Abstract
This paper proposed a multi-objective, multi-disciplinary design optimization and multi-attribute evaluation method for the manned lunar lander descent stage. A system design model is established considering multiple disciplines such as propulsion, structure, trajectory and cost. With the goal of minimizing mass, minimizing cost and maximizing velocity increment, the overall scheme for hybrid rocket motors was optimized by altering various grain shapes and feed systems, acting as an alternative propulsion scheme for the manned lunar lander. Under the same design conditions, the optimal scheme of hybrid rocket motors considering continuous and discrete attributes was studied and compared with that of liquid rocket engines to elucidate the characteristics of the hybrid rocket motors for deep space exploration. The results showed that the evaluation results obtained by considering only continuous attributes were different from those by considering both continuous and discrete attributes. The liquid propulsion scheme with liquid oxygen/kerosene is superior to the hybrid propulsion schemes due to its excellent cost and specific impulse performance when only continuous attributes are considered. However, hybrid rocket motors have shown good performance in terms of operability, manufacturability, safety and environmental protection. So, after introducing discrete attributes, the hybrid propulsion schemes show greater potential. In brief, based on the multi-attribute evaluation method considering comprehensive attributes, the hybrid rocket motor provided with tube grain and gas pressure feed system was considered as the optimal propulsion system for the lunar lander. Furthermore, the parametric analysis showed that the fuel grain outside diameter, the initial design thrust and the initial oxygen-to-fuel ratio had a significant influence on the performance of the hybrid rocket motor for the lunar lander, and in particular, the effect of the fuel grain outside diameter was more than 50%.
1. Introduction
Recently, a worldwide race for lunar exploration has resumed. NASA took the opportunity to launch the Space Launch System (SLS) heavy rocket on 16 November 2022, a key step in its return to the moon. With the historic successes achieved by Chang’e 5, China has successfully finished the third phase of its lunar exploration program, and targets manned lunar landing by 2030. This series of moves has set off a new round of manned lunar landing efforts all over the world.
It is necessary to perform maneuver control on the lunar lander and search for a suitable landing point during descent, which has high requirements on the variable thrust performance of the lunar descent engine. Conventional liquid rocket engines (LREs) provide the ability of thrust adjustment. Up to now, all the plans for successful lunar missions (such as Apollo 11 and Altair) [1] have adopted the LREs, which can be used as feasible solutions.
However, the liquid propellants commonly used by LREs are toxic or low temperature, and the flow rates of oxidizer and fuel need to be adjusted simultaneously during thrust adjustment, which brings some problems in application. Hybrid rocket motors (HRMs) employing liquid oxidizer and solid fuel grain which remain separate before ignition [2] provide good safety, low cost, high reliability, restart characteristics and a wide range of thrust regulation [3,4,5]. Therefore, high mission flexibility make HRMs a fair candidate for deep space exploration missions such as lunar landing [6].
Many space entities are now developing HRMs for future space exploration. Virgin Galactic’s hybrid-powered SpaceShip2 VSS Unity completed its first fully crewed space flight in 2021 [7]. In 2022, we saw the first launch of the Taiwan ARRC team’s HTTP-3A hybrid-powered vertical takeoff and landing sounding rocket [8]. Research on HRM-powered launch vehicles was also in full swing by the Nammo team in Norway [9], Vaya Space in the U.S. [10], and Gilmour in Australia [11]. In deep space exploration, the ORPHEE (Operational Research Project on Hybrid Engine in Europe) project evaluated the suitability of hybrid systems for small vehicles, lunar landers, and Mars landers [12]. Di Torino analyzed the optimal design of the propulsion system for a potential Mars ascent vehicle and verified the feasibility of a hybrid alternative scheme [13]. Moreover, Koc University proposed a scheme of preparing metal-based HRMs by utilizing most-abundant metals such as magnesium and aluminum in lunar soil, and has successfully carried out ground-based tests [14]. In more recent research, Korean Aerospace University conducted a laboratory-scale ground-based test of an HRM and validated the applicability of the hybrid propulsion system on lunar landers, indicating that the HRM-powered lunar lander has reached a high level of technological maturity [15]. The above research has demonstrated that HRMs have considerable potential for lunar lander propulsion systems.
Large-scale aerospace engineering projects such as lunar exploration programs require an increasing amount of technical, financial and material resources. More and more attention has been paid to the impact of non-technical attributes such as the costs in technical solutions, involving multi-attribute representation, quantification and evaluation. Preliminary research on multi-attribute assessment has been carried out internationally in the field of aerospace. In 2011, Ullah adopted an entropy-based multi-attribute evaluation (MAE) strategy to evaluate the rocket performance [16]. In 2015, he further proposed a comprehensive method for improving the subjectivity of constant-valued triangular fuzzy numbers [17]. In 2020, Wang proposed a comprehensive MAE method for small launch vehicles. The results showed that the solid propulsion system was the optimal solution when considering only the technical attributes such as take-off mass, thrust-to-weight ratio and mass fraction. However, the ranking was changed after the non-technical attributes were taken into account [18]. During the conceptual design phase of vehicles, it is essential to evaluate the impact of non-technical features to make the selection more accurate and reliable.
A comprehensive evaluation is also required for lunar exploration propulsion technology. Although there already exists research into various optimization schemes for different aspects of the lunar landing power systems [19,20], non-technical factors are hardly taken into account. Taking the descent power system of Apollo 11 lunar module as the object, the multi-disciplinary, multi-objective design optimization (MODO) was carried out on the HRM alternatives with different grain shapes and feed systems. Finally, the characteristics of the HRMs for deep space exploration were analyzed by comparing the optimal scheme of the HRMs considering multi-attributes with that of LREs under the same design conditions.
The paper is organized as follows: Section 2 gives a detailed description of the problem and model, and the multi-disciplinary, multi-objective design optimization and multi-attribute evaluation method considered in this study. Section 3 provides the framework of the overall optimal design system and the practical application of the proposed method through the case study. The results and discussions are listed in Section 4, and some conclusions are summarized in Section 5.
2. A Detailed Description of the Problem and Model
2.1. Problem under Study
The Apollo 11 lunar module consists of a descent stage and an ascent stage, which are relatively independent of each other. The descent stage does its main work during the descent and landing from the lunar orbit to the lunar surface. As the landing platform of the lunar module and the launch platform of the ascent stage, the descent stage uses variable thrust rocket engines to provide deceleration, maneuvering and landing cushion for a phase of the arrival at the moon. The Apollo 11 descent stage contains the descent motor, four landing legs, four instrument compartments, four storage compartments and the outer envelope, as shown in Figure 1 [21].
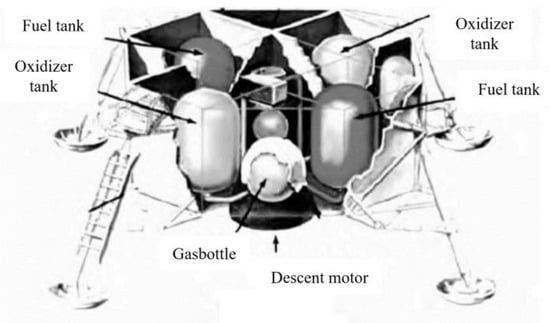
Figure 1.
Structure diagram of lunar module descent engine.
The Apollo 11 descent stage has an outside diameter of about 4.2 m [22,23] and a height of about 3.2 m [24]. The mass of the descent motor is 10,282 kg [22]; together with the mass of the structural components and the upper stage, the total mass of the Apollo 11 is about 16,000 kg. The actual design of Apollo 11 during the descent is 2261 m/s [25], the total propellant mass is 18,260.5 lb [26] and the specific impulse is 305 s [27], which translates into a total impulse of 2.48 × 107 N·s.
Referring to the design of Apollo 11, the descent stage of the manned lunar lander is to be designed subject to the following constraints:
- (1)
- The diameter and height of the outer envelope of the descent stage shall not exceed 4.2 m and 3.2 m, respectively;
- (2)
- The mass of the descent motor and the complete lunar lander shall not exceed 10,282 kg and 16,000 kg, respectively;
- (3)
- The total impulse and total velocity increment of the descent motor shall not be less than 2.48 × 107 N·s and 2261 m/s, respectively;
- (4)
- During descent and landing, the propulsion system hovering in the weak lunar gravitational field shall meet the requirements on a wider range of thrust regulation.
Taking the Apollo 11 descent engine as the design target, this paper carries out MODO using different types of LRE and HRM alternatives, and then MAE is conducted on the design results to investigate the characteristics of the HRM applied to the descent stage.
2.2. Modeling of HRM/LRE-Propelled Lunar Lander
The manned lunar lander is a complex physical system, and its design involves the features of multiple disciplines. In the process of modeling, many interdisciplinary coupling variables need to be continuously transmitted and iterated along with the design process of each system and the performance analysis models of involved disciplines. Therefore, it is necessary to decouple and simplify the involved disciplines of the manned lunar lander before modeling.
Since the manned lunar lander mainly works in a vacuum, the effects of aerodynamics can be ignored. Therefore, the modelling on the manned lunar lander is decomposed into three parts: propulsion, structure and trajectory. A total of six propulsion schemes are used in present study. Four types of HRM propulsion models are developed: the HRM with a tube grain and a gas pressure feed system (HRM-TGGF), the HRM with a tube grain and electric pump feed system (HRM-TGPF), the HRM with a wheel grain and a gas pressure feed system (HRM-WGGF) and the HRM with a wheel grain and an electric pump feed system (HRM-WGPF). As comparative scenarios, the LREs with two alternative types of propellants N2O4/Unsymmetrical Dimethylhydrazine—(LRE-ND) and liquid oxygen/kerosene (LRE-LK) are also modelled. The objective of structural optimization is mainly the mass and dimensional characteristics of the main propulsion system components, and other structural parameters follow those of Apollo 11. Achieving a soft landing over the lunar surface is the main goal of the descent stage, so only the velocity increment needs to be considered in the trajectory discipline.
2.2.1. Propulsion
- Hybrid rocket motor
Considering the safety and environmental protection, specific impulse performance and other characteristics, 98%H2O2/60%HTPB + 28%Al + 10%Mg + 2%C is selected as the propellant combination for HRMs. As mentioned in Section 2.1, two types of grains (tube grain and wheel grain) and two different oxidizer feed systems (gas pressure feed system and electric pump feed system) are adopted. The design variables of HRMs consist of the initial grain shape parameters and initial design parameters.
As shown in Figure 2, the initial grain shape parameters for the tube grain include the grain outer diameter Dp and fuel grain thickness e; while the initial grain shape parameters for the wheel grain include the grain outer diameter Dp, grain thickness e, wheel number N and the diameter of the center hole Di (set N as 6 and Di as 0.16Dp). The specific expressions of Ab and the channel area Ap can be derived from geometric relationships using the initial grain shape parameters.
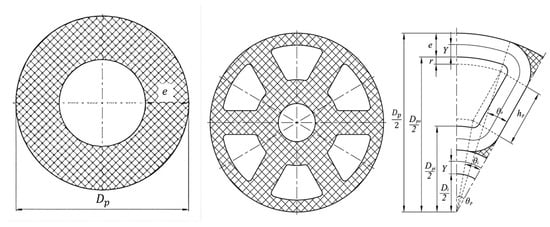
Figure 2.
Different grain shapes.
The initial thrust Fi, initial oxidizer-to-fuel ratio , expansion ratio of nozzle and initial chamber pressure Pci are selected as the initial design parameters. Figure 3 [28] shows the steps involved in general design procedure of HRMs. Based on these input variables, the internal ballistic calculations can be performed by solving the differential equation of the combustion chamber pressure Pc.
where is the regression rate which is closely related to channel area Ap and oxidizer mass flow rate [29,30,31,32], Γ is a function of the specific heat ratio, c* is the characteristic velocity provided by thermodynamic calculation, Vc is the free volume of chamber, At is the nozzle throat area, is the fuel mass flow rate, Ab is the combustion surface area which is the product of the combustion line (Sc) and the length of the grain (Lp), a is the regression rate coefficient and n is the flux rate exponent.
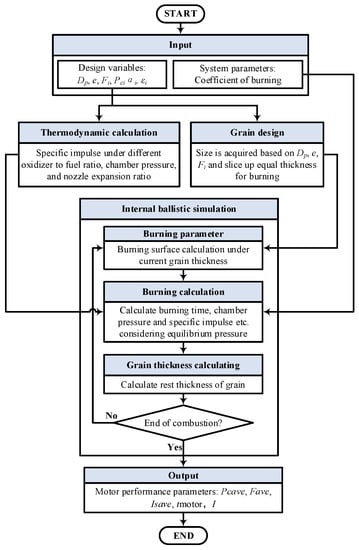
Figure 3.
The steps involved in general design procedure of HRMs.
As shown in Figure 3, grain design and thermodynamic calculation are the basis of the internal ballistic simulation. The grain design is mainly based on the geometric relationship to calculate Ab and Ap under the different rest thickness of grain. Thermodynamic calculations are based on isenthalpy and isentropic relations. Generally speaking, the oxidizer-to-fuel ratio changes all the time during the working process of HRMs. When working at the optimum oxidizer-to-fuel ratio, the main total reaction of the propellant combination is the following:
After completing the grain design, thermodynamic calculation and internal ballistic simulation, the following data are obtained for the HRM: average chamber pressure Pcave, average vacuum specific impulse Isave, average thrust Fave, motor operating time tmotor, impulse I and other propulsion performance parameters.
Furthermore, Ref. [33] provides the validation of the internal ballistic simulation model of HRMs compared with the data of HRM firing tests, which shows that the model can be used as the basis for the overall design of HRMs in the paper.
Liquid rocket engine
The propulsion model for LREs mainly includes two types of modules: thermal calculation and internal ballistic simulation. The chamber pressure Pc, vacuum specific impulse Isvac, thrust F, impulse I, mass flux qm and other propulsion performance parameters are computed from the initial design parameters, including Fi, , , Pci and motor operating time tmotor. The method of mass flux solution is obtained from the following equation:
where ηIs is efficiency of specific impulse.
With reference to manned lunar module Apollo11’s design, the liquid propellants are fed to the chamber by the gas pressure system, resulting in a low chamber pressure. For liquid oxygen/kerosene and N2O4/Unsymmetrical Dimethylhydrazine (UDMH), we have built databases of performance parameters by the theoretical analysis software RPA and selected some special points according to the application scope (vacuum environment) of this paper and plotted Figure 4. Figure 4 gives the relationships between vacuum-specific impulse Isvac and oxidizer-to-fuel ratio under four different chamber pressures (1 MPa, 2 MPa, 3 MPa, 4 MPa) and three nozzle expansion ratios ε(60, 80, 100). The curves indicate that the optimal of both liquid oxygen/kerosene and N2O4/UDMH is around 2.6.
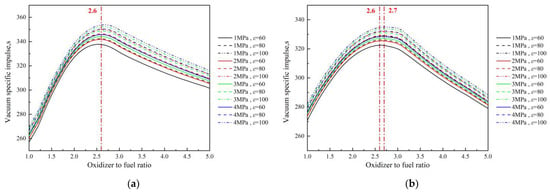
Figure 4.
Isvac- curves under different chamber pressure/nozzle expansion ratio. (a) liquid oxygen/kerosene; (b) N2O4/UDMH.
2.2.2. Structure
The structure discipline focuses on the mass and dimensional characteristics of the manned lunar lander. As shown in Figure 1, the descent stage mainly consists of the descent engine, four instrument compartments and four propellant tank compartments. The four instrument compartments contain payloads and gas cylinders. The dimensional characteristics of the manned lunar lander are mainly determined by the dimensions of motors and tanks (considering that the nozzle needs to be staggered with the tanks), as shown in the following Equation (6):
where DD and LD are the diameter and length of the descent stage, Dc and Dtank are the diameters of the chamber and tank, and Lc, Ltank and Lnozzle are the lengths of the chamber, tank and nozzle, respectively. The dimension parameters of the chamber of HRMs mainly depend on the grain parameters, nozzle throat area At and . The dimension parameters of LREs mainly depend on the characteristic chamber length, mass flux, nozzle throat area At, and .
As an important interdisciplinary coupling parameter, the mass of the manned lunar lander is basically composed of two parts: ascent stage mass MA and descent stage mass MD.
where the ascent stage mass is set to be 4800 kg, and the descent stage mass MD is determined by the following equation:
where Mm is the total mass of the propulsion system which is determined by Equation (9), the structural mass Ms = 500 kg comprises the mass of the outer envelope and landing legs, and the load mass Mload is set to be 500 kg.
where Mp is the propellant mass; Mc is the mass of the chamber; Mtank is the mass of the tanks (four oxidizer tanks for HRM; two oxidizer tanks and two fuel tanks for LRE); Mgasbottle is the mass of the gas bottle; Mfeed system is the mass of the feed system (the gas pressure feed system includes pipeline valves; the electric pump feed system includes pipeline valves and electric pump, etc.); the electric pump mass is evaluated as in Ref. [34] and Melse is the residual mass(set to be 300 kg). In detail, the total propellant mass is divided into the mass of the grain, which is determined by the grain’s length and shape, and the mass of the oxidizer, which is determined by the oxidizer mass flow rate and the operating time. The thrust chamber is made up of the combustion chamber and the nozzle. The dimensions of the combustion chamber are determined by the dimensions of the grain. The shell thickness of the cylinder section of the combustion chamber can be estimated by the third strength theory, and the mass of the combustion chamber can be further obtained. The size, shape and mass of the nozzle can be calculated according to the size of the combustion chamber and the nozzle expansion ratio. The volume of the tank is determined by the mass of the oxidizer, and the volume of the gas bottle is calculated through the adiabatic expansion process of the ideal gas. Similar to the combustion chamber, the thicknesses of the tank and the gas bottle are calculated by the third strength theory. At the same time, the mass of pipeline and valves was estimated according to the oxidizer mass flow rate and pressure.
The main dimensions and mass parameters of the HRM and LRE components, mainly including total mass, length and effective propellant mass fraction of engine ηi, are deduced from the propellant mass, mass flux and the pressure relationship among chamber, tank and gas bottle.
Each kind of structure and its material are listed in Table 1, where CF is the abbreviation of carbon fiber and “——” indicates that the scheme does not contain this structure.

Table 1.
Main structure of the manned lunar lander’s propulsion system.
2.2.3. Trajectory
The lunar lander performs velocity increment about 2081 m/s [26] to decelerate from a nominal orbit to a soft landing. However, due to the actual loss of descent and the effects of manual hover, etc., the actual pre-mission design of Apollo 11 is 2261 m/s [25]. To ensure successful descent completion, the theoretical of the design schemes should be no less than 2261 m/s. Reza has found that the results of Ziolkovsky-based formulas and three-degree-of-freedom simulations provide similar velocity distribution profiles [35]. Therefore, can be calculated by the Ziolkovsky formula. The mass and specific impulse parameters required for calculating are provided according to the principles of propulsion and structure.
2.3. Multi-Attribute Evaluation Method
To obtain better design results, the overall design of the manned lunar lander needs to balance the relationship between technical and non-technical performance. This section mainly focuses on the modeling and analysis of non-technical attributes.
2.3.1. Technical Performance
Three parameters, including total mass, mass fraction of motor and velocity increment, are chosen to represent the technical performance of lunar lander descent stage. Smaller total mass achieves better performance of the vehicle. Mass fraction is the ratio of the effective propellant mass to the motor mass, which can directly reflect the design level of the vehicle. The velocity increment can reflect the main trajectory performance of the lunar lander. Therefore, these three technical attributes are calculated from the design model described in Section 2.2.
2.3.2. Non-Technical Performance
According to whether the continuous mathematical model can be used to describe the attributes, non-technical attributes are divided into continuous and discrete attributes. The continuous non-technical attribute is mainly focused on cost. The discrete non-technical attributes include operability, manufacturability, safety, etc. Among the non-technical attributes, the cost can be modeled based on the structural mass, propellant mass and other performance parameters. Meanwhile, the empirical values of discrete attributes are given by expert scoring.
- Continuous non-technical attributes: cost
- Liquid rocket engine
Ref. [36] has provided an LRE cost estimation method based on overall parameters, so this paper adopts the cost model based on structural mass to acquire the total cost of the LRE:
where Cliquid is the cost of the LRE, C1 is the cost of chamber, pipes and valves ( for upper stage LRE [37]), Cotank is the oxidizer tank cost, CFtank is the fuel tank cost, Cgastank is the gas bottle cost and Cp is the propellant cost. Both gas bottle and tank are pressure vessels with similar structure and shape. As shown in Equation (11), there is a basically positive correlation between their costs and surface areas. When considering factors such as liquid oxygen cryopreservation and hydrogen peroxide compatibility treatment, the corresponding coefficients shall be multiplied according to the following equation [36]:
where St is the surface area of the tank or the gas bottle.
It is noted that the coefficient term in Refs. [36,37] represents the price level in the 1960s and 1970s, so its application in the current era needs to consider the price effects. In this paper, the cost model is modified according to the production price index PPI, which represents the changing trend of production and processing costs over time.
- Hybrid rocket motor
HRMs are assembled with several typical components from both solid rocket engines (SREs) and LREs. The cost model based on structural mass can also be applied to acquire the total cost of the HRM:
where Chybrid is the cost of the HRM; C1 is the cost of feed system (including pipes, valves, pump, etc.), Ctank is the oxidizer tank cost; Cgastank is the gas bottle cost; Ch,dry is the cost of chamber shell and other dry weight; Ch,p is the solid propellant cost; Co is the liquid propellant cost. The costs of the components from LREs (including pipes and valves, gas bottle, tank, etc.) can refer to LREs, and this section mainly describes the costs of the components from SREs (including fuel grain, combustion chamber shell, nozzles, etc.).
According to Ref. [38], the dry weight cost and solid propellant cost are modeled as Equations (13) and (14), respectively.
where learning factor LC takes a constant value of 0.9, Cs1 is a coefficient, Wsol is the total mass of motor and NN is the number of nozzles.
Since HRMs adopt similar combustion chamber material, nozzle configuration and material to SREs, the dry weight cost of an HRM can be estimated according to the proportion of the dry weight cost of an SRE. Considering that the charge shape and manufacturing process of HRMs are simpler than those of SREs, the charge cost of the HRM can be calculated by Equation (17).
where c1 and c2 are the coefficients related to grain shape and grain unit price, taking 0.9 and 0.5, respectively.
- Discrete non-technical attribute modeling analysis method
Discrete non-technical attributes mainly include operability, manufacturability, flexibility and safety/environmental friendliness. The expert scoring is used to model the discrete attributes [18]. Triangular fuzzy number is used to quantify the subjective characteristics of expert evaluation for each attribute.
The specific process is shown in Figure 5. A total of K experts evaluate m alternatives based on n evaluation attributes, and the evaluation range is between 0 and 1.It indicates that, for the index j of alternative scheme i, there are a total of K scores from different experts, namely to . The k scores are transformed into the triangular fuzzy number , where represent the lower bound, the most possible value and the upper bound, respectively.
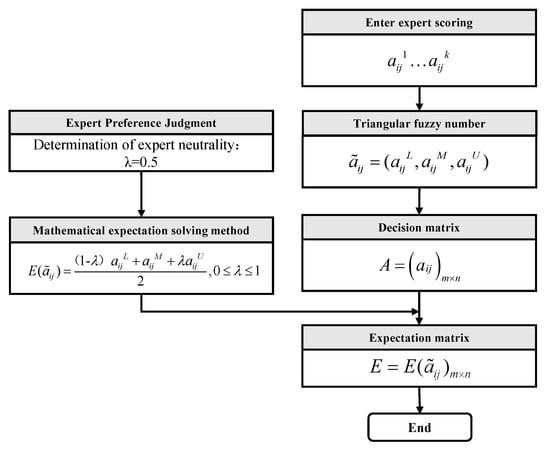
Figure 5.
Non-technical attribute modeling method (expert scoring).
The triangular fuzzy numbers form the decision matrix . After obtaining the decision matrix, the expectation value can be calculated by:
where is the expert preference judgement, 0.5 in this paper.
is the quantitative result of the index j of alternative scheme i, and will participate in TOPSIS evaluation.
In the above process, the quantitative modeling of non-technical attributes is completed by expert scoring.
2.3.3. Multi-Attribute Evaluation Strategy Based on Entropy Weight Method-TOPSIS
The Order Preference by Similarity to Ideal Solution (TOPSIS) process is shown in Figure 6. The key problem lies in the index weight distribution, which is solved by the introduction of entropy weight.
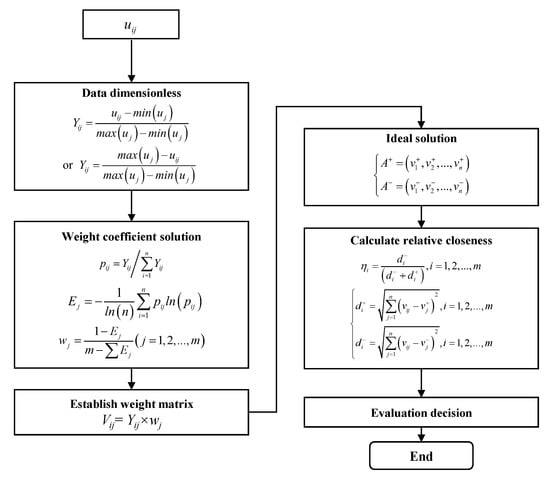
Figure 6.
TOPSIS process based on entropy weight method.
The modeling results of the continuous attributes (technical performance and cost) and the quantitative evaluations of the discrete attributes for each scheme are the initial input data uij to TOPSIS. Firstly, the original data matrix is normalized to obtain a standard decision matrix . Secondly, the information entropy of each index Ej can be obtained by the Equation (19), and the index weights can be further calculated by the Equation (20). Additionally, the weighted decision matrix Vij is obtained by multiplying the standard decision matrix with the weight vector. The best/worst values of each column in the weighted decision matrix form the best/worst solution vector (A+/A−). The distances between the current solution and the best/worst solutions are achieved by Euclidean metrics and finally ranked according to the relative closeness as the basis for evaluating the advantages and disadvantages of each solution.
where .
Compared with other multi-attribute evaluation methods, TOPSIS does not need an objective function and consistency test, and has fewer constraints on inputs, resulting in a more concise calculation process.
3. Design Optimization and MAE
MODO and MAE are applied to the lunar lander descent motor, and the process is shown in Figure 7. Referring to the design of Apollo 11, six types of propulsion systems (HRM-TGGF, HRM-TGPF, HRM-WGGF, HRM-WGPF, LRE-ND and LRE-LK) are selected as possible design schemes. The MODO and TOPSIS method are utilized to conduct the multi-attribute decision making for the infinite scheme of the lunar lander with the six different propulsion systems under the continuous model. Then, on the basis of quantitative modeling of discrete attributes (empirical values obtained by expert scoring), combined with the above results of multi-attribute decision making, the MAE method is adopted to select the optimal scheme. Section 3.1 and Section 3.2 give a detailed description on the design optimization model and discrete attribute scoring process for six types of propulsion systems, respectively.
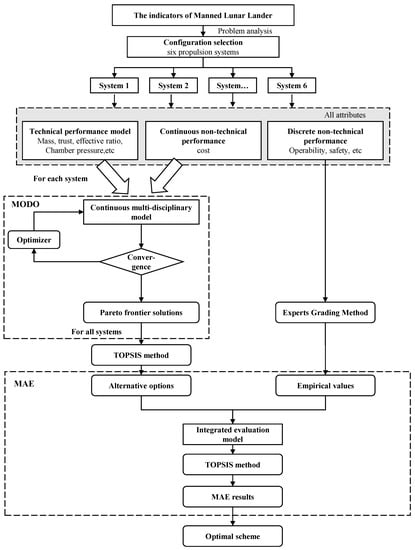
Figure 7.
The process of MODO and MAE.
3.1. MODO of Manned Lunar Lander
As analyzed in Section 2, the design variables, objective function and constraints of two types of manned lunar landers can readily be obtained. The design optimization models for HRM and LRE are shown as Equations (21) and (22), where x is the vector of design variables. The input variables used in the HRM model include grain outer diameter Dp, thickness fraction e/Dp, initial combustion chamber pressure Pci, initial thrusts Fi, initial oxidizer-to-fuel ratio αi and nozzle expansion ratio ε. The mass M, motor cost C(Cliquid or Chybrid) and velocity increment ΔV are set as the optimal objectives. Considering the dimensions and specifications of the manned lunar lander and the required lunar landing capability mentioned in Section 2.1, the velocity increment ΔV, impulse I, mass M, diameter DD and length LD are calculated as constraints.
The input variables, optimization objectives and constraints in the LRE MODO model are similar to those in the HRM MODO model.
The non-dominated sorting genetic algorithm (NSGA-II) is used as the optimization algorithm. The NSGA-II algorithm is a fast, non-dominated multi-objective optimization algorithm with elite retention strategy which allows individuals near the Pareto region to evenly diffuse to the entire Pareto region while maintaining the diversity of the population. The characteristics of NSGA-II are discussed in detail in Refs. [39,40]. In this manuscript, the population size and number of generations are set as 20 and 1000, respectively. In addition, the computer running the algorithm is configured as a laptop with Intel Core i7-1165G7, 2.8 GHz,4C-8T CPU, and 16 GB, LPDDR4x 4266 MHz RAM. The algorithm design is implemented using C#.
3.2. MAE Process
Three experts are invited to evaluate the design of the manned lunar lander. Table 2, Table 3, Table 4 and Table 5 give the original expert evaluation scores (numbers in brackets), evaluation results in the form of triangular fuzzy numbers (numbers after brackets) and an average score of each index. Some exclusive indexes (marked as ‘(——)’ in the tables) are regarded as (1,1,1).

Table 2.
Operability results of expert evaluations.

Table 3.
Manufacturability results of expert evaluations.

Table 4.
Flexibility results of expert evaluations.

Table 5.
Safety/environmental-friendliness results of expert evaluations.
4. Results and Discussions
4.1. MODO Results
A series of Pareto solutions are obtained for the three objectives of cost, mass and velocity increment.
4.1.1. Hybrid Scheme Optimization Results
The optimized results are shown in Figure 8, Figure 9, Figure 10 and Figure 11, which represent the relationship between the three objectives. The frontier solutions are represented by blue points through which an optimal frontier surface can be clearly observed, and the black points are the projections on each coordinate plane.
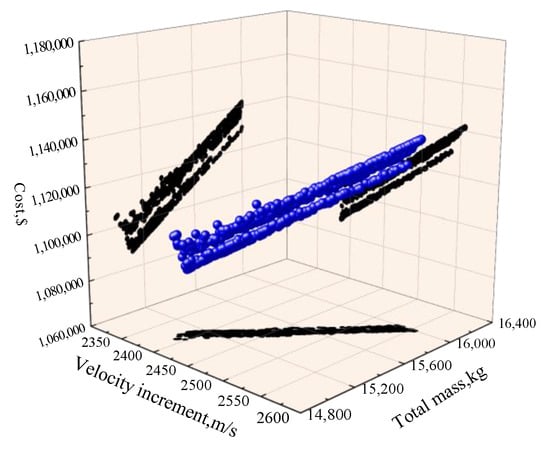
Figure 8.
Pareto solution set of HRM-TGGF.
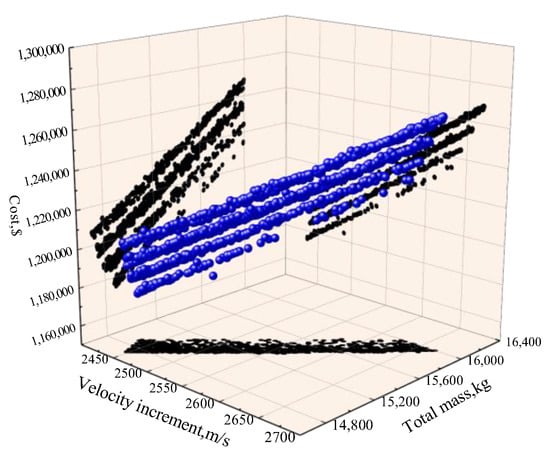
Figure 9.
Pareto solution set of HRM-TGPF.
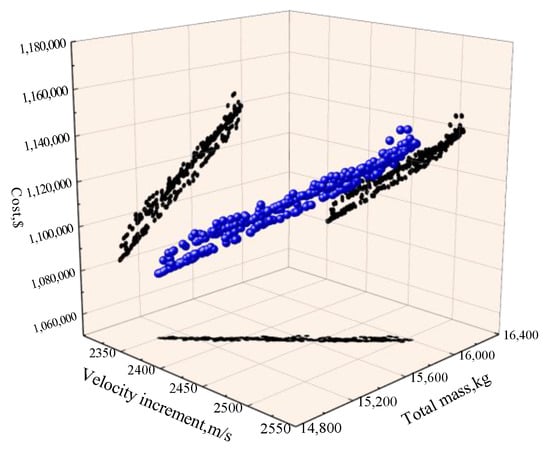
Figure 10.
Pareto solution set of HRM-WGGF.
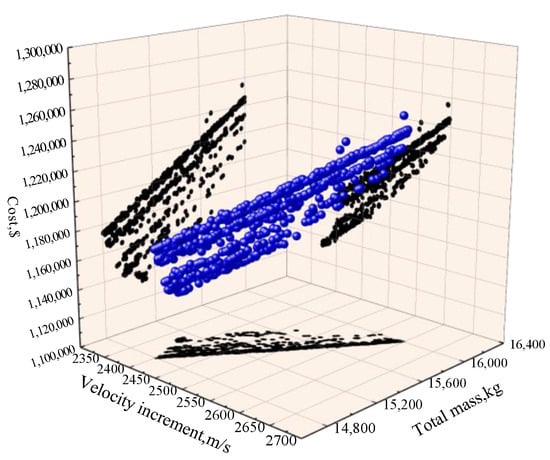
Figure 11.
Pareto solution set of HRM-WGPF.
HRM-TGGF is selected as a typical case to further analyze the Pareto frontier solutions. The curved surface between cost, mass and velocity increment is fitted to obtain the relationship shown in the Equation (23), where R2 = 0.9806. The correlation coefficient suggests that the cost is strongly correlated with velocity increment and total mass.
The Pareto frontier solution sets of the other three schemes (HRM-TGPF, HRM-WGGF, HRM-WGPF) are used as test sets, and the corresponding mean absolute percentage errors (MAPEs) are 0.0443, 0.0431 and 0.0608, respectively. It shows that the fitting formula has high applicability in the optimization design of HRMs utilizing various grain shapes and feed systems.
4.1.2. Liquid Scheme Optimization Results
Compared with hybrid propulsion systems, liquid propulsion systems have fewer optimization variables and simpler optimization process. The optimized results for liquid propulsion systems are shown in Figure 12 and Figure 13. The Pareto points of the LRE-LK scheme are used to fit the curved surface and obtain the Equation (24), where R2 = 0.9828.
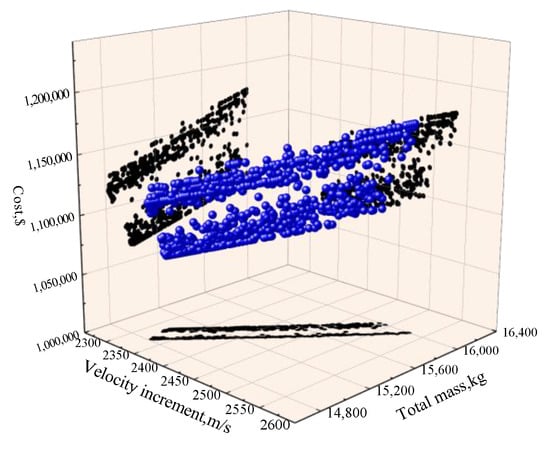
Figure 12.
Feasible solution set of LRE-LK.
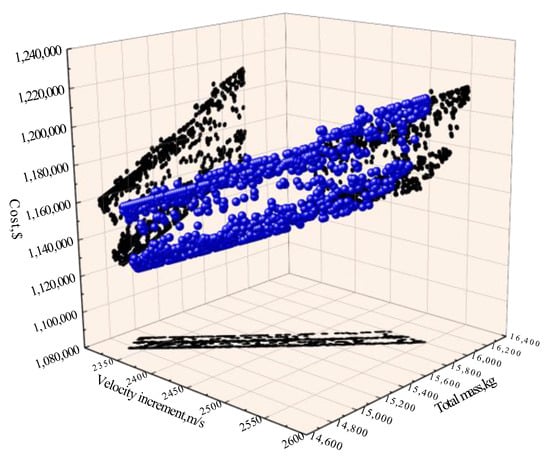
Figure 13.
Feasible solution set of LRE-ND.
The correlation coefficient suggests that there is a high degree of matching. Pareto data of LRE-ND are used for testing, and the corresponding MAPE is 0.0410. The results show that the fitting formula is applicable to the optimal design of LRE-LK and LRE-ND, and can provide a reference for the cost estimation of the vehicles with similar missions and configurations.
4.2. Analysis of MAE Results
According to MODO, each propulsion system is given a series of Pareto frontier solutions, 3755 in total. It is necessary to select the solution that provides the best overall performance from the total Pareto frontier solutions. Considering that the propulsion systems of the same type have almost the same discrete non-technical attributes, MAE can be decomposed into two steps. The first step only takes the continuous attributes including three technical attributes (lunar lander mass, velocity increment, propellant mass fraction) and one non-technical attribute (cost) as evaluation indicators, and selects an optimal design scheme for each type of propulsion system. The second step conducts a multi-attribute evaluation considering all technical and non-technical attributes on these six alternative propulsion systems.
4.2.1. Results of Continuous Attributes Evaluation for All Pareto Front Solutions
The results of continuous attributes evaluation for all Pareto frontier solutions are summarized in Table 6. As shown in Section 2.3.3, the relative closeness of each solution is the evaluation indicator of performance. When the continuous attributes are used as the evaluation criterion, the LRE using liquid oxygen/kerosene propellants has the highest closeness. The relative closeness of HRM-TGGF and HRM-WGGF is slightly lower. However, it means that HRM-TGGF and HRM-WGGF do not differ much from LRE-LK, indicating that the HRMs have some alternative possibilities on the manned lunar lander.

Table 6.
Main performance of continuous attributes assessment results.
It is not difficult to conclude that the six alternative propulsion systems have similar total mass. Among them, the HRM-TGPF has the smallest total mass and the largest velocity increment. In terms of total mass, the HRMs with electric feed system have advantages over the LREs, mainly because a complex liquid rocket feed system requires more pipes and valves which are the dead weight of the engine. In terms of mass and effective propellant mass fraction, the HRMs with tube grain have advantages over those with wheel grain, mainly because the wheel grain cannot be fully burned to no fuel residue. Since no high upstream pressure is required, the gas bottle and tank mass of the electric pump feed system is significantly reduced, leading to a significant reduction in its total mass compared with the gas pressure feed system. In two liquid scenarios, the total mass of the LRE-LK is lower than that of the LRE-ND, which reflects the excellent specific impulse performance of the liquid oxygen/kerosene propellants.
In terms of cost, two types of LREs have significant advantages over four types of HRMs. This is because the unit cost of hydrogen peroxide is much higher than that of liquid oxygen, kerosene and other propellants. If the demand for hydrogen peroxide is significantly increased and large-scale production is carried out, the hybrid solutions can bring new possibilities. Among the four types of HRMs, the pump feed system offers smaller mass but higher cost. Even today, the manufacture of hydrogen peroxide pumps still looks expensive, which prevents the overall price of the feed system from being more attractive. With the further development of pump, battery, controller and motor manufacturing, the electric pump feed system can offer more feasibility.
In a word, HRMs have shown great potential for lunar landing in terms of both technical and continuous non-technical attributes, and can be an important supplement to LREs.
4.2.2. The MAE Results
Table 7 lists the MAE results of the six schemes considering all technical and non-technical attributes and the relative closeness of the six schemes. Figure 14 shows the weight distribution of each attribute by using the TOPSIS method. Based on the decision analysis results, HRM-TGGF is considered as the optimal propulsion system for the lunar lander. The mass parameters of the motor in this propulsion system are shown in Table 8, and the internal ballistic results are shown in Figure 15. The figure indicates that, for HRMs, the combustion chamber pressure and thrust decrease slightly with the operation process, and the oxidizer-to-fuel ratio changes with time. When the oxidizer-to-fuel ratio deviates greatly, the specific impulse is at a lower level. Compared to the results in Section 4.2.1, there is an elevated rating for the hybrid scenarios after considering the discrete non-technical attributes, which also indicates that the non-technical attributes affect the selection of the design scheme. The hybrid solutions are deficient in cost and specific impulse compared to the liquid solutions. However, HRMs adopt non-toxic propellants, with a simpler structural layout and less complex components such as the pipes and valves of the feeding system, so they have shown good performance in terms of operability, manufacturability, safety and environmental protection. LREs would be more cost-effective for large scale vehicles with high thrust. In short, HRMs have a relatively broad application prospect and unique advantages in their application to lunar landers.

Table 7.
MAE results.
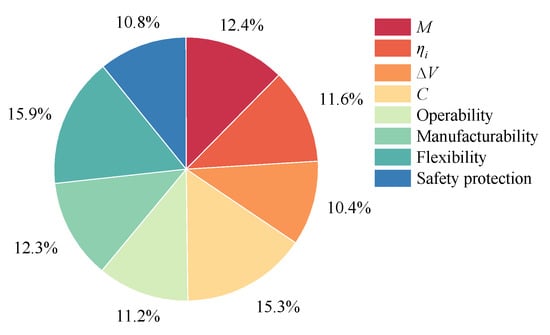
Figure 14.
Weight distribution of each attribute.

Table 8.
The descent motor mass of HRM-TGGF.
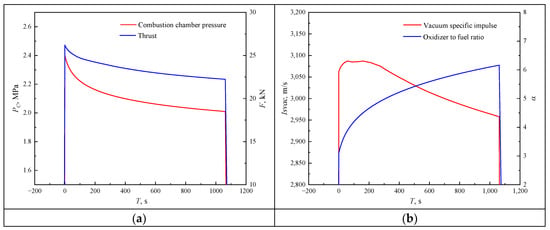
Figure 15.
Internal ballistic simulation results for HRM-TGGF. (a) Pc-T and F-T; (b) Isvac-T and α-T.
4.3. Parametric Analysis of HRM
The parametric analysis (PA) is adopted to analyze the effects of design variables on the performance parameters of the HRM-powered lunar lander, which provides a theoretical reference for the design optimization of similar aerospace vehicles.
The parametric analysis of main responses are revealed in Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20 (e represents e/Dp in these figures). The blue bars show the positive correlation and the red bars indicate the negative correlation.
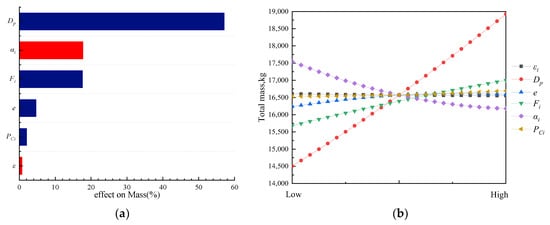
Figure 16.
Parametric analysis of design variables to mass. (a) Pareto diagram; (b) main effect plot.
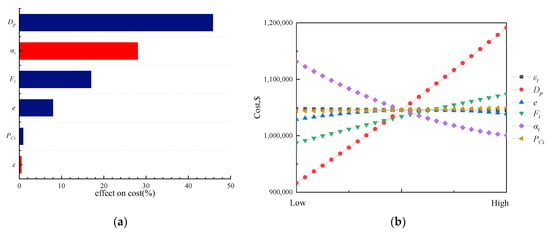
Figure 17.
Parametric analysis of design variables to cost. (a) Pareto diagram; (b) main effect plot.
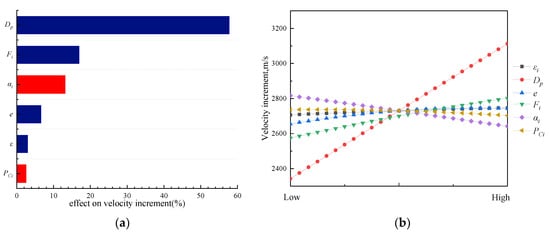
Figure 18.
Parametric analysis of design variables to velocity increment. (a) Pareto diagram; (b) main effect plot.
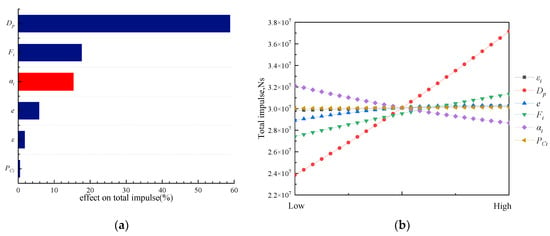
Figure 19.
Parametric analysis of design variables to total impulse. (a) Pareto diagram; (b) main effect plot.
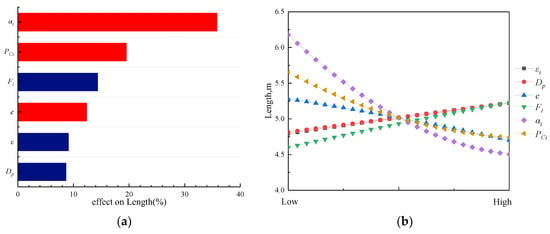
Figure 20.
Parametric analysis of design variables to the motor length. (a) Pareto diagram; (b) main effect plot.
Each design parameter has a similar impact on mass and cost, among which the grain diameter Dp, initial oxidizer-to-fuel ratio and initial thrust Fi have a disproportionate impact. In particular, the effect of Dp was more than 50%.
When other parameters such as initial thrust, initial oxidizer-to-fuel ratio, initial pressure and thickness fraction are unchanged, the initial propellant flow rates basically remain the same. For any grain type, when the thickness fraction and grain shape parameters remain unchanged, the increase in the grain outer diameter will lead to the equal increase in the combustion line (Sc) (Sc~Dp) and the square of the channel area (Ap) (Ap~Dp2). According to Equation (25):
where , n depends on the grain performance, greater than 0 in this paper. Therefore, , where is proportional to the 2n−1 power of . The total mass of the grain depends on the product of its length and cross-sectional area. Consequently, there is . As increases, the grain mass will increase, and the shell mass and oxidizer mass will also increase accordingly, which will further affect the total mass and cost of HRMs. This conclusion is consistent with the results of principal component effect analysis.
Meanwhile, affects not only the oxidizer-to-fuel ratio but also the specific impulse performance of various propellant combinations. These two factors also have an impact on the mass of the propellants and structure. It is easy to understand the effect of initial thrust on total mass. As the initial thrust increases, the grain length increases, resulting in an increased total mass.
As the paramount parameters of the lunar lander, the velocity increment and total impulse can be used to determine whether a successful lunar landing can be achieved. The main factors affecting these two parameters are also similar, among which Dp has the greatest impact when all other factors remain unchanged. As the grain outer diameter increases, the grain mass increases. Assuming a constant specific impulse, the total impulse and velocity increment will also increase with the increase in the mass of the propellant participating in the reaction.
The influence of coefficients of various design parameters on the total length of HRMs are significantly different from those on the total mass and cost, among which has the most influence. As changes, both the fuel and oxidizer flow rates and the grain length required for the same initial thrust will change. The grain is an important part of the combustion chamber, and the change in grain length will greatly change the total length of HRMs. As seen in Figure 19, the combustion chamber pressure Pci also has a great influence on the total length of HRMs. The nozzle throat diameter is usually determined by the initial combustion chamber pressure. Assuming constant nozzle configuration and nozzle expansion ratio , as Pci changes, both the throat diameter and total length of the nozzle will change. Furthermore, the main effect plot shows that the grain outer diameter Dp has a slightly positive effect on the total length of HRMs. As in the above analysis, and n > 0.5 for this paper, and the results match the theoretical analysis.
In a word, the same variations of design parameters will have different effects on the change trend of different performance parameters, which also reveals the necessity of adopting the MODO method for comprehensive selection.
5. Conclusions
The present study has successfully established a MODO and MAE framework to conduct an optimization design for a lunar lander descent engine. The MAE process is decomposed into two phases according to whether the discrete attributes have been considered. The MODO and MAE method has been verified to realize the comprehensive consideration of multi-attributes. The final evaluation has proven that HRM-TGGF is the optimal propulsion system and HRMs are considered to be feasible as the propulsion systems of the lunar lander descent stage. In addition, parametric analysis reveals the influence of input parameters on output response. The results show that, Dp, Fi and αi generally have a significant impact on the overall performance of the manned lunar lander. These parameters directly or indirectly affect the thrust, length and total mass of propulsion systems. In the design optimization process, more consideration should be paid to the design space of these parameters.
However, further study is still needed to take into account the input uncertainty variables, model uncertainty and the transmission of uncertain variables in the MODO process. Meanwhile, future research will adopt the evolutionary algorithm based on the HV index to improve the convergence and distribution of the solution sets. Furthermore, the weight calculation using the entropy weight method depends entirely on the input data, ignoring the subjective judgment of the importance of each attribute. In the future, the combinations of subjective and objective weights will be used to conduct the evaluation.
Author Contributions
Conceptualization, Y.L. and P.W.; methodology, Y.L. and X.L.; validation, X.L.; investigation, Y.L. and X.L.; resources, G.C. and X.Z.; data curation, Y.L. and X.L.; writing—original draft preparation, Y.L. and X.L.; writing—review and editing, X.Z. and H.Z.; supervision, G.C.; project administration, G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Funds for the Central Universities.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cohen, M.M. From Apollo LM to Altair: Design, Environments, Infrastructure, Missions, and Operations. In Proceedings of the AIAA SPACE 2009 Conference & Exposition, Pasadena, CA, USA, 14–17 September 2009. [Google Scholar] [CrossRef]
- Meyer, C.; Maul, W. The Application of Neural Networks to the SSME Startup Transient. In Proceedings of the 27th Joint Propulsion Conference, Sacramento, CA, USA, 24–26 June 1991. [Google Scholar] [CrossRef]
- Dinesh, M.; Rajput, S.S.; Kumar, R. Protrusion Effect on the Performance of Hybrid Rocket with Liquefying and Non-Liquefying Fuels. Acta Astronaut. 2021, 178, 536–547. [Google Scholar] [CrossRef]
- Kuo, K.K.; Chiaverini, M.J. (Eds.) Fundamentals of Hybrid Rocket Combustion and Propulsion; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2007. [Google Scholar]
- Schmierer, C.; Kobald, M.; Tomilin, K.; Fischer, U.; Schlechtriem, S. Low Cost Small-Satellite Access to Space Using Hybrid Rocket Propulsion. Acta Astronaut. 2019, 159, 578–583. [Google Scholar] [CrossRef]
- Jens, E.T.; Cantwell, B.J.; Hubbard, G.S. Hybrid Rocket Propulsion Systems for Outer Planet Exploration Missions. Acta Astronaut. 2016, 128, 119–130. [Google Scholar] [CrossRef]
- Virgin Galactic Successfully Completes First Fully Crewed Spaceflight. Vayu Aerosp. Def. Rev. 2021, 4, 82–84. Available online: https://www.proquest.com/scholarly-journals/virgin-galactic-successfully-completes-first/docview/2580731010/se-2 (accessed on 9 August 2022).
- Wei, S.S.; Lee, M.C.; Huang, J.W.; Lu, Y.; Kang, C.H.; Kao, S.T.; Lu, S.J.; Huang, C.H.; Zhan, J.J.; Chen, Z.R.; et al. Demonstration of Tethered Hovering Flight of HTTP-3AT Hybrid Rocket. Acta Astronaut. 2022, 191, 279–292. [Google Scholar] [CrossRef]
- Faenza, M.G.; Boiron, A.J.; Haemmerli, B.; Verberne, O. The Nammo Nucleus Launch: Norwegian Hybrid Sounding Rocket over 100km. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019. [Google Scholar] [CrossRef]
- DAUNTLESS 2021 Vaya Space SmallSat Launch Company and Hybrid Engine Sales. Available online: https://www.vayaspace.com/post/vaya-space-awarded-multiple-patents-for-vortex-hybrid-engine-technology (accessed on 9 August 2022).
- GILMOUR. Available online: https://www.gspace.com/post/gilmour-space-completes-final-qualification-test-of-sirius-rocket-engine (accessed on 8 November 2022).
- Martin, F.; Chapelle, A.; Orlandi, O.; Yvart, P. Hybrid Propulsion Systems for Future Space Applications. In Proceedings of the 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Nashville, TN, USA, 25–28 July 2010. [Google Scholar]
- Casalino, L.; Masseni, F.; Pastrone, D. Optimal Design of Electrically Fed Hybrid Mars Ascent Vehicle. Aerospace 2021, 8, 181. [Google Scholar] [CrossRef]
- Yelken, U.; Yalcintas, A.; Kara, O.; Baysal, M.; Karabeyoglu, M.A. Experimental Study of Lunar-Based Hybrid Rocket Engine. In Proceedings of the AIAA Propulsion and Energy 2021 Forum, Virtual Online, 9–11 August 2021. [Google Scholar]
- Lee, D.; Han, S.; Moon, H. Development of 200 N-Class Throttleable Hybrid Rocket Motor for Lunar Module Application. FirePhysChem 2021, 1, 251–259. [Google Scholar] [CrossRef]
- Ullah, R.; Zhou, D.Q.; Zhou, P.; Hussain, M.; Amjad Sohail, M. An Approach for Space Launch Vehicle Conceptual Design and Multi-Attribute Evaluation. Aerosp. Sci. Technol. 2013, 25, 65–74. [Google Scholar] [CrossRef]
- Ullah, R.; Zhou, D.Q.; Zhou, P.; Baseer, M. A Novel Weight Allocation and Decision Making Method for Space Launch Vehicle Design Concept Selection. Int. J. Ind. Syst. Eng. 2015, 19, 155–168. [Google Scholar] [CrossRef]
- Wang, P.; Zhu, H.; Xie, L.; Xiao, M.; Tian, H.; Cai, G. Multi-attribute evaluation approach for small launch vehicle with multi-objective multi-discipline design optimization. In Proceedings of the International Astronautical Congress, IAC, Virtual Online, 12–14 October 2020; Agenzia Spaziale Italiana (ASI): Rome, Italy, 2020. [Google Scholar]
- Moon, Y.; Jang, T.S.; Park, C.; Kwon, S. Requirements Analysis of Propulsion Systems for Lunar-Exploration Mission. J. Spacecr. Rockets 2013, 50, 620–631. [Google Scholar] [CrossRef]
- Zhu, H.; Tian, H.; Cai, G.B.; Bao, W.M. Uncertainty Analysis and Probabilistic Design Optimization of Hybrid Rocket Motors for Manned Lunar Landing. Sci. China Technol. Sci. 2015, 58, 1234–1241. [Google Scholar] [CrossRef]
- Kelly, T.J. Manned Lunar Lander Design—The Project Apollo Lunar Module (LM). In Proceedings of the Space Programs and Technologies Conference, Huntsville, AL, USA, 24–27 March 1992. [Google Scholar] [CrossRef]
- Apollo 11 Lunar Module/EASEP. Available online: https://nssdc.gsfc.nasa.gov/nmc/spacecraft/display.action?id=1969-059C (accessed on 28 October 2022).
- Smith, P.D. Apollo Experience Report: Spacecraft Structure Subsystem; National Aeronautics and Space Administration: Washington, DC, USA, 1974. [Google Scholar]
- Lunar Module. Available online: https://history.nasa.gov/alsj/CSM08_LM_&_SLA_Overview_pp61-68.pdf (accessed on 5 June 2018).
- Wilhite, A.W.; Wagner, J.; Tolson, R.; Moen, M.M. Lunar Module Descent Mission Design. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Honolulu, Hawaii, 18–21 August 2008. [Google Scholar] [CrossRef]
- Bennett, F.V. Apollo Experience Report: Mission Planning for Lunar Module Descent and Ascent; National Aeronautics and Space Administration: Washington, DC, USA, 1972. [Google Scholar]
- Hammock, W.R.; Currie, E.C.; Fisher, A.E. Apollo Experience Report: Descent Propulsion System; National Aeronautics and Space Administration: Washington, DC, USA, 1973. [Google Scholar]
- Wang, P.; Xu, W.; Zhu, H.; Tian, H.; Cai, G. An Application of Analytical Target Cascading for a Hierarchical Multidisciplinary System: The Preliminary Design of a Launch Vehicle Powered by Hybrid Rocket Motors. Aerospace 2022, 9, 778. [Google Scholar] [CrossRef]
- Ahn, B.; Kang, H.; Lee, E.; Yun, Y.; Kwon, S. Design of Multiport Grain with Hydrogen Peroxide Hybrid Rocket. J. Propuls. Power 2018, 34, 1189–1197. [Google Scholar] [CrossRef]
- Okninski, A. On Use of Hybrid Rocket Propulsion for Suborbital Vehicles. Acta Astronaut. 2018, 145, 1–10. [Google Scholar] [CrossRef]
- Casalino, L.; Masseni, F.; Pastrone, D. Robust Design Approaches for Hybrid Rocket Upper Stage. J. Aerosp. Eng. 2019, 32, 1–13. [Google Scholar] [CrossRef]
- Rao, D.; Cai, G.; Zhu, H.; Tian, H. Design and Optimization of Variable Thrust Hybrid Rocket Motors for Sounding Rockets. Sci. China Technol. Sci. 2012, 55, 125–135. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, P.; Xu, W.; Zhang, Y.; Tian, H.; Cai, G. Design Optimization and Parameter Analysis of a Hybrid Rocket Motor-Powered Small LEO Launch Vehicle. Int. J. Aerosp. Eng. 2021, 2021, 5574436. [Google Scholar] [CrossRef]
- Lobanoff, V.S.; Ross, R.R. Centrifugal Pumps: Design and Application; Elsevier: Amsterdam, The Netherlands, 2013; ISBN 0080500854. [Google Scholar]
- Jamilnia, R.; Naghash, A. Simultaneous Optimization of Staging and Trajectory of Launch Vehicles Using Two Different Approaches. Aerosp. Sci. Technol. 2012, 23, 85–92. [Google Scholar] [CrossRef]
- Frank, C.P.; Atanian, M.F.; Pinon-Fischer, O.J.; Mavris, D.N. A conceptual design framework for performance, life-cycle cost, and safety evaluation of suborbital vehicles. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Friedland, E.I.; Nieroski, J.S. Liquid Rocket Engine Cost Estimating Relationships. In Proceedings of the 2nd Annual Meeting, San Francisco, CA, USA, 26–29 July 1965. [Google Scholar]
- Frank, C.P.; Pinon-Fischer, O.J.; Mavris, D.N. A Flexible Multi-Disciplinary Environment for Performance, Life-Cycle Cost, and Safety Evaluation of Suborbital Vehicles. Aerosp. Sci. Technol. 2018, 77, 555–562. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V. A Comprehensive Review on NSGA-II for Multi-Objective Combinatorial Optimization Problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).