3.1. Overall Results for European Cities
The number of the available clear-sky MODIS–LST imagery for the period June to August 2017 varied significantly across cities, from 38 images for Amsterdam to 245 for Lisbon (average value: 119 images per city). Intra-urban spatial variability was found approximately twice as high during daytime compared to nighttime, with an average LST standard deviation of 2.1 K and 1.1 K, respectively. After normalization, the LST products MOD11A1 and MYD11A1 showed high similarity for each study area, for both their daytime and nighttime average LSTs (rho = 0.886 and non-statistically significant differences after a paired sample t-test). Thereby, the thermal spatial patterns and the statistical analysis for a given city were to a great extent overlapping between the two MODIS satellites; thus, the results presented in this section were derived only from Aqua (MYD11A1 product), which corresponds to overpassing times at fully developed daytime and nocturnal urban boundary layers.
Spearman’s
rho linear correlation coefficients between the urban surface parameters and LST by day are presented in
Table 4. For the majority of the cities the
λimp–LST relationship had a statistically significant positive correlation (
p < 0.05), with an average value for all cases of
rho = 0.54. For cities characterized by warmer and dryer summer conditions (southern European cities; Bsh and Csa climate types in
Table 1), the correlation was noticeably weaker and, in two cases, negative (Nicosia and Madrid). Bivariate correlations between
λimp and the other two surface features were also high; mainly for the case of
λb (average
rho = 0.83) and to a lesser extent for
H (
rho = 0.54)—all the pairwise correlations among the three morphological parameters can be found in the
Appendix A (
Table A1). Thus, not surprisingly,
λb showed a somewhat similar connection to LST in the daytime (average
rho = 0.40) as that of
λimp. The pairwise relation of
H with LST yielded higher variability across cities and generally lower
rho values (average
rho = 0.29). Depending on the city, the
H–LST correlation varied from strongly negative (e.g., Madrid) or with no obvious association (e.g., Athens, London) to moderately/strongly positive—for most cases. Nighttime correlations (
Table 5) were generally more consistent across study areas. All measures of cover and structure were detected to be strongly, positively correlated with LST at night; average
rho was equal to 0.55, 0.52, and 0.51 for
λimp,
λb, and
H, respectively. Hence, in contrast to daytime hours,
H at night was found positively correlated to LST in all but one case (Dublin) and with
rho values of similar magnitude to those for
λimp. It should be noted that all results in
Table 4 and
Table 5 correspond to statistically significant correlations (
p < 0.05), except for the
λimp–LST and
H–LST correlations for daytime Rome.
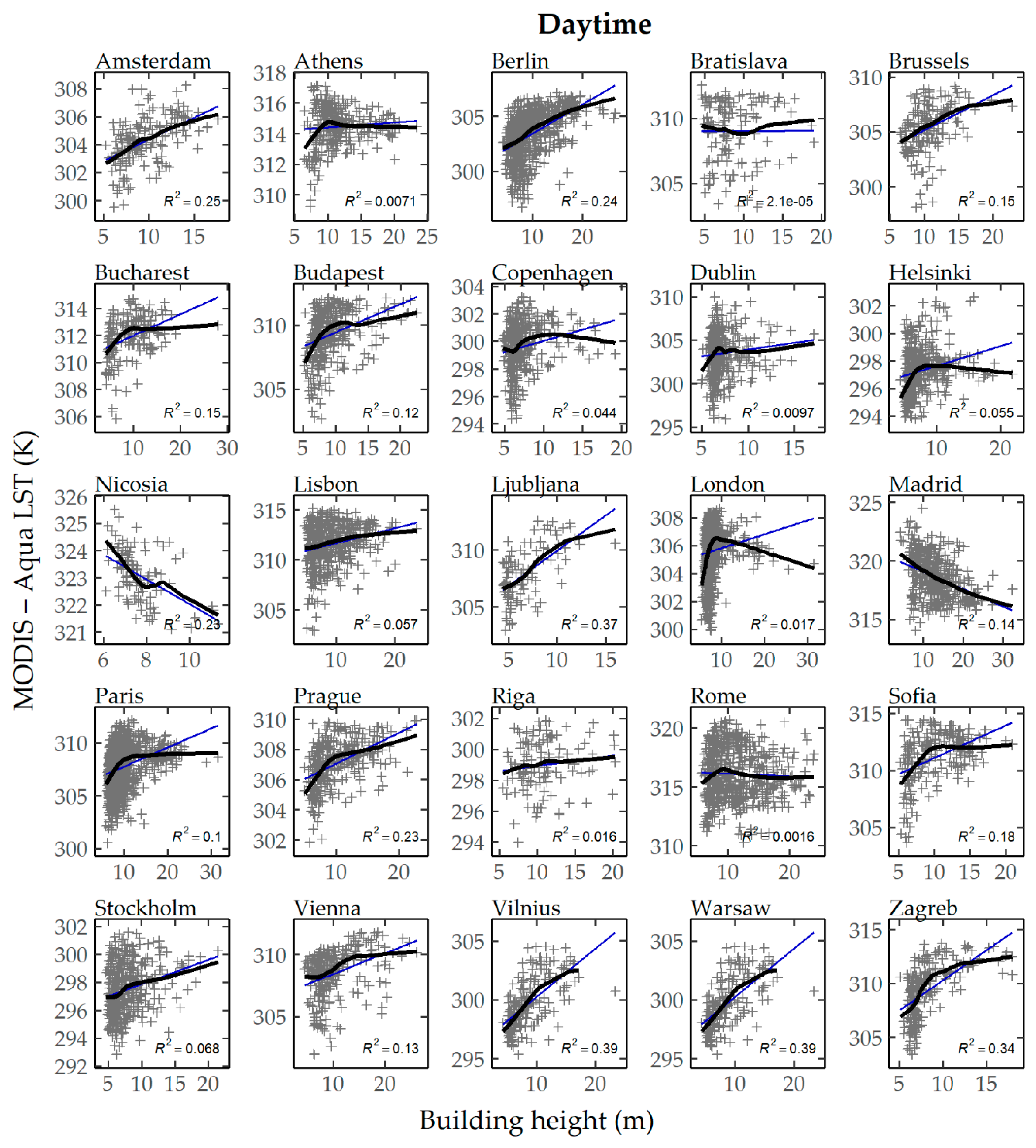
The relationship between the examined urban features and MODIS–LST was examined in more detail using scatter plots and deriving the non-parametric best fitting functions from lowess regression. For
λimp an almost linear relation with LST was determined, observed both in daytime and nighttime observations. This relationship was obtained both when examining each city independently (not shown) and when aggregating all study areas, as presented in
Figure 5a,d. To avoid oversampling the larger cities in
Figure 5, 100 randomly distributed pixels for each case were prior selected. A similar, approximately linear relationship was obtained for
λb–LST (
Figure 5b,e). Greater complexity can be observed for the relationship of
H and LST. Specifically, during daytime (
Figure 5c), for the values above a critical building height (approximately one standard deviation above the mean
H), the lowess regression results in a less steep increasing curve, while no obvious relation can be observed. A significant number of observations can also be detected in the upper left region of
Figure 5c—corresponding to low
H and high LST. At night (
Figure 5f), LST was found to increase more consistently with
H.
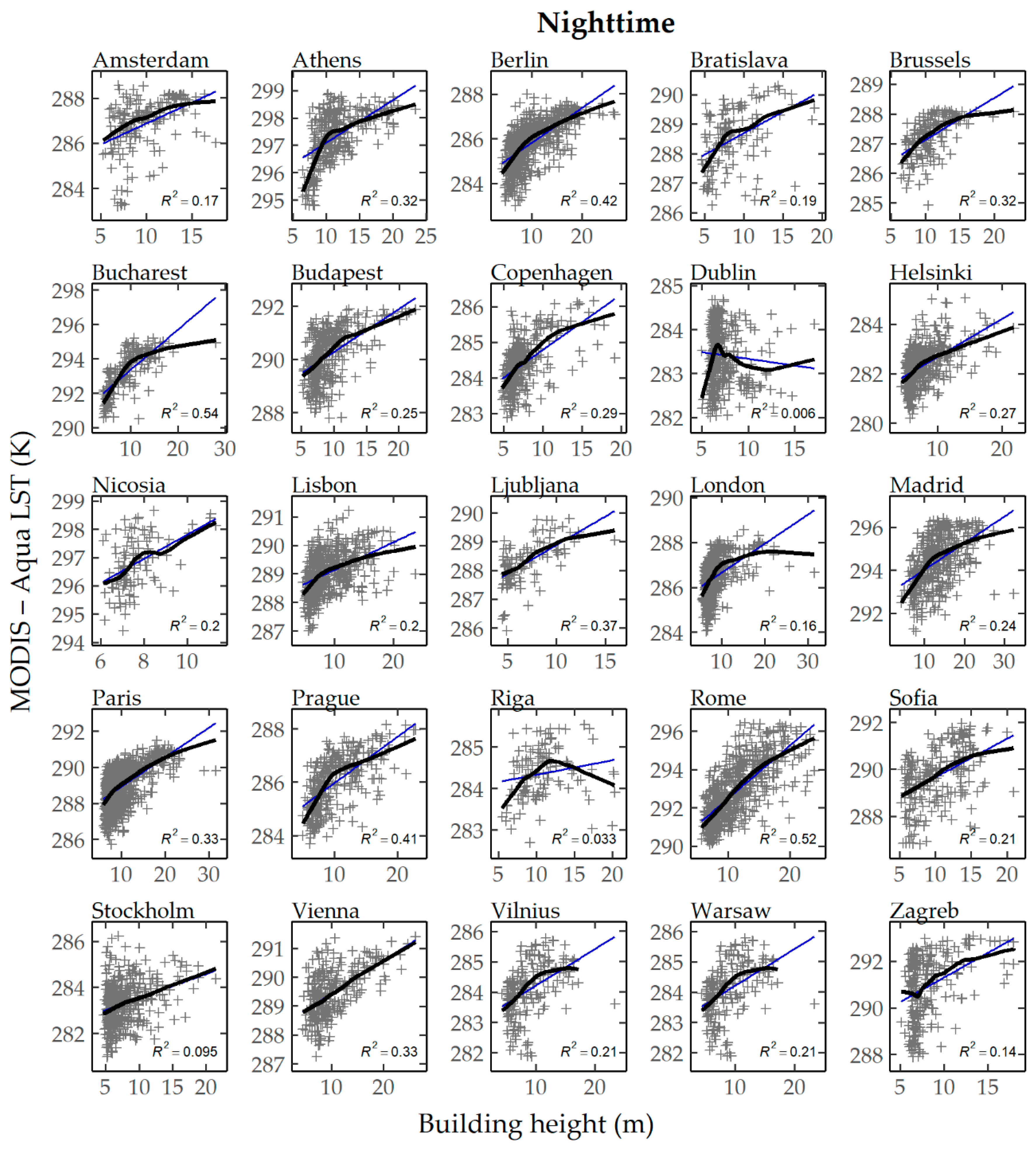
To achieve a more detailed investigation of the
H–LST relationship, the individual scatter plots and the associated lowess regression fit per city are given in
Figure 6 and
Figure 7. In
Figure 6 (daytime surface temperatures) several distinguishing interlinks can be detected across study areas. For a significant number of occasions—most noticeably for Athens, Copenhagen, Paris, and London—daytime LST increased approximately linearly up to maximum value at intermediate heights, above which the positive association levels off or is reversed. In a few cities (e.g., Amsterdam and Brussels) as
H increased, LST values were consistently larger. Finally, mainly for southern/Mediterranean cities, a particularly weak (Lisbon and Rome) or negative (Madrid and Nicosia) relation between
H and LST was observed. Conversely, during nighttime (
Figure 7)
H and LST presented a more consistent association across cities; LST was positively affected by increasing building height for the vast majority of the examined cases.
As noted previously, strong intercorrelations were found for
λimp,
λb, and
H; thereby the independent effect of each variable on LST may to an extent be concealed in the pairwise correlations. The relative influence of each surface parameter after adjusting for the others was assessed within multiple regression models. The overall results of the regression analysis are given in
Table 6, where regression coefficients are standardized (beta coefficients).
The main findings for the surface influences during daytime can be summarized as follows: The impervious fraction (
λimp) was shown to be the stronger controlling factor of LST; for almost all cities it had statistically significant positive beta coefficients, larger in magnitude than
λb and
H. Besides, it can be observed that after adjusting for the other two surface parameters,
λimp exerted a positive influence on LST also for all southern European cities. Regarding
λb and
H, the sign and statistical significance of beta coefficients had larger variability among different study areas. However, all statistically significant coefficients for
λb were negative (apart from Stockholm), with a value ranging between −0.88 and −0.10. For
H, cities with a consistent positive relationship in
Figure 6, resulted in positive regression coefficients. On the other hand, when daytime LST was decreasing with increasing
H or had a peak at intermediate heights, the regression coefficients were statistically significant negative, however, with a weaker effect on LST than that exerted by
λimp.
For nighttime observations, the strength and direction of the influence on LST was found to be much more evenly distributed among surface parameters. The impervious fraction was no longer the prevailing determining factor of LST; in some cases, it had a negative association with LST, however, for the majority of the statistically significant beta coefficients, the effect was positive. For λb and H, the nighttime regression results were noticeably different from those by day. Firstly, for the majority of the cases, beta coefficients increased in value, which was often accompanied by a change of their sign. Furthermore, the statistically significant coefficients for λb and H were positive and of similar magnitude to those for λimp.
The coefficient of determination (
R2) of the multiple regression models had an average value of 0.45 and 0.42 in daytime and nighttime, respectively. Despite the intercorrelation between surface paraments, the multicollinearity metric VIF had moderate values, below the theoretical, critical threshold of 5 (average VIF for all regression models: 3.40). As can be seen in
Table 6 for six cities, that the original regression models resulted in a VIF value over 5, only
λimp and
H were finally included in the analysis to avoid the emerging multicollinearity effects.
Besides the central role of urban morphology discussed above, sea breeze has also been found to be an important determinant of the urban heat island intensity, usually exerting a strong moderating influence [
101,
102,
103]. To include the effects of the sea breeze in the current statistical analysis, further regression models were developed incorporating the proximity to the sea—the distance between the center of a given image pixel and the coastline (
d)—as an additional independent variable. Only the urban areas within ten kilometers of the coast were considered, in order to ensure a strong influence of the local sea breeze circulation, irrespective of other local characteristics of each study area. As can be seen from
Table 7, during daytime for all the examined urban areas, a larger distance from the coast resulted in higher surface temperatures. For five of the seven cases, the cooling effect of the sea breeze was also found to be statistically significant. At night, the developing land breeze provided more diverging results—which may be attributed to local influences not taken into account in the current analysis. Nevertheless, as expected, for the majority of the nighttime cases, the proximity to the sea results in a positive influence on LST. In addition, the statistically significant results of all 4-variable regression models were in agreement with the findings presented previously (
Table 6) regarding the control of urban form—i.e., that closely packed and/or high-rise buildings tend to result in lower temperatures during daytime and to higher LST values at night.
Statistically significant and relatively high was the spatial autocorrelation of the multiple regression models. The average Moran’s I measure of spatial autocorrelation was found equal to 0.61 in the daytime and 0.66 at nighttime. Hence, spatial regression models were used to incorporate in the analysis of the neighboring influences on the LST values. Specifically, spatial lag models (SLM) were developed, assuming that the spatial influence was constrained to the eight direct neighbors of a given pixel. Different choices regarding the adjacency weights did not lead to improved accuracy, thus were not included in the findings. A summary of the spatial regression results is given in
Table 8; regression coefficients are standardized, and they correspond to the total influence—the sum of direct and indirect effects—of the independent variables according to [
104].
The results of SLM models were generally in agreement with the OLS regression regarding the direction of urban structure controls on LST. By day, on almost all occasions, the statistically significant spatial regression coefficients were positive for λimp and negative—also smaller in magnitude—for λb and H. In contrast, during nighttime, almost all statistically significant coefficients were positive for all three surface parameters. In some cases, non-statistically significant sign changes were observed in comparison to the multiple regression results. An inter-comparison of the accuracy of the two regression types can be derived using the Akaike information criterion (AIC), where a lower value corresponds to better performance of the model. The reduction of AIC when using SLM—by an average of 67% in the daytime and 81.6% at night compared to the OLS regression—highlights the improvement in modeling LST when spatial autocorrelation was taken into account.
3.2. Urban Area of Athens
In the previous section, a broad statistical assessment of the relation between surface parameters and LST was conducted for 25 European cities. A more focused analysis was carried out next for the city of Athens in order to highlight the aspects of urban form and the physical processes that drive the derived associations. A point of concern in the previous discussion was the high intercorrelations among
λimp,
λb, and
H. It is common that in urban areas, impervious fraction, building density, and building height increase largely concurrently—typically from the city outskirts to the city center [
105]. Although multiple regression allows the isolation of the independent effect of a given variable, statistical analysis is accompanied by uncertainties and its underlying assumptions are not fully satisfied in practice. The particular characteristics of the urban environment of Athens enable us to define well-distinguished zones of differing three-dimensional structures, controlling in this way for vegetation variations.
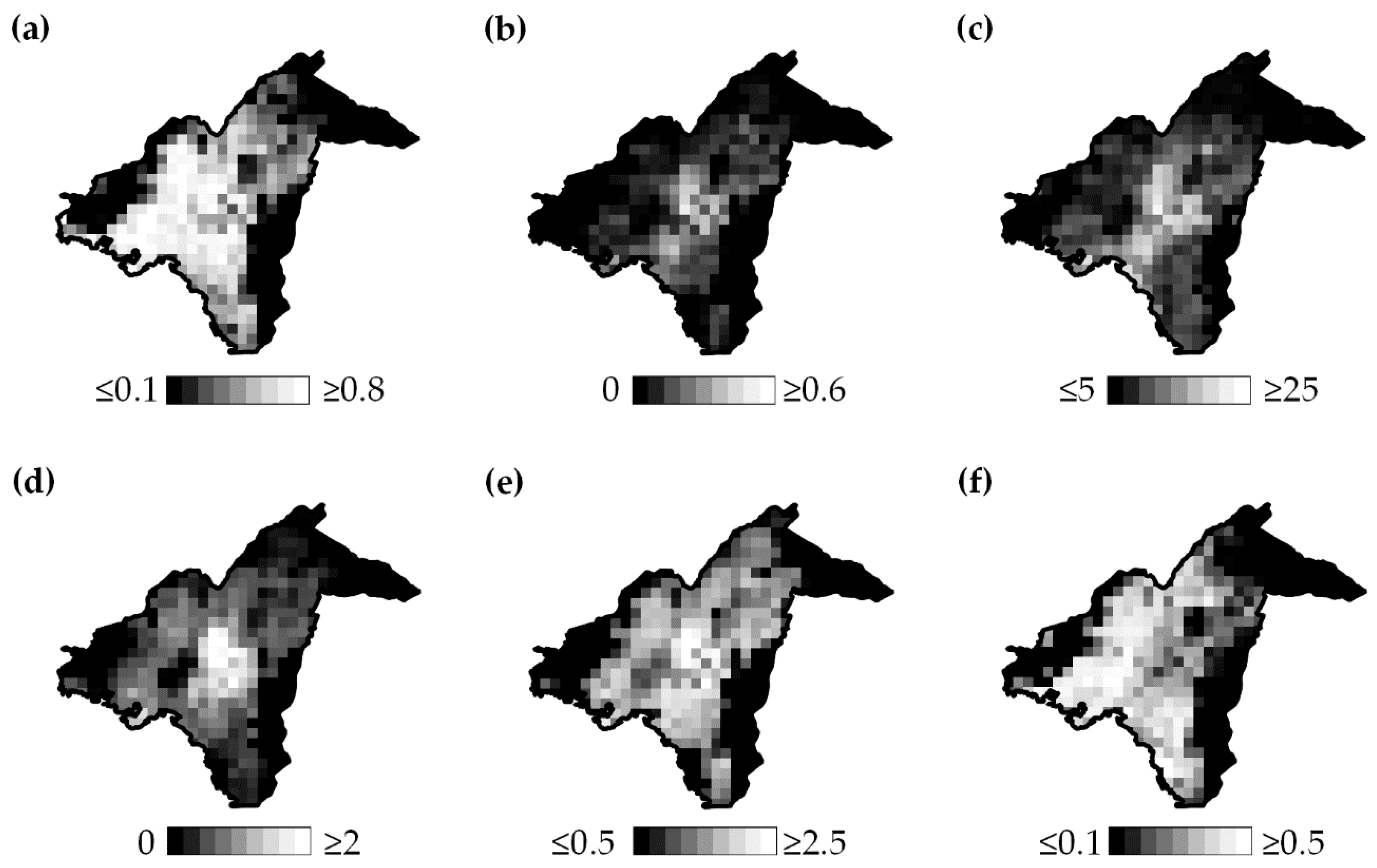
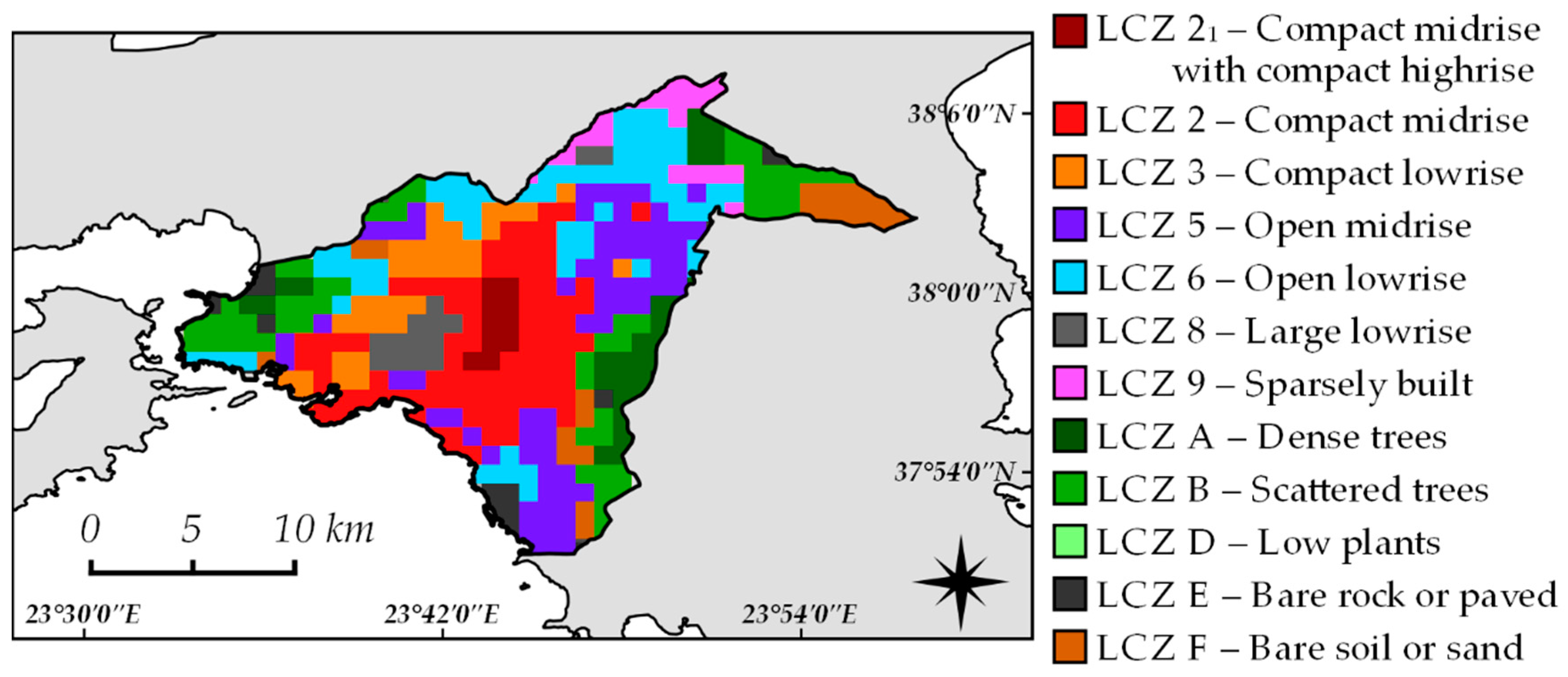
As follows from
Figure 3, a clear division can be observed for Athens, between the well-vegetated, less densely built northeastern part of the city (to a lesser extent also for the southeastern districts) and the central areas. Focusing on the urban core—as defined in
Figure 2—the following characteristics can be outlined: The inner-city area (LCZ 2
1 and LCZ 2,
Figure 4) corresponds to neighborhoods of dense and high-rise structure; vegetation is generally scarce except for few fragmented urban parks (see
Figure 2). In close proximity, there is an extended area of light industrial use, mainly with open set low-rise buildings (LCZ 8). Moreover, the western districts of the urban core correspond to compact housing with medium/low building height (LCZ 2 and mostly LCZ 3).
For all the above-mentioned zones, vegetation density is low and similar across the LCZs; the average
λimp inside the urban core was found equal to 0.66, 0.66, 0.70, and 0.69 for LCZ 2
1, LCZ 2, LCZ 3, and LCZ 8, respectively. For this calculation, as well as in the following discussions, three pixels inside the urban core that include extended urban parks were not taken into account.
Figure 8 shows the average surface temperature of Athens during the summer months of 2017 using the product MODIS LST product (clear sky observations of Aqua). It can be observed that the northeastern regions of the urban area were associated, both during daytime and nighttime, with lower surface temperatures. That is in accordance to the results of
Figure 5 and
Table 6 and
Table 7 for Athens, regarding the negative relation of
λimp with LST. Overall, the classes LCZ 5, 6, and 9 had an average lower LST by ≈ 1.9 Κ in comparison to the other urban LCZs. Of more interest is the spatial variability inside the urban core of the city. There, during daytime pixels included in the LCZ 8 class (high values of
λimp and relatively low values of
λb and
H) were clearly distinguished as the warmer spots in Athens (LST ≈ 317 K). The districts where closely-packed, high-rise buildings prevail (LCZ 2
1) were characterized by notably lower temperatures (LST ≈ 315.3 K). Thus, the negative relation of
H with daytime LSTs that was previously derived for Athens using multiple regression analysis (
Table 6) can also be detected here. The western periphery tends to be characterized by intermediate values of
λb and
H that was subsequently mirrored in the observed LSTs. The thermal patterns of the urban core were reversed when examining the nighttime spaceborne observations: The densely built-up neighborhoods exhibited in this case higher LST than the LCZ 8 zone. In
Table 9, the overall surface temperature statistics are shown per LCZ (natural type LCZs were not included).
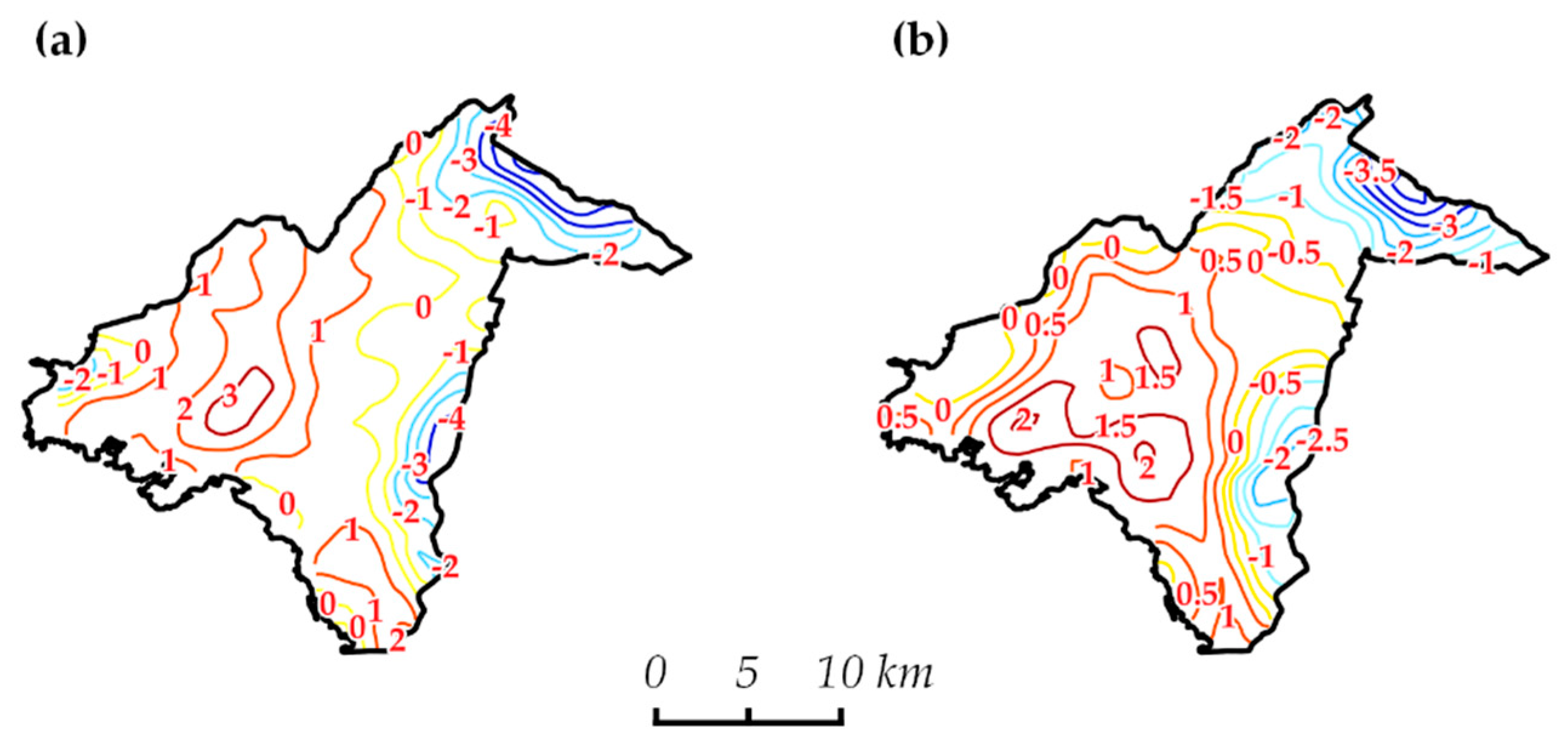
The local differentiations across the city can be more clearly outlined deriving the normalized—the temperature anomaly relative to the average value of LST for the study area—isotherms. As can be observed in
Figure 9, the center of the LCZ 8 class was by day, on average, 3 °C warmer than the average temperature of the study area and up to 2 °C than the neighboring densely built central area. At night—where in general LST variability was weaker—a local minimum can be detected in LCZ 8, with a lower LST up to 1 °C compared to the adjacent areas. Furthermore, in the broader region, three distinct centers of excess heat were developed.
The thermal signature of the local climate zones is driven by the vegetation density and the characteristics of urban structure, with the latter being the determining influence for the urban core of Athens. In
Section 3.1, the average building height
H was used as a means of accounting the total three-dimensional effects (i.e., used as a proxy variable).
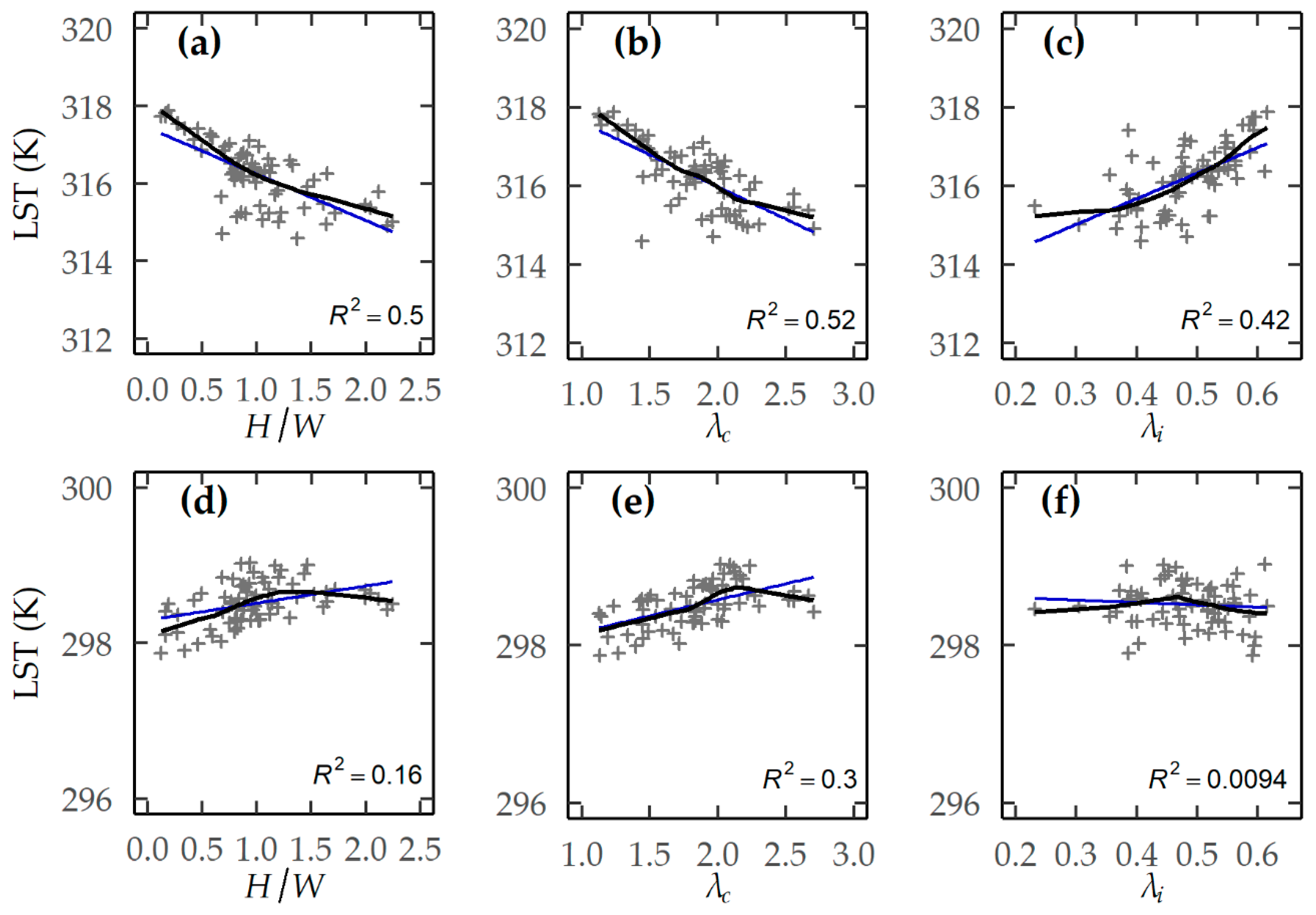
Figure 10 shows the relation of LST with two additional surface parameters of the urban structure (
H/
W and
λc) and a parameter that describes the fraction of impervious ground (i.e., impervious surface without buildings) (
λi). During the daytime,
H/
W had a similar association with LST, as shown previously for
H in
Figure 6. Specifically, LST is increasing with
H/
W for the range 0 to ≈1, while for larger height-to-width ratios, there is a noticeable decline in LSTs. No obvious relation is found for
λc (
Figure 10b), whereas
λi (
Figure 10c) shows a remarkable linearity and strong correlation with LST (
rho = 0.70,
p <0.01). For nighttime observations, all three parameters exerted a positive influence on LSTs (
Figure 10d–f).
The surface temperatures of the urban districts of Athens in close proximity to the sea were expected to be influenced by the presence of the local sea breeze circulation. To quantify the magnitude of this effect, the sea breeze days for June–August 2017 were firstly identified, considering the cases when the wind direction was between 150° and 280° during daytime hours and between 300° and 130° at night [
106]. For the remaining dates, the city was under the influence of the synoptic flow (northern wind). As seen from
Table 10, depending on the circulation type, the neighborhoods that were close to the seashore—distance lower than 3 km—were generally relatively cooler during daytime and warmer at night, in agreement to
Table 7.
To isolate the influence of the urban structure, the corresponding scatterplots and lowess regression lines for the urban core—which was characterized by little variability in green areas (after excluding the main urban parks) and was less influenced by the sea breeze—are in given in
Figure 11 (total number of pixels: 70). For
H/
W and
λc, the association with LST had an obvious dependence on the time of the day. The above features had a statistically significant (
p < 0.01) strong negative relation with LST in the daytime (
rho = −0.68 and −0.70 for
H/
W and
λc, respectively) and positive at night (
rho = 0.45 and 0.59, respectively). For
H/
W > 2 and
λc > 2.5 the nocturnal LST slightly decreased; however, the included number of pixels in this range was limited. As expected, LST increased consistently with
λi during daytime (
rho = 0.65,
p < 0.01); at night, no significant correlation was evident within the urban core. Surface parameters
H/
W and
λc showed a high bivariate correlation with
H (
rho = 0.71 and 0.84, respectively), which can explain the similarity of their observed influence on LST.
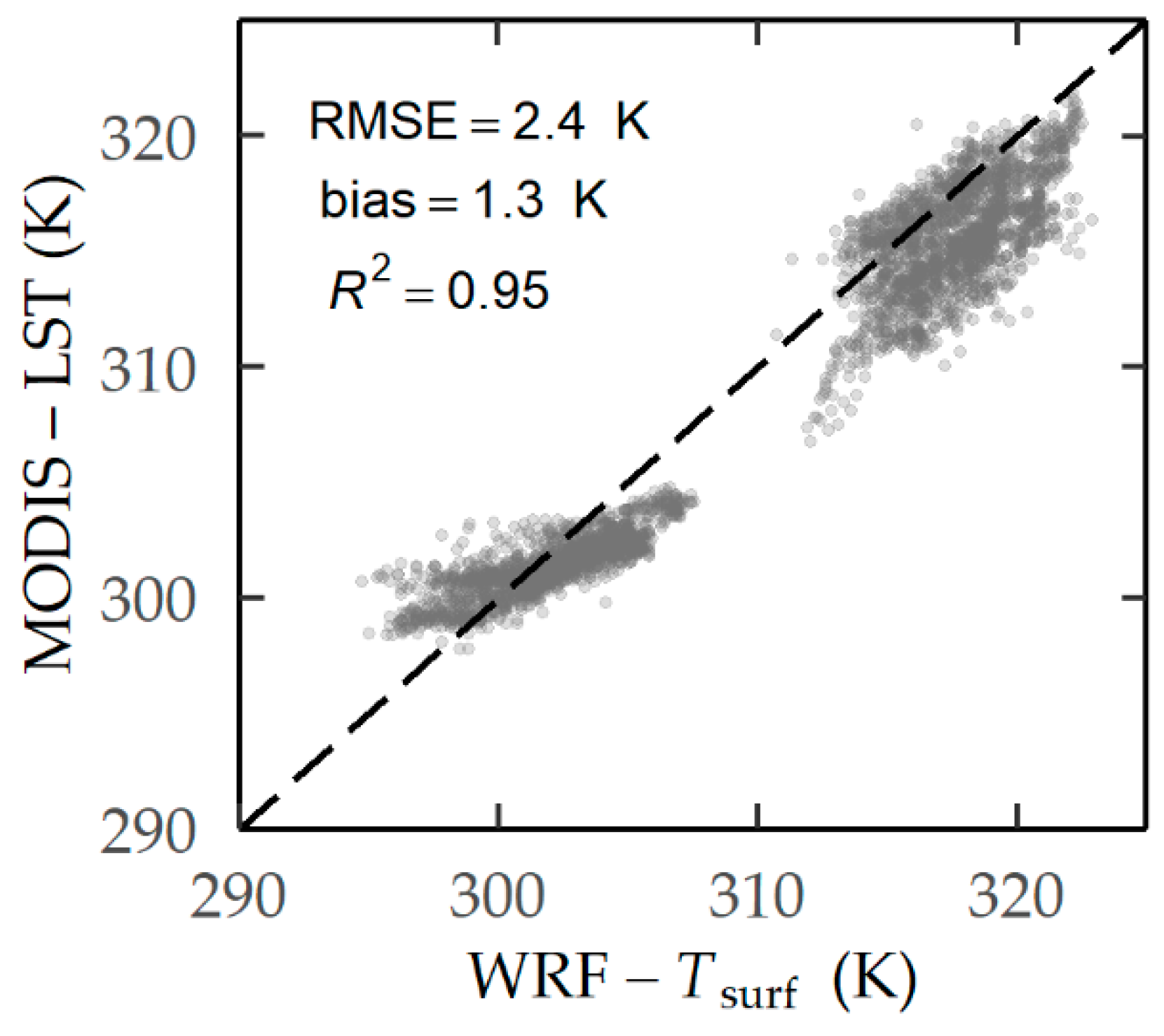
Next, the urban thermal climate of Athens was investigated using the WRF model for a five-day case-study (7–11 August 2017). The simulated surface temperature (
Ts) was tested against cloud-free MODIS LST (Terra and Aqua) images. A reasonable agreement was found for the urban fabric—i.e., for the urban cells,
λurb > 0—with an average RMSE = 2.4 K and a Mean Absolute Error (MAE) equal to 2.0 K. For the total study area—including the forested areas at the city boundaries—RMSE and MAE were 2.8 K and 2.3 K, respectively. However, as can be seen from
Figure 12, the modeled surface temperature was generally systematically overestimated. The mean
Ts–LST error (bias) was 1.3 K (2.0 K during daytime and 0.6 K at night). In addition, in the nighttime the highly vegetated neighborhoods (LCZ 5, 6, and 9) exhibited a slight to moderate underestimation of
Ts (average bias = −0.4 K).
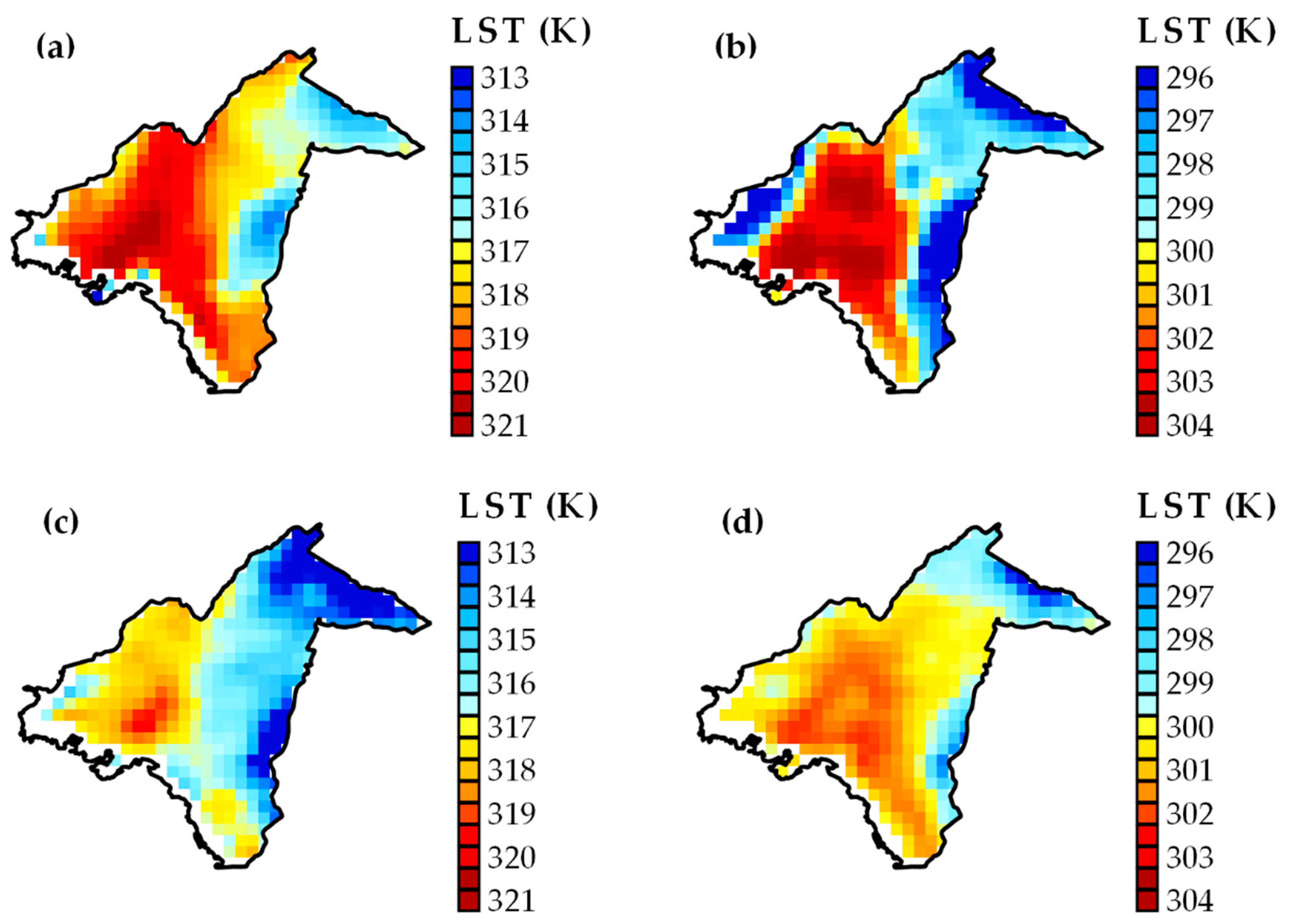
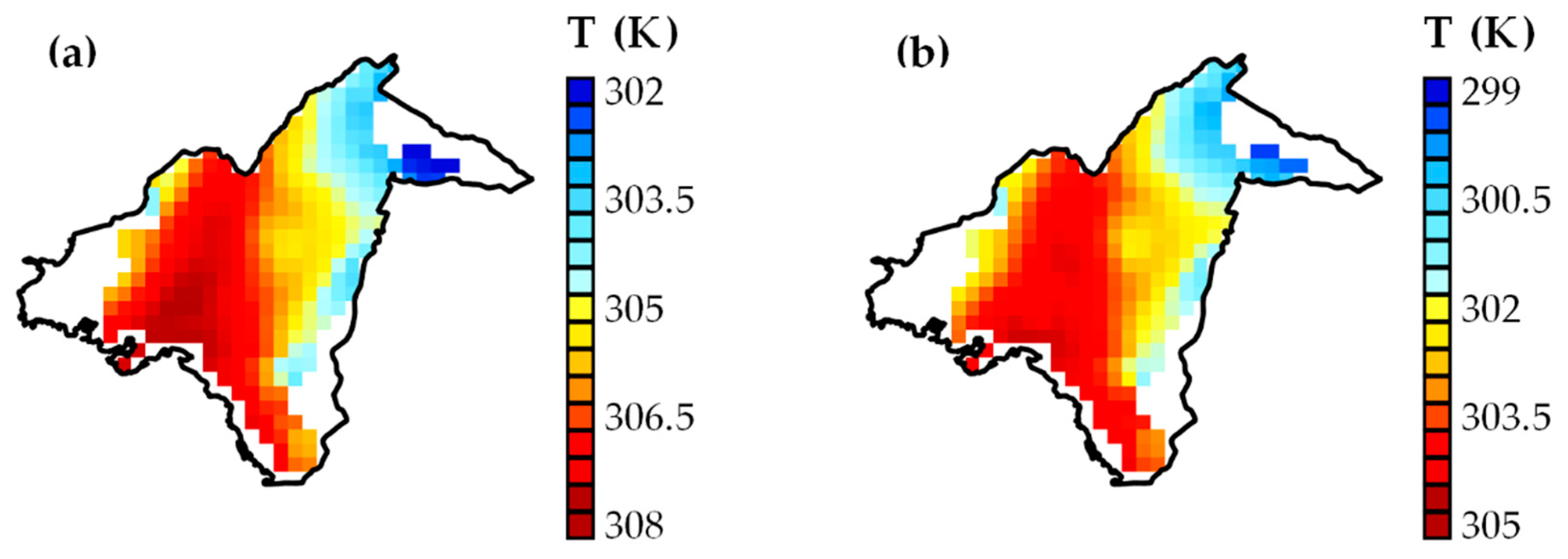
The above discrepancies can be better highlighted in the spatial mapping of
Ts presented in
Figure 13 (average model estimations compared against synchronous average LST values retrieved from MODIS Aqua). Nevertheless, despite the systematic differences, it can be observed that WRF–SLUCM was capable of matching to a fairly good extent the spatial patterns of satellite-derived LST.
By day (
Figure 13a) LCZ 8 (high
λi and low
H/
W) was correctly simulated to have a higher surface temperature of ≈2 Κ compared to the neighboring densely built districts (LCZ 2
1 and LCZ 2). At night, the center of the open set LCZ 8 zone corresponded to a local minimum, 0.5–1 K cooler than the central areas with closely packed buildings (
Figure 13b), in agreement to Aqua observations (
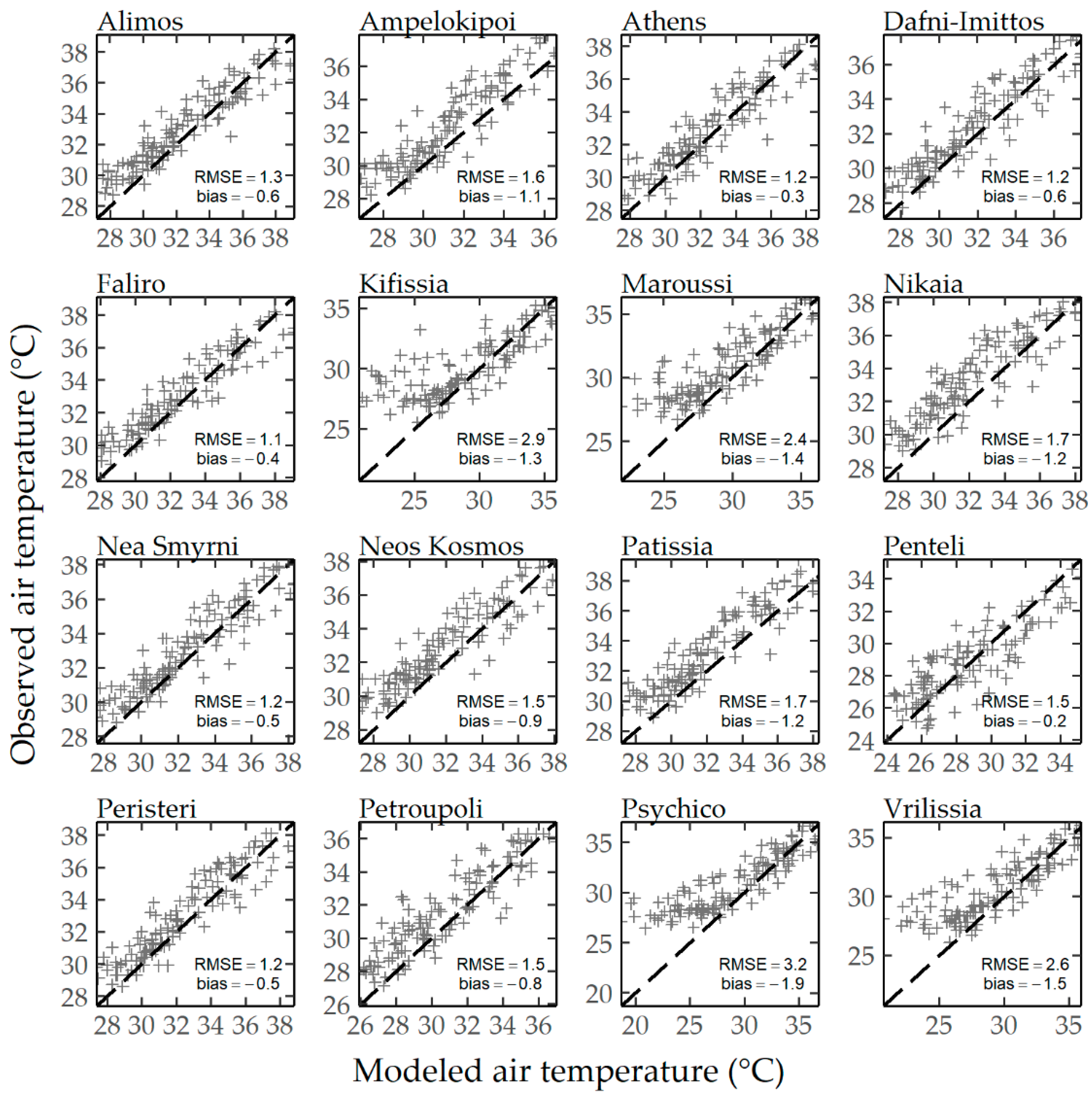
Figure 13d). In addition, the model-observation comparison demonstrates that WRF noticeably captured the differentiation between the highly built-up and the heavily vegetated urban districts. However, the intra-urban variations were overestimated at nighttime because of the previously noted systematic errors. The evaluation of the model’s ability to predict the near-surface air temperature (
Tas) is given in
Figure 14. In general, WRF provided good estimates for the majority of the stations, with an RMSE varying from 1.2 to 3.2 Κ and an average value of 1.7 K. The larger errors were obtained for the less densely built-up LCZs as a result of significant underestimation of nocturnal
Tas (average bias equal to −0.9 K for all stations). In addition to a general underestimation of the nocturnal thermal stress in well-vegetated urban areas that was also observed previously for
Ts, the disagreement between modeled and observed values are considered to be further influenced by the location of the automatic meteorological stations. Specifically, while the majority of the stations are located within or near residential districts, modeled
Tas corresponds to the aggregated temperature of both the impervious and the vegetated tile of the urban grid cell. Limiting the evaluation only to the impervious part of the modeled temperatures (
Tas,urb), the negative bias was seen to consistently decrease (average bias = −0.1 K for all stations), while RMSE also became smaller, from 1.7 Κ to 1.1 Κ (
Figure 15).
The considerably low bias using
Tas,urb as a diagnostic output variable is reflected on the average modeled air temperature per LCZ for the total examined period (
Table 11); results are divided into daytime (7 a.m. to 8 p.m. local time) and nighttime (9 p.m. to 7 a.m. local time) hours. It can be observed that the average thermal conditions for the different LCZs were well predicted. As expected, the less densely developed sites demonstrated lower average temperatures (also influenced by greater elevation). The variability among LCZs was observed to be relatively stable for daytime and nighttime estimates.
Figure 16 gives the spatial distribution of the modeled near-surface, considering only the urban tile (
Tas,urb). Similar to the surface temperature variability in
Figure 8 and
Figure 13, the closely packed LCZs of the broader center of Athens (LCZ 2
1 and LCZ 2) had a lower temperature in the order of 0.5 Κ than the adjacent LCZ 8 by day. At night, a difference of similar magnitude was observed, however, this time with higher
Tas,urb for LCZ 2
1 and LCZ 2.