Attribution and Prediction of Precipitation and Temperature Trends within the Sydney Catchment Using Machine Learning
Abstract
1. Introduction
2. Data and Methodology
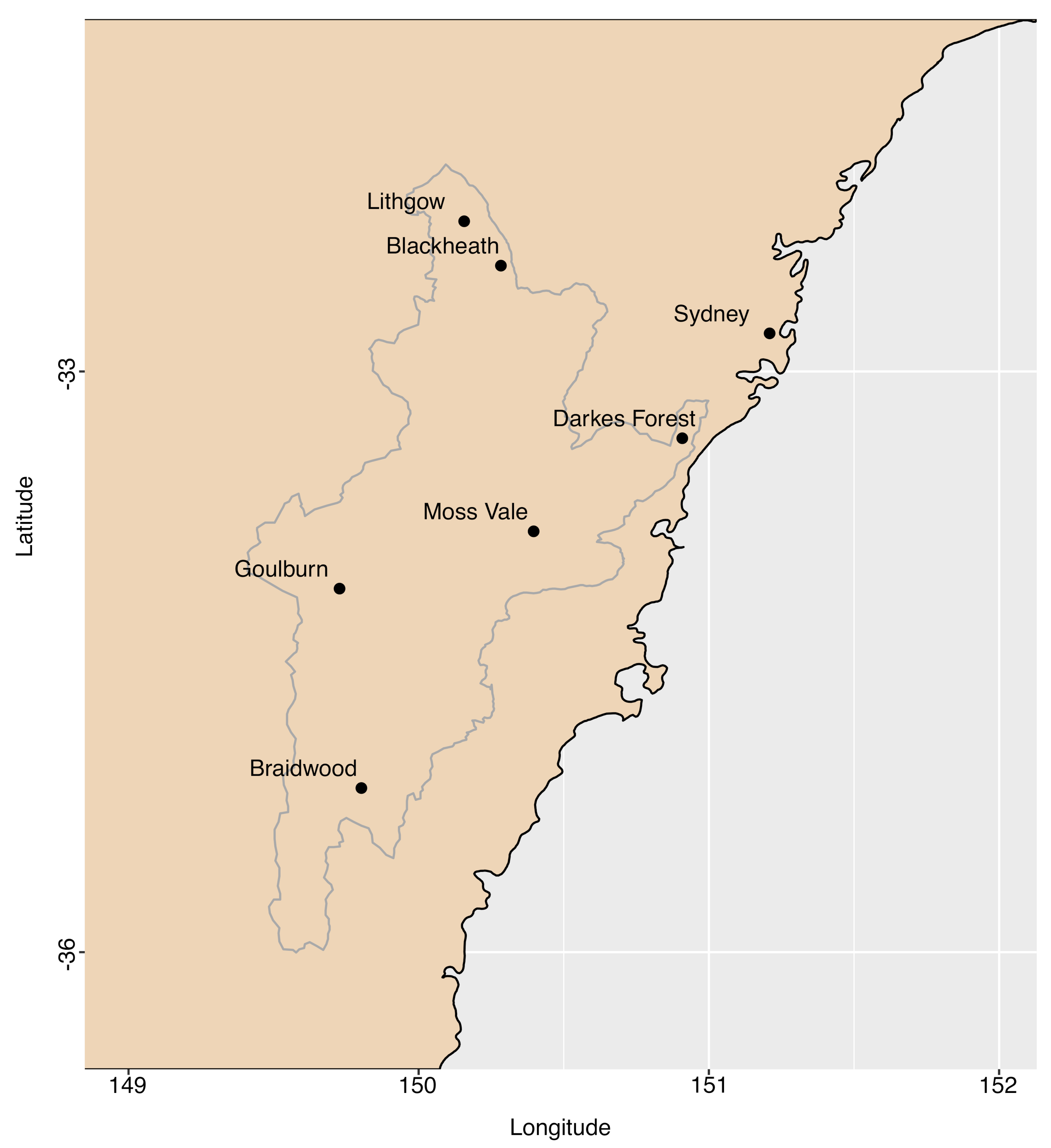
2.1. Data
2.2. Statistical Analysis
2.3. Attribute Selection and Prediction
3. Results
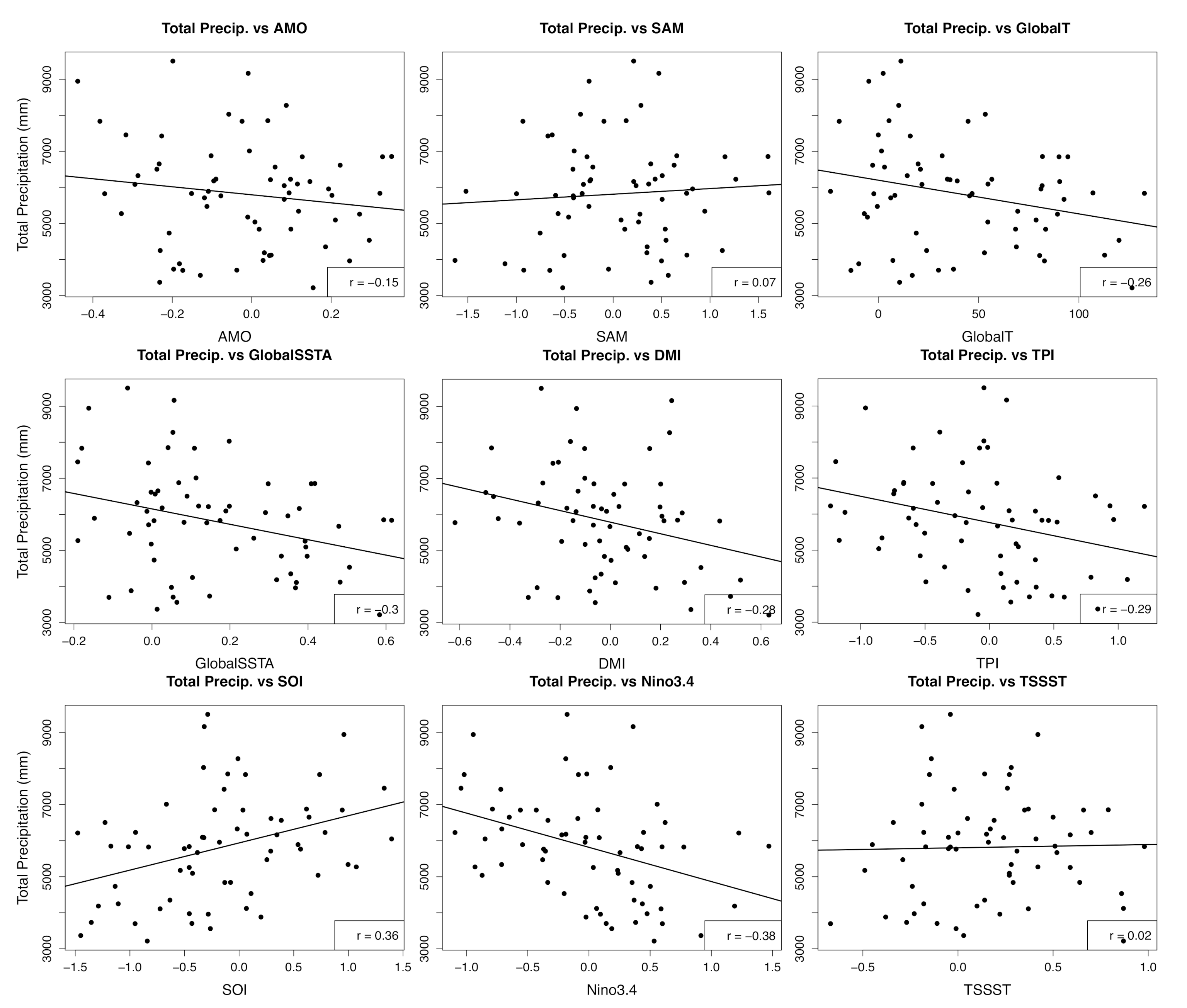
3.1. Evolution of Precipitation
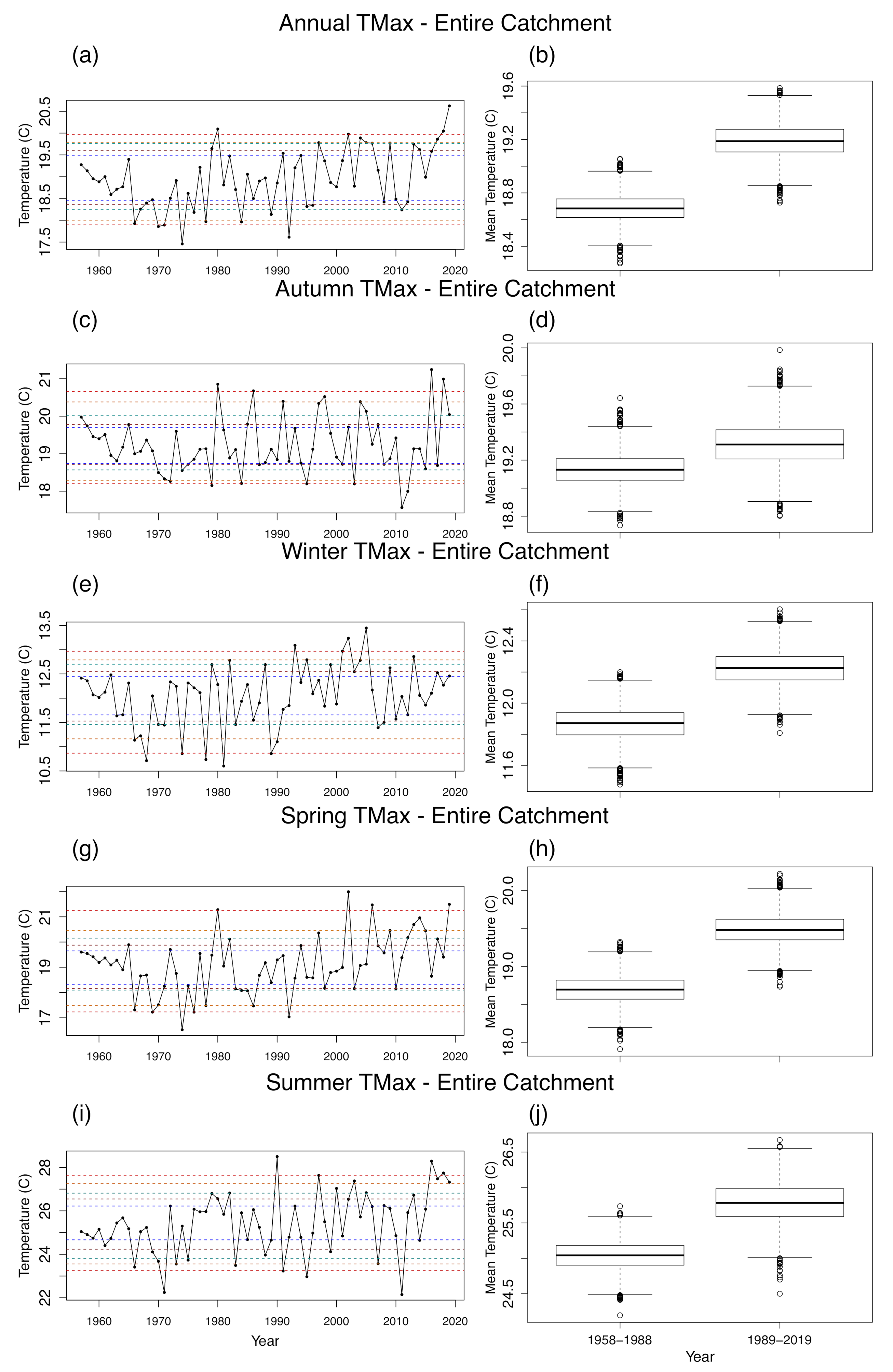
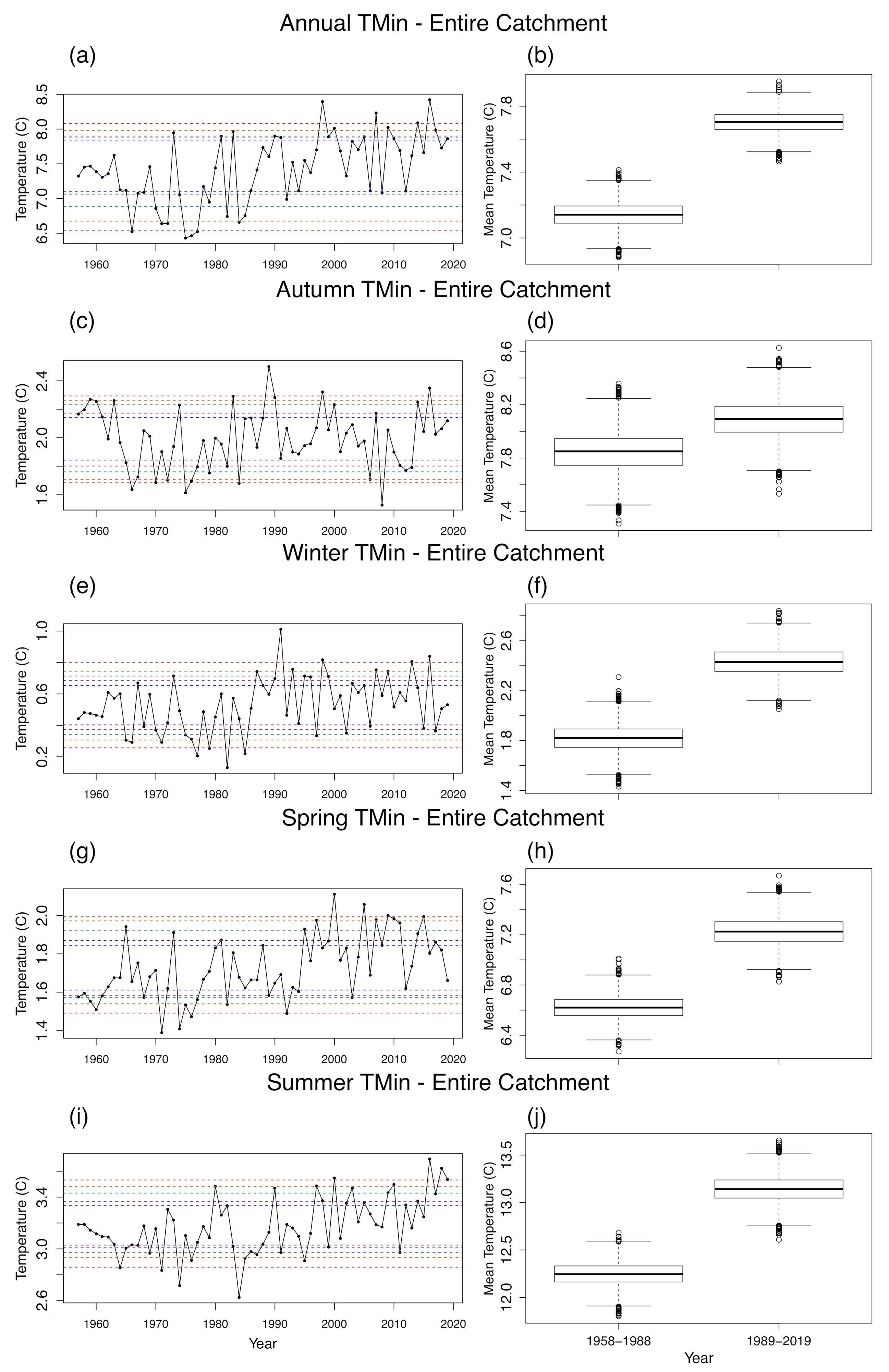
3.2. Evolution of Temperature
3.3. Wavelet Analysis of Precipitation
3.4. Wavelet Analysis of Temperature
3.5. Attribution and Prediction of Annual Precipitation
3.6. Attribution and Prediction of Autumn Precipitation
3.7. Attribution and Prediction of Winter Precipitation
4. Discussion
4.1. Drought Vulnerability
4.2. Attribution and Prediction
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability
References
- Kiem, A.S.; Johnson, F.; Westra, S.; van Dijk, A.; Evans, J.P.; O’Donnell, A.; Rouillard, A.; Barr, C.; Tyler, J.; Thyer, M.; et al. Natural hazards in Australia: Droughts. Clim. Chang. 2016, 139, 37–54. [Google Scholar] [CrossRef]
- Richman, M.B.; Leslie, L.M. Machine Learning for Attribution of Heat and Drought in Southwestern Australia. Procedia Comput. Sci. 2019, 168, 3–10. [Google Scholar] [CrossRef]
- Mukherjee, S.; Mishra, A.; Trenberth, K. Climate Change and Drought: A Perspective on Drought Indices. Curr. Clim. Chang. Rep. 2018, 4, 145–163. [Google Scholar] [CrossRef]
- Cheeseman, J. Food Security in the Face of Salinity, Drought, Climate Change, and Population Growth. In Halophytes for Food Security in Dry Lands; Elsevier: Amsterdam, The Netherlands, 2016; pp. 111–123. [Google Scholar]
- Stanke, C.; Kerac, M.; Prudhomme, C.; Medlock, J.; Murray, V. Health Effects of Drought: A Systematic Review of the Evidence. PLoS Curr. 2013, 5. [Google Scholar] [CrossRef] [PubMed]
- Dowdy, A.; Pepler, A.; Di Luca, A.; Cavicchia, L.; Mills, G.; Evans, J.; Louis, S.; McInnes, K.; Walsh, K. Review of Australian east coast low pressure systems and associated extremes. Clim. Dyn. 2019, 53, 4887–4910. [Google Scholar] [CrossRef]
- Sydney Water. Sydney’s Drought: Aquabumps Shows Just How Dry it Got. 2020. Available online: https://www.sydneywater.com.au/SW/about-us/our-publications/Media/sydney-s-drought–aquabumps-shows-just-how-dry-it-got/index.htm (accessed on 1 August 2020).
- Bureau of Meteorology. The “Federation Drought”, 1895–1902. 2009. Available online: https://webarchive.nla.gov.au/awa/20090330051442/http://pandora.nla.gov.au/pan/96122/20090317-1643/www.bom.gov.au/lam/climate/levelthree/c20thc/drought1.html (accessed on 4 June 2020).
- The World War II Droughts 1937–1945. Available online: https://webarchive.nla.gov.au/awa/20090330051442/http://pandora.nla.gov.au/pan/96122/20090317-1643/www.bom.gov.au/lam/climate/levelthree/c20thc/drought3.html (accessed on 4 June 2020).
- Chiew, F.H.S.; Potter, N.J.; Vaze, J.; Petheram, C.; Zhang, L.; Teng, J.; Post, D.A. Observed hydrologic non-stationarity in far south-eastern Australia: Implications for modelling and prediction. Stoch. Environ. Res. Risk Assess. 2014, 28, 3–15. [Google Scholar] [CrossRef]
- Richman, M.B.; Leslie, L.M. Uniqueness and Causes of the California Drought. Procedia Comput. Sci. 2015, 61, 428–435. [Google Scholar] [CrossRef]
- Richman, M.B.; Leslie, L.M. The 2015–2017 Cape Town Drought: Attribution and Prediction Using Machine Learning. Procedia Comput. Sci. 2018, 140, 248–257. [Google Scholar] [CrossRef]
- Diffenbaugh, N.S.; Swain, D.L.; Touma, D. Anthropogenic warming has increased drought risk in California. Proc. Natl. Acad. Sci. USA 2015, 112, 3931–3936. [Google Scholar] [CrossRef]
- Niang, I.; Ruppel, O.C.; Abdrabo, M.A.; Essel, A.; Lennard, C.; Padgham, J.; Urquhart, P. 2014: Africa. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Technical Report; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 1199–1265. [Google Scholar]
- Speer, M.; Leslie, L.; Fierro, A. Australian east coast rainfall decline related to large scale climate drivers. Clim. Dyn. 2011, 36, 1419–1429. [Google Scholar] [CrossRef]
- Timbal, B.; Fawcett, R. A Historical Perspective on Southeastern Australian Rainfall since 1865 Using the Instrumental Record. J. Clim. 2013, 26, 1112–1129. [Google Scholar] [CrossRef]
- Timbal, B.; Drosdowsky, W. The relationship between the decline of Southeastern Australian rainfall and the strengthening of the subtropical ridge. Int. J. Climatol. 2013, 33, 1021–1034. [Google Scholar] [CrossRef]
- Post, D.A.; Timbal, B.; Chiew, F.H.S.; Hendon, H.H.; Nguyen, H.; Moran, R. Decrease in southeastern Australian water availability linked to ongoing Hadley cell expansion. Earth’s Future 2014, 2, 231–238. [Google Scholar] [CrossRef]
- Australian Bureau of Statistics. Australian Demographic Statistics; Technical Reportl Cat. No. 3101.0; Australian Bureau of Statistics: Canberra, Australia, 2019; 44p. [Google Scholar]
- Choudhury, D.; Mehrotra, R.; Sharma, A.; Gupta, A.; Sivakumar, B. Effectiveness of CMIP5 Decadal Experiments for Interannual Rainfall Prediction Over Australia. Water Resour. Res. 2019, 55, 7400–7418. [Google Scholar] [CrossRef]
- Deo, R.C.; Şahin, M. Application of the Artificial Neural Network model for prediction of monthly Standardized Precipitation and Evapotranspiration Index using hydrometeorological parameters and climate indices in eastern Australia. Atmos. Res. 2015, 161, 65–81. [Google Scholar] [CrossRef]
- Bagirov, A.M.; Mahmood, A.; Barton, A. Prediction of monthly rainfall in Victoria, Australia: Clusterwise linear regression approach. Atmos. Res. 2017, 188, 20–29. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteor. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Lau, K.M.; Weng, H. Climate Signal Detection Using Wavelet Transform: How to Make a Time Series Sing. Bull. Am. Meteor. Soc. 1995, 76, 2391–2402. [Google Scholar] [CrossRef]
- Hartigan, J.; MacNamara, S.; Leslie, L. Application of Machine Learning to Attribution and Prediction of Seasonal Precipitation and Temperature Trends in Canberra, Australia. Climate 2020, 8, 76. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Cai, W.; Cowan, T. Dynamics of late autumn rainfall reduction over southeastern Australia. Geophys. Res. Lett. 2008, 35, L09708. [Google Scholar] [CrossRef]
- Cai, W.; Cowan, T.; Briggs, P.; Raupach, M. Rising temperature depletes soil moisture and exacerbates severe drought conditions across southeast Australia. Geophys. Res. Lett. 2009, L21709. [Google Scholar] [CrossRef]
- Kirono, D.; Chiew, F.; Kent, D. Identification of best predictors for forecasting seasonal rainfall and runoff in Australia. Hydrol. Process. 2010, 24, 1237–1247. [Google Scholar] [CrossRef]
- Maldonado, S.; Weber, R. A wrapper method for feature selection using Support Vector Machines. Inf. Sci. 2009, 179, 2208–2217. [Google Scholar] [CrossRef]
- Hsu, C.-W.; Chang, C.-C.; Lin, C.-J. A Practical Guide to Support Vector Classification; Technical Report; National Taiwan University: Taipei, Taiwan, 2003; p. 16. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: San Diego, CA, USA, 2011; Volume 100. [Google Scholar]
- Trenberth, K. Changes in precipitation with climate change. Clim. Res. 2011, 47, 123–138. [Google Scholar] [CrossRef]
- Trenberth, K.; Dai, A.; van der Schrier, G.; Jones, P.; Barichivich, J.; Briffa, K.; Sheffield, J. Global warming and changes in drought. Nat. Clim. Chang. 2014, 4, 17–22. [Google Scholar] [CrossRef]
- Adler, R.; Gu, G.; Sapiano, M.; Wang, J.J.; Huffman, G. Global Precipitation: Means, Variations and Trends During the Satellite Era (1979–2014). Surv. Geophys. 2017, 38, 679–699. [Google Scholar] [CrossRef]
- Stocker, T.; Qin, D.; Plattner, G.K.; Tignor, M.; Allen, S.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- McBride, J.L.; Nicholls, N. Seasonal Relationships between Australian Rainfall and the Southern Oscillation. Mon. Weather Rev. 1983, 111, 1998–2004. [Google Scholar] [CrossRef]
- Kucharski, F.; Kang, I.S.; Farneti, R.; Feudale, L. Tropical Pacific response to 20th century Atlantic warming. Geophys. Res. Lett. 2011, 38, 5. [Google Scholar] [CrossRef]
- Kucharski, F.; Ikram, F.; Molteni, F.; Farneti, R.; Kang, I.S.; No, H.H.; King, M.; Giuliani, G.; Mogensen, K. Atlantic forcing of Pacific decadal variability. Clim. Dyn. 2016, 46, 2337–2351. [Google Scholar] [CrossRef]
- Johnson, Z.; Chikamoto, Y.; Luo, J.J.; Mochizuki, T. Ocean Impacts on Australian Interannual to Decadal Precipitation Variability. Climate 2018, 6, 61. [Google Scholar] [CrossRef]
- Bureau of Meteorology. Climate Glossary. 2012. Available online: http://www.bom.gov.au/climate/glossary/elnino.shtml (accessed on 1 August 2020).
- Ummenhofer, C.; Gupta, A.; Briggs, P.; England, M.; McIntosh, P.; Meyers, G.; Pook, M.; Raupach, M.; Risbey, J. Indian and Pacific Ocean Influences on Southeast Australian Drought and Soil Moisture. J. Clim. 2011, 24, 1313–1336. [Google Scholar] [CrossRef]
- Risbey, J.S.; Pook, M.J.; McIntosh, P.C.; Wheeler, M.C.; Hendon, H.H. On the Remote Drivers of Rainfall Variability in Australia. Mon. Weather Rev. 2009, 137, 3233–3253. [Google Scholar] [CrossRef]
- Ummenhofer, C.C.; England, M.H.; McIntosh, P.C.; Meyers, G.A.; Pook, M.J.; Risbey, J.S.; Gupta, A.S.; Taschetto, A.S. What causes southeast Australia’s worst droughts? Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Hansen, J.; Ruedy, R.; Sato, M.; Lo, K. Global Surface Temperature Change. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Power, S.; Casey, T.; Folland, C.; Colman, A.; Mehta, V. Inter-decadal modulation of the impact of ENSO on Australia. Clim. Dyn. 1999, 15, 319–324. [Google Scholar] [CrossRef]
- Verdon, D.; Wyatt, A.; Kiem, A.; Franks, S. Multidecadal variability of rainfall and streamflow: Eastern Australia. Water Resour. Res. 2004, 40, W10201. [Google Scholar] [CrossRef]
- Kiem, A.; Franks, S. Multi-decadal variability of drought risk, eastern Australia. Hydrol. Process. 2004, 18, 2039–2050. [Google Scholar] [CrossRef]
- Folland, C.; Renwick, J.; Salinger, M.; Mullan, A. Relative influences of the Interecadal Pacific Oscillation and ENSO on the South Pacific Convergence Zone. Geophys. Res. Lett. 2002, 29, 21–1–21–4. [Google Scholar] [CrossRef]
- Hall, M.A. Correlation-Based Feature Selection for Machine Learning. Ph.D. Thesis, University of Waikato, Hamilton, New Zealand, 1999. [Google Scholar]
- Prasad, R.; Deo, R.C.; Li, Y.; Maraseni, T. Input selection and performance optimization of ANN-based streamflow forecasts in the drought-prone Murray Darling Basin region using IIS and MODWT algorithm. Atmos. Res. 2017, 197, 42–63. [Google Scholar] [CrossRef]
- Benoit, L.; Vrac, M.; Mariethoz, G. Nonstationary stochastic rain type generation: Accounting for climate drivers. Hydrol. Earth Syst. Sci. 2020, 24, 2841–2854. [Google Scholar] [CrossRef]
- Hartigan, J. Precipitation and Temperature Data for the Sydney Catchment Area, Australia. 2020. Available online: https://doi.org/10.5281/zenodo.4037473 (accessed on 19 September 2020).

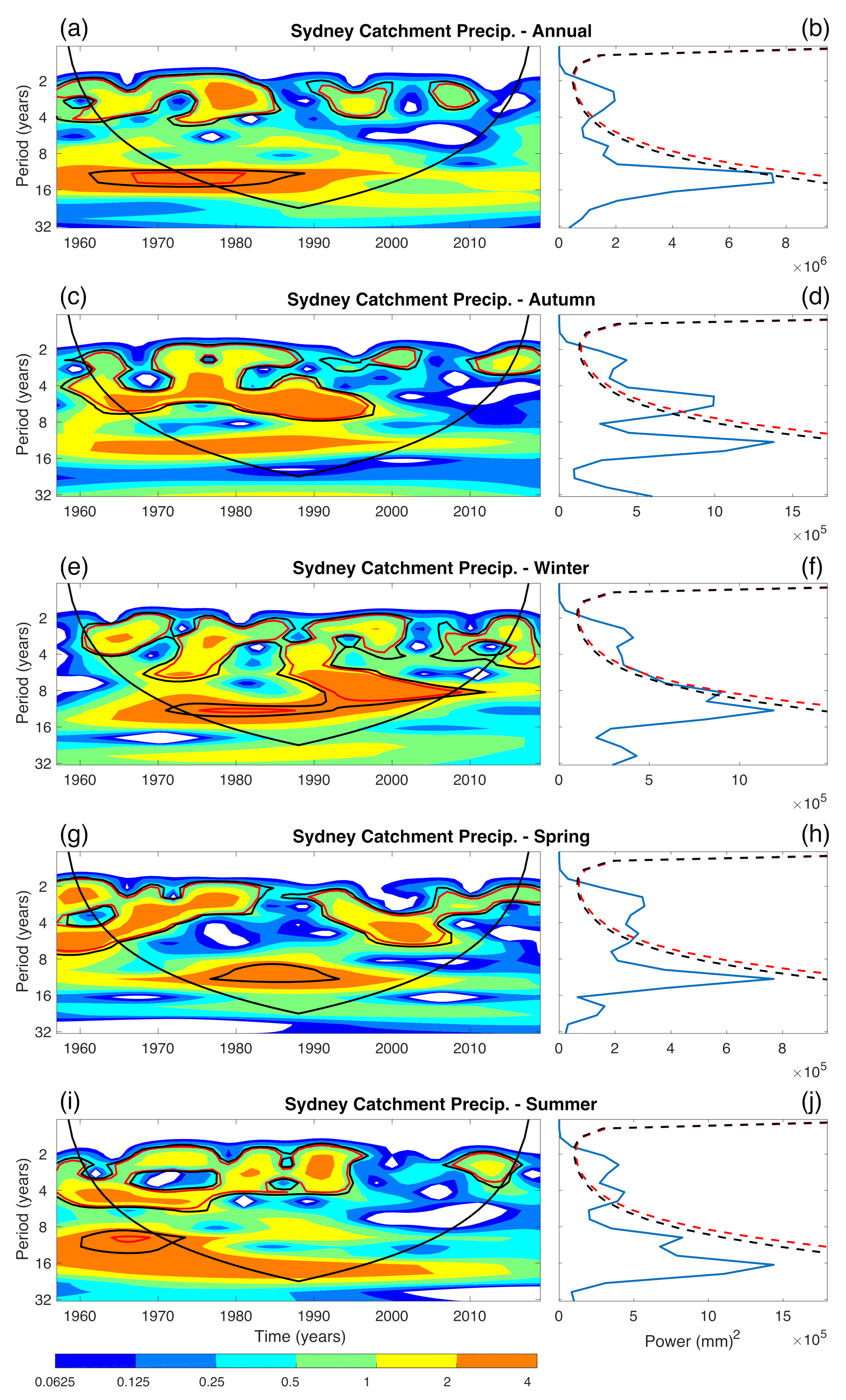
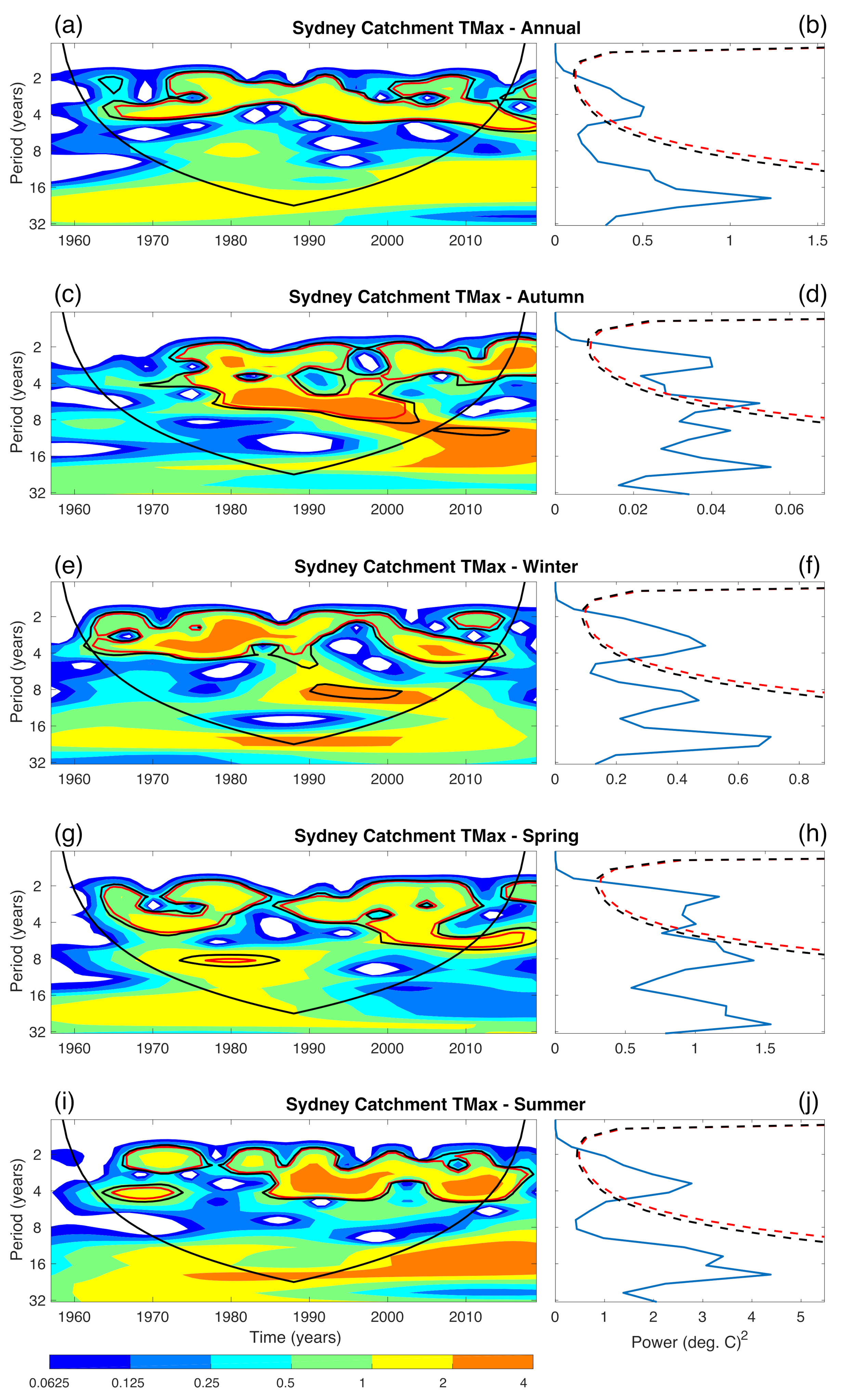
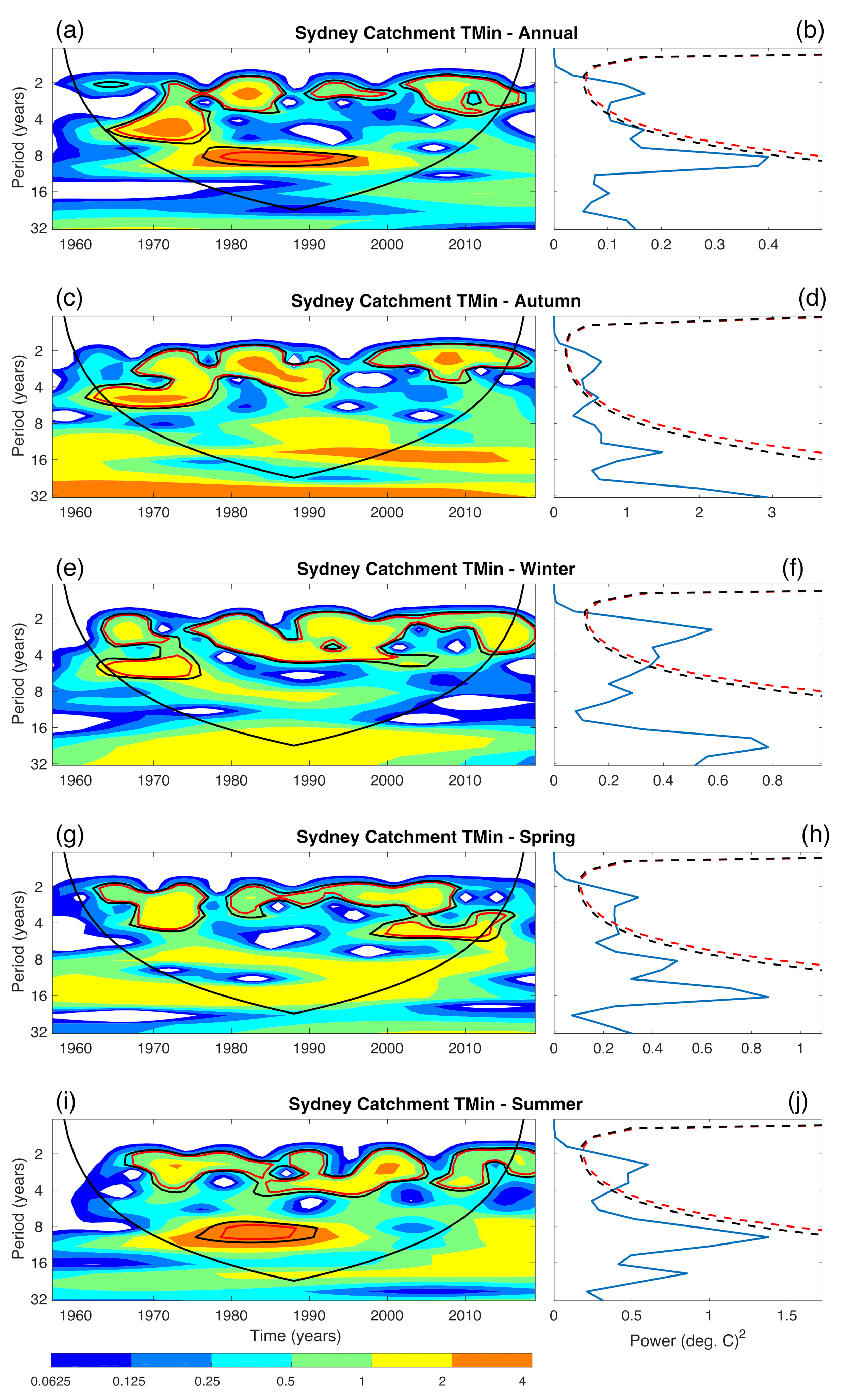
| Attribute | LR | SVR (RBF) | SVR (Poly) | RF | Attribute | LR | SVR (RBF) | SVR (Poly) | RF |
|---|---|---|---|---|---|---|---|---|---|
| AMO | 30 | 100 | 80 | 40 | DMI*TSSST | 90 | 80 | 60 | 20 |
| DMI | 0 | 70 | 80 | 30 | GlobalSSTA*GlobalT | 0 | 60 | 80 | 10 |
| GlobalSSTA | 0 | 80 | 80 | 30 | GlobalSSTA*Niño3.4 | 10 | 60 | 80 | 40 |
| GlobalT | 80 | 40 | 90 | 20 | GlobalSSTA*TPI | 20 | 60 | 80 | 40 |
| Niño3.4 | 60 | 30 | 90 | 20 | GlobalSSTA*SAM | 0 | 90 | 70 | 30 |
| TPI | 10 | 60 | 80 | 30 | GlobalSSTA*SOI | 10 | 60 | 90 | 30 |
| SAM | 20 | 80 | 90 | 20 | GlobalSSTA*TSSST | 0 | 70 | 60 | 30 |
| SOI | 60 | 60 | 80 | 40 | GlobalT*Niño3.4 | 30 | 40 | 90 | 30 |
| TSSST | 10 | 30 | 90 | 10 | GlobalT*TPI | 0 | 60 | 90 | 20 |
| AMO*DMI | 60 | 80 | 70 | 40 | GlobalT*SAM | 0 | 100 | 80 | 50 |
| AMO*GlobalSSTA | 10 | 90 | 80 | 40 | GlobalT*SOI | 10 | 50 | 80 | 30 |
| AMO*GlobalT | 10 | 80 | 70 | 40 | GlobalT*TSSST | 10 | 70 | 50 | 50 |
| AMO*Niño3.4 | 20 | 50 | 70 | 30 | Niño3.4*TPI | 0 | 40 | 70 | 30 |
| AMO*TPI | 0 | 70 | 50 | 30 | Niño3.4*SAM | 40 | 80 | 70 | 30 |
| AMO*SAM | 30 | 80 | 90 | 40 | Niño3.4*SOI | 0 | 40 | 60 | 30 |
| AMO*SOI | 10 | 80 | 90 | 30 | Niño3.4*TSSST | 0 | 40 | 70 | 30 |
| AMO*TSSST | 0 | 50 | 60 | 20 | TPI*SAM | 30 | 70 | 80 | 30 |
| DMI*GlobalSSTA | 10 | 10 | 80 | 70 | TPI*SOI | 10 | 50 | 70 | 30 |
| DMI*GlobalT | 10 | 30 | 80 | 50 | TPI*TSSST | 40 | 50 | 70 | 20 |
| DMI*Niño3.4 | 50 | 40 | 90 | 40 | SAM*SOI | 0 | 80 | 60 | 40 |
| DMI*TPI | 40 | 60 | 70 | 40 | SAM*TSSST | 20 | 100 | 90 | 50 |
| DMI*SAM | 30 | 80 | 80 | 30 | SOI*TSSST | 10 | 40 | 60 | 40 |
| DMI*SOI | 20 | 70 | 80 | 60 |
| Years | Precipitation | TMax | TMin |
|---|---|---|---|
| Annual | |||
| Mean | 0.0258 | 0.0036 | 0.0000 |
| Variance | 0.0280 | 0.2570 | 0.2300 |
| Autumn | |||
| Mean | 0.0778 | 0.3600 | 0.2470 |
| Variance | 0.2180 | 0.0914 | 0.8190 |
| Winter | |||
| Mean | 0.6850 | 0.0226 | 0.0004 |
| Variance | 0.8430 | 0.9290 | 0.7860 |
| Spring | |||
| Mean | 0.0228 | 0.0070 | 0.0002 |
| Variance | 0.0802 | 0.5840 | 0.2680 |
| Summer | |||
| Mean | 0.6390 | 0.0440 | 0.0000 |
| Variance | 0.0438 | 0.0408 | 0.3980 |
| Model | LR | SVR (RBF) | SVR (Poly) | RF |
|---|---|---|---|---|
| RMSE (mm) | 764.971 | 651.478 | 613.704 | 780.455 |
| Skill | 0.567 | 0.686 | 0.721 | 0.550 |
| Correlation | 0.815 | 0.761 | 0.921 | 0.622 |
| R | 0.663 | 0.579 | 0.848 | 0.387 |
| Residuals Mean (mm) | 258.617 | −22.463 | 310.671 | 98.182 |
| Residuals SD (mm) | 763.600 | 690.585 | 561.365 | 821.221 |
| Residuals Skewness | 1.365 | 0.084 | 0.566 | 0.283 |
| Residuals Kurtosis | 0.705 | −1.314 | −1.158 | −1.729 |
| Model | LR | SVR (RBF) | SVR (Poly) | RF |
|---|---|---|---|---|
| RMSE (mm) | 418.036 | 597.255 | 515.242 | 621.334 |
| Skill | 0.445 | −0.133 | 0.157 | −0.226 |
| Correlation | 0.679 | 0.116 | 0.493 | 0.094 |
| R | 0.461 | 0.013 | 0.243 | 0.009 |
| Residuals Mean (mm) | 118.211 | 138.001 | 162.255 | −112.422 |
| Residuals SD (mm) | 425.297 | 616.342 | 518.692 | 648.147 |
| Residuals Skewness | −0.545 | −0.360 | −0.044 | 0.469 |
| Residuals Kurtosis | −0.856 | −0.864 | −1.148 | −1.414 |
| Model | LR | SVR (RBF) | SVR (Poly) | RF |
|---|---|---|---|---|
| RMSE (mm) | 533.319 | 502.886 | 439.781 | 522.228 |
| Skill | 0.179 | 0.270 | 0.442 | 0.213 |
| Correlation | 0.514 | 0.521 | 0.703 | 0.461 |
| R | 0.264 | 0.272 | 0.494 | 0.212 |
| Residuals Mean (mm) | −147.827 | 58.190 | 145.452 | 67.985 |
| Residuals SD (mm) | 543.506 | 529.808 | 440.207 | 549.193 |
| Residuals Skewness | 0.585 | −0.217 | −0.205 | 1.009 |
| Residuals Kurtosis | −0.745 | −1.356 | −1.202 | −0.444 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hartigan, J.; MacNamara, S.; Leslie, L.M.; Speer, M. Attribution and Prediction of Precipitation and Temperature Trends within the Sydney Catchment Using Machine Learning. Climate 2020, 8, 120. https://doi.org/10.3390/cli8100120
Hartigan J, MacNamara S, Leslie LM, Speer M. Attribution and Prediction of Precipitation and Temperature Trends within the Sydney Catchment Using Machine Learning. Climate. 2020; 8(10):120. https://doi.org/10.3390/cli8100120
Chicago/Turabian StyleHartigan, Joshua, Shev MacNamara, Lance M. Leslie, and Milton Speer. 2020. "Attribution and Prediction of Precipitation and Temperature Trends within the Sydney Catchment Using Machine Learning" Climate 8, no. 10: 120. https://doi.org/10.3390/cli8100120
APA StyleHartigan, J., MacNamara, S., Leslie, L. M., & Speer, M. (2020). Attribution and Prediction of Precipitation and Temperature Trends within the Sydney Catchment Using Machine Learning. Climate, 8(10), 120. https://doi.org/10.3390/cli8100120






