Performance Evaluation of Satellite-Based Rainfall Products over Nigeria
Abstract
1. Introduction
2. Materials and Methods
2.1. Rainfall Data Description
2.1.1. Gauge Rainfall
2.1.2. Satellite Rainfall
2.2. Quality Control
2.3. Methodology
3. Results and Discussions
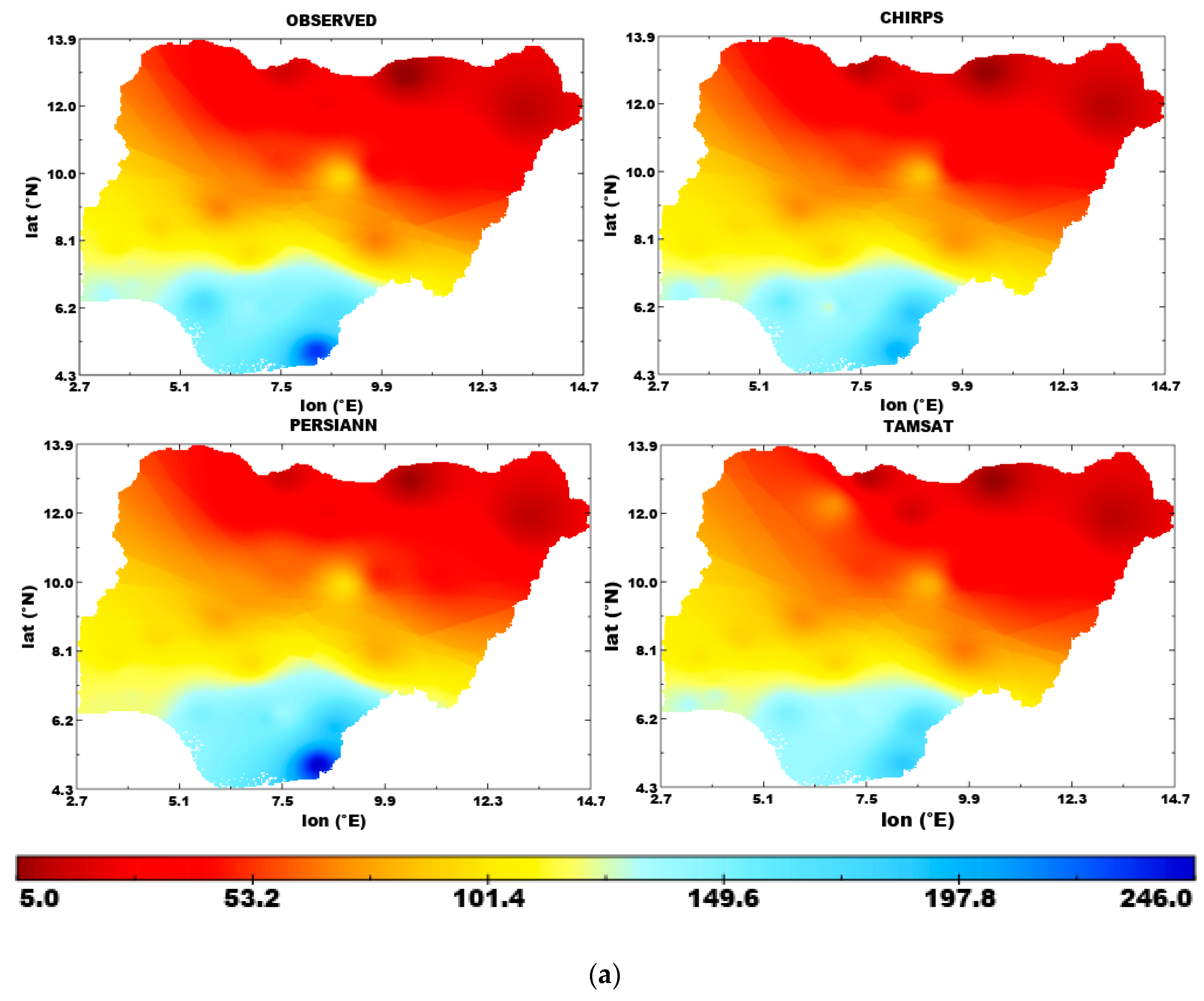
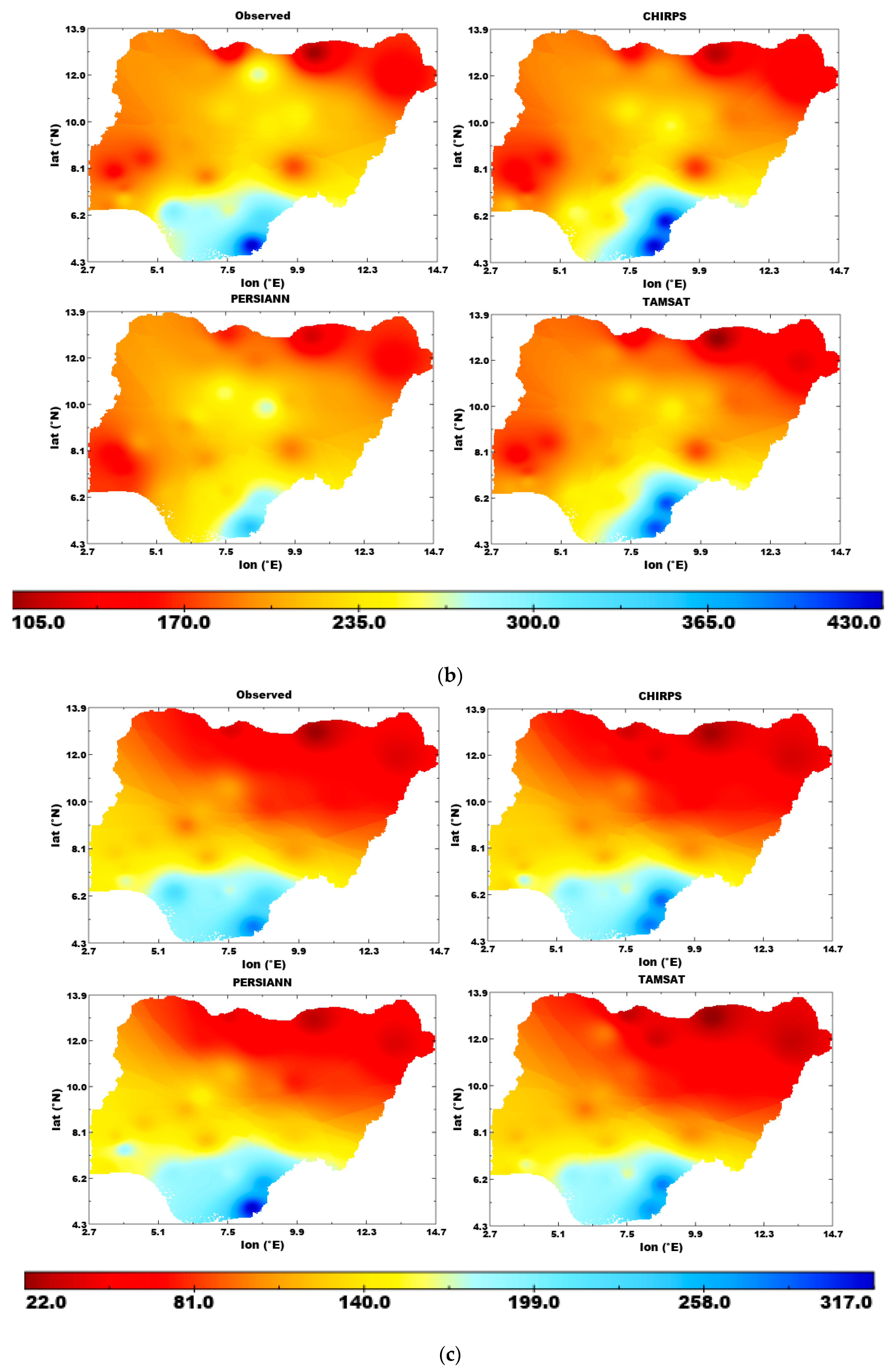
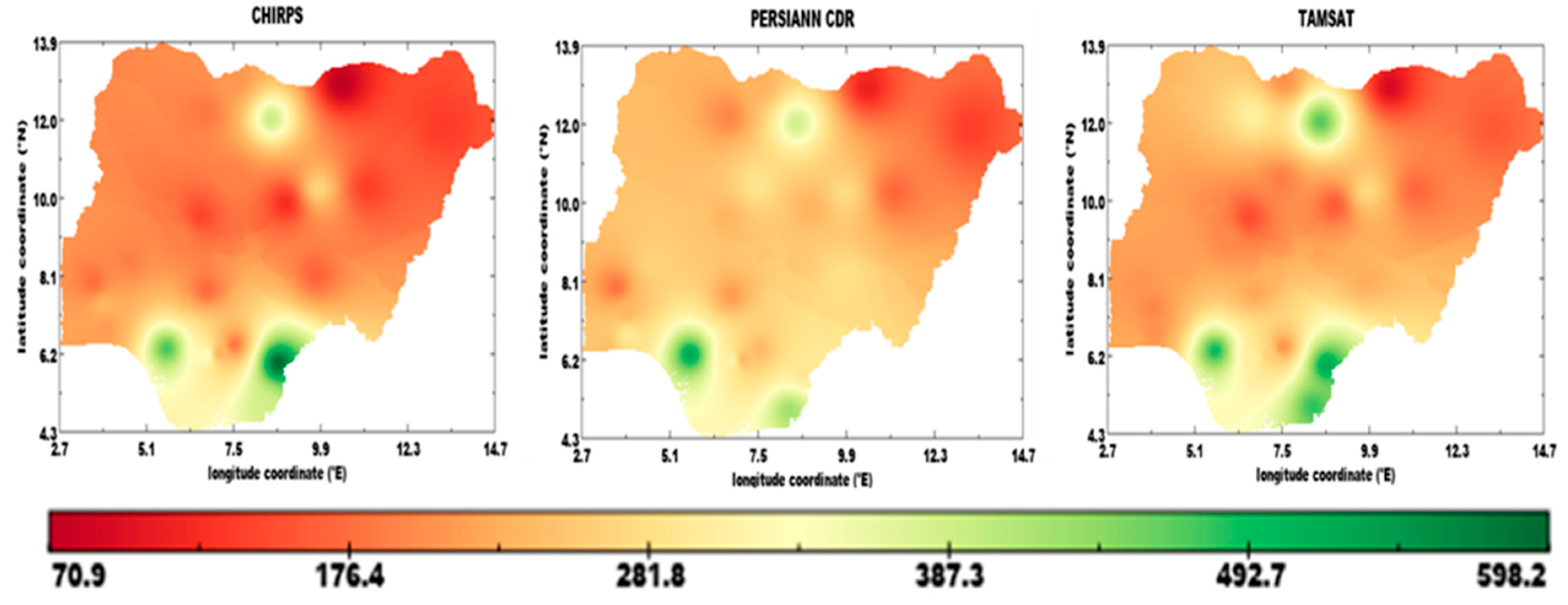
3.1. Seasonal Climatology
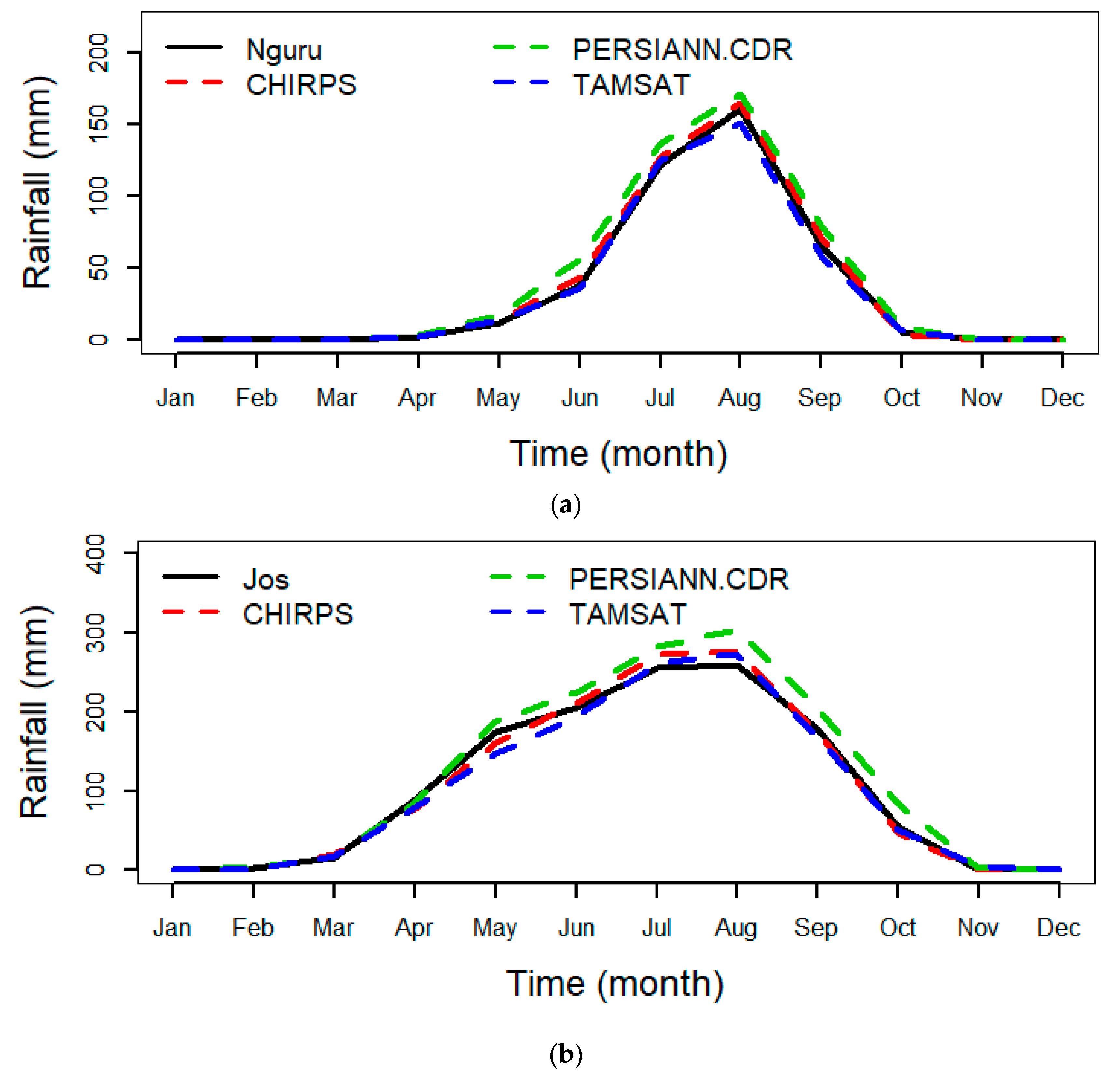
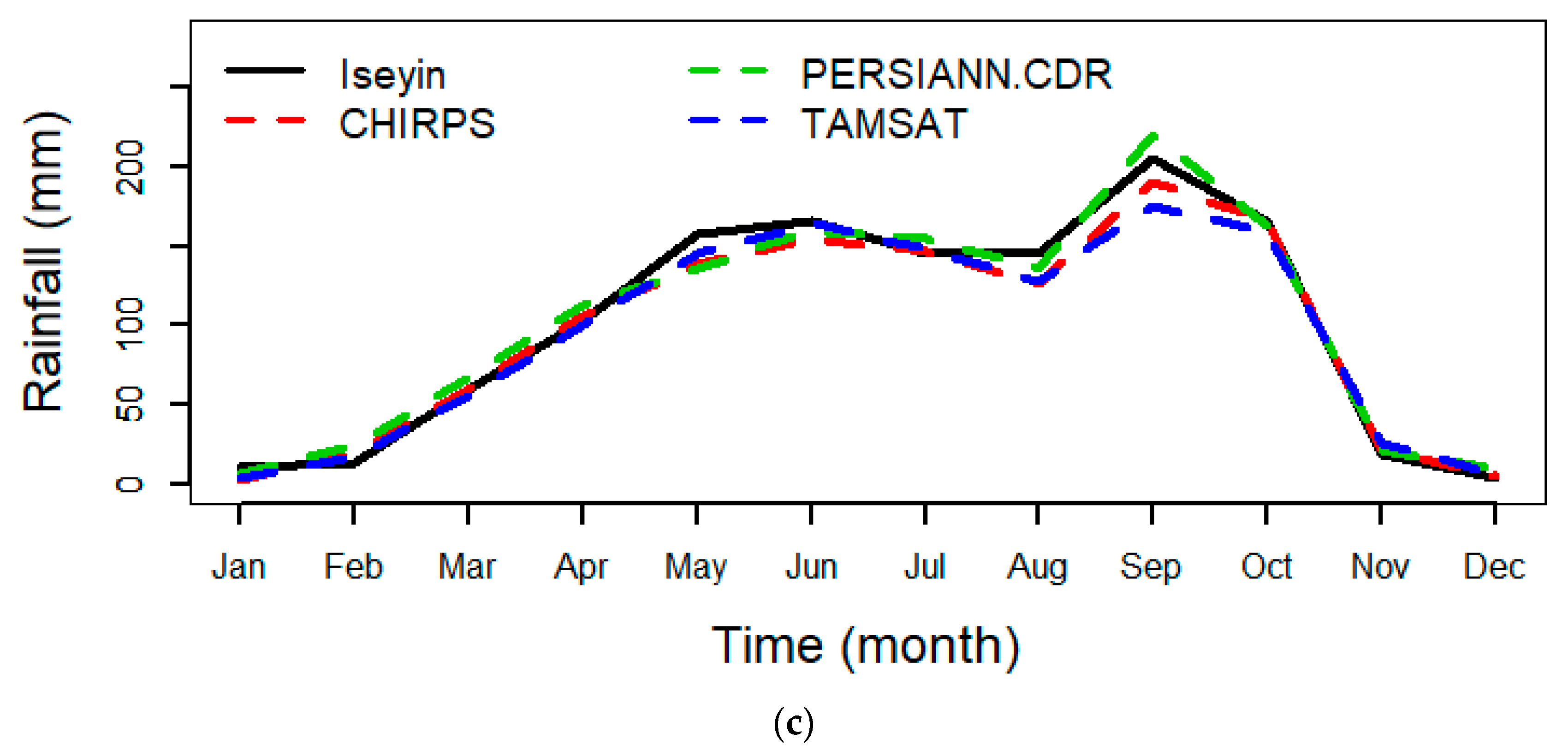
3.2. Annual Cycle of Mean Monthly Rainfall
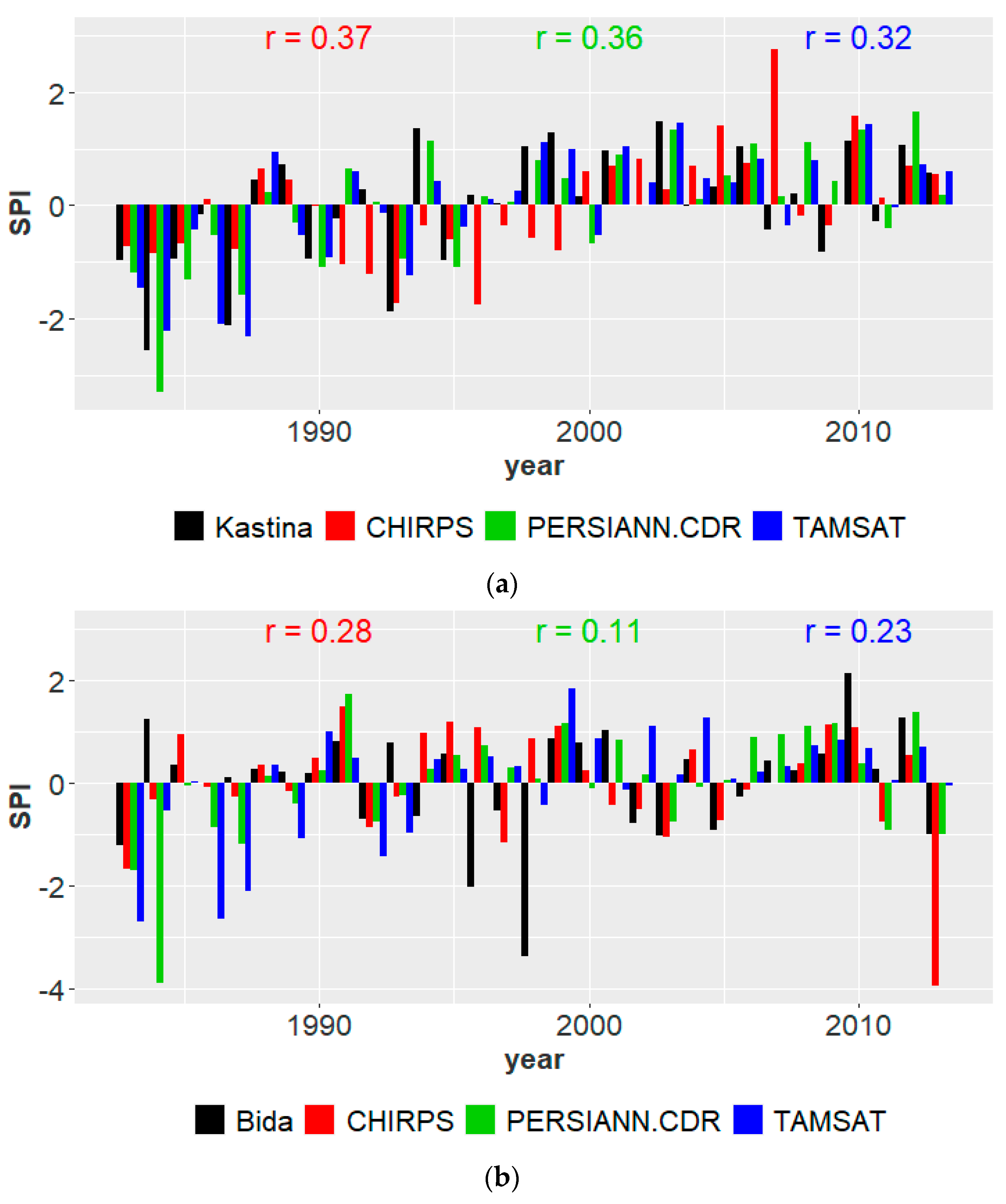
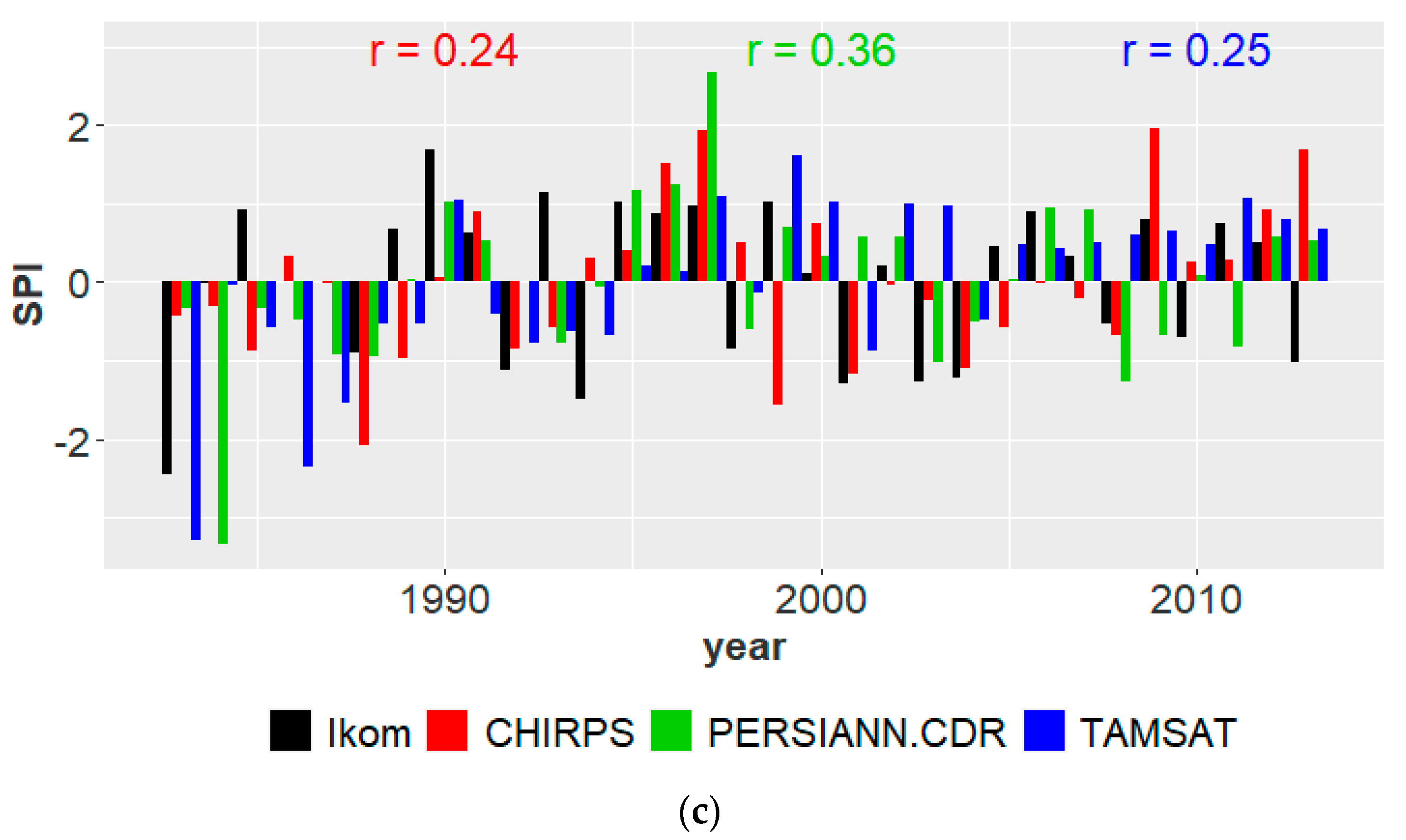
3.3. Inter-Annual Rainfall Anomaly
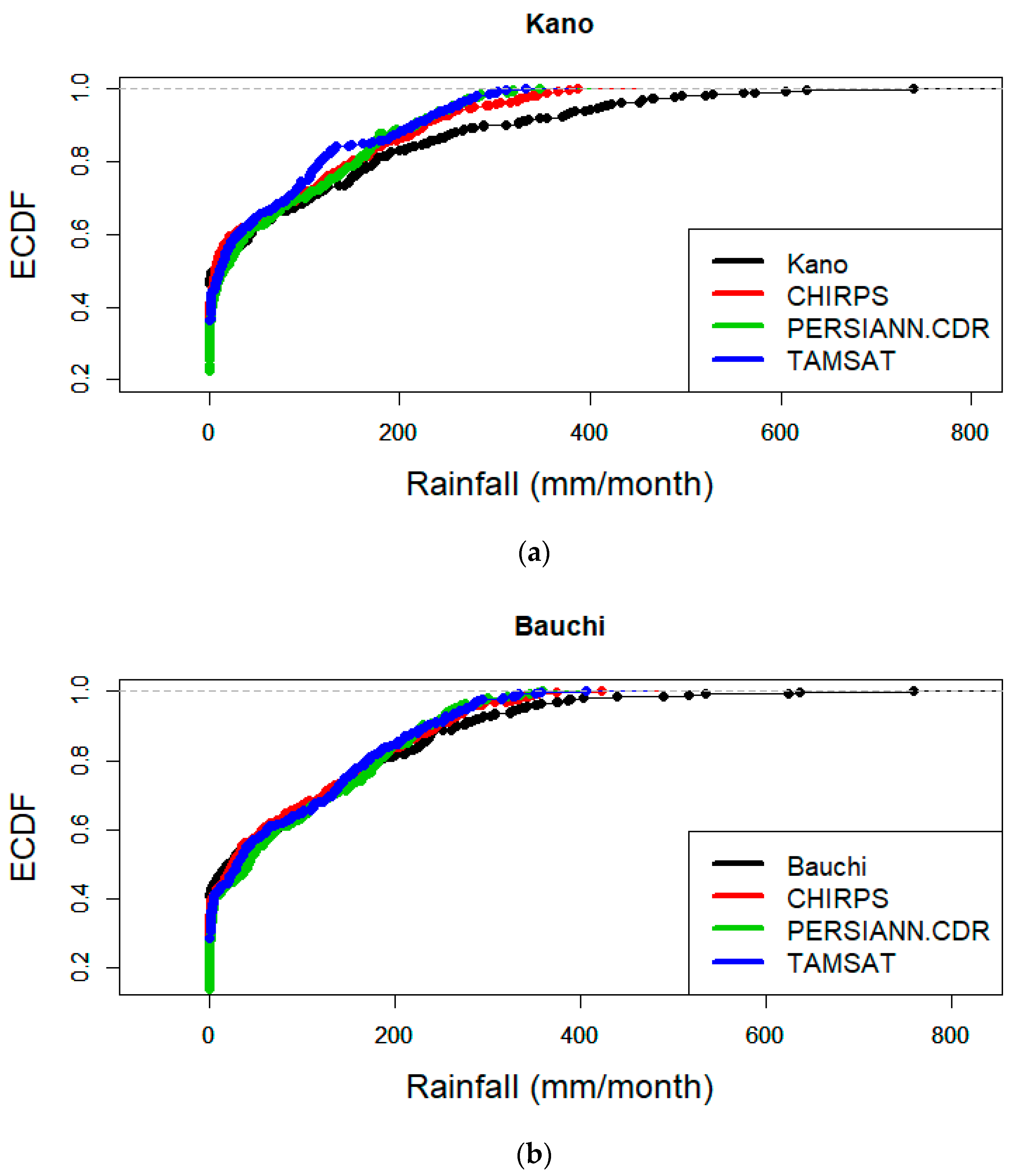
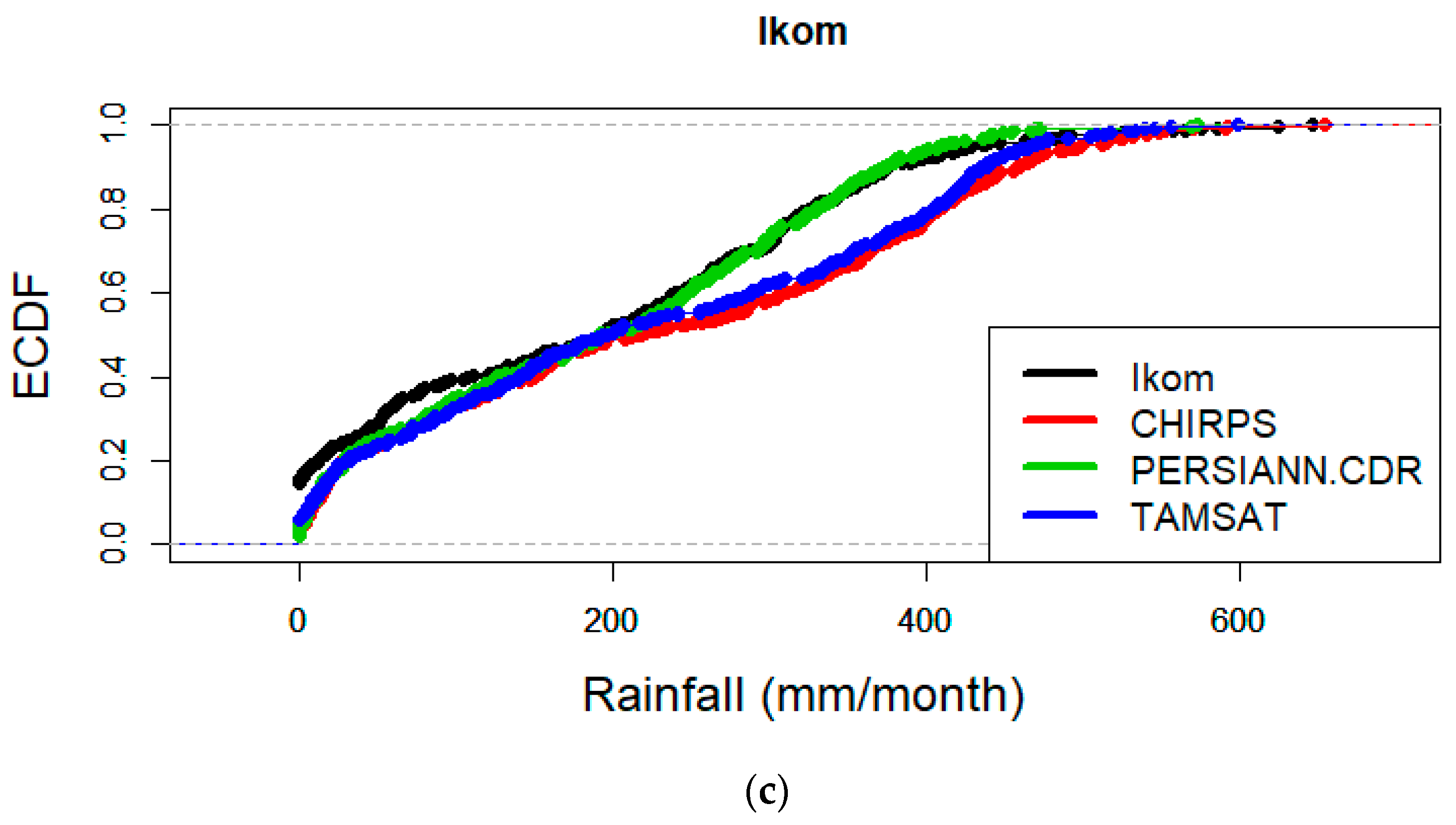
3.4. Empirical Cumulative Distribution Frequency
3.5. Trend Analysis
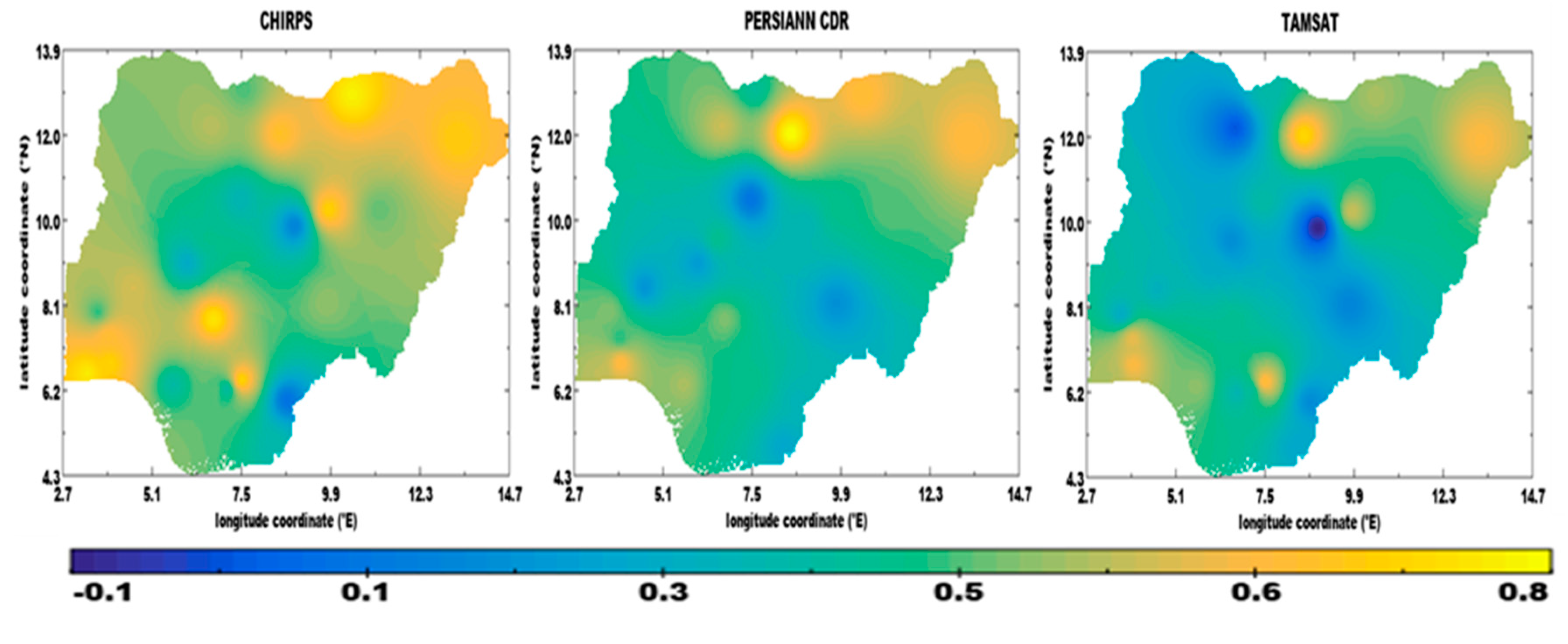
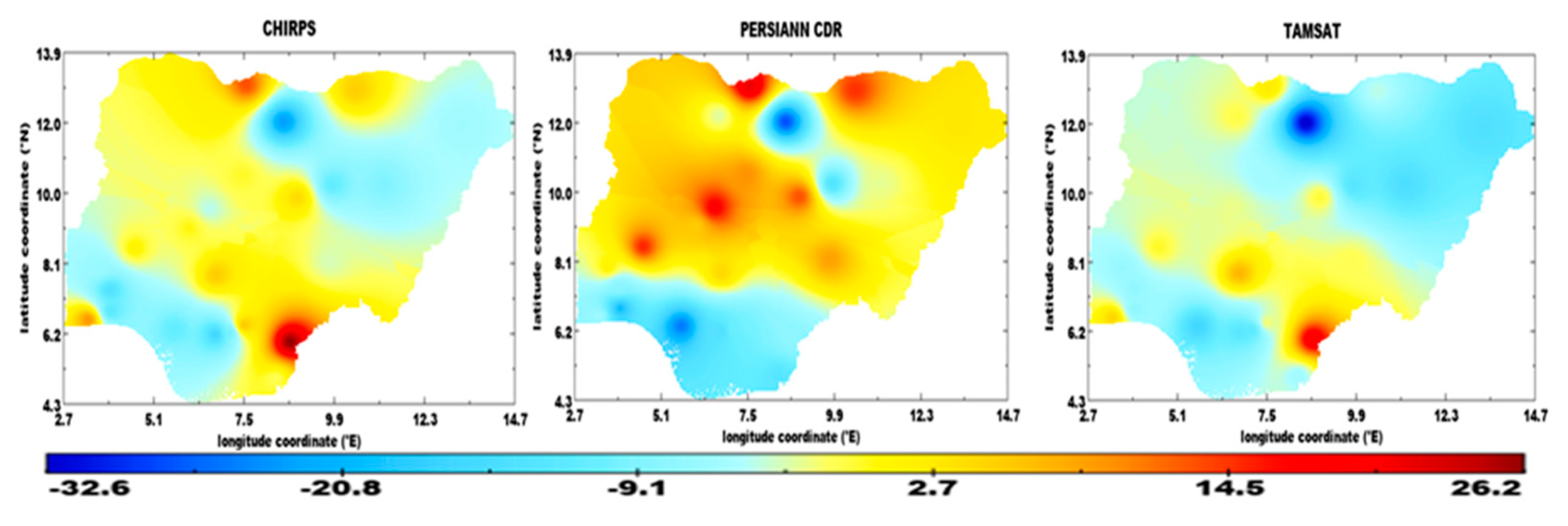
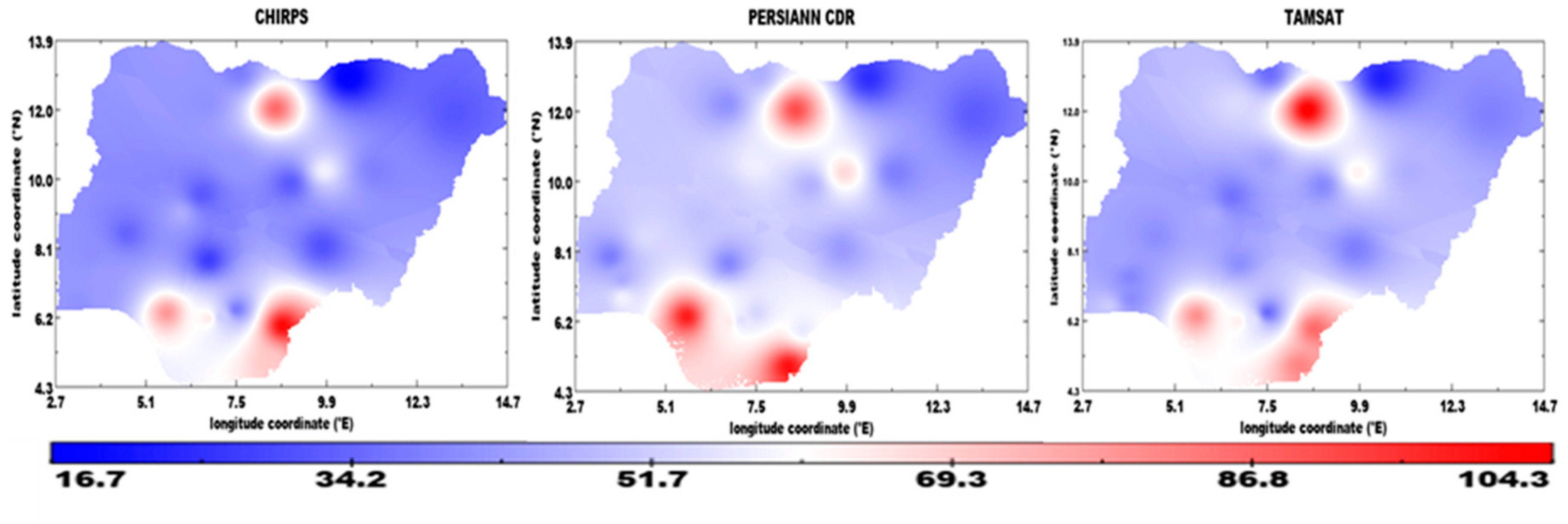
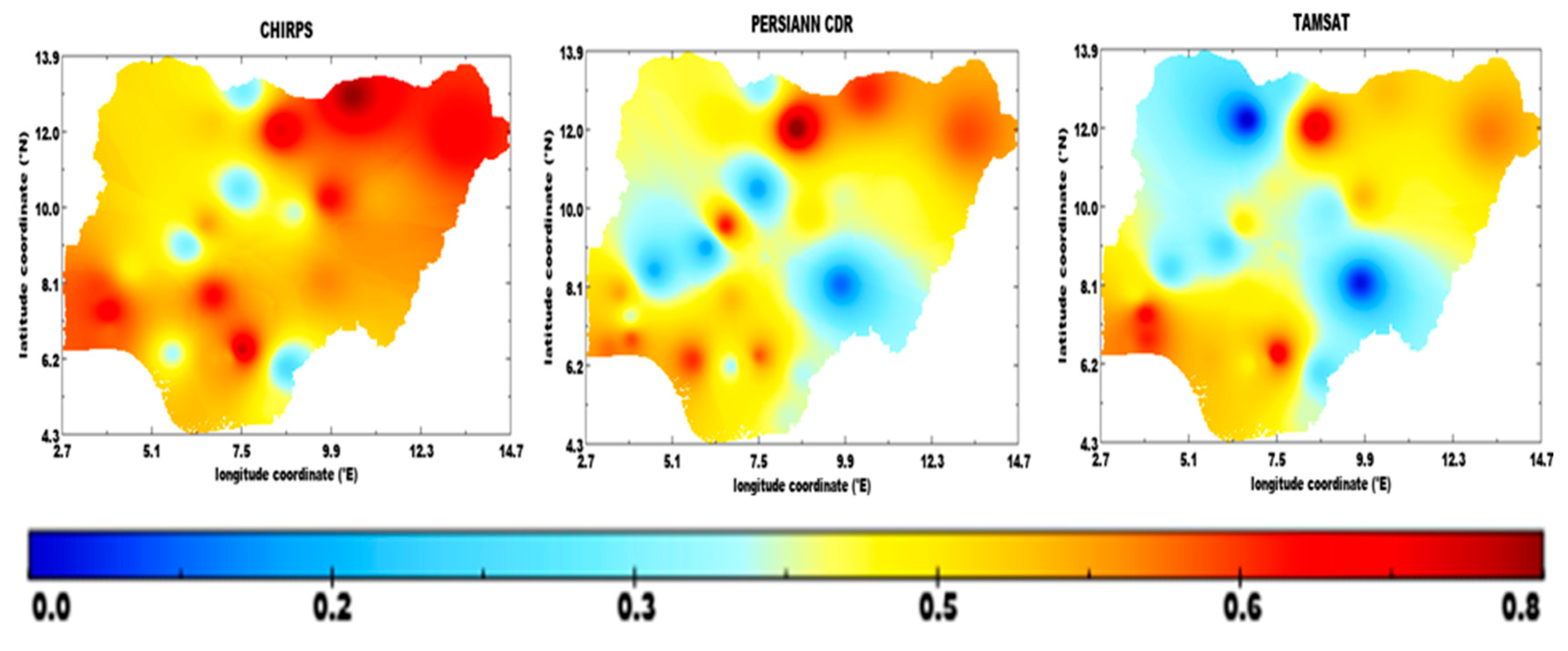
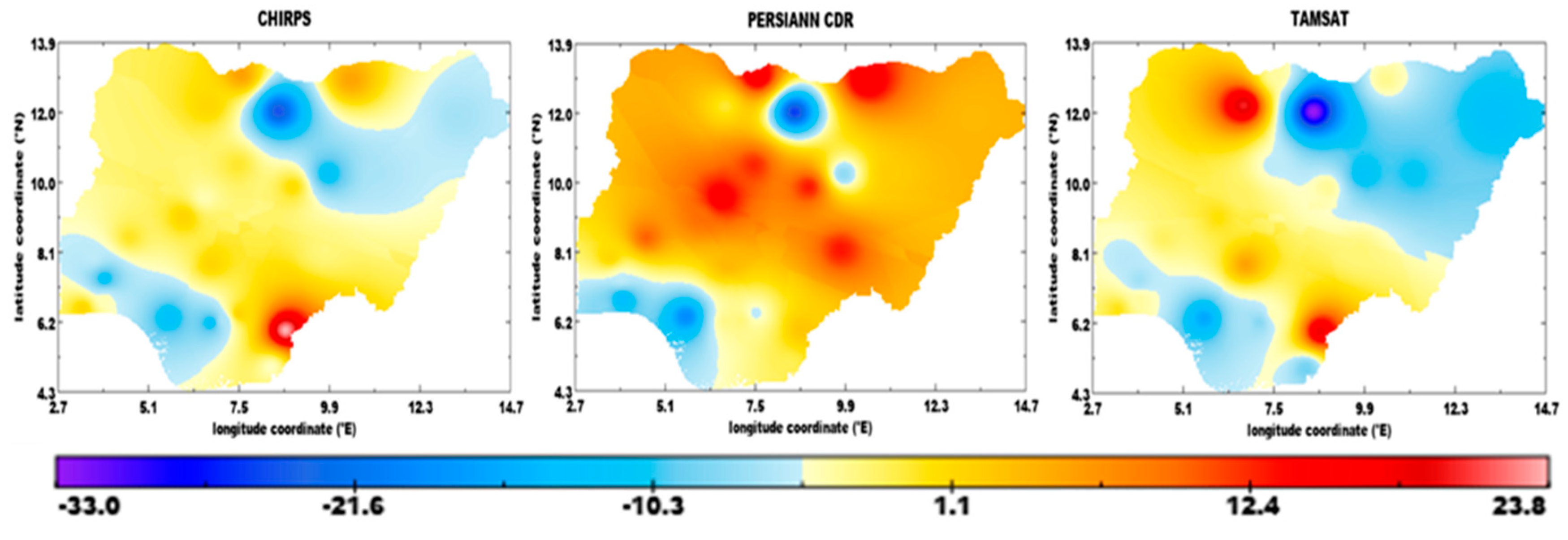
3.6. Evaluation of Satellite Rainfall Products
3.6.1. Inter-Annual Variation of Mean Seasonal Rainfall
3.6.2. Inter-Annual Variation of Mean Annual Rainfall
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dembélé, M.; Zwart, S.J. Evaluation and comparison of satellite-based rainfall products in Burkina Faso, West Africa. Int. J. Remote Sens. 2016, 37, 3995–4014. [Google Scholar] [CrossRef]
- Fall, C.M.N.; Lavaysse, C.; Drame, M.S.; Panthou, G.; Gaye, A.T. Wet and dry spells in Senegal: Evaluation of satellite-based and model re-analysis rainfall estimates. Nat. Hazards Earth Syst. Sci. Discuss. 2019, 1–29. [Google Scholar] [CrossRef]
- Pellarin, T.; Román-Cascón, C.; Baron, C.; Bindlish, R.; Brocca, L.; Camberlin, P.; Fernández-Prieto, D.; Kerr, Y.H.; Massari, C.; Panthou, G.; et al. The Precipitation Inferred from Soil Moisture (PrISM) Near Real-Time Rainfall Product: Evaluation and Comparison. Remote Sens. 2020, 12, 481. [Google Scholar] [CrossRef]
- Usman, M.; Nichol, J.E.; Ibrahim, A.T.; Buba, L.F. A spatio-temporal analysis of trends in rainfall from long term satellite rainfall products in the Sudano Sahelian zone of Nigeria. Agric. For. Meteorol. 2018, 260–261, 273–286. [Google Scholar] [CrossRef]
- Gebrechorkos, S.H.; Hülsmann, S.; Bernhofer, C. Evaluation of multiple climate data sources for managing environmental resources in East Africa. Hydrol. Earth Syst. Sci. 2018, 22, 4547–4564. [Google Scholar] [CrossRef]
- Le Coz, C.; Van De Giesen, N. Comparison of rainfall products over sub-saharan africa. J. Hydrometeorol. 2020, 21, 553–596. [Google Scholar] [CrossRef]
- Akinyemi, D.F.; Ayanlade, O.S.; Nwaezeigwe, J.O.; Ayanlade, A. A Comparison of the Accuracy of Multi-satellite Precipitation Estimation and Ground Meteorological Records Over Southwestern Nigeria. Remote Sens. Earth Syst. Sci. 2019, 1–12. [Google Scholar] [CrossRef]
- Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T.; Gadain, H.; Ceccato, P. Validation of the CHIRPS satellite rainfall estimates over eastern Africa. Q. J. R. Meteorol. Soc. 2018, 144, 292–312. [Google Scholar] [CrossRef]
- Satgé, F.; Ruelland, D.; Bonnet, M.-P.; Molina, J.; Pillco, R. Consistency of satellite-based precipitation products in space and over time compared with gauge observations and snow- hydrological modelling in the Lake Titicaca region. Hydrol. Earth Syst. Sci. 2019, 23, 595–619. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 1–21. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Maidment, R.I.; Grimes, D.; Allan, R.P.; Tarnavsky, E.; Stringer, M.; Hewison, T.; Roebeling, R.; Black, E. The 30 year TAMSAT African Rainfall Climatology And Time series (TARCAT) data set. J. Geophys. Res. Atmos. 2014, 119, 10619–10644. [Google Scholar] [CrossRef]
- Tarnavsky, E.; Grimes, D.; Maidment, R.; Black, E.; Allan, R.P.; Stringer, M.; Chadwick, R.; Kayitakire, F. Extension of the TAMSAT satellite-based rainfall monitoring over Africa and from 1983 to present. J. Appl. Meteorol. Climatol. 2014, 53, 2805–2822. [Google Scholar] [CrossRef]
- Ayehu, G.T.; Tadesse, T.; Gessesse, B.; Dinku, T. Validation of new satellite rainfall products over the Upper Blue Nile Basin, Ethiopia. Atmos. Meas. Tech. 2018, 11, 1921–1936. [Google Scholar] [CrossRef]
- Romilly, T.G.; Gebremichael, M. Evaluation of satellite rainfall estimates over Ethiopian river basins. Hydrol. Earth Syst. Sci. 2011, 15, 1505–1514. [Google Scholar] [CrossRef]
- Larbi, I.; Hountondji, F.C.C.; Annor, T.; Agyare, W.A.; Gathenya, J.M.; Amuzu, J. Spatio-temporal trend analysis of rainfall and temperature extremes in the Vea catchment, Ghana. Climate 2018, 6, 87. [Google Scholar] [CrossRef]
- Hassan, I.; Kalin, R.M.; White, C.J.; Aladejana, J.A. Evaluation of Daily Gridded Meteorological Datasets over the Niger Delta Region of Nigeria and Implication to Water Resources Management. Atmos. Clim. Sci. 2020, 10, 21–39. [Google Scholar] [CrossRef]
- Poméon, T.; Diekkrüger, B.; Springer, A.; Kusche, J.; Eicker, A. Multi-Objective Validation of SWAT for Sparsely-Gauged West African River Basins—A Remote Sensing Approach. Water 2018, 10, 451. [Google Scholar] [CrossRef]
- Oyerinde, G.T.; Fademi, I.O.; Denton, O.A. Modeling runoff with satellite-based rainfall estimates in the Niger basin. Cogent Food Agric. 2017, 3, 1363340. [Google Scholar] [CrossRef]
- Akande, A.; Costa, A.C.; Mateu, J.; Henriques, R. Geospatial Analysis of Extreme Weather Events in Nigeria (1985-2015) Using Self-Organizing Maps. Adv. Meteorol. 2017, 217, 8576150. [Google Scholar] [CrossRef]
- Ogungbenro, S.B.; Morakinyo, T.E. Rainfall distribution and change detection across climatic zones in Nigeria. Weather Clim. Extrem. 2014, 5–6, 1–6. [Google Scholar] [CrossRef]
- Abatan, A.A.; Abiodun, B.J.; Lawal, K.A.; Gutowski, W.J. Trends in extreme temperature over Nigeria from percentile-based threshold indices. Int. J. Climatol. 2016, 36, 2527–2540. [Google Scholar] [CrossRef]
- Gbode, I.E.; Adeyeri, O.E.; Menang, K.P.; Intsiful, J.D.K.; Ajayi, V.O.; Omotosho, J.A.; Akinsanola, A.A. Observed changes in climate extremes in Nigeria. Meteorol. Appl. 2019, 26, 642–654. [Google Scholar] [CrossRef]
- Poméon, T.; Jackisch, D.; Diekkrüger, B. Evaluating the performance of remotely sensed and reanalysed precipitation data over West Africa using HBV light. J. Hydrol. 2017, 547, 222–235. [Google Scholar] [CrossRef]
- Wang, X.L.; Chen, H.; Wu, Y.; Feng, Y.; Pu, Q. New techniques for the detection and adjustment of shifts in daily precipitation data series. J. Appl. Meteorol. Climatol. 2010, 49, 2416–2436. [Google Scholar] [CrossRef]
- Wang, X.L.; Feng, Y. RHtests_dlyPrcp User Manual; Climate Research Division, Atmospheric Science and Technology Directorate, Science and Technology Branch, Environment Canada: Toronto, ON, Canada, 2013; 17p. [Google Scholar]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference of Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Kendall, M. Rank Correlation Methods, 4th ed.; Charles Griffin: London, UK, 1975. [Google Scholar]
- Adeyeri, O.E.; Lawin, A.E.; Laux, P.; Ishola, K.A.; Ige, S.O. Analysis of climate extreme indices over the Komadugu-Yobe basin, Lake Chad region: Past and future occurrences. Weather Clim. Extrem. 2019, 23, 100194. [Google Scholar] [CrossRef]
- Okafor, G.C.; Ogbu, K.N. Assessment of the impact of climate change on the freshwater availability of Kaduna River basin, Nigeria. J. Water Land Dev. 2018, 38, 105–114. [Google Scholar] [CrossRef]
- Akinsanola, A.A.; Ajayi, V.O.; Adejare, A.T.; Adeyeri, O.E.; Gbode, I.E.; Ogunjobi, K.O.; Nikulin, G.; Abolude, A.T. Evaluation of rainfall simulations over West Africa in dynamically downscaled CMIP5 global circulation models. Theor. Appl. Climatol. 2018, 132, 437–450. [Google Scholar] [CrossRef]
- Pool, S.; Vis, M.; Seibert, J. Evaluating model performance: Towards a non-parametric variant of the Kling-Gupta efficiency. Hydrol. Sci. J. 2018, 63, 1941–1953. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical note: Inherent benchmark or not? Comparing Nash-Sutcliffe and Kling-Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Ayugi, B.; Tan, G.; Gnitou, G.T.; Ojara, M.; Ongoma, V. Historical evaluations and simulations of precipitation over East Africa from Rossby centre regional climate model. Atmos. Res. 2020, 232, 104705. [Google Scholar] [CrossRef]
- Hofstra, N.; Haylock, M.; New, M.; Jones, P.; Frei, C. Comparison of six methods for the interpolation of daily, European climate data. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Chen, T.; Ren, L.; Yuan, F.; Yang, X.; Jiang, S.; Tang, T.; Liu, Y.; Zhao, C.; Zhang, L. Comparison of spatial interpolation schemes for rainfall data and application in hydrological modeling. Water 2017, 9, 342. [Google Scholar] [CrossRef]
- Yang, X.; Xie, X.; Liu, D.L.; Ji, F.; Wang, L. Spatial Interpolation of Daily Rainfall Data for Local Climate Impact Assessment over Greater Sydney Region. Adv. Meteorol. 2015, 2015, 563629. [Google Scholar] [CrossRef]
- Adeniyi, M.O.; Dilau, K. Seasonal prediction of precipitation over Nigeria. J. Sci. Technol. 2015, 35, 102–113. [Google Scholar] [CrossRef][Green Version]
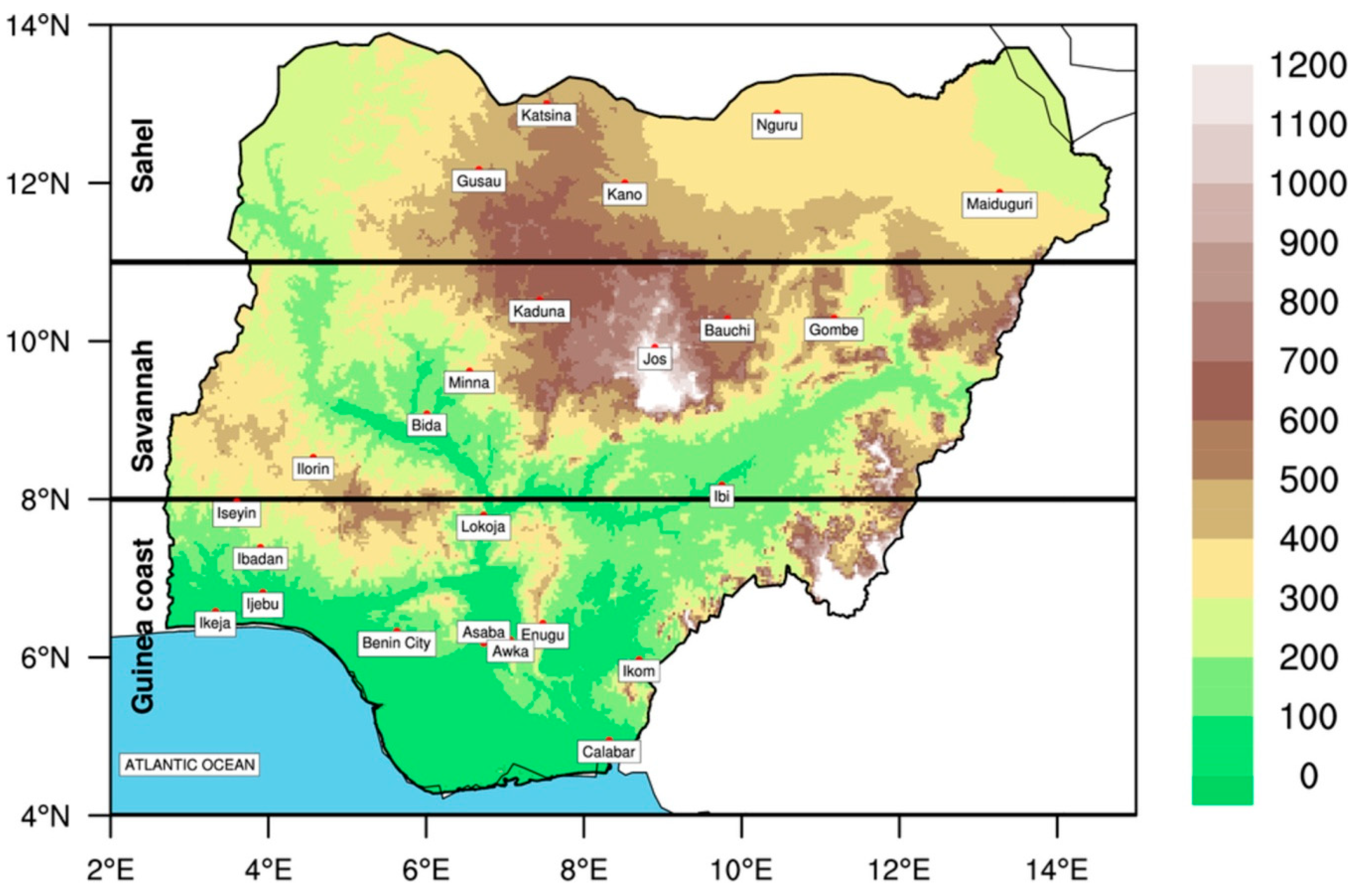
| Station | Region | Longitude (N) | Latitude (E) | Elevation (m) |
|---|---|---|---|---|
| Asaba | Guinea coast | 6.73 | 6.18 | 60 |
| Awka | 7.07 | 6.22 | 100 | |
| Benin | 5.63 | 6.33 | 80 | |
| Calabar | 8.32 | 4.95 | 80 | |
| Enugu | 7.48 | 6.43 | 300 | |
| Ibadan | 3.90 | 7.39 | 200 | |
| Ijebu | 3.93 | 6.82 | 60 | |
| Ikeja | 3.33 | 6.58 | 40 | |
| Ikom | 8.70 | 5.97 | 40 | |
| Iseyin | 3.60 | 7.97 | 300 | |
| Lokoja | 6.73 | 7.80 | 180 | |
| Bauchi | Savannah | 9.82 | 10.28 | 600 |
| Bida | 6.01 | 9.08 | 140 | |
| Gombe | 11.17 | 10.29 | 440 | |
| Ibi | 9.75 | 8.18 | 120 | |
| Ilorin | 4.57 | 8.53 | 280 | |
| Jos | 8.90 | 9.92 | 1160 | |
| Kaduna | 7.44 | 10.52 | 580 | |
| Minna | 6.55 | 9.62 | 280 | |
| Gusau | Sahel | 6.67 | 12.17 | 420 |
| Kano | 8.52 | 12.00 | 460 | |
| Katsina | 7.53 | 13.00 | 440 | |
| Maiduguri | 13.27 | 11.88 | 280 | |
| Nguru | 10.45 | 12.88 | 340 |
| Satellite Product | Temporal Coverage | Spatial Coverage | Instrument | Spatial Resolution | Temporal Resolution |
|---|---|---|---|---|---|
| CHIRPS | 1981–present | 50° N–50° S | MW, IR, RG | 0.05° | Daily |
| PERSIANN–CDR | 1983–present | 60° N–60° S | MW, IR, RG | 0.25° | Daily |
| TAMSAT | 1983–present | Africa | IR, RG | 0.0375° | Daily |
| Station | Region | CHIRPS | PERSIANN–CDR | TAMSAT |
|---|---|---|---|---|
| Asaba | Guinea coast | 28.3 | 28.3 | 23.6 |
| Awka | 19.1 | 22.8 | 22.8 | |
| Benin | 29.4 | 49.1 | 35.5 | |
| Calabar | 22.1 | 45.9 | 30.8 | |
| Enugu | 12.9 | 24.2 | 11.8 | |
| Ibadan | 21.1 | 18.1 | 11.7 | |
| Ijebu | 20.4 | 34.1 | 14.8 | |
| Ikeja | 21.2 | 27.0 | 20.6 | |
| Ikom | 60.1 | 31.2 | 50.2 | |
| Iseyin | 9.6 | 10.0 | 11.2 | |
| Lokoja | 9.2 | 12.4 | 12.7 | |
| Bauchi | Savannah | 15.9 | 20.7 | 17.7 |
| Bida | 8.1 | 14.7 | 7.2 | |
| Gombe | 15.8 | 12.3 | 20.8 | |
| Ibi | 13.8 | 15.1 | 12.1 | |
| Ilorin | 11.2 | 23.2 | 7.7 | |
| Jos | 9.5 | 20.3 | 10.4 | |
| Kaduna | 13.3 | 18.9 | 16.2 | |
| Minna | 8.7 | 26.0 | 7.5 | |
| Gusau | Sahel | 13.5 | 15.2 | 37.7 |
| Kano | 35.6 | 45.7 | 48.5 | |
| Katsina | 15.7 | 16.5 | 11.7 | |
| Maiduguri | 6.8 | 4.8 | 11.4 | |
| Nguru | 3.0 | 8.7 | 3.9 |
| Station | Region | CHIRPS | PERSIANN–CDR | TAMSAT |
|---|---|---|---|---|
| Asaba | Guinea coast | 0.56 | 0.38 | 0.49 |
| Awka | 0.54 | 0.47 | 0.56 | |
| Benin | 0.37 | 0.66 | 0.56 | |
| Calabar | 0.44 | 0.40 | 0.41 | |
| Enugu | 0.77 | 0.61 | 0.75 | |
| Ibadan | 0.67 | 0.41 | 0.68 | |
| Ijebu | 0.61 | 0.63 | 0.69 | |
| Ikeja | 0.62 | 0.60 | 0.63 | |
| Ikom | 0.24 | 0.36 | 0.25 | |
| Iseyin | 0.67 | 0.57 | 0.48 | |
| Lokoja | 0.65 | 0.50 | 0.46 | |
| Bauchi | Savannah | 0.68 | 0.43 | 0.55 |
| Bida | 0.28 | 0.11 | 0.23 | |
| Gombe | 0.55 | 0.42 | 0.44 | |
| Ibi | 0.56 | 0.10 | 0.05 | |
| Ilorin | 0.43 | 0.11 | 0.23 | |
| Jos | 0.36 | 0.43 | 0.29 | |
| Kaduna | 0.31 | 0.13 | 0.40 | |
| Minna | 0.56 | 0.69 | 0.50 | |
| Gusau | Sahel | 0.48 | 0.48 | 0.02 |
| Kano | 0.76 | 0.83 | 0.76 | |
| Katsina | 0.37 | 0.36 | 0.32 | |
| Maiduguri | 0.74 | 0.71 | 0.64 | |
| Nguru | 0.75 | 0.64 | 0.59 |
| Station | Data | Annual | MAM | JJAS | SON | Climatic Zone |
|---|---|---|---|---|---|---|
| Gusau | Observed | 0.20 | 0.92 | –0.95 | –0.82 | Sahel |
| CHIRPS | 0.82 | –0.31 | 0.82 | 0.71 | ||
| PERSIANN | 2.65 | 2.26 | 2.14 | 2.69 | ||
| TAMSAT | 2.51 | 2.60 | 1.39 | 2.53 | ||
| Kano | Observed | 3.81 | 1.56 | 3.74 | 2.86 | |
| CHIRPS | 2.35 | 0.92 | 2.41 | 1.33 | ||
| PERSIANN | 3.09 | 1.94 | 3.37 | 2.35 | ||
| TAMSAT | 3.03 | 1.14 | 3.03 | 2.46 | ||
| Katsina | Observed | 3.06 | 2.67 | 2.58 | 1.36 | |
| CHIRPS | 2.31 | 0.74 | 2.34 | 1.22 | ||
| PERSIANN | 3.71 | 2.58 | 2.43 | 2.04 | ||
| TAMSAT | 3.16 | 1.43 | 0.00 | 1.58 | ||
| Maiduguri | Observed | 3.64 | 0.73 | 3.26 | 1.97 | |
| CHIRPS | 2.11 | 2.11 | 2.07 | 1.22 | ||
| PERSIANN | 3.26 | 1.73 | 3.26 | 2.44 | ||
| TAMSAT | 3.60 | 1.04 | 3.37 | 2.87 | ||
| Nguru | Observed | 2.58 | 0.48 | 2.75 | 0.89 | |
| CHIRPS | 2.45 | 2.14 | 2.28 | 1.29 | ||
| PERSIANN | 3.74 | 2.14 | 3.77 | 2.58 | ||
| TAMSAT | 3.88 | 1.34 | 3.88 | 2.21 | ||
| Bauchi | Observed | 3.94 | –0.64 | 4.08 | 1.87 | Savannah |
| CHIRPS | 2.11 | –0.95 | 2.18 | 0.44 | ||
| PERSIANN | 2.01 | 1.33 | 1.94 | 2.31 | ||
| TAMSAT | 2.94 | 1.16 | 3.03 | 2.35 | ||
| Bida | Observed | 0.48 | –0.88 | 0.17 | 1.05 | |
| CHIRPS | 0.03 | –0.41 | –0.85 | 0.61 | ||
| PERSIANN | 2.55 | 2.58 | 0.75 | 2.79 | ||
| TAMSAT | 2.51 | 2.60 | 1.39 | 2.53 | ||
| Gombe | Observed | 0.65 | –1.63 | 0.58 | 0.85 | |
| CHIRPS | 1.33 | 0.17 | 1.29 | 1.87 | ||
| PERSIANN | 1.39 | 0.51 | 1.67 | 3.20 | ||
| TAMSAT | 4.22 | 1.19 | 3.74 | 3.06 | ||
| Ibi | Observed | 0.00 | –0.54 | –0.85 | 2.11 | |
| CHIRPS | 0.99 | –0.30 | 0.07 | 2.11 | ||
| PERSIANN | 1.33 | 2.17 | –0.48 | 3.23 | ||
| TAMSAT | 1.71 | 2.62 | 2.38 | 2.84 | ||
| Ilorin | Observed | 0.41 | –0.10 | 0.00 | 2.24 | |
| CHIRPS | 1.33 | –0.75 | 0.51 | 3.63 | ||
| PERSIANN | 1.67 | 1.46 | –0.17 | 3.23 | ||
| TAMSAT | 2.71 | 1.63 | 1.16 | 2.75 | ||
| Jos | Observed | 1.50 | 0.37 | 0.08 | 1.73 | |
| CHIRPS | 1.97 | –0.20 | 2.35 | 0.00 | ||
| PERSIANN | 2.45 | 2.52 | 1.43 | 1.84 | ||
| TAMSAT | 3.84 | 2.65 | 3.60 | 2.28 | ||
| Kaduna | Observed | 1.60 | 0.71 | 0.92 | 1.80 | |
| CHIRPS | 0.92 | –0.03 | 0.20 | 0.14 | ||
| PERSIANN | 3.43 | 1.70 | 2.75 | 2.72 | ||
| TAMSAT | 4.01 | 2.69 | 3.06 | 2.33 | ||
| Minna | Observed | 1.53 | 0.31 | 1.56 | 2.65 | |
| CHIRPS | 0.75 | 0.37 | –0.34 | 1.77 | ||
| PERSIANN | 3.09 | 2.62 | 0.82 | 2.86 | ||
| TAMSAT | 3.20 | 2.99 | 1.92 | 3.33 | ||
| Asaba | Observed | 0.31 | 0.75 | –0.73 | 0.27 | Guinea |
| CHIRPS | 1.60 | 1.29 | 0.10 | 1.70 | ||
| PERSIANN | 0.24 | 1.16 | –2.28 | 1.02 | ||
| TAMSAT | 3.30 | 3.16 | 1.80 | 3.03 | ||
| Awka | Observed | 1.73 | 1.80 | –0.92 | 0.88 | |
| CHIRPS | 1.09 | 0.74 | –0.17 | 2.24 | ||
| PERSIANN | 0.51 | 1.90 | –2.41 | 2.10 | ||
| TAMSAT | 3.81 | 3.71 | 1.87 | 3.16 | ||
| Benin | Observed | 2.31 | 2.86 | 1.12 | 2.67 | |
| CHIRPS | 0.17 | 0.92 | –0.31 | 1.12 | ||
| PERSIANN | 0.37 | 1.12 | –1.67 | 1.50 | ||
| TAMSAT | 3.09 | 3.21 | 1.63 | 3.06 | ||
| Calabar | Observed | 2.65 | 0.88 | 2.11 | 0.54 | |
| CHIRPS | 2.41 | 0.10 | 2.44 | –0.24 | ||
| PERSIANN | 1.09 | 1.77 | –1.94 | –1.70 | ||
| TAMSAT | 3.94 | 3.23 | 0.03 | 2.41 | ||
| Enugu | Observed | 2.28 | 1.12 | 1.19 | 4.39 | |
| CHIRPS | 1.12 | 1.70 | 0.51 | 1.84 | ||
| PERSIANN | 1.05 | 2.28 | –1.53 | 2.62 | ||
| TAMSAT | 3.57 | 3.94 | 1.94 | 3.23 | ||
| Ibadan | Observed | 1.09 | 0.20 | 1.36 | 2.31 | |
| CHIRPS | 0.54 | –0.99 | 0.00 | 2.31 | ||
| PERSIANN | 1.16 | 0.48 | –0.10 | 3.16 | ||
| TAMSAT | 2.78 | 2.18 | 0.61 | 3.23 | ||
| Ijebu | Observed | 3.17 | 0.25 | 2.45 | 2.57 | |
| CHIRPS | 1.77 | 0.14 | 0.54 | 2.24 | ||
| PERSIANN | 2.04 | 0.446 | –0.24 | 3.06 | ||
| TAMSAT | 3.47 | 2.58 | 0.88 | 2.82 | ||
| Ikeja | Observed | 1.83 | 0.84 | 0.81 | 2.78 | |
| CHIRPS | 1.05 | 0.41 | 0.07 | 0.20 | ||
| PERSIANN | 1.35 | 0.24 | –0.24 | 2.21 | ||
| TAMSAT | 3.91 | 2.55 | 1.53 | 2.69 | ||
| Ikom | Observed | 1.67 | 0.65 | –0.17 | 1.73 | |
| CHIRPS | -0.03 | 0.20 | –1.56 | 0.85 | ||
| PERSIANN | 0.88 | 2.35 | –2.75 | 2.41 | ||
| TAMSAT | 3.40 | 2.41 | 1.70 | 2.86 | ||
| Iseyin | Observed | 1.05 | 0.10 | 0.03 | 2.04 | |
| CHIRPS | 1.90 | –0.20 | 0.00 | 2.79 | ||
| PERSIANN | 2.04 | 0.71 | 0.37 | 3.54 | ||
| TAMSAT | 3.16 | 1.56 | 0.53 | 3.30 | ||
| Lokoja | Observed | 0.68 | 1.46 | –0.48 | 0.99 | |
| CHIRPS | 0.85 | –0.27 | 0.34 | 1.60 | ||
| PERSIANN | 0.37 | 1.63 | –1.43 | 2.21 | ||
| TAMSAT | 2.48 | 2.99 | 1.05 | 2.48 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ogbu, K.N.; Hounguè, N.R.; Gbode, I.E.; Tischbein, B. Performance Evaluation of Satellite-Based Rainfall Products over Nigeria. Climate 2020, 8, 103. https://doi.org/10.3390/cli8100103
Ogbu KN, Hounguè NR, Gbode IE, Tischbein B. Performance Evaluation of Satellite-Based Rainfall Products over Nigeria. Climate. 2020; 8(10):103. https://doi.org/10.3390/cli8100103
Chicago/Turabian StyleOgbu, Kingsley N., Nina Rholan Hounguè, Imoleayo E. Gbode, and Bernhard Tischbein. 2020. "Performance Evaluation of Satellite-Based Rainfall Products over Nigeria" Climate 8, no. 10: 103. https://doi.org/10.3390/cli8100103
APA StyleOgbu, K. N., Hounguè, N. R., Gbode, I. E., & Tischbein, B. (2020). Performance Evaluation of Satellite-Based Rainfall Products over Nigeria. Climate, 8(10), 103. https://doi.org/10.3390/cli8100103






