Ushering in the New Era of Radiometric Intercomparison of Multispectral Sensors with Precision SNO Analysis
Abstract
:1. Introduction
2. The Comparison Conditions
2.1. The Instruments
2.2. General Issues
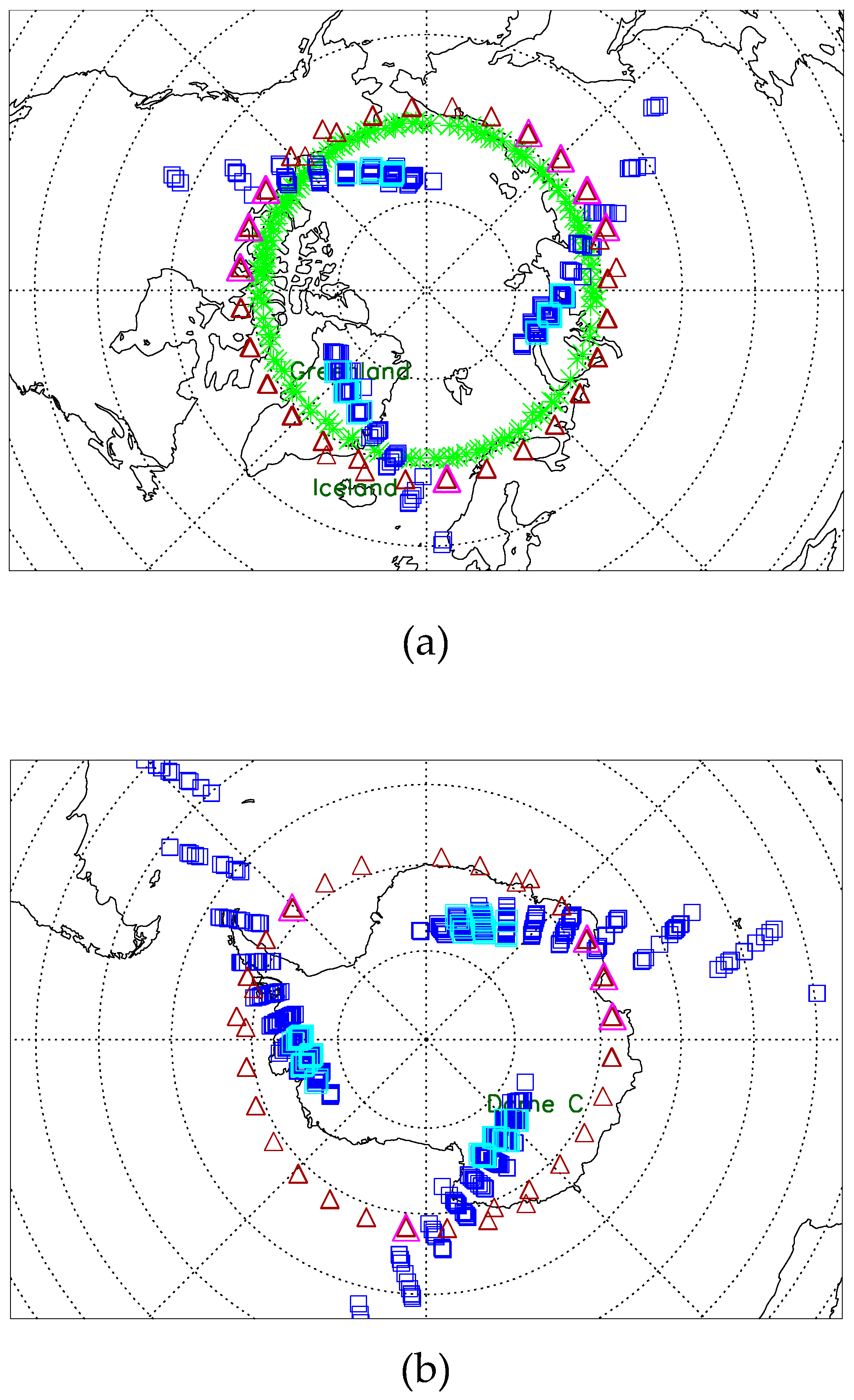
2.2.1. SNO Geolocation and Scenes
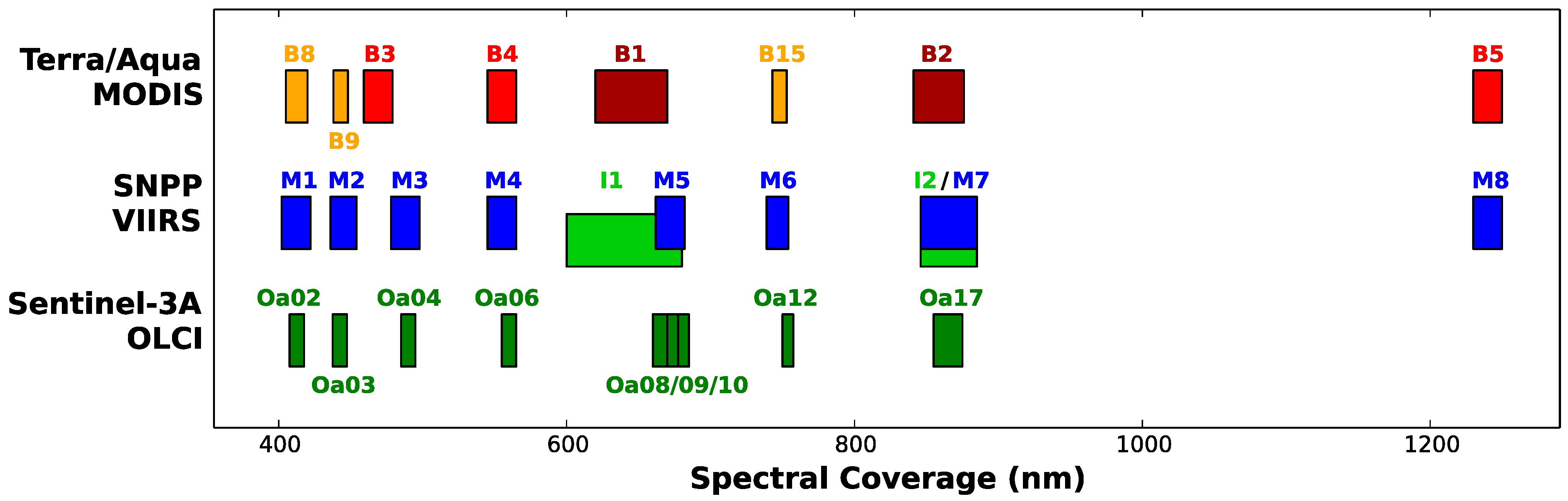
2.2.2. Spectral Match
2.2.3. Dynamic Range
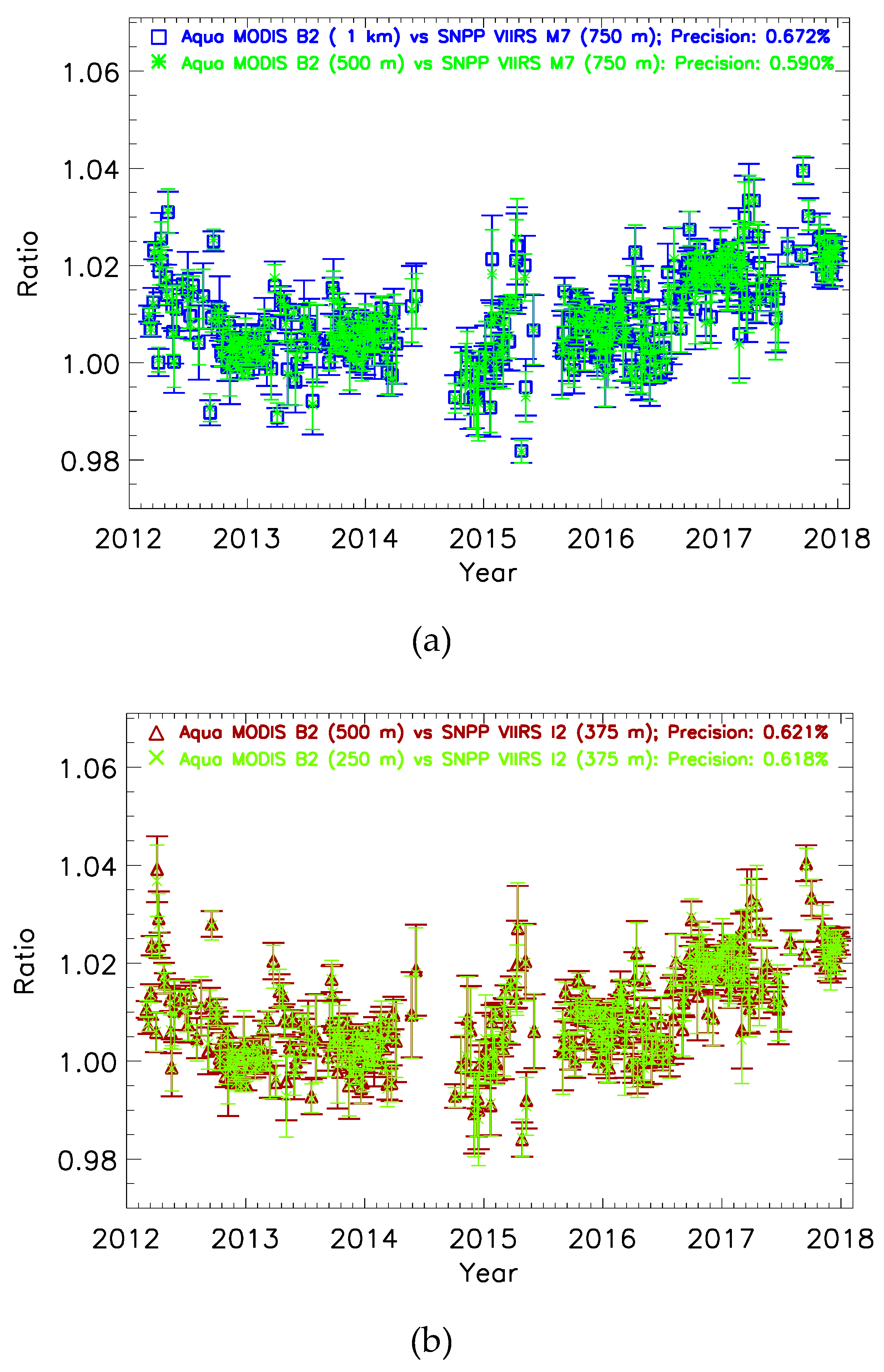
2.2.4. Spatial Resolution
3. The Examination of Radiometric Intersensor Comparison
3.1. Procedure and Setup
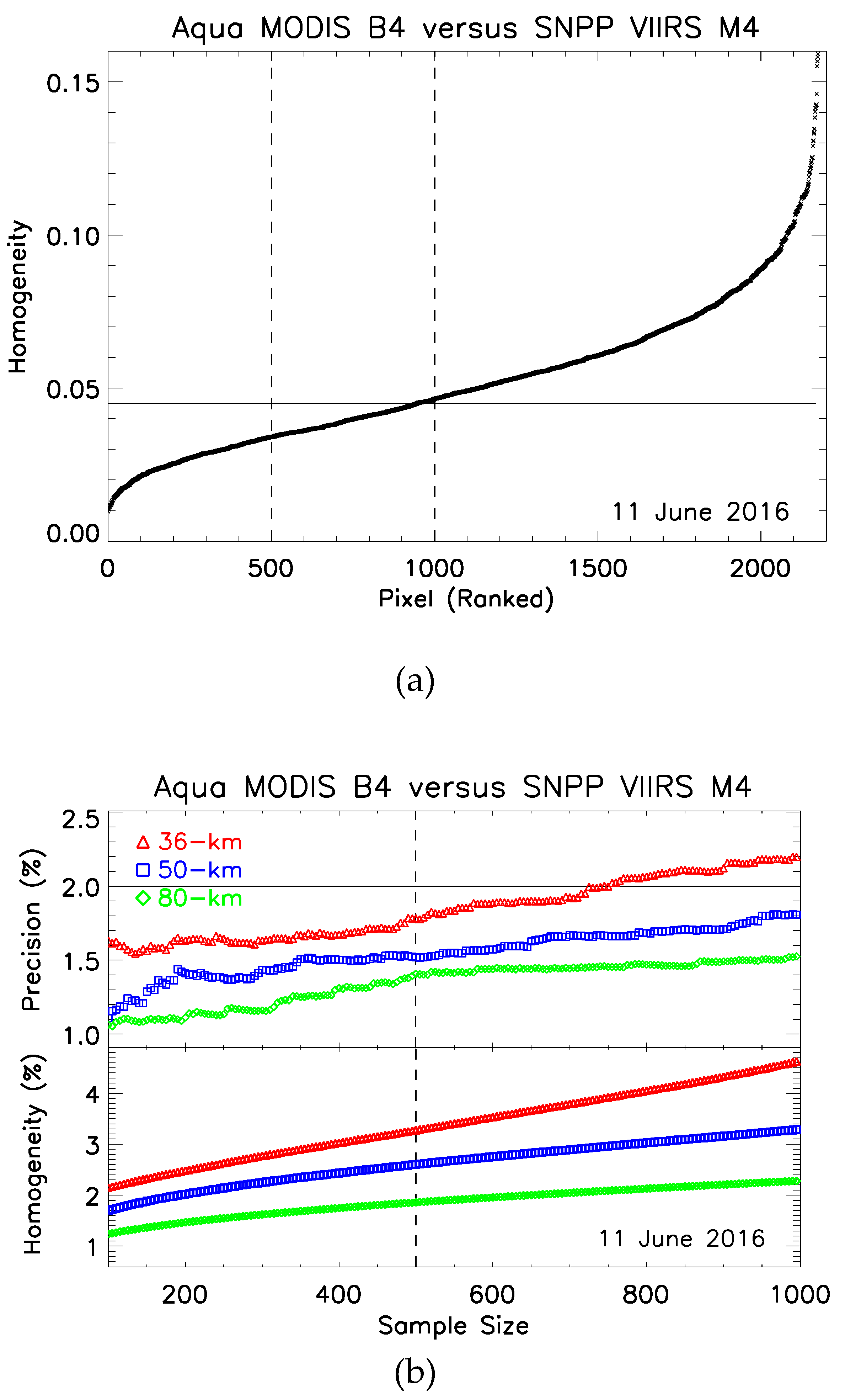
3.2. Homogeneity
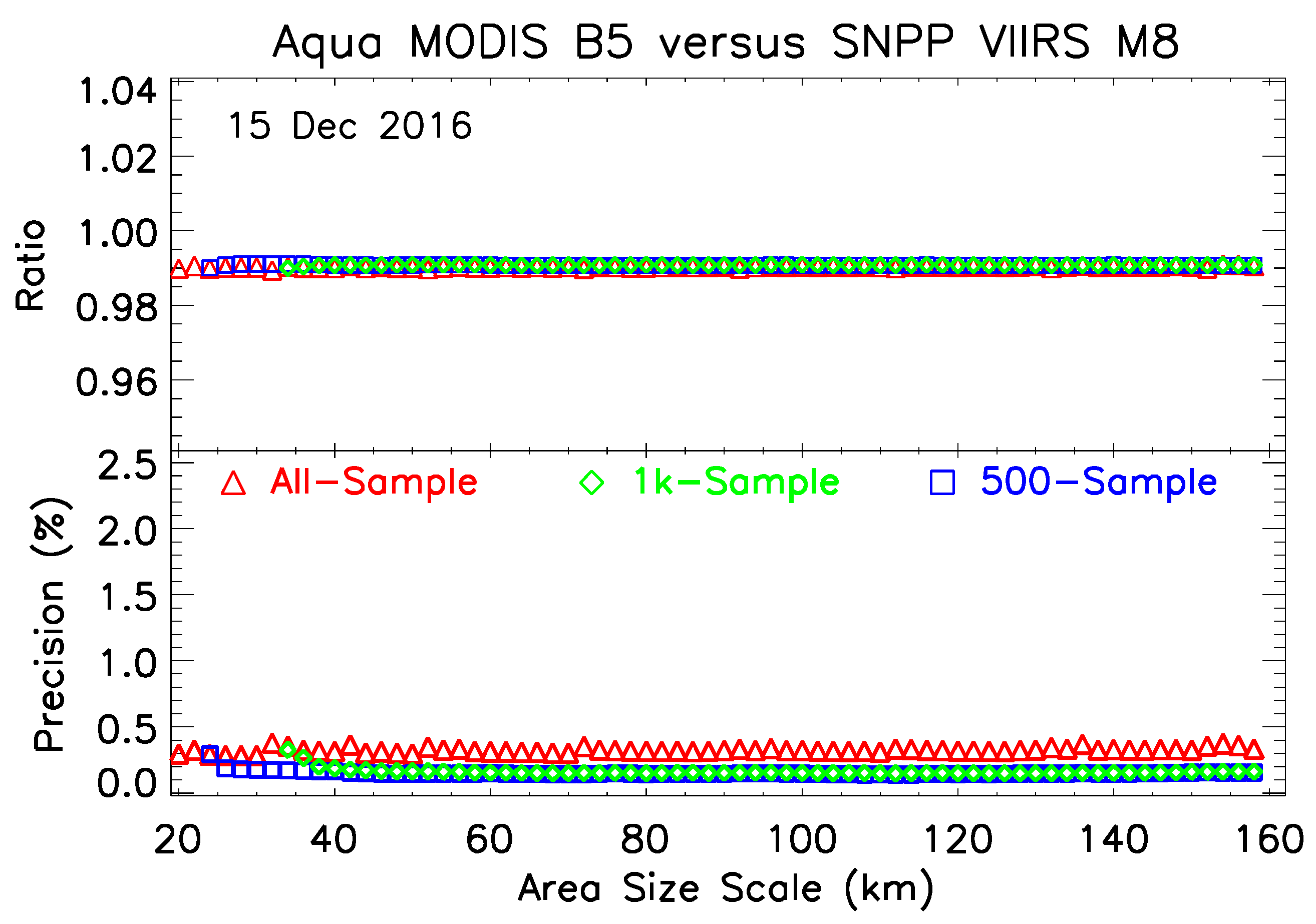
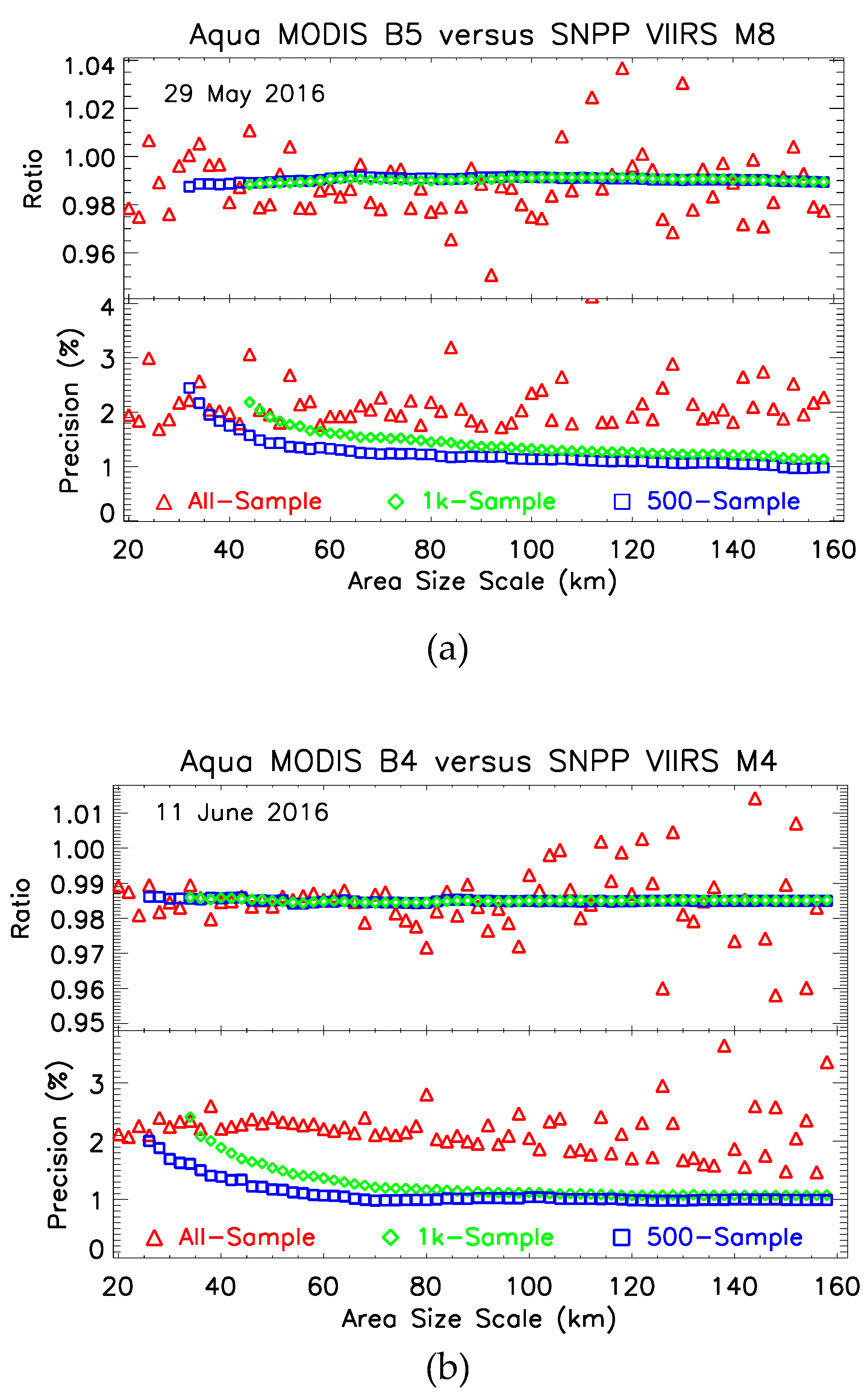
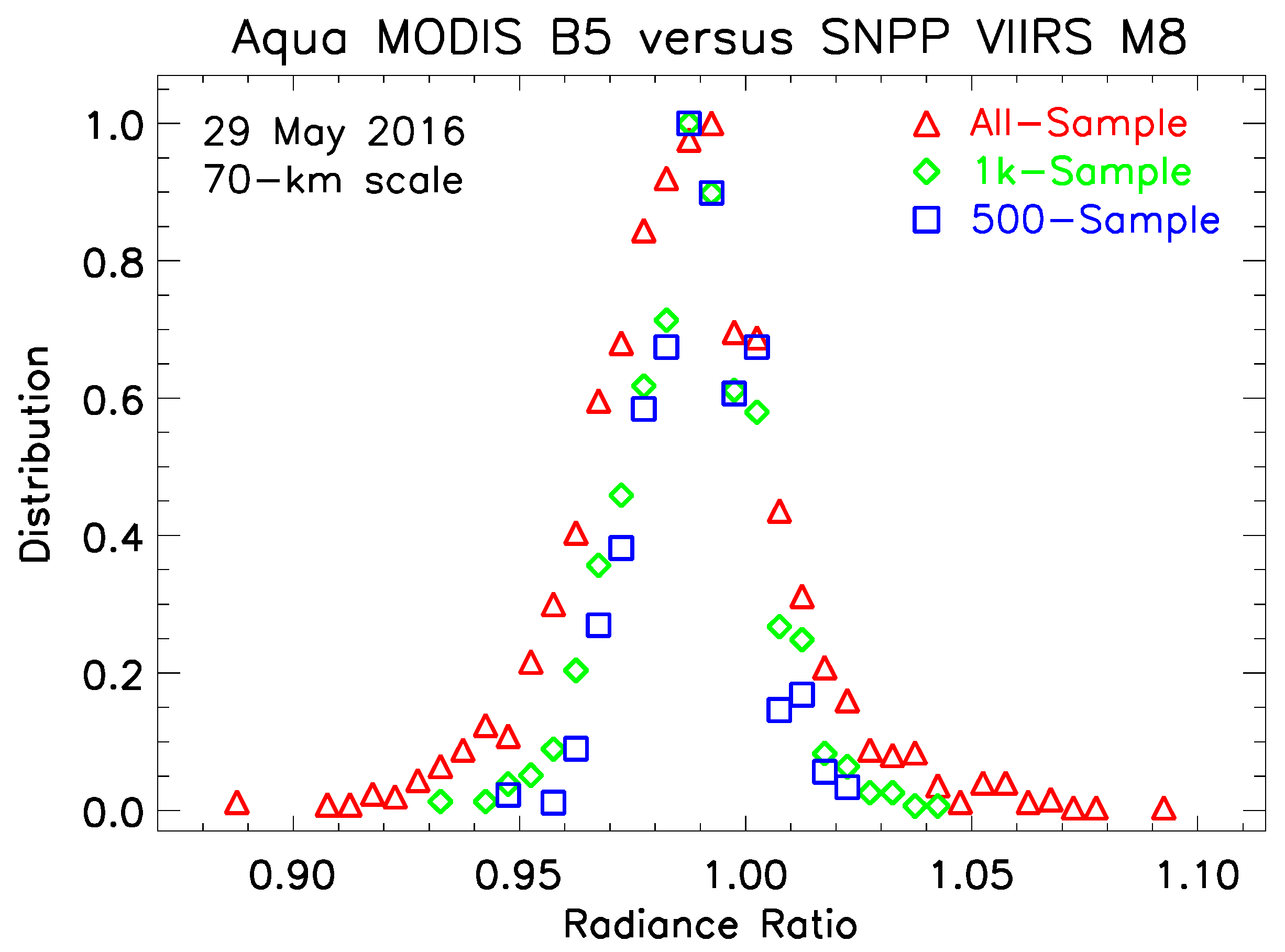
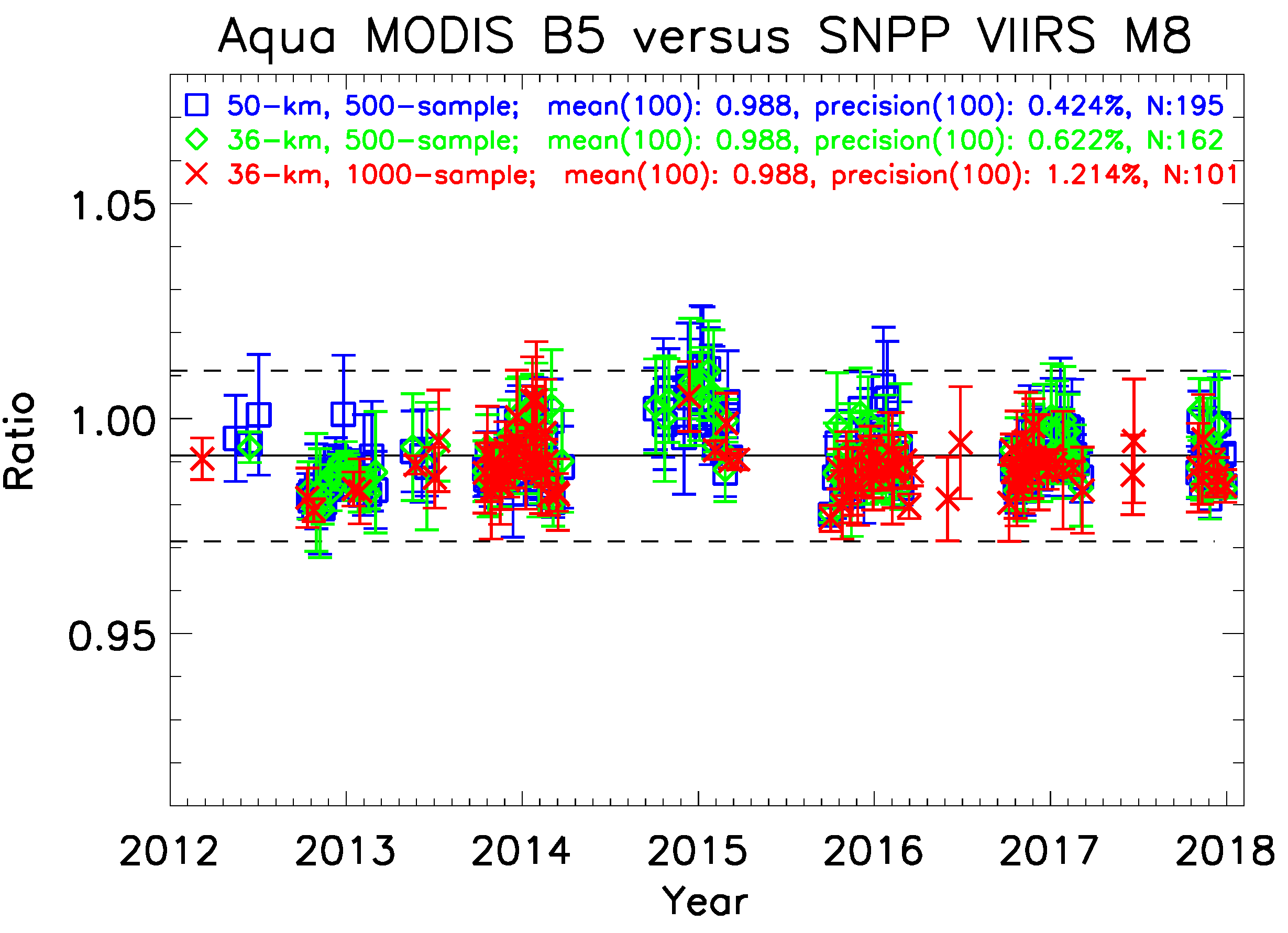
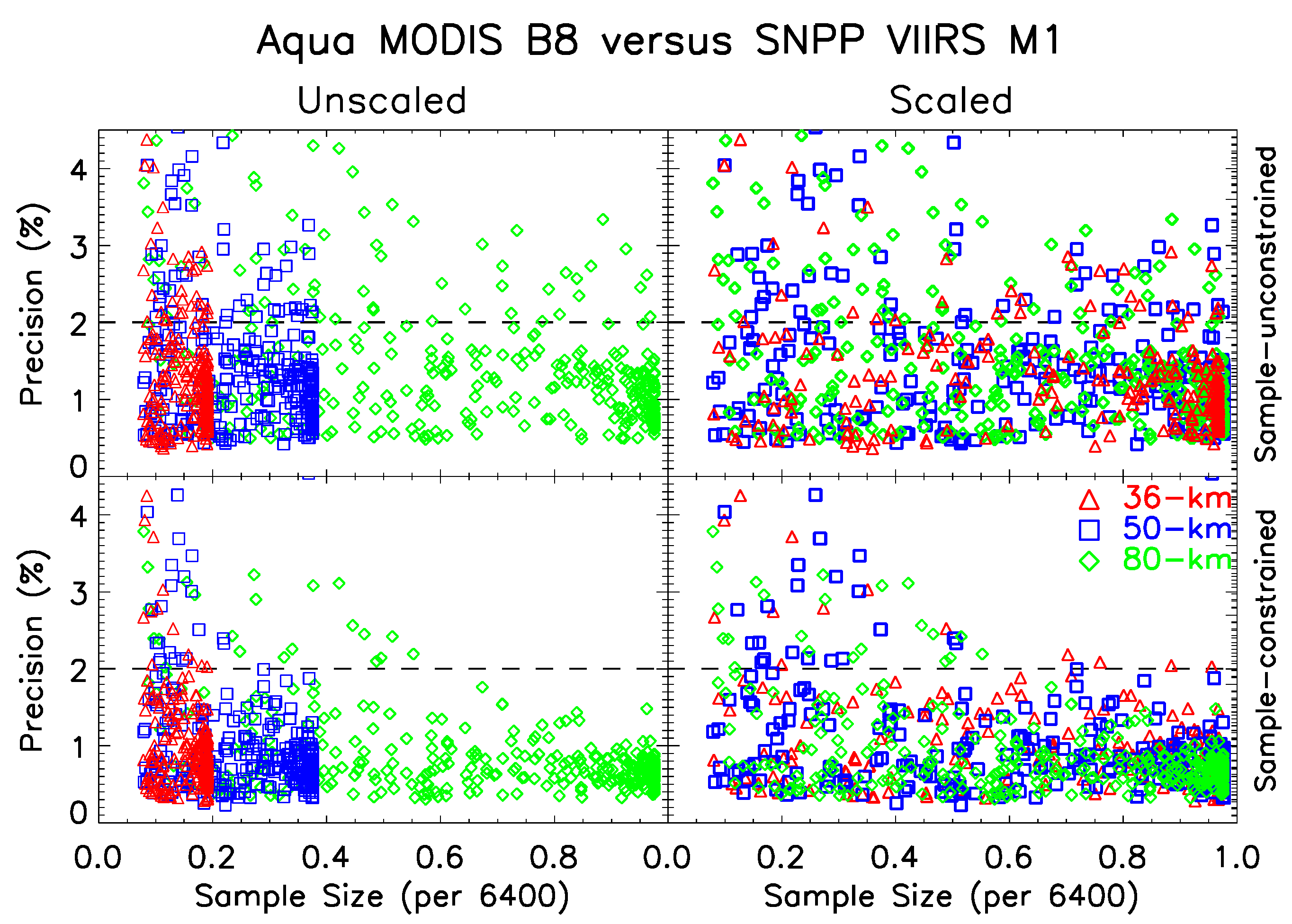
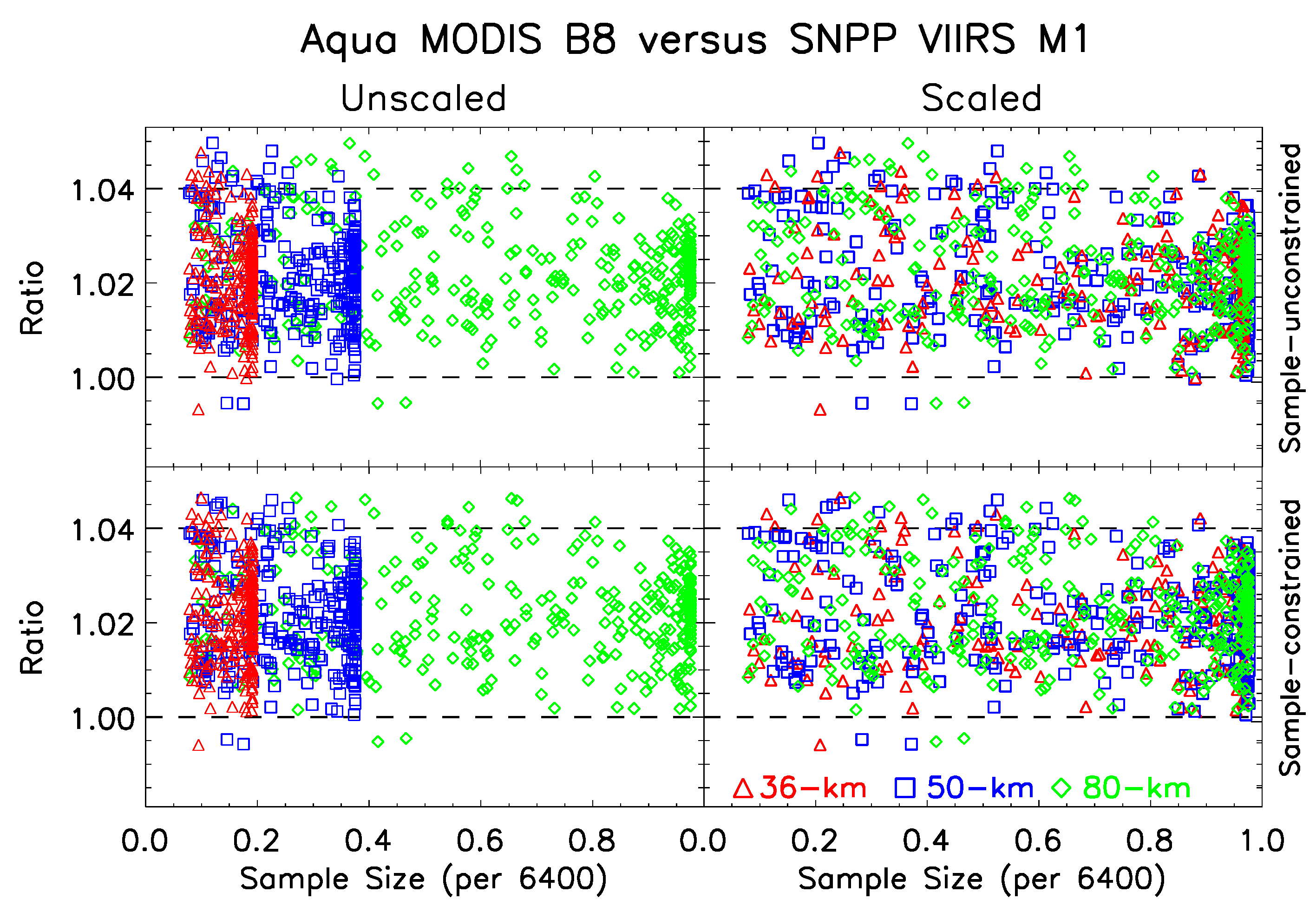
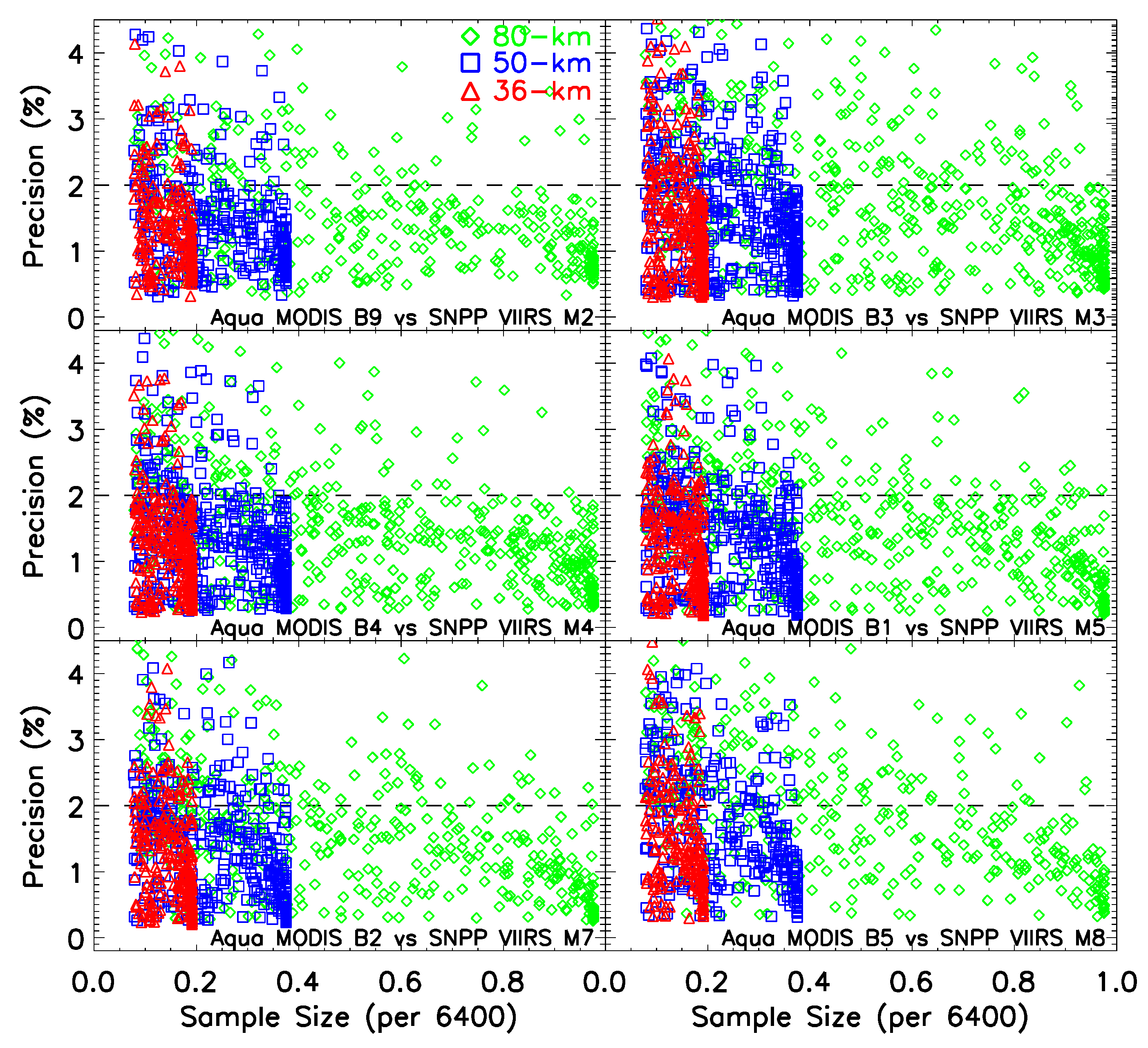
3.3. Area Size and Sample Size Constraint
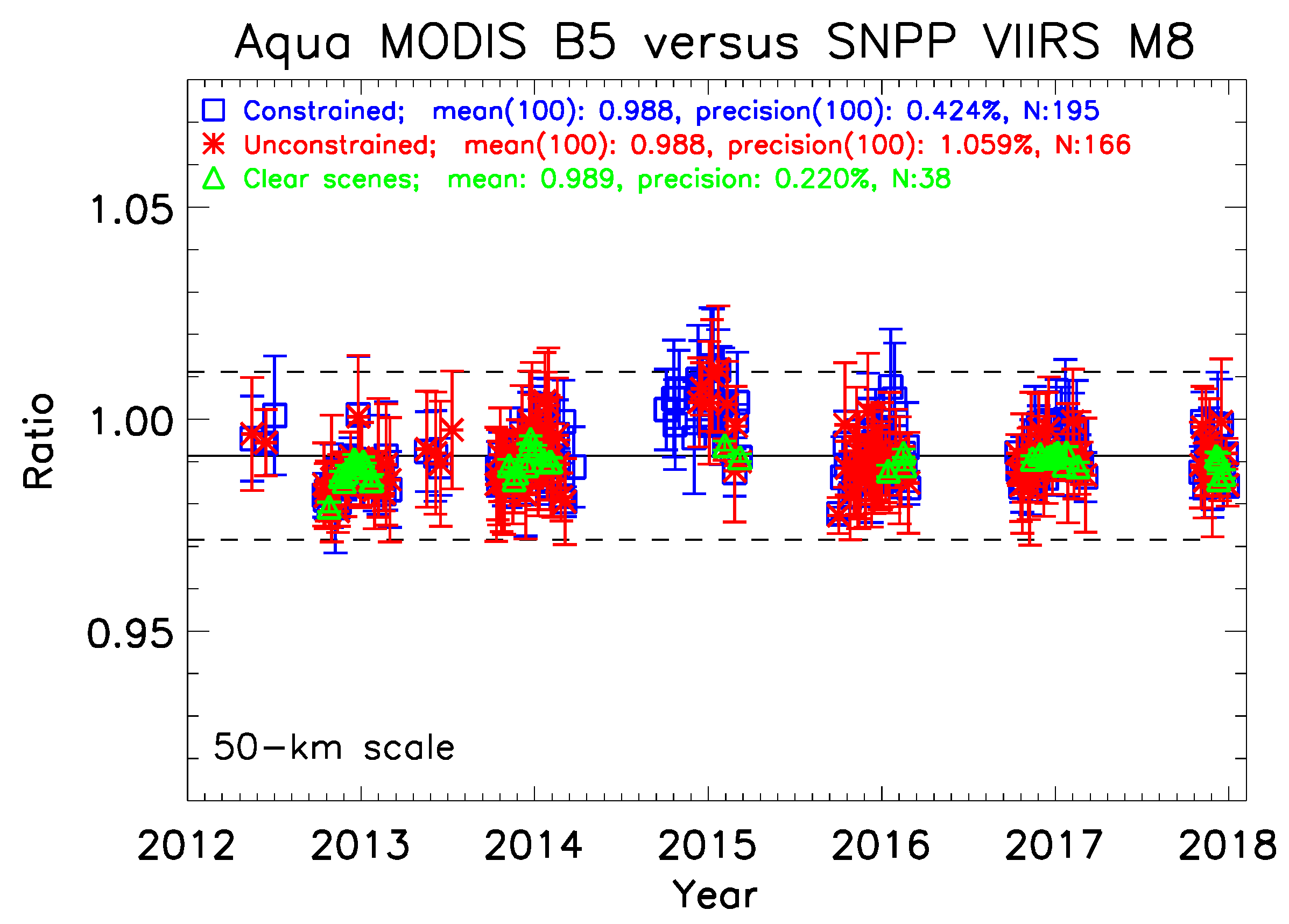
3.4. Examination of Pixel Quality
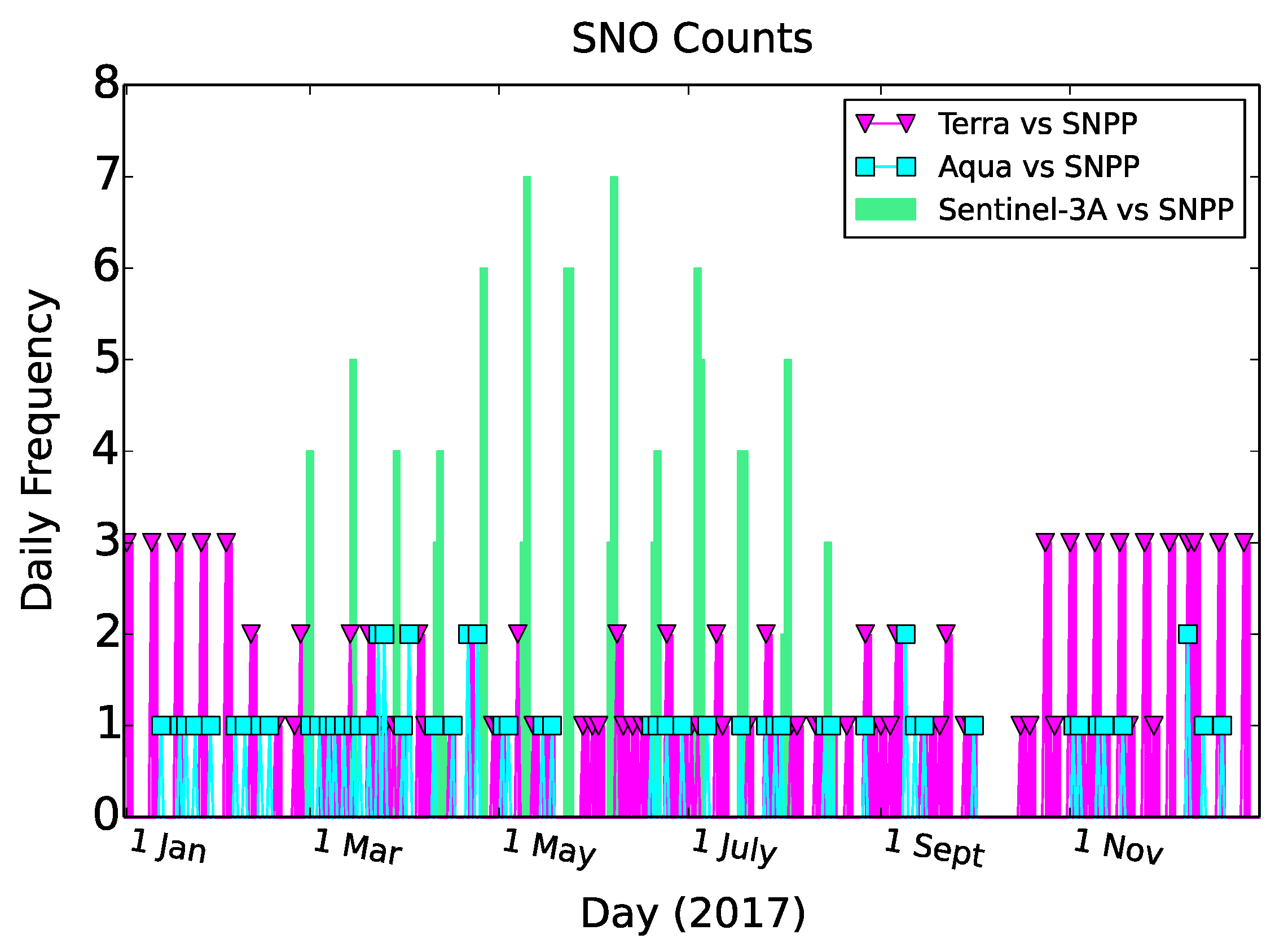
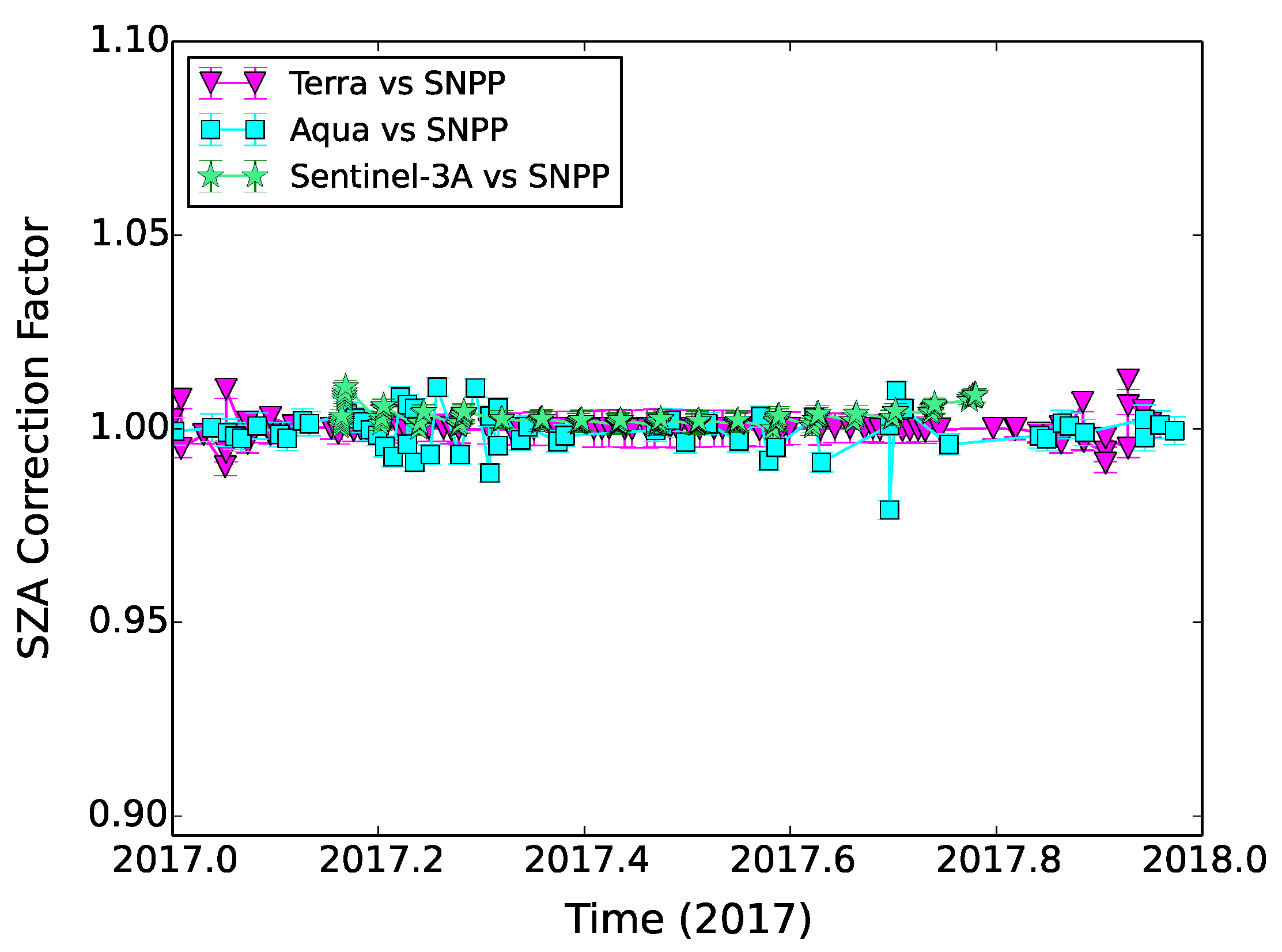
3.5. Application and Result
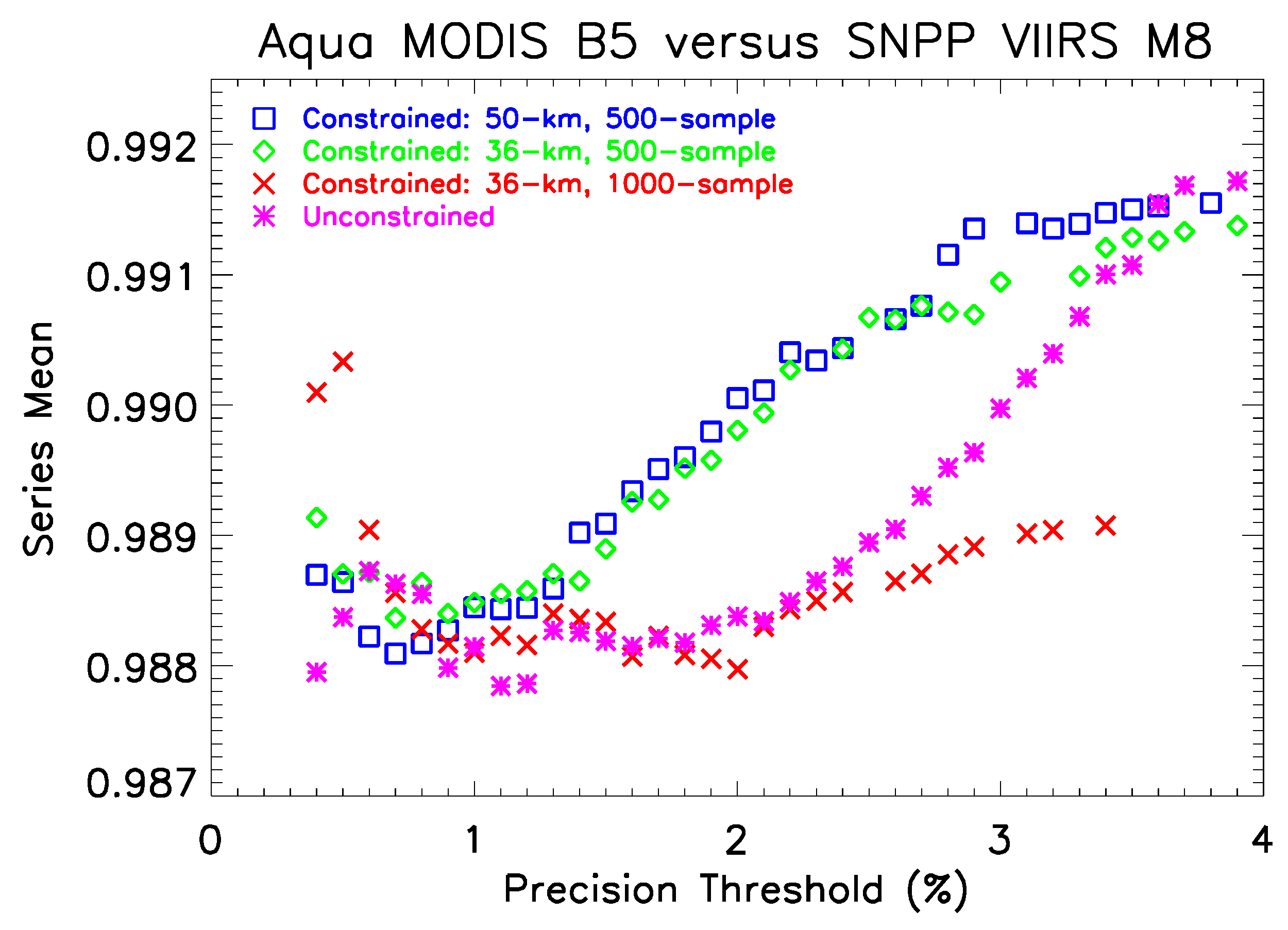
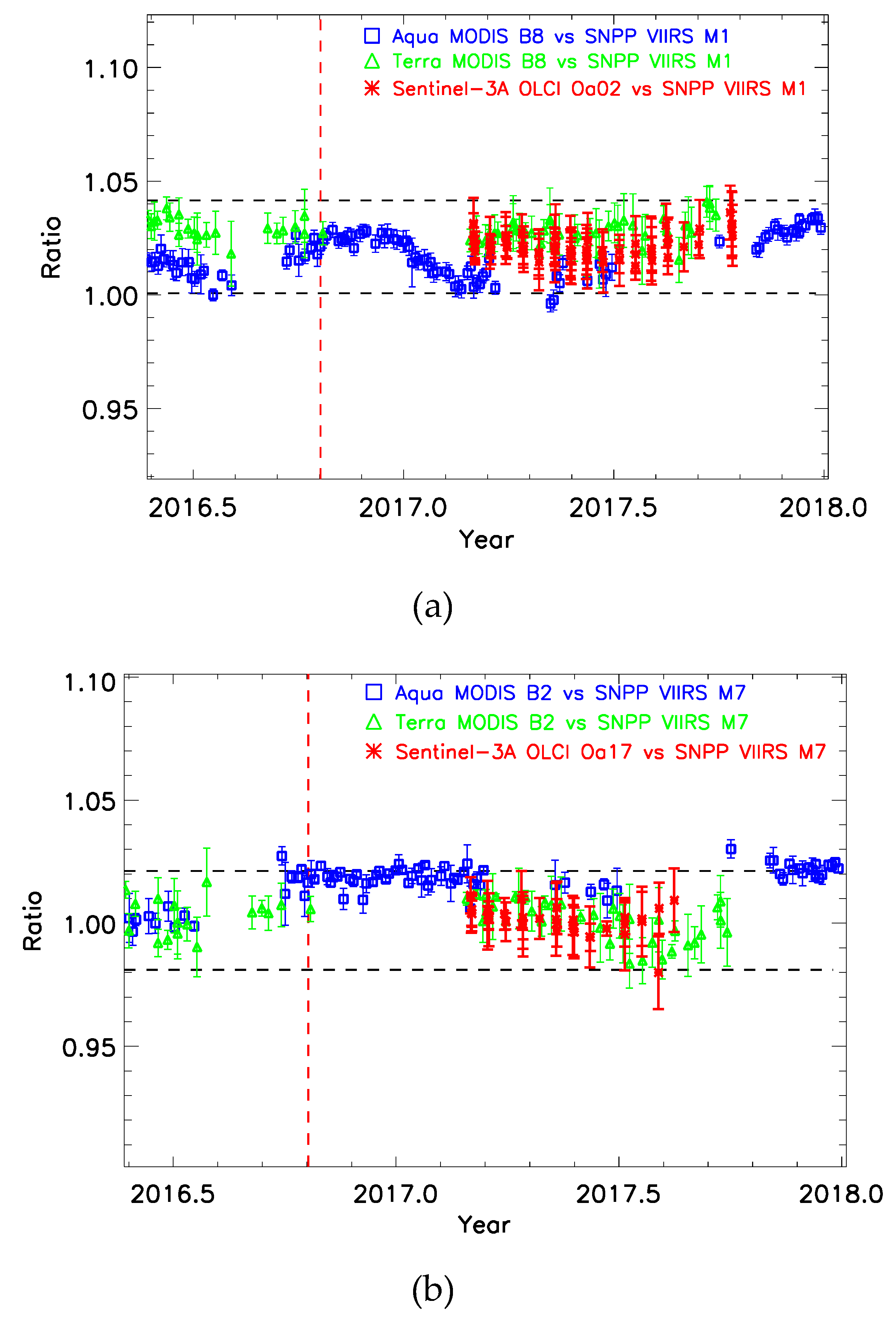
3.6. Impact of Precision Threshold on the Time Series
3.7. Scaling Phenomenon in MODIS versus SNPP VIIRS
3.8. Scale-Dependence in Sentinel-3A OLCI versus SNPP VIIRS
3.9. Discussion and Summary
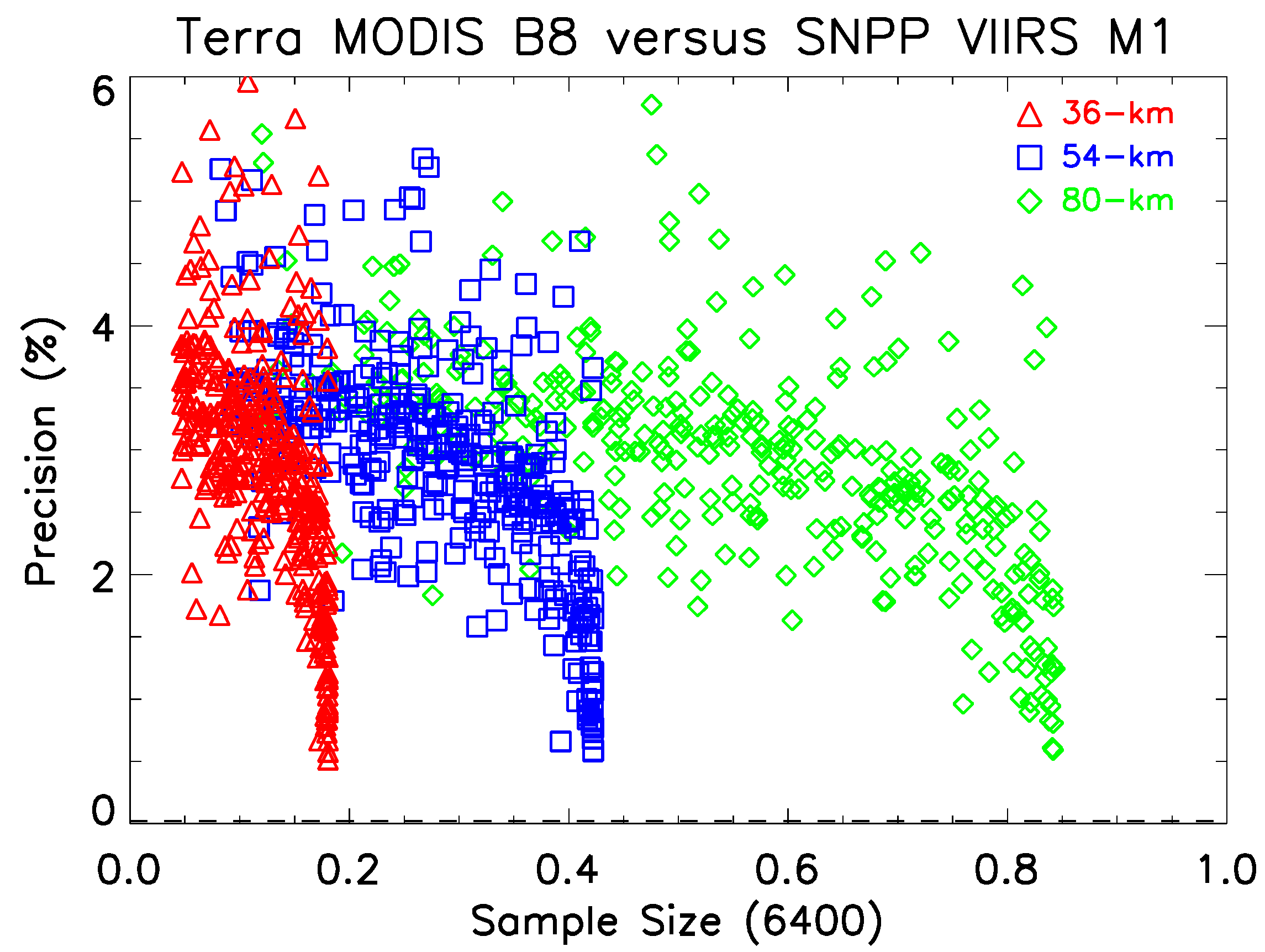
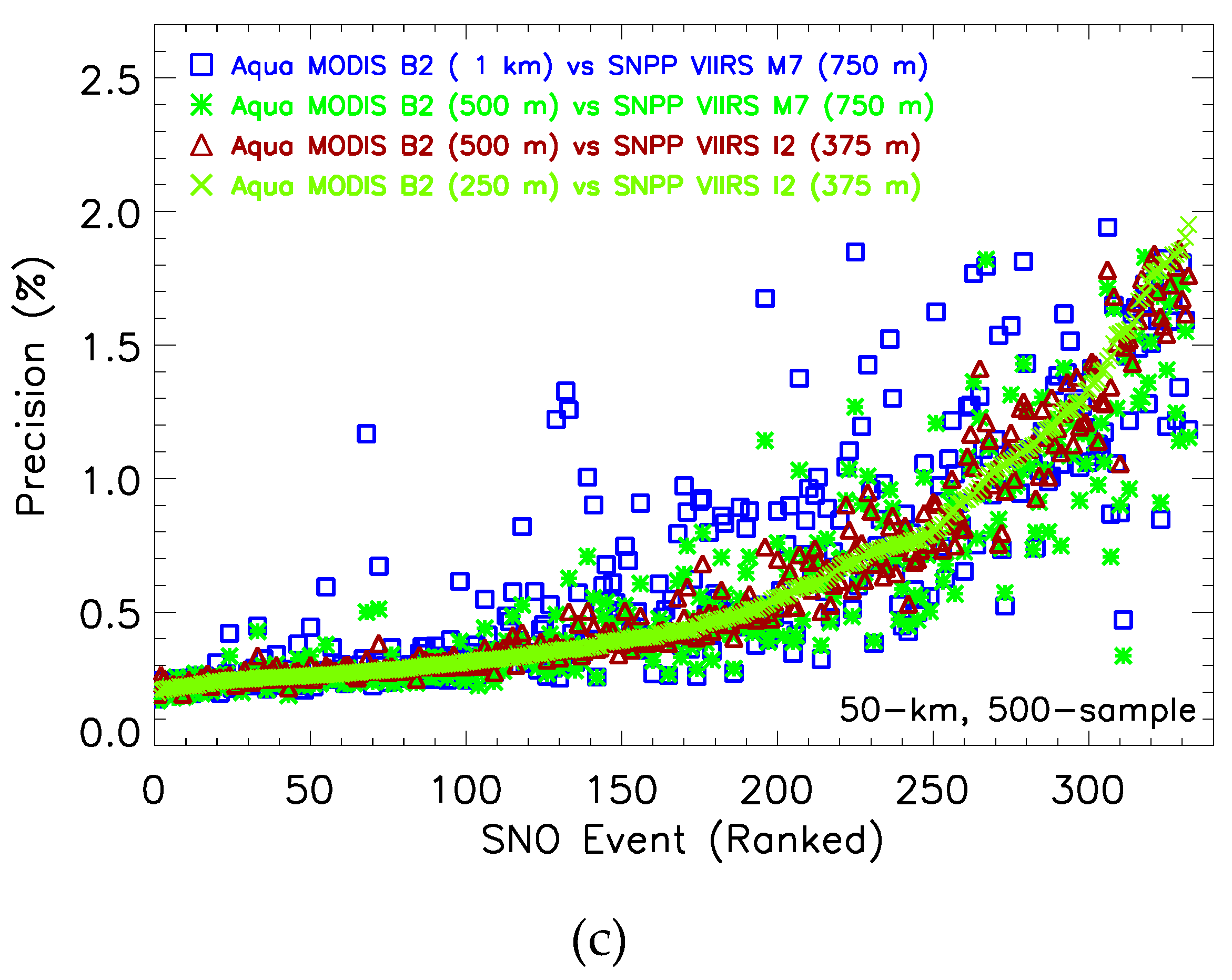
4. Capability at Different Regimes of Spatial Resolution
5. Multi-instrument Cross-Comparison
5.1. Aqua MODIS, Sentinel-3A OLCI and SNPP VIIRS Comparisons
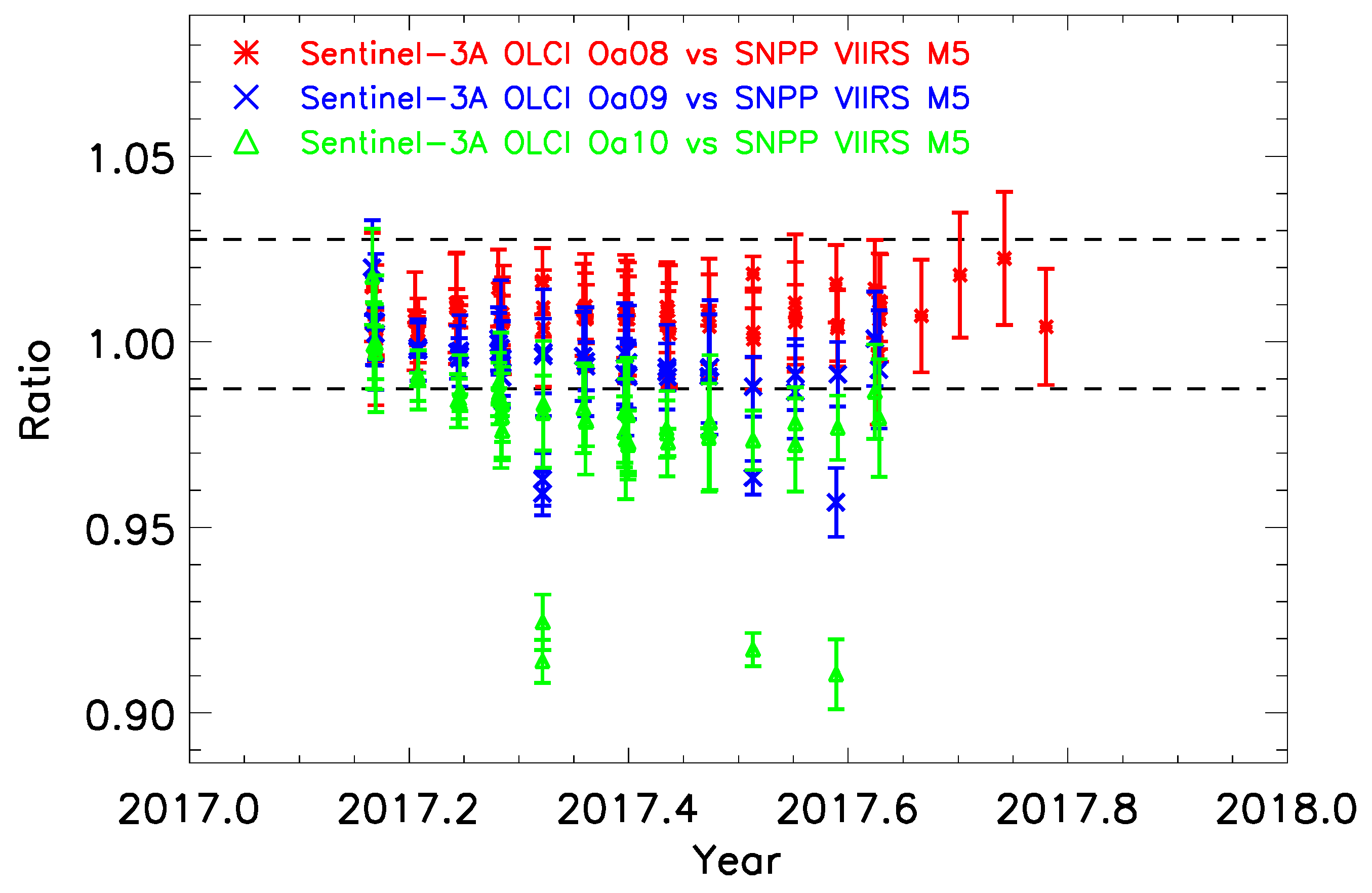
5.2. Impact of RSR Mismatch: Sentinel-3A Oa08-Oa10 versus SNPP VIIRS M5
6. General Discussions
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barnes, W.L.; Salomonson, V.V. MODIS: A global imaging spectroradiometer for the Earth Observing System. Crit. Rev. Opt. Sci. Technol. 1993, CR47, 285–307. [Google Scholar]
- Guenther, B.; Barnes, W.; Knight, E.; Barker, J.; Harnden, J.; Weber, R.; Roberto, M.; Godden, G.; Montgomery, H.; Abel, P. MODIS Calibration: A brief review of the strategy for the at-launch calibration approach. J. Atmos. Ocean. Technol. 1996, 12, 274–285. [Google Scholar] [CrossRef]
- Suomi NPP Home Page. Available online: https://www.nasa.gov/mission_pages/NPP/main/index.html (accessed on 1 February 2018).
- Cao, C.; Deluccia, F.; Xiong, X.; Wolfe, R.; Weng, F. Early on-orbit performance of the Visible Infrared Imaging Radiometer Suite onboard the Suomi National Polar-orbiting Partnership (S-NPP) satellite. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1142–1156. [Google Scholar] [CrossRef]
- Wu, A.; Xiong, X.; Cao, C.; Chiang, K. Assessment of SNPP VIIRS VIS/NIR radiometric calibration stability using Aqua MODIS and invariant surface targets. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2918–2924. [Google Scholar] [CrossRef]
- Uprety, S.; Blonski, S.; Cao, C. On-orbit radiometric performance characterization of S-NPP VIIRS reflective solar bands. In Proceedings of the Earth Observing Missions and Sensors: Development, Implementation and Characterization IV, New Delhi, India, 4–7 April 2016; Volume 9881, p. 98811H. [Google Scholar]
- Chu, M.; Sun, J.; Wang, M. Performance evaluation of on-orbit calibration of SNPP reflective solar bands via intersensor comparison with Aqua MODIS. J. Atmos. Ocean. Technol. 2018, 35, 385–403. [Google Scholar] [CrossRef]
- Cao, C.; Heidinger, A.K. Inter-comparison of the long-wave infrared channels of MODIS and AVHRR/NOAA-16 using simultaneous nadir observations at orbit intersections. In Earth Observing Systems VII; Barnes, W.L., Ed.; International Society for Optical Engineering: Bellingham, WA, USA, 2002; Volume 4814, pp. 306–316. [Google Scholar] [CrossRef]
- Heidinger, A.K.; Cao, C.; Sullivan, J.T. Using Moderate Resolution Imaging Spectroradiometer (MODIS) to calibrate Advanced Very High Resolution Radiometer reflectance channels. J. Geophys. Res. 2002, 107, 4702. [Google Scholar] [CrossRef]
- Cao, C.; Weinreb, M.; Xu, H. Predicting simultaneous nadir overpasses among polar-orbiting meteorological satellites for the intersatellite calibration of radiometers. J. Atmos. Ocean. Technol. 2004, 21, 21537–21542. [Google Scholar] [CrossRef]
- Chander, G.; Hewison, T.J.; Fox, N.; Wu, X.; Xiong, X.; Blackwell, W.J. Overview of Intercalibration of Satellite Instruments. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1056–1080. [Google Scholar] [CrossRef]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.-H.; Féménias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C.; et al. The global monitoring for environment and security (GMES) sentinel-3 mission. Remote Sens. Environ. 2012, 120, 37–57. [Google Scholar] [CrossRef]
- JPSS Series Satellites: NOAA-20 Home Page. Available online: https://www.nesdis.noaa.gov/jpss-1 (accessed on 1 February 2018).
- Tabata, T.; Andou, A.; Bessho, K.; Date, K.; Dojo, R.; Hosaka, K.; Mori, N.; Murata, H.; Nakayama, R.; Okuyama, A.; et al. Himawari-8/AHI latest performance of navigation and calibration. In Proceedings of the Earth Observing Missions and Sensors: Development, Implementation, and Characterization IV, New Delhi, India, 4–7 April 2016; Volume 9881, p. 98811H. [Google Scholar]
- Meteorological Satellite Center (MSC) of JMA, Himawari-8 Imager (AHI) Home Page. Available online: https://www.data.jma.go.jp/mscweb/en/himawari89/space_segment/spsg_ahi.html.
- Schmit, T.J.; Gunshor, M.M.; Menzel, W.P.; Gurka, J.J.; Li, J.; Bachmeier, A.S. Introducing the next-generation Advanced Baseline Imager on GOES-R. Bull. Am. Meteorol. Soc. 2005, 86, 1079–1096. [Google Scholar] [CrossRef]
- Schmit, T.J.; Griffith, P.; Gunshor, M.M.; Daniels, J.M.; Goodman, S.J.; Lebair, W.J. A Closer Look at the ABI on the GOES-R Series. Bull. Am. Meteorol. Soc. 2017, 98, 681–698. [Google Scholar] [CrossRef]
- GOES-R Series Home Page. Available online: https://www.goes-r.gov (accessed on 10 June 2019).
- Sun, J.; Angal, A.; Xiong, X.; Chen, H.; Geng, X.; Wu, A.; Choi, T.; Chu, M. MODIS reflective solar bands calibration improvements in Collection 6. In Proceedings of the Earth Observing Missions and Sensors: Development, Implementation, and Characterization II, Kyoto, Japan, 29 October–1 November 2012; Volume 8528, p. 85280N. [Google Scholar]
- Sun, J.; Xiong, X.; Angal, A.; Chen, H.; Wu, A.; Geng, X. Time-dependent response versus scan angle for MODIS reflective solar bands. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3159–3174. [Google Scholar] [CrossRef]
- NASA EARTHDATA: LAADS DAAC Home Page. Available online: https://ladweb.modaps.eosdis.nasa.gov (accessed on 1 February 2018).
- NOAA CLASS Home Page. Available online: https://www.bou.class.noaa.gov (accessed on 1 February 2018).
- ESA Copernicus Open Access Hub Home Page. Available online: https://scihub.copernicus.eu (accessed on 1 February 2018).
- Tansock, J.; Bancroft, D.; Butler, J.; Cao, C.; Datla, R.; Hansen, S.; Helder, D.; Kacker, R.; Latvakoski, H.; Mylnczak, M.; et al. Guidelines for Radiometric Calibration of Electro-Optical Instruments for Remote Sensing, Space Dynamics Lab Publications 2015. Paper 163. Available online: https://digitalcommons.usu.edu/sdl_pubs/163 (accessed on 10 June 2019). [CrossRef]
- Chu, M.; Sun, J.; Wang, M. Radiometric Evaluation of SNPP VIIRS Band M11 via Sub-Kilometer Intercomparison with Aqua MODIS Band 7 over Snowy Scenes. Remote Sens. 2018, 10, 413. [Google Scholar] [CrossRef]
- Sun, J.; Wang, M. Visible Infrared Imaging Radiometer Suite solar diffuser calibration and its challenges using solar diffuser stability monitor. Appl. Opt. 2014, 53, 8571–8584. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Wang, M. On-orbit calibration of the Visible Infrared Imaging Radiometer Suite reflective solar bands and its challenges using a solar diffuser. Appl. Opt. 2015, 54, 7210–7223. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Wang, M. Radiometric calibration of the Visible Infrared Imaging Radiometer Suite reflective solar bands with robust characterizations and hybrid calibration coefficients. Appl. Opt. 2015, 54, 9331–9342. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Chu, M.; Wang, M. Degradation nonuniformity in the solar diffuser bidirectional reflectance distribution function. Appl. Opt. 2016, 55, 6001–6016. [Google Scholar] [CrossRef] [PubMed]
- Chu, M.; Sun, J.; Wang, M. The inter-sensor radiometric comparison of SNPP VIIRS reflective solar bands with Aqua MODIS updated through June 2017. In Proceedings of the Earth Observing Systems XXII, San Diego, CA, USA, 6–10 August 2017; Volume 10402, p. 1040222. [Google Scholar]
- Chu, M.; Dodd, J. Examination of Radiometric Deviations in Bands 29, 31 and 31 of MODIS. IEEE Trans. Geosci. Remote Sens. 2019. [Google Scholar] [CrossRef]



| Sentinel-3A: OLCI | SNPP: VIIRS | Terra: MODIS | Aqua: MODIS | |
|---|---|---|---|---|
| Satellite Repeat Cycles (Days) | 27 | 16 | 16 | 16 |
| Satellite Local Crossing Time | Descending: 10:00 am | Ascending: 1:30 pm | Descending: 10:30 am | Ascending: 1:30 pm |
| Satellite Altitude (km) | 814 | 834 | 705 | 705 |
| Satellite Orbit Inclination | 98.6 | 98.7 | 98.2 | 98.2 |
| Sensor: Swath (km) | 1270 | 3040 | 2330 | 2330 |
| Sensor: Resolution at SSP (m) | 300 m | 750 m, 350 m | 1 km, 500 m, 250 m | 1 km, 500 m, 250 m |
| Sensor: Number of Bands | 21 | 22 | 36 | 36 |
| Sensor: RSB/TEB/Other | 21/0 | 14/7/1 | 20/26 | 20/26 |
| Sentinel-3A OLCI | SNPP VIIRS | Terra/Aqua MODIS | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | Band | Spectral Range (nm) | Center λ (nm) | Spatial Resolution (m) | Lmax | Band | Spectral Range (nm) | Center λ (nm) | Spatial Resolution (m) | Lmax | Band | Spectral Range (nm) | Center λ (nm) | Spatial Resolution (m) | Lmax |
| VIS | Oa02 | 407–417 | 412.5 | 300 | 501.3 | M1 | 402–422 | 410 | 750 | 135/615 | B8 | 405–420 | 412 | 1000 | 175 |
| Oa03 | 438–448 | 442.5 | 300 | 466.1 | M2 | 436–454 | 443 | 750 | 127/687 | B9 | 438–448 | 443 | 1000 | 133 | |
| Oa04 | 485–495 | 490 | 300 | 483.3 | M3 | 478–498 | 486 | 750 | 107/702 | B3 | 459–479 | 469 | 500/1000 | 593 | |
| Oa06 | 555–565 | 560 | 300 | 524.5 | M4 | 545–565 | 551 | 750 | 78/667 | B4 | 545–565 | 555 | 500/1000 | 518 | |
| Oa08/(Oa09)/(Oa10) | 660–670/(670–677.5)/(677.5–685) | 665/(673.75)/(681.25) | 300 | 364.9/(443.1)/(350.3) | M5 | 662–682 | 671 | 750 | 59/651 | B1 | 620–670 | 645 | 250/500/100 | 685 | |
| I1 | 600–680 | 640 | 375 | 718 | |||||||||||
| NIR | Oa12 | 750–757.5 | 753.75 | 300 | 377.7 | M6 | 739–754 | 745 | 750 | 41 | B15 | 743–753 | 748 | 1000 | 26 |
| Oa17 | 856–876 | 865 | 300 | 229.5 | M7 | 846–885 | 862 | 750 | 29/349 | B2 | 841–876 | 859 | 250/500/1000 | 285 | |
| I2 | 846–885 | 862 | 375 | 349 | |||||||||||
| SWIR | (N/A) | M8 | 1230–1250 | 1238 | 750 | 165 | B5 | 1230–1250 | 1240 | 500/1000 | 110 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, M.; Dodd, J. Ushering in the New Era of Radiometric Intercomparison of Multispectral Sensors with Precision SNO Analysis. Climate 2019, 7, 81. https://doi.org/10.3390/cli7060081
Chu M, Dodd J. Ushering in the New Era of Radiometric Intercomparison of Multispectral Sensors with Precision SNO Analysis. Climate. 2019; 7(6):81. https://doi.org/10.3390/cli7060081
Chicago/Turabian StyleChu, Mike, and Jennifer Dodd. 2019. "Ushering in the New Era of Radiometric Intercomparison of Multispectral Sensors with Precision SNO Analysis" Climate 7, no. 6: 81. https://doi.org/10.3390/cli7060081
APA StyleChu, M., & Dodd, J. (2019). Ushering in the New Era of Radiometric Intercomparison of Multispectral Sensors with Precision SNO Analysis. Climate, 7(6), 81. https://doi.org/10.3390/cli7060081





