Study on Temporal Variations of Surface Temperature and Rainfall at Conakry Airport, Guinea: 1960–2016
Abstract
1. Introduction
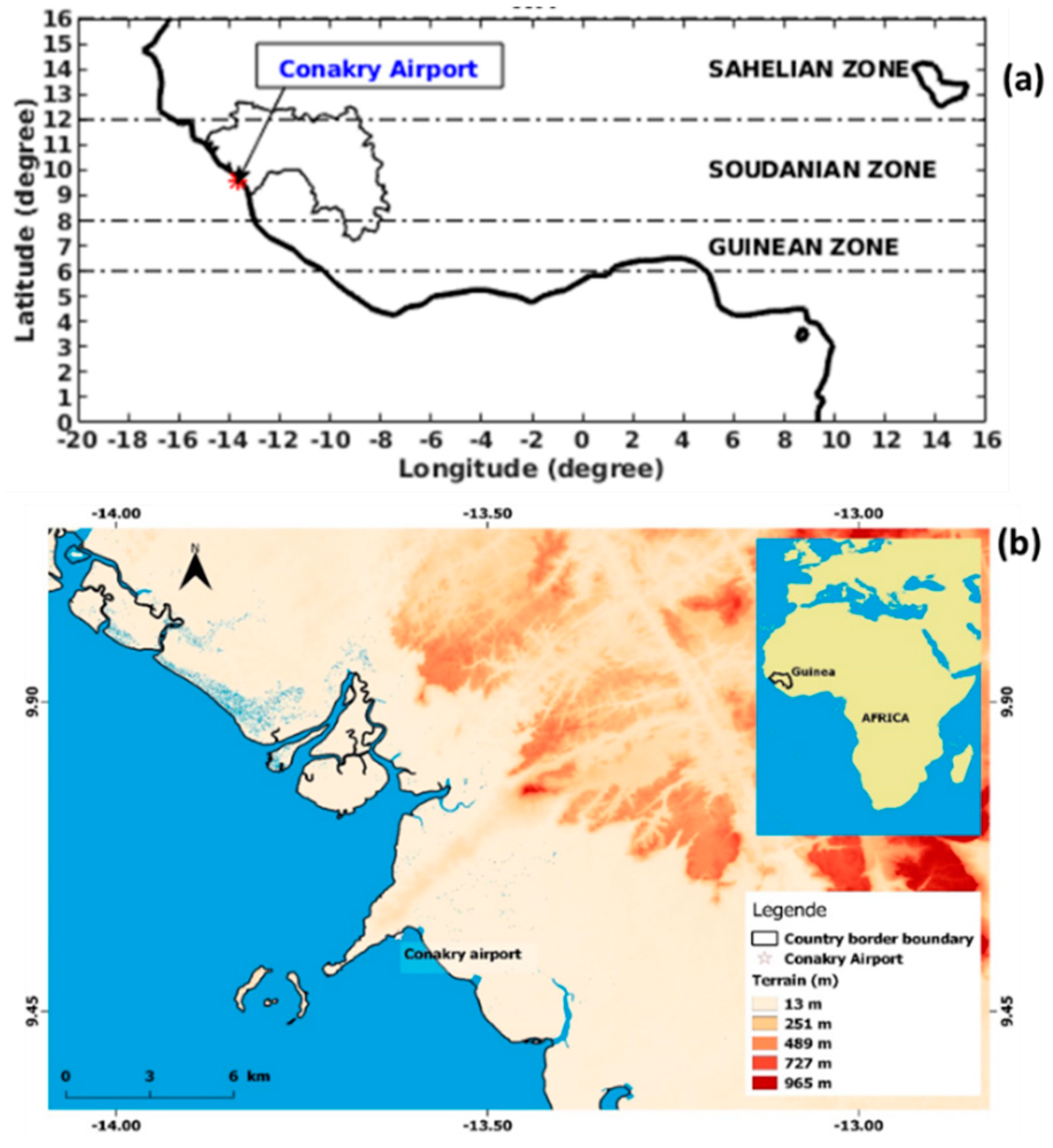
2. Materials and Methods
2.1. Data
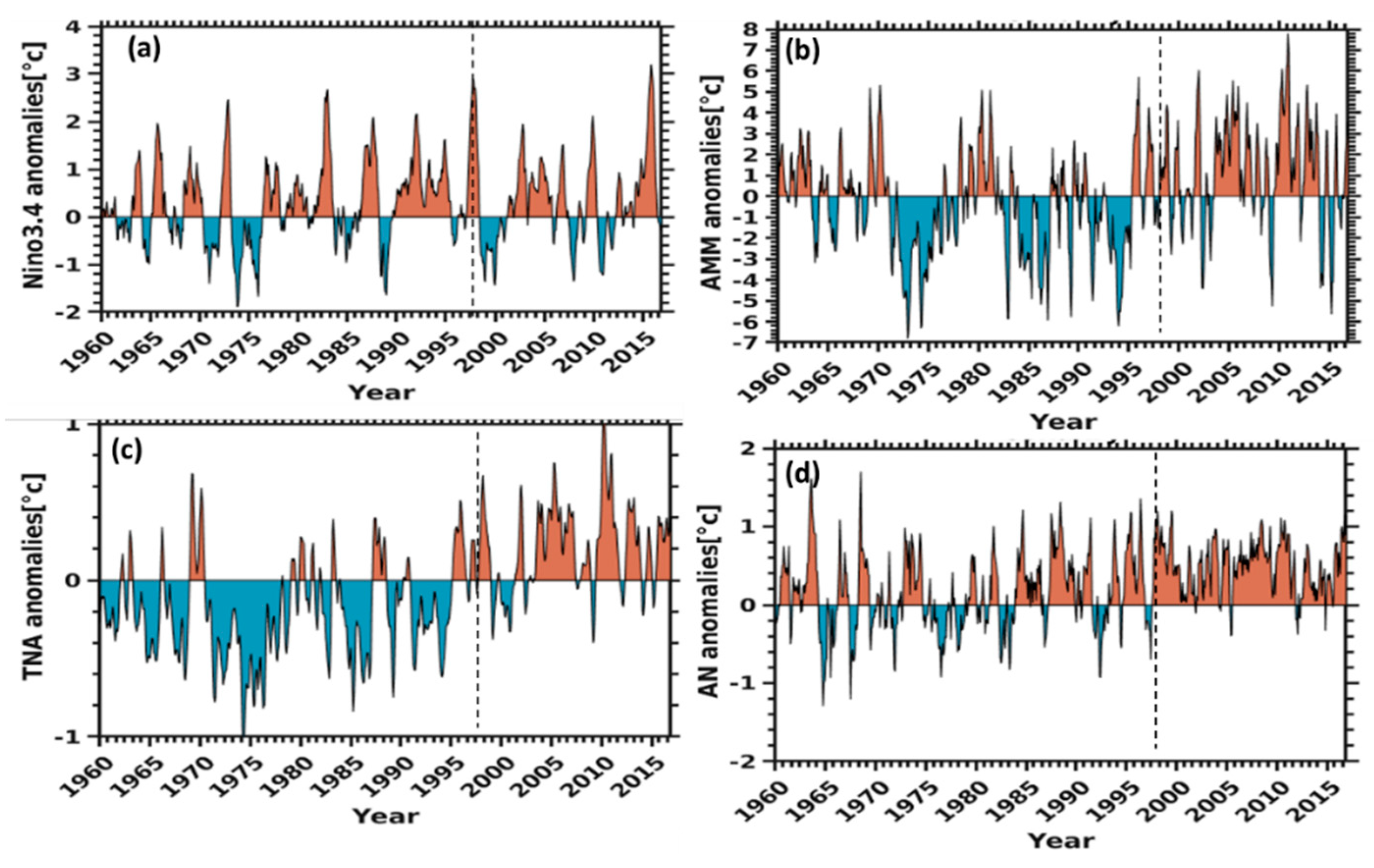
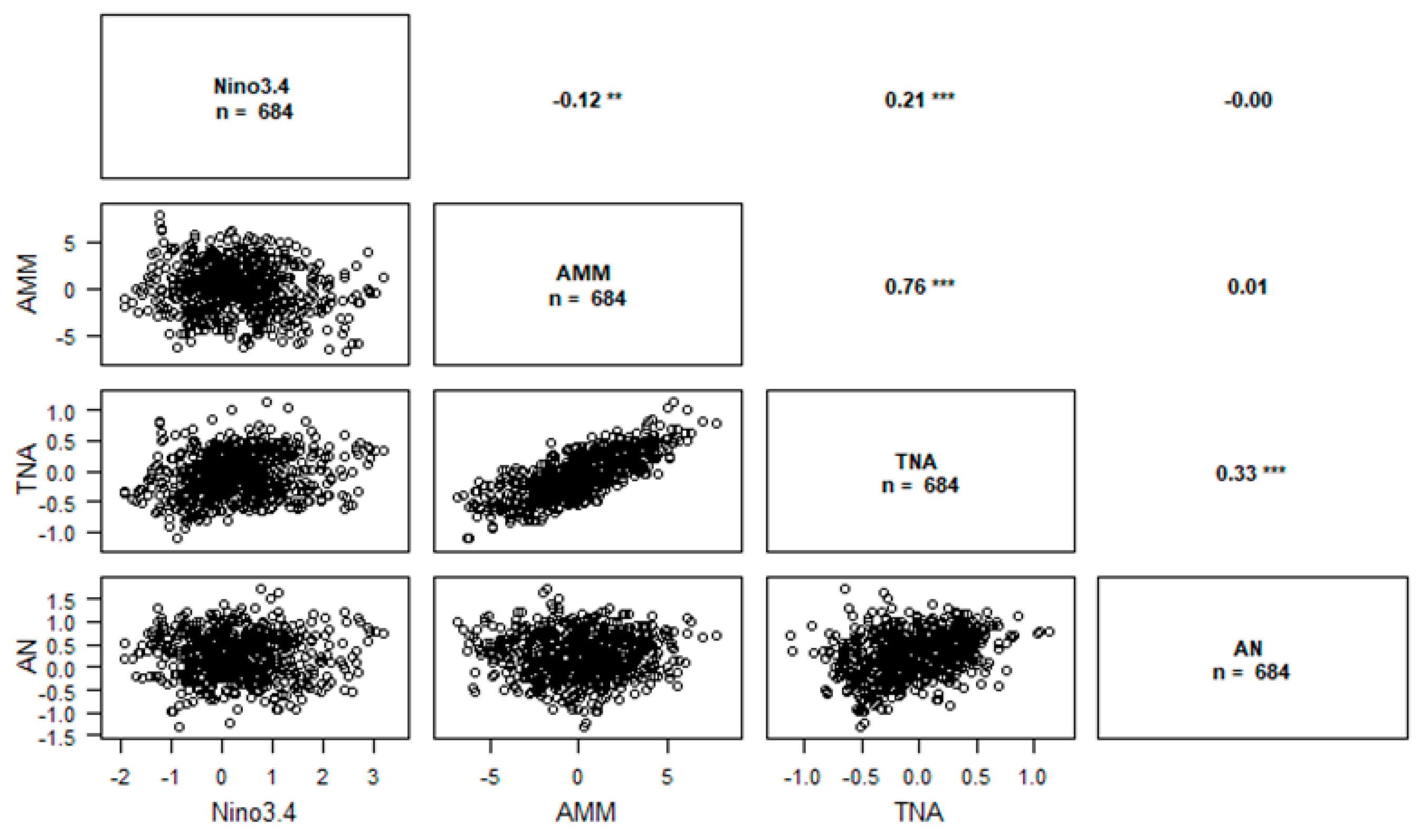
- Niño3.4 monthly mean time series from 1960 to 2016 (684 measurements) were downloaded from the National Oceanic and Atmospheric Administration (NOAA) website (https://www.esrl.noaa.gov/psd_wgsp/Timeseries). The Niño3.4 index is calculated by taking the area-averaged sea-surface temperature (SST) within the Niño3.4 region, which extends from 5° N to 5° S in latitude and from 120° W to 170° W in longitude (in the Pacific Ocean). We use Niño3.4 averages calculated from the HadISST SST dataset, which is given by 1° in latitude–longitude.
- Atlantic Meridional Mode (AMM) SST index from 1960 to 2016 (684 data) were downloaded from the National Oceanic and Atmospheric Administration (NOAA) website (https://www.esrl.noaa.gov/psd/data/timeseries/monthly). The AMM time series is calculated by projecting SST on to the spatial structure resulting from Maximum Covariance Analysis (MCA) to sea surface temperature (SST) over the region of 21° S–32° N, 74° W–15° E.
- Tropical Northern Atlantic index (TNA) is the anomaly of the monthly averaged SST values. The TNA SST index is defined as region-averaged SST anomalies in the domain (0°–20° N, 60° W–20° E) [24]. TNA monthly mean time series from 1960 to 2016 (684 data) were downloaded from the NOAA website (https://www.esrl.noaa.gov/psd/data/climateindices/list/#TNA).
- The Atlantic Niño (AN) or Atlantic Equatorial Mode is a quasiperiodic interannual climate pattern of the equatorial Atlantic Ocean. The term Atlantic Niño comes from its close similarity with the El Niño-Southern Oscillation (ENSO) that dominates the tropical Pacific basin [25]. The Atlantic Niño (AN) index is defined as the SST anomaly in the central-eastern tropical Atlantic: (3° S–3° N; 20° W–0° E) [26]. The AN monthly mean time series from 1960 to 2016 (684 measurements) were download from KNMI website (https://climexp.knmi.nl/start.cgi). The equatorial warming and cooling events associated with the Atlantic Niño are known to be strongly related to atmospheric climate anomalies, especially in African countries bordering the Gulf of Guinea [27]. As Conakry is a coastal region in west Africa, we used AN in our study.
2.2. Method
2.2.1. Mann-Kendal Test
2.2.2. Multilinear Regression
2.2.3. Theil-Sen’s Estimator
2.2.4. Wavelet Analysis
3. Results
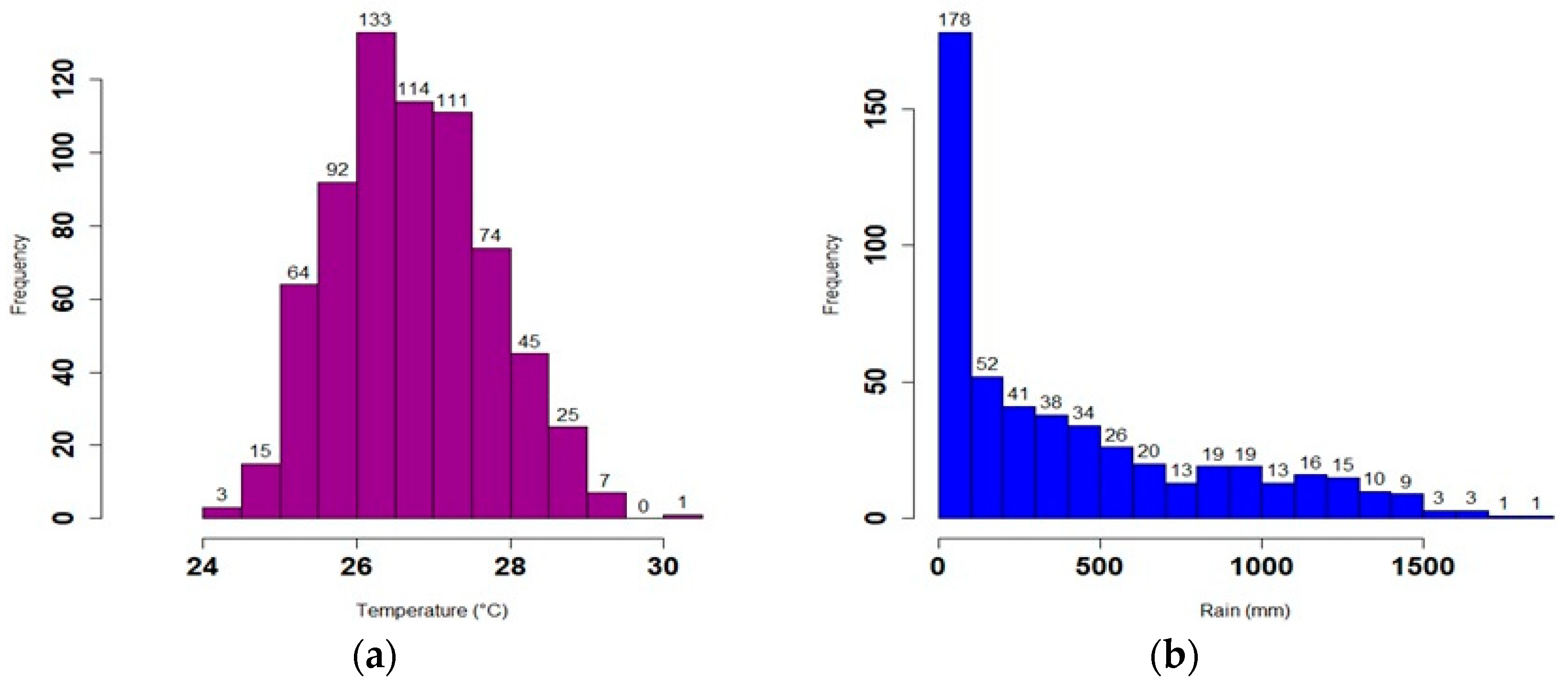
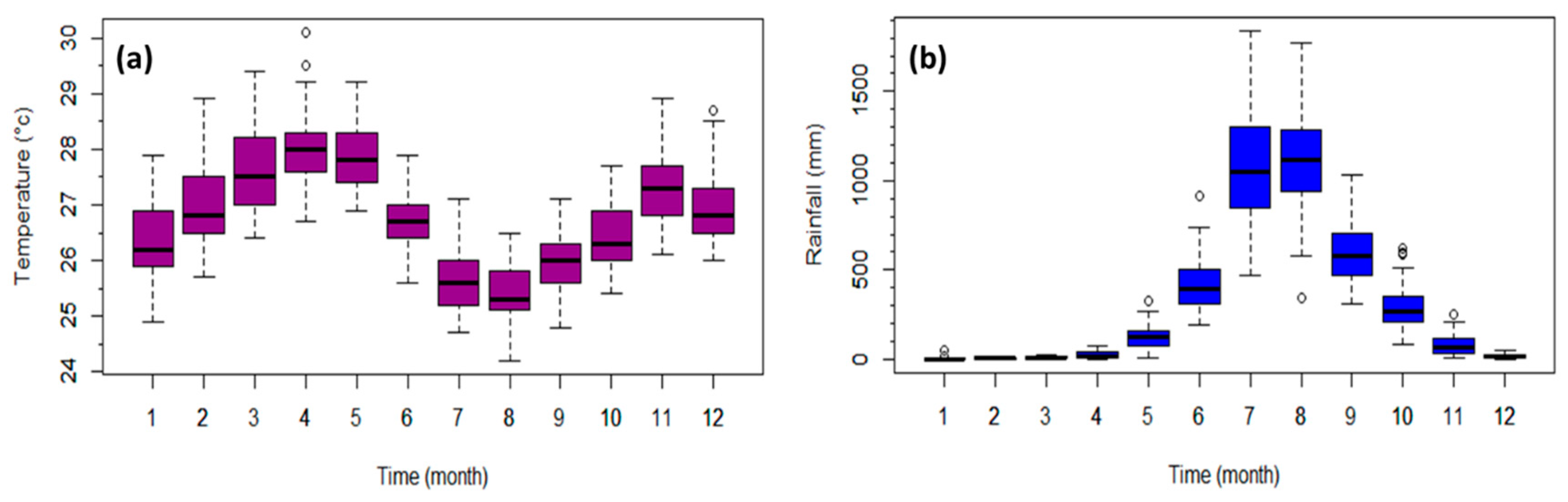
3.1. Climatology and Seasonality of Temperature and Rainfall
3.1.1. Inter-Annual Variation of Temperature and Rainfall
3.1.2. Monthly Climatological Variations
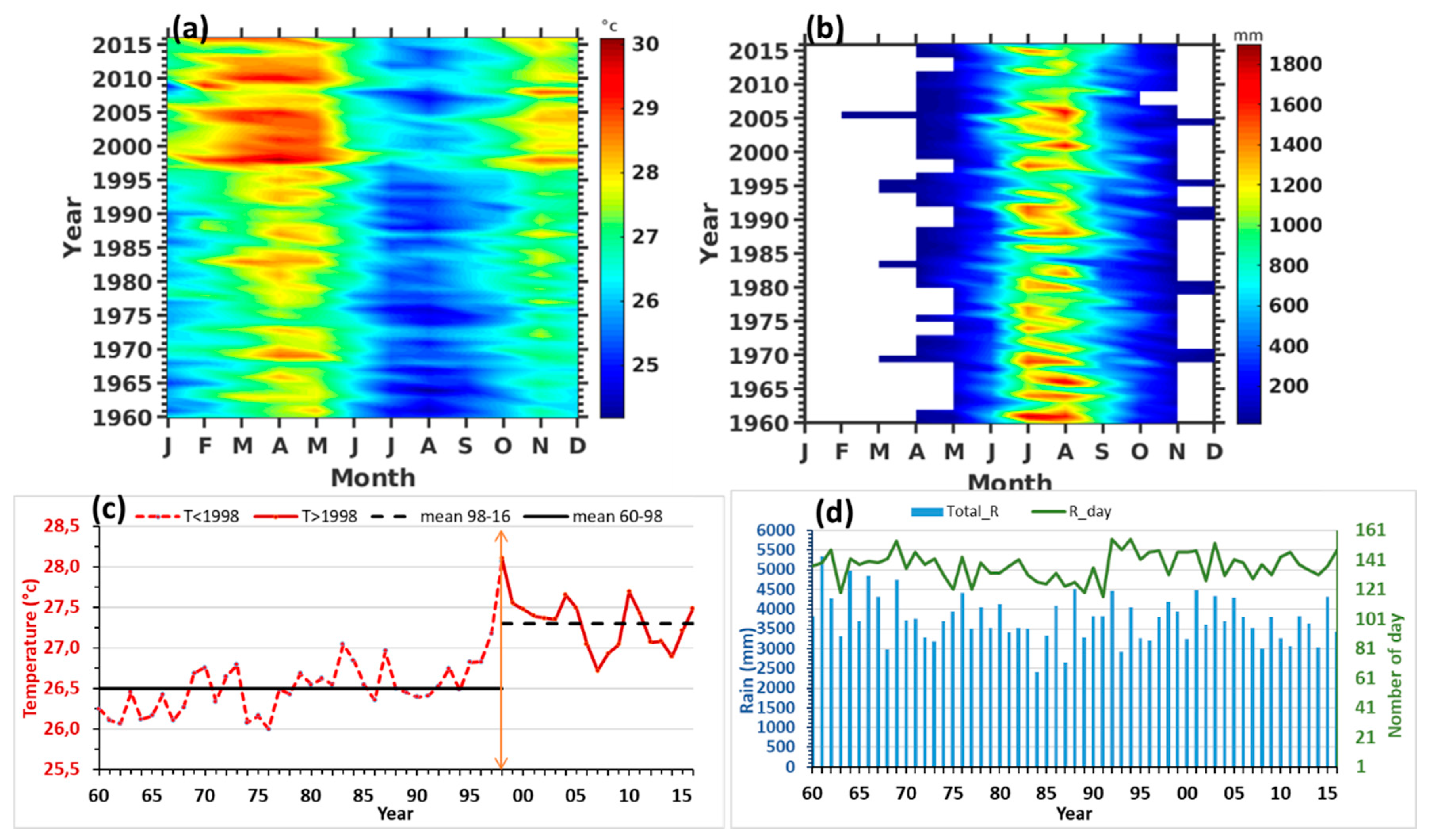
3.1.3. Temperature and Rainfall Anomalies
- (a) the cold class: it corresponds to periods with negative anomalies (1960–1962; 1964–1965; 1967–1968; 1971; 1974–1976; 1986);
- (b) the quiet or normal class with temperature anomalies close to zero (1963; 1966; 1977–1978; 1985–1986; 1988–1992, 1994) and;
- (c) the warm class with positive anomalies (1969–1970; 1972–1973; 1979–1984; 1987; 1993; 1995–2006). The last period of the warm class is the warmest and longest one, it lasts about 12 years (1995–2006).
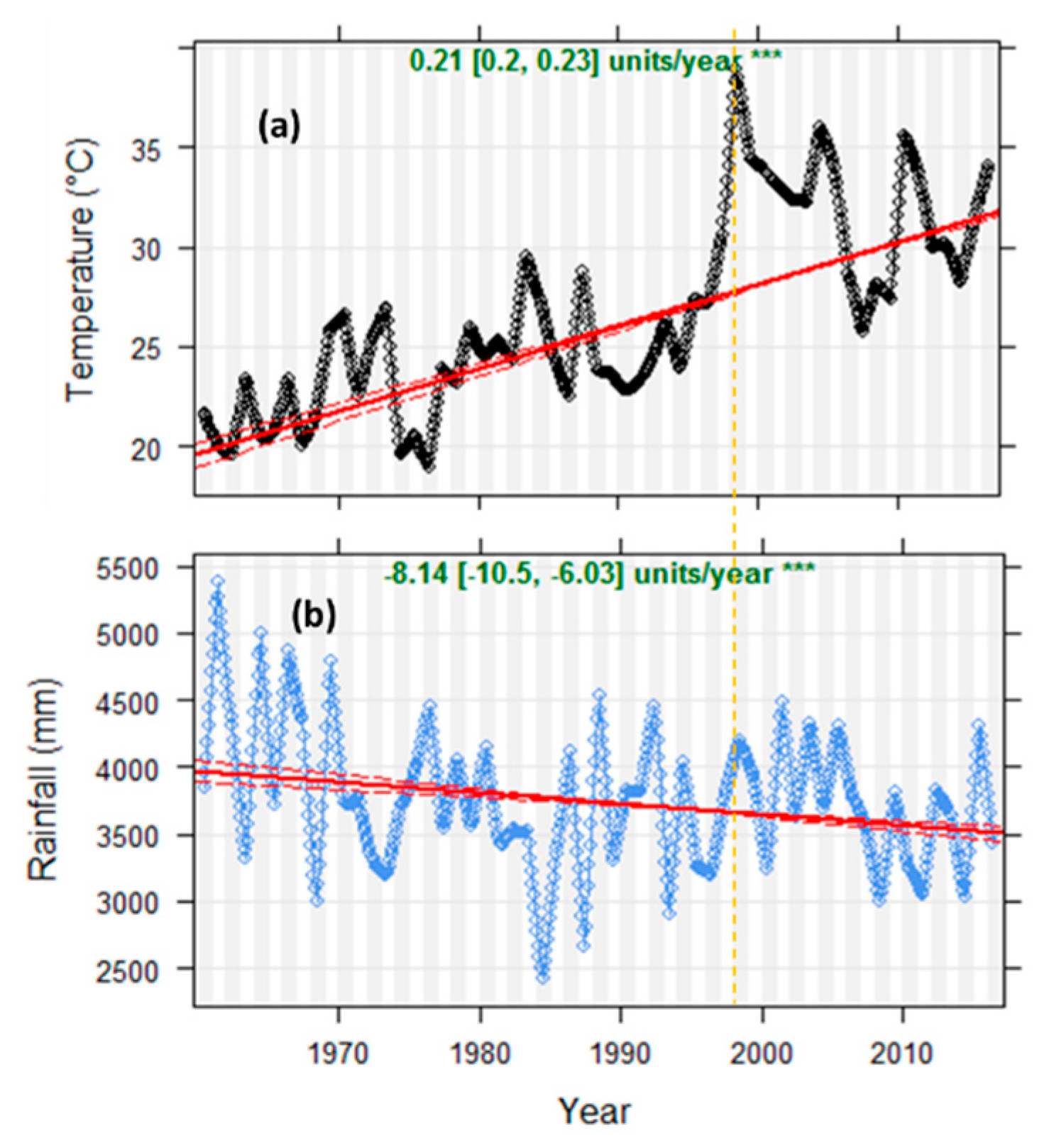
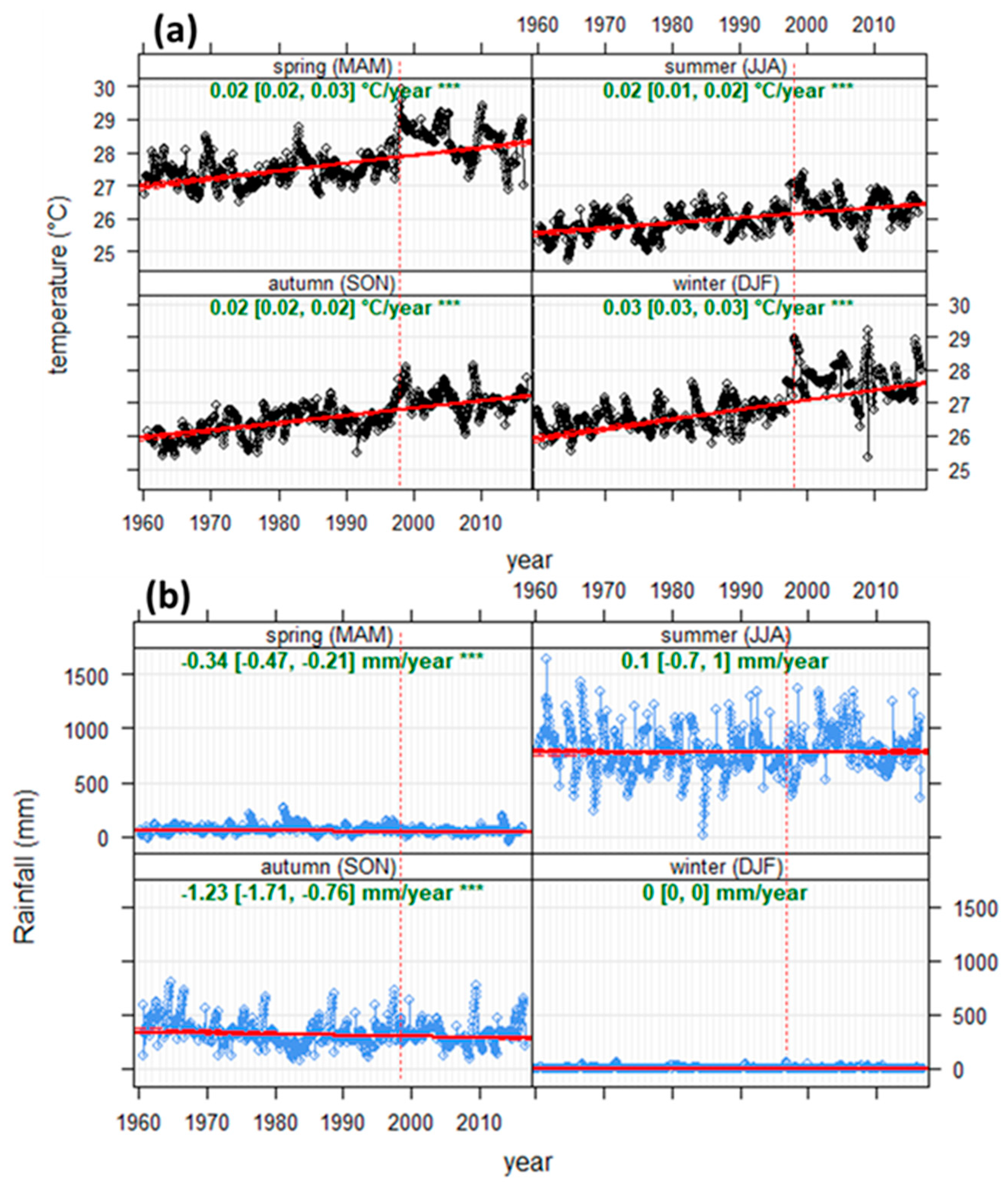
3.2. Trend Analysis of Temperature and Rainfall
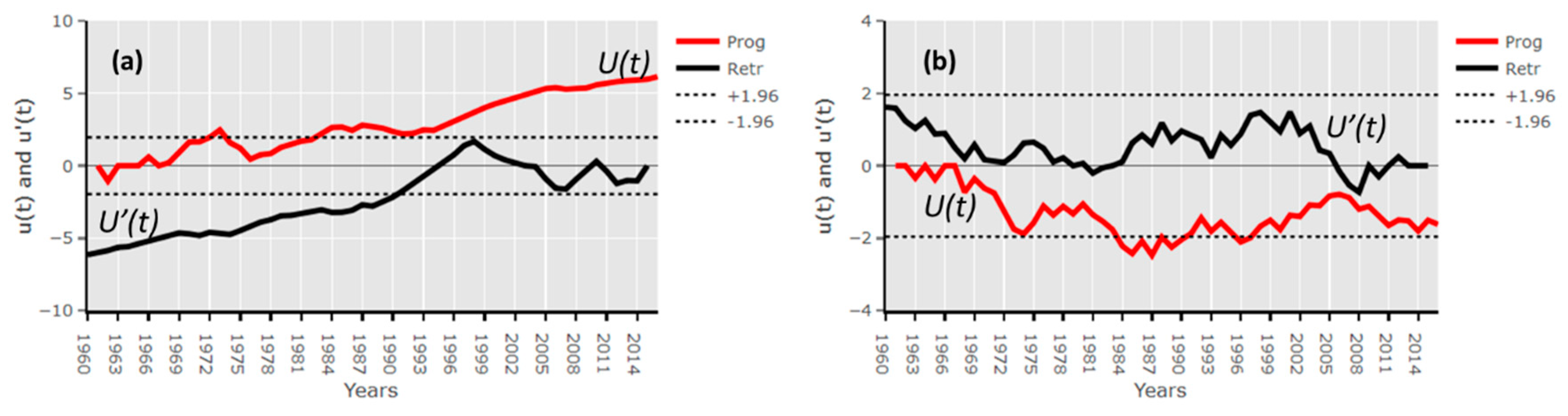
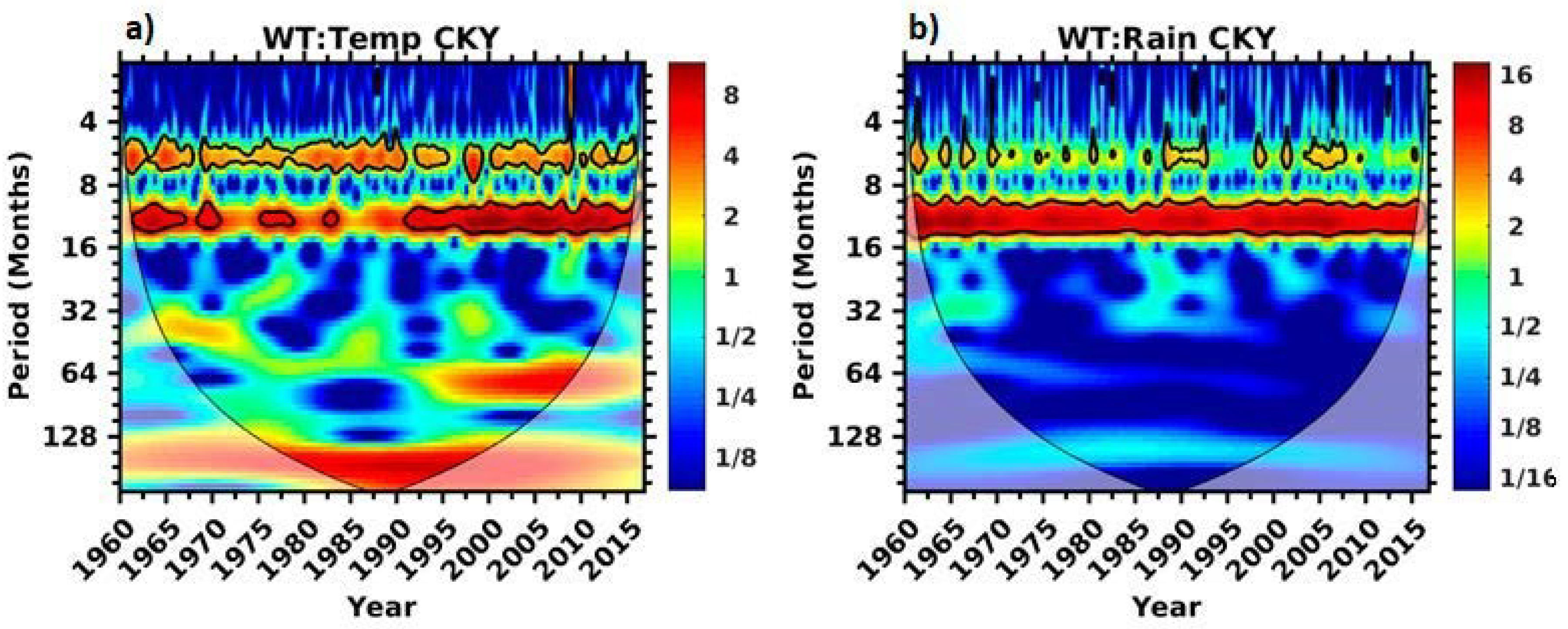
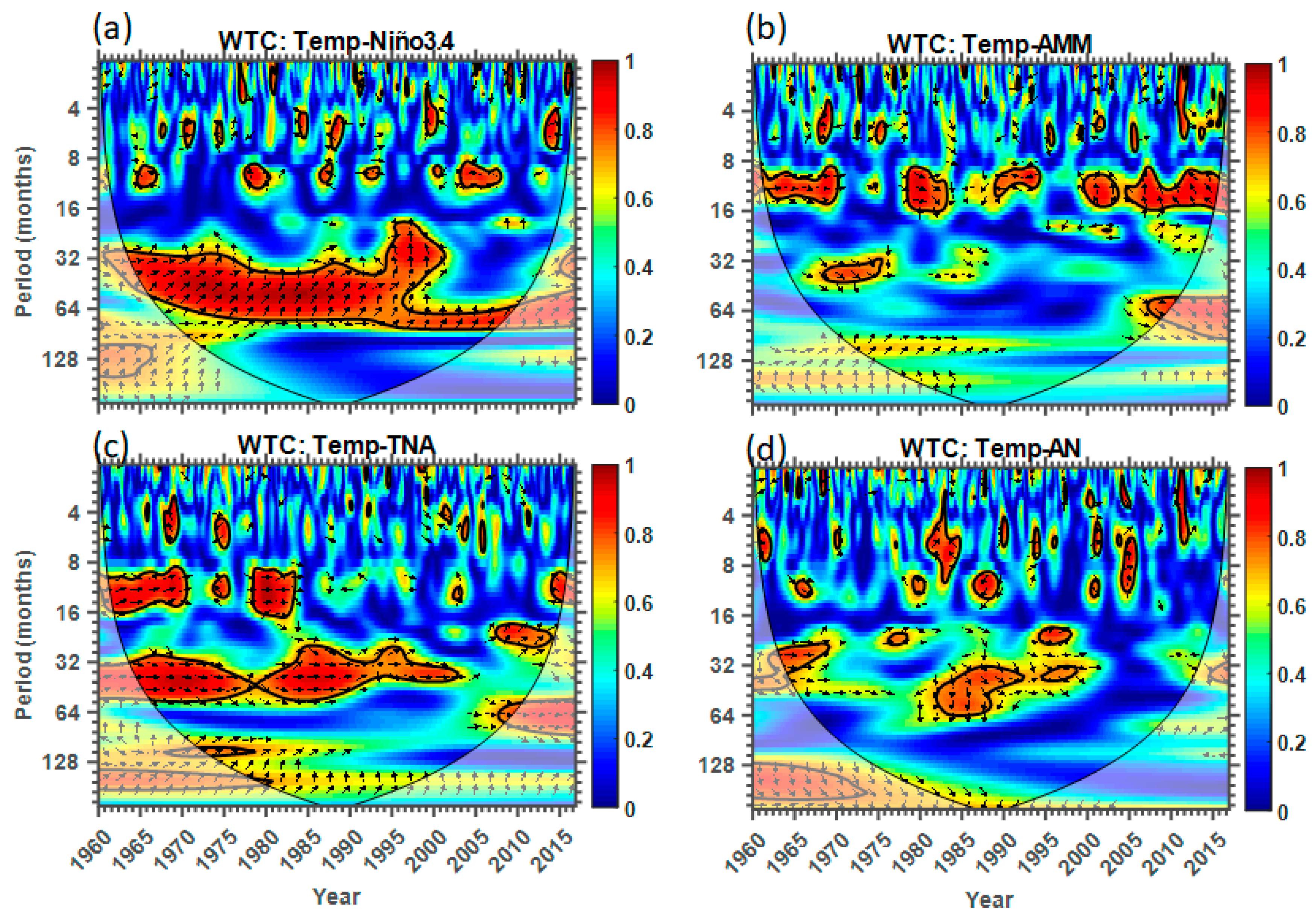
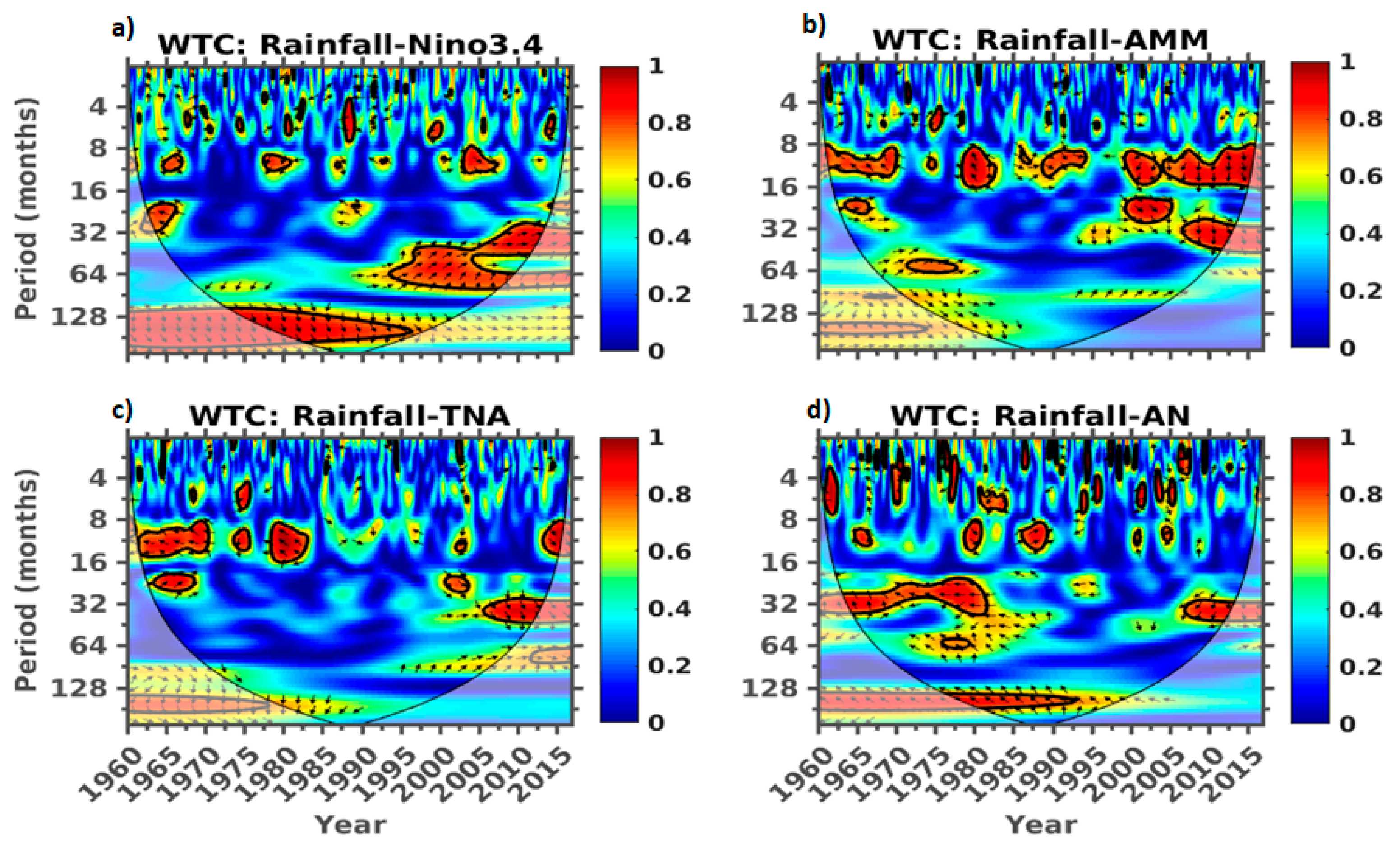
3.3. Wavelet Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Serra, C.; Burgueño, A.; Lana, X. Analysis of maximum and minimum daily temperatures recorded at Fabra Observatory (Barcelona, NE Spain) in the period 1917–1998. Int. J. Climatol. 2001, 21, 617–636. [Google Scholar] [CrossRef]
- Conway, D. Adapting climate research for development in Africa. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 428–450. [Google Scholar] [CrossRef]
- Zerbo, J.-L.; Ouattara, F.; Nanéma, E. Solar Activity and Meteorological Fluctuations in West Africa: Temperatures and Pluviometry in Burkina Faso, 1970–2012. Int. J. Astron. Astrophys. 2013, 3, 408–411. [Google Scholar] [CrossRef][Green Version]
- Schulte, J.A.; Najjar, R.G.; Li, M. The influence of climate modes on streamflow in the Mid-Atlantic region of the United States. J. Hydrol. Reg. Stud. 2016, 5, 80–99. [Google Scholar] [CrossRef]
- Gbobaniyi, E.; Sarr, A.; Sylla, M.B.; Diallo, I.; Lennard, C.; Dosio, A.; Dhiédiou, A.; Kamga, A.; Klutse, N.A.B.; Hewitson, B.; et al. Climatology, annual cycle and interannual variability of precipitation and temperature in CORDEX simulations over West Africa. Int. J. Climatol. 2014, 34, 2241–2257. [Google Scholar] [CrossRef]
- Rodrigues, L.R.L.; García-Serrano, J.; Doblas-Reyes, F. Seasonal forecast quality of the West African monsoon rainfall regimes by multiple forecast systems. J. Geophys. Res. Atmos. 2014, 119, 7908–7930. [Google Scholar] [CrossRef]
- Sylla, M.B.; Dell’Aquila, A.; Ruti, P.M.; Giorgi, F. Simulation of the intraseasonal and the interannual variability of rainfall over West Africa with RegCM3 during the monsoon period. Int. J. Climatol. 2010, 30, 1865–1883. [Google Scholar] [CrossRef]
- Vizy, E.K.; Cook, K.H. Development and application of a mesoscale climate model for the tropics: Influence of sea surface temperature anomalies on the West African monsoon. J. Geophys. Res. Atmos. 2002, 107. [Google Scholar] [CrossRef]
- Loua, R.T.; Beavogui, M.; Bencherif, H.; Barry, A.B.; BAMBA, Z.; Amory-Mazaudier, C. Climatology of Guinea: Study of Climate Variability in N’zerekore. J. Agric. Sci. Technol. A 2017, 7, 115–233. [Google Scholar]
- Paeth, H.; Hense, A. On the linear response of tropical African climate to SST changes deduced from regional climate model simulations. Theor. Appl. Climatol. 2006, 83, 1–19. [Google Scholar] [CrossRef]
- Okumura, Y.; Xie, S.-P. Interaction of the Atlantic equatorial cold tongue and the African monsoon. J. Clim. 2004, 17, 3589–3602. [Google Scholar] [CrossRef]
- Joly, M.; Voldoire, A. Role of the Gulf of Guinea in the inter-annual variability of the West African monsoon: What do we learn from CMIP3 coupled simulations? Int. J. Climatol. 2010, 30, 1843–1856. [Google Scholar] [CrossRef]
- Fitzpatrick, R.G.J.; Bain, C.L.; Knippertz, P.; Marsham, J.H.; Parker, D.J. The West African Monsoon Onset: A Concise Comparison of Definitions. J. Clim. 2015, 28, 8673–8694. [Google Scholar] [CrossRef]
- Sultan, B.; Janicot, S. The West African Monsoon Dynamics. Part II: The “Preonset” and “Onset” of the Summer Monsoon. J. Clim. 2003, 16, 3407–3427. [Google Scholar] [CrossRef]
- Sultan, B.; Janicot, S.; Diedhiou, A. The West African Monsoon Dynamics. Part I: Documentation of Intraseasonal Variability. J. Clim. 2003, 16, 3389–3406. [Google Scholar] [CrossRef]
- Nicholson, S.E. Rainfall and Atmospheric Circulation during Drought Periods and Wetter Years in West Africa. Mon. Weather Rev. 1981, 109, 2191–2208. [Google Scholar] [CrossRef]
- Nicholson, S.E. The West African Sahel: A Review of Recent Studies on the Rainfall Regime and Its Interannual Variability. Available online: https://www.hindawi.com/journals/isrn/2013/453521/ (accessed on 15 December 2017).
- Citeau, J.; Guillot, B.; Lahuec, J.-P.; ORSTOM (Eds.) Champs Thermiques de Surface de L’océan Atlantique: Convection et Fronts Thermiques Sur le Continent Africain: Essai de Mise en Relation; Initiation-Documentations Techniques; Télédetection; ORSTOM: Lannion, France, 1985; ISBN 978-2-7099-0770-5. [Google Scholar]
- Okoola, R.E.; Ambenje, P.G. Transition from the Southern to the Northern Hemisphere summer of zones of active convection over the Congo Basin. Meteorol. Atmos. Phys. 2003, 84, 255–265. [Google Scholar] [CrossRef]
- Espinoza Villar, J.C.; Ronchail, J.; Guyot, J.L.; Cochonneau, G.; Naziano, F.; Lavado, W.; De Oliveira, E.; Pombosa, R.; Vauchel, P. Spatio-temporal rainfall variability in the Amazon basin countries (Brazil, Peru, Bolivia, Colombia, and Ecuador). Int. J. Climatol. 2009, 29, 1574–1594. [Google Scholar] [CrossRef]
- Kouassi, A.; Assamoi, P.; Bigot, S.; Diawara, A.; Schayes, G.; Yoroba, F.; Kouassi, B. Étude du climat ouest-africain à l’aide du modèle atmosphérique régional MAR. Climatologie 2010, 7, 39–55. [Google Scholar]
- Carter, R.C.; Parker, A. Climate change, population trends and groundwater in Africa. Hydrol. Sci. J. 2009, 54, 676–689. [Google Scholar] [CrossRef]
- Tu, X.; Du, Y.; Singh, V.P.; Chen, X. Joint distribution of design precipitation and tide and impact of sampling in a coastal area. Int. J. Climatol. 2018, 38, e290–e302. [Google Scholar] [CrossRef]
- Chen, S.-F.; Wu, R. An enhanced influence of sea surface temperature in the tropical northern Atlantic on the following winter ENSO since the early 1980s. Atmos. Ocean. Sci. Lett. 2017, 10, 175–182. [Google Scholar] [CrossRef]
- Wang, C. ENSO, Atlantic Climate Variability, and the Walker and Hadley Circulations. In The Hadley Circulation: Present, Past and Future; Diaz, H.F., Bradley, R.S., Eds.; Springer: Dordrecht, The Netherlands, 2004; Volume 21, pp. 173–202. ISBN 978-90-481-6752-4. [Google Scholar]
- Rodríguez-Fonseca, B.; Polo, I.; García-Serrano, J.; Losada, T.; Mohino, E.; Mechoso, C.R.; Kucharski, F. Are Atlantic Niños enhancing Pacific ENSO events in recent decades? Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Zebiak, S.E. Air-Sea Interaction in the Equatorial Atlantic Region. J. Clim. 1993, 6, 1567–1586. [Google Scholar] [CrossRef]
- WMO. Directives de L’OMM Pour le Calcul Des Normales Climatiques; OMM, Édition 2017; OMM: Geneva, Switzerland, 2017; ISBN 978-92-63-21203-0. [Google Scholar]
- WMO. Calculation of Monthly and Annual 30-Year Standat Normals; WMO: Washington, DC, USA, 1989; Volume 10. [Google Scholar]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann-Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Okafor, G.C.; Jimoh, O.D.; Larbi, K.I. Detecting Changes in Hydro-Climatic Variables during the Last Four Decades (1975–2014) on Downstream Kaduna River Catchment, Nigeria. Atmos. Clim. Sci. 2017, 7, 161–175. [Google Scholar] [CrossRef]
- Sneyers, R. On the Statistical Analysis of Series of Observations; World Meteorological Organization: Geneva, Switzerland, 1990; pp. 143–192. [Google Scholar]
- Rahman, M.A.; Yunsheng, L.; Sultana, N. Analysis and prediction of rainfall trends over Bangladesh using Mann-Kendall, Spearman’s rho tests and ARIMA model. Meteorol. Atmos. Phys. 2017, 129, 409–424. [Google Scholar] [CrossRef]
- Chen, Y.; Guan, Y.; Shao, G.; Zhang, D. Investigating Trends in Streamflow and Precipitation in Huangfuchuan Basin with Wavelet Analysis and the Mann-Kendall Test. Water 2016, 8, 77. [Google Scholar] [CrossRef]
- Mbatha, N.; Xulu, S. Time Series Analysis of MODIS-Derived NDVI for the Hluhluwe-Imfolozi Park, South Africa: Impact of Recent Intense Drought. Climate 2018, 6, 95. [Google Scholar] [CrossRef]
- Khan, A.; Chatterjee, S.; Bisai, D. On the long-term variability of temperature trends and changes in surface air temperature in Kolkata Weather Observatory, West Bengal, India. Meteorol. Hydrol. Water Manag. 2015, 3, 9–16. [Google Scholar] [CrossRef]
- Dang, X.; Peng, H.; Wang, X.; Zhang, H. Theil-Sen Estimators in a Multiple Linear Regression Model. Olemiss Edu, 2008. Available online: http://home.olemiss.edu/~xdang/papers/MTSE.pdf (accessed on 1 January 2019).
- Theil, H. A rank-invariant method of linear and polynomial regression analysis, 3; confidence regions for the parameters of polynomial regression equations. Inproceding. 1950, 53, 386–392. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Chang, C.; Glover, G.H. Time-frequency dynamics of resting-state brain connectivity measured with fMRI. NeuroImage 2010, 50, 81–98. [Google Scholar] [CrossRef]
- Bilbao, J.; Román, R.; Yousif, C.; Mateos, D.; de Miguel, A. Total ozone column, water vapour and aerosol effects on erythemal and global solar irradiance in Marsaxlokk, Malta. Atmos. Environ. 2014, 99, 508–518. [Google Scholar] [CrossRef]
- FAO Update on FAO’s Activities in Relation to the 1997/98 El Niño and La Niña: October 1998. Available online: http://www.fao.org/english/newsroom/global/elnin3-e.htm (accessed on 1 January 2019).
- Nicholson, S.E.; Some, B.; Kone, B. An Analysis of Recent Rainfall Conditions in West Africa, Including the Rainy Seasons of the 1997 El Niño and the 1998 La Niña Years. J. Clim. 2000, 13, 2628–2640. [Google Scholar] [CrossRef]
- Angell, J.K. Comparison of surface and tropospheric temperature trends estimated from a 63-Station Radiosonde Network, 1958–1998. Geophys. Res. Lett. 1999, 26, 2761–2764. [Google Scholar] [CrossRef]
- Maidment, R.I.; Allan, R.P.; Black, E. Recent observed and simulated changes in precipitation over Africa. Geophys. Res. Lett. 2015, 42, 8155–8164. [Google Scholar] [CrossRef]
- Khodri, M.; Izumo, T.; Vialard, J.; Janicot, S.; Cassou, C.; Lengaigne, M.; Mignot, J.; Gastineau, G.; Guilyardi, E.; Lebas, N.; et al. Tropical explosive volcanic eruptions can trigger El Niño by cooling tropical Africa. Nat. Commun. 2017, 8, 778. [Google Scholar] [CrossRef]
- Liu, F.; Chai, J.; Wang, B.; Liu, J.; Zhang, X.; Wang, Z. Global monsoon precipitation responses to large volcanic eruptions. Sci. Rep. 2016, 6, 24331. [Google Scholar] [CrossRef]
- Wang, S.; Gong, D. Enhancement of the warming trend in China. Geophys. Res. Lett. 2000, 27, 2581–2584. [Google Scholar] [CrossRef]
- Foster, G.; Rahmstorf, S. Global temperature evolution 1979–2010. Environ. Res. Lett. 2011, 6, 044022. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Caron, J.M.; Stepaniak, D.P.; Worley, S. Evolution of El Niño-Southern Oscillation and global atmospheric surface temperatures. J. Geophys. Res. Atmos. 2002, 107. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T. An apparent hiatus in global warming? Earths Future 2013, 1, 19–32. [Google Scholar] [CrossRef]
- Djigbo, F.B.; Afouda, A.; Diekkrüger, B.; Kapangaziwiri, E. Investigation on the 1970s and 1980s Droughts in Four Tributaries of the Niger River Basin (West Africa). In Proceedings, The Hague. 2015. Available online: http://rgdoi.net/10.13140/RG.2.1.1559.0485 (accessed on 1 January 2019).
- Masih, I.; Maskey, S.; Mussá, F.E.F.; Trambauer, P. A review of droughts on the African continent: A geospatial and long-term perspective. Hydrol. Earth Syst. Sci. 2014, 18, 3635–3649. [Google Scholar] [CrossRef]
- Sylla, M.B.; Diallo, I.; Pal, J.S. West African Monsoon in State-of-the-Science Regional Climate Models, In Tech. 2013. Available online: https://www.intechopen.com/books/climate-variability-regional-and-thematic-patterns/west-african-monsoon-in-state-of-the-science-regional-climate-models (accessed on 1 January 2019).
- El Niño en 97-98 El Niño en 97-98|Espace des Sciences. Available online: https://www.espace-sciences.org/multimedia/blogs/57931/billet/el-nino-en-97-98 (accessed on 19 February 2019).
- Simmons, A.J.; Berrisford, P.; Dee, D.P.; Hersbach, H.; Hirahara, S.; Thépaut, J.-N. A reassessment of temperature variations and trends from global reanalyses and monthly surface climatological datasets. Q. J. R. Meteorol. Soc. 2016, 143, 101–119. [Google Scholar] [CrossRef]
- Peel, M.C.; Pegram, G.G.S.; Mcmahon, T.A. Global analysis of runs of annual precipitation and runoff equal to or below the median: Run length. Int. J. Climatol. 2004, 24, 807–822. [Google Scholar] [CrossRef]
- Nicholson, S.E. The nature of rainfall variability over Africa on time scales of decades to millenia. Glob. Planet. Chang. 2000, 26, 137–158. [Google Scholar] [CrossRef]
- Bonnecase, V. Retour sur la famine au Sahel du début des années 1970: La construction d’un savoir de crise, Building knowledge on a crisis. Famine in Sahelian Africa in the early 1970s. Politique Afr. 2010, 3, 23–42. [Google Scholar] [CrossRef]
- Ouedraogo, M.; Paturel, J.-E.; Mahe, G. Conséquences de la Sécheresse Observée Depuis le Début des Années 1970 en Afrique de L’Ouest et Centrale: Normes Météorologiques et Hydrologiques; IAHS Press: Cape Town, South Africa, 2002; Volume 274, pp. 149–155. [Google Scholar]
- Suhaila, J.; Yusop, Z. Trend analysis and change point detection of annual and seasonal temperature series in Peninsular Malaysia. Meteorol. Atmos. Phys. 2018, 130, 565–581. [Google Scholar] [CrossRef]
- Chiang, J.C.H.; Vimont, D.J. Analogous Pacific and Atlantic Meridional Modes of Tropical Atmosphere-Ocean Variability. J. Clim. 2004, 17, 4143–4158. [Google Scholar] [CrossRef]
- Ruiz-Barradas, A.; Carton, J.A.; Nigam, S. Role of the Atmosphere in Climate Variability of the Tropical Atlantic. J. Clim. 2003, 16, 2052–2065. [Google Scholar] [CrossRef]
- Servain, J. Simple climatic indices for the tropical Atlantic Ocean and some applications. J. Geophys. Res. 1991, 96, 15137–15146. [Google Scholar] [CrossRef]
- Xie, S.-P.; Carton, J.A. Tropical Atlantic Variability: Patterns, Mechanisms, and Impacts. In Geophysical Monograph Series; Wang, C., Xie, S.P., Carton, J.A., Eds.; American Geophysical Union: Washington, DC, USA, 2004; pp. 121–142. ISBN 978-1-118-66594-7. [Google Scholar]
- Smirnov, D.; Vimont, D.J. Variability of the Atlantic Meridional Mode during the Atlantic Hurricane Season. J. Clim. 2011, 24, 1409–1424. [Google Scholar] [CrossRef]
- Merle, J.; Fieux, M.; Hisard, P. Annual signal and interannual anomalies of sea surface temperature in the eastern equatorial Atlantic Ocean. In Oceanography and Surface Layer Meteorology in the B/C Scale; Elsevier: Amsterdam, The Netherlands, 1980; pp. 77–101. ISBN 978-1-4832-8366-1. [Google Scholar]
- Doi, T.; Tozuka, T.; Yamagata, T. The Atlantic Meridional Mode and Its Coupled Variability with the Guinea Dome. J. Clim. 2010, 23, 455–475. [Google Scholar] [CrossRef]
- Chen, S.; Wu, R.; Chen, W. The Changing Relationship between Interannual Variations of the North Atlantic Oscillation and Northern Tropical Atlantic SST. J. Clim. 2015, 28, 485–504. [Google Scholar] [CrossRef]
- Rugg, A.; Foltz, G.R.; Perez, R.C. Role of Mixed Layer Dynamics in Tropical North Atlantic Interannual Sea Surface Temperature Variability. J. Clim. 2016, 29, 8083–8101. [Google Scholar] [CrossRef]
- Nnamchi, H.C.; Li, J.; Kucharski, F.; Kang, I.-S.; Keenlyside, N.S.; Chang, P.; Farneti, R. Thermodynamic controls of the Atlantic Niño. Nat. Commun. 2015, 6, 8895. [Google Scholar] [CrossRef]
- Philander, S.G. El Niño, La Niña, and the Southern Oscillation; International Geophysics Series; Academy Press: San Diego, CA, USA, 1990; ISBN 978-0-12-553235-8. [Google Scholar]
- Jury, M.R.; Enfield, D.B.; Mélice, J.-L. Tropical monsoons around Africa: Stability of El Niño–Southern Oscillation associations and links with continental climate. J. Geophys. Res. 2002. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (Ed.) Climate Change 2013—The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014; ISBN 978-1-107-41532-4. [Google Scholar]
- IPCC. Special Report on the impacts of global warming of 1.5 °C above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change, sustainable development, and efforts to eradicate poverty. 2018. In Press. Available online: https://www.ipcc.ch/sr15/ (accessed on 1 January 2019).
- Foltz, G.R.; McPhaden, M.J.; Lumpkin, R. A Strong Atlantic Meridional Mode Event in 2009: The Role of Mixed Layer Dynamics. J. Clim. 2012, 25, 363–380. [Google Scholar] [CrossRef]
- Preethi, B.; Sabin, T.P.; Adedoyin, J.A.; Ashok, K. Impacts of the ENSO Modoki and Other Tropical Indo-Pacific Climate-Drivers on African Rainfall. Sci. Rep. 2015, 5, 16653. [Google Scholar] [CrossRef]
- Ruchith, R.D.; Sivakumar, V. Influence of aerosol-cloud interaction on austral summer precipitation over Southern Africa during ENSO events. Atmos. Res. 2018, 202, 1–9. [Google Scholar] [CrossRef]
- Narasimha, R.; Bhattacharyya, S. A wavelet cross-spectral analysis of solar–ENSO–rainfall connections in the Indian monsoons. Appl. Comput. Harmon. Anal. 2010, 28, 285–295. [Google Scholar] [CrossRef]
- Wang, C. Atmospheric Circulation Cells Associated with the El Niño-Southern Oscillation. J. Clim. 2002, 15, 399–419. [Google Scholar] [CrossRef]
- Uvo, C.B.; Repelli, C.A.; Zebiak, S.E.; Kushnir, Y. The Relationships between Tropical Pacific and Atlantic SST and Northeast Brazil Monthly Precipitation. J. Clim. 1998, 11, 551–562. [Google Scholar] [CrossRef]
- Sun, M.; Li, X.; Kim, G. Correlation Analysis of Climate Indices and Precipitation Using Wavelet Image Processing Approach. In Lecture Notes in Electrical Engineering, Proceedings of the International Conference on Frontier Computing; Springer: Singapore, 2017; pp. 231–240. [Google Scholar]
- Bhattacharyya, S. Possible association between Indian monsoon rainfall and solar activity. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Hastenrath, S.; Polzin, D. Long-term variations of circulation in the tropical Atlantic sector and Sahel rainfall. Int. J. Climatol. 2011, 31, 649–655. [Google Scholar] [CrossRef]
- Rodríguez-Fonseca, B.; Mohino, E.; Mechoso, C.R.; Caminade, C.; Biasutti, M.; Gaetani, M.; Garcia-Serrano, J.; Vizy, E.K.; Cook, K.; Xue, Y.; et al. Variability and Predictability of West African Droughts: A Review on the Role of Sea Surface Temperature Anomalies. J. Clim. 2015, 28, 4034–4060. [Google Scholar] [CrossRef]
- Mbata, A.; Jean Marie, T.; Phuku Phuati, E.; Kyamakya, K.; Keto, F.; Bopili Mbotia, R.; Ndotoni, Z. Continuous wavelet analysis of rainfall fluctuations at interannual and decennial scales on the south-eastern part in the Democratic Republic of the Congo between 1940 and 1997. Int. J. Innov. Sci. Res. 2016, 27, 2351–8014. [Google Scholar]
- Giannini, A.; Saravanan, R.; Chang, P. Oceanic Forcing of Sahel Rainfall on Interannual to Interdecadal Time Scales. Science 2003, 302, 1027–1030. [Google Scholar] [CrossRef]
- Davey, M.K.; Brookshaw, A.; Ineson, S. The probability of the impact of ENSO on precipitation and near-surface temperature. Clim. Risk Manag. 2014, 1, 5–24. [Google Scholar] [CrossRef]
- Bose, M.; Kasim, I.; Mande, H.; Abdullah, A. Rainfall Trend Detection in Northern Nigeria over the Period of 1970–2012. J. Environ. Earth Sci. 2015, 5, 94–99. [Google Scholar]
- Sanogo, S.; Fink, A.H.; Omotosho, J.A.; Ba, A.; Redl, R.; Ermert, V. Spatio-temporal characteristics of the recent rainfall recovery in West Africa. Int. J. Climatol. 2015, 35, 4589–4605. [Google Scholar] [CrossRef]
- Andam-Akorful, S.A.; Ferreira, V.G.; Ndehedehe, C.E.; Quaye-Ballard, J.A. An investigation into the freshwater variability in West Africa during 1979–2010. Int. J. Climatol. 2017, 37, 333–349. [Google Scholar] [CrossRef]
- Dennett, M.D.; Elston, J.; Rodgers, J.A. A reappraisal of rainfall trends in the sahel. J. Climatol. 1985, 5, 353–361. [Google Scholar] [CrossRef]
- Fontaine, B.; Janicot, S. Sea Surface Temperature Fields Associated with West African Rainfall Anomaly Types. J. Clim. 1996, 9, 2935–2940. [Google Scholar] [CrossRef]
- Aguilar, E.; Barry, A.A.; Brunet, M.; Ekang, L.; Fernandes, A.; Massoukina, M.; Mbah, J.; Mhanda, A.; do Nascimento, D.J.; Peterson, T.C.; et al. Changes in temperature and precipitation extremes in western central Africa, Guinea Conakry, and Zimbabwe, 1955–2006. J. Geophys. Res. Atmos. 2009, 114, 2039–2055. [Google Scholar] [CrossRef]
- Panthou, G.; Lebel, T.; Vischel, T.; Quantin, G.; Sane, Y.; Ba, A.; Ndiaye, O.; Diongue-Niang, A.; Diopkane, M. Rainfall intensification in tropical semi-arid regions: The Sahelian case. Environ. Res. Lett. 2018, 13, 064013. [Google Scholar] [CrossRef]
- Lübbecke, J.F.; Rodríguez-Fonseca, B.; Richter, I.; Martín-Rey, M.; Losada, T.; Polo, I.; Keenlyside, N.S. Equatorial Atlantic variability-Modes, mechanisms, and global teleconnections. Wiley Interdiscip. Rev. Clim. Chang. 2018, 9, e527. [Google Scholar] [CrossRef]
- Bjerknes, J. Atmospheric teleconnections from the equatorial pacific. Mon. Weather Rev. 1969, 97, 163–172. [Google Scholar] [CrossRef]
- Nnamchi, H.C.; Li, J.; Kucharski, F.; Kang, I.-S.; Keenlyside, N.S.; Chang, P.; Farneti, R. An Equatorial-Extratropical Dipole Structure of the Atlantic Niño. J. Clim. 2016, 29, 7295–7311. [Google Scholar] [CrossRef]
- Adejuwon, J.O.; Balogun, E.E.; Adejuwon, S.A. On the annual and seasonal patterns of rainfall fluctuations in sub-saharan West Africa. Int. J. Climatol. 1990, 10, 839–848. [Google Scholar] [CrossRef]
- Janicot, S.; Moron, V.; Fontaine, B. Sahel droughts and ENSO dynamics. Geophys. Res. Lett. 1996, 23, 515–518. [Google Scholar] [CrossRef]
- Srivastava, G.; Chakraborty, A.; Nanjundiah, R.S. Multidecadal see-saw of the impact of ENSO on Indian and West African summer monsoon rainfall. Clim. Dyn. 2018, 1–17. [Google Scholar] [CrossRef]
- Christensen, J.H.; Hewitson, B.; Busuioc, A.; Chen, A.; Gao, X.; Held, R.; Jones, R.; Kolli, R.K.; Kwon, W.K.; Laprise, R.; et al. Regional Climate Projections. Available online: http://epic.awi.de/17617/ (accessed on 15 January 2019).

| Variables | Estimate | Std. Error | t-Value | p-Value | Significance |
|---|---|---|---|---|---|
| Niño 3.4 | −0.11653 | 0.04722 | −2.468 | 0.0138 | * |
| AMM | −0.14055 | 0.02675 | −5.254 | 1.99 × 107 | *** |
| TNA | 1.79296 | 0.20497 | 8.747 | 2 × 1016 | *** |
| AN | 0.14372 | 0.08790 | 1.635 | 0.1025 |
| Variables | Estimate | Std. Error | t-Value | p-Value | Significance |
|---|---|---|---|---|---|
| Niño 3.4 | 43.55 | 21.55 | 2.020 | 0.04374 | * |
| AMM | 34.89 | 12.21 | 2.857 | 0.00441 | ** |
| TNA | −278.57 | 93.56 | −2.977 | 0.00301 | ** |
| AN | −13.49 | 40.12 | −0.336 | 0.73691 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loua, R.T.; Bencherif, H.; Mbatha, N.; Bègue, N.; Hauchecorne, A.; Bamba, Z.; Sivakumar, V. Study on Temporal Variations of Surface Temperature and Rainfall at Conakry Airport, Guinea: 1960–2016. Climate 2019, 7, 93. https://doi.org/10.3390/cli7070093
Loua RT, Bencherif H, Mbatha N, Bègue N, Hauchecorne A, Bamba Z, Sivakumar V. Study on Temporal Variations of Surface Temperature and Rainfall at Conakry Airport, Guinea: 1960–2016. Climate. 2019; 7(7):93. https://doi.org/10.3390/cli7070093
Chicago/Turabian StyleLoua, René Tato, Hassan Bencherif, Nkanyiso Mbatha, Nelson Bègue, Alain Hauchecorne, Zoumana Bamba, and Venkataraman Sivakumar. 2019. "Study on Temporal Variations of Surface Temperature and Rainfall at Conakry Airport, Guinea: 1960–2016" Climate 7, no. 7: 93. https://doi.org/10.3390/cli7070093
APA StyleLoua, R. T., Bencherif, H., Mbatha, N., Bègue, N., Hauchecorne, A., Bamba, Z., & Sivakumar, V. (2019). Study on Temporal Variations of Surface Temperature and Rainfall at Conakry Airport, Guinea: 1960–2016. Climate, 7(7), 93. https://doi.org/10.3390/cli7070093







