Abstract
The main features of the instrumental global mean surface temperature (GMST) are reasonably well described by a simple linear response model driven by anthropogenic, volcanic and solar forcing. This model acts as a linear long-memory filter of the forcing signal. The physical interpretation of this filtering is the delayed response due to the thermal inertia of the ocean. This description is considerably more accurate if El Niño Southern Oscillation (ENSO) and the Atlantic Multidecadal Oscillation (AMO) are regarded as additional forcings of the global temperature and hence subject to the same filtering as the other forcing components. By considering these as predictors in a linear regression scheme, more than 92% of the variance in the instrumental GMST over the period 1870–2017 is explained by this model, in particular, all features of the 1998–2015 hiatus, including its death. While the more prominent pauses during 1870–1915 and 1940–1970 can be attributed to clustering in time of strong volcanic eruptions, the recent hiatus is an unremarkable phenomenon that is attributed to ENSO with a small contribution from solar activity.
1. Introduction
According to instrumental observations [1], the global mean surface temperature (GMST) has risen at an increasing rate throughout the instrumental period, 1850–2017, the Common Era (CE). This rise, however, has been interrupted by three pauses of no, or even negative, growth. These are the periods 1870–1915, 1940–1970, and 1998–2014. The last hiatus was the shortest and least spectacular of these, and the reason for the great attention it has received is primarily that it is the first pause observed since global warming became a scientific and political issue in the 1980s. The existence of the most recent pause has been challenged in several recent papers, partly justified by new corrected estimates of the GMST which point out biases in older estimates (see, for instance, the review by Jones (2016) [2]. The most prominent of these biases is gradual introduction of new measurement methods of sea surface temperature (SST) since the outbreak of World War III [3,4]. These recent corrections, however, are quite modest and do not remove the visual impression of a deviation throughout the 1998–2014 interval from the long-term temperature trend of the longer 1970–2017 interval. Whether or not this deviation deserves to be classified as a hiatus is a matter of definition and is not the subject of the present paper.
Multiple linear regression was applied to explain the GMST satellite record for the 1979–2011 period by Foster and Rahmstorf (2011) [5]. Their emphasis was on eliminating the effects of volcanic and solar forcing, and the El Niño Southern Oscillation (ENSO), to recover the anthropogenic trend in the data. Lean and Rind (2008) [6] applied such regression with the volcanic, solar, and anthropogenic forcing signals, and, in addition, the multivariate ENSO index, as predictors for the instrumental GMST for the 1889–2006 period. This description captured the initial part of the hiatus for the 1998–2006 period, but not the pauses during the 1870–1915 and 1940–1970 intervals.
Other authors (e.g., Zhou et al. (2012) [7] and Canty et al. (2013) [8]) have also used the Atlantic Multidecadal Oscillation (AMO) index as a predictor in addition to ENSO and the various forcing components. Zhou et al. (2012) replaced the anthropogenic forcing by a linear trend and used total solar irradiance (TSI), volcanic aerosol optical depth, and ENSO as predictors. The resulting explained signal contains an unexplained oscillation with period of approximately 60 years which is roughly in phase with the AMO. By introducing AMO as a predictor, most of this oscillation is explained.
Recently Folland et al. [9] published a comprehensive study considering a substantial number of predictors and regression against several GMST datasets with monthly resolution and a number of reconstructions of forcing and indices for various modes. The predictors corresponding to components of the radiative forcing were filtered by convolving them with a response kernel composed of two exponential functions with time constants of 4–5 years and 200 years. This form of the linear GMST response function has been found from experiments with Earth system models [10]. A special feature of that study was to analyze time intervals of pauses and strong warming in isolation, and then perform the regression analysis limited to those particular intervals with a variable number of predictors customized for each interval.
The Folland et al. paper reflects a trend in attribution research towards higher model complexity and the use of more data with higher resolution. However, increased model complexity is not without problems. One important issue is overfitting: a large number of predictors with sufficiently diverse spectral structure will typically produce high explained variance even when no causal connection between predictors and observation exists. Analysis of shorter time intervals in isolation also increases the chance of overfitting since the regression coefficients are allowed to be different in different intervals, thus increasing the effective number of predictors.
What is gained by analyzing data with monthly rather than annual resolution? As recognized by Folland et al., the GMST responds on time scales of a few years up to centuries, i.e., the climate system acts as a low-pass filter to remove forced variability on monthly time scales. This means that temporal structure on time scales shorter than this cannot be attributed to the variability of radiative forcing. Climatic modes used as predictors are related to interannual, decadal, or multidecadal dynamical mechanisms, and thus, the monthly variability of indices characterizing these modes should be perceived and treated as noise. If inclusion of this noise in the predictors and observations increases the explained variance, it is an indication that both predictors and observations are subject to the same noise. For instance, a particular climate mode index and the GMST can be influenced by the same large-scale weather events which are unrelated to any of the climate modes used as predictors. This leads to a spurious correlation between the mode predictor and the GMST which will attribute more of the variance to this mode. In fact, the mode dynamics may be completely unrelated to the GMST, but the correlated high-frequency components will still attribute part of the GMST to this mode.
Chylek et al. (2014) [11] adopted a parsimonious approach, managing to explain 93% of the variance by employing only greenhouse gas (GHG) forcing and the AMO at annual resolution as predictors. This paper is interesting because it illustrates the potential pitfalls of regression analysis involving climate modes as predictors when the selection and form of the predictors are not sufficiently guided by physics. The AMO index with annual resolution is correlated with ENSO and the volcanic forcing signal on interannual time scales (just as the GMST is). For instance, the strong 1997 El Niño is present as a very prominent peak in the annual resolution AMO. We know that this high-frequency variability in the AMO index has no connection to the multidecadal dynamics governing the AMO, but is a reflection of the dynamics of ENSO and volcanic forcing. It is methodologically flawed to analyze AMO with annual resolution because it will incorrectly attribute the GMST variability caused by ENSO and volcanic forcing to AMO when ENSO and volcanic forcing are not used as predictors. Since the AMO also oscillates in phase with the slow 60-year oscillation observed in the GMST, it is not surprising that the explained variance can be very high with GHG forcing and annual resolution AMO as the only predictors.
The present paper also takes an approach based on the principle of parsimony, but great care is taken in the selection of predictors that are physically sound, for instance, by using low-pass filtered forcing similar to that of Folland et al. (2018), and have a form that prevents spurious attribution due to physical dependence between modes or forcings on certain time scales. The latter is prevented by using high resolution predictors for interannual modes and low-resolution (smoothed) predictors for multidecadal modes.
The objective is to explain the deviations from the expected anthropogenic warming on decadal and multidecacdal time scales. The deviations on these time scales have been used by some to cast doubt about the reality of human-induced climate change. Explaining monthly or annual variability is not the focus of interest, and hence, this kind of change is excluded from the analysis by using annual means of the data and employing a response filter that effectively eliminates these time scales from the analysis. A goal is also to find the most parsimonious description (the lowest number of predictors) that explains the most essential features of the observed GMST signal, i.e., those features necessary for concluding that the pauses under examination all can be attributed to natural variability. The main result of the paper is that we do not need a host of different data sets of high resolution and a large number of predictors to reach that conclusion, and we single out those predictors that are essential and those may be left out in the most parsimonious, yet sufficient, description.
The paper is a follow-up from Rypdal (2015) [12] who employed a long-memory response filter to the three forcing components (solar, volcanic and anthropogenic) and applied the AMO index as a predictor in addition to the forcing components and the Niño3.4 index. This approach explains 89% of the variance in the 1880–2010 GMST and captures all three pauses. A characteristic result of all these approaches is a relatively strong AMO footprint and a weaker volcanic footprint compared to what one would expect from estimates of volcanic aerosol forcing like the ones presented in Hansen et al. (2011) [13].
It will be demonstrated that two analysis features of many earlier papers may exaggerate the AMO footprint at the expense of the volcanic footprint. One is the the use of the forcing components themselves as predictors and not a long-memory filtered response that respects that the surface temperature responds to forcing on multiple time scales [10,14]. This long-range memory response to volcanic eruptions may explain part of the slow oscillation that remains unexplained when the AMO is not used as a predictor. Another feature is that the three forcing components are treated as independent predictors thus ignoring theoretical estimates of their relative magnitudes. In addition to discarding such estimates, this approach increases the number of regression coefficients from three to five, and hence, increases the risk of overfitting, i.e., high degree of explained variance from an incorrect statistical model with too many degrees of freedom.
The main purpose of the present paper is to extend the results of [12] to the 1870–2017 period and hence, capture the “death” of the 1998–2014 hiatus, but also seeks to reduce the model complexity to avoid overfitting. The regression model is simpler than the one employed in [12] in the sense that the long-memory temperature response to the sum of anthropogenic, volcanic, and solar forcing is treated as one predictor, rather than three independent predictors (the one-forcing model). In Section 4.2, we also compare this to the model where the volcanic forcing is separated from the sum of solar and anthropogenic forcing as an independent predictor (the two-forcing model). The long-memory response to the ENSO and AMO indices are treated as predictors, rather than being the indices themselves. This means that, in the one-forcing model, the number of predictors are reduced from five to three, and hence, the chance of overfitting is considerably reduced. This enhances the confidence we can have in the model. In spite of the reduction of model complexity, the explained variance increases to 92%. This may be attributed to using the long-memory response to the ENSO index as predictor, rather than the index itself, but updated and longer data sets may also play roles. The effects of systematically increasing the number of predictors are studied in more detail in Section 4.
The forcing signals used as a basis for the predictors are shown in Figure 1. Figure 1a displays the sum of volcanic, solar and anthropogenic forcing, and Figure 1b displays the individual components of the forcing. Figure 1c,d display the AMO and the ENSO indices, respectively. Section 2.1 explains how these signals are filtered into signals that exhibit the temporal fingerprints of the GMST responses to these forcing signals. By means of a linear multiple regression, these fingerprints (or predictors) and the instrumental GMST are used to estimate regression coefficients which allow the formation of a weighted sum to represent the best fit to the instrumental data. Here, each weighted fingerprint is denoted as the footprint of the specific forcing or index, since it can be interpreted as the component of that forcing or index present in the instrumental GMST.
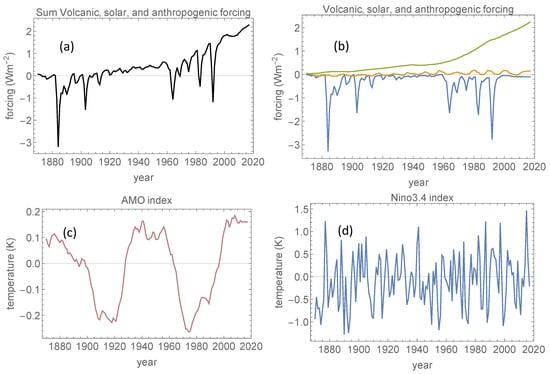
Figure 1.
Forcing signals used in the regression analysis. (a) The sum of volcanic, solar and anthropogenic forcing. (b) The blue curve depicts the volcanic forcing, the yellow curve depicts the solar forcing and the green curve depicts the total anthropogenic forcing, including greenhouse gases, land use change and anthropogenic aerosols. (c) The Atlantic Multidecadal Oscillation (AMO) index. (d) the Niño3.4 index. These indices are not in units of forcing, but the corresponding forcing is assumed to be proportional to the indices.
2. Results
2.1. Estimating the Long-Memory Exponent for the GMST-Response
If the GMST is supposed to respond linearly to radiative forcing, , the general form of the response has the form of a convolution integral:
where is the temperature change relative to the time, . Here, stochastic forcing is also added, where is a Gaussian white-noise stochastic process. It is supposed to represent the random forcing on the GMST arising from atmospheric weather systems, but it is not a priori clear as to how to include distinct climatic modes like the AMO and ENSO in this description. It was shown by Rypdal and Rypdal (2014) [14] that by adding a white-noise forcing to the known deterministic forcing, , the residual internal variability (the climate noise) of on time scales from years to centuries is well described by a response function of the power-law form:
It can be shown that, if , the resulting internal variability exhibits a power spectral density of the form . This property is called scale invariance, or simply scaling, because the statistical properties of the signal are independent of scale. Crudely stated, the signal looks the same if we zoom in or out. It was shown in reference [14] that this scaling is a feature of the residual climate noise of the instrumental GMST, and this has also been found in long control runs of atmospheric–ocean general circulation models [15]. In both cases, the scaling seems to be reasonably valid on time scales from years to centuries with , although it has been recognized that ENSO poses a problem to this picture [16].
The spectral exponent, , measures the long-range memory in the temperature signal; corresponds to no memory (white noise), while characterizes a “pink noise” process. For in this range, the stochastic process is a stationary persistent fractional Gaussian noise, while, for , it is a fractional Brownian motion which is a non-stationary process.
This methodology includes internal modes like AMO and ENSO as part of the long-memory climate noise. This may be problematic, since the spectral density of these modes peak in distinct frequency ranges and tend to break the scale invariance implied by the assumed scaling of the GMST signal. As a means to solve this problem, it is proposed here that AMO and ENSO are included in the deterministic forcing signal. These indices are not given in units of forcing, so the magnitudes of forcing that they represent are not known. However, this is unimportant, because it is only their temporal structure that is used in the regression. Their magnitude, and hence their footprints, are determined through the estimation of the regression coefficients.
A brief sketch of the the method of estimating is given below. Details can be found in Section 4.2. The fingerprints of the deterministic forcing, AMO and ENSO are found by convolving the forcing signal and the AMO and ENSO indices by the response function given by Equation (2). The convolution has the form shown in Equation (1). The three footprints contain multiplicative constants, , which serve as regression coefficients in a linear multiple regression, where the fingerprints are the predictors. The exponent is assumed to be the same for all fingerprints. By varying in the range 0.3–0.9 in steps of 0.1, the total footprint is computed for each by regressing against the instrumental GMST, and the residual is computed by subtracting the footprint from the observed signal. The estimated scaling exponent, , for the residual is then computed from the estimated power spectrum or from some other estimator. Here, the variogram estimator is used (see, for instance, Rypdal et al. (2013) [17] for definitions and discussion of various estimators). It measures how the variance of the cumulative sum of the signal depends on the time, , over which it is summed. If the signal is scale invariant, this variance follows a powe -law, , where is the estimated Hurst exponent. The relation between and is [17].
In Figure 2a, the blue curve depicts the estimate versus the assumed used in the response function, and the yellow curve is just the line through the origin with unit slope. The two curves intersect where , i.e., at the value where for which the response model is self-consistent. This value is a bit lower than the value of that was estimated in reference [14] and should be considered as a correction due to the elimination of AMO and ENSO from the residual.
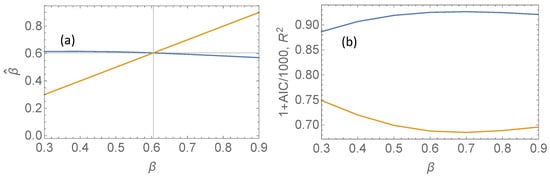
Figure 2.
(a) The blue curve is plotted against which was estimated from the variogram of the residual signal obtained after regression using fingerprints obtained from filtering forcing signals by the response function, . The yellow curve is the straight line through the origin with unit slope. (b) The blue curve is of the regression plotted against which was used in the response function. The yellow curve is versus , where is the Akaike information criterion.
This result suggests that is the preferred choice to use as a filter exponent to define the individual fingerprints. This choice is strengthened by computing the coefficient of explained variance, (see [12]), against . This is shown as the blue curve in Figure 2b, which peaks in the vicinity of this -value. The yellow curve is a plot derived from the so-called Akaike information criterion (AIC) (which is plotted as , see reference [12]). This criterion measures the explained variance with a penalty for model complexity. Of two statistical models, the one with the lower AIC is preferable to the other in an information-theoretical sense. The AIC curve has a minimum in the vicinity of and hence, supports this as the preferred value of the exponent in the subsequent analysis.
2.2. Instrumental GMST Explained
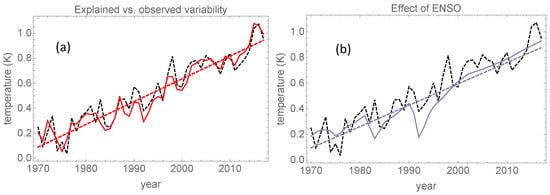
Figure 3a shows the results of the regression analysis with and with the fingerprints of deterministic forcing, AMO and ENSO used as predictors. The regression determines the three coefficients, , and the total footprint (the red curve) explains of the variance of the observed GMST (the black, dashed curve). One can observe that the three pauses discussed in Section 1 are all explained by the superpositions of these three footprints.
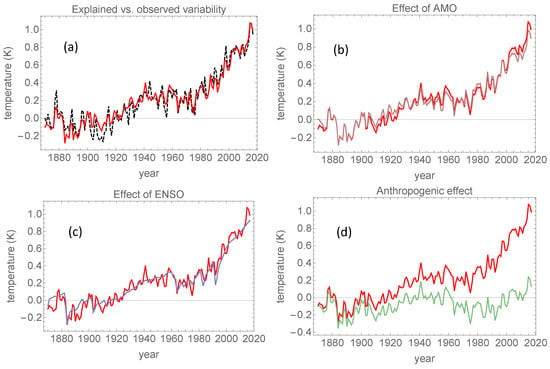
Figure 3.
In all four panels, the red curve is the total explained global mean surface temperature (GMST, or the total footprint) from the regression. (a) The black, dashed curve is the HadCrut4 GMST signal. (b) The brown curve is the signal obtained after the AMO footprint is subtracted from the total footprint. (c) The blue curve is the signal obtained after the El Niño Southern Oscillation (ENSO) footprint is subtracted from the total footprint. (d) The green curve is the signal obtained after the anthropogenic footprint issubtracted from the total footprint.
One would perhaps have expected that the AMO would explain a considerable part of the two first pauses and part of the most recent hiatus, but the effect of AMO is, in fact, quite small. This is seen in Figure 3b, where the total footprint (red) is plotted along with the signal obtained with the AMO footprint subtracted (brown). The two first pauses give the graph of the entire time series an appearance of a slow oscillation that is more or less in phase with the AMO and superposed on a rising trend, but this oscillation is not primarily created by the AMO. It is caused by the clustered structure of the volcanic forcing—one cluster in the 1880–1920 CE interval, and another in the 1960–2000 CE interval. Actually, this phase coincidence suggests that the AMO may be paced by this clustering. This assertion is supported by repeating the analysis without using the AMO as a predictor. The results are not substantially different, as shown in Section 3.
In Figure 3c, the blue curve shows the total footprint with the ENSO footprint subtracted. As expected, the two first pauses are not substantially altered by removing the effect of ENSO, but the most recent hiatus essentially disappears. After subtracting the effect of ENSO, the negative spikes caused by volcanic eruptions appear much more clearly. This shows that volcanic and ENSO footprints are of comparable magnitude and operate on the same time scale.
The anthropogenic influence is demonstrated explicitly in Figure 3d, where the green curve is the total footprint with the anthropogenic footprint subtracted. This green curve is the natural footprint, comprised of the footprints of volcanic and solar forcing with a weak contribution from AMO and a strong contribution from ENSO (see Figure 1). The slow oscillation with period around 60 years is mainly caused by the clustering of volcanic eruptions; the fast annual to decadal scale fluctuations are a combination of fast responses to volcanic eruptions and ENSO, with a weak contribution from the 11-year solar cycle.
2.3. The Recent Hiatus and Warming Trend
Figure 4a is a close-up on Figure 3a for the period 1970–2017, and Figure 4b is a close-up of Figure 3c. The red, dashed line is a linear fit to the total footprint (the red, full curve), and the slope corresponds to 0.182 K per decade. The blue, full curve in Figure 4b shows that as the effect of ENSO is removed, the actual temperature rise during 2000–2017 follows the linear fit line to this curve for the 1970–2017 period, which has a slope of 0.166 K per decade. Thus, with the ENSO footprint included, the variability of this period is very accurately explained, including the hiatus. When ENSO is removed, the hiatus disappears and what remains is a linearly growing trend on which we observe the effect of three volcanic eruptions prior to the turn of the century. During the hiatus period, the hiatus is completely replaced by this linear trend when ENSO is removed, so we can conclude that the 1998–2014 hiatus and its death during the years 2014–2017 are, first and foremost, effects of ENSO.
3. Discussion
Rypdal (2015) [12] obtained (89%), slightly smaller than that obtained here (92%) by using volcanic, solar and anthropogenic fingerprints as independent predictors in addition to AMO and ENSO. In other words, in that paper, five predictors gave no better results than we obtained here with three. On the other hand, the AIC found there was −244, while the present analysis found AIC = −312 due to the reduced model complexity. One of the major differences in these two analyses is that in reference [12], the volcanic to anthropogenic footprint ratio was reduced by a factor of two compared to the fingerprint ratios, while the AMO footprint was enhanced. A plausible interpretation of this difference is that the freedom of allowing different effective sensitivities to the volcanic, solar and anthropogenic forcing components results in unphysical overfitting. The situation is complex, however, since a number of other factors were different between these analyses. For instance, the data series in the present work were longer (1870–2017 versus 1880–2010), and both the GMST time series and the forcing time series have been updated. From an information-theoretical viewpoint, the present analysis is preferable, and the data used are likely more correct. The reduced AMO footprint has the interesting implication that the slow oscillation of a period of about 60 years, giving rise to the 1870–1915 and 1940–1970 pauses, can be attributed to the clustering of volcanic eruptions. Moreover, since the AMO phase coincides with this oscillation, it opens the possibility that during the 20th century, AMO was paced by volcanic activity. The effects of long-memory filtering and an increasing number of predictors are presented systematically for the new and extended datasets in Section 4.2.
Another conclusion that can be drawn from comparing these results with those obtained by Lean and Rind (2008) [6] and by Rypdal (2015) [12] using a zero-memory (instantaneous) response function is that a long-memory response is required to fully reproduce this slow oscillation as a response to the clustering of volcanic activity. Hence, it serves as a confirmation of the usefulness of the long-memory response description and emphasizes that volcanic forcing has effects not only a few years after eruptions, but also on multidecadal time scales (see also Figure 5, Figure 6, Figure 7 and Figure 8 and the discussion in Section 4.2).
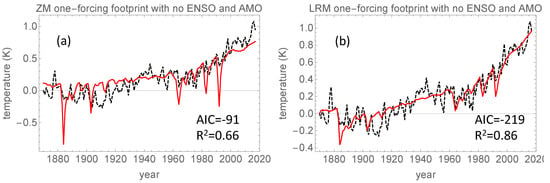
Figure 5.
(a) The red curve is the total explained GMST (or the total footprint) from the regression when the only predictor (fingerprint) is the unfiltered sum of solar, volcanic and anthropogenic forcing (the total forcing). The black, dashed curve is the HadCrut4 GMST signal. (b) The same as (a) with the long-memory filtered () forcing as a predictor.
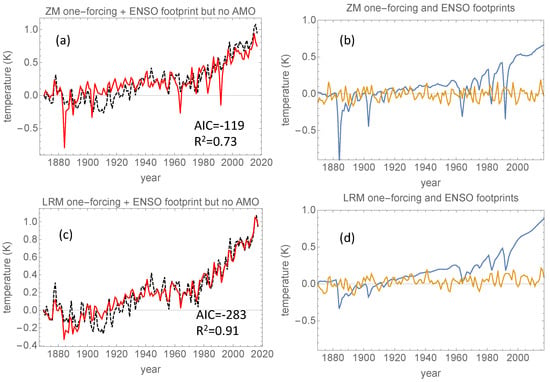
Figure 6.
(a) The red curve is the total explained GMST (or the total footprint) from the regression where the fingerprints are the unfiltered total forcing and ENSO index. The black, dashed curve is the HadCrut4 GMST signal. (b) The individual footprints whose sum is the red curve in panel (a). The blue curve is the total forcing and the yellow curve represents the ENSO footprints, respectively. Panels (c,d) show the results of the same analysis as panels (a,b), but with fingerprints filtered with .
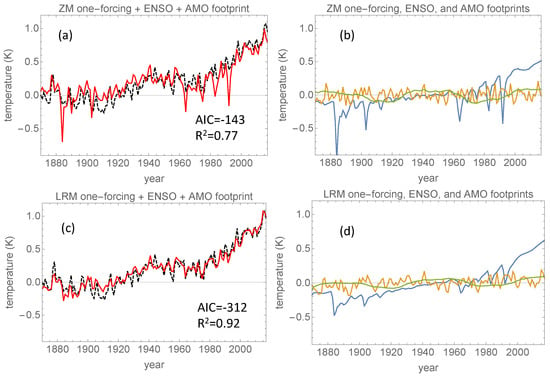
Figure 7.
(a) The red curve is the total explained GMST (or the total footprint) from the regression when the fingerprints are the unfiltered total forcing and the ENSO and AMO indices. The black, dashed curve is the HadCrut4 GMST signal. (b) The individual footprints, whose sum is the red curve in panel (a). The blue curve is the total forcing, the yellow curve is the ENSO, and the green curve is the AMO footprints, respectively. Panels (c,d) show the results of the same analysis as panels (a,b), but with fingerprints filtered with .
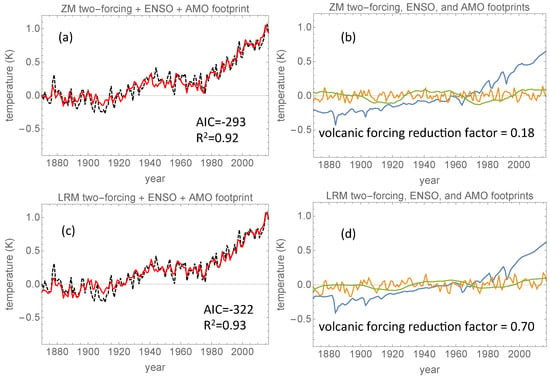
Figure 8.
(a) The red curve is the total explained GMST (or the total footprint) from the regression when the fingerprints are the unfiltered solar and anthropogenic forcing, the unfiltered volcanic forcing, and the unfiltered ENSO and AMO indices. The black, dashed curve is the HadCrut4 GMST signal. (b) The individual footprints, whose sum is the red curve in panel (a). The blue curve is the total forcing, the yellow curve is the ENSO, and the green curve is the AMO footprints, respectively. Panels (c,d) show the results of the same analysis as panels (a,b), but with fingerprints filtered with .
By including AMO and ENSO as a part of the deterministic forcing, and hence excluding these signals from the residual climate noise background, the present work obtains a better scaling description of this background on time scales from years to a few decades, and a memory exponent of (corresponding to a Hurst exponent of ) has been obtained. This eliminates a problem that plagues many studies, whereby ENSO creates difficulties for computing scaling exponents (see, e.g., Fredriksen and Rypdal (2016) [16]).
Seen under the context of the entire instrumental 1870–2017 GMST record, the most remarkable feature of the the 1998–2014 deviation from the long-term warming trend is how unremarkable it is. The duration of the period with a weaker GMST trend is considerably shorter than those of the 1870–1915 and 1940–1970 pauses, during which the trends were actually not zero, but negative. There have been no strong volcanic eruptions since the Mount Pinatubo eruption of 1993, but a particularly deep solar minimum occurred in 2009 and a weak solar cycle 24 during the following decade lead to the dip in the total forcing during the first decade of this century observed in Figure 1a. At first sight, this might suggest that the entire hiatus could be attributed to this low solar forcing, but this is not supported by Figure 4b, where the elimination of the ENSO footprint also essentially eliminates the reduction of the trend. On the other hand, the solar footprint may explain the slightly higher slope of the trend line in Figure 4a (0.182 K per decade) compared to 0.166 K per decade in Figure 4b. Figure 3b and Figure 7d show that AMO is responsible for a positive temperature anomaly of about 0.1 K during the 2000–2017 intreval, but this perturbation is almost constant during the period and does not significantly influence the shape of the GMST curve during this period.
It is worth mentioning, though, that other combinations of modes than AMO and ENSO have been used to explain the most recent hiatus. For instance, Steinman et al. (2015) [18] employed a semi-empirical approach combining observations and global circulation model simulations to attribute this slowdown to a combination of the positive phase of AMO and negative trending of the Pacific multidecadal oscillation (PMO). However, the study deals with Northern hemisphere (not global) temperature, and the data series end in 2012. Hence, it does not capture the interannual variability associated with ENSO and, in particular, does not capture the “death” of the hiatus associated with the strong 2015 El Niño. The present paper shows that neither AMO, nor a combination of AMO and PMO, are necessary to fully explain the recent hiatus.
The overall conclusion is that the 1998–2014 deviation from the long-term warming trend is an unremarkable phenomenon that can be attributed to the influence of ENSO on the global mean surface temperature, with a slightly reduced warming trend due to low solar activity.
4. Materials and Methods
4.1. Data and Its Use
The GMST data used in this paper is the HadCrut4 global temperature time series [1] (data available at https://crudata.uea.ac.uk/cru/data/temperature/HadCRUT4-gl.dat).
The forcing data is an updated version of [13] (data available at http://www.columbia.edu/~mhs119/Forcings/).
This data series goes to 2015. The two last data points for 2017 and 2016 used in the analysis were obtained by linear extrapolation.
The AMO index data is the AMO-smoothed, long time series, derived from the Kaplan SST data set [19] (data availble at https://www.esrl.noaa.gov/psd/data/timeseries/AMO/).
The Nino3.4 index is described in reference [20] (data available at https://www.esrl.noaa.gov/psd/data/correlation/nina34.data).
The data were analyzed with annual resolution, including the AMO. All datasets were downloaded with monthly resolution, and from these monthly data, annual averages were computed by averaging over calendar years. However, the AMO monthly data set used here is really an 11-year moving average. The reason for this choice is that the AMO is a multidecadal oscillation, i.e., its dynamics involve time scales longer than a decade. The variability of the AMO index on an annual scale is not related to this mode. This variability is comprised of regional climate noise uncorrelated with the GMST and possibly, some variability that contributes to the GMST and is correlated with it. If we include this latter variability as part of a predictor in the regression analysis, we, in effect, use the GMST as a predictor of itself, and this may spuriously enhance the weight of its footprint. It turned out, however, that using unsmoothed data made almost no difference. This indicates that annual scale fluctuations in the AMO-index are essentially uncorrelated with the GMST and therefore, do not have any significant effect on the results of the regression analysis.
The same reasoning cannot be applied to ENSO because it is an interannual mode. Since ENSO also has a significant seasonal structure, one could argue that monthly resolution in the analysis would have been more appropriate. However, the inclusion of seasonal variability would add many complications in the interpretation of the analysis and was not the kind of variability that we seeked to explain. The important thing was that the annual means were all computed the same way for all data.
4.2. Methods
Let be the total forcing signal plotted in Figure 1a, is the AMO index in Figure 1c, and is the Nino3.4-index in Figure 1d. The predictors corresponding to these signals are the filtered functions, , , , which may be perceived as the fingerprints of the signals to be detected in the GMST response. The response function (or the predictand) is the linear combination:
The multiple linear regression determined the regression coefficients, , , that minimize the square deviation between and the observed GMST. This section also presents results for other choices of predictors. In Figure 5, the only predictor is the fingerprint of the total forcing (the one-forcing, one-predictor model); in Figure 6, the ENSO fingerprint is added to the total forcing (the one-forcing, two-predictor model); in Figure 7, the AMO fingerprint is added to the total forcing and ENSO (the one-forcing, three-predictor model); and finally, in Figure 8, the forcing is split into one component consisting of the sum of solar and anthropogenic and another of the volcanic forcing (the two-forcing, four-predictor model). The reason why the volcanic signal was separated out was to demonstrate that the regression procedure tends to suppress the volcanic footprint in order to reduce the unexplained variance caused by the strong negative spikes in the volcanic forcing signal.
The regression coefficients were obtained by the LinearModelFit command in Mathematica. To select the optimal , we computed the diagnostic (coefficient of determination) for each , which measures the fraction of the total variance in the observed record that is explained by the predictand. In the model selection assessments, we used model selection criteria based on the information theory where the likelihood function is used as a measure of the goodness of the fit, which is subject to a penalty for model complexity (the number of predictors). One of those used was the Akaike information criterion (AIC) [21]. This criterion produces a real number that can be positive or negative, and the model giving the smaller number was, in this particular sense, preferable. These diagnostics are directly available as options in LinearModelFit.
The main effect of the long-memory filtering is to smear out the responses to forcing features that are localized in time, such as volcanic eruptions and ENSO events, but it also causes some redistribution of the weight that is given to slower features, such as the AMO footprint versus the volcanic footprint. This is illustrated in Figure 5, Figure 6, Figure 7 and Figure 8 which are discussed in the following text.
In Figure 5a the regression is shown without any filtering of the forcing signal, i.e., the fingerprint that is used as predictor is the forcing signal itself. In Figure 5b, the fingerprint is the forcing smoothed with the filter. Figure 5a, compared to Figure 5b, shows that the absence of filtering yields excessively strong short-time responses to the volcanic eruptions. These spikes in Figure 5a could be reduced by a lower weight, but then the rising trend of the forcing signal would be much lower than observed which would decrease the explained variance. The explained variance with this model was only 66% and the AIC was −91, which indicates that this is a poor model even though the model complexity is low. By using the long-memory filtered fingerprint, the volcanic spikes were wider and reduced in amplitude. This gave a higher weight of the volcanic footprint which yielded a considerably higher explained variance () and . This shows that long-memory smoothing of the fingerprint provides a considerably better statistical model.
The inclusion of the ENSO fingerprint as an additional predictor, as shown in Figure 6, increased from 66% to 73% for zero-memory (unfiltered) fingerprints and from 86% to 91% for long-memory filtered fingerprints. Even though the model complexity increased, the AIC for zero memory decreased from −91 to −119 and for long-memory filtering, it decreased from −219 to −283. Hence, the inclusion of ENSO provides a better model, but the use of long-memory filtered fingerprints is significantly more important than including ENSO when it comes to producing a better model according to the information-theoretic model-selection criteria. Again, the reason for this is that the long-memory filtering reduces and widens the volcanic spikes.
By adding the AMO fingerprint to the forcing and ENSO predictors in Figure 7, increased from 73% to 77% for zero memory, and from 91% to 92% for long memory. The AIC decreased from −119 to −143 for zero memory and from −283 to −312 for long memory. Thus, including AMO made a better model, but the improvement is rather insignificant compared to what was obtained by inclusion of ENSO.
The most surprising observation from these three figures is that the long-memory, one-predictor model (no ENSO and AMO), with and outperformed the zero-memory, three-predictor model (with ENSO and AMO), with and .
Figure 8 shows the result of treating the solar and anthropogenic forcing and the volcanic forcing as separate predictors in addition to ENSO and AMO (the two-forcing, four-predictor model). With four predictors, we necessarily increased the explained variance.
For the zero-memory model (Figure 8a,b), increased from 77% to 92% because now the volcanic footprint could be suppressed independently of the solar and anthropogenic forcing. The AIC was also quite low, it reduced from −143 to −293, indicating that from an information-theoretic viewpoint, this model is preferable to the all the previous zero-memory models, but not to the one-forcing, three-predictor long-memory model. The reason for the higher explained variance is that we can keep the high anthropogenic trend and still suppress the volcanic spikes. The weight of the volcanic footprint reduced by a factor 0.18, so this model puts very little emphasis on volcanic forcing. In fact, very similar results were obtained by removing the volcanic forcing as a predictor, hence this result is quite similar to those obtained by Chylek et al. [11]. The main difference is that ENSO has been included here and AMO has been smoothed by a ten-year moving average. Thus, this figure shows the volcanic suppression effect of using unfiltered predictors for the volcanic signal which is also present in [11].
This suppression of the volcanic footprint is the result of the combined use of the unphysical, unfiltered fingerprint for the temperature response to the volcanic forcing and treating this fingerprint as an independent predictor. There are physical reasons to assume that the ratio between the magnitudes of the volcanic forcing and the solar and anthropogenic forcing is close to that presented in the forcing data used in [13]. By treating them as independent predictors, the regression analysis is made blind to this constraint.
The long-memory, two-forcing, four-predictor model (Figure 8c,d) behaves quite differently. The smoothing of the volcanic spikes causes less need for suppression of the volcanic signal, it was only reduced by a factor 0.70, and thus, the end result was quite similar to the long-memory, three-predictor model shown in Figure 7c,d. The explained variance only increased from 92% to 93% and the AIC reduced from −312 to −322. The fact that it made little difference if we separated the forcing into two independent fingerprints is reassuring. This is an indication that the long-memory three- and four-predictor models are physically sound.
It is apparent from Figure 7b,d and Figure 8b,d that the long-memory filtering reduced the AMO footprint by approximately 50%. The reason for this is that the long-memory filtered volcanic signal contains a slow component that is more or less in phase with the AMO and contributes to the two earlier pauses at the start and middle of the 20th century.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Morice, C.P.; Kennedy, J.J.; Rayner, N.A.; Jones, P.D. Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The HadCRUT4 dataset. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Jones, P. The reliability of recent global and hemispheric temperature records. Adv. Atmos. Sci. 2016, 33, 269–282. [Google Scholar] [CrossRef]
- Karl, T.R.; Arguez, A.; Huang, B.; Lawrimore, J.H.; McMahon, J.R.; Menne, M.M.J.; Peterson, T.C.; Vose, R.S.; Zhang, H.-M. Possible artifacts of data biases in the recent global surface warming hiatus. Science 2015, 348, 1469–1472. [Google Scholar] [CrossRef] [PubMed]
- Hausfather, Z.; Cowtan, K.; Clarke, D.C.; Jacobs, P.; Richardson, M.; Rohde, R. Assessing recent warming using instrumentally homogeneneous sea surface temperature records. Sci. Adv. 2017, 3, e1601207. [Google Scholar] [CrossRef] [PubMed]
- Foster, G.; Rahmstorf, S. Global temperature evolution 1979–2010. Environ. Res. Lett. 2011, 6, 044022. [Google Scholar] [CrossRef]
- Lean, J.L.; Rind, D.H. How natural and anthropogenic influences alter global and regional surface temperatures: 1889 to 2006. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Zhou, J.; Tung, K.-K. Deducing multidecadal anthropogenic global warming trends using multiple linear regression analysis. J. Atmos. Sci. 2012, 70, 3–8. [Google Scholar] [CrossRef]
- Canty, T.; Mascioli, N.R.; Smarte, M.D.; Salawitch, R.J. An empirical model of global climate—Part 1: A critical evaluation of volcanic cooling. Atmos. Chem. Phys. 2013, 13, 3997–4031. [Google Scholar] [CrossRef]
- Folland, C.K.; Boucher, O.; Colman, A.; Parker, D.E. Causes of irregularities in trends of global mean surface temperature since the late 19th century. Sci. Adv. 2018, 4, eeao5297. [Google Scholar] [CrossRef] [PubMed]
- Geoffroy, O.; Saint-Martin, D.; Olivié, D.J.L.; Voldoire, A.; Bellon, G.; Tytcá, S. Transient Climate Response in a Two-Layer Energy-Balance Model. Part I: Analytical Solution and Parameter Calibration Using CMIP5 AOGCM Experiments. J. Clim. 2013, 6, 1841–1857. [Google Scholar] [CrossRef]
- Chylek, P.; Klett, J.D.; Lesins, G.; Dubey, M.K.; Hengartner, N. The Atlantic Multidecadal Oscillation as dominant factor of oceanic influence on climate. Geophys. Res. Lett. 2014, 41, 1689–1697. [Google Scholar] [CrossRef]
- Rypdal, K. Attribution in the presence of a long-memory climate response. Earth Syst. Dyn. 2015, 6, 719–730. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M.; Kharecha, P.; von Schuckmann, K. Earth’s energy imbalance and implications. Atmos. Chem. Phys. 2011, 11, 13421–13449. [Google Scholar] [CrossRef]
- Rypdal, M.; Rypdal, K. Long-memory effects in linear-response models of Earth’s temperature and implications for future global warming. J. Clim. 2014, 27, 5240–5258. [Google Scholar] [CrossRef]
- stvand, L.; Nilsen, T.; Rypdal, K.; Divine, D.; Rypdal, M. Long-range memory in internal and forced dynamics of millennium-long climate model simulation. Earth Syst. Dyn. 2014, 5, 295–308. [Google Scholar] [CrossRef]
- Fredriksen, H.-B.; Rypdal, K. Spectral characteristics of instrumental and climate model surface temperatures. J. Clim. 2016, 29, 1253–1268. [Google Scholar] [CrossRef]
- Rypdal, K.; Østvand, L.; Rypdal, M. Long-range memory in Earth’s surface temperature on time scales from months to centuries. J. Geophys. Res. 2013, 118, 7046–7062. [Google Scholar] [CrossRef]
- Steinman, B.A.; Mann, M.E.; Miller, S.K. Atlantic and Pacfic multidecadal oscillations and Northern Hemisphere temperatures. Science 2015, 347, 988–991. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, A.; Cane, M.; Kushnir, Y.; Clement, A.; Blumenthal, M.; Rajagopalan, B. Analyses of global sea surface temperature 1856–1991. J. Geophys. Res. 1998, 103, 18567–18589. [Google Scholar] [CrossRef]
- Trenberth, K.E. The Definition of El Niño. Bull. Am. Meteorol. Soc. 1997, 78, 2771–2777. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel inference: Understanding AIC and BIC in model selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).