The Hiatus in Global Warming and Interactions between the El Niño and the Pacific Decadal Oscillation: Comparing Observations and Modeling Results
Abstract
1. Introduction
2. Materials
Tie Pints, or Dated Events
3. Methods
3.1. Pretreatment of the Data
3.2. Quantifying Running Leading-Lagging Relation for Pairs of Variables
3.3. Auxiliary Methods
4. Results
5. Discussion
5.1. Raw and Smoothed Time Series
5.2. Paired Series
5.3. Comparing Observations and Simulations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, S.Y.; L’Heureux, M.; Yoon, J.H. Are Greenhouse Gases Changing ENSO Precursors in the Western North Pacific? J. Clim. 2013, 26, 6309–6322. [Google Scholar] [CrossRef]
- Taylor, E.K.; Stouffer, R.J.; Meehl, G.A. An Overview of Cmip5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Overland, J.; Rodionov, S.; Minobe, S.; Bond, N. North Pacific regime shifts: Definitions, Issues and Recent Transitions. Prog. Oceanogr. 2008, 77, 92–102. [Google Scholar] [CrossRef]
- Reid, P.C.; Hari, R.E.; Beaugrand, G.; Livingstone, D.M.; Marty, C.; Straile, D.; Barichivich, J.; Goberville, E.; Adrian, R.; Aono, Y.; et al. Global Impacts of the 1980s Regime Shift. Glob. Chang. Biol. 2016, 22, 682–703. [Google Scholar] [CrossRef] [PubMed]
- Parrenin, F.; Masson-Delmotte, V.; Kohler, P.; Raynaud, D.; Paillard, D.; Schwander, J.; Barbante, C.; Landais, A.; Wegner, A.; Jouzel, J. Synchronous Change of Atmospheric CO2 and Antarctic Temperature during the Last Deglacial Warming. Science 2013, 339, 1060–1063. [Google Scholar] [CrossRef] [PubMed]
- Mehta, V.M.; Wang, H.; Mendoza, K. Decadal Predictability of Tropical Basin Average and Global Average Sea Surface Temperatures in CMIP5 Experiments with the HadCM3, GFDL-CM2.1, NCAR-CCSM4, and MIROC5 Global Earth System Models. Geophys. Res. Lett. 2013, 40, 2807–2812. [Google Scholar] [CrossRef]
- Trenberth, K.E. Has There Been a Hiatus? Science 2015, 349, 691–692. [Google Scholar] [CrossRef] [PubMed]
- Gehne, M.; Kleeman, R.; Trenberth, K.E. Irregularity and Decadal Variation in ENSO: A Simplified Model Based on Principal Oscillatory Petterns. Clim. Dyn. 2014, 43, 3327–3350. [Google Scholar] [CrossRef]
- Wills, R.C.; Schneider, T.J.; Wallace, M.; Battisti, D.S.; Hartmann, D.L. Disentangling Global Warming, Multidecadal Variability, and El Nino in Pacific Temperatures. Geophys. Res. Lett. 2018, 45, 2487–2496. [Google Scholar] [CrossRef]
- Minobe, S.A. 50–70 Year Climatic Oscillation over the North Pacific and North America. Geophys. Res. Lett. 1997, 24, 683–686. [Google Scholar] [CrossRef]
- Chen, X.Y.; Wallace, J.M. ENSO-Like Variability: 1900–2013. J. Clim. 2015, 8, 9623–9641. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T. An apparent Hiatus in Global Warming? Earths Future 2015, 1, 19–32. [Google Scholar] [CrossRef]
- Medhaug, I.; Stolpe, M.B.; Fischer, E.M.; Knutti, R. Reconciling Controversies about Global Warming Hiatus. Nature 2017, 545, 41–47. [Google Scholar] [CrossRef] [PubMed]
- Hedemann, C.; Mauritsen, T.; Jungclaus, J.; Marotzke, J. The Subtle Origins of Surface-Warming Hiatuses. Nat. Clim. Chang. 2017, 7, 336. [Google Scholar] [CrossRef]
- Stevenson, S.; Otto-Bliesner, B.; Fasullo, J.; Brady, E. El Nino Like Hydroclimate Responses to Last Millennium Volcanic Eruptions. J. Clim. 2016, 29, 2907–2921. [Google Scholar] [CrossRef]
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-Spectral Methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.H.; Deyle, E.; Fogarty, M.; Munch, S. Detecting Causality in Complex Ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef] [PubMed]
- Stips, A.; Macias, D.; Coughlan, C.; Garcia-Gorriz, E.; Liang, X.S. On the Causal Structure between CO2 and Global Temperature. Sci. Rep. 2016, 6, 21691. [Google Scholar] [CrossRef] [PubMed]
- Kestin, T.S.; Karoly, D.J.; Yang, J.I.; Rayner, N.A. Time-Frequency Variability of ENSO and Stochastic Simulations. J. Clim. 1998, 11, 2258–2272. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.N.; Yen, N.C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Seip, K.L.; McNown, R. The Timing and Accuracy of Leading and Lagging Business Cycle Indicators: A new Approach. Int. J. Forecast. 2007, 22, 277–287. [Google Scholar] [CrossRef]
- Seip, K.L. and Grøn, O. Leading the Game, Losing the Competition: Identifying Leaders and Followers in a Repeated Game. PLoS ONE 2016, 11, e0150398. [Google Scholar] [CrossRef] [PubMed]
- Seip, K.L.; Grøn, Ø. A New Method for Identifying Possible Causal Relationships between CO2, Total Solar Irradiance and Global Temperature Change. Theor. Appl. Climatol. 2017, 127, 923–938. [Google Scholar] [CrossRef]
- Newman, M.; Shin, S.I.; Alexander, M.A. Natural Variation in ENSO Flavors. Geophys. Res. Lett. 2011, 38, 65. [Google Scholar] [CrossRef]
- Newman, M.; Alexander, M.A.; Ault, T.R.; Cobb, K.M.; Deser, C.; Lorenzo, E.D.; Mantua, N.J.; Miller, A.J.; Minobe, S.; Nakamura, H.; et al. The Pacific Decadal Oscillation, Revisited. J. Clim. 2016, 29, 4399–4427. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, M.C.; Long, S.R.; Shen, S.S.P.; Qu, W.D.; Gloersen, P.; Fan, K.L. A Confidence Limit for the Empirical Mode Decomposition and Hilbert Spectral Analysis. Proc. R. Soc. Math. Phys. Eng. Sci. 2003, 459, 2317–2345. [Google Scholar] [CrossRef]
- Wu, S.; Liu, Z.Y.; Zhang, R.; Delworth, T.L. On the Observed Relationship between the Pacific Decadal Oscillation and the Atlantic Multi-Decadal Oscillation. J. Oceanogr. 2011, 67, 27–35. [Google Scholar] [CrossRef]
- Power, S.; Haylock, M.; Colman, R.; Wang, X. The predictability of interdecadal changes in ENSO activity and ENSO teleconnections. J. Clim. 2006, 19, 4755–4771. [Google Scholar] [CrossRef]
- Seip, K.L.; Reynolds, C.S. Phytoplankton Functional Attributes along Trophic Gradient and Season. Limnol. Oceanogr. 1995, 40, 589–597. [Google Scholar] [CrossRef]
- Imbrie, J.; Berger, A.; Boyle, E.A.; Clemens, S.C.; Duffy, A.; Howard, W.R.; Kukla, G.; Kutzbach, J.; Martinson, D.G.A.; Mcintyre, A.C.; et al. On the Structure and Origin of Major Glaciation Cycles 2. The 100,000-Year Cycle. Paleoceanography 1993, 8, 699–735. [Google Scholar] [CrossRef]
- Doyle, A.C. The memoirs of Sherlock Holmes; George Newnes: Lonton, UK, 1893. [Google Scholar]
- Torrence, C.; Webster, P.J. Interdecadal Changes in the ENSO-Monsoon System. J. Clim. 1999, 12, 2679–2690. [Google Scholar] [CrossRef]
- Wunsch, C. The Interpretation of Short Climate Records, with Comments on the North Atlantic and Southern Oscillations. Bull. Am. Meteorol. Soc. 1999, 80, 245–255. [Google Scholar] [CrossRef]
- Knutson, T.R.; Sirutis, J.J.; Zhao, M.; Tuleya, R.E.; Bender, M.; Vecchi, G.A.; Villarini, G.; Chavas, D. Global Projections of Intense Tropical Cyclone Activity for the Late Twenty-First Century from Dynamical Downscaling of CMIP5/RCP4.5 Scenarios. J. Clim. 2015, 28, 7203–7224. [Google Scholar] [CrossRef]
- Patra, P.K.; Maksyutov, S.; Ishizawa, M.; Nakazawa, T.; Takahashi, T.; Ukita, J. Interannual and Decadal Changes in the Sea-Air CO2 Flux from Atmospheric CO2 Inverse Modeling. Glob. Biogeochem. Cycles 2005. [Google Scholar] [CrossRef]
- Mehta, V.M.; Mendoza, K.; Wang, H. Predictability of Phases and Magnitudes of Natural Decadal Climate Variability Phenomena in CMIP5 Experiments with the UKMO HadCM3, GFDL-CM2.1, NCAR-CCSM4, and MIROC5 Global Earth System Models. Clim. Dyn. 2017. [Google Scholar] [CrossRef]
- DeVries, T.; Holzer, M.; Primeau, F. Recent increase in carbon uptake driven by weaker upper-ocean overturning. Nature 2017, 542, 215–220. [Google Scholar] [CrossRef] [PubMed]
- Meehl, G.A.; Hu, A.; Arblaster, J.M.; Fasullo, J.; Trenberth, K.E. Externally Forced and Internally Generated Decadal Climate Variability Associated with the Interdecadal Pacific Oscillation. J. Clim. 2013, 26, 7298–7310. [Google Scholar] [CrossRef]
- Loeb, N.G.; Thorsen, T.J.; Norris, J.R.; Wang, H.; Su, W. Changes in Earth’s Energy Budget during and after the “Pause” in Global Warming: An Observational Perspective. Climate 2018, 6, 18. [Google Scholar] [CrossRef]
- Seip, K.L.; Grøn, Ø. On the Statistical Nature of Distinct Cycles in Global Warming Variables. Clim. Dyn. 2016. [Google Scholar] [CrossRef]

| Variables | Raw Dta, High Frequency | Smoothed Data, Low Frequency | ||
|---|---|---|---|---|
| Regression, r2 | p | Regression, r2 | p | |
| El Niño, Obs, PDO, Obs | 0.518 | <0.001 | 0.208 | 0.012 |
| El Niño, Sim, PDO, Sim | 0.392 | <0.001 | 0.452 | <0.001 |
| El Niño, Obs, El Niño sim. | 0.147 | 0.08 | 0.001 | 0.987 |
| PDO, Obs, PDO sim. | 0.071 | 0.40 | 0.005 | 0.676 |
| LL(N,P) obs GTAslope 21–93 | 0.024 | 0.21 | 0.090 | 0.01 |
| LL(N,P)Sim GTAslope 21–93 | 0.424 | <0.001 | 0.452 | <0.001 |
| Rows | Variable | Observed/Simulated | Cycle Length, Years | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | |||
| I | LL(El Niño, PDO) | Obs. | 5 | 11, 13 | 26 | 31 | |||
| Sim. | 5 | 11, 16 | 26 | 31 | |||||
| II | El Niño | Obs. | 21 | 31 | 44 | 72 | |||
| Sim. | 11 | 32 | 48 | 62 | 72 | ||||
| III | PDO | Obs. | 8 | 22 | 28 | 46 | 70 | ||
| Sim. | 7 | 11 | 20 | 31 | 49 | 62 | 72 | ||
| IV | El Nño-PDO | Obs. | 7.9 ± 2.5 | 24.5 ± 3.2 | |||||
| Sim. | 8.4 ± 4.0 | 23.9±3.0 | |||||||
| No. | Criteria | Significant/Similarities | Clues | Figure/Table |
|---|---|---|---|---|
| A | Regressions between pairs in observations and simulations | Observed El Niño and PDO are similar as is the simulated pair, Observed and simulated El Niño are different, as is the PDO pair. | Tie points may realign time series | Table 1 |
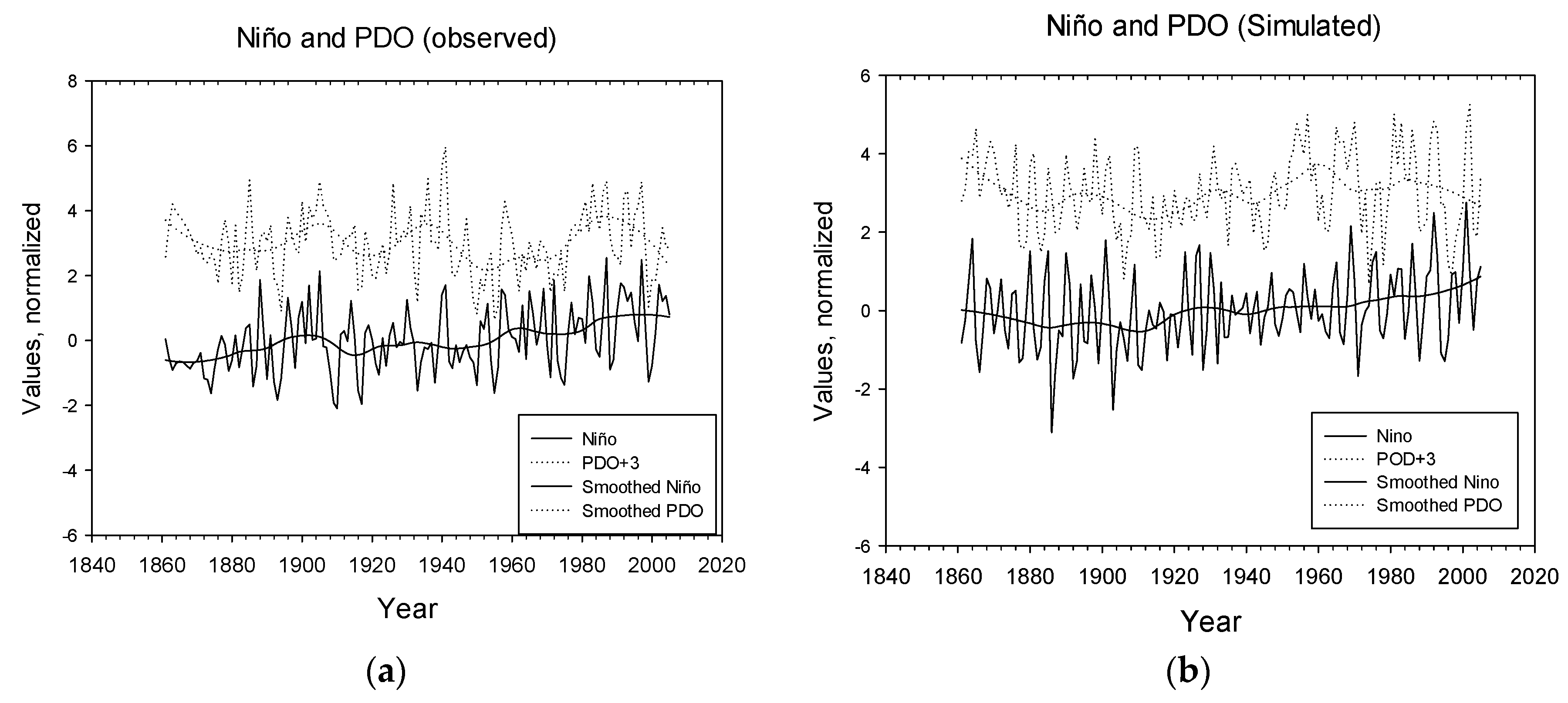
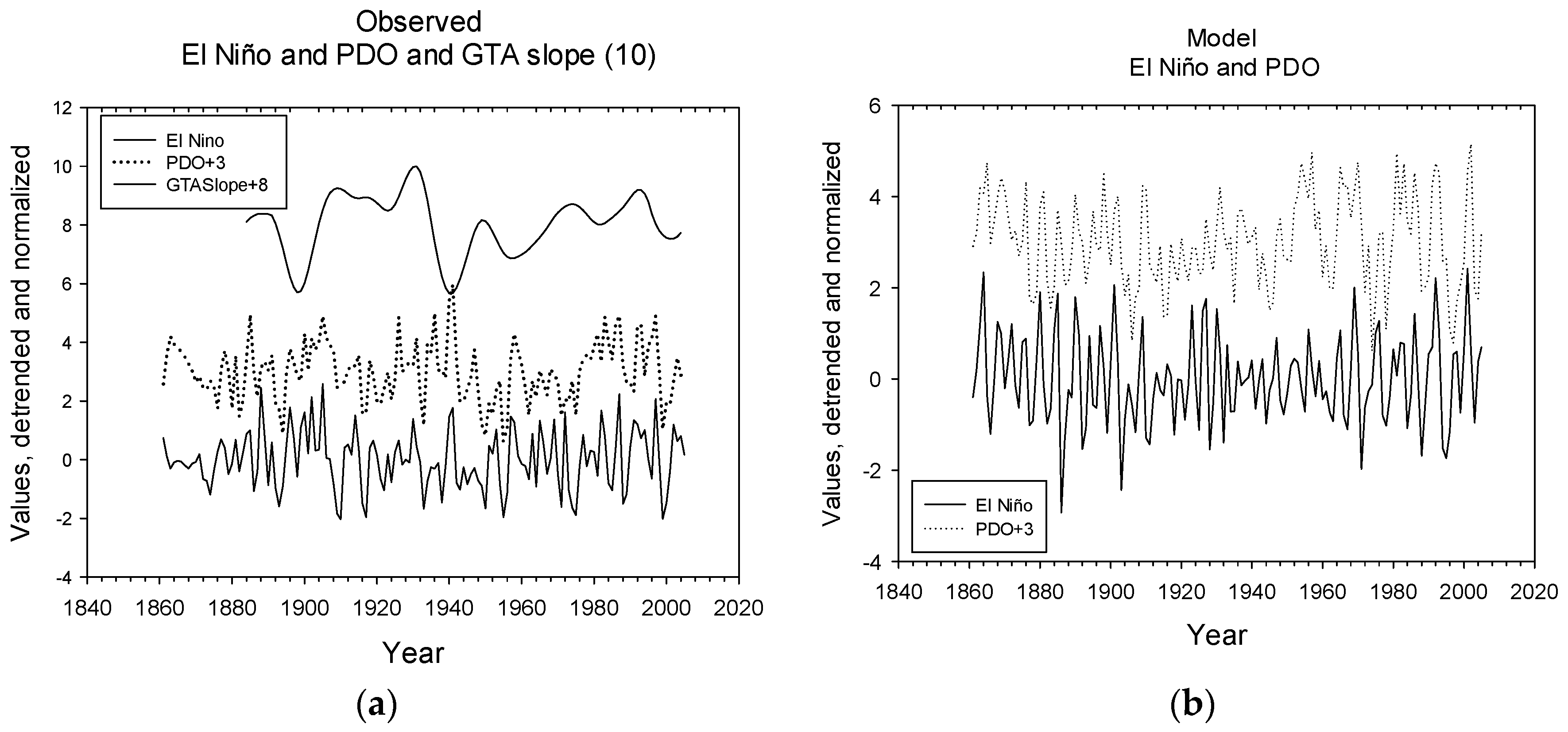
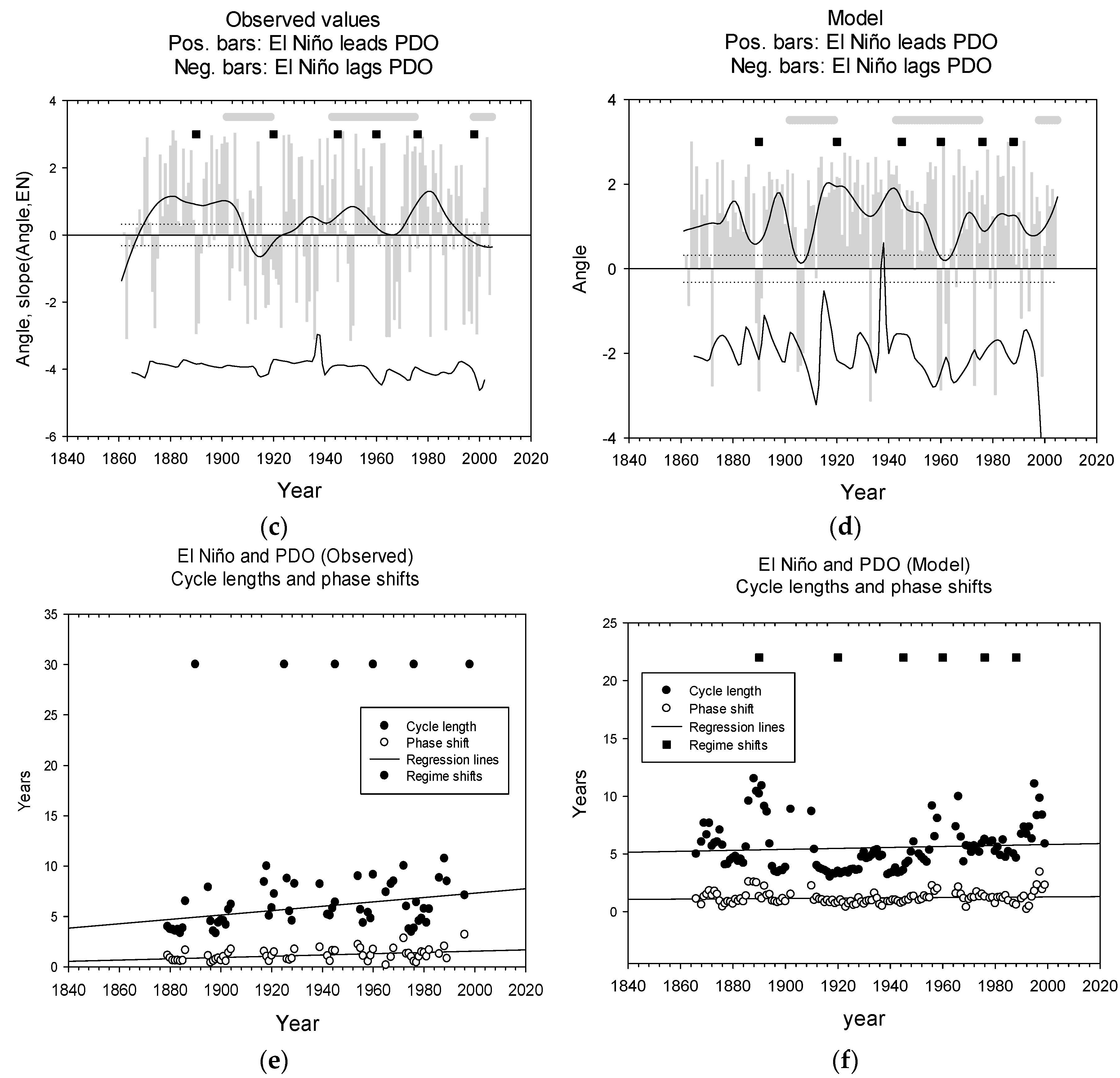
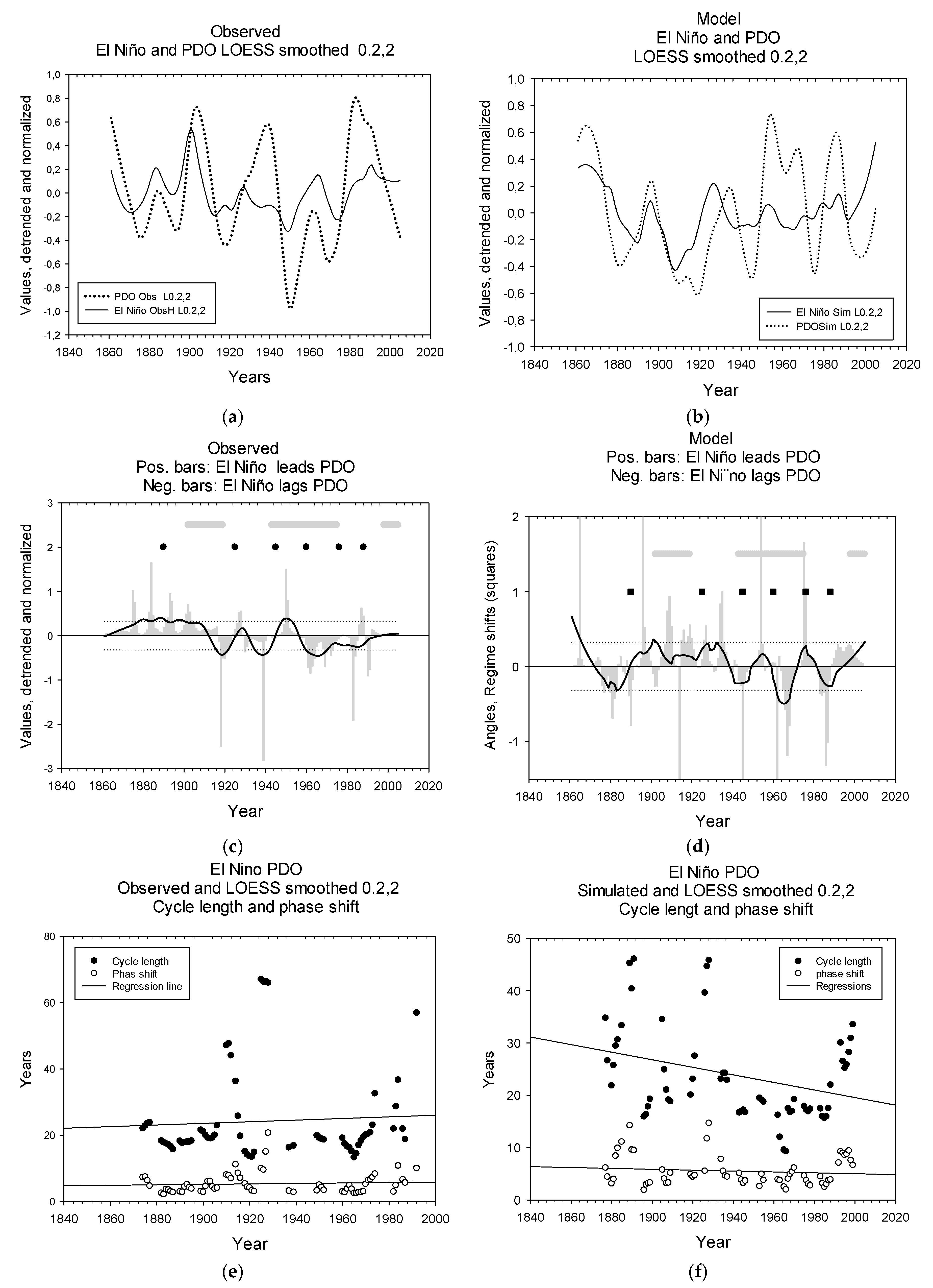
| B | LL-relations, time series | El Niño and PDO LL-relations have common traits, but are not significantly correlated | Similar features in 1910, 1960, 2000 | Figure 2c,d Figure 3c,d |
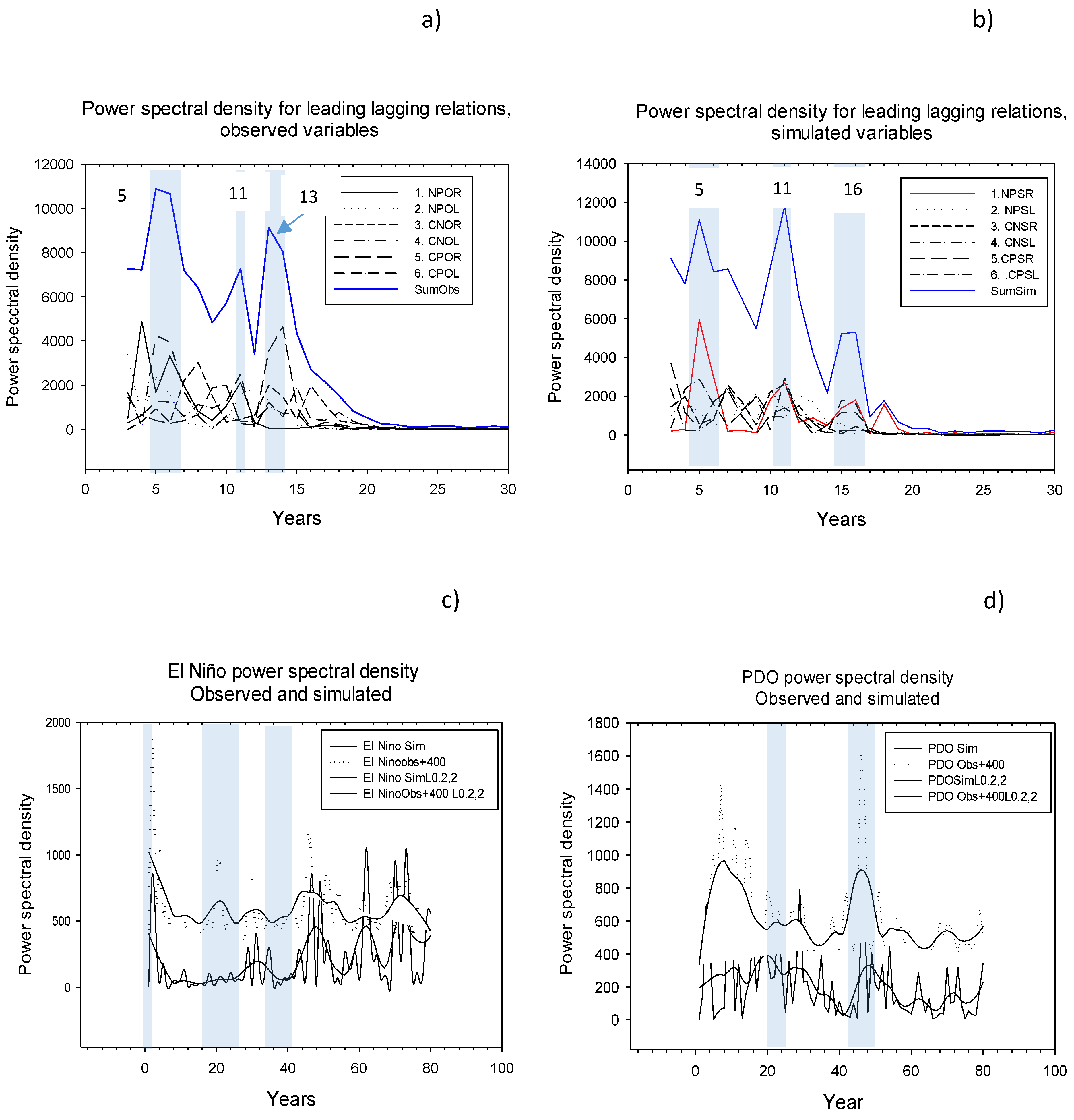
| C | Power spectral density, LL-relations | Peak at 5 and 13 years strongest in observation, peak at 11 years strongest in simulation | Unimodal and bimodal patterns, c.f. (1) | Figure 4c,d |
| D | Power spectral density- single series | Peak at 31 years in observed and simulated El Niño; peak at ≈ 7 years and ≈ 28–31 years in observed and simulated PDO | Longer cycle lengths may exist | Figure 5c,d |
| E | Common cycle lengths: Time series | Raw series are similar ≈ 8 years. Smoothed series are similar ≈ 24 years. | Longer cycle lengths may exist. | Figure 3e,f Figure 4e,f |
| F | Phase shifts: time series | Raw series show similar phase shifts, ≈ 1 year; smoothed series show similar phase shift ≈ 5 years. | Longer phase shifts exist. | Figure 3e,f Figure 4e,f |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seip, K.L.; Wang, H. The Hiatus in Global Warming and Interactions between the El Niño and the Pacific Decadal Oscillation: Comparing Observations and Modeling Results. Climate 2018, 6, 72. https://doi.org/10.3390/cli6030072
Seip KL, Wang H. The Hiatus in Global Warming and Interactions between the El Niño and the Pacific Decadal Oscillation: Comparing Observations and Modeling Results. Climate. 2018; 6(3):72. https://doi.org/10.3390/cli6030072
Chicago/Turabian StyleSeip, Knut L., and Hui Wang. 2018. "The Hiatus in Global Warming and Interactions between the El Niño and the Pacific Decadal Oscillation: Comparing Observations and Modeling Results" Climate 6, no. 3: 72. https://doi.org/10.3390/cli6030072
APA StyleSeip, K. L., & Wang, H. (2018). The Hiatus in Global Warming and Interactions between the El Niño and the Pacific Decadal Oscillation: Comparing Observations and Modeling Results. Climate, 6(3), 72. https://doi.org/10.3390/cli6030072





