Development of Automatic Labels for Cold Front Detection in South America: A 2009 Case Study for Deep Learning Applications

Abstract

Deep learning models for atmospheric pattern recognition require spatially consistent training labels that align precisely with input meteorological fields. This study introduces an automatic cold front detection method using the ERA5 reanalysis dataset from the European Centre for Medium-Range Weather Forecasts (ECMWF) at 850 hPa, specifically designed to generate physically consistent labels for machine learning applications. The approach combines the Thermal Front Parameter (TFP) with temperature advection (AdvT), applying optimized thresholds (TFP < 5 × 10⁻¹¹ K m⁻²; AdvT < −1 × 10⁻⁴ K s⁻¹), morphological filtering, and polynomial smoothing. Comparison against 1426 manual charts from 2009 revealed systematic spatial displacement, with mean offsets of ~502 km. Although pixel-level overlap was low, with Intersection over Union (IoU) = 0.013 and Dice coefficient (Dice) = 0.034, spatial concordance exceeded 99%, confirming both methods identify the same synoptic systems. The automatic method detects 58% more fronts over the South Atlantic and 44% fewer over the Andes compared to manual charts. Seasonal variability shows maximum activity in austral winter (31.3%) and minimum in summer (20.1%). This is the first automatic front detection system calibrated for South America that maintains direct correspondence between training labels and reanalysis input fields, addressing the spatial misalignment problem that limits deep learning applications in atmospheric sciences.

1. Introduction

Cold fronts play a crucial role in the development of extreme weather events over South America, including heavy rainfall and abrupt temperature drops, with critical impacts on human activities [1]. These systems form when polar air masses advance over warmer air, forcing it to rise and triggering condensation processes that lead to torrential rainfall [2]. As these fronts move inland their rainfall can cause flood and landslide risks, especially in urbanized coastal areas [3]. From a meteorological perspective, cold front passages are commonly associated with sharp temperature drops, often exceeding 10 °C within a 24 h period, which can severely impact agricultural production and livestock activities [4]. These events also have public health implications, with hospital admissions for respiratory illnesses increasing by up to 25% during extreme cold episodes [5].

The identification of cold fronts over South America has traditionally relied on manual analysis of surface synoptic charts, following classical polar front theory [6], which integrate observations of thermal gradients, mean sea level pressure, and wind patterns [2,7]. However, this approach faces significant challenges, primarily due to its dependence on subjective human interpretation, which can lead to discrepancies between analysts, particularly in regions with complex terrain. In South America, the presence of the Andes Mountain range acts as a major orographic barrier, substantially modifying atmospheric circulation patterns and the trajectories of cold fronts [8]. Additionally, regions such as the Gran Chaco and the Brazilian Highlands exhibit observational limitations due to sparse meteorological networks, where data gaps are prevalent (35% of stations report failures exceeding 20% [9] and temporal inconsistencies among national data sources further hinder the accurate detection of frontal gradients [10]. These combined factors compromise the standardization of frontal analyses and reduce the reliability of weather forecasts at local and regional scales.

The development of frontal detection methods has advanced significantly, evolving from classical techniques such as the Thermal Front Parameter (TFP), originally proposed by Berry et al. [11] and later refined by Feng et al. [12], to modern machine learning approaches. Modern deep learning architectures, particularly convolutional neural networks [13,14], have revolutionized pattern recognition in environmental sciences [15,16]. Contemporary methods include convolutional neural networks applied to reanalysis datasets [17] and multivariate random forest algorithms [12], achieving accuracy rates exceeding 92% in the Northern Hemisphere. However, these approaches require high-quality, spatially consistent labeled datasets for training. In South America, the lack of such datasets, combined with the challenges of manual analysis, represents a critical barrier to implementing deep learning solutions for operational cold front detection

Although these advances demonstrate high performance, their specific application to South America remains limited, representing a critical gap in the literature [18,19,20]. The success of deep learning models in meteorology fundamentally depends on the quality and spatial consistency of the training datasets. In semantic segmentation tasks, such as cold front detection, systematic misalignments between input meteorological fields and binary labels can introduce spurious correlations, ultimately compromising the models’ generalization capability [21,22,23].

Architectures such as convolutional neural network (U-Net) [24,25,26] have demonstrated strong effectiveness in the automatic identification of atmospheric features. U-Net is a convolutional neural network architecture originally designed for biomedical image segmentation, characterized by its encoder–decoder structure with skip connections that preserve both local and global spatial information, making it particularly effective for pixel-level classification tasks in atmospheric sciences due to its ability to capture multi-scale features while maintaining spatial precision [16,27]. Recent applications include [17], who successfully applied U-Net for automatic atmospheric river detection using global reanalysis data, achieving detection accuracies exceeding 85% when compared to manual expert analysis, and [28], who employed U-Net architectures for tropical cyclone eye detection in satellite imagery, demonstrating the method’s capability to identify complex atmospheric patterns across different scales and regions. However, their performance depends directly on the accuracy of the input labels. In the case of cold fronts, this aspect is particularly critical due to the inherent complexity, spatial variability, and subjectivity associated with their delineation.

The success of deep learning applications in meteorology fundamentally depends on the spatial alignment between input meteorological fields and training labels [29]. Convolutional neural networks, particularly U-Net architectures used for atmospheric pattern segmentation [17,26], learn spatial relationships by associating local atmospheric features with corresponding target classifications. When training labels are systematically displaced from their associated physical patterns as occurs when using synoptic chart labels with reanalysis input data models learn spurious spatial correlations that compromise generalization performance [23]. This spatial misalignment problem is particularly acute for cold front detection, where manual synoptic analyses often represent frontal boundaries at different locations than the underlying thermal gradients captured in reanalysis data [6,11,30,31]. The development of automatic labeling methods that maintain direct correspondence with input meteorological fields is therefore essential for advancing machine learning applications in atmospheric sciences [27].

The main objective of this study is to develop an automatic method for cold front identification at 850 hPa over South America using ERA5 reanalysis data, specifically designed to generate physically consistent labels for future deep learning applications. We compare our automatic detection with Center for Weather Forecasting and Climate Studies (CPTEC/INPE—National Institute for Space Research) charts to characterize the systematic differences between automatic and manual approaches, demonstrating that these differences reflect distinct methodological perspectives rather than deficiencies. The automatic method provides labels that maintain direct correspondence with the atmospheric fields that will be used as input in machine learning models. Additionally, we present an analysis of seasonal patterns and frontal characteristics during 2009, providing a georeferenced dataset of automatically generated front labels as a foundation for future machine learning applications.

2. Materials and Methods

2.1. Data Sources

The data used in this study were obtained from the ERA5 reanalysis dataset, produced by the European Centre for Medium-Range Weather Forecasts (ECMWF; [32]), with a 6 h frequency (0000, 0600, 1200, and 1800 UTC). The ERA5 dataset, used here at its native spatial resolution of 0.25° × 0.25°, is widely recognized for its high quality, refined spatial resolution, and strong consistency with observational data [33,34,35,36]. The 850 hPa pressure level was selected as the primary diagnostic level because it represents a region of the lower troposphere where thermal and dynamical contrasts associated with cold fronts are often more pronounced. Several studies have shown that frontal baroclinicity tends to reach a maximum at this level [30], which makes it a common reference in objective front diagnostics. In our case, the use of 850 hPa ensures that the labels are directly aligned with the ERA5 predictors employed in the machine learning framework. Mean sea level pressure (MSLP) was used only as a complementary field for visualization and synoptic interpretation, but it was not included in the automatic detection. Future developments of this methodology may incorporate multiple vertical levels to capture a more complete frontal structure

The extracted variables included: zonal and meridional wind components (u, v) temperature (T), and mean sea level pressure (MSLP)

The temporal coverage spans the entire year of 2009, providing a complete annual cycle for seasonal analysis. This period was selected to establish a baseline methodology for automatic cold front detection over South America, serving as a foundation for future multi-annual applications.

For comparison, operational synoptic charts from the CPTEC were used, with a 6 h frequency, covering the same period. Out of a total of 1460 possible observations for the year 2009 (365 days × 4 daily observations), only 1426 had manual data available, resulting in a completeness rate of 97.7%. The 34 missing observations (2.3%) were scattered throughout the year due to the unavailability of some synoptic charts in the CPTEC archive.

2.2. Cold Front Detection Methods

This study employs two distinct approaches for cold front identification: an automatic method (ERA5-based) and a manual method (synoptic chart-based). The automatic method was developed based on an approach that combines the Thermal Front Parameter (TFP) and temperature advection (AdvT), adapted to South American conditions following the work of [12]. Their methodology provided the initial foundation for the automatic detection of cold fronts in reanalysis data and was adjusted in the present work to account for regional specificities such as South America’s topography and local climate patterns [37,38]. The manual method relies on operational synoptic charts from CPTEC, where cold fronts are identified through traditional meteorological analysis. It is important to emphasize that manual CPTEC charts were considered the reference dataset, while the automatic detection represents an experimental approach restricted to 850 hPa.

2.2.1. Automatic Method

The automatic approach uses thermodynamic parameters calculated from ERA5 reanalysis data. The processing steps are described below:

$$\mathrm{TFP}=-\nabla \left|\nabla \theta \right|·{\displaystyle \frac{\nabla \theta }{\left|\nabla \theta \right|}}$$

(1)

where $\mathrm{TFP}$ is the Thermal Front Parameter, $\theta$ is the potential temperature (K), is the direction normal to the temperature gradient, and $\nabla$ represents the horizontal gradient operator.

$$\theta =T {\left({\displaystyle \frac{1000}{P}}\right)}^{0.286}$$

(2)

where $\theta$ is the potential temperature (K), $T$ is the air temperature (K), $P$ is the atmospheric pressure (hPa), and $P$₀ = 1000 hPa is the reference pressure.

Additionally, temperature advection (AdvT) is given by:

$$\mathrm{AdvT}=-\nu ·\nabla \mathrm{T}$$

(3)

where AdvT is the horizontal temperature advection (K s⁻¹), $\nu$ = $\left(u, v\right)$ is the horizontal wind vector, with $u$ the zonal (east–west) wind component (m s⁻¹) and $v$ the meridional (north–south) wind component (m s⁻¹), $\mathrm{T}$ is the air temperature (K), and $\nabla$T denotes the horizontal gradient of temperature (K m⁻¹).

A point is classified as part of a cold front if TFP < threshold TFP and AdvT < 0, indicating strong baroclinicity and cold air advection, respectively. Based on the TFP and thermal advection fields, the cold frontal zone was objectively defined as the set of grid points simultaneously satisfying both criteria: TFP ≤ 5 × 10⁻¹¹ K m⁻² and AdvT ≤ −1 × 10⁻⁴ K s⁻¹. Compared to the thresholds proposed by Feng et al. 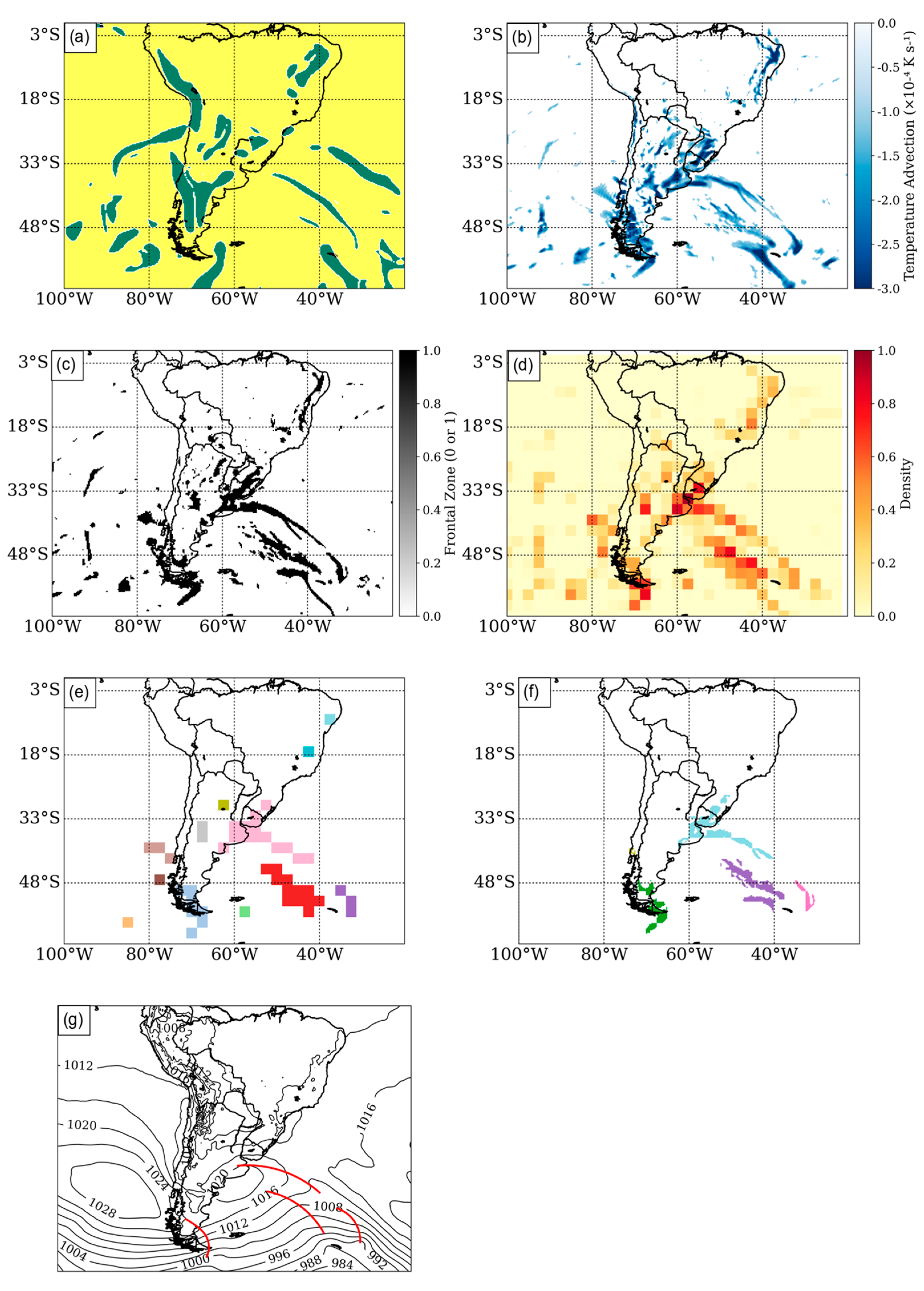[12] (|TFP| ≤ 2 × 10⁻¹¹ K m⁻²; AdvT ≤ −1 × 10⁻⁴ K s⁻¹), the present study adopts a more permissive TFP threshold (|TFP| ≤ 5 × 10⁻¹¹ K m⁻²) while retaining a similar advection threshold (AdvT ≤ −1 × 10⁻⁴ K s⁻¹). The increase in the TFP threshold was necessary to improve sensitivity to broader and weaker thermal gradients, which are frequently observed over the South Atlantic and other South American sectors, thereby avoiding false negatives in diffuse oceanic frontal zones. The advection threshold was kept at the same order of magnitude to ensure that detected zones remain associated with meaningful cold-air advection. These choices were informed by sensitivity and percentile analyses and were complemented by morphological filtering (density threshold = 35%) and a minimum frontal extent criterion (600 km) to suppress spurious mesoscale detections. Together, this configuration balances sensitivity to diffuse fronts with robustness against noise in tropical and complex-terrain regions.

Cells with a density greater than 35% were considered candidates for frontal regions. This threshold was established through a sensitivity analysis in which values between 20% and 50% were tested. Thresholds below 30% led to excessive noise and isolated mesoscale detections, while thresholds above 40% suppressed diffuse but meteorologically relevant fronts, especially over the South Atlantic. The choice of 35% therefore represents an optimal balance, maximizing the detection of synoptic-scale fronts while minimizing spurious signals (Figure 1d).

Thermodynamic Parameters and Preprocessing

Reanalysis data were used to derive the AdvT and TFP fields, as shown in Figure 1a,b. ERA5 data were processed at their native 0.25° × 0.25° resolution for initial field calculations. Temperature was smoothed using a five-point filter applied iteratively over 100 cycles, employing a standard 3 × 3 convolution kernel, as suggested Feng et al. [12]. This extensive smoothing is essential to reduce high-frequency meteorological noise that can create false frontal signals while preserving the mesoscale thermal gradients that characterize genuine atmospheric fronts. Subsequently, horizontal gradients of the smoothed temperature field were calculated considering the Earth’s spherical geometry. The distances corresponding to variations in latitude and longitude were adjusted using the Earth’s mean radius (6371 km) and projection corrections based on latitude. Based on the TFP and thermal advection fields, the cold frontal zone was objectively defined as the set of grid points simultaneously satisfying the following criteria: 5 × 10⁻¹¹ K m⁻² and AdvT ≤ −1 × 10⁻⁴ K s⁻¹.

These thresholds were selected based on previous studies [11,12,30,31] and refined through an exploratory analysis of the percentiles of the dynamic and thermodynamic fields in the study region.

Aggregation, Connectivity and Filtering

The points classified as part of the frontal zone were marked in a binary matrix with a resolution of 0.25°, corresponding to the native grid of the ERA5 data. The thresholds were adjusted to better represent South American conditions (Figure 1c). To spatially consolidate the frontal signals and eliminate isolated noise, the original 0.25° × 0.25° grid was aggregated into a coarser 2.5° × 2.5° grid. For each cell of this new grid, the relative density of cold frontal points was calculated. Cells with a density greater than 35% were considered candidates for frontal regions. This threshold was determined through a sensitivity analysis and represents the optimal value that maximizes the detection of meteorologically significant fronts while minimizing the inclusion of mesoscale atmospheric noise (Figure 1d).

Next, a nearest-neighbor connectivity method was applied to group adjacent cells into continuous regions. This connectivity analysis identifies which cells belong to the same frontal structure by examining the eight neighboring cells (8-connectivity) for each frontal candidate. Adjacent cells that meet the density threshold are assigned the same label, creating connected frontal zones as shown in Figure 1e.

Polynomial Refinement

Following the connectivity analysis described above, the connected frontal zones were considered part of the same frontal structure and visually distinguished by different labels (Figure 1e). These labels were then projected back onto the high-resolution grid (0.25° × 0.25°), preserving the detailed spatial location of the fronts. The high-resolution frontal grids (0.25° × 0.25°) within the low-resolution boundaries (2.5° × 2.5°) are shown in Figure 1f.

Only those frontal regions whose horizontal extent, calculated as the maximum distance between any two points within the structure, exceeded 600 km were retained as valid cold fronts (Figure 1f). This minimum extent criterion was established through iterative testing and represents the optimal threshold that removes small-scale noise structures without discarding meteorologically relevant cold front.

To represent the cold fronts in a continuous and visually coherent manner, a second-order polynomial fit was applied to the set of coordinates corresponding to frontal grid points with the same identification. This smoothing procedure allowed the generation of traces that better match the expected morphology of meteorological fronts, as typically observed in synoptic charts and operational analysis fields. Fronts with fewer than three valid points were discarded at this stage to avoid overfitting and to ensure statistical robustness in the interpolation process.

The resulting polynomial curves were then used for both visualization and export of the results, maintaining compatibility with conventional representations of cold fronts in meteorological analyses. As illustrated in Figure 1g, the identified cold fronts exhibit clear and continuous spatial organization. The example selected for 00 UTC on January 1, 2009, shows three distinct fronts: two located over the South Atlantic Ocean and one positioned over southern Argentina.

Temporal Independence of Detection

It is important to clarify that this study performs independent cold front detection at each time step, without temporal tracking between consecutive analyses. Each 6-hourly ERA5 field is processed independently to identify cold fronts present at that specific time, as the primary objective is to generate training labels for machine learning models that typically process individual snapshots. Therefore, the comparison with CPTEC synoptic charts is performed on a time-by-time basis, matching each automatic detection with its corresponding chart from the same date and time. The 1426 comparisons represent individual temporal instances, not tracked cold front, avoiding the additional complexity of trajectory analysis that is not relevant to the label generation process.

2.2.2. Manual Method

The synoptic charts used in this study were provided by the CPTEC for the same temporal coverage as the ERA5 analysis—6-hourly intervals throughout 2009. Each chart was processed independently, with no temporal tracking between consecutive charts. Initially, the lines representing cold fronts were manually vectorized in Python (v3.12), focusing on the dashed blue lines that indicate cold fronts. The geometries were converted into shapefiles and subsequently rasterized onto a 0.25° × 0.25° grid using nearest-neighbor interpolation. Pixels intersected by the front lines were assigned a value of 1 (front), while all others received a value of 0. Small holes (<50 km²), disconnected components, and overlapping features were removed. Thus, both methods produce binary matrices with the same structure: 1 for frontal pixels and 0 for non-frontal pixels. The result was a set of binary masks compatible with the automatic detection data, enabling direct time-by-time comparison where each automatic frontal map is compared with its corresponding manual chart from the same date and UTC time (Figure 2).

2.3. Spatial Comparison Metrics

The spatial comparison between the automatic labels (derived from ERA5 data) and the manual labels (from synoptic charts) was carried out using classical binary segmentation metrics, applied over a regular 0.25° × 0.25° grid. These metrics quantify the spatial agreement between methods, though it is important to note that low overlap does not indicate poor performance for machine learning applications, as the methods represent fundamentally different approaches to front identification. The metrics considered were:

• Precision: The proportion of pixels classified as cold front by the automatic method that matched those in the manual chart.

$$\mathrm{Precision}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP} + \mathrm{FP}}}$$

(4)

where Precision is the proportion of pixels classified as cold front by the automatic method that match those in the manual chart, $\mathrm{TP}$ denotes the true positives (pixels identified as cold front by both methods), and $\mathrm{FP}$ denotes the false positives (pixels identified as cold front only by the automatic method).

• Recall: The proportion of manual fronts correctly detected by the automatic method.

$$\mathrm{Recall}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP} + \mathrm{FN}}}$$

(5)

where Recall is the proportion of manual fronts correctly detected by the automatic method, $\mathrm{TP}$ denotes the true positives, and $\mathrm{FN}$ denotes the false negatives (pixels identified as cold front only by the manual method).

• F1-score: The harmonic mean of Precision and Recall, balancing both aspects.

$$\mathrm{F}1\text{-}\mathrm{score}=2\times {\displaystyle \frac{\mathrm{Precision} \times \mathrm{Recall}}{\mathrm{Precision} + \mathrm{Recall}}}$$

(6)

where F1-score is the harmonic mean of Precision and Recall, balancing both aspects.

• Coefficient Dice: A measure of spatial similarity dice

$$\mathrm{Dice}={\displaystyle \frac{2\times \left|A {\displaystyle \cap } B\right|}{\left|A\right|+\left|B\right|}}$$

(7)

• Intersection over Union (IoU): The ratio between the intersection and the union of the binary masks.

$$\mathrm{IoU}={\displaystyle \frac{ \left|A {\displaystyle \cap } B\right| }{\left|A {\displaystyle \cup } B\right|}}={\displaystyle \frac{ TP }{\mathrm{TP} +\mathrm{FP} + \mathrm{FN}}}$$

(8)

where $A$ and $B$ are the sets of pixels identified as cold fronts by the automatic and manual methods, respectively; ${\displaystyle \cap }$ denotes the intersection (common pixels between the two sets), ${\displaystyle \cup }$ denotes the union (all pixels belonging to at least one set), $TP$ denotes true positives, $\mathrm{FP}$ false positives, and $\mathrm{FN}$ false negatives.

Confusion matrix components were defined as follows:

• TP (True Positive): pixels identified as cold front by both methods
• FP (False Positive): pixels identified as cold front only by the automatic method
• FN (False Negative): pixels identified as cold front only by the manual method
• TN (True Negative): pixels not identified as cold front by either method

For all metrics, values range from 0 (no overlap) to 1 (perfect overlap), where higher values indicate better performance and greater spatial agreement between automatic and manual labels. Metrics such as Dice and IoU are particularly sensitive to spatial overlap and are widely used in image segmentation evaluations and meteorological event detection comparison. This approach follows well-established practices in both machine learning and meteorological forecast verification [39,40,41,42,43,44].

It is important to note that low pixel-level overlap between automatic and manual methods does not imply poor performance for machine learning applications. The key requirement is that the automatic labels maintain direct spatial correspondence with the ERA5 input fields. This physical consistency is more relevant for convolutional neural network training than achieving exact pixel-level agreement with manual charts, which are systematically displaced from the underlying thermal gradients.

To harmonize the rasterized manual fronts (average thickness ≈ 12.4 pixels) and the automatic ERA5-derived masks (average thickness ≈ 9.0 pixels), we applied a binary dilation to the automatic masks using a 3 × 3 structuring element with one iteration. This operation increased the mean automatic line width to be comparable with the manual charts, thereby reducing systematic discrepancies caused by line thickness differences and avoiding bias in pixel-based comparison metrics. The dilation parameters were chosen based on the measured average thickness of the two datasets, ensuring full consistency between datasets. 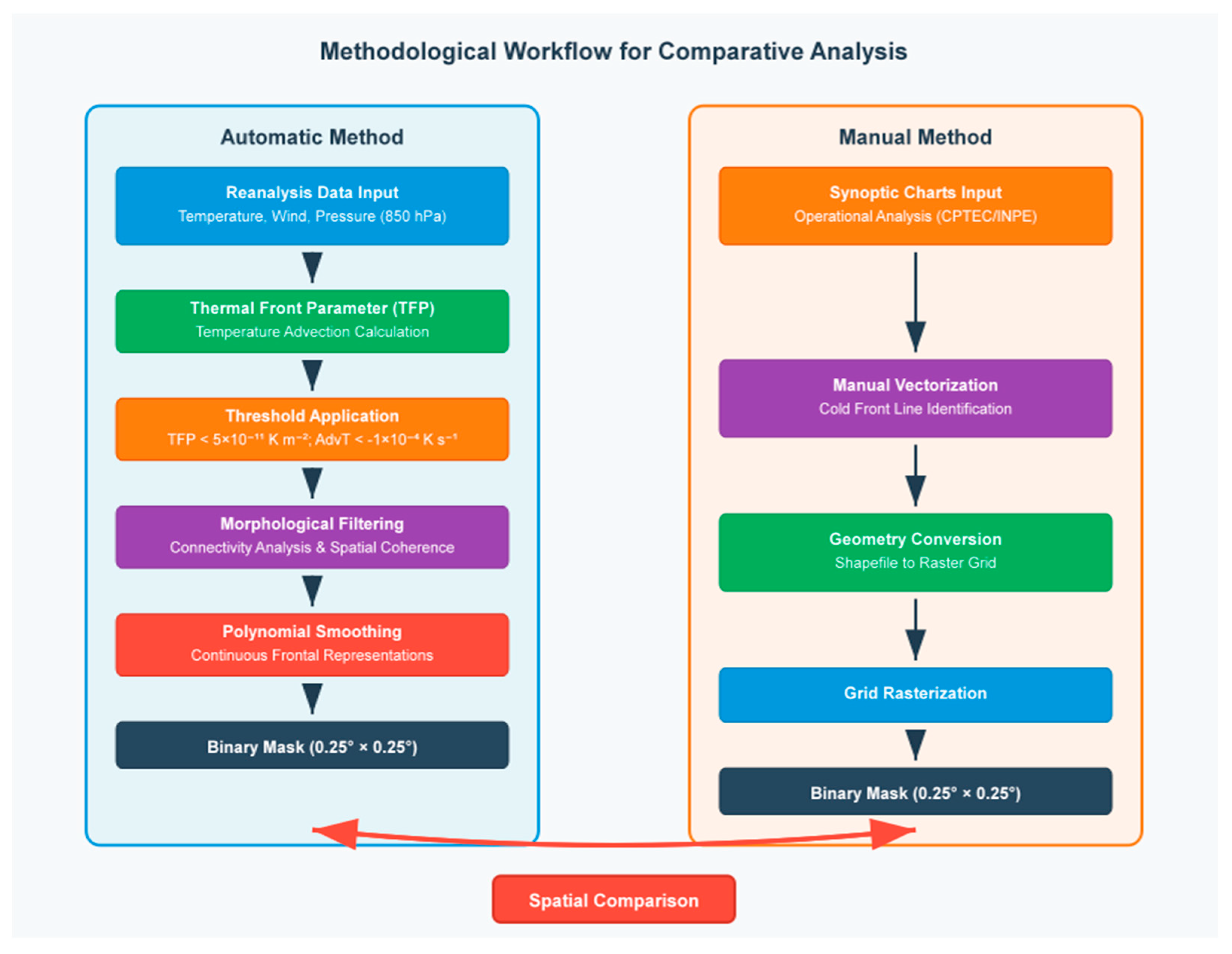Figure 3 illustrates the methodological framework employed in this study to compare automatic and manual cold front detection approaches. The automatic method (left panel) processes ERA5 reanalysis data through a sequential pipeline: calculation of thermodynamic parameters (TFP and temperature advection), application of optimized thresholds, morphological filtering for spatial coherence, and polynomial smoothing to generate continuous frontal representations. In parallel, the manual method (right panel) digitizes cold fronts from operational CPTEC synoptic charts through vectorization and subsequent rasterization onto the same 0.25° × 0.25° grid. Both methodologies produce binary masks where pixels are classified as frontal (1) or non-frontal (0), enabling direct pixel-by-pixel comparison using standard spatial metrics. This comparative framework allows for quantitative assessment of systematic differences between automatic and manual front identification approaches.

3. Results and Discussion

3.1. Seasonal and Spatial Patterns of Cold Front Detection

The sensitivity analysis of the thresholds (Figure 4) demonstrates the robustness of the developed cold front detection method. The distribution of the TFP (Figure 4a) exhibits a log-normal behavior, with the optimized threshold of 5 × 10⁻¹¹ K m⁻² effectively capturing the most significant frontal events. The temperature advection (Figure 4b) shows a distribution centered near zero, with the threshold of −1 × 10⁻⁴ K s⁻¹ appropriately selecting cases of cold advection. The sensitivity map (Figure 4c) reveals that the chosen combination of thresholds maximizes the detection of frontal points (40–41%), maintaining a balance between sensitivity and specificity. The percentile analysis (Figure 4d) confirms that the advection threshold corresponds approximately to the 25th percentile, ensuring adequate selectivity. The spatial results (Figure 4e,f) show that the detected fronts exhibit climatologically consistent patterns over South America, with well-defined temperature gradients in regions of higher frontal activity, validating the effectiveness of the optimized thresholds.

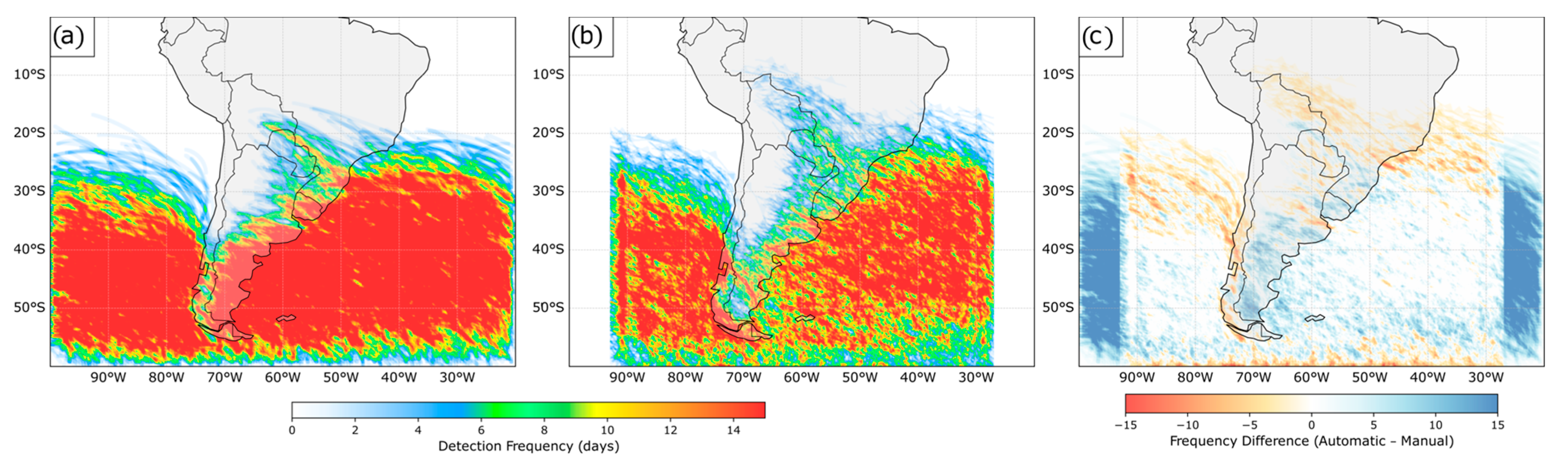
The analysis of cold front detection frequency throughout 2009 (Figure 5), based on 1426 temporal observations (6 h intervals), revealed distinct spatial and seasonal patterns between the automatic and manual methods. Figure 5 presents the spatial distribution of detection frequency, highlighting significant regional discrepancies that reflect the differing natures of the methods employed.

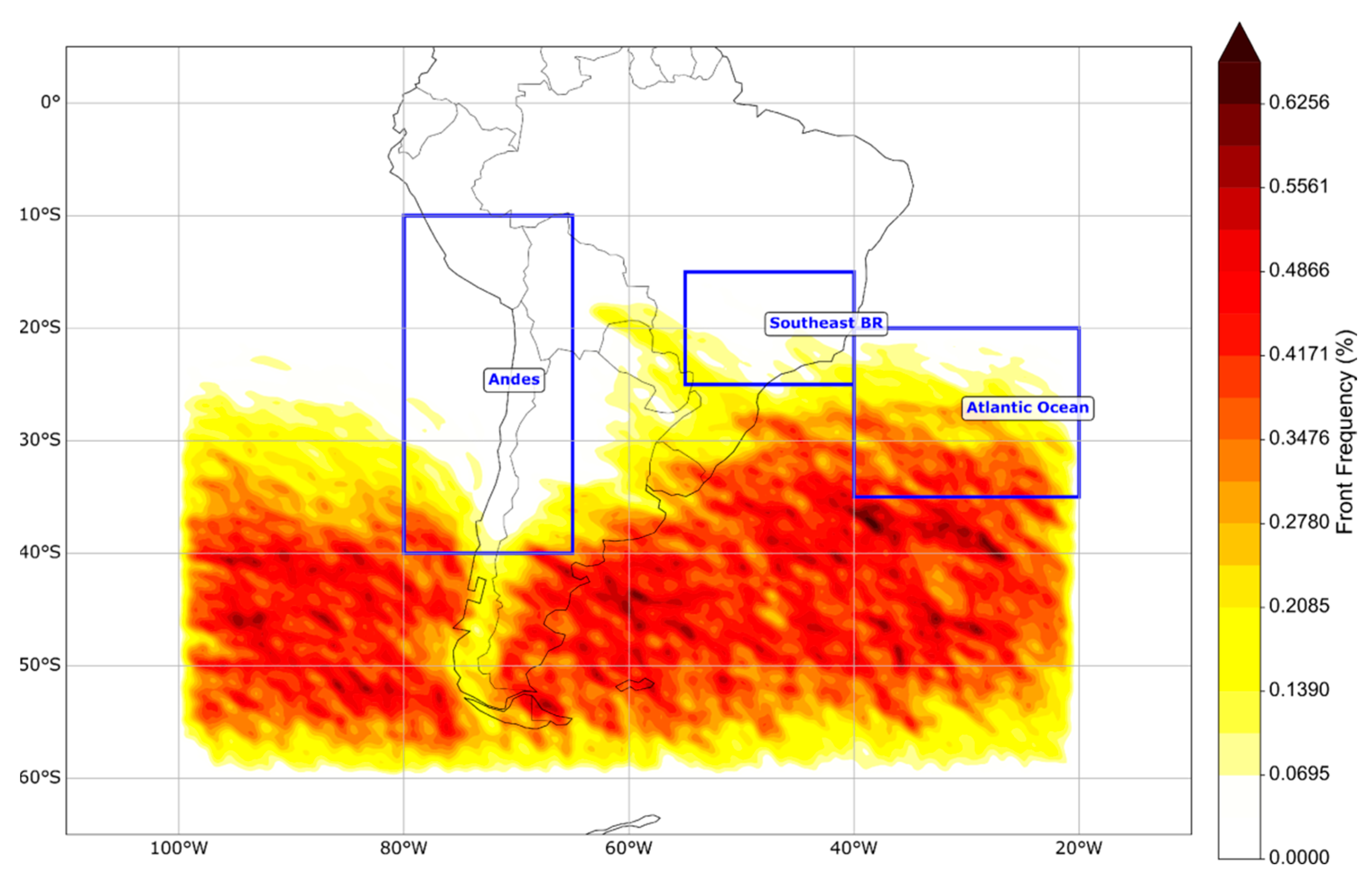
In the southwestern Atlantic Ocean sector (40° W–30° W), the automatic method detected cold fronts in 39% of the analyzed time steps (554 out of 1426 observations), exceeding the frequency recorded by the manual charts (25%, or 350 observations) by ≈59%. This discrepancy can be attributed to the greater sensitivity of ERA5 to oceanic thermal gradients, which are smoothed by the spatial interpolation inherent to the reanalysis but are often underestimated in manual analyses due to the lower observational density over the ocean [32].

In contrast, along the eastern slopes of the Andes (70° W–65° W), the automatic method exhibited systematic underdetection, identifying fronts in only 18% of the cases (262 out of 1426 observations), representing a ≈44% reduction compared to the manual analyses (33%, or 467 observations). Importantly, the manual CPTEC analyses were treated as the reference dataset, while the automatic detection at 850 hPa was evaluated against these operational charts to assess its skill under simplified diagnostic conditions. The purpose of the automatic method is not to replicate the full operational analysis but to provide spatially consistent labels aligned with reanalysis data for machine learning applications. This discrepancy also reflects the well-known challenges faced by numerical models in adequately representing complex orographic effects, particularly the channeling and modification of polar airflows by the Andean barrier [32,45].

The southeastern region of Brazil, characterized by a higher observational density and moderately complex terrain, showed relative agreement between the methods, with detection frequencies around 28% for both approaches. This convergence validates the robustness of the automatic method in well-instrumented regions and suggests that the discrepancies observed in other areas are related to the specific limitations of each technique.

3.2. Comparative Analysis: Automatic vs. Manual Front Labels

3.2.1. Morphological and Spatial Differences

Figure 6 presents two representative cases that clearly demonstrate the key differences between automatic and manual front labeling. During the summer event (3 January 2009, 18 UTC), a distinct core of strong negative temperature advection is centered south of the Rio Grande do Sul coast, with values exceeding −2 × 10⁻⁴ K s⁻¹. The 850 hPa wind vectors, mainly from the northwest, support the presence of cold-air advection toward the subtropical coastline.

The comparison between the front delineations reveals a systematic spatial misalignment: the manual front (depicted in red) is consistently displaced southward and eastward, whereas the automatic contours (in dark blue) closely follow the thermal gradient at 850 hPa. This displacement, ranging from 100 to 150 km across different segments, highlights the fundamental conceptual distinction between these representations. Manual charts integrate surface observations with heuristic, analyst-driven interpretations, while the automatic detection relies solely on the physical structure of thermal gradients in the lower troposphere as captured by the reanalysis data.

In the winter case (22 July 2009, 12 UTC), the agreement between methods shows marked improvement compared to the summer case. The broad lobe of cold air advection, extending from Patagonia to southeastern Brazil, is associated with a deep cyclonic circulation typical of winter cold fronts. The spatial alignment between the delineations is substantially better, with discrepancies generally reduced to less than 100 km in most regions. This improved agreement suggests that during winter, when cold fronts are more intense and well-defined, both the manual analysis and the automatic detection converge toward similar representations of the baroclinic zones, reflecting the clearer thermal gradients characteristic of stronger cold fronts.

It is important to emphasize that these discrepancies reflect the inherent differences between methodologies. The automatic approach is highly sensitive to oceanic thermal gradients represented in ERA5, while manual analyses tend to underestimate these regions due to sparse observational coverage. Conversely, in the Andes, human analysts can interpret orographic modifications of polar airflows that remain a limitation for reanalysis-based methods. Therefore, these discrepancies indicate methodological complementarity rather than deficiencies.

3.2.2. Methodological Comparison: Quantifying Systematic Differences

The regional evaluation (

Table 1. Pixel-based comparison metrics between the automatic and manual methods for cold front detection, by region.

Region	Precision (%)	Recall (%)	F1-Score (%)	TP	FP	FN	Total Comparisons
Atlantic Ocean	6.2	3.1	4.1	320,764	4,862,849	9,968,270	1426
Andes	1.8	0.8	1.1	30,406	1,657,310	3,617,080	1426
Southern Brazil	7.2	2.0	3.1	17,065	219,798	846,194	1426

) highlights the pronounced spatial heterogeneity in the agreement between the automatic and manual methods. The analysis was based on 1426 coincident timestamps, corresponding to periods in which both automatic labels and manual labels were available. This represents 97.7% of the total possible observations for 2009, with the remaining 34 cases (2.3%) excluded due to the unavailability of some manual charts in the institutional archive.

The quantitative assessment of methodological differences is presented in Table 1, which summarizes pixel-based comparison metrics across three distinct geographical regions [43,46]. The South Atlantic Ocean demonstrates the automatic method’s higher detection frequency with 320,764 coincident pixels but generates 4,862,849 additional detections not present in manual charts. This 15:1 ratio of automatic-to-manual detections reflects the method’s enhanced sensitivity to mesoscale thermal gradients over oceanic regions, features systematically smoothed or omitted in operational manual analysis due to lower observational density and time constraints. The resulting precision and recall values of 6.2% and 3.1%, respectively, indicate substantial methodological divergence rather than performance deficiencies.

In contrast, the Andes Region shows the manual method identifying 3,617,080 frontal pixels not detected automatically, while the automatic method finds only 30,406 coincident detections. This 119:1 ratio (manual-to-automatic) highlights the superior performance of human analysts in interpreting complex orographic effects, where numerical models struggle with terrain-modified atmospheric flows. The extremely low precision (1.8%) and recall (0.8%) values in this region do not indicate methodological deficiencies, but rather underscore the fundamental challenges faced by gradient-based automatic methods in mountainous terrain where thermal gradients are disrupted by complex topography.

Southeastern Brazil shows intermediate behavior with more balanced detection ratios (≈50:1 manual-to-automatic), consistent with this region’s moderate terrain complexity and higher observational density, where both methods perform closer to their optimal conditions. The relatively higher precision (7.2%) compared to other regions, though still modest, reflects the more favorable conditions for automatic detection in areas with moderate topographic complexity.

It is crucial to interpret these pixel-based metrics within the proper methodological context. These values reflect fundamental differences in spatial representation approaches between methods that operate at different scales and serve different purposes: automatic detection captures mesoscale thermal gradients at 850 hPa with high spatial resolution, while manual analysis identifies synoptic-scale frontal zones through multi-level atmospheric interpretation. For machine learning applications, the physical consistency provided by automatic labels is more valuable than pixel-perfect overlap with manual charts. The systematic spatial displacement (median ≈ 502 km) observed between methods would introduce significant label noise if manual charts were used as ground truth for training convolutional neural networks. Models would learn to associate atmospheric patterns at one location with frontal boundaries at systematically displaced positions, severely compromising their generalization capability. The high spatial concordance (99.7%) demonstrates that automatic labels correctly identify frontal events while maintaining direct correspondence with the meteorological fields that serve as model inputs.

3.2.3. Interpretation Framework

The regional pixel-based metrics in Table 1 must be interpreted alongside the global comparison results presented in

Table 2. Global comparison metrics between the automatic and manual methods front labels.

Metric	Value	Interpretation
IoU	0.013	Low spatial overlap
Dice	0.034	Limited binary similarity
Precision	0.052	High false positive rate
Recall	0.025	High false negative rate
Spatial Concordance	0.997	Excellent event detection

, which reveal a critical distinction between spatial localization accuracy and event detection capability. As expected for methods measuring fundamentally different atmospheric representations, pixel-level overlap metrics are low (IoU = 0.013), while event-level detection shows excellent agreement (spatial concordance = 0.997), confirming both methods identify the same synoptic systems with different spatial representations.

This apparent contradiction between low pixel-based overlap and high event detection accuracy reflects the fundamental scale mismatch between methodologies. The automatic method detects mesoscale thermal gradients (50–200 km) at 850 hPa with high spatial resolution, while manual analysis identifies synoptic-scale frontal zones (500–1000 km) through multi-level atmospheric interpretation. The spatial concordance metric accounts for this displacement, revealing that both methods identify the same meteorological phenomena but represent them at different scales and locations.

The low IoU (0.013) and Dice (0.034) coefficients should therefore not be interpreted as indicating methodological failure, but rather as evidence of this systematic spatial displacement between fundamentally different approaches to front representation. The excellent spatial concordance (0.997) provides critical insight: both methods successfully identify the same frontal events despite their different spatial representations. This distinction is essential for understanding why automatic labels are superior for machine learning training—they maintain direct spatial correspondence with the physical atmospheric fields that will be used as model inputs, while manual labels introduce systematic displacement that would compromise neural network performance.

3.2.4. Implications for Machine Learning Applications

The high spatial concordance (0.997) provides strong evidence for the automatic method’s effectiveness in Machine Learning (ML) applications, demonstrating that it reliably identifies frontal events even when precise pixel locations differ from manual analysis. This event-level accuracy is more relevant for ML training than pixel-perfect overlap, as models need to learn the atmospheric patterns associated with frontal activity rather than memorize specific pixel positions.

The automatic method’s advantages for ML training become clear when considering both detection reliability and methodological consistency. The objective criteria eliminate analyst-dependent biases that would compromise model generalization, while the consistent detection threshold prevents overfitting to individual analyst preferences. The higher detection frequency over oceanic regions (15:1 ratio) captures meteorologically significant mesoscale frontal activity that operational analysis typically omits, providing more comprehensive training examples.

Furthermore, the physical grounding in 850 hPa thermal gradients ensures direct correspondence between labels and input meteorological fields, enabling models to learn physically meaningful relationships rather than subjective interpretations. The systematic spatial consistency maintains reliable correspondence with temperature, wind, and pressure fields, which is essential for robust model training.

3.2.5. Methodological Complementarity

Rather than competing approaches, these methods serve complementary purposes where automatic labels are optimal for ML training, climatological studies, and objective research, while manual labels remain essential for operational forecasting, emergency response, and meteorological interpretation. The regional calibration framework (Section 3.5) leverages this complementarity by applying method-specific strengths to appropriate geographical domains.

3.2.6. Geometric and Morphological Characteristics

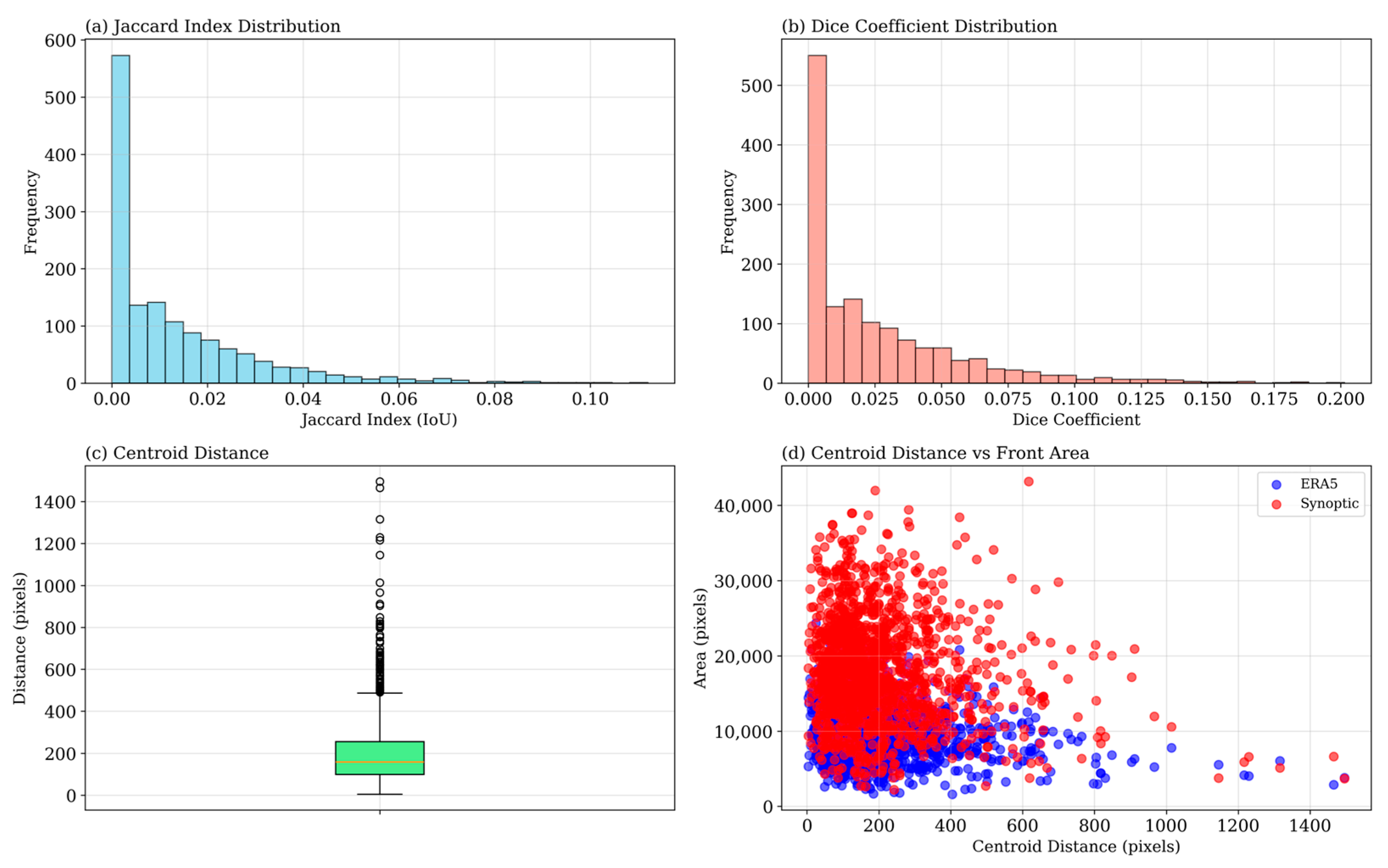
The analysis of the geometric characteristics of the identified fronts (Figure 7) reveals systematic differences between the methods. The Jaccard Index histogram (Figure 7a) shows a strongly skewed distribution, with 78% of the samples exhibiting an IoU < 0.05, indicating minimal spatial overlap [47,48]. The Dice coefficient (Figure 7b) confirms this pattern, with a median value of 0.032 and 85% of values below 0.10.

The distance between the centers of mass of the corresponding fronts (Figure 7c) has a median of 6.3 degrees of latitude/longitude (≈700 km), with interquartile range between 4.1° and 8.7°. The presence of extreme outliers (distances > 15°) indicates cases where fronts are identified in entirely different sectors of the domain, suggesting fundamental differences in the interpretation of the atmospheric structure.

The scatter plot (Figure 7d) between the distance of centers and the mean area of the fronts reveals that manual fronts tend to be 25% larger in area compared to automatic fronts (means of 2847 vs. 2141 pixels, respectively). This difference suggests that manual delineations are less precise spatially, possibly due to the tendency to “connect” multiple baroclinic cores into a single frontal structure.

3.3. Seasonal Variability During 2009

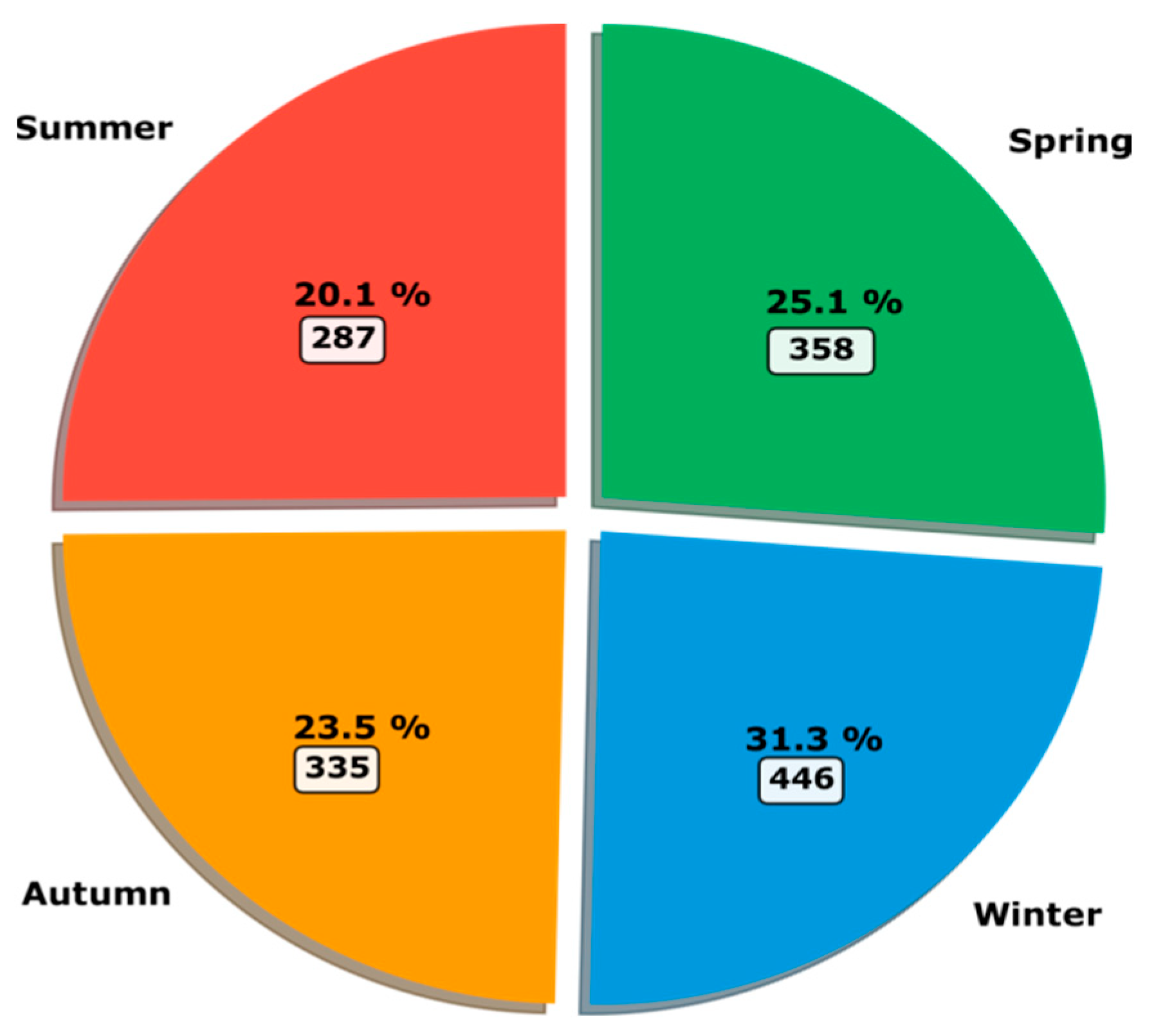
The seasonal analysis of cold front occurrence during 2009 reveals patterns consistent with the expected atmospheric dynamics of South America. During the austral winter (June–August), the highest frequency of cold fronts was observed (31.3% of detected events, 446 detections), characterized by more intense systems and preferred trajectories along the Argentina–Southern Brazil corridor. Spring (September–November) exhibited an intermediate frequency (25.1% of frontal events, 358 detections), marked by transitional fronts with less pronounced thermal characteristics. Autumn (March–May) displayed a transitional pattern (23.5%, 335 detections), with a gradual resumption of cyclogenetic activity over the South Atlantic, while austral summer (December–February) recorded the lowest frontal activity (20.1% of total detections, 287 detections), mostly concentrated over the far south of the continent. These seasonal patterns, totaling 1426 cold front detections throughout 2009, are consistent with multi-year studies reported in the literature [2,49,50,51] though a single year of analysis cannot establish climatological trends (Figure 8).

3.4. Implications for Deep Learning Applications

The results indicate that directly using manual charts as ground truth for training convolutional neural networks would introduce systematic location noise [15]. Models such as U-Net, when trained with manual labels, would learn patterns that do not align with the physical gradients at 850 hPa, thereby compromising their generalization capability.

The average misalignment of approximately 700 km between the centroids of the fronts corresponds to about 2.8 grid cells (at 0.25° resolution), which is significant considering that typical frontal structures span 3–5 degrees of longitude. This systematic displacement would introduce spurious correlations during training, leading models to learn incorrect atmospheric patterns.

The low spatial overlap (IoU = 0.013) suggests that networks trained with manual labels would exhibit a high false positive rate when applied to reanalysis data, thus limiting their operational applicability. In contrast, automatic labels, due to their direct alignment with physical gradients, provide a more robust foundation for the development of automatic cold front detection systems.

3.5. Proposed Calibration Framework

Based on the identified regional discrepancies, we propose a calibration framework to optimize the use of the automatic labels across different regions (

Table 3. Regional Adjustment Factors Applied to Automatic Cold Front Labels Based on Geographical Characteristics.

Region	Adjustment Factor (%)	Weight	Justification
South Atlantic Ocean	−38% (Reduction)	0.62	Corrects over-detection of thermal gradients over the ocean.
Andean Region (>1500 m)	+78% (Amplification)	1.78	Corrects under-detection due to orographic complexity.
Lowland Continental Areas	0% (No Adjustment)	1.00	Maintains original parameters due to robust performance.

).

This regional calibration framework preserves the physical objectivity of the automatic labels while correcting identified systematic biases, resulting in a dataset that more accurately represents the atmospheric conditions over South America for machine learning applications.

The spatial distribution of cold front density for the year 2009 (Figure 9) reveals distinct regional patterns with well-defined statistical variability across the three analysis regions. The South Atlantic Ocean exhibits the highest frontal activity, with an average density of 0.40% and a maximum of 1.51%, along with the highest standard deviation (0.24%), indicating significant spatial variability in the occurrence of fronts over this oceanic region. In contrast, the Andes and southeastern Brazil present similar average densities (0.22% and 0.24%, respectively) but with distinct characteristics. The Andes recorded 185,609 frontal points distributed across an extensive area of 540,000 pixels, resulting in a relatively low density due to the orographic influence of the mountain range. Meanwhile, southeastern Brazil registered 81,540 frontal points over just 135,000 pixels, demonstrating greater frontal detection efficiency per unit area. The global maximum density of 1.51% was observed over the South Atlantic Ocean, confirming this region as the primary corridor for cold fronts over South America. The direction vectors highlight the typical west-to-east propagation pattern of cold fronts during 2009, with systems maintaining their intensity as they traverse the continent and concentrating their maximum activity over oceanic areas, where more favorable conditions for development and propagation are found.

3.6. Quantitative Assessment of Spatial Misalignment Impact

To quantify the systematic spatial displacement between automatic and manual labeling approaches, we conducted a comprehensive spatial analysis using 1426 matched timestamp pairs covering the complete available dataset from 2009. This analysis directly addresses the core motivation for developing automatic labels: demonstrating why manual chart labels are unsuitable for training convolutional neural networks.

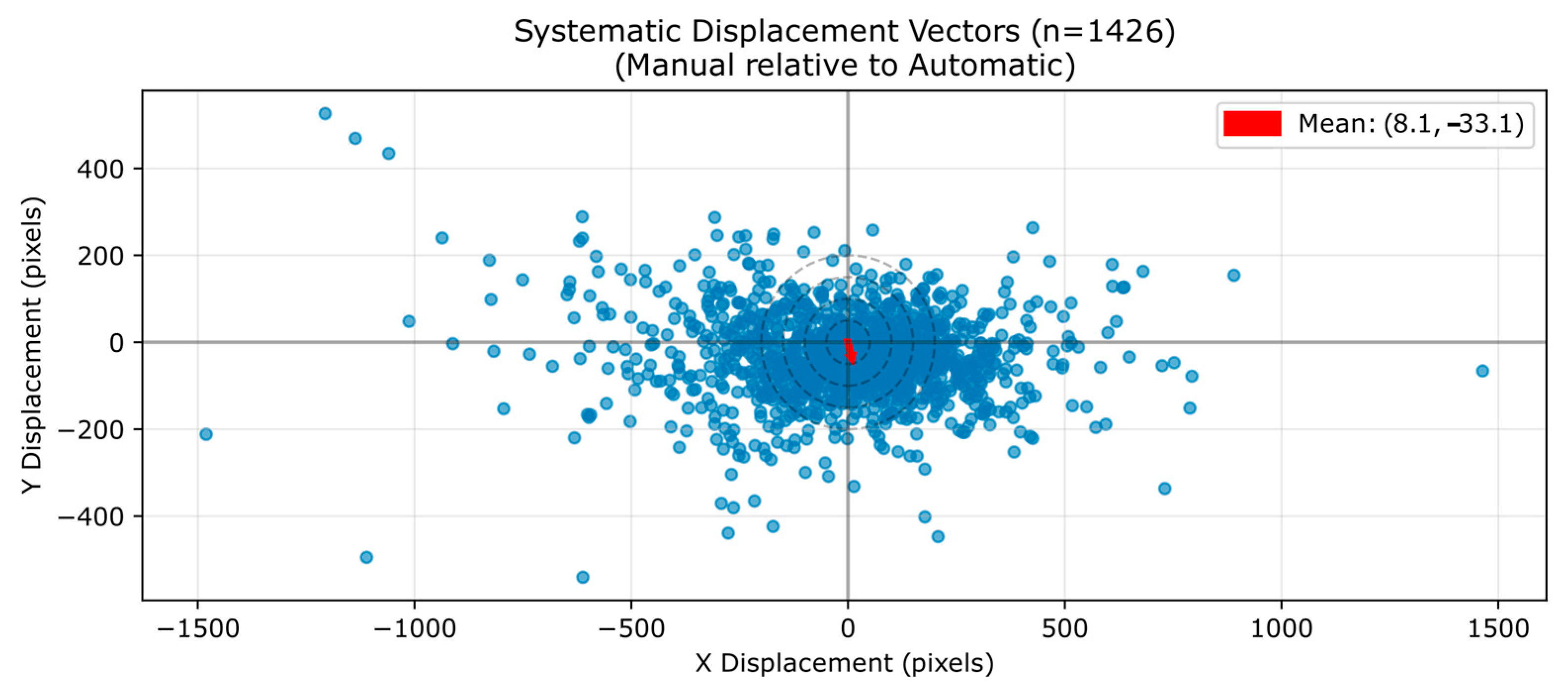
The displacement vector analysis reveals systematic spatial misalignment between methodologies, with mean center-to-center distance of 201.0 ± 163.7 pixels, corresponding to approximately 502 km at the 0.25° resolution of our analysis grid (Figure 10). The displacement pattern shows a consistent south-southeastward bias, with mean displacement vector of (8.1, −33.1) pixels, indicating that manual labels are systematically positioned south-southeast of their corresponding automatic counterparts. This systematic displacement reflects the fundamental difference in detection approaches: automatic labels precisely identify thermal gradient locations at 850 hPa, while manual analyses integrate multi-level atmospheric patterns through human interpretation, often positioning frontal boundaries at different locations than the underlying physical gradients captured in reanalysis data.

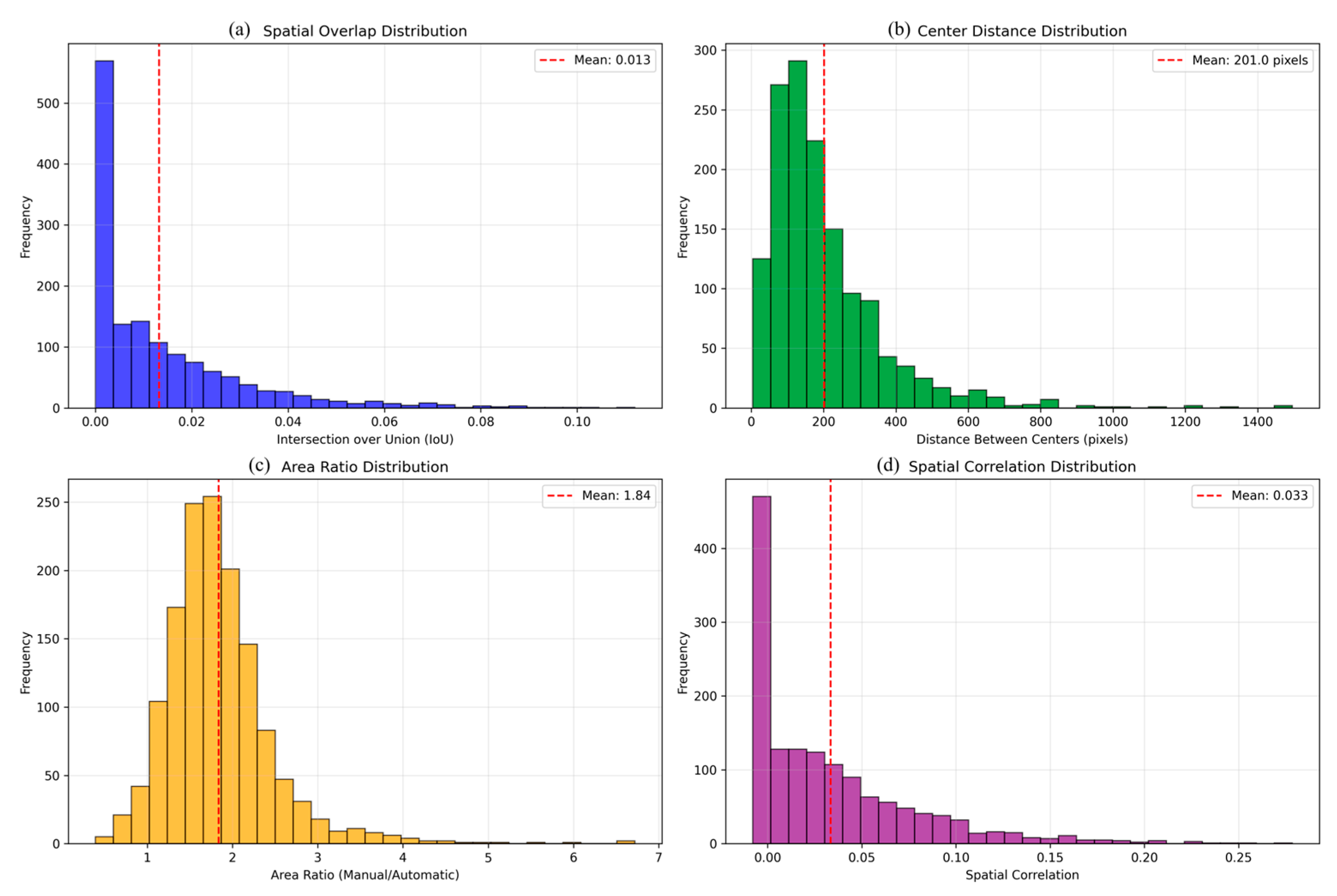
The comprehensive statistical assessment confirms the magnitude of methodological differences across multiple metrics (Figure 11). Pixel-level spatial overlap was minimal (IoU = 0.013 ± 0.017), confirming negligible direct spatial correspondence between methods. Area analysis revealed that manual labels are systematically larger, with mean ratio of 1.84 ± 0.63, indicating that manual analysis delineates frontal zones approximately 84% more extensive compared to the precise gradient-based detection of the automatic method. Even after morphological dilation to account for scale differences, spatial correlation remained extremely low (r = 0.033 ± 0.044), emphasizing the fundamental scale mismatch between approaches.

These quantitative results demonstrate why manual chart labels introduce systematic noise when used to train convolutional neural networks with reanalysis input data. The mean displacement of ~502 km corresponds to approximately 2.0 grid cells at standard resolution, which would cause models to learn incorrect spatial associations between atmospheric patterns and frontal boundaries. For U-Net architectures specifically, this spatial misalignment would manifest as false spatial correlations, reduced generalization, and degraded performance when applied to new data or regions. The systematic clustering of displacement vectors combined with consistently low statistical correspondence confirms that while both methods identify the same synoptic-scale meteorological phenomena, they represent them at systematically displaced spatial locations, thereby validating that automatic labels provide superior spatial consistency for machine learning applications.

4. Conclusions

This study successfully developed an automatic methodology for cold front identification over South America by integrating the Thermal Front Parameter (TFP) with temperature advection from reanalysis data. The approach generated physically consistent labels at 850 hPa using optimized thresholds (TFP < 5 × 10⁻¹¹ K m⁻² and AdvT < –1 × 10⁻⁴ K s⁻¹), revealing characteristic seasonal patterns with peak activity during austral winter (31.3% of cases) and the South Atlantic as the primary propagation corridor. Comparison with manual charts indicated substantial spatial discrepancies (mean IoU = 0.013, median displacement ≈ 700 km); however, these differences reflect the fundamentally distinct nature of the methodologies rather than deficiencies. The automatic approach precisely delineates physical gradients, whereas manual analyses integrate multi-level heuristic interpretations. Regional differences, including oceanic over-detection (58% higher) and Andean under-detection (44% lower), were effectively addressed through the proposed calibration framework. Although the detection metrics are modest from an operational forecasting standpoint, they provide a valuable proof of concept and highlight the potential of physically consistent automatic labeling to advance machine learning applications in atmospheric sciences.

The key contributions of this work address a critical methodological gap in atmospheric machine learning applications. First, it develops the first automatic cold front detection system for South America that maintains direct spatial correspondence between training labels and reanalysis input fields, thereby solving the systematic displacement problem that limits deep learning performance. Second, it demonstrates quantitatively that automatic labels provide superior consistency and physical grounding compared to manual charts for convolutional neural network applications. Finally, it creates a comprehensive, georeferenced dataset with regional calibration factors that optimize detection across different geographical domains.

It should also be reinforced that CPTEC synoptic charts were explicitly treated as the operational reference dataset throughout this study, whereas the automatic detection was evaluated only as an experimental approach restricted to 850 hPa, specifically designed for generating physically consistent labels for machine learning applications.

A limitation of this study is the focus on 850 hPa as the diagnostic level for automatic detection. This methodological choice ensures spatial consistency between labels and ERA5 predictors, which was the primary goal of this work. Nevertheless, we recognize that cold fronts are inherently multi-level phenomena, and other levels (e.g., MSLP, 925 hPa, 700 hPa, moisture, vertical wind shear) could enhance the robustness of future implementations.

Another important limitation of this study is the restriction to a single year (2009). While this period provides a useful proof of concept, it does not capture the full range of interannual variability or seasonal contrasts that characterize South American frontal activity. Future work should extend the methodology to multiple years and diverse seasonal regimes, which would allow a more robust evaluation of detection consistency, the identification of regional biases, and the assessment of climatological relevance.

A further limitation is the absence of temporal tracking. While the automatic detection provides spatially consistent labels at each time step, it does not establish continuity between successive frontal positions. This restricts its direct applicability to operational forecasting and to dynamic analyses that require trajectory information. Future developments should focus on incorporating temporal linking algorithms or trajectory-based approaches, which would enable more comprehensive modeling of cold front behavior and improve the operational value of the method.

This research also addresses the spatial misalignment problem that has hindered the application of state-of-the-art deep learning models to South American meteorology [32]. By ensuring that training labels correspond precisely to the locations of thermal gradients in reanalysis data, the methodology enables robust model training without the spurious spatial correlations introduced by manual charts. The automatic approach provides the consistency and physical correspondence essential for advancing computational meteorology, with demonstrated transferability to other regions through the regional calibration framework. Future research directions include the use of transfer learning approaches that exploit automatic labels for pre-training across different regions, the integration of multi-level atmospheric data to better capture complex frontal structures, and the development of ensemble methods that combine multiple physical parameters to enhance detection accuracy.