Let Us Change the Aerodynamic Roughness Length as a Function of Snow Depth
Abstract
1. Introduction
2. Data and Methods
2.1. Site Descriptions
2.2. Field Data Collection
2.3. Data Processing
2.4. Data Analysis
2.5. Sublimation Estimation
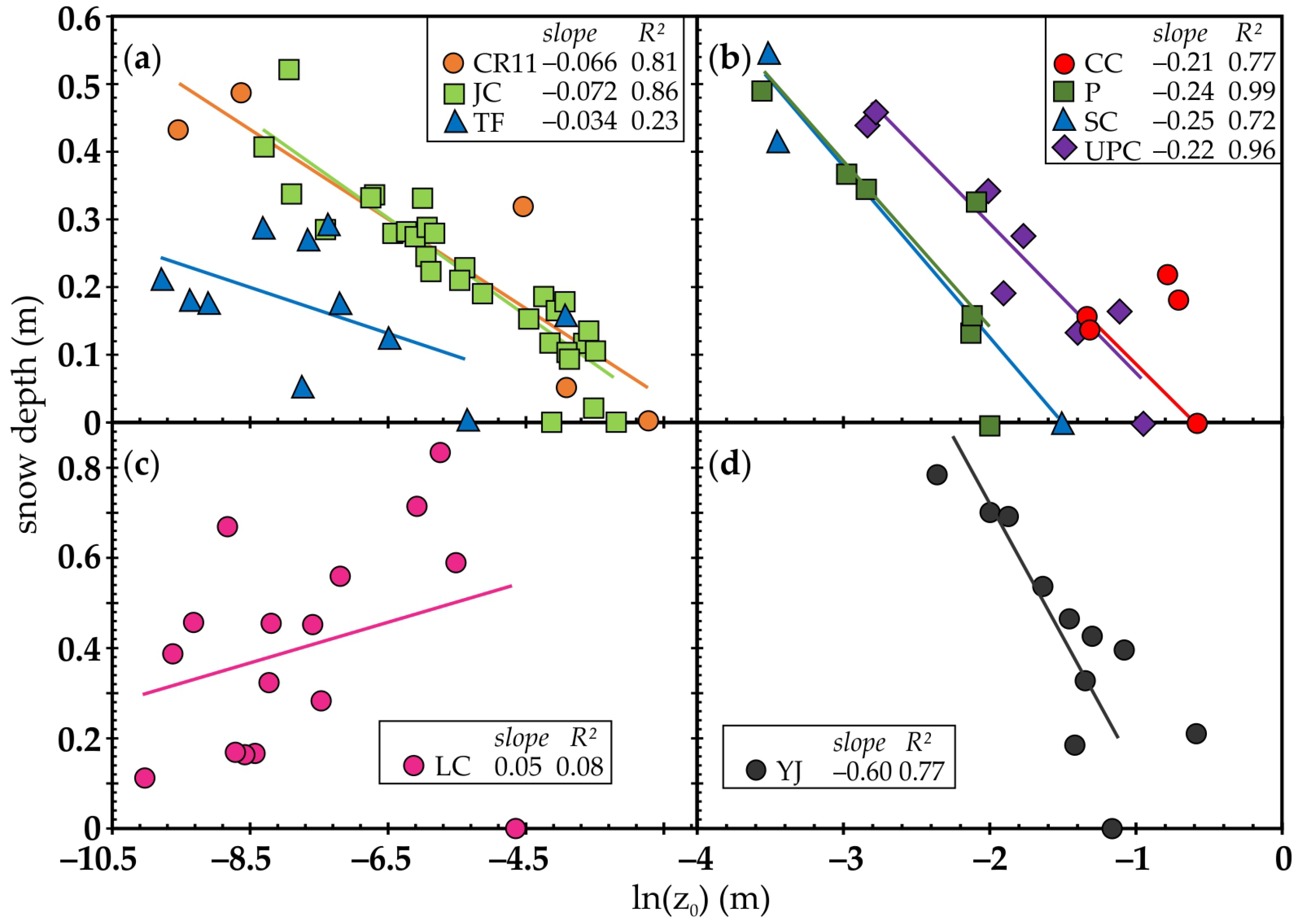
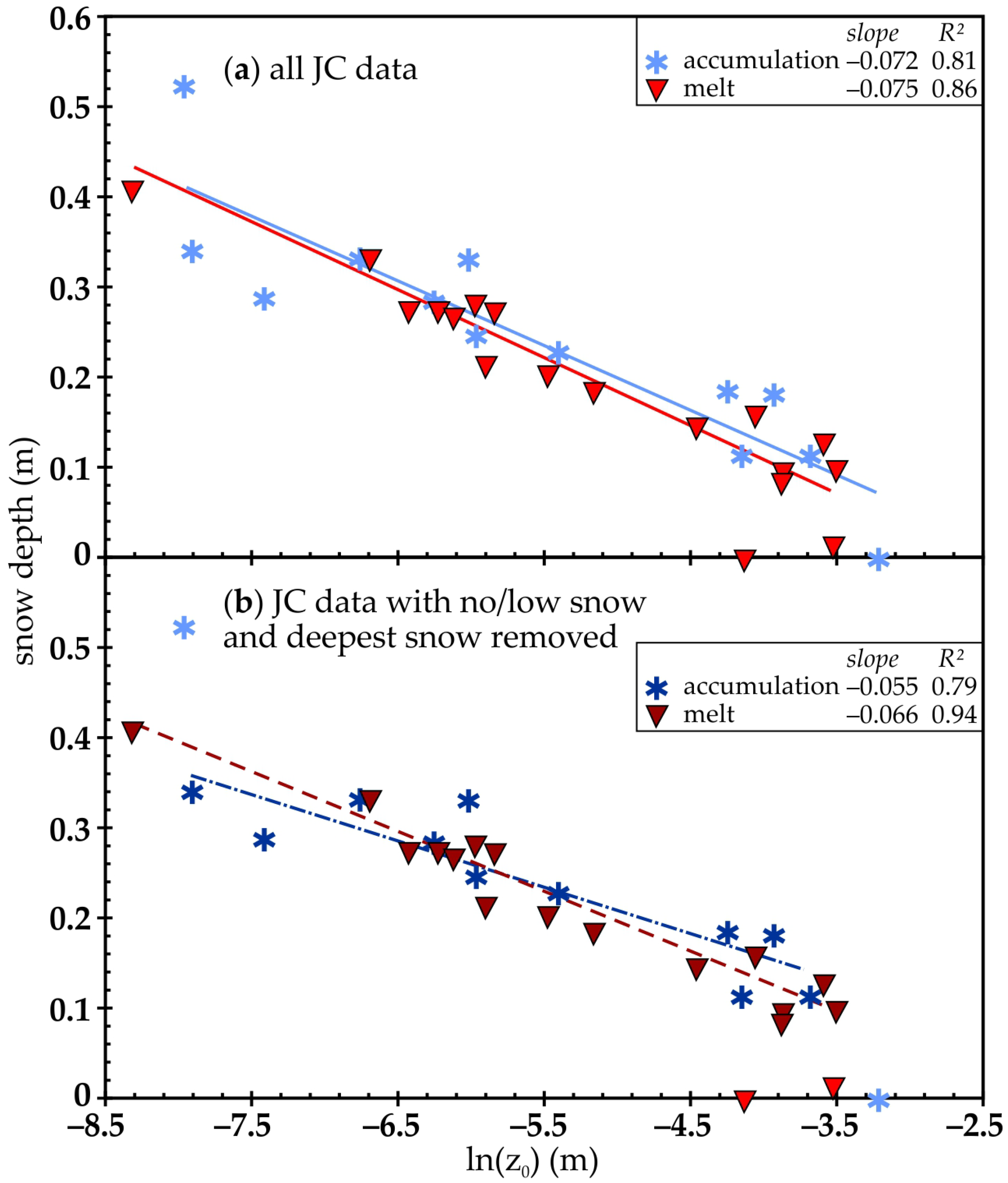
3. Results
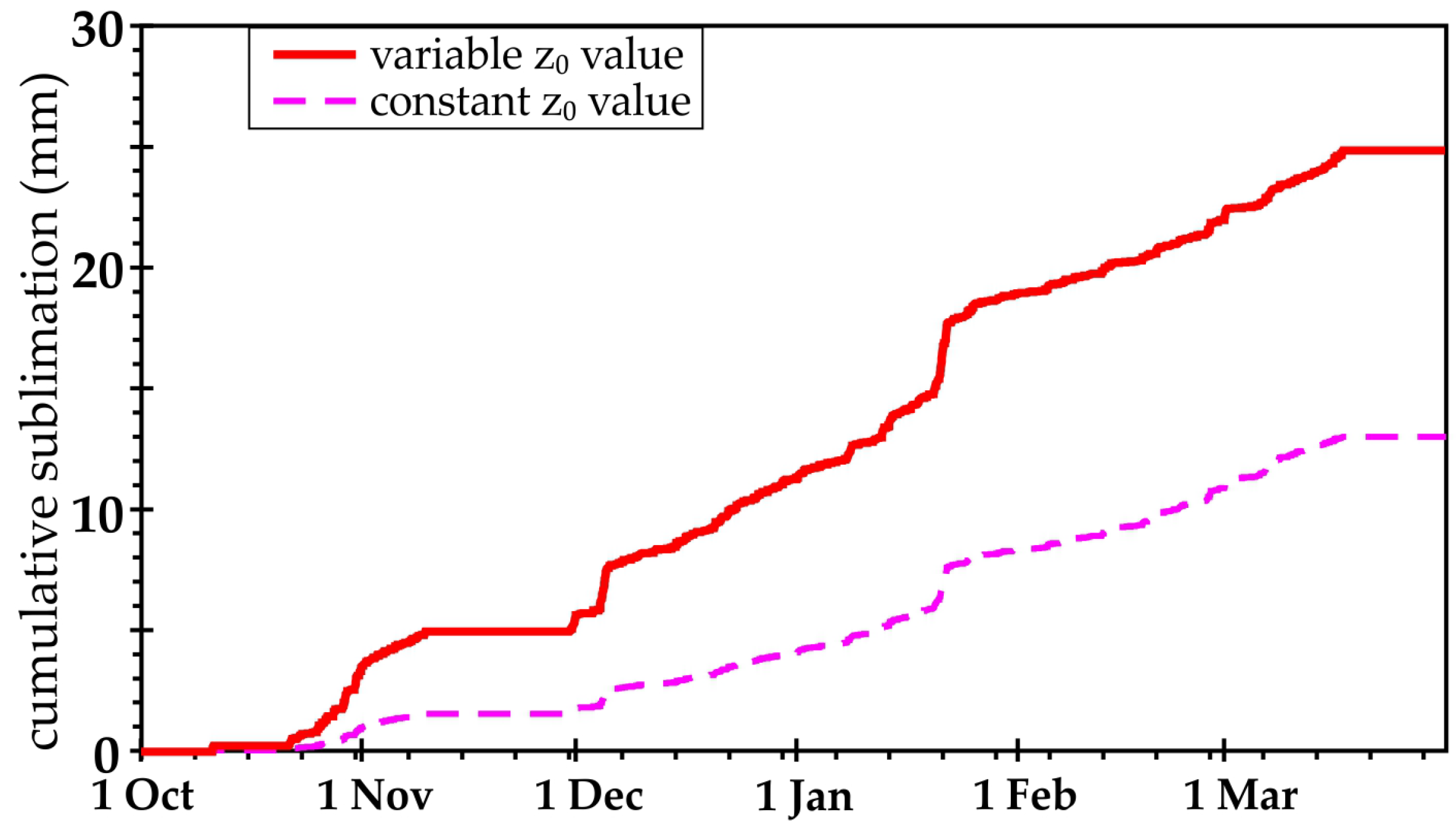
Cumulative Sublimation
4. Discussion
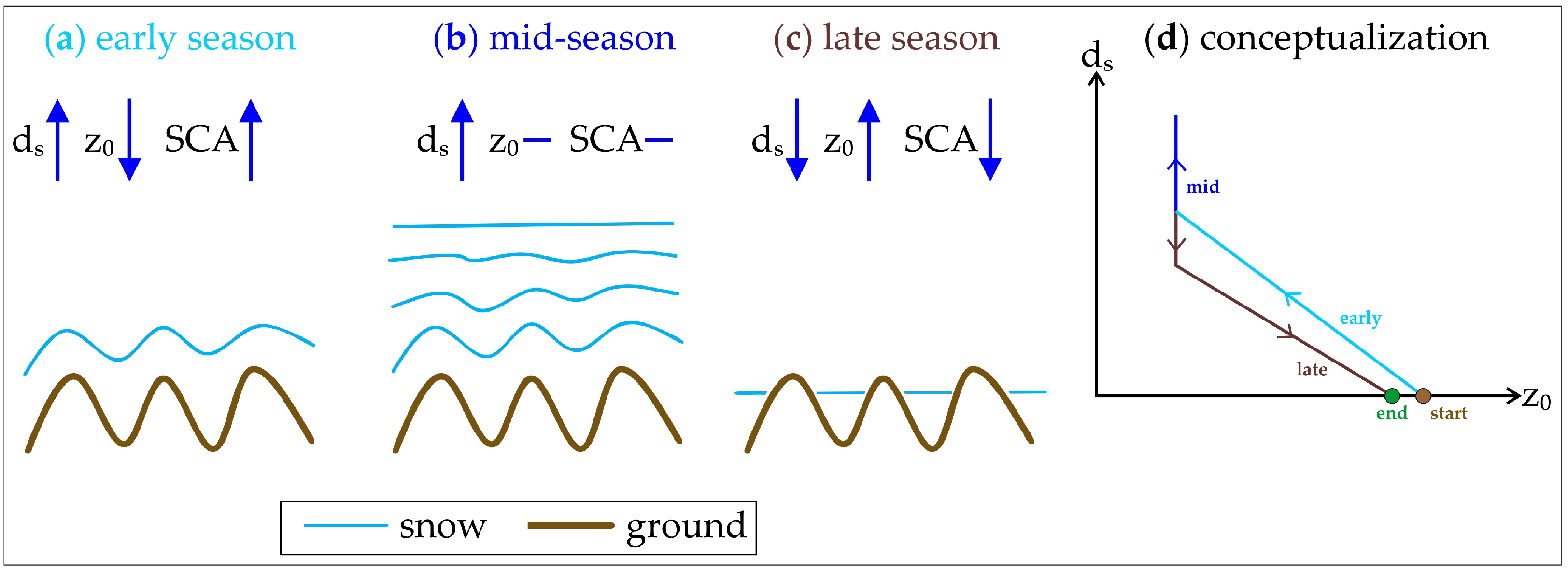
4.1. Implications
4.2. Next Steps
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Snowpack Modeling
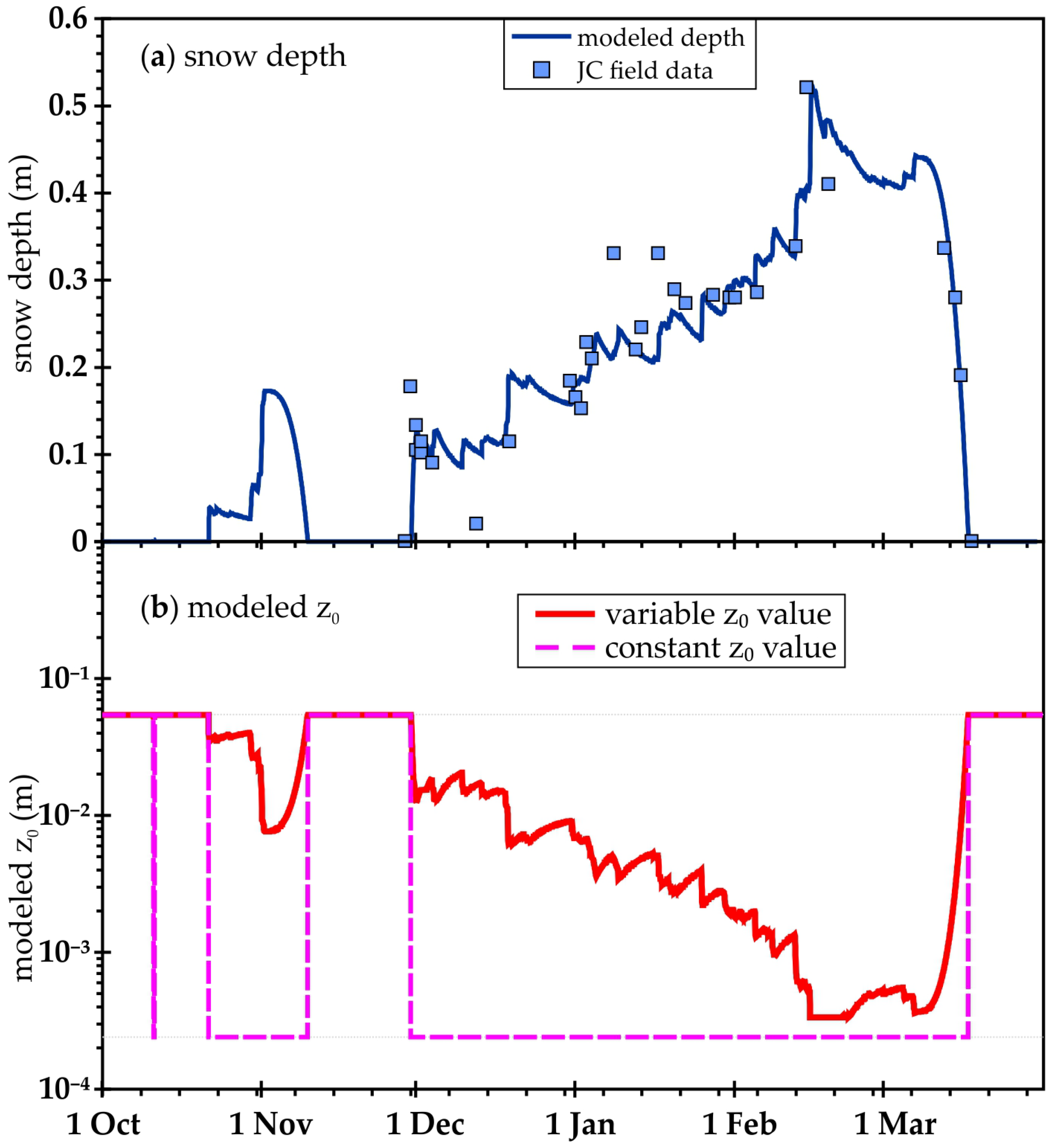
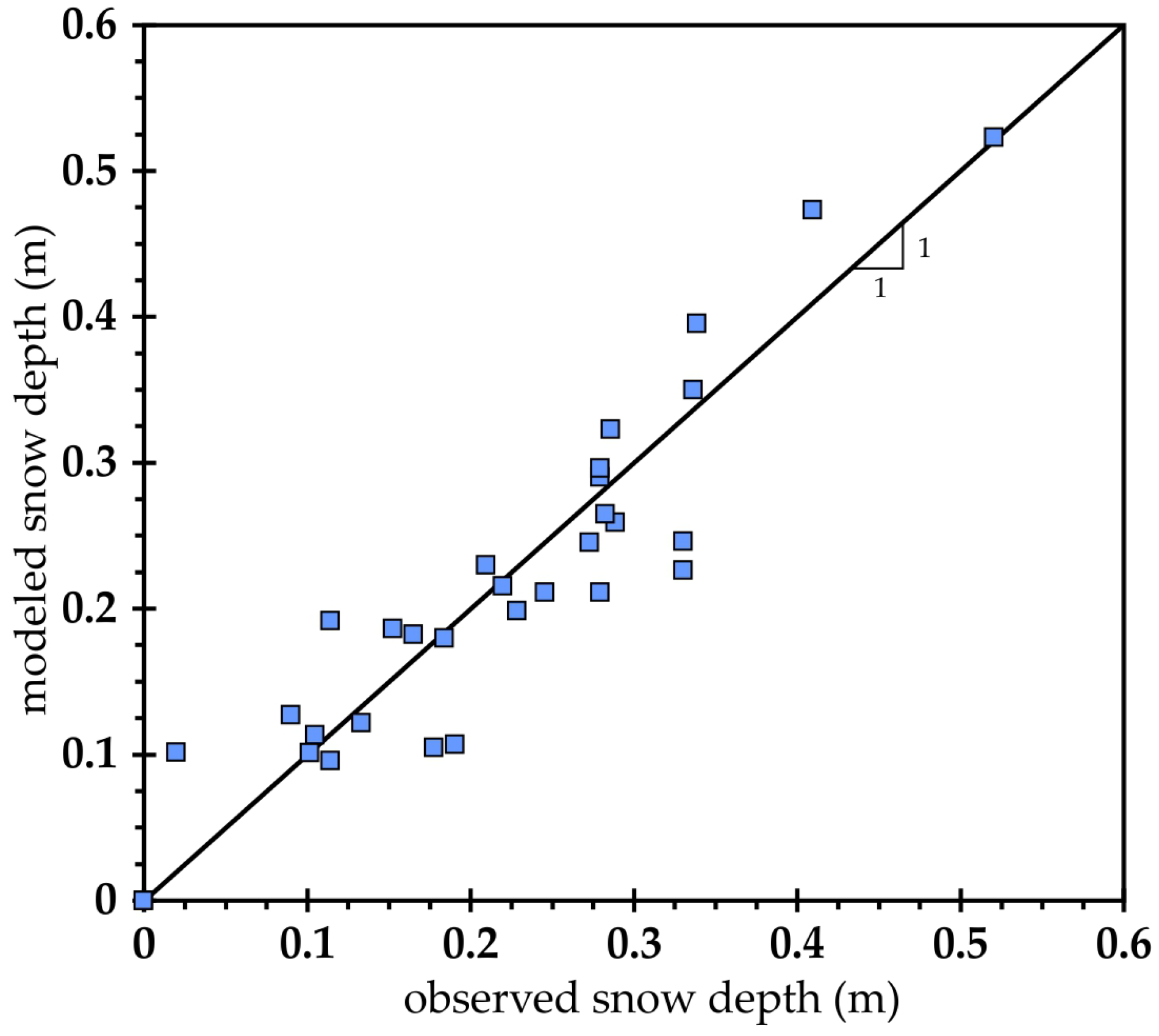
Appendix B. The Data
| Site | Date | Snow Depth (m) | (× m) | Regression Slope | Regression |
|---|---|---|---|---|---|
| CR11 | 6 January 2020 | 0.32 | 10.9 | −0.066 | 0.81 |
| 29 January 2020 | 0.43 | 0.0724 | |||
| 10 February 2020 | 0.49 | 0.176 | |||
| 11 March 2020 | 0.05 | 20.0 | |||
| 16 March 2020 | 0 | 65.8 | |||
| Julie Circle | 25 Nov 2019 | 0 | 40 | −0.072 | 0.86 |
| 26 November 2019 | 0.18 | 19.7 | |||
| 27 November 2019 | 0.13 | 27.4 | |||
| 27 November 2019 | 0.11 | 30.0 | |||
| 28 November 2019 | 0.10 | 20.7 | |||
| 28 November 2019 | 0.11 | 25.2 | |||
| 30 November 2019 | 0.09 | 20.3 | |||
| 8 December 2019 | 0.02 | 29.3 | |||
| 14 December 2019 | 0.11 | 15.8 | |||
| 25 December 2019 | 0.18 | 14.3 | |||
| 26 December 2019 | 0.17 | 17.2 | |||
| 27 December 2019 | 0.15 | 11.6 | |||
| 28 December 2019 | 0.23 | 4.50 | |||
| 29 December 2019 | 0.21 | 4.19 | |||
| 2 January 2020 | 0.33 | 1.17 | |||
| 6 January 2020 | 0.22 | 2.74 | |||
| 7 January 2020 | 0.27 | 2.57 | |||
| 10 January 2020 | 0.33 | 2.44 | |||
| 13 January 2020 | 0.29 | 2.57 | |||
| 15 January 2020 | 0.27 | 2.21 | |||
| 20 January 2020 | 0.28 | 1.93 | |||
| 23 January 2020 | 0.28 | 1.99 | |||
| 24 January 2020 | 0.28 | 1.63 | |||
| 28 January 2020 | 0.29 | 0.606 | |||
| 4 February 2020 | 0.34 | 0.365 | |||
| 6 February 2020 | 0.52 | 0.351 | |||
| 10 February 2020 | 0.41 | 0.247 | |||
| 2 March 2020 | 0.36 | 1.24 | |||
| 4 March 2020 | 0.28 | 2.91 | |||
| 5 March 2020 | 0.19 | 5.72 | |||
| Trout Farm | 26 December 2019 | 0.05 | 0.427 | −0.034 | 0.23 |
| 30 December 2019 | 0.13 | 1.49 | |||
| 2 January 2020 | 0.18 | 0.0836 | |||
| 6 January 2020 | 0.18 | 0.737 | |||
| 19 January 2020 | 0.18 | 0.109 | |||
| 24 January 2020 | 0.21 | 0.0562 | |||
| 4 February 2020 | 0.27 | 0.467 | |||
| 10 February 2020 | 0.29 | 0.631 | |||
| 25 February 2020 | 0.29 | 0.246 | |||
| 11 March 2020 | 0 | 4.76 | |||
| Cathedral Creek | 11 Oct 2019 | 0 | 563 | −0.21 | 0.77 |
| 3 January 2020 | 0.16 | 264 | |||
| 16 January 2020 | 0.15 | 268 | |||
| Piceance | 15 November 2019 | 0 | 137 | −0.24 | 0.99 |
| 2 December 2019 | 0.16 | 120 | |||
| 30 December 2019 | 0.34 | 124 | |||
| 24 January 2020 | 0.36 | 58.3 | |||
| 11 February 2020 | 0.50 | 28.8 | |||
| 3 March 2020 | 0.38 | 51 | |||
| 12 March 2020 | 0.14 | 121 | |||
| Spring Creek | 15 November 2019 | 0 | 222 | −0.25 | 0.72 |
| 3 January 2020 | 0.43 | 32.4 | |||
| 11 February 2020 | 0.56 | 30.3 | |||
| Upper Piceance | 15 November 2019 | 0 | 389 | −0.22 | 0.96 |
| 2 December 2019 | 0.14 | 246 | |||
| 8 January 2020 | 0.28 | 172 | |||
| 24 January 2020 | 0.35 | 135 | |||
| 11 February 2020 | 0.47 | 63 | |||
| 25 February 2020 | 0.45 | 59.3 | |||
| 12 March 2020 | 0.20 | 149 | |||
| 24 March 2020 | 0.17 | 329 | |||
| Lost Creek | 8 Oct 2019 | 0 | 9.41 | 0.045 | 0.08 |
| 27 November 2019 | 0.17 | 0.172 | |||
| 28 November 2019 | 0.11 | 0.0476 | |||
| 6 December 2019 | 0.17 | 0.203 | |||
| 11 December 2019 | 0.17 | 0.231 | |||
| 27 December 2019 | 0.33 | 0.281 | |||
| 30 December 2019 | 0.39 | 0.0732 | |||
| 7 January 2020 | 0.46 | 0.295 | |||
| 14 January 2020 | 0.57 | 0.788 | |||
| 28 January 2020 | 0.68 | 0.157 | |||
| 26 February 2020 | 0.85 | 3.38 | |||
| 4 March 2020 | 0.73 | 2.35 | |||
| 11 March 2020 | 0.60 | 4.02 | |||
| 26 March 2020 | 0.46 | 0.53 | |||
| 31 March 2020 | 0.47 | 0.0976 | |||
| 7 Apr 2020 | 0.29 | 0.598 | |||
| Yellow Jacket | 9 October 2019 | 0 | 328 | −0.60 | 0.77 |
| 21 October 2019 | 0.18 | 255 | |||
| 27 November 2019 | 0.33 | 275 | |||
| 30 December 2019 | 0.54 | 205 | |||
| 28 January 2020 | 0.71 | 144 | |||
| 26 February 2020 | 0.79 | 100 | |||
| 4 March 2020 | 0.70 | 163 | |||
| 26 March 2020 | 0.43 | 288 | |||
| 31 March 2020 | 0.47 | 245 |
| Site Name | Slope | Y-Intercept |
|---|---|---|
| CR11 | −12.3 | −2.7 |
| Julie Circle (JC) | −12 | −2.7 |
| Trout Farm (TF) | −6.7 | −6.7 |
| Cathedral Creek (CC) | −4.8 | −0.58 |
| Piceance (P) | −4.1 | −0.79 |
| Spring Creek (SC) | −3.8 | −1.6 |
| Upper Piceance (UPC) | −2.9 | −1.7 |
| Yellow Jacket (YJ) | −1.3 | −0.96 |
| Lost Creek (LC) | 1.8 | −8.4 |
References
- Mialon, A.; Fily, M.; Royer, A. Seasonal snow cover extent from microwave remote sensing data: Comparison with existing ground and satellite based measurements. EARSeL eProc. 1994, 4, 215–225. [Google Scholar]
- Fassnacht, S.R.; Williams, M.W.; Corrao, M.V. Changes in the surface roughness of snow from millimetre to metre scales. Ecol. Complex. 2009, 6, 221–229. [Google Scholar] [CrossRef]
- Barnett, T.P.; Pierce, D.W.; Hidalgo, H.G.; Bonfils, C.; Santer, B.D.; Das, T.; Bala, G.; Wood, A.W.; Nozawa, T.; Mirin, A.A.; et al. Human induced changes in the hydrology of the western United States. Science 2008, 319, 1080–1083. [Google Scholar] [CrossRef] [PubMed]
- Fassnacht, S.R.; Heath, J.T.; Venable, N.B.H.; Elder, K.J. Snowmobile impacts on snowpack physical and mechanical properties. Cryosphere 2018, 12, 1121–1135. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Venable, N.B.H.; McGrath, D.; Patterson, G.G. Sub-seasonal snowpack trends in the Rocky Mountain National Park area, Colorado, USA. Water 2018, 10, 562. [Google Scholar] [CrossRef]
- Niu, G.; Yang, Z.L. An observation-based formulation of snow cover fraction and its evaluation over large North American river basins. J. Geophys. Res. 2007, 112, D21101. [Google Scholar] [CrossRef]
- Anttila, K.; Manninen, T.; Karjalainen, T.; Lahtinen, P.; Riihela, A.; Siljamo, N. The temporal and spatial variability in submeter scale surface roughness of seasonal snow in Sodankyla Finnish Lapland in 2009–2010. J. Geophys. Res. Atmos. 2014, 119, 9236–9252. [Google Scholar] [CrossRef]
- Trujillo, E.; Molotch, N.P. Snowpack regimes of the Western United States. Water Resour. Res. 2014, 50, 5611–5623. [Google Scholar] [CrossRef]
- Luce, C.H.; Tarboton, D.G. The application of depletion curves for parameterization of subgrid variability of snow. Hydrol. Processes 2004, 18, 1409–1422. [Google Scholar] [CrossRef]
- Smith, M.W. Roughness in the earth sciences. Earth Sci. Rev. 2014, 136, 202–225. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Stednick, J.D.; Deems, J.S.; Corrao, M.V. Metrics for assessing snow surface roughness from digital imagery. Water Resour. Res. 2009, 45, W00D31. [Google Scholar] [CrossRef]
- Moeser, D.; Stahli, M.; Jonas, T. Improved snow interception modeling using canopy parameters derived from airborne LIDAR data. Water Resour. Res. 2015, 51, 5041–5059. [Google Scholar] [CrossRef]
- Liston, G.E. Representing subgrid snow cover heterogeneities in regional and global models. J. Clim. 2004, 17, 1381–1397. [Google Scholar] [CrossRef]
- Blöschl, G. Scaling issues in snow hydrology. Hydrol. Process 1999, 13, 2149–2175. [Google Scholar] [CrossRef]
- Neville, R.A.; Shipman, P.D.; Fassnacht, S.R.; Sanow, J.E.; Pasquini, R.; Oprea, I. A geometric-based aerodynamic roughness length formulation and code applied to lidar-derived snow surfaces. Remote Sens. 2025, 17, 1984. [Google Scholar] [CrossRef]
- Magand, C.; Ducharne, A.; Le Moine, N. Introducing hysteresis in snow depletion curves to improve the water budget of a land surface model in alpine catchment. J. Hydrometeorol. 2014, 15, 631–649. [Google Scholar] [CrossRef]
- Brock, B.; Willis, I.; Sharp, M. Measurement and parameterization of aerodynamic roughness length variations at Haut Glacier d’Arolla, Switzerland. J. Glaciol. 2006, 52, 281–297. [Google Scholar] [CrossRef]
- Quincey, D.; Smith, M.; Rounce, D.; Ross, A.; King, O.; Watson, C. Evaluating morphological estimates of the aerodynamic roughness of debris covered glacier ice. Earth Surf. Processes Landforms 2017, 42, 2541–2553. [Google Scholar] [CrossRef]
- Manes, C.; Guala, M.; Löwe, H.; Bartlett, S.; Egli, L.; Lehning, M. Statistical properties of fresh snow roughness. Water Resour. Res. 2008, 44, 1–9. [Google Scholar] [CrossRef]
- Sanow, J.E.; Fassnacht, S.R.; Kamin, D.J.; Sexstone, G.A.; Bauerle, W.L.; Oprea, I. Geometric versus anemometric surface roughness for a shallow accumulating snowpack. Geosciences 2018, 8, 463. [Google Scholar] [CrossRef]
- Swenson, S.C.; Lawrence, D.M. A new fractional snow-covered area parameterization for the Community Land Model and its effect on the surface energy balance. J. Geophys. Res. 2012, 117, D21107. [Google Scholar] [CrossRef]
- Luce, C.H.; Tarboton, D.G.; Cooley, K.R. Sub-grid parameterization of snow distribution for an energy and mass balance snow cover model. Hydrol. Processes 1999, 13, 1921–1933. [Google Scholar] [CrossRef]
- DeBeer, C.M.; Pomeroy, J.W. Influence of snowpack and melt energy heterogeneity on snow cover depletion and snowmelt runoff simulation in a cold mountain environment. J. Hydrol. 2017, 553, 199–213. [Google Scholar] [CrossRef]
- Hock, R.; Hutchings, J.K.; Lehning, M. Grand challenges in cryospheric sciences: Toward better predictability of glaciers, snow, and sea ice. Front. Earth Sci. 2017, 5, 1–14. [Google Scholar] [CrossRef]
- Sanow, J.E.; Fassnacht, S.R.; Suzuki, K. How does a dynamic surface roughness affect snowpack modelling? Polar Sci. 2024, 41, 101110. [Google Scholar] [CrossRef]
- Desert Research Institute. Western Regional Climate Center. Available online: https://wrcc.dri.edu/ (accessed on 28 July 2025).
- Blue Maestro. Available online: https://bluemaestro.com/ (accessed on 28 July 2025).
- Faro. Available online: https://www.faro.com/ (accessed on 17 July 2025).
- CloudCompare. Available online: https://www.danielgm.net/cc/ (accessed on 17 July 2025).
- Golden Software–Surfer. Available online: https://www.goldensoftware.com/products/surfer/ (accessed on 17 July 2025).
- Lettau, H. Note on aerodynamic roughness-parameter estimation on the basis of roughness-element description. J. Appl. Meteorol. 1969, 8, 828–832. [Google Scholar] [CrossRef]
- Fassnacht, S.R. Temporal changes in small scale snowpack surface roughness length for sublimation estimates in hydrological modelling. Cuad. Investig. Geográfica 2010, 36, 43. [Google Scholar] [CrossRef]
- UCAR. Community Land Model (CLM). Available online: https://www.cesm.ucar.edu/models/clm (accessed on 21 October 2025).
- Hultstrand, D.M.; Fassnacht, S.R. The Sensitivity of Snowpack Sublimation Estimates to Instrument and Measurement Uncertainty Perturbed in a Monte Carlo Framework. Front. Earth Sci. 2018, 12, 728–738. [Google Scholar] [CrossRef]
- Reba, M.L.; Pomeroy, J.; Marks, D.; Link, T.E. Estimating surface sublimation losses from snowpacks in a mountain catchment using eddy covariance and turbulent transfer calculations. Hydrol. Process. 2012, 26, 3699–3711. [Google Scholar] [CrossRef]
- NOAA. National Centers for Environmental Information. Available online: https://www.ncdc.noaa.gov/cdo-web/ (accessed on 21 October 2025).
- Judson, A.; Doesken, N. Density of freshly fallen snow in the central Rocky Mountains. Bull. Am. Meteorol. Soc. 2000, 81, 1577–1588. [Google Scholar] [CrossRef]
- Verseghy, D.L. CLASS—A Canadian land surface scheme for GCMs. I. Soil model. Int. J. Climatol. 1991, 11, 111–133. [Google Scholar] [CrossRef]
- Chapman, G.; Cleese, J.; Idle, E.; Gilliam, T.; Jones, T.; Palin, M. Monty Python and the Holy Grail; EMI Films: London, UK, 1975. [Google Scholar]
- Gromke, C.; Manes, C.; Walter, B.; Lehning, M.; Guala, M. Aerodynamic roughness length of fresh snow. Bound.-Layer Meteorol. 2011, 141, 21–34. [Google Scholar] [CrossRef]
- Musselman, K.N.; Pomeroy, J.W.; Essery, R.L.; Leroux, N. Impact of windflow calculations on simulations of alpine snow accumulation, redistribution, and ablation. Hydrol. Processes 2015, 29, 3983–3999. [Google Scholar] [CrossRef]
- Bales, R.C.; Molotch, N.P.; Painter, T.H.; Dettinger, R.R.; Dozier, J. Mountain hydrology of the western United States. Water Resour. Res. 2006, 42, W08432. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Suzuki, K.; Nemoto, M.; Sanow, J.E.; Kosugi, K.; Tedesche, M.E.; Frey, M.M. Location Dictates Snow Aerodynamic Roughness. Glacies 2024, 1, 1–16. [Google Scholar] [CrossRef]
- Sturm, M.; Liston, G.E. Revisiting the Global Seasonal Snow Classification: An Updated Dataset for Earth System Applications. J. Hydrometeor. 2021, 22, 2917–2938. [Google Scholar] [CrossRef]
- Raleigh, M.S.; Landry, C.C.; Hayashi, M.; Quinton, W.L.; Lundquist, J.D. Approximating snow surface temperature from standard temperature and humidity data: New possibilities for snow model and remote sensing evaluation. Water Resour. Res. 2013, 49, 8053–8069. [Google Scholar] [CrossRef]
- Harpold, A.; Brooks, P.; Rajagopal, S.; Heidbuchel, I.; Jardine, A.; Stielstra, C. Changes in snowpack accumulation and ablation in the intermountain west. Water Resour. Res. 2012, 48, 11501. [Google Scholar] [CrossRef]
- Davison, B.J. Snow Accumulation in a Distributed Hydrological Model. Unpublished Master’s Thesis, Civil Engineering, University of Waterloo, Waterloo, ON, Canada, 2004. 108pp + appendices. [Google Scholar]
- Lundquist, J.D.; Vano, J.; Gutmann, E.; Hogan, D.; Schwat, E.; Haugeneder, M.; Mateo, E.; Oncley, S.; Roden, C.; Osenga, E.; et al. Sublimation of Snow. Bull. Amer. Meteor. Soc. 2024, 105, E975–E990. [Google Scholar] [CrossRef]
- Naple, P.; Skiles, S.M.; Lang, O.I.; Rittger, K.; Lenard, S.J.P.; Burgess, A.; Painter, T.H. Dust on snow radiative forcing and contribution to melt in the Colorado River Basin. Geophys. Res. Lett. 2025, 52, e2024GL112757. [Google Scholar] [CrossRef]
- Wayand, N.E.; Marsh, C.B.; Shea, J.M.; Pomeroy, J.W. Globally scalable alpine snow metrics. Remote Sens. Environ. 2018, 213, 61–72. [Google Scholar] [CrossRef]
- Flerchinger, G.N.; Xaio, W.; Marks, D.; Sauer, T.J.; Yu, Q. Comparison of algorithms for incoming atmospheric long-wave radiation. Water Resour. Res. 2009, 45, W03423. [Google Scholar] [CrossRef]
- Bryan, Z.L. Bad News; Belting Bronco: Los Angeles, CA, USA, 2025. [Google Scholar]
- Liston, G.E. Local advection of momentum, heat, and moisture during the melt of patchy snow covers. J. Appl. Meteorol. 1995, 34, 1705–1715. [Google Scholar] [CrossRef]
- Sanow, J.E. The Dynamic Nature of Snow Surface Roughness. Ph.D. Dissertation, Watershed Science, Colorado State University, Fort Collins, CO, USA, 2022, unpublished. [Google Scholar]


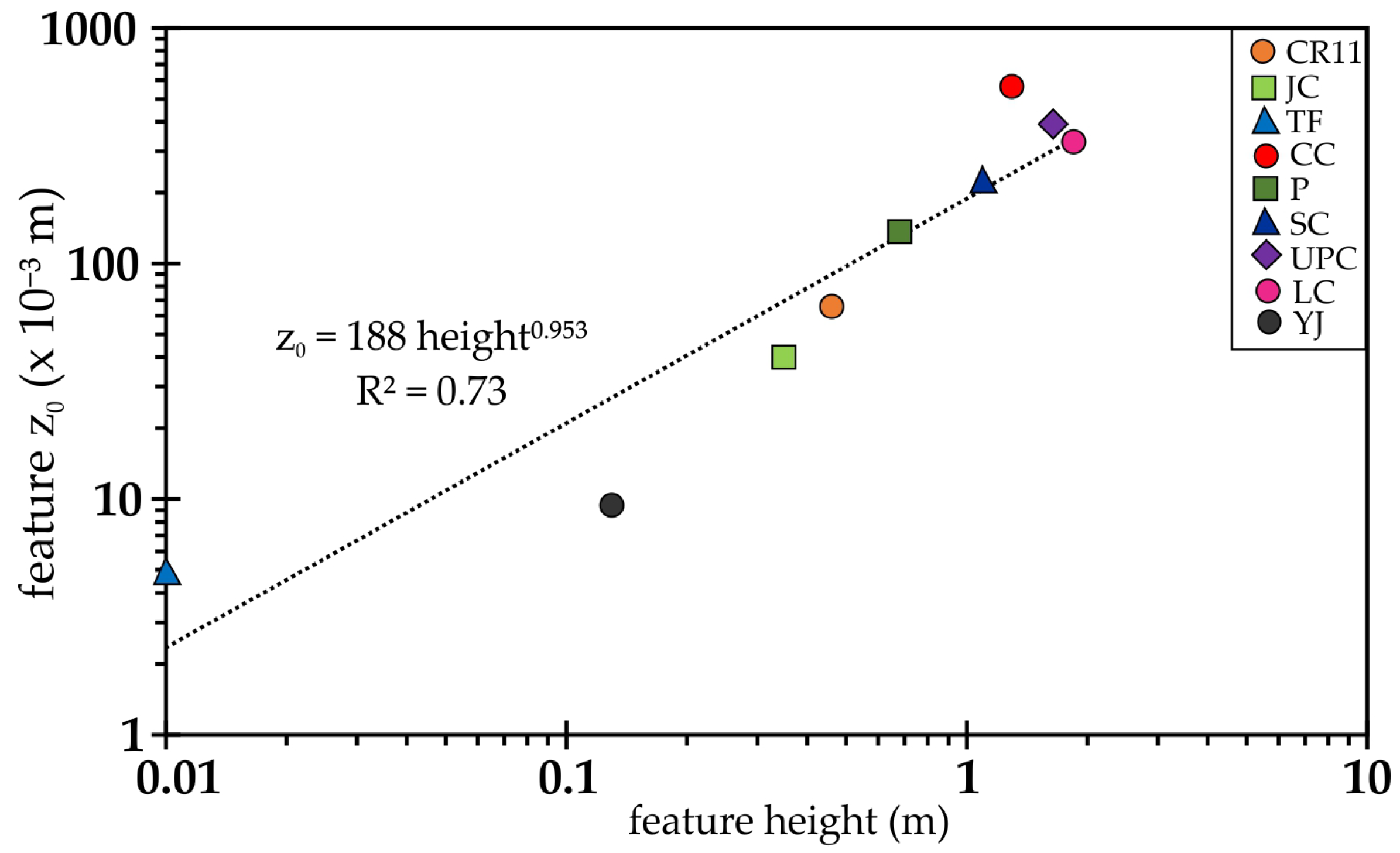

| Site Name | Scan Frequency | Primary Roughness Feature Height (m) | Initial ( m) |
|---|---|---|---|
| Yellow Jacket (YJ) | Tri-weekly | 1.85 | 330 |
| Trout Farm (TF) | Weekly | 0.01 | 5.0 |
| Julie Circle (JC) | Every storm | 0.35 | 40 |
| Lost Creek (LC) | Weekly | 0.13 | 9.0 |
| Spring Creek (SC) | Monthly | 1.10 | 220 |
| Cathedral Creek (CC) | Bi-weekly | 1.30 | 570 |
| Piceance (P) | Bi-weekly | 0.68 | 110 |
| CR11 | Bi-weekly | 0.46 | 66 |
| Upper Piceance (UPC) | Bi-weekly | 1.65 | 390 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanow, J.E.; Fassnacht, S.R. Let Us Change the Aerodynamic Roughness Length as a Function of Snow Depth. Climate 2025, 13, 226. https://doi.org/10.3390/cli13110226
Sanow JE, Fassnacht SR. Let Us Change the Aerodynamic Roughness Length as a Function of Snow Depth. Climate. 2025; 13(11):226. https://doi.org/10.3390/cli13110226
Chicago/Turabian StyleSanow, Jessica E., and Steven R. Fassnacht. 2025. "Let Us Change the Aerodynamic Roughness Length as a Function of Snow Depth" Climate 13, no. 11: 226. https://doi.org/10.3390/cli13110226
APA StyleSanow, J. E., & Fassnacht, S. R. (2025). Let Us Change the Aerodynamic Roughness Length as a Function of Snow Depth. Climate, 13(11), 226. https://doi.org/10.3390/cli13110226






