Abstract
Climate change has had several negative effects, including more severe storms, warmer oceans, high temperatures and, in particular, increased drought, directly affecting the water availability in a region. The Northeast Region of Brazil (NEB) is known to have scarce rainfall, especially in the northeastern semiarid region. Droughts and high temperatures in the NEB negatively affect water resources in the region, resulting in a gradual decrease in the storage volume in the reservoirs and contributing to unprecedented water scarcity. The objective of this research was to investigate the spatiotemporal behavior of the number of days without rain (DWR) in a region of northeastern Brazil, making use of the spatiotemporal geostatistical methodology. Cross-validation resulted in an R2 of 71%, indicating a good performance of spatiotemporal kriging for predicting DWRs. The results indicate a spatial dependence for a radius of up to 39 km and that the DWR observations in a certain location influence its estimates in the next 2.8 years. The projection maps from 2021 to 2030 identified a growing trend in the DWRs. With the results presented in our study, it is expected that they can be used by government agencies for the adoption of public policies aiming to minimize the possible damage caused by long periods of drought.
1. Introduction
Climate change has had several negative effects, including more severe storms, warmer oceans, loss of species, high temperatures and, in particular, increased drought, directly affecting the water availability in a region. According to the United Nations report [1], periods of drought aggravated by global warming have been increasingly common in regions already susceptible to water shortages, increasing the risk of agricultural and ecological droughts.
Climate change has made droughts more frequent and prolonged, causing negative consequences such as the risk of forest fires, acceleration of the desertification process and water scarcity [2]. Thus, effective modeling of the droughts in a region becomes inevitable, applying different indices and statistical methodologies that allow the presentation of scenarios so that the destructive impacts of this phenomenon can be minimized.
The growth of the human population has increasingly required an increase in agricultural production. However, the effects of drought have caused significant reductions in production [3]. A study on the impacts of drought on the yield of irrigated and rainfed crops in the state of Texas showed a greater impact on winter wheat (Triticum aestivum L.) and corn (Zea mays L.); differently, the production of cotton (Gossypium spp.) and sorghum [Sorghum bicolor(L.) Moench] were less impacted by drought effects [4]. A review of water management in dry regions pointed out that places with dry seasons need adaptations on the part of the phenology of the plant and also on water savings to guarantee stable yields, concluding that it is essential to understand the water stress in a region to propose efficient measures to mitigate this stress [5].
The Northeast Region of Brazil (NEB) is known to have scarce rainfall, especially in the northeastern semiarid region. Droughts and high temperatures in the NEB negatively affect water resources in the region, resulting in a gradual decrease in the storage volume in the reservoirs and contributing to unprecedented water scarcity [6].
In general, droughts in the NEB generate profound environmental, social and economic impacts. In dry years, when rainfall is insufficient for harvesting and water storage, farmers residing in the northeastern semiarid region interrupt agricultural production, causing a social calamity, unemployment, because the region does not offer other job opportunities, forcing the inhabitants to abandon their lands and migrate to the great centers of Brazil, such as the regions of São Paulo, Rio de Janeiro and Brasília [7].
The state of Paraíba, which makes up one of the nine federative units of the NEB, has been impacted by droughts in recent years. It is estimated that 94.60% of the territory of Paraíba presents an area susceptible to desertification as a result of soil degradation caused by the combination of human activities and climate change [8]. Due to the migratory processes caused by the droughts in Paraíba, municipalities in this region have the highest rates of population aging, since young people leave their lands in search of employment opportunities [9].
Agricultural production throughout the State of Paraíba has been suffering negative impacts due to the droughts that affect the entire region. In the period from 2012 to 2016, due to the droughts and high temperatures that affected the state, the productivity of crops such as maize, cowpea and rice showed a drastic reduction in relation to the planted area [10].
The standardized precipitation index (SPI) has been commonly used for drought monitoring and analysis in different regions of the globe [11,12,13]. Several studies have modeled drought rates in regions of the State of Paraíba through the SPI. An analysis in the Alto Paraíba basin between 2012 and 2017 revealed a strong influence of droughts on the spatiotemporal variability of vegetation in this region [14]. A study using the SPI identified rainy and dry periods across the region, concluding that the months from September to December are the driest in the entire state [15]. Research on drought trends in Paraíba from 1998 to 2017 concluded, through the SPI, that drought events tend to have a higher temporal frequency and tend to be more severe [16]. Although the aforementioned studies have presented interpolated maps of drought-related indices, they did not take into account the joint, space–time dependence of these attributes and did not present projections so that government agencies can use them to minimize the damage caused by long periods without rain.
In view of this, the impacts on a region related to natural disasters such as droughts undoubtedly cause several upsets to society and the environment. Therefore, there is a need to apply strategic planning to minimize the impacts generated by these disasters. The construction of cisterns, weirs and dams can be adopted by governments to solve this serious problem. In addition, to adopt efficient public policies, statistical analysis becomes an indispensable tool for planning, providing precious information based on the historical series of rainfall in the region and presenting projections so that the needs of the entire society can be anticipated.
Therefore, the main objective of this research was to investigate the spatiotemporal behavior of the number of days without rain in the year throughout the state of Paraíba, thus presenting high resolution maps of this attribute so that government agencies can use them as tools in the presentation of projects to minimize the impacts generated by droughts.
2. Materials and Methods
The study area corresponds to the State of Paraíba, located in the Northeast Region of Brazil, with a territorial extension of 56,467 km2, which corresponds to 0.664% of the entire territory of Brazil [17]. To obtain an idea of the extent of this region, countries on the European continent, such as Slovakia (48,845 km2), Denmark (43,094 km2) and Switzerland (41,290 km2) have areas smaller than the State of Paraíba. The state is divided into four mesoregions (Sertão Paraibano, Borborema, Agreste Paraibano and Mata Paraibana) with different climatic and environmental conditions (Figure 1).
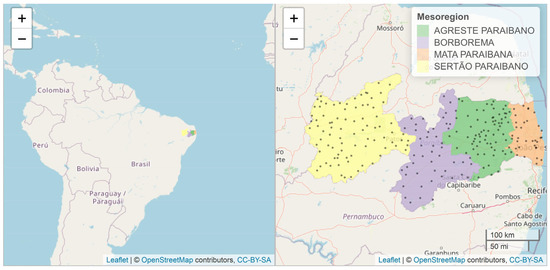
Figure 1.
Map of South America (left side) with details for the region under study (right side) accompanied by the location of the 238 rainfall stations in the state of Paraíba.
The dataset used in this study consisted of 238 rainfall stations irregularly distributed throughout the study region (Figure 1). The original dataset refers to the daily rainfall recorded at each of the rainfall stations from 1994 to 2020. We consider a day without rain as a day when there was no record of rainfall on the day (0 mm). At each rainfall station, the total number of days without rain (DWR) per year was extracted, considering only stations with more than 180 days without rain in the year. The dataset was provided by AESA—Executive Agency for Water Management of the State of Paraíba (http://www.aesa.pb.gov.br/aesa-website/ (accessed on 1 December 2022.)).
In this study, we considered the stochastic process where represents the geographic coordinates and represents the temporal dimension. In this model, we can decompose the space–time component ( in the following expression:
In Equation (1), the stochastic process was decomposed by the tendency components () and the stochastic error (). In our modeling, we assumed that the random error was second-order stationary, mutually independent and spatially isotropic [18].
For tendency modeling, we performed a preliminary analysis using scatter plots, considering the DWR as the dependent variable and the geographic coordinates and the year as independent variables. To adjust this component, we adjusted multiple linear regression, followed by the t test to verify the significance of the parameters related to the linear effects of latitude, longitude and temporal index and the quadratic effect of longitude. The coefficient of determination (R2) was calculated to determine how much of the variability in the DWR is explained by the tendency.
The residuals of the regression model were submitted to an empirical spatiotemporal variogram. The generalized product-sum theoretical model, with the exponential function in the spatial and temporal components, was adjusted to the point cloud of the empirical variogram. The generalized sum-product has been widely used in spatiotemporal geostatistical analysis by presenting a nonseparable space–time structure and providing suitable adjustments to kriging [19,20].
To obtain the interpolated maps, ordinary spatiotemporal kriging was first applied to the residuals, which is expressed by the following expression:
In Equation (2), the term concerns the interpolated residue of the DWR at spatial position and time . The component represents the transposed vector of the residual covariance between the “observed” residuals (estimated by the trend) with the estimated one for the point (). represents the inverse matrix of residual covariances, and is the vector of the residuals of the trend-adjusted model. The final predictor of DWR (Equation (3)) at position and at time is given by:
Equation (3) is known as spatiotemporal regression kriging [18,20]. The terms and are obtained by tendency fitting and ordinary spatiotemporal kriging, respectively. The “leave-one-out” cross-validation was used to extract the metrics to present the results of the quality of fit of the DWR estimates obtained by Equation (3). The metrics used were the mean absolute error and the coefficient of determination between the observed and interpolated values.
Finally, for the construction of spatiotemporal kriging maps, a grid with 28,300 points distributed regularly in the region under study was constructed, resulting in a spatial resolution of 1 point every 2 km2.
Statistical analyses were performed in R software [21]. In the software, the main libraries used were ggplot2 [22] and gstat [23] for graphical presentation and for geostatistical modeling, respectively.
3. Results and Discussion
Table 1 shows a descriptive analysis of the DWR of the mesoregions that make up the state of Paraíba between 1994 and 2020. The Zona da Mata region draws attention by having the lowest average number of 240 days a year without rain and the greatest variability, with a coefficient of variation of 15.86%. However, Borborema presented the highest average of 325 days in the year without rain, with a low variability between the rainfall stations that make up this region.

Table 1.
Descriptive measures for the number of days without rain in the state of Paraíba from 1994 to 2020.
Figure 2 shows the spatial distribution of the average annual number of DWRs for the State of Paraíba from 1994 to 2020. As already described in Table 1, the Zona da Mata mesoregion presented the lowest average DWR, and most rainfall stations presented a maximum of 240 days without rain in the year. However, some rainfall stations located in the Borborema mesoregion showed the highest average DWR values, with at least 330 days a year without rainfall.
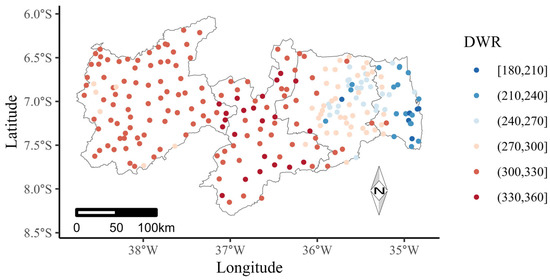
Figure 2.
Average annual number of days without rain (DWR) for the State of Paraíba in the period from 1994 to 2020.
The dryness phenomenon occurs when there is a delay of more than 15 days in the rainy season, implying a reduction of 60% or more of the historical monthly rainfall averages [24]. According to this author, drought is the occurrence of prolonged dryness, causing a significant reduction in water reserves in a region. In the State of Paraíba, 1984 occurrences of drought were recorded in the period from 1994 to 2012, with at least 212 municipalities affected by this type of natural disaster. These municipalities are located in the different mesoregions of the state; however, a significant number of these records occurred in the central region of the state, where the Agreste Paraibano and Borborema mesoregions are located, totaling 1205 drought records [25]. However, among the four mesoregions, Sertão Paraibano presents the highest number of natural disaster records, with 711 occurrences.
The year 2012 drew attention in the region under study for presenting a high density of DWRs in all mesoregions (Figure 3). According to the Brazilian Atlas of Natural Disasters [25], in 2012, they presented the highest occurrences of prolonged drought in the State of Paraíba, with a total of 391 records, 20% of the records during the period from 1991 to 2012.
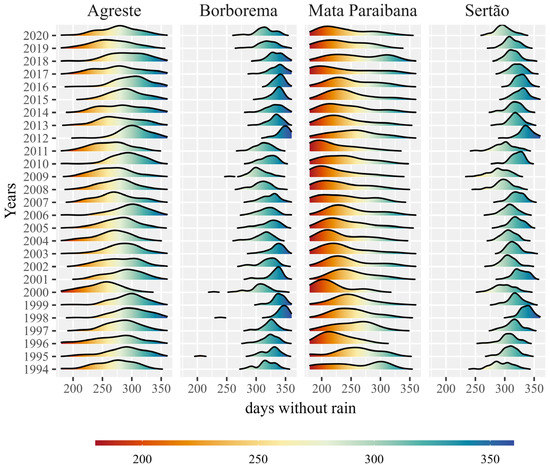
Figure 3.
Density of the annual number of days without rain (DWR) for the Paraíba mesoregions from 1994 to 2020.
When analyzing the percentage of storage volumes in reservoirs across the state, a downward trend was noted for the period from 2012 to 2015, from 50% storage of reservoirs in 2012 to less than 20% in 2015 [26]. The Brazil Drought Monitor pointed out that in Paraíba, between 2014 and 2019, the presence of droughts classified as S3 (extreme drought) and S4 (exceptional drought), indicated losses of crops and a pastures and lack of water in reservoirs, resulting in emergency situations [27].
Figure 4 shows an exploratory analysis to investigate the relationship between the DWR variable and the geographic coordinates of longitude and latitude. We can clearly see a quadratic effect between DWR and longitude (Figure 4a). However, there is no causal relationship between the variable and latitude (Figure 4b).
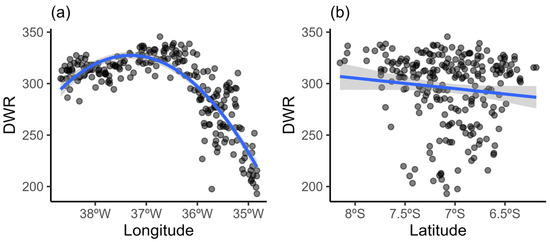
Figure 4.
Analysis of the trend between the annual number of days without rain (DWR) and the geographic coordinates longitude (a) and latitude (b) in the state of Paraíba.
Table 2 shows the results of the multiple linear regression adjustment considering the linear and quadratic effects of longitude.

Table 2.
Results of the multiple regression adjustment for the number of days without rain in the State of Paraíba in the period from 1994 to 2020.
The results of the multiple regression fit indicate that the linear and quadratic effects of longitude were statistically significant (p < 0.05) for the DWR. It was noted that 55.64% of the DWR variability was explained by tendency adjustment.
It is clearly noted that the space–time distribution of rainfall in the State of Paraíba shows a trend in relation to the geographic coordinates, and that more than half of this variability is due to the effect of the trend, with prior modeling of this component being of fundamental importance. The authors in [15] constructed interpolated maps of descriptive measures related to rainfall in Paraíba, which clearly showed a spatial tendency of these estimates, which was not considered by the authors.
Therefore, we can see the great importance of first modeling the trend so that, after removing it, we proceed to the analysis of spatiotemporal dependence. A study on the space–time distribution of monthly accumulated precipitation in the State of Paraíba found the presence of a tendency for this variable as a function of latitude and longitude geographical coordinates, with an R2 of 29% [18].
After removing the trend, the experimental variograms and the theoretical generalized product-sum were obtained (Figure 5). In this figure, we can see that the greatest contribution to the space–time variability of the DWR was due to the spatial component.
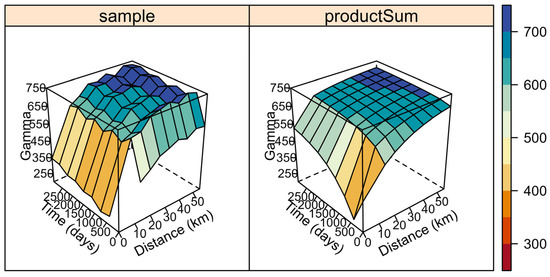
Figure 5.
Experimental variograms (left side) and the theoretical generalized product-sum (right side) for the number of days without rain in the year after removing the tendency.
Table 3 shows the estimates of the parameters of the generalized product-sum model. As mentioned in Figure 5, the variability of the spatial component (sill = 272.274) was greater than that of the temporal component (sill = 3.176), indicating that the variability of the DWR was more related to space than to time. The results showed that there is a spatial dependence of the DWR between neighboring points separated by a radius of up to 39 km. However, the number of days without rain in the year of a location presents a temporal dependence, and what happens today in the region influences the results in the next 2.8 years.

Table 3.
Estimates of the generalized product-sum theoretical model adjusted to the number of days without rain per year in the State of Paraíba.
When using the generalized product-sum model, we consider in the modeling that the DWR presents a space–time interaction of its variability, thus making it possible to interpolate this variable in nonsampled locations and in nonobserved times, thus creating forecast maps.
A study on the variability of dry and rainy periods in the State of Paraíba used geostatistical techniques for interpolation; however, this research did not take into account the existence of temporal dependence of rainfall in the region [15].
Figure 6 shows the result of the “leave-one-out” cross-validation when space–time kriging is applied to the number of days without rain in the year. Figure 6a shows that the mean absolute error varied between 0 and 75 days, and Agreste Paraibano had stations that presented the largest and the smallest errors, an expected result due to the high variability of the DWR between the rainfall stations located in this region. In Figure 6b, we have the scatter plot between the observed and estimated values by space–time kriging, in which we observed a good performance of the method, reaching a coefficient of determination of 71%.
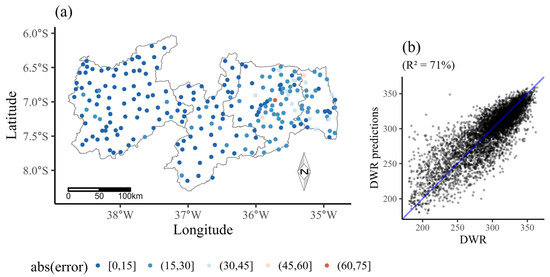
Figure 6.
Leave-one-out cross-validation results for the annual number of days without rain (DWR) for the State of Paraíba. Figure (a) is the mean absolute error (abs(error)) at each station, and Figure (b) represents the relationship between the observed and predicted DWR data.
The generalized product-sum theoretical model has been shown to be suitable for modeling indexed phenomena in space–time. Ref. [18], when using the geostatistical methodology for spatiotemporal modeling of monthly rainfall, found that the generalized product-sum model, with adjustments of the Gaussian model in the temporal and spatial components, presented excellent results, reaching an R2 of 85% in the “leave-one-out” cross-validation. Research on the space–time distribution of pests and predators in maize production used the generalized product-sum model. However, they only verified the adequacy of this model to the point cloud of the empirical variogram, not using cross-validation to verify the predictive quality of the fit [28].
Figure 7 shows the results of the space–time kriging of the DWR from 2021 to 2030. The results indicate an increase in the number of dry days in the coming years in all mesoregions. As expected, the Borborema mesoregion is the one with the highest estimates, followed by the Sertão Paraibano.
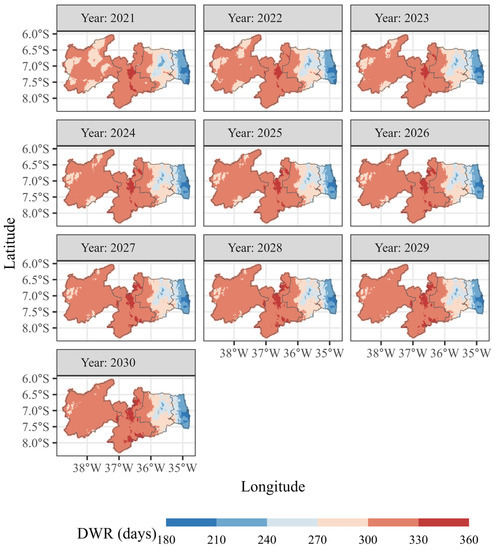
Figure 7.
Spatiotemporal kriging for the annual number of days without rain (DWR) in the State of Paraíba.
Comparing the years 2021 and 2030, it is possible to see that in some areas of Sertão Paraibano, the minimum number of dry days will increase from 270 to 300 days in the year, corresponding to a whole month without rainfall, which can result in unprecedented water scarcity. A study on the quantity, duration and intensity of drought events in Paraíba from 1998 to 2017 showed that the highest and lowest records of these events were for Sertão and Mata Paraibana, respectively [29].
An important point to be discussed in our research is the fact that we do not model drought rates, but we present estimates for the number of days without rain, which is directly related to drought events. It is known that drought is a phenomenon that is influenced by various physical and biological processes, making it a difficult task to understand [2,30]. The difficulty is the very definition of drought and what is the best index to be used for its characterization [30]. Ref. [2] presents a discussion on the different indicators used for modeling droughts, showing that these indications must be improved so that they can result in more reliable and accurate estimates. The authors in [30], similarly, carried out a review of the past–future models used to create drought scenarios, commenting that the climatic changes provoked by the droughts depend, initially, on how this was defined and the use of different statistical indicators becomes a little precise investigation. Thus, it is evident that studies on droughts present weaknesses and open up space for discussions, from its definition to the use of its indexes and statistical methods. However, in our manuscript we emphasized modeling the annual number of days without rain becoming a tool for diagnosis and impact caused by climate change in the region under study and that this should be used as an additional tool for conclusions about droughts in the region.
As previously mentioned, the Borborema region presented the highest estimates of DWR in the year; however, this region presents a great contribution to the water supply in the State of Paraíba. Located in Borborema, the Alto Rio Paraíba Basin has great importance for the water resources of Paraíba since it is responsible for supplying the second largest water reservoir in the state [31]. Ref. [32] asserts, based on a historical analysis from 1950 to 2013, that this region of the basin has presented a process of desertification. However, this process has not been directly impacted by the low levels of rainfall but possibly by human activities that have led to soil and vegetation degradation.
Finally, our study modeled the annual number of dry days. Although a region may have 330 or more dry days a year, we can say nothing about its rainfall levels since in a single day a significant amount can occur. However, DWR estimates are directly related to water availability, making it an additional tool for preventing natural disasters caused by prolonged dry spells. To verify the relationship between DWR and accumulated annual rainfall, a map of correlations between these two variables was proposed (Figure 8).
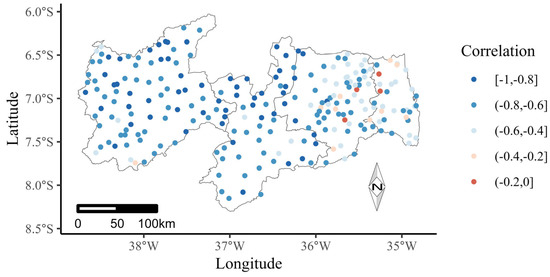
Figure 8.
Spatial distribution of the Spearman correlation between the annual number of days without rain and the annual accumulated rainfall in the State of Paraíba.
As expected, the region showed an inversely proportional relationship between the DWR and the annual accumulated rainfall at the rainfall stations. The highest ratios are found in the Sertão Paraibano and Borborema mesoregions, with a negative coefficient greater than 0.80. However, we have low correlations in the Agreste Paraibano and Mata Paraíba mesoregions, places where we have the highest rainfall volumes and the lowest DWR.
Additionally, the densities of the total annual rainfall in the different mesoregions were constructed (Figure 9).
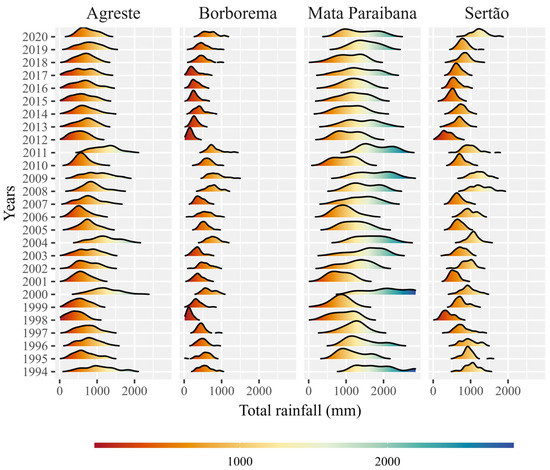
Figure 9.
Density of the total annual rainfall for the Paraíba mesoregions from 1994 to 2020.
In comparison with the density for the DWR (Figure 3), it is noted in relation to the total annual rainfall. Similar to DWR, the year 2012 presented the lowest levels of total rainfall, with Mata Paraibana and Borborema presenting the highest and lowest distributions of annual rainfall, respectively.
4. Final Remarks
The annual number of days without rain directly affects the water availability of a region. Our research aimed to analyze the spatiotemporal pattern of the DWR, making use of the spatiotemporal geostatistical methodology. Cross-validation showed an adequate adjustment of the methodology proposed in this research. The results indicate a spatial dependence for a radius of up to 39 km, and the DWR observations in a certain location influence its estimates for the next 2.8 years.
The projection maps from 2021 to 2030 identified a growing trend in the number of dry days in the Borborema and Sertão Paraibano mesoregions. Given this, it is expected that our results can be used by government agencies as a tool for the adoption of public policies aiming to minimize the possible damage caused by long periods of drought.
Knowing that the region under study clearly presents a spatiotemporal pattern of DWR, there is a need for work that employs the geostatistical spatiotemporal methodology for modeling the annual maximum number of consecutive days without rain and on drought rates.
Author Contributions
Conceptualization, E.S.d.M., R.R.d.L. and C.A.C.d.S.; Methodology, E.S.d.M. and R.R.d.L.; Software, E.S.d.M.; Validation, E.S.d.M. and R.R.d.L.; Formal analysis, E.S.d.M. and R.R.d.L.; Investigation, E.S.d.M., R.R.d.L. and C.A.C.d.S.; Resources, E.S.d.M.; Data curation, E.S.d.M. and C.A.C.d.S.; Writing—original draft preparation, E.S.d.M., R.R.d.L. and C.A.C.d.S.; Writing—review and editing, E.S.d.M., R.R.d.L. and C.A.C.d.S.; Visualization, E.S.d.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Council for Scientific and Technological Development (CNPq), grant number 314996/2021-4, and the APC was funded by Climate (ISSN 2225-1154).
Data Availability Statement
The data supporting reported results can be found at http://doi.org/10.13140/RG.2.2.15863.29606 (accessed on 6 December 2022). The computational code can be accessed at http://dx.doi.org/10.13140/RG.2.2.22574.18241 (accessed on 6 December 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- United Nations: Causes and Effects of Climate Change. Available online: https://www.un.org/site-search/ (accessed on 25 November 2022).
- Mukherjee, S.; Mishra, A.; Trenberth, K.E. Climate Change and Drought: A Perspective on Drought Indices. Curr. Clim. Chang. Rep. 2018, 4, 145–163. [Google Scholar] [CrossRef]
- Iqbal, M.S.; Singh, A.K.; Ansari, M.I. Effect of Drought Stress on Crop Production. In New Frontiers in Stress Management for Durable Agriculture; Springer: Singapore, 2020; pp. 35–47. [Google Scholar]
- Ray, R.L.; Fares, A.; Risch, E. Effects of Drought on Crop Production and Cropping Areas in Texas. Agric. Environ. Lett. 2018, 3, 170037. [Google Scholar] [CrossRef]
- Bodner, G.; Nakhforoosh, A.; Kaul, H.-P. Management of Crop Water under Drought: A Review. Agron. Sustain. Dev. 2015, 35, 401–442. [Google Scholar] [CrossRef]
- Raulino, J.B.S.; Silveira, C.S.; Lima Neto, I.E. Assessment of Climate Change Impacts on Hydrology and Water Quality of Large Semi-Arid Reservoirs in Brazil. Hydrol. Sci. J. 2021, 66, 1321–1336. [Google Scholar] [CrossRef]
- Denys, E.; Engle, N.L.; Magalhães, A.R. Secas No Brasil: Política e Gestão Proativas; Centro de Gestão e Estudos Estratégicos—CGEE: Brasília, Brazil, 2016; ISBN 978-85-5569-116-4. [Google Scholar]
- CGEE—Centro de Gestão e Estudos Estratégicos. Desertificação, Degradação Da Terra e Secas No Brasil; Centro de Gestão e Estudos Estratégicos: Brasília, Brazil, 2016; ISBN 978-85-5569. [Google Scholar]
- MMA—Ministério do Meio Ambiente. Atlas de Áreas Susceptíveis a Desertificação No Brasi; Santana, M.O., Ed.; Secretária de Recursos Hídricos, Universidade Federal da Paraíba: Brasília, Brazil, 2007; ISBN 978-85-7738-075-6. [Google Scholar]
- CONAB: Companhia Nacional de Abastecimento. Acompanhamento da Safra Brasileira de Grãos; Levantamento/Agosto 2017, Safra 2016/2017, Monitamento Agricola Safra; Companhia Nacional de Abastecimento: Brasília, Brazil, 2017; Volume 4, pp. 1–171. [Google Scholar]
- Livada, I.; Assimakopoulos, V.D. Spatial and Temporal Analysis of Drought in Greece Using the Standardized Precipitation Index (SPI). Theor. Appl. Climatol. 2007, 89, 143–153. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Sheffield, J.; Pan, M.; Wood, E.F. Evaluation of the Tropical Rainfall Measuring Mission Multi-Satellite Precipitation Analysis (TMPA) for Assessment of Large-Scale Meteorological Drought. Remote Sens. Environ. 2015, 159, 181–193. [Google Scholar] [CrossRef]
- Tirivarombo, S.; Osupile, D.; Eliasson, P. Drought Monitoring and Analysis: Standardised Precipitation Evapotranspiration Index (SPEI) and Standardised Precipitation Index (SPI). Phys. Chem. Earth Parts A/B/C 2018, 106, 1–10. [Google Scholar] [CrossRef]
- Ferreira da Silva, G.J.; de Oliveira, N.M.; Santos CA, G.; da Silva, R.M. Spatiotemporal Variability of Vegetation due to Drought Dynamics (2012–2017): A Case Study of the Upper Paraíba River Basin, Brazil. Nat. Hazards 2020, 102, 939–964. [Google Scholar] [CrossRef]
- Rodrigues, E.L.; Sousa, F.D.A.S.; Lopes, R.F.C. Analysis of the Variability of Dry and Rainy Periods of Rainfall in the State of Paraíba Using the Standardized Precipitation Index (SPI). Rev. Bras. Geogr. Física 2022, 15, 2544. [Google Scholar] [CrossRef]
- Brasil Neto, R.M.; Santos, C.A.G.; Silva, R.M.; Santos, C.A.C. Evaluation of TRMM Satellite Dataset for Monitoring Meteorological Drought in Northeastern Brazil. Hydrol. Sci. J. 2022, 67, 2100–2120. [Google Scholar] [CrossRef]
- IBGE—Instituto Brasileiro de Geografia e Estatística Cidades e Estados. Available online: https://www.ibge.gov.br/cidades-e-estados/pb.html (accessed on 16 February 2022).
- Medeiros, E.S.; Lima, R.R.; Olinda, R.A.; Santos, C.A.C. Modeling Spatiotemporal Rainfall Variability in Paraíba, Brazil. Water 2019, 11, 1843. [Google Scholar] [CrossRef]
- Tadić, J.; Williams, I.; Tadić, V.; Biraud, S. Towards Hyper-Dimensional Variography Using the Product-Sum Covariance Model. Atmosphere 2019, 10, 148. [Google Scholar] [CrossRef]
- Medeiros, E.S.; Lima, R.R.; Olinda, R.A.; Dantas, L.G.; Santos, C.A.C. Space–Time Kriging of Precipitation: Modeling the Large-Scale Variation with Model GAMLSS. Water 2019, 11, 2368. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Wickham, H. Ggplot2-Positioning Elegant Graphics for Data Analysis; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 978-0-387-98140-6. [Google Scholar]
- Graler, B.; Pebesma, E.; Heuvelink, G. Spatio-Temporal Interpolation Using Gstat. R J. 2016, 8, 204. [Google Scholar] [CrossRef]
- Castro, A.L.C. Manual de Desastres: Desastres Naturais; Ministério da Integração Nacional: Brasília, Brazil, 2003.
- CEPED—Centro Universitário sobre Estudos e Pesquisa sobre Desastres. Atlas Brasileiro de Desastres Naturais: 1991–2012; Centro Universitário Sobre Estudos e Pesquisa Sobre Desastres: Paraíba, Brazil, 2013; 105p. [Google Scholar]
- Martins, E.S.P.; De Nys, E.; Molejón, C.; Biazeto, B.; Silva, R.F.V.; Engle, N.L. Monitor de Secas do Nordeste, Em Busca de um Novo Paradigma Para a Gestão de Secas; The World Bank: Brasília, Brazil, 2015; Volume 10, ISBN 978-85-88192-16-4. [Google Scholar]
- ANA—Agência Nacional De Águas. O Monitor de Secas. Available online: https://monitordesecas.ana.gov.br/ (accessed on 25 October 2022).
- Mello, M.N.; Dias, C.T.S.; Medeiros, E.S.; Martins, I.C.F.; Campos, L.D. Spatiotemporal Analysis of Distribution of Pest and Predator in Corn Crops. Arq. Inst. Biol. 2021, 88, 1–11. [Google Scholar] [CrossRef]
- Brasil Neto, R.M.; Santos, C.A.G.; da Costa Silva, J.F.C.B.; da Silva, R.M.; dos Santos, C.A.C.; Mishra, M. Evaluation of the TRMM Product for Monitoring Drought over Paraíba State, Northeastern Brazil: A Trend Analysis. Sci. Rep. 2021, 11, 1097. [Google Scholar] [CrossRef] [PubMed]
- Cook, B.I.; Mankin, J.S.; Anchukaitis, K.J. Climate Change and Drought: From Past to Future. Curr. Clim. Chang. Rep. 2018, 4, 164–179. [Google Scholar] [CrossRef]
- Dornellas, P.C.; Xavier, R.A.; Silva, R.M.; da Silva Seabra, V. Morphometric Analyses of High Paraiba River Basin, Semiarid Region of Paraiba State. Rev. Bras. Geomorfol. 2020, 21, 601–614. [Google Scholar] [CrossRef]
- Alves, T.L.B.; de Azevedo, P.V.; Santos, C.A.C. Influence of Climate Variability on Land Degradation (Desertification) in the Watershed of the Upper Paraíba River. Theor. Appl. Climatol. 2017, 127, 741–751. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).