Direct and Indirect Effects under Sample Selection and Outcome Attrition
Abstract
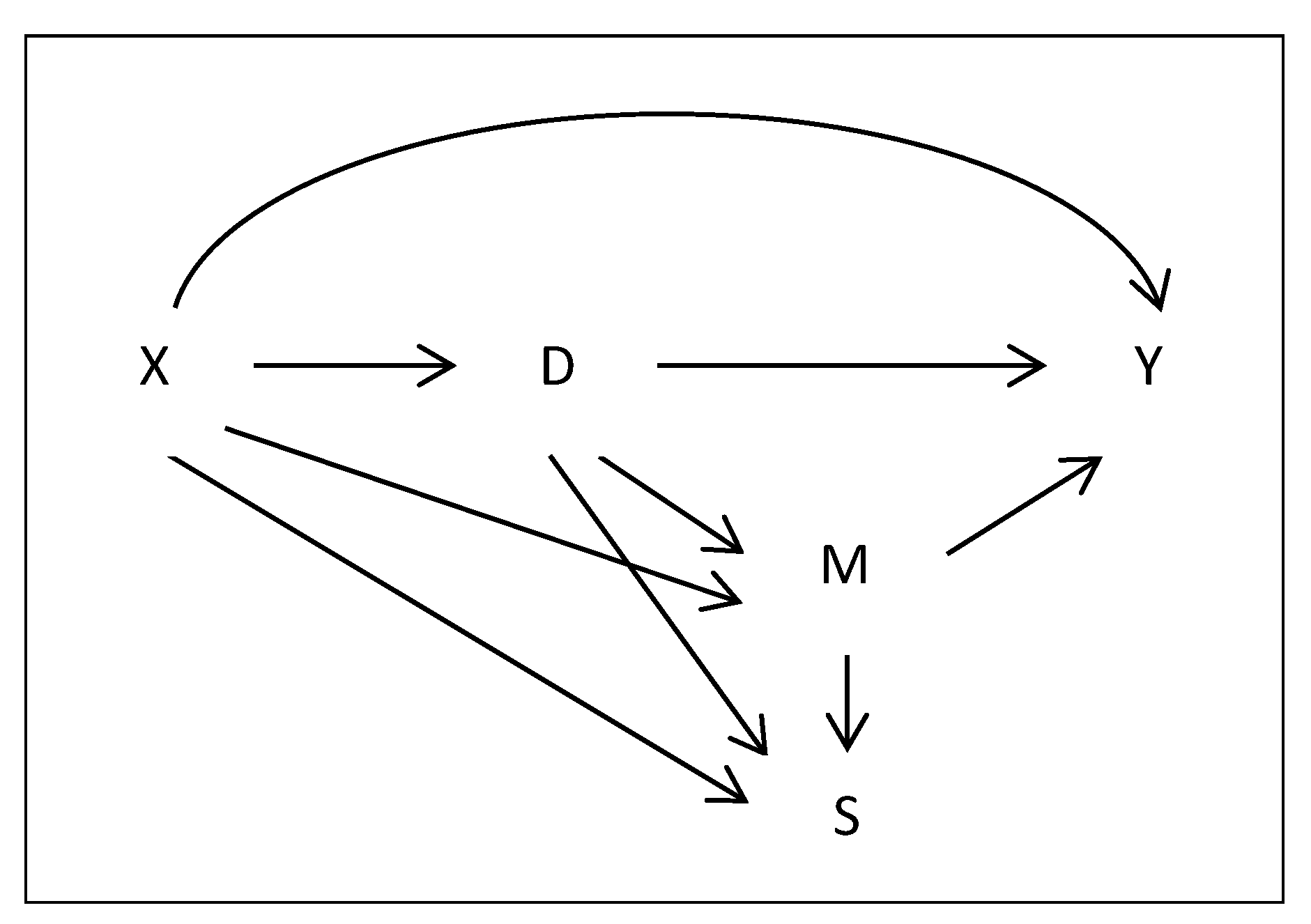
1. Introduction
2. Identification
2.1. Parameters of Interest
2.2. Assumptions and Identification Results under MAR
- (i)
- Under Assumptions 1–4, for d∈,
- (ii)
- Under Assumptions 1(a), 2–4, and M following a discrete distribution,
2.3. Assumptions and Identification Results under Selection Related to Unobservables
- (i)
- Under Assumptions 1, 2, 5, and 6 for d∈,
- (ii)
- Under Assumptions 1(a), 2, 5, and 6, and M following a discrete distribution,
2.4. Extensions to Further Populations, Parameters, and Variable Distributions
3. Estimation
4. Simulation Study
5. Empirical Application
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Theorem 1
Appendix A.2. Proof of Theorem 2
Appendix A.3. Proof of Theorem 3
References
- Abowd, John M., Bruno Crépon, and Francis Kramarz. 2001. Moment Estimation With Attrition: An Application to Economic Models. Journal of the American Statistical Association 96: 1223–30. [Google Scholar] [CrossRef]
- Ahn, Hyungtaik, and James L. Powell. 1993. Semiparametric Estimation of Censored Selection Models with a Nonparametric Selection Mechanism. Journal of Econometrics 58: 3–29. [Google Scholar] [CrossRef]
- Albert, Jeffrey M. 2008. Mediation analysis via potential outcomes models. Statistics in Medicine 27: 1282–304. [Google Scholar] [CrossRef]
- Albert, Jeffrey M., and Suchitra Nelson. 2011. Generalized causal mediation analysis. Biometrics 67: 1028–38. [Google Scholar] [CrossRef] [PubMed]
- Angrist, Joshua, Eric Bettinger, and Michael Kremer. 2006. Long-Term Educational Consequences of Secondary School Vouchers: Evidence from Administrative Records in Colombia. American Economic Review 96: 847–62. [Google Scholar] [CrossRef]
- Angrist, Joshua D., Guido W. Imbens, and Donald B. Rubin. 1996. Identification of Causal Effects using Instrumental Variables. Journal of American Statistical Association 91: 444–72. [Google Scholar] [CrossRef]
- Baron, Reuben M., and David A. Kenny. 1986. The Moderator-Mediator Variable Distinction in Social Psychological Research: Conceptual, Strategic, and Statistical Considerations. Journal of Personality and Social Psychology 51: 1173–82. [Google Scholar] [CrossRef] [PubMed]
- Blinder, Alan S. 1973. Wage Discrimination: Reduced Form and Structural Estimates. Journal of Human Resources 8: 436–55. [Google Scholar] [CrossRef]
- Blundell, Richard W., and James L. Powell. 2004. Endogeneity in Semiparametric Binary Response Models. The Review of Economic Studies 71: 655–79. [Google Scholar] [CrossRef]
- Bodory, Hugo, and Martin Huber. 2018. The Causalweight Package for Causal Inference in R. SES Working Paper 493. Fribourg: University of Fribourg. [Google Scholar]
- Brunello, Giorgio, Margherita Fort, Nicole Schneeweis, and Rudolf Winter-Ebmer. 2016. The Causal Effect of Education on Health: What is the Role of Health Behaviors? Health Economics 25: 314–36. [Google Scholar] [CrossRef]
- Busso, Matias, John E. DiNardo, and Justin McCrary. 2009. New Evidence on the Finite Sample Properties of Propensity Score Matching and Reweighting Estimators. IZA Discussion Paper No. 3998. Available online: https://ssrn.com/abstract=1351162 (accessed on 28 November 2020).
- Carroll, Raymond J., David Ruppert, and Leonard A. Stefanski. 1995. Measurement Error in Nonlinear Models. London: Chapman and Hall. [Google Scholar]
- Castiglioni, Laura, Klaus Pforr, and Ulrich Krieger. 2008. The Effect of Incentives on Response Rates and Panel Attrition: Results of a Controlled Experiment. Survey Research Methods 2: 151–58. [Google Scholar]
- Chetty, Raj, John N. Friedman, Nathaniel Hilger, Emmanuel Saez, Diane Whitmore Schanzenbach, and Danny Yagan. 2011. How Does Your Kindergarten Classroom Affect Your Earnings? Evidence from Project Star. The Quarterly Journal of Economics 126: 1593–660. [Google Scholar] [CrossRef] [PubMed]
- Conti, Gabriella, James J. Heckman, and Rodrigo Pinto. 2016. The Effects of Two Influential Early Childhood Interventions on Health and Healthy Behaviour. The Economic Journal 126: F28–F65. [Google Scholar] [CrossRef]
- Crump, Richard K., V. Joseph Hotz, Guido W. Imbens, and Oscar A. Mitnik. 2009. Dealing with limited overlap in estimation of average treatment effects. Biometrika 96: 187–99. [Google Scholar] [CrossRef]
- Das, Mitali, Whitney K. Newey, and Francis Vella. 2003. Nonparametric Estimation of Sample Selection Models. Review of Economic Studies 70: 33–58. [Google Scholar] [CrossRef]
- d’Haultfoeuille, Xavier. 2010. A new instrumental method for dealing with endogenous selection. Journal of Econometrics 154: 1–15. [Google Scholar]
- Finn, Jeremy D., and Charles M. Achilles. 1990. Answers and Questions about Class Size: A Statewide Experiment. American Educational Research Journal 27: 557–77. [Google Scholar] [CrossRef]
- Finn, Jeremy D., DeWayne Fulton, Jayne Zaharias, and Barbara A. Nye. 1989. Carry-Over Effects of Small Classes. Peabody Journal of Education 67: 75–84. [Google Scholar] [CrossRef]
- Fitzgerald, John, Peter Gottschalk, and Robert Moffitt. 1998. An Analysis of Sample Attrition in Panel Data: The Michigan Panel Study of Income Dynamics. Journal of Human Resources 33: 251–99. [Google Scholar] [CrossRef]
- Flores, Carlos A., and Alfonso Flores-Lagunes. 2009. Identification and Estimation of Causal Mechanisms and Net Effects of a Treatment under Unconfoundedness. IZA DP No. 4237. Available online: https://ssrn.com/abstract=1423353 (accessed on 28 November 2020).
- Folger, John, and Carolyn Breda. 1989. Evidence from Project STAR about Class Size and Student Achievement. Peabody Journal of Education 67: 17–33. [Google Scholar] [CrossRef]
- Frangakis, Constantine E., and Donald B. Rubin. 1999. Addressing complications of intention-to-treat analysis in the combined presence of all-or-none treatment-noncompliance and subsequent missing outcomes. Biometrika 86: 365–79. [Google Scholar] [CrossRef]
- Fricke, Hans, Markus Frölich, Martin Huber, and Michael Lechner. 2020. Endogeneity and Non-Response Bias in Treatment Evaluation—Nonparametric Identification of Causal Effects by Instruments. Journal of Applied Econometrics 35: 481–504. [Google Scholar] [CrossRef]
- Frölich, Markus. 2004. Finite Sample Properties of Propensity-Score Matching and Weighting Estimators. The Review of Economics and Statistics 86: 77–90. [Google Scholar] [CrossRef]
- Frölich, Markus, and Martin Huber. 2014. Treatment evaluation with multiple outcome periods under endogeneity and attrition. Journal of the American Statistical Association 109: 1697–711. [Google Scholar] [CrossRef]
- Frölich, Markus, and Martin Huber. 2017. Direct and Indirect Treatment Effects—Causal Chains and Mediation Analysis with Instrumental Variables. Journal of the Royal Statistical Society: Series B 79: 1645–66. [Google Scholar] [CrossRef]
- Gershenson, Seth, Alison Jacknowitz, and Andrew Brannegan. 2017. Are Student Absences Worth the Worry in U.S. Primary Schools? Education Finance and Policy 12: 137–65. [Google Scholar] [CrossRef]
- Gottfried, Michael A. 2009. Excused Versus Unexcused: How Student Absences in Elementary School Affect Academic Achievement. Educational Evaluation and Policy Analysis 31: 392–415. [Google Scholar] [CrossRef]
- Gronau, Reuben. 1974. Wage comparisons-a selectivity bias. Journal of Political Economy 82: 1119–43. [Google Scholar] [CrossRef]
- Hausman, Jerry A., and David A. Wise. 1979. Attrition Bias In Experimental and Panel Data: The Gary Income Maintenance Experiment. Econometrica 47: 455–73. [Google Scholar] [CrossRef]
- Heckman, James J. 1976. The Common Structure of Statistical Models of Truncation, Sample Selection, and Limited Dependent Variables, and a Simple Estimator for such Models. Annals of Economic and Social Measurement 5: 475–92. [Google Scholar]
- Heckman, James J. 1979. Sample Selection Bias as a Specification Error. Econometrica 47: 153–61. [Google Scholar] [CrossRef]
- Hirano, Keisuke, Guido W. Imbens, and Geert Ridder. 2003. Efficient Estimation of Average Treatment Effects Using the Estimated Propensity Score. Econometrica 71: 1161–89. [Google Scholar] [CrossRef]
- Hong, Guanglei. 2010. Ratio of mediator probability weighting for estimating natural direct and indirect effects. In Proceedings of the American Statistical Association, Biometrics Section. Alexandria: American Statistical Association, pp. 2401–15. [Google Scholar]
- Horvitz, Daniel G., and Donovan J. Thompson. 1952. A Generalization of Sampling without Replacement from a Finite Population. Journal of American Statistical Association 47: 663–85. [Google Scholar] [CrossRef]
- Hsu, Joanne W., Maximilian D. Schmeiser, Catherine Haggerty, and Shannon Nelson. 2017. The Effect of Large Monetary Incentives on Survey Completion: Evidence from a Randomized Experiment with the Survey of Consumer Finances. Public Opinion Quarterly 81: 736–47. [Google Scholar] [CrossRef]
- Hsu, Yu-Chin, Martin Huber, Ying-Ying Lee, and Layal Lettry. 2018. Direct and Indirect Effects of Continuous Treatments Based on Generalized Propensity Score Weighting. SES Working Papers 495. Fribourg: University of Fribourg. [Google Scholar]
- Huber, Martin. 2012. Identification of average treatment effects in social experiments under alternative forms of attrition. Journal of Educational and Behavioral Statistics 37: 443–474. [Google Scholar] [CrossRef]
- Huber, Martin. 2014a. Identifying causal mechanisms (primarily) based on inverse probability weighting. Journal of Applied Econometrics 29: 920–43. [Google Scholar] [CrossRef]
- Huber, Martin. 2014b. Treatment evaluation in the presence of sample selection. Econometric Reviews 33: 869–905. [Google Scholar] [CrossRef]
- Huber, Martin. 2015. Causal pitfalls in the decomposition of wage gaps. Journal of Business and Economic Statistics 33: 179–91. [Google Scholar] [CrossRef]
- Huber, Martin, and Blaise Melly. 2015. A Test of the Conditional Independence Assumption in Sample Selection Models. Journal of Applied Econometrics 30: 1144–68. [Google Scholar] [CrossRef]
- Imai, Kosuke. 2009. Statistical analysis of randomized experiments with non-ignorable missing binary outcomes: An application to a voting experiment. Journal of the Royal Statistical Society Series C 58: 83–104. [Google Scholar] [CrossRef]
- Imai, Kosuke, Luke Keele, and Teppei Yamamoto. 2010. Identification, Inference and Sensitivity Analysis for Causal Mediation Effects. Statistical Science 25: 51–71. [Google Scholar] [CrossRef]
- Imai, Kosuke, and Teppei Yamamoto. 2011. Identification and Sensitivity Analysis for Multiple Causal Mechanisms: Revisiting Evidence from Framing Experiments. in press. [Google Scholar]
- Imbens, Guido W. 2004. Nonparametric Estimation of Average Treatment Effects under Exogeneity: A Review. The Review of Economics and Statistics 86: 4–29. [Google Scholar] [CrossRef]
- Imbens, Guido W., and Joshua D. Angrist. 1994. Identification and Estimation of Local Average Treatment Effects. Econometrica 62: 467–75. [Google Scholar] [CrossRef]
- Imbens, Guido W., and Whitney K. Newey. 2009. Identification and Estimation of Triangular Simultaneous Equations Models Without Additivity. Econometrica 77: 1481–512. [Google Scholar]
- Judd, Charles M., and David A. Kenny. 1981. Process Analysis: Estimating Mediation in Treatment Evaluations. Evaluation Review 5: 602–19. [Google Scholar] [CrossRef]
- Khan, Shakeeb, and Elie Tamer. 2010. Irregular Identification, Support Conditions, and Inverse Weight Estimation. Econometrica 78: 2021–42. [Google Scholar]
- Krueger, Alan B. 1999. Experimental Estimates of Education Production Functions. Quarterly Journal of Economics 114: 497–532. [Google Scholar] [CrossRef]
- Krueger, Alan B., and Diane M. Whitmore. 2001. The Effect of Attending a Small Class in the Early Grades on College-Test Taking and Middle School Test Results: Evidence from Project STAR. The Economic Journal 111: 1–28. [Google Scholar] [CrossRef]
- Little, Roderick J.A., and Donald B. Rubin. 1987. Statistical Analysis with Missing Data. New York: Wiley. [Google Scholar]
- Little, Roderick J.A. 1995. Modeling the Drop-Out Mechanism in Repeated-Measures Studies. Journal of the American Statistical Association 90: 1112–21. [Google Scholar] [CrossRef]
- Morrissey, Taryn W., Lindsey Hutchison, and Adam Winsler. 2014. Family Income, School Attendance, and Academic Achievement in Elementary School. Developmental Psychology 50: 741–53. [Google Scholar] [CrossRef]
- Newey, Whitney K., James L. Powell, and Francis Vella. 1999. Nonparametric Estimation of Triangular Simultaneous Equations Models. Econometrica 67: 565–603. [Google Scholar] [CrossRef]
- Newey, Whitney K. 1984. A method of moments interpretation of sequential estimators. Economics Letters 14: 201–6. [Google Scholar] [CrossRef]
- Newey, Whitney K. 2007. Nonparametric continuous/discrete choice models. International Economic Review 48: 1429–39. [Google Scholar] [CrossRef]
- Nye, Barbara, Larry V. Hedges, and Spyros Konstantopoulos. 2001. The Long-Term Effects of Small Classes in Early Grades: Lasting Benefits in Mathematics Achievement at Grade 9. The Journal of Experimental Education 69: 245–57. [Google Scholar] [CrossRef]
- Oaxaca, Ronald. 1973. Male-Female Wage Differences in Urban Labour Markets. International Economic Review 14: 693–709. [Google Scholar] [CrossRef]
- Odongo, David Otieno, W. J. Wakhungu, and Omuterema Stanley. 2017. Causes of variability in prevalence rates of communicable diseases among secondary school Students in Kisumu County, Kenya. Journal of Public Health 25: 161–66. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Pearl, Judea. 1995. Causal Diagrams for Empirical Research. Biometrika 82: 669–710. [Google Scholar] [CrossRef]
- Pearl, Judea. 2001. Direct and indirect effects. In Proceedings of the Seventeenth Conference on Uncertainty in Artificial Intelligence. San Francisco: Morgan Kaufman, pp. 411–20. [Google Scholar]
- Petersen, Maya L., Sandra E. Sinisi, and Mark J. van der Laan. 2006. Estimation of Direct Causal Effects. Epidemiology 17: 276–84. [Google Scholar] [CrossRef]
- Pforr, Klaus, Michael Blohm, Annelies G. Blom, Barbara Erdel, Barbara Felderer, Mathis Fräßdorf, Kristin Hajek, Susanne Helmschrott, Corinna Kleinert, Achim Koch, and et al. 2015. Are Incentive Effects on Response Rates and Nonresponse Bias in Large-scale, Face-to-face Surveys Generalizable to Germany? Evidence from Ten Experiments. Public Opinion Quarterly 79: 740–68. [Google Scholar] [CrossRef]
- Ready, Douglas D. 2010. Socioeconomic Disadvantage, School Attendance, and Early Cognitive Development: The Differential Effects of School Exposure. Sociology of Education 83: 271–86. [Google Scholar] [CrossRef]
- Robins, James M. 2003. Semantics of causal DAG models and the identification of direct and indirect effects. In Highly Structured Stochastic Systems. Edited by P. Green, N. Hjort and S. Richardson. Oxford: Oxford University Press, pp. 70–81. [Google Scholar]
- Robins, James M., and Sander Greenland. 1992. Identifiability and Exchangeability for Direct and Indirect Effects. Epidemiology 3: 143–55. [Google Scholar] [CrossRef] [PubMed]
- Robins, James M., and Thomas S. Richardson. 2010. Alternative graphical causal models and the identification of direct effects. In Causality and Psychopathology: Finding the Determinants of Disorders and Their Cures. Edited by P. Shrout, K. Keyes and K. Omstein. Oxford: Oxford University Press. [Google Scholar]
- Robins, James M., Andrea Rotnitzky, and Lue Ping Zhao. 1994. Estimation of Regression Coefficients When Some Regressors Are not Always Observed. Journal of the American Statistical Association 90: 846–66. [Google Scholar] [CrossRef]
- Robins, James M., Andrea Rotnitzky, and Lue Ping Zhao. 1995. Analysis of Semiparametric Regression Models for Repeated Outcomes in the Presence of Missing Data. Journal of American Statistical Association 90: 106–21. [Google Scholar] [CrossRef]
- Rubin, Donald B. 1974. Estimating Causal Effects of Treatments in Randomized and Nonrandomized Studies. Journal of Educational Psychology 66: 688–701. [Google Scholar] [CrossRef]
- Rubin, Donald B. 1976. Inference and Missing Data. Biometrika 63: 581–92. [Google Scholar] [CrossRef]
- Rubin, Donald B. 1990. Formal Modes of Statistical Inference for Causal Effects. Journal of Statistical Planning and Inference 25: 279–92. [Google Scholar] [CrossRef]
- Rubin, Donald B. 2004. Direct and Indirect Causal Effects via Potential Outcomes. Scandinavian Journal of Statistics 31: 161–70. [Google Scholar] [CrossRef]
- Shah, Amrik, Nan Laird, and David Schoenfeld. 1997. A Random-Effects Model for Multiple Characteristics With Possibly Missing Data. Journal of the American Statistical Association 92: 775–79. [Google Scholar] [CrossRef]
- Tchetgen, Eric J. Tchetgen, and Ilya Shpitser. 2012. Semiparametric theory for causal mediation analysis: Efficiency bounds, multiple robustness, and sensitivity analysis. The Annals of Statistics 40: 1816–45. [Google Scholar] [CrossRef]
- Tchetgen, Eric J. Tchetgen, and Tyler J. VanderWeele. 2014. On Identification of Natural Direct Effects when a Confounder of the Mediator is Directly Affected by Exposure. Epidemiology 25: 282–91. [Google Scholar] [CrossRef]
- Ten Have, Thomas R., Marshall M. Joffe, Kevin G. Lynch, Gregory K. Brown, Stephen A. Maisto, and Aaron T. Beck. 2007. Causal mediation analyses with rank preserving models. Biometrics 63: 926–34. [Google Scholar] [CrossRef] [PubMed]
- VanderWeele, Tyler J. 2009. Marginal Structural Models for the Estimation of Direct and Indirect Effects. Epidemiology 20: 18–26. [Google Scholar] [CrossRef] [PubMed]
- Vansteelandt, Stijn, Maarten Bekaert, and Theis Lange. 2012. Imputation Strategies for the Estimation of Natural Direct and Indirect Effects. Epidemiologic Methods 1: 129–58. [Google Scholar] [CrossRef]
- Waernbaum, Ingeborg. 2012. Model misspecification and robustness in causal inference: Comparing matching with doubly robust estimation. Statistics in Medicine 31: 1572–81. [Google Scholar] [CrossRef]
- Wooldridge, Jeffrey M. 2002. Inverse Probability Weigthed M-Estimators for Sample Selection, Attrition and Stratification. Portuguese Economic Journal 1: 141–62. [Google Scholar] [CrossRef]
- Wooldridge, Jeffrey M. 2007. Inverse probability weighted estimation for general missing data problems. Journal of Econometrics 141: 1281–301. [Google Scholar] [CrossRef]
- Zheng, Wenjing, and Mark J. van der Laan. 2012. Targeted Maximum Likelihood Estimation of Natural Direct Effects. The International Journal of Biostatistics 8: 1–40. [Google Scholar] [CrossRef]
| 1 | The idea of using inverse probability weighting to control for selection problems goes back to (Horvitz and Thompson 1952). |
| 2 | The estimators considered in the simulation study and the empirical application are available in the ‘causalweight’ package by (Bodory and Huber 2018) for the statistical software ‘R’. |
| 3 | Robins (2003); Robins and Greenland (1992) refer to this parameter as the total or pure direct effect and (Flores and Flores-Lagunes 2009) as net average treatment effect. |
| 4 | Robins (2003); Robins and Greenland (1992) refer to this parameter as the total or pure indirect effect and (Flores and Flores-Lagunes 2009) as mechanism average treatment effect. |
| 5 | See for instance (Imai 2009) for an alternative set of restrictions, assuming that selection is related to the outcome but is independent of the treatment conditional on the outcome and other observable variables. |
| 6 | Note that , which means that fixing the treatment and the potential mediator yields the potential outcome. |
| 7 | We implicitly also impose the Stable Unit Treatment Value Assumption (SUTVA, see (Rubin 1990)), stating that the potential mediators and outcomes for any individual are stable in the sense that their values do not depend on the treatment allocations in the rest of the population. |
| 8 | In the latter case, even the stronger condition holds. |
| 9 | Several studies in the mediation literature discuss identification in the presence of post-treatment confounders of the mediator that may themselves be affected by the treatment. See for instance (Albert and Nelson 2011; Huber 2014a; Imai and Yamamoto 2011; Robins and Richardson 2010; Tchetgen and VanderWeele 2014). |
| 10 | As an alternative set of IV restrictions in the context of selection, (d’Haultfoeuille 2010) permits the instrument to be associated with the outcome, but assumes conditional independence of the instrument and selection given the outcome. |
| 11 | Control function approaches have been applied in semi- and nonparametric sample selection models, e.g., (Ahn and Powell 1993; Das et al. 2003; Newey 2007), and and Huber (2012, 2014b) as well as in nonparametric instrumental variable models, see for example (Blundell and Powell 2004; Imbens and Newey 2009; Newey et al. 1999). |
| 12 | This implies that the following relation between the conditional means of potential and observed outcomes holds: , where the first equality follows from iterated expectations, the second from Assumptions 1 and 5, the third from Assumptions 2 and 5, the fourth from Assumption 5, and the fifth from the fact that conditional on and , the potential outcome corresponds to the observed outcome Y. |
| 13 | For instance, the weighted versions of the parameters identified in Theorem 1 correspond to
|
| 14 | Results are very similar when and therefore omitted. |
| 15 | Note that in spite of , estimation based on (the incorrect) Theorem 3 is consistent because the distribution of U is not associated with S conditional on . |
| 16 | Results are very similar when setting and therefore omitted. |
| 17 | Odongo et al. (2017) find a positive correlation between school size and communicable disease prevalence rates in Kenya. We are, however, not aware of any such study considering class (rather than school) size. |
| 18 | We do not consider IPW IV estimation based on Theorems 2 and 3, as our data do not contain credible instruments. |
| 19 | See (Huber 2015) on the equivalence of conventional wage gap decompositions and a simple mediation model. |
| 20 | Following (Chetty et al. 2011), we consider regular class size with and without additional teaching aid to be one treatment. |
| 21 | For example, Ready (2010) reports a stronger negative impact of absenteeism on early literacy outcomes for students with lower socioeconomic status, which implies that socioeconomic status and absenteeism interact in explaining the outcome. If socioeconomic status in addition affects absenteeism, it is a confounder of the association between absenteeism and the literacy outcomes. |
| 22 | 5276 students joined the program in subsequent years. About 2200 entered the experiment in the first grade, 1600 in the second and 1200 in the third grade. |
| 23 | Less than 1% of students in the sample are Asian, Hispanic, Native American or other race. In our analysis, they are included in one group with black students. |

| bias | std | rmse | bias | std | rmse | bias | std | rmse | bias | std | rmse | |
| , | ||||||||||||
| IPW w. | −0.16 | 0.14 | 0.21 | −0.17 | 0.16 | 0.23 | −0.01 | 0.15 | 0.15 | −0.02 | 0.11 | 0.12 |
| IPW MAR | 0.03 | 0.28 | 0.28 | 0.01 | 0.20 | 0.20 | −0.03 | 0.13 | 0.14 | −0.05 | 0.14 | 0.15 |
| IPW IV | −0.01 | 0.30 | 0.30 | −0.02 | 0.31 | 0.31 | −0.02 | 0.18 | 0.18 | −0.03 | 0.15 | 0.15 |
| , | ||||||||||||
| IPW w. | −0.16 | 0.07 | 0.18 | −0.17 | 0.08 | 0.19 | 0.00 | 0.08 | 0.08 | −0.01 | 0.06 | 0.06 |
| IPW MAR | 0.01 | 0.15 | 0.15 | 0.01 | 0.10 | 0.10 | −0.02 | 0.07 | 0.07 | −0.03 | 0.08 | 0.09 |
| IPW IV | −0.01 | 0.15 | 0.15 | −0.02 | 0.16 | 0.16 | −0.01 | 0.09 | 0.09 | −0.02 | 0.08 | 0.08 |
| bias | std | rmse | bias | std | rmse | bias | std | rmse | bias | std | rmse | |
| , | ||||||||||||
| IPW w. | −0.28 | 0.13 | 0.31 | −0.27 | 0.16 | 0.32 | 0.07 | 0.16 | 0.18 | 0.07 | 0.12 | 0.14 |
| IPW MAR (Theorem 1) | −0.09 | 0.30 | 0.31 | −0.11 | 0.21 | 0.24 | 0.06 | 0.14 | 0.15 | 0.04 | 0.15 | 0.16 |
| IPW IV (Theorem 3) | 0.02 | 0.32 | 0.32 | −0.01 | 0.31 | 0.31 | −0.02 | 0.18 | 0.18 | −0.05 | 0.16 | 0.16 |
| , | ||||||||||||
| IPW w. | −0.28 | 0.07 | 0.29 | −0.28 | 0.08 | 0.29 | 0.08 | 0.08 | 0.12 | 0.09 | 0.06 | 0.11 |
| IPW MAR (Theorem 1) | −0.11 | 0.16 | 0.20 | −0.11 | 0.10 | 0.15 | 0.06 | 0.07 | 0.09 | 0.06 | 0.09 | 0.11 |
| IPW IV (Theorem 3) | 0.01 | 0.17 | 0.17 | −0.01 | 0.16 | 0.16 | −0.02 | 0.09 | 0.09 | −0.04 | 0.08 | 0.09 |
| , | ||||||||||||
| IPW w. | −0.37 | 0.13 | 0.39 | −0.35 | 0.15 | 0.38 | 0.05 | 0.16 | 0.16 | 0.07 | 0.12 | 0.14 |
| IPW MAR (Theorem 1) | −0.20 | 0.30 | 0.36 | −0.20 | 0.21 | 0.28 | 0.03 | 0.14 | 0.14 | 0.04 | 0.15 | 0.16 |
| IPW IV (Theorem 3) | −0.14 | 0.32 | 0.34 | −0.16 | 0.31 | 0.35 | −0.02 | 0.18 | 0.18 | −0.05 | 0.16 | 0.16 |
| , | ||||||||||||
| IPW w. | −0.38 | 0.07 | 0.38 | −0.36 | 0.08 | 0.36 | 0.06 | 0.08 | 0.10 | 0.09 | 0.06 | 0.11 |
| IPW MAR (Theorem 1) | −0.22 | 0.16 | 0.27 | −0.20 | 0.10 | 0.22 | 0.04 | 0.07 | 0.08 | 0.06 | 0.09 | 0.11 |
| IPW IV (Theorem 3) | −0.14 | 0.16 | 0.22 | −0.16 | 0.16 | 0.23 | −0.01 | 0.09 | 0.09 | −0.04 | 0.08 | 0.09 |
| bias | std | rmse | bias | std | rmse | bias | std | rmse | bias | std | rmse | |
| , | ||||||||||||
| IPW w. | −0.11 | 0.13 | 0.17 | −0.09 | 0.15 | 0.17 | 0.05 | 0.16 | 0.16 | 0.07 | 0.12 | 0.14 |
| IPW IV w. (Theorem 2) | 0.00 | 0.21 | 0.21 | −0.03 | 0.23 | 0.23 | 0.02 | 0.17 | 0.17 | −0.01 | 0.12 | 0.12 |
| , | ||||||||||||
| IPW w. | −0.12 | 0.07 | 0.14 | −0.10 | 0.08 | 0.12 | 0.06 | 0.08 | 0.10 | 0.09 | 0.06 | 0.11 |
| IPW IV w. (Theorem 2) | 0.01 | 0.10 | 0.10 | −0.02 | 0.11 | 0.12 | 0.03 | 0.08 | 0.08 | −0.00 | 0.06 | 0.06 |
| Variable | Total | Difference | p-Value | ||
|---|---|---|---|---|---|
| Student’s gender: male | 0.51 | 0.51 | 0.51 | 0.00 | 0.96 |
| [0.50] | [0.50] | [0.50] | (0.01) | ||
| Student’s race: white | 0.67 | 0.67 | 0.68 | 0.01 | 0.42 |
| [0.47] | [0.47] | [0.47] | (0.02) | ||
| Free lunch | 0.48 | 0.49 | 0.47 | −0.02 | 0.25 |
| [0.50] | [0.50] | [0.50] | (0.02) | ||
| Born 1978 | 0.01 | 0.01 | 0.00 | −0.01 | 0.00 |
| [0.08] | [0.09] | [0.05] | (0.00) | ||
| Born 1979 | 0.23 | 0.22 | 0.25 | 0.03 | 0.04 |
| [0.42] | [0.42] | [0.43] | (0.01) | ||
| Born 1980 | 0.76 | 0.77 | 0.74 | −0.02 | 0.09 |
| [0.43] | [0.42] | [0.44] | (0.01) | ||
| Born 1981 | 0.00 | 0.00 | 0.00 | 0.00 | 0.87 |
| [0.03] | [0.03] | [0.03] | (0.00) | ||
| Kindergarten days absent | 10.51 | 10.72 | 10.01 | −0.71 | 0.02 |
| [9.76] | [9.95] | [9.29] | (0.31) | ||
| Math SAT grade 1 | 534.54 | 531.52 | 541.25 | 9.73 | 0.00 |
| [43.83] | [42.92] | [45.10] | (2.14) |
| Total Effect | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| est. | s.e. | -Value | est. | s.e. | -Value | est. | s.e. | -Value | est. | s.e. | -Value | est. | s.e. | -Value | |
| IPW MAR | 8.74 | 2.37 | 0.00 | 8.52 | 2.36 | 0.00 | 7.75 | 2.70 | 0.00 | 0.99 | 0.79 | 0.21 | 0.23 | 0.13 | 0.09 |
| Lin w. , no X | 9.73 | 2.16 | 0.00 | 9.46 | 2.17 | 0.00 | 9.55 | 2.15 | 0.00 | 0.27 | 0.18 | 0.12 | 0.18 | 0.13 | 0.16 |
| IPW w. , no X | 9.73 | 2.16 | 0.00 | 9.55 | 2.15 | 0.00 | 9.43 | 2.18 | 0.00 | 0.30 | 0.21 | 0.16 | 0.18 | 0.13 | 0.15 |
| IPW w. | 9.20 | 2.14 | 0.00 | 9.01 | 2.14 | 0.00 | 8.77 | 2.19 | 0.00 | 0.43 | 0.32 | 0.18 | 0.19 | 0.14 | 0.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huber, M.; Solovyeva, A. Direct and Indirect Effects under Sample Selection and Outcome Attrition. Econometrics 2020, 8, 44. https://doi.org/10.3390/econometrics8040044
Huber M, Solovyeva A. Direct and Indirect Effects under Sample Selection and Outcome Attrition. Econometrics. 2020; 8(4):44. https://doi.org/10.3390/econometrics8040044
Chicago/Turabian StyleHuber, Martin, and Anna Solovyeva. 2020. "Direct and Indirect Effects under Sample Selection and Outcome Attrition" Econometrics 8, no. 4: 44. https://doi.org/10.3390/econometrics8040044
APA StyleHuber, M., & Solovyeva, A. (2020). Direct and Indirect Effects under Sample Selection and Outcome Attrition. Econometrics, 8(4), 44. https://doi.org/10.3390/econometrics8040044




