Trajectory-Assisted Municipal Agent Mobility: A Sensor-Driven Smart Waste Management System
Abstract
1. Introduction
2. Related Work and Motivation
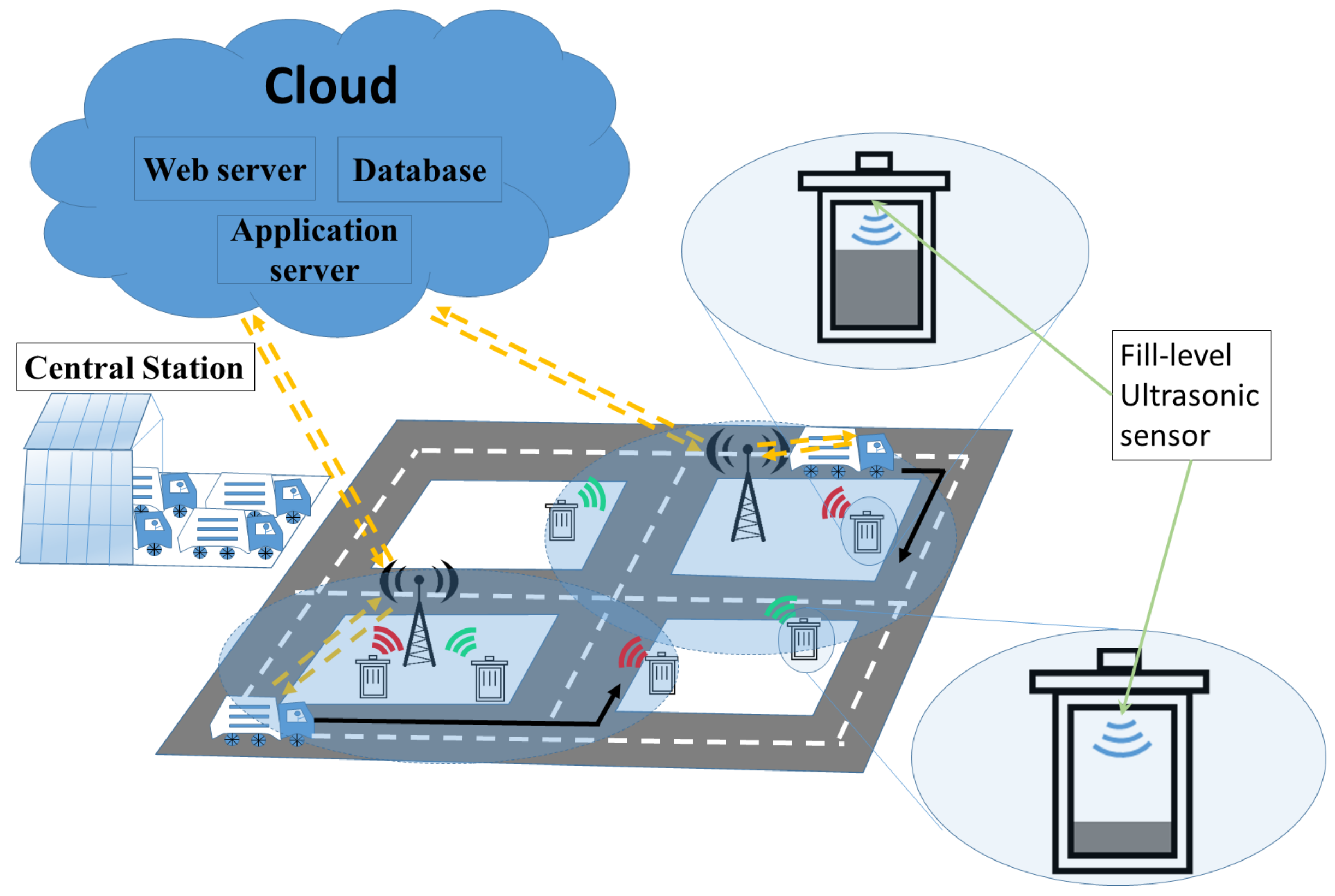
3. System Model
4. Optimization Model for WSN-Based Waste Management in Smart Cities
4.1. Cost-Based Optimization Model
4.2. Delay-Based Optimization Model
5. Heuristics for WSN-Based Waste Management in Smart Cities
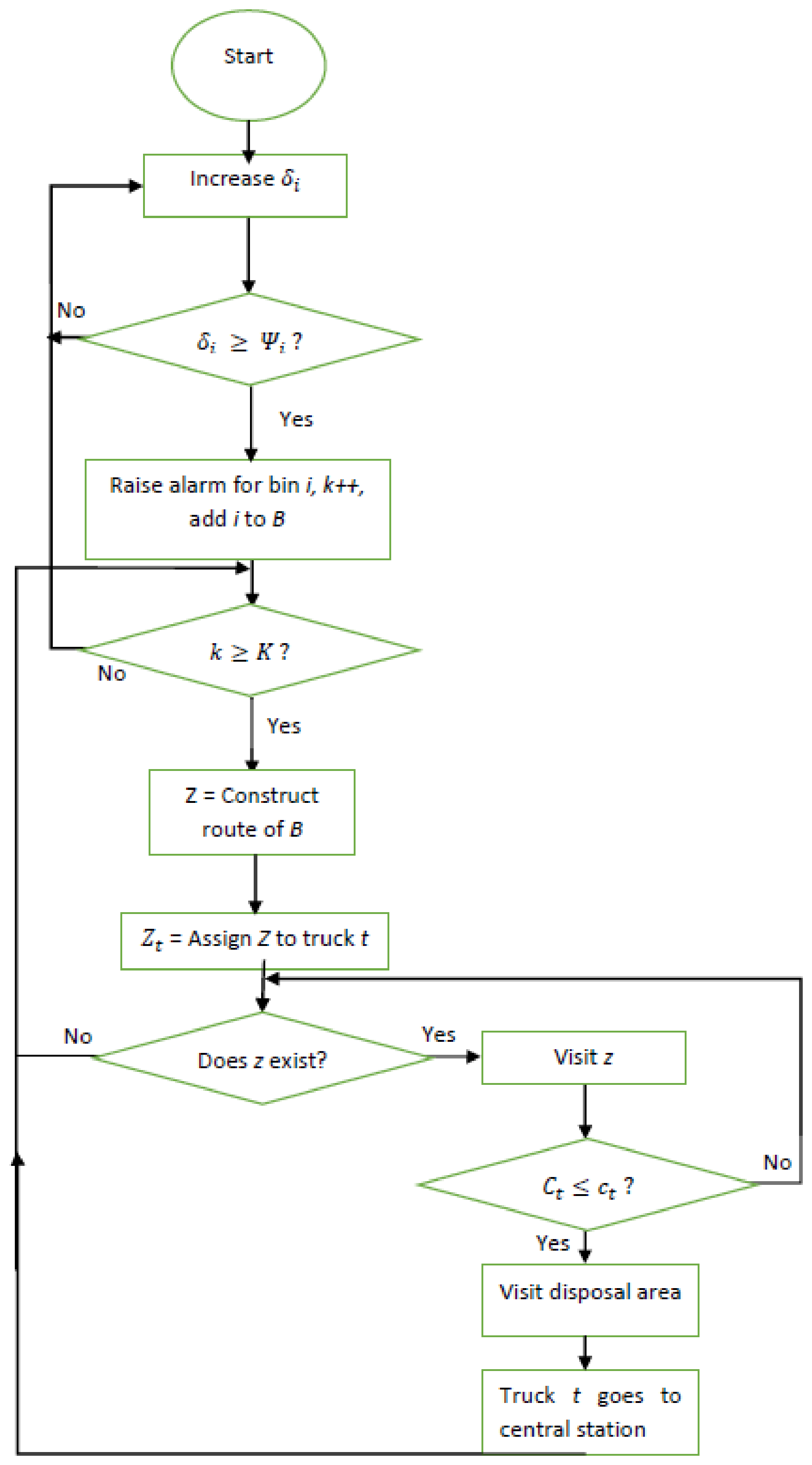
5.1. Closest Vehicle First: A Locality-Based Baseline Solution
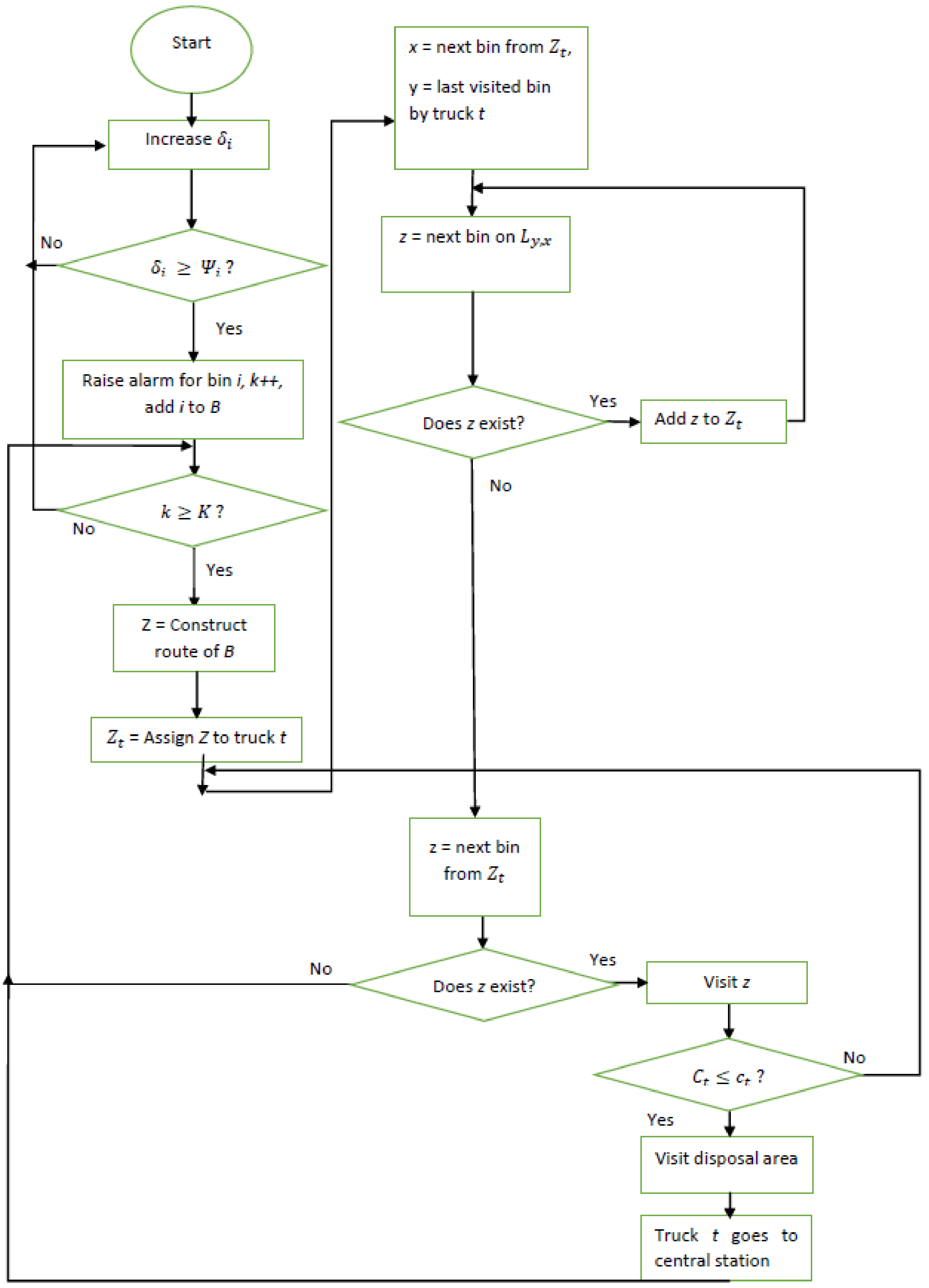
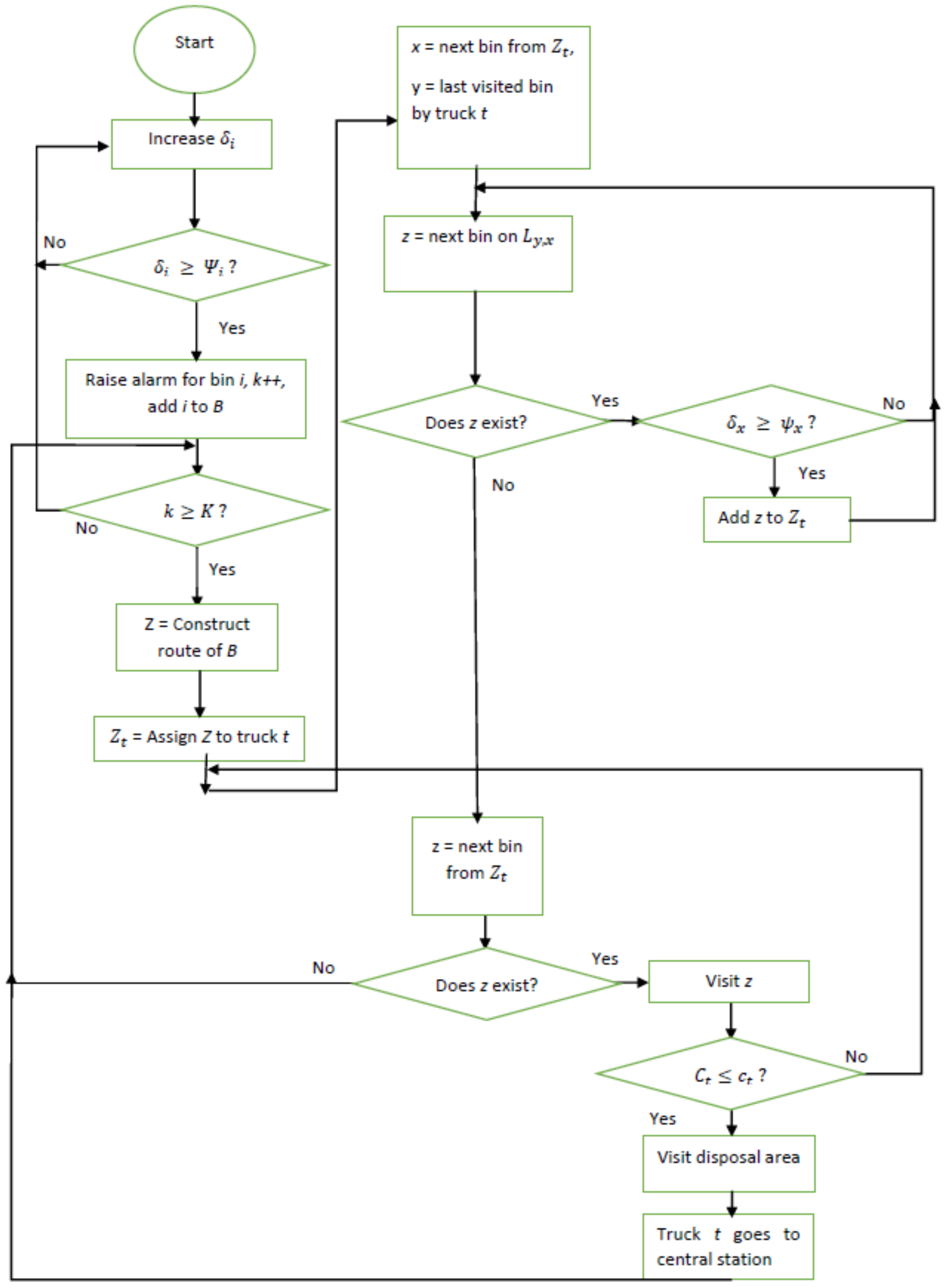
5.2. Proposed Nearly-Optimal Heuristics
5.2.1. Collect based on Upper Threshold
5.2.2. Collect based on Upper and Lower Threshold
6. Performance Evaluation
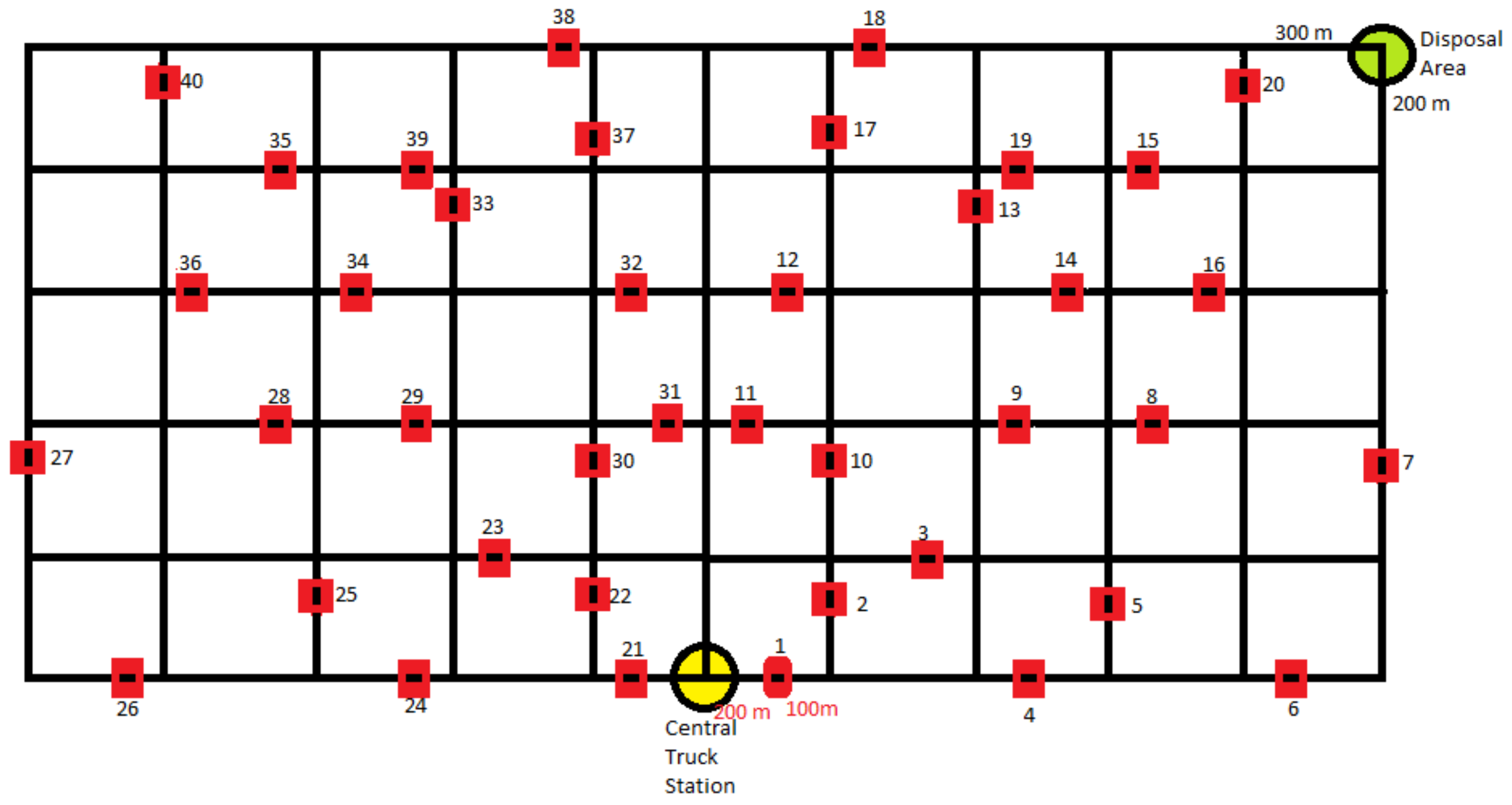
6.1. Simulation Settings
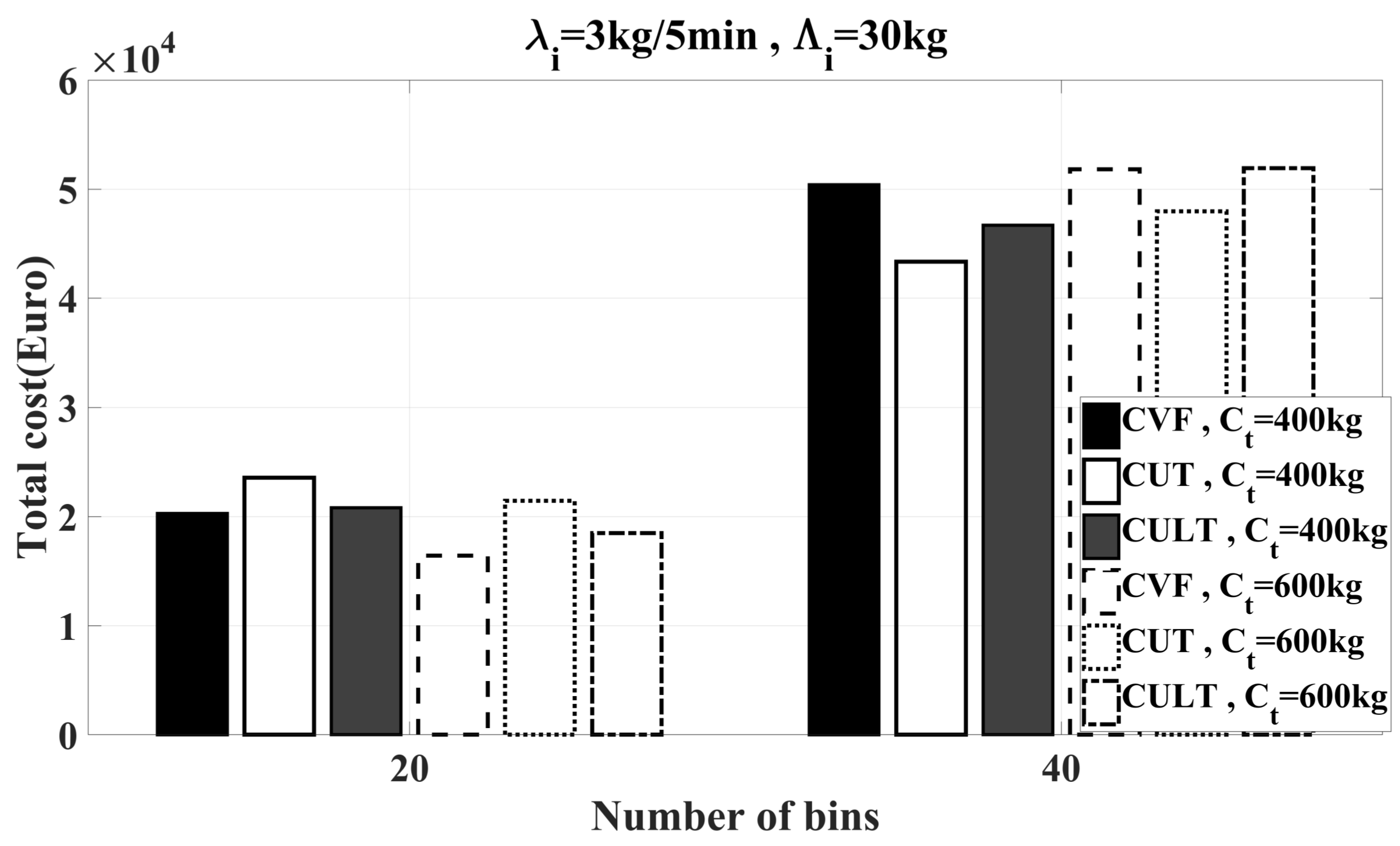
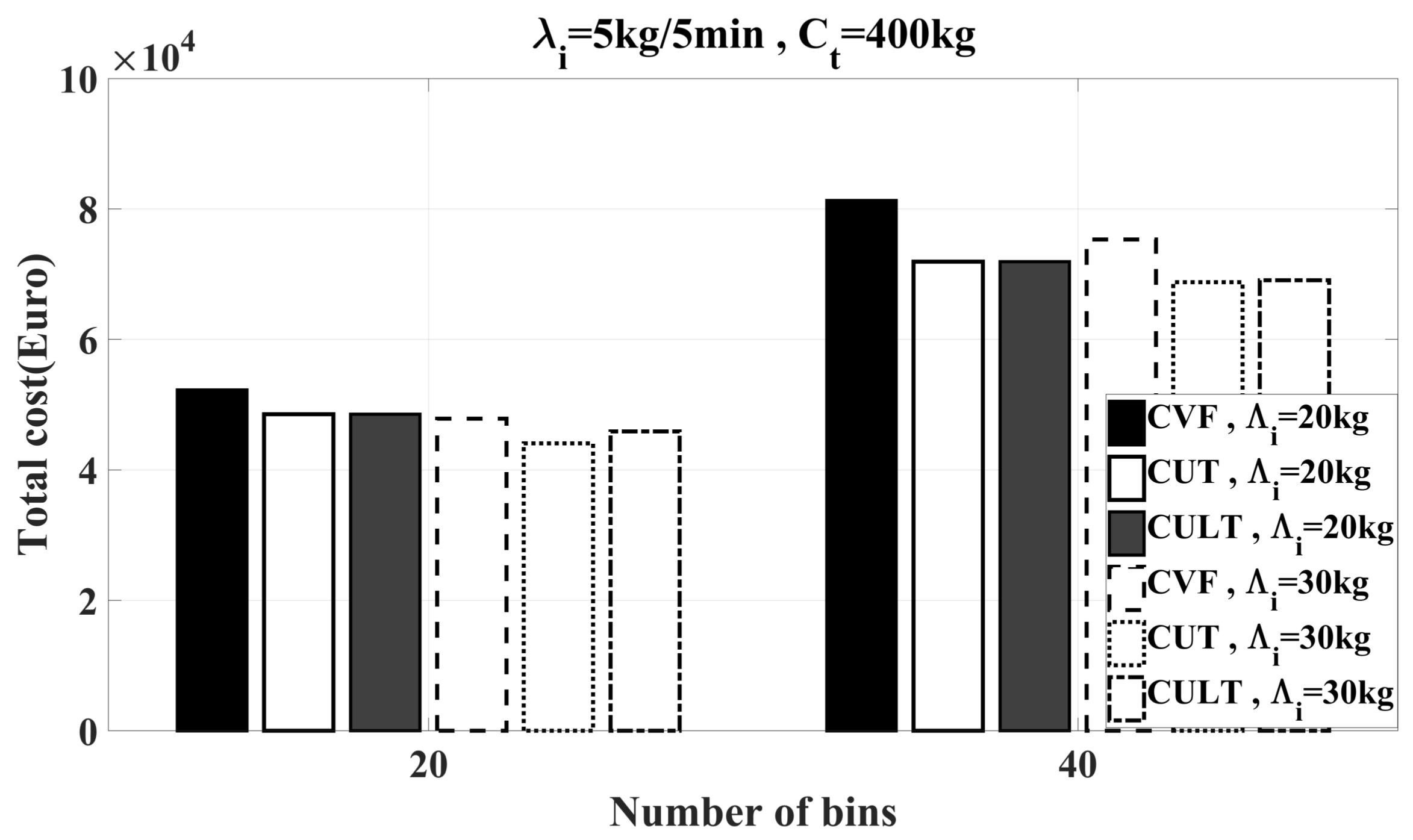
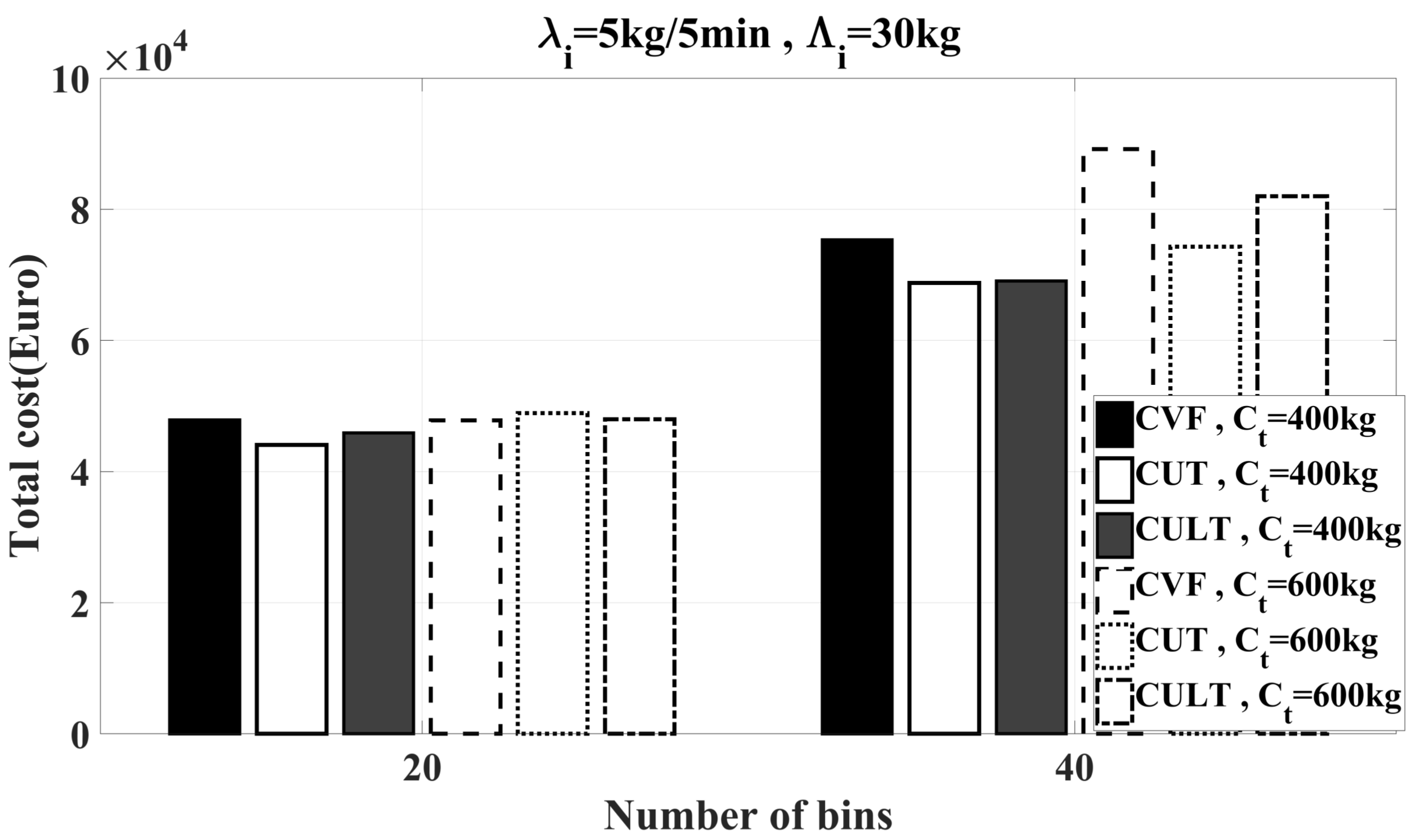
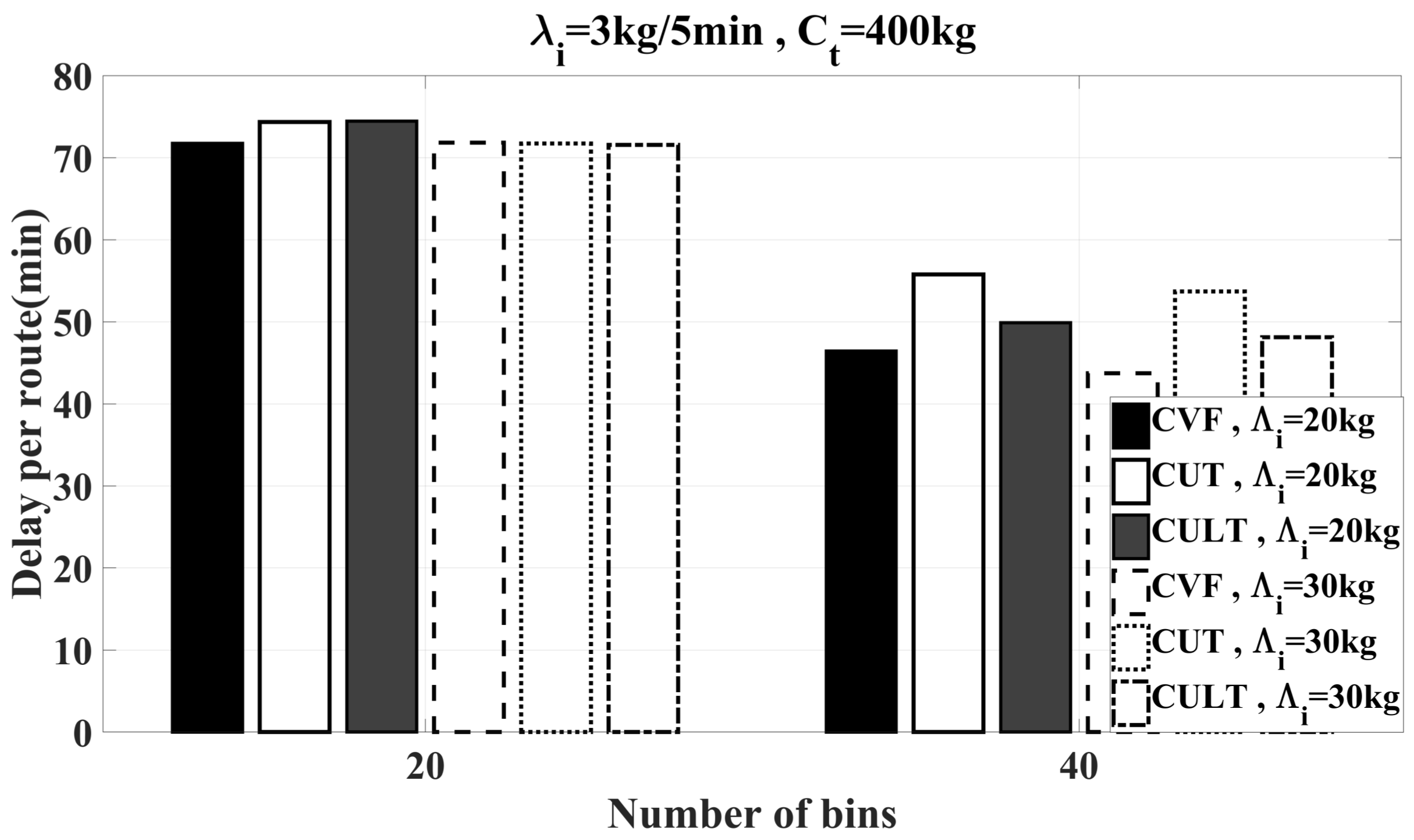
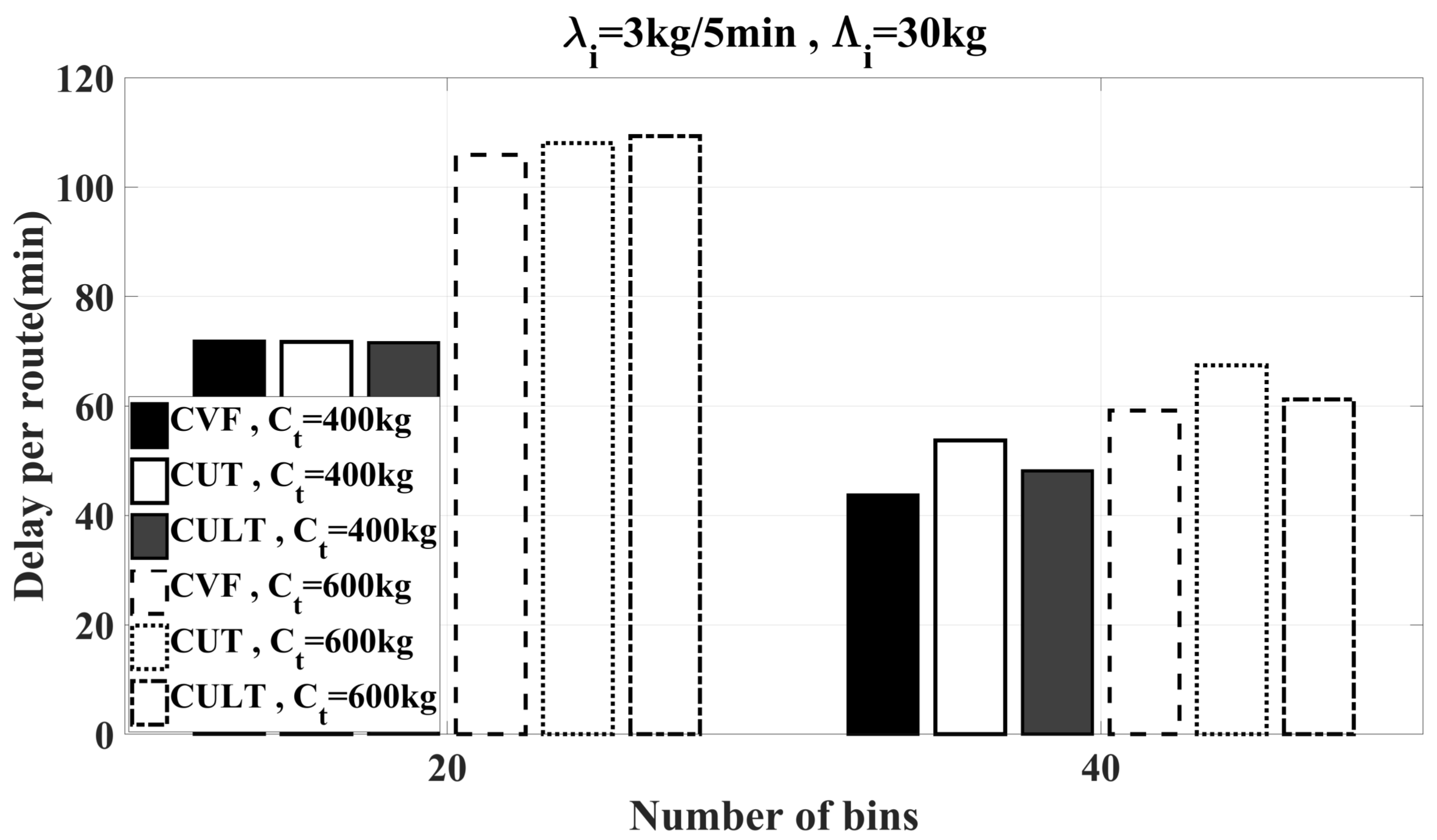
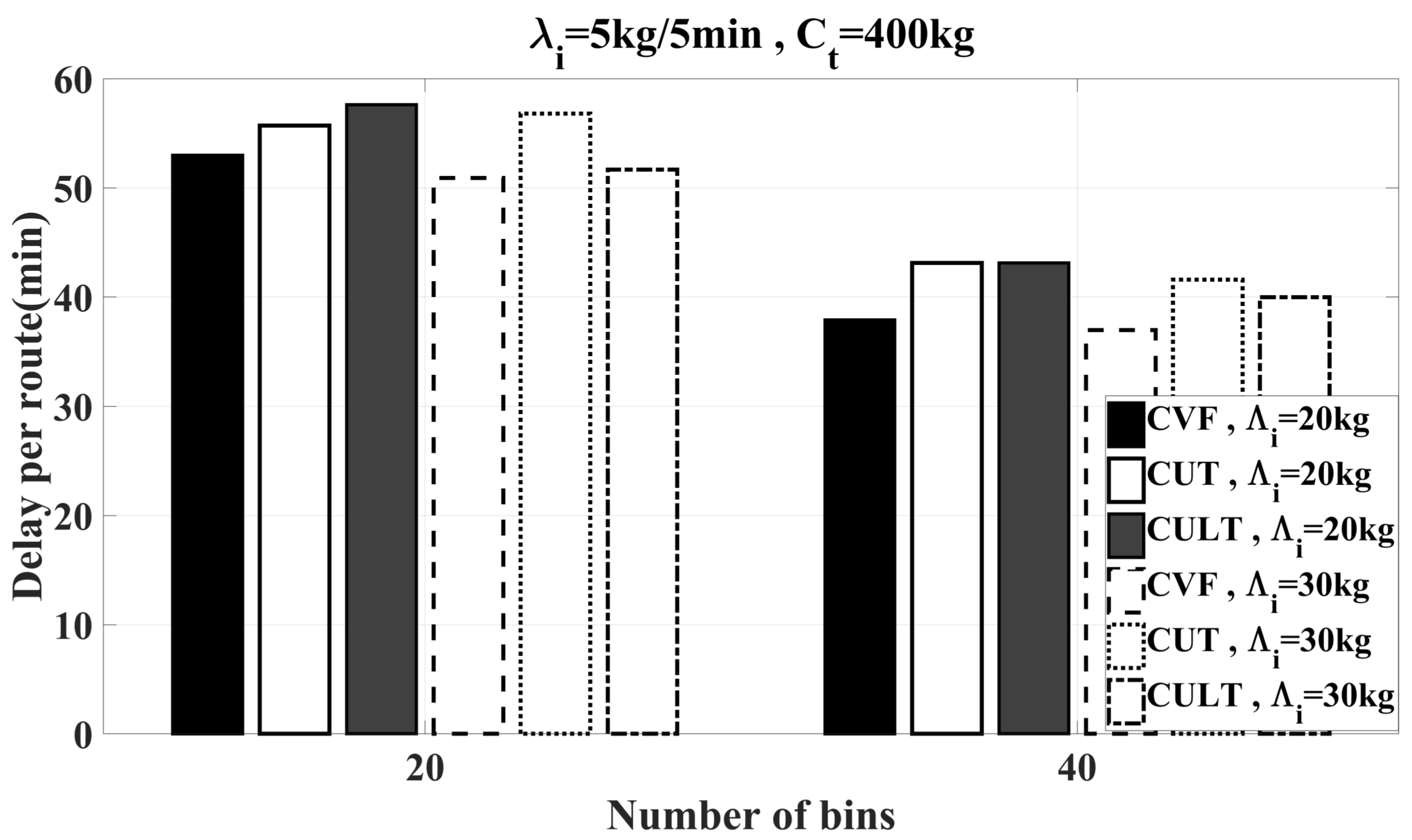
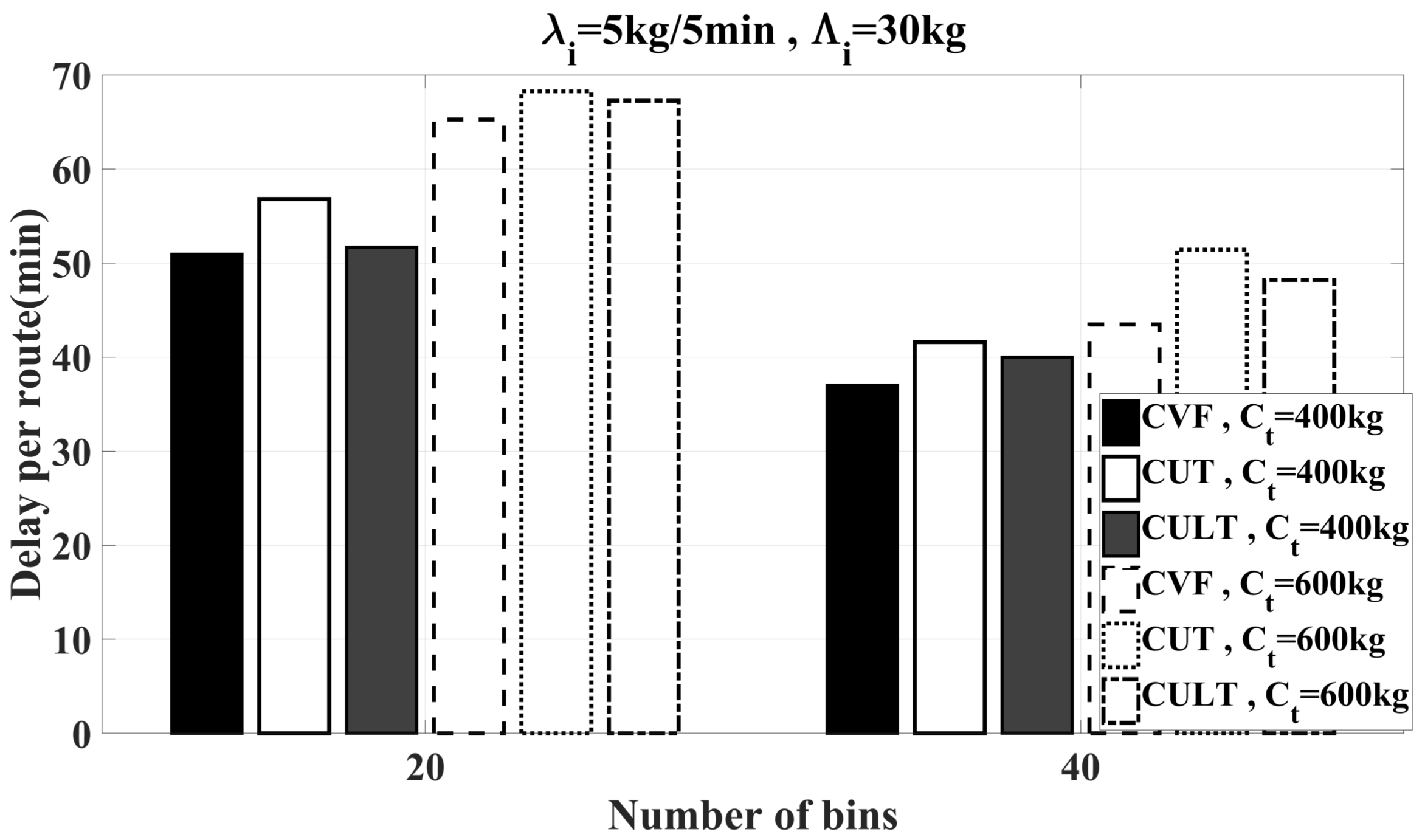
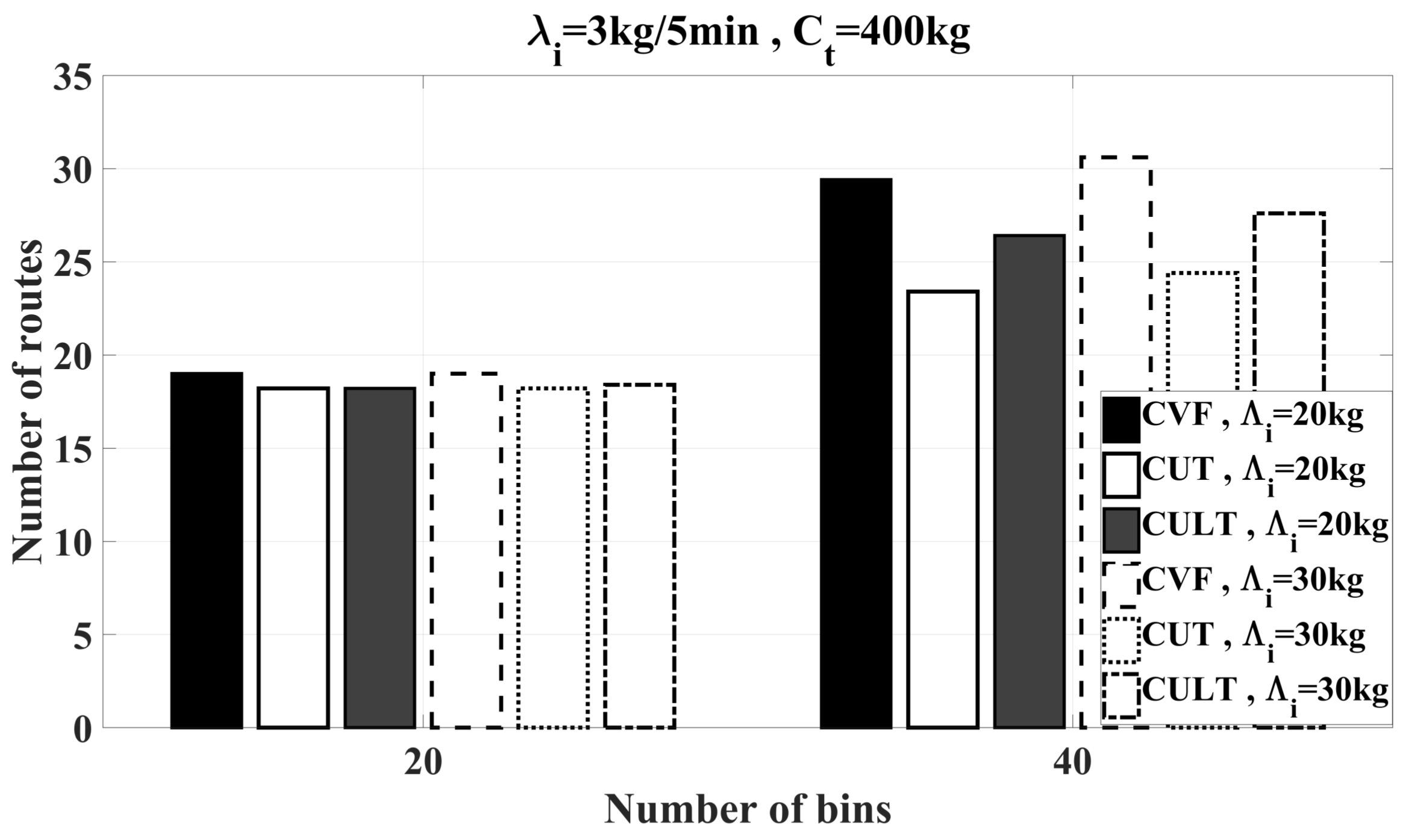
6.2. Simulation Results
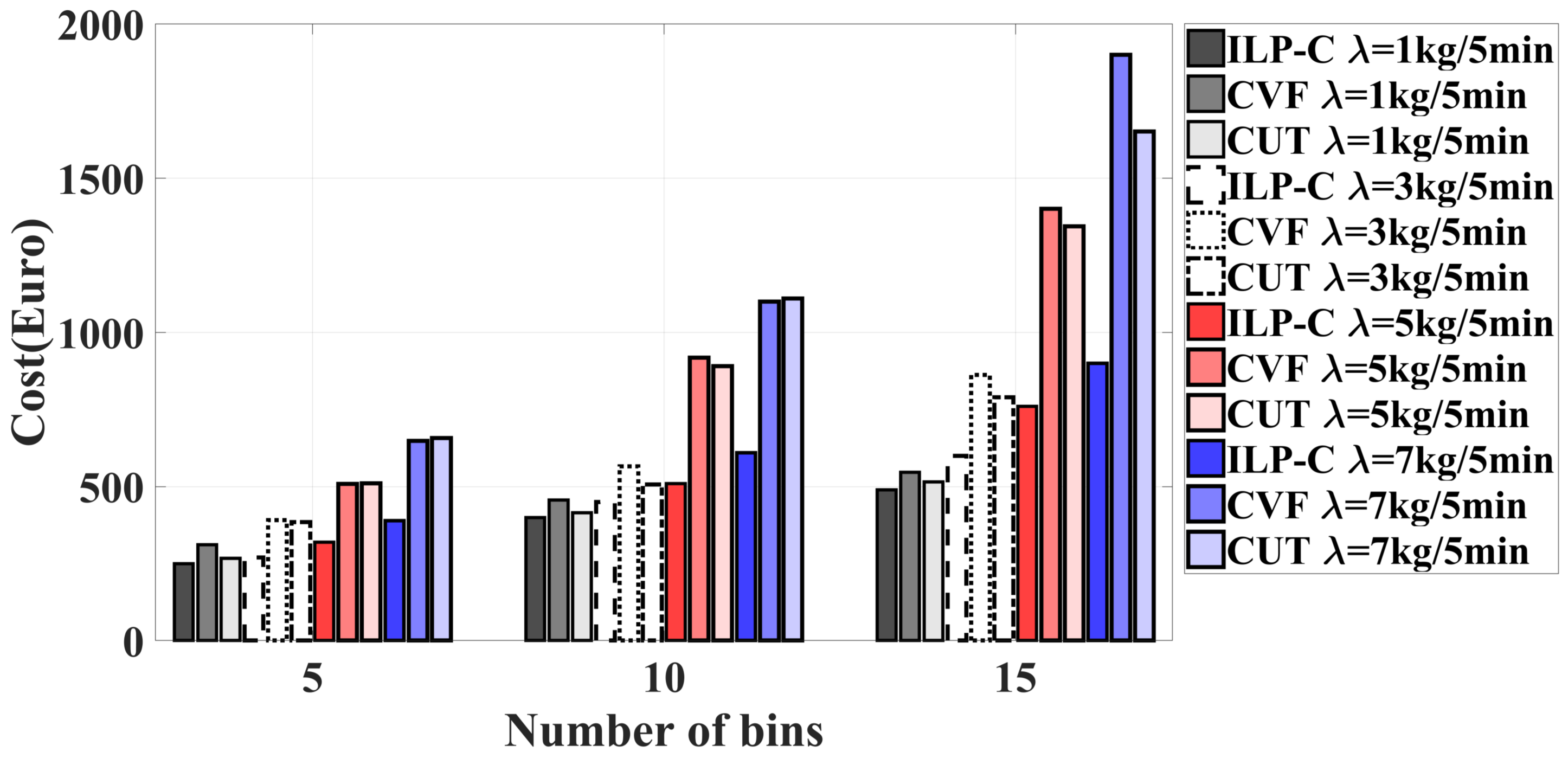
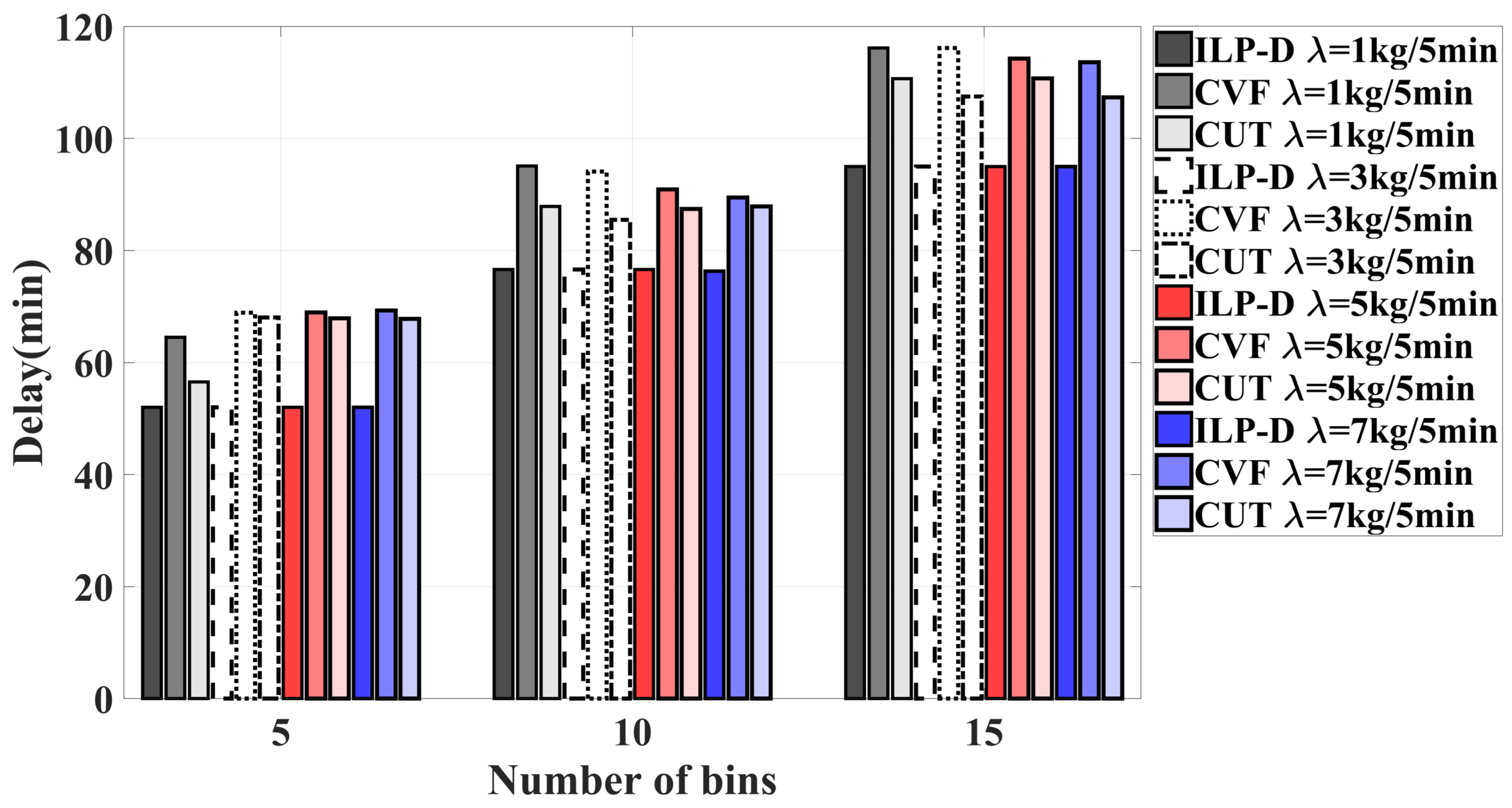
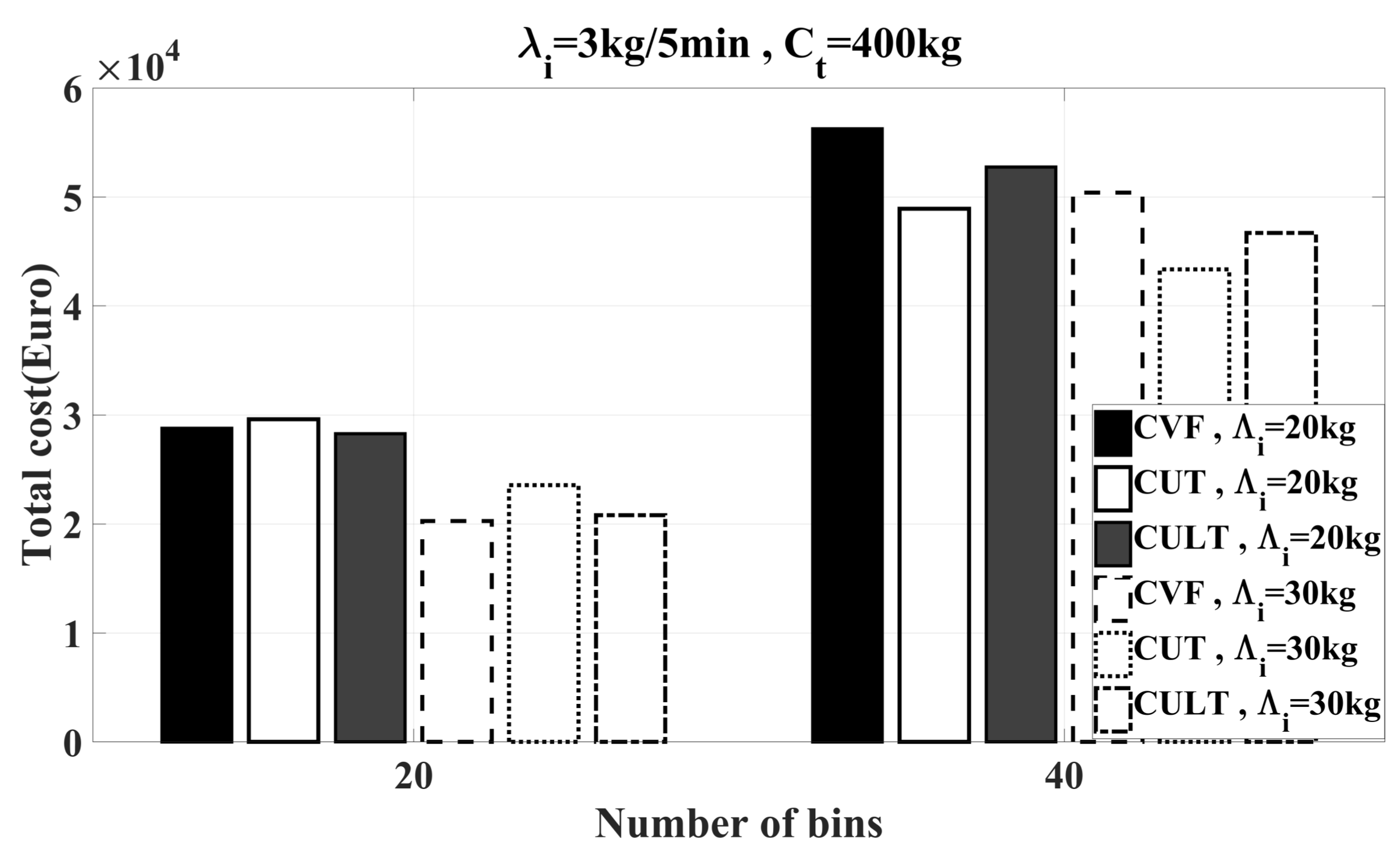
6.2.1. Optimality Assessment of the Heuristics
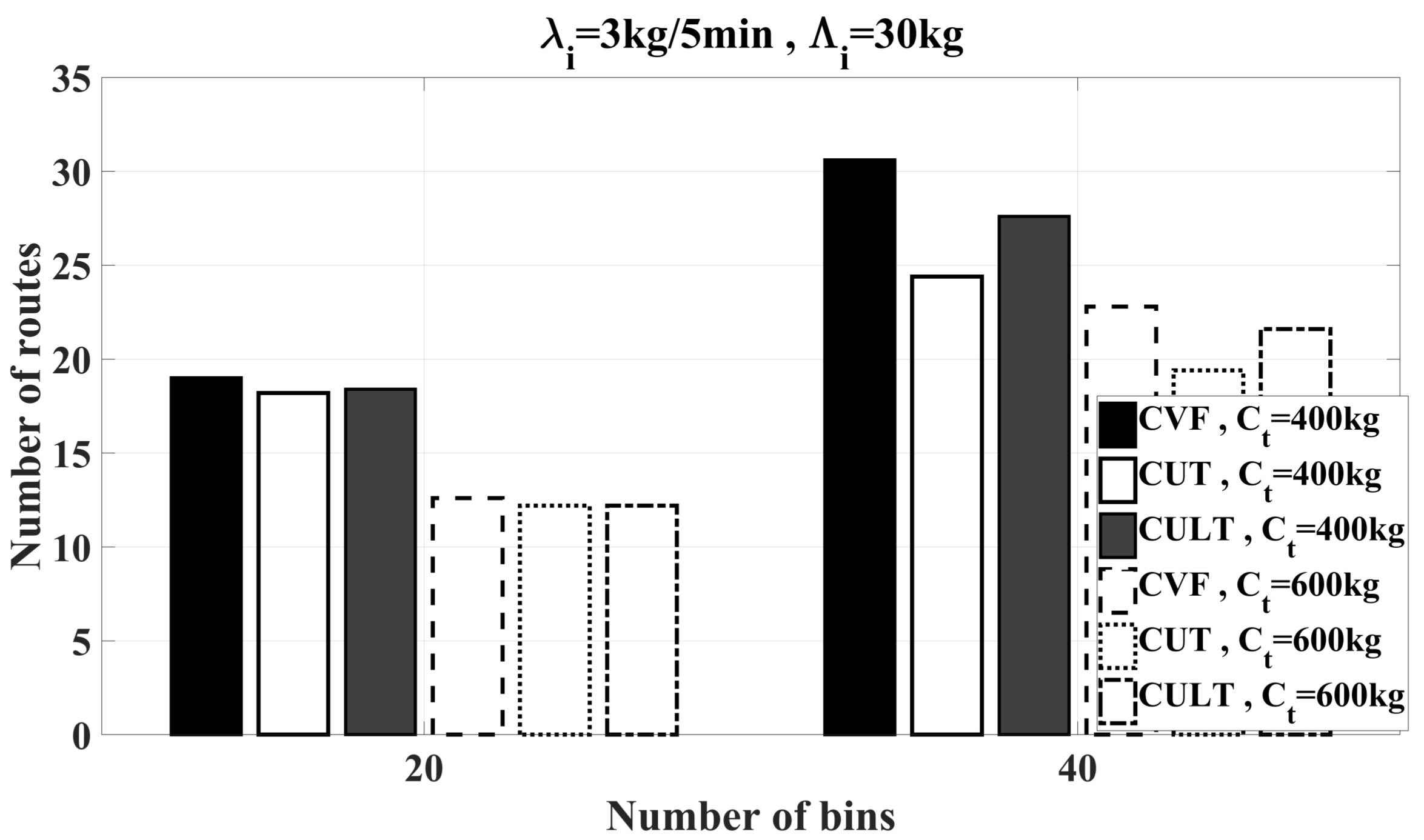
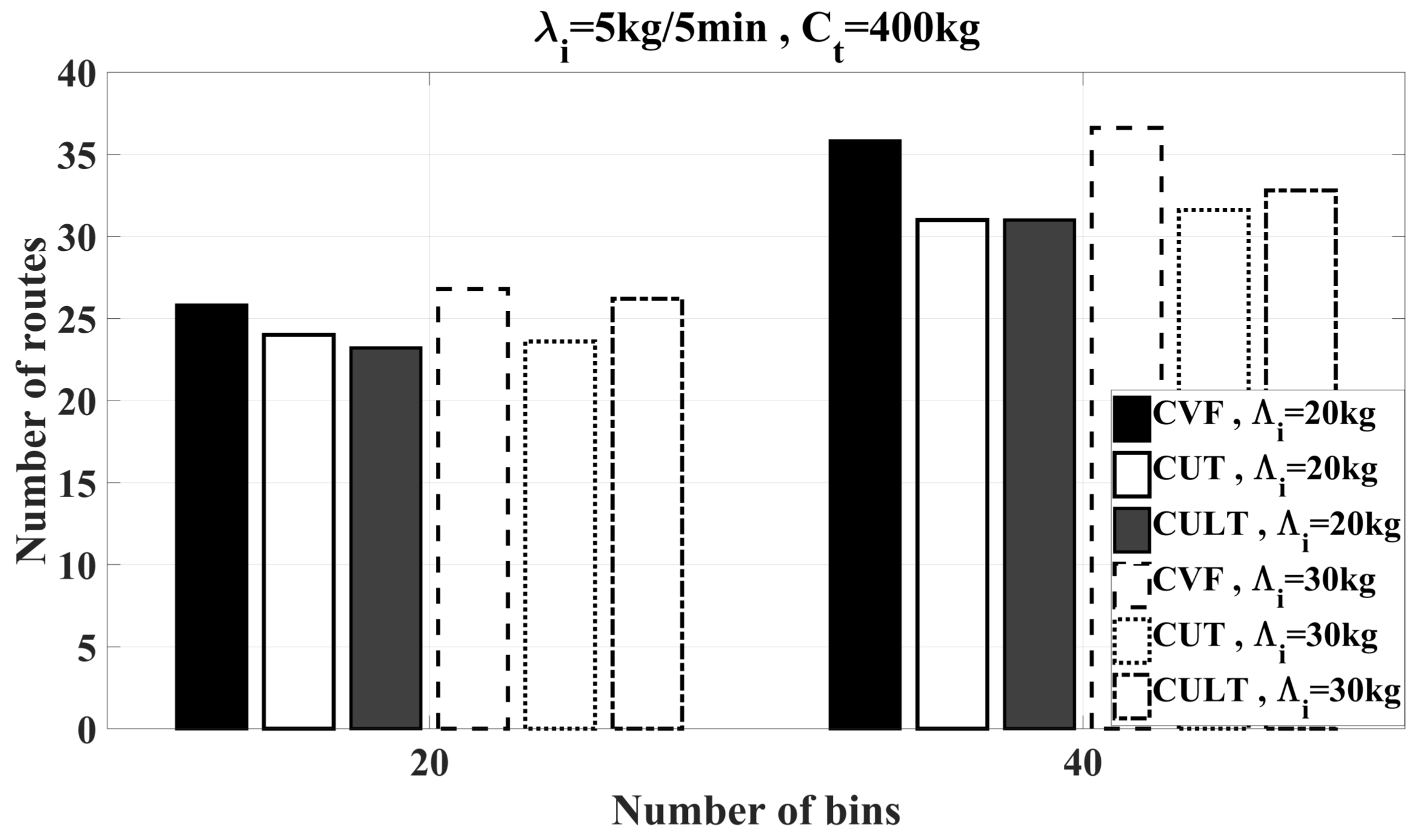
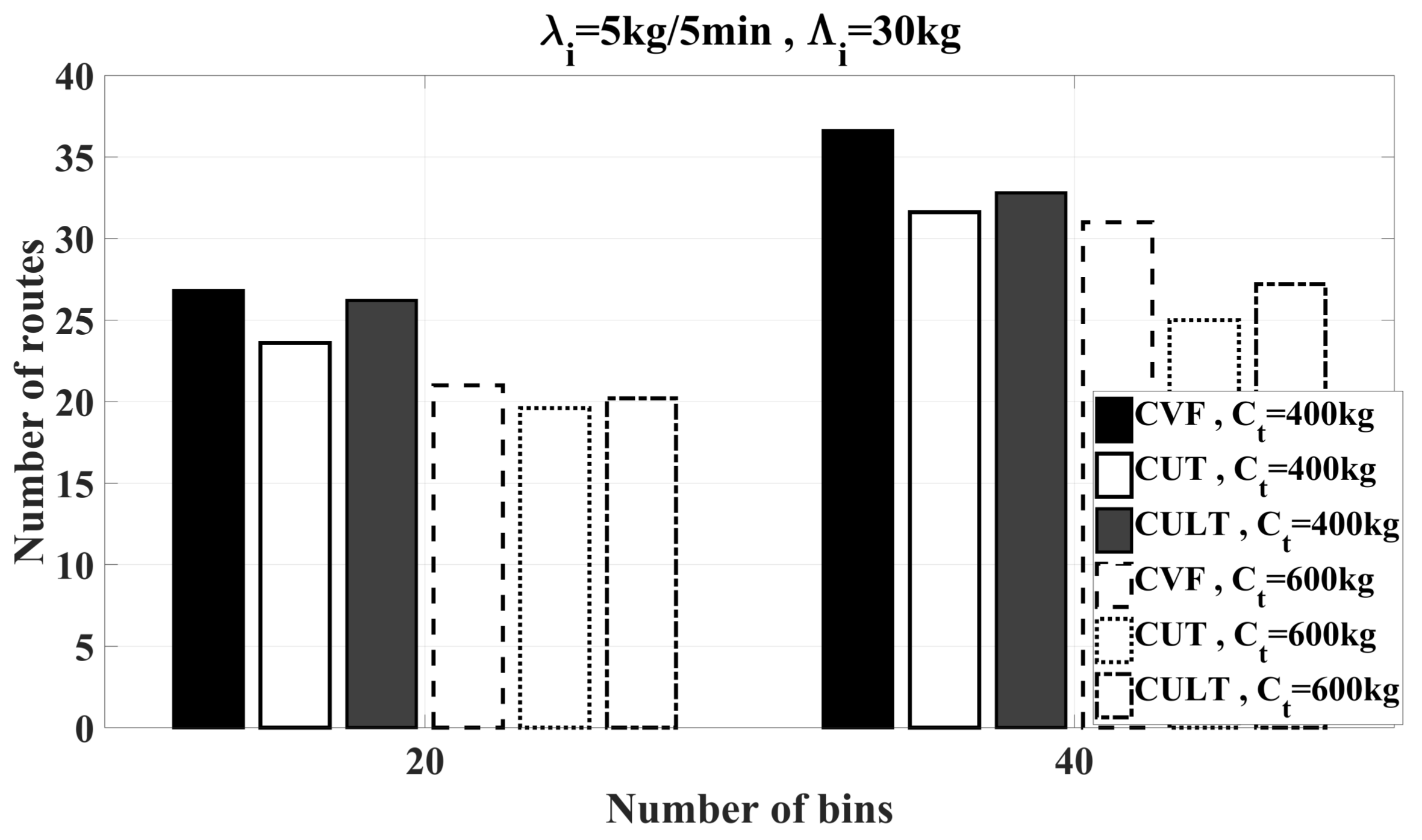
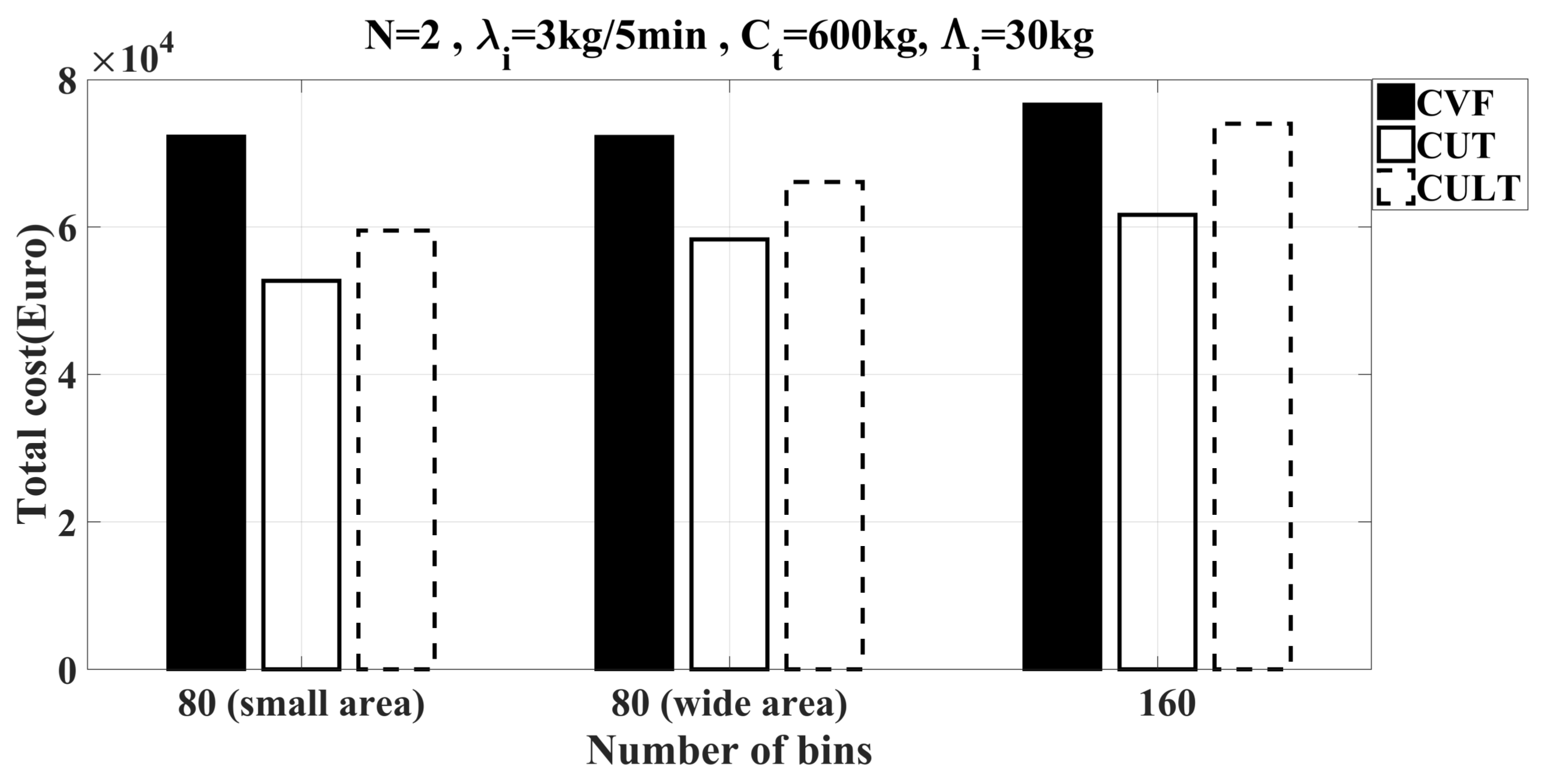
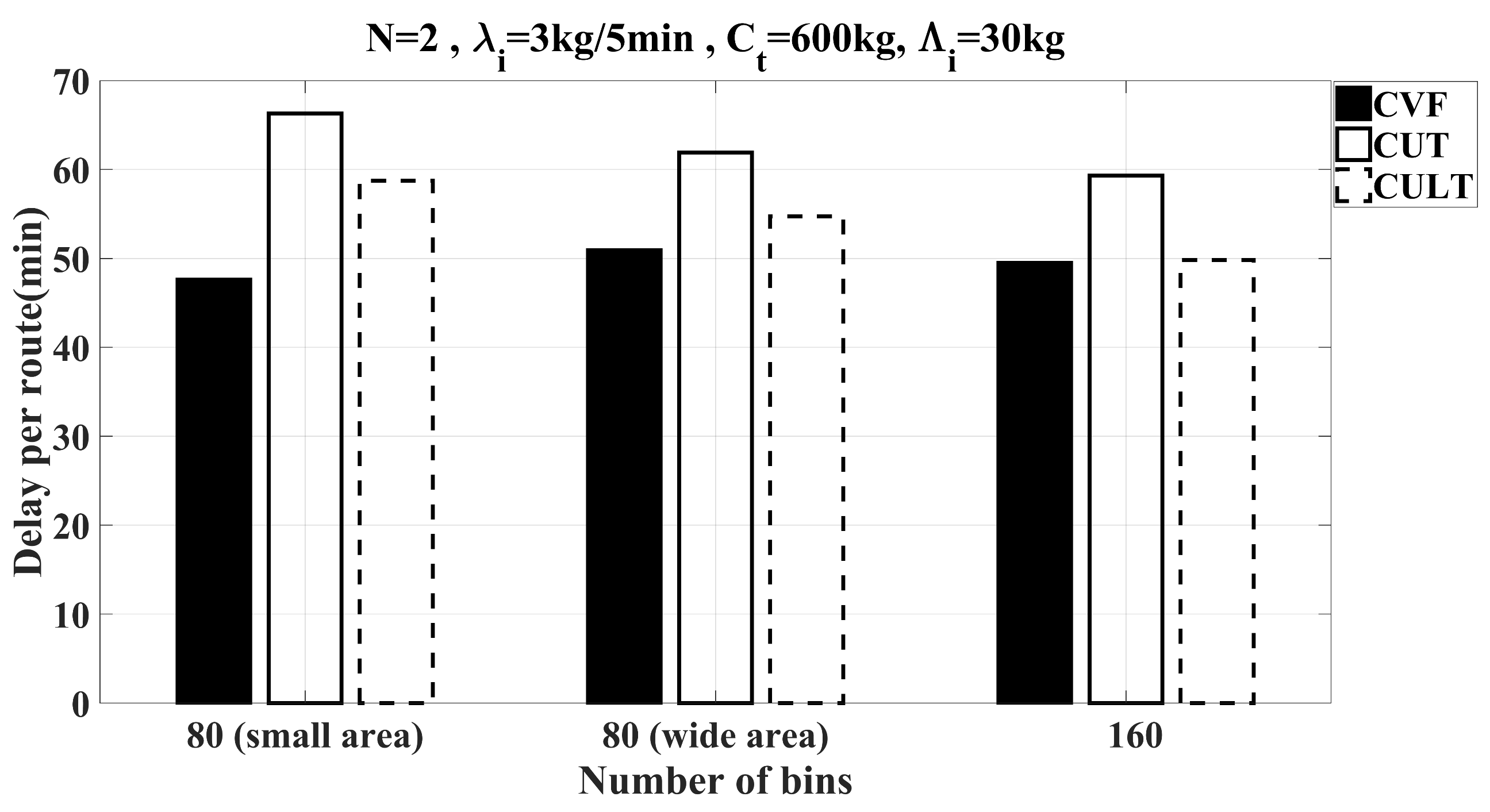
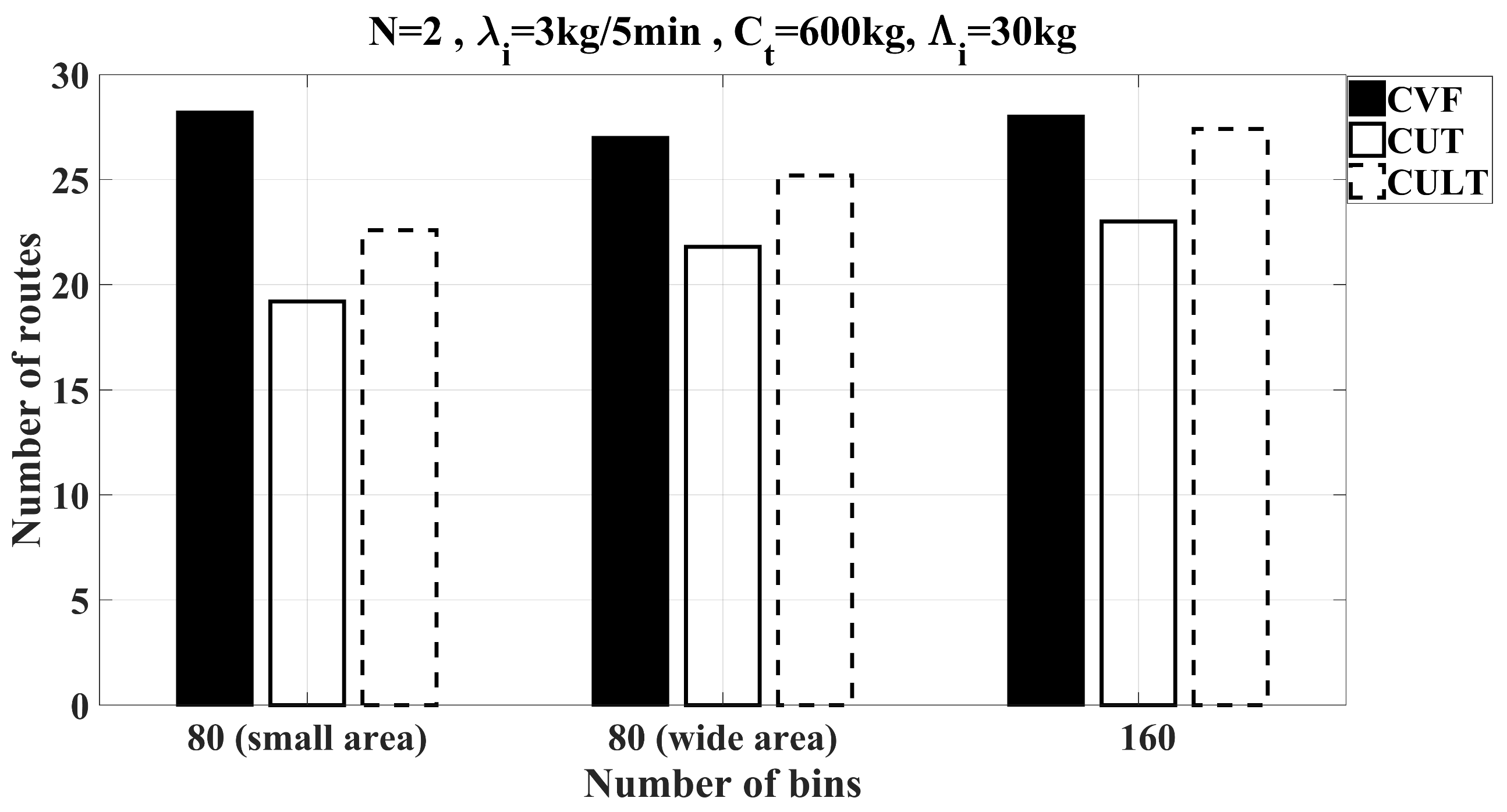
6.2.2. Feasibility Study of Heuristics
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Habibzadeh, H.; Qin, Z.; Soyata, T.; Kantarci, B. Large Scale Distributed Dedicated- and Non-Dedicated Smart City Sensing Systems. IEEE Sens. J. 2017, 17, 7649–7658. [Google Scholar] [CrossRef]
- Shyam, G.K.; Manvi, S.S.; Bharti, P. Smart waste management using Internet-of-Things (IoT). In Proceedings of the 2nd International Conference on Computing and Communications Technologies (ICCCT), Chennai, India, 23–24 February 2017; pp. 199–203. [Google Scholar]
- Habibzadeh, H.; Boggio-Dandry, A.; Qin, Z.; Soyata, T.; Kantarci, B.; Mouftah, H.T. Soft Sensing in Smart Cities: Handling 3Vs Using Recommender Systems, Machine Intelligence, and Data Analytics. IEEE Commun. Mag. 2018, 56, 78–86. [Google Scholar] [CrossRef]
- Page, A.; Hijazi, S.; Askan, D.; Kantarci, B.; Soyata, T. Research Directions in Cloud-Based Decision Support Systems for Health Monitoring Using Internet-of-Things Driven Data Acquisition. Int. J. Serv. Comput. 2016, 4, 18–34. [Google Scholar]
- Pouryazdan, M.; Kantarci, B.; Soyata, T.; Song, H. Anchor-Assisted and Vote-Based Trustworthiness Assurance in Smart City Crowdsensing. IEEE Access 2016, 4, 529–541. [Google Scholar] [CrossRef]
- Pouryazdan, M.; Kantarci, B. The Smart Citizen Factor in Trustworthy Smart City Crowdsensing. IT Prof. 2016, 18, 26–33. [Google Scholar] [CrossRef]
- Hijazi, S.; Page, A.; Kantarci, B.; Soyata, T. Machine Learning in Cardiac Health Monitoring and Decision Support. IEEE Comput. 2016, 49, 38–48. [Google Scholar] [CrossRef]
- Silva, B.N.; Khan, M.; Han, K. Towards sustainable smart cities: A review of trends, architectures, components, and open challenges in smart cities. Sustain. Cities Soc. 2018, 38, 697–713. [Google Scholar] [CrossRef]
- Atzori, L.; Iera, A.; Morabito, G. Understanding the Internet of Things: Definition, potentials, and societal role of a fast evolving paradigm. Ad Hoc Netw. 2017, 56, 122–140. [Google Scholar] [CrossRef]
- Strzelecka, A.; Ulanicki, B.; Koop, S.; Koetsier, L.; van Leeuwen, K.; Elelman, R. Integrating Water, Waste, Energy, Transport and ICT Aspects into the Smart City Concept. Procedia Eng. 2017, 186, 609–616. [Google Scholar] [CrossRef]
- Gruler, A.; Quintero-Araújo, C.L.; Calvet, L.; Juan, A.A. Waste collection under uncertainty: A simheuristic based on variable neighbourhood search. Eur. J. Ind. Eng. 2017, 11, 228–255. [Google Scholar] [CrossRef]
- Aazam, M.; St-Hilaire, M.; Lung, C.H.; Lambadaris, I. Cloud-based smart waste management for smart cities. In Proceedings of the IEEE 21st International Workshop on Computer Aided Modelling and Design of Communication Links and Networks (CAMAD), Toronto, ON, Canada, 23–25 October 2016; pp. 188–193. [Google Scholar]
- Coban, A.; Ertis, I.F.; Cavdaroglu, N.A. Municipal solid waste management via multi-criteria decision making methods: A case study in Istanbul, Turkey. J. Clean. Prod. 2018, 180, 159–167. [Google Scholar] [CrossRef]
- Minghua, Z.; Xiumin, F.; Rovetta, A.; Qichang, H.; Vicentini, F.; Bingkai, L.; Giusti, A.; Yi, L. Municipal solid waste management in Pudong New Area, China. Waste Manag. 2009, 29, 1227–1233. [Google Scholar] [CrossRef] [PubMed]
- Fussa, M.; Barros, R.T.V.; Poganietz, W.R. Designing a framework for municipal solid waste managementtowards sustainability in emerging economy countries—An application to a case study in Belo Horizonte (Brazil). J. Clean. Prod. 2018, 178, 655–664. [Google Scholar] [CrossRef]
- Ikhlayel, M. Development of management systems for sustainable municipal solid waste in developing countries: A systematic life cycle thinking approach. J. Clean. Prod. 2018, 180, 571–586. [Google Scholar] [CrossRef]
- Guerrero, L.A.; Maas, G.; Hogland, W. Solid waste management challenges for cities in developing countries. Waste Manag. 2013, 33, 220–232. [Google Scholar] [CrossRef] [PubMed]
- Marshall, R.E.; Farahbakhsh, K. Systems approaches to integrated solid waste management in developing countries. Waste Manag. 2013, 33, 988–1003. [Google Scholar] [CrossRef] [PubMed]
- Henry, R.K.; Yongsheng, Z.; Jun, D. Municipal solid waste management challenges in developing countries—Kenyan case study. Waste Manag. 2006, 26, 92–100. [Google Scholar] [CrossRef] [PubMed]
- Anagnostopoulos, T.; Kolomvatsos, K.; Anagnostopoulos, C.; Zaslavsky, A.; Hadjiefthymiades, S. Assessing dynamic models for high priority waste collection in smart cities. J. Syst. Softw. 2015, 110, 178–192. [Google Scholar] [CrossRef]
- Manqele, L.; Adeogun, R.; Dlodlo, M.; Coetzee, L. Multi-objective decision-making framework for effective waste collection in smart cities. In Proceedings of the Global Wireless Summit (GWS), Cape Town, South Africa, 15–18 October 2017; pp. 155–159. [Google Scholar]
- UNEP—United Nations Environment Programme. Municipal Solid Waste: Is it Garbage or Gold? 2013. Available online: https://na.unep.net/geas/getUNEPPageWithArticleIDScript.php?article_id=105 (accessed on 10 March 2018).
- Johansson, O.M. The effect of dynamic scheduling and routing in a solid waste management system. Waste Manag. 2006, 26, 875–885. [Google Scholar] [CrossRef] [PubMed]
- Jouhara, H.; Czajczyńska, D.; Ghazal, H.; Krzyzynska, R.; Anguilano, L.; Reynolds, A.; Spencer, N. Municipal waste management systems for domestic use. Energy 2017, 139, 485–506. [Google Scholar] [CrossRef]
- Nuortioa, T.; Kytöjoki, J.; Niskaa, H.; Braysy, O. Improved route planning and scheduling of waste collection and transport. Expert Syst. Appl. 2006, 30, 223–232. [Google Scholar] [CrossRef]
- Arebey, M.; Hannan, M.; Begum, R.; Basri, H. Solid waste bin level detection using gray level co-occurrence matrix feature extraction approach. J. Environ. Manag. 2012, 104, 9–18. [Google Scholar] [CrossRef] [PubMed]
- Chenga, S.; Chanb, C.; Huang, G. An integrated multi-criteria decision analysis and inexact mixed integer linear programming approach for solid waste management. Eng. Appl. Artif. Intell. 2006, 16, 543–554. [Google Scholar] [CrossRef]
- Mamun, M.A.A.; Hannan, M.A.; Hussain, A.; Basri, H. Theoretical model and implementation of a real time intelligent bin status monitoring system using rule based decision algorithms. Expert Syst. Appl. 2016, 48, 76–88. [Google Scholar] [CrossRef]
- Apaydin, O. Route optimization for solid waste collection: Trabzon (Turkey) case study. Glob. NEST J. 2007, 9, 6–11. [Google Scholar]
- Ramos, T.R.P.; de Morais, C.S.; Barbosa-Póvoa, A.P. The smart waste collection routing problem: Alternative operational management approaches. Expert Syst. Appl. 2018, 103, 146–158. [Google Scholar] [CrossRef]
- Ramson, S.J.; Moni, D.J. Wireless sensor networks based smart bin. Comput. Electr. Eng. 2017, 64, 337–353. [Google Scholar] [CrossRef]
- Data analytics approach to create waste generation profiles for waste management and collection. Waste Manag. 2018, 77, 477–485.
- MATLAB Optimization Toolbox, version 8.0 (MATLAB R2017b). Available online: https://www.mathworks.com/products/optimization.html (accessed on 10 March 2018).
| Notations | Equations | Sections | Definition |
|---|---|---|---|
| D | 2; 43 | 4.1; 5.1 | Cost of (un)dumping per bin (from a bin to a truck) (€) |
| H | 2; 43 | 4.1; 5.1 | Cost of human resource (€)/h |
| G | 2; 43 | 4.1; 5.1 | Cost of gas mileage (€)/km |
| S | 6; 26; 47 | 4.1; 4.2; 5.1 | Average speed in the town (km/h) |
| W | 2; 26 | 4.1; 4.2 | Time needed to collect waste from a bin (minutes) |
| N | 2 | 4.1 | Total number of trucks |
| M | 2; 13; 36; 43 | 4.1; 4.2; 5.1 | Total number of bins |
| 21; 38 | 4.1; 4.2 | The upper bound of variable | |
| - | 5 | Upper threshold for the waste amount of bin i | |
| - | 5 | Lower threshold for the waste amount of bin i | |
| 2; 43 | 4.1; 5.1 | Penalty of bin i per kg (€) | |
| 6; 26; 47 | 4.1; 4.2; 5.1 | Time needed to empty truck t at the dumping area and prepare it for the next trip (minutes) | |
| ℏ | 5; 26; 47 | 4.1; 4.2; 5.1 | Distance from the dumping area to the central station (meters) |
| 5 | 4.1 | Distance between bin i and bin j (meters) | |
| 20; 26 | 4.1; 4.2 | Time needed to move from bin i to bin j (minutes) | |
| 8; 32 | 4.1; 4.2 | Distance from bin i to the dumping area (meters) | |
| 7; 33 | 4.1; 4.2 | Distance from the central station to bin i (meters) | |
| 17; 23; 37 | 4.1; 4.2 | Average waste arrival at bin i (kg) | |
| 2; 43 | 4.1; 5.1 | Number of workers in truck t | |
| 2; 43 | 4.1; 5.1 | Capacity of bin i (kg) | |
| 17; 37 | 4.1; 4.2 | Initial load for bin i (kg) | |
| 17; 37 | 4.1; 4.2 | Capacity of truck t (kg) | |
| 20 | 4.1 | Time from the central station to first bin i (minutes) | |
| - | 5 | Initial load of truck t (kg) | |
| K | - | 5 | Threshold for the count of bins that have alarmed |
| k | - | 5 | Number of bins that have alarmed |
| - | 5 | Alarm status of bin i | |
| B | - | 5 | List of bins that have alarmed |
| - | 5 | Route of truck t | |
| - | 5 | List of bins on the shortest path between bin i and j | |
| 7–21; 27–29; 31–38 | 4.1; 4.2 | The binary variable is one if bin i is the n-th collected bin by truck t | |
| 5; 9; 10; 11; 16; 26–30 | 4.1; 4.2 | The binary variable defines the multiplication of | |
| 17; 18; 19; 37; 38; 39 | 4.1; 4.2 | The integer variable defines the multiplication of by | |
| 20; 21; 22; 23 | 4.1 | The integer variable defines the multiplication of by | |
| 2; 3; 5; 6; 44 | 4.1; 5.1 | The integer variable defines the total distance covered by truck t (meters) | |
| d | 2; 3; 43; 44 | 4.1; 5.1 | The integer variable defines the total distance covered by Ntrucks (meters) |
| 2; 47 | 4.1; 4.2; 5.1 | The integer variable defines the distance from the central station to first bin of truck t (meters) | |
| 2; 47 | 4.1; 4.2; 5.1 | The integer variable defines the distance from last bin of truck t to the dumping area (meters) | |
| 4; 6 | 4.1 | The integer variable defines the total time of truck t (minutes) | |
| 2; 4; 43; 45 | 4.1; 5.1 | The integer variable defines the total time of the Ntrucks (minutes) | |
| 15; 16; 30; 34; 45 | 4.1; 4.2; 5.1 | The integer variable defines the total number of bins collected by truck t | |
| 2; 23; 43 | 4.1; 5.1 | The integer variable defines the final load of bin i (kg) | |
| 18; 20; 21; 23; 38–41 | 4.1; 4.2 | The integer variable defines the pick up time of bin i (minutes) | |
| - | 5 | List of visited bins by truck t |
| Notations | Value |
|---|---|
| Cost of emptying bin (D) | 1.62 €/bin |
| Cost of human resource (H) | 39 €/h |
| Cost of gas mileage (G) | 20 €/km |
| Average speed in the town (S) | 20 km/h |
| Time needed to collect waste from a bin (W) | 2.5 min |
| Total number of trucks (N) | 2 |
| Total number of bins (M) | {5, 10, 15, 20, 40, 80, 160} |
| The upper bound of variable () | 10 |
| The upper threshold for the waste amount of bin i () | [10–15] kg |
| The lower threshold for the waste amount of bin i () | [5–8] kg |
| Penalty of the overflowed bin () | 5 €/kg |
| Time needed to empty truck t at the dumping area and prepare it for the next trip () | 12 min |
| Distance from the dumping area to the central station (ℏ) | 2500 m |
| Distance between bin i and bin j () | [200–2300] m |
| Time needed to move from bin i to bin j () | [0.6–6.9] min |
| Distance from bin i to the dumping area () | [400–2300] m |
| Distance from the central station to bin i () | [200–2300] m |
| Average waste arrival rate at a bin () | {1, 3, 5, 7} kg/5 min |
| Number of workers in a truck () | 3 |
| Maximum capacity of a bin () | {20, 30} kg |
| Initial load for bin i () | [0–30] kg |
| Maximum capacity of a truck () | {400, 600} kg |
| Time from the central station to the first bin i () | [0.6–6.9] min |
| Initial load of a truck t () | [0–600] kg |
| Threshold for the count of bins that have alarmed (K) | {1,2,3} |
| Number of bins that have alarmed (k) | [0–160] |
| Alarm status of bin i () | {On, Off} |
| Method | Bin Count | Bin Capacity (kg) | Truck Capacity (kg) | Cost (€) | Delay per Route | No. of Routes |
|---|---|---|---|---|---|---|
| 20 | 20 | 400 | 5354.16 | 193.78 | 5.8 | |
| 20 | 20 | 400 | 6246.67 | 205.16 | 6 | |
| 20 | 20 | 400 | 5542.85 | 199.41 | 5.8 | |
| 20 | 30 | 400 | 4343.99 | 155.17 | 5.8 | |
| 20 | 30 | 400 | 4953.32 | 187.85 | 5.6 | |
| 20 | 30 | 400 | 4229.57 | 143.68 | 6.2 | |
| 20 | 30 | 600 | 4189.10 | 305.8 | 2.8 | |
| 20 | 30 | 600 | 4936.05 | 345.12 | 3 | |
| 20 | 30 | 600 | 4134.74 | 330.23 | 2.6 | |
| 40 | 20 | 400 | 11,188.28 | 109.36 | 12 | |
| 40 | 20 | 400 | 14,950.88 | 126.79 | 10 | |
| 40 | 20 | 400 | 11,801.55 | 112.27 | 11.6 | |
| 40 | 30 | 400 | 5926.93 | 104.85 | 12 | |
| 40 | 30 | 400 | 11,722.18 | 116.95 | 10.4 | |
| 40 | 30 | 400 | 6634.55 | 104.22 | 12 | |
| 40 | 30 | 600 | 5665.45 | 158.35 | 8 | |
| 40 | 30 | 600 | 11,579.94 | 17,726 | 7 | |
| 40 | 30 | 600 | 6066.07 | 157.86 | 8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Omara, A.; Gulen, D.; Kantarci, B.; Oktug, S.F. Trajectory-Assisted Municipal Agent Mobility: A Sensor-Driven Smart Waste Management System. J. Sens. Actuator Netw. 2018, 7, 29. https://doi.org/10.3390/jsan7030029
Omara A, Gulen D, Kantarci B, Oktug SF. Trajectory-Assisted Municipal Agent Mobility: A Sensor-Driven Smart Waste Management System. Journal of Sensor and Actuator Networks. 2018; 7(3):29. https://doi.org/10.3390/jsan7030029
Chicago/Turabian StyleOmara, Ahmed, Damla Gulen, Burak Kantarci, and Sema F. Oktug. 2018. "Trajectory-Assisted Municipal Agent Mobility: A Sensor-Driven Smart Waste Management System" Journal of Sensor and Actuator Networks 7, no. 3: 29. https://doi.org/10.3390/jsan7030029
APA StyleOmara, A., Gulen, D., Kantarci, B., & Oktug, S. F. (2018). Trajectory-Assisted Municipal Agent Mobility: A Sensor-Driven Smart Waste Management System. Journal of Sensor and Actuator Networks, 7(3), 29. https://doi.org/10.3390/jsan7030029







