Figure 1.
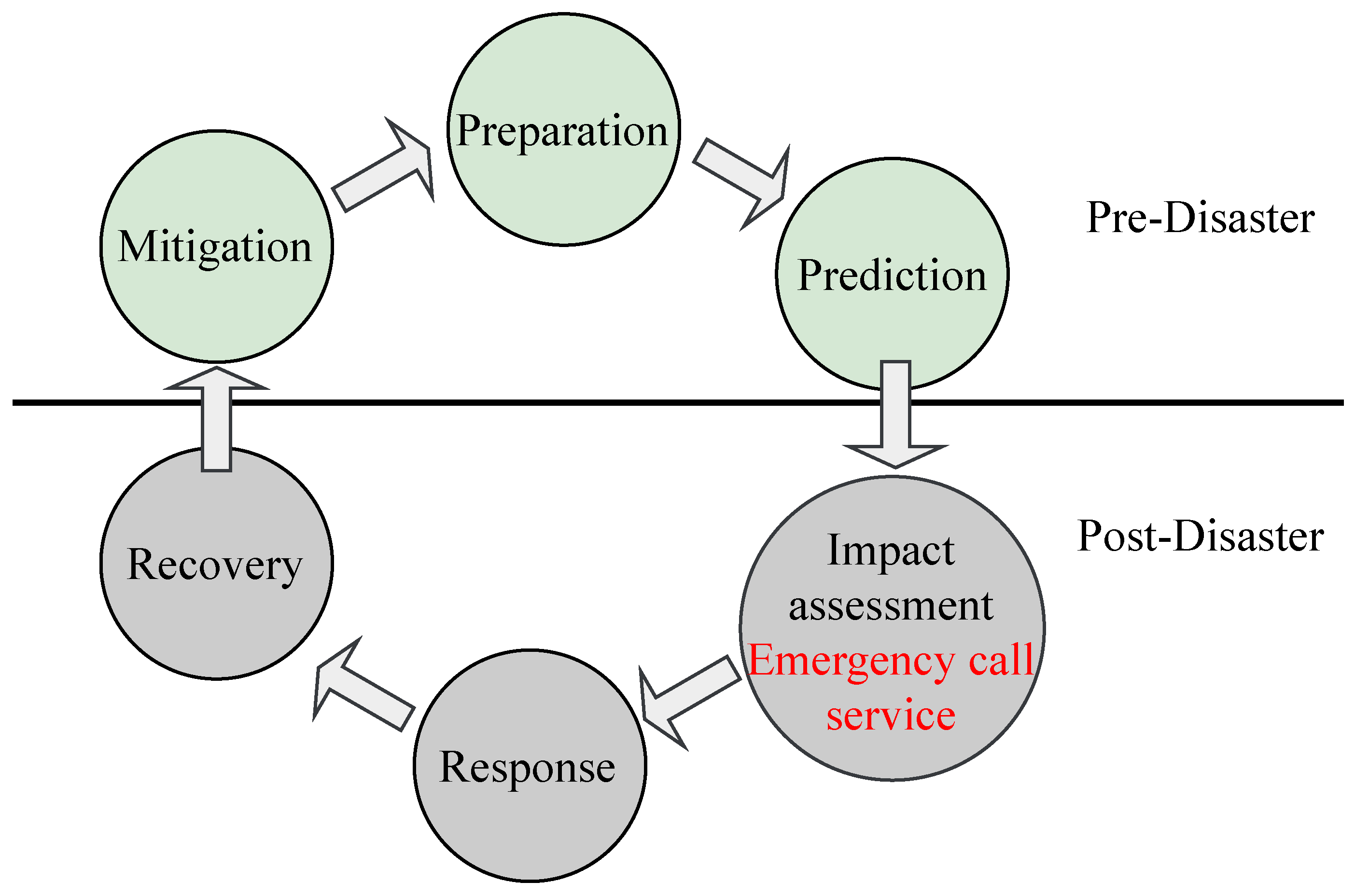
The phases of disaster management cycle during pre-disaster and post-disaster stages.
Figure 1.
The phases of disaster management cycle during pre-disaster and post-disaster stages.
Figure 2.
Evolution of the 3GPP specifications for missions critical/emergency scenarios using proximity-based services under each release from 11–17.
Figure 2.
Evolution of the 3GPP specifications for missions critical/emergency scenarios using proximity-based services under each release from 11–17.
Figure 3.
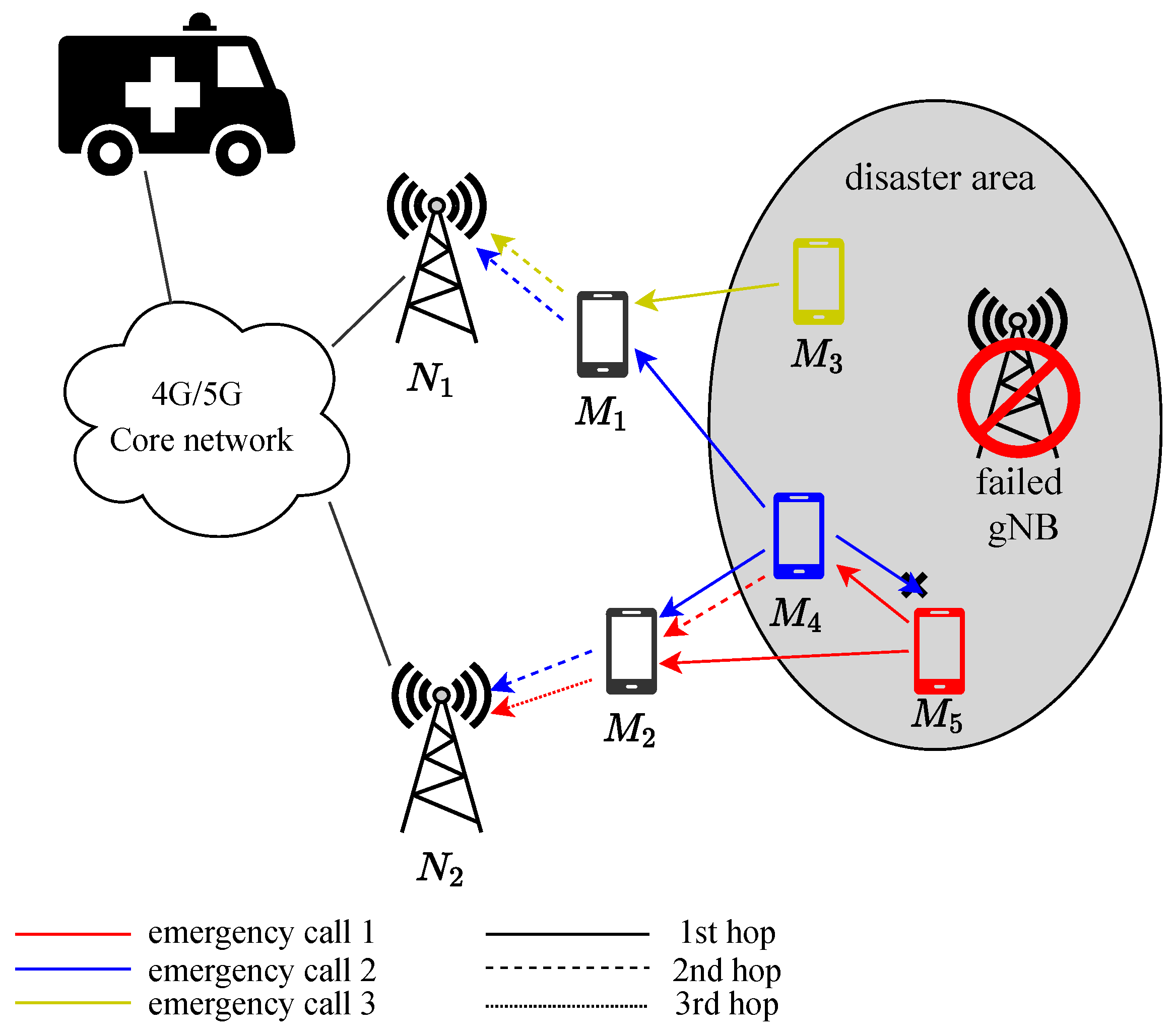
The proposed emergency call service architecture. Emergency UEs in the disaster area forward their calls in the direction of the functioning gNBs via relay UEs in the neighborhood. Distinct emergency calls generated by each emergency UE are represented by the color of the arrow. Solid lines indicate the D2D communication mode, while dashed lines indicate the classical communication between gNB and UE.
Figure 3.
The proposed emergency call service architecture. Emergency UEs in the disaster area forward their calls in the direction of the functioning gNBs via relay UEs in the neighborhood. Distinct emergency calls generated by each emergency UE are represented by the color of the arrow. Solid lines indicate the D2D communication mode, while dashed lines indicate the classical communication between gNB and UE.
Figure 4.
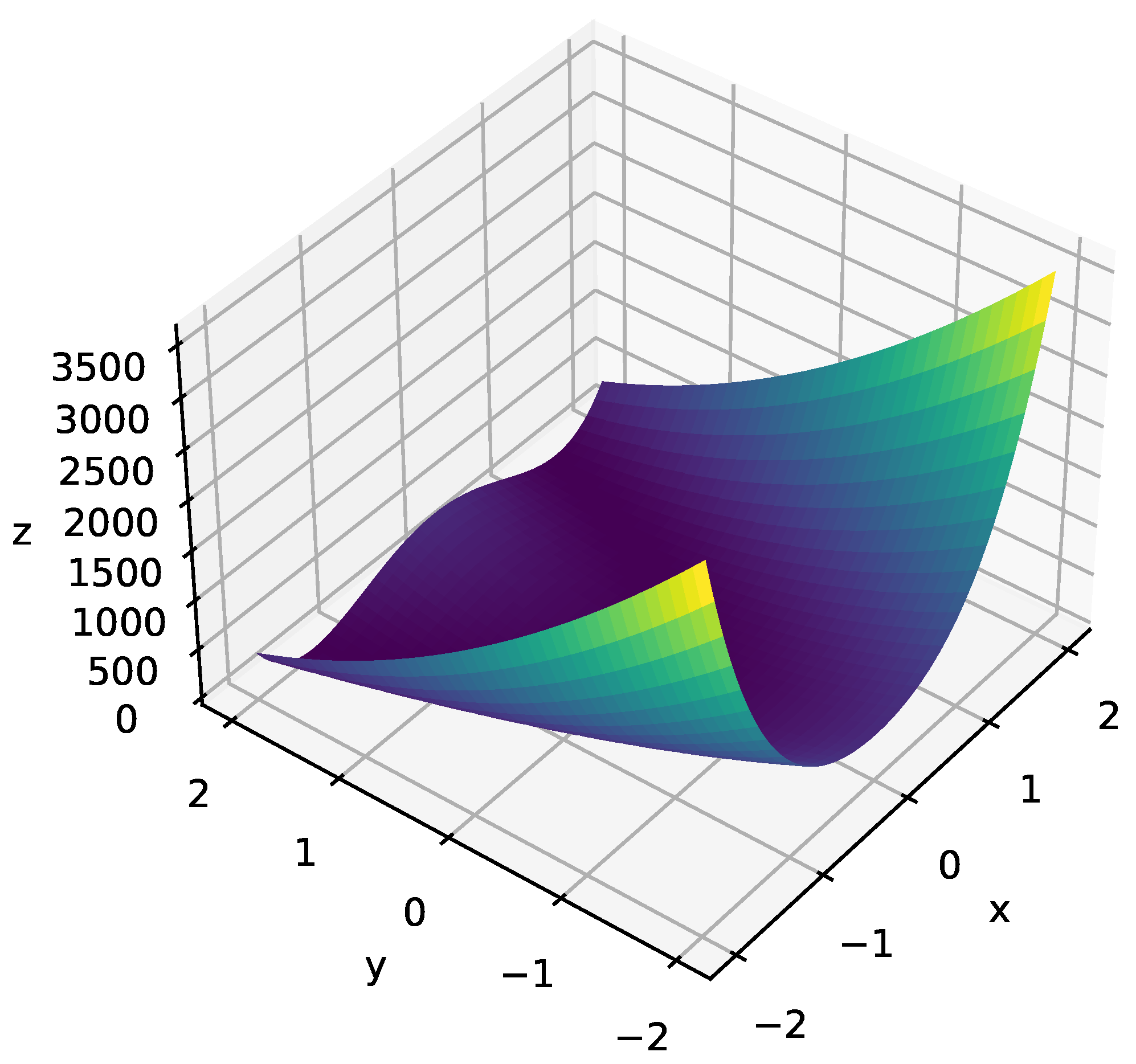
Illustration of the standard Rosenbrock function defined by two variables and given by
. Here, we assume a = 1, b = 100, and the minimum value of zero is at (1,1). The adaptive
given in (
5) is based on the Rosenbrock function.
Figure 4.
Illustration of the standard Rosenbrock function defined by two variables and given by
. Here, we assume a = 1, b = 100, and the minimum value of zero is at (1,1). The adaptive
given in (
5) is based on the Rosenbrock function.
Figure 5.
A relay UE gives higher priority for a far emergency UE than a near UE using the RSSI ratio. The RSSI ratio in (
4) is lower for a far UE than a near UE. The relay UE waits a lesser time, hence relays faster the transmissions of the far UE emergency call in the direction of a functioning gNB.
Figure 5.
A relay UE gives higher priority for a far emergency UE than a near UE using the RSSI ratio. The RSSI ratio in (
4) is lower for a far UE than a near UE. The relay UE waits a lesser time, hence relays faster the transmissions of the far UE emergency call in the direction of a functioning gNB.
Figure 6.
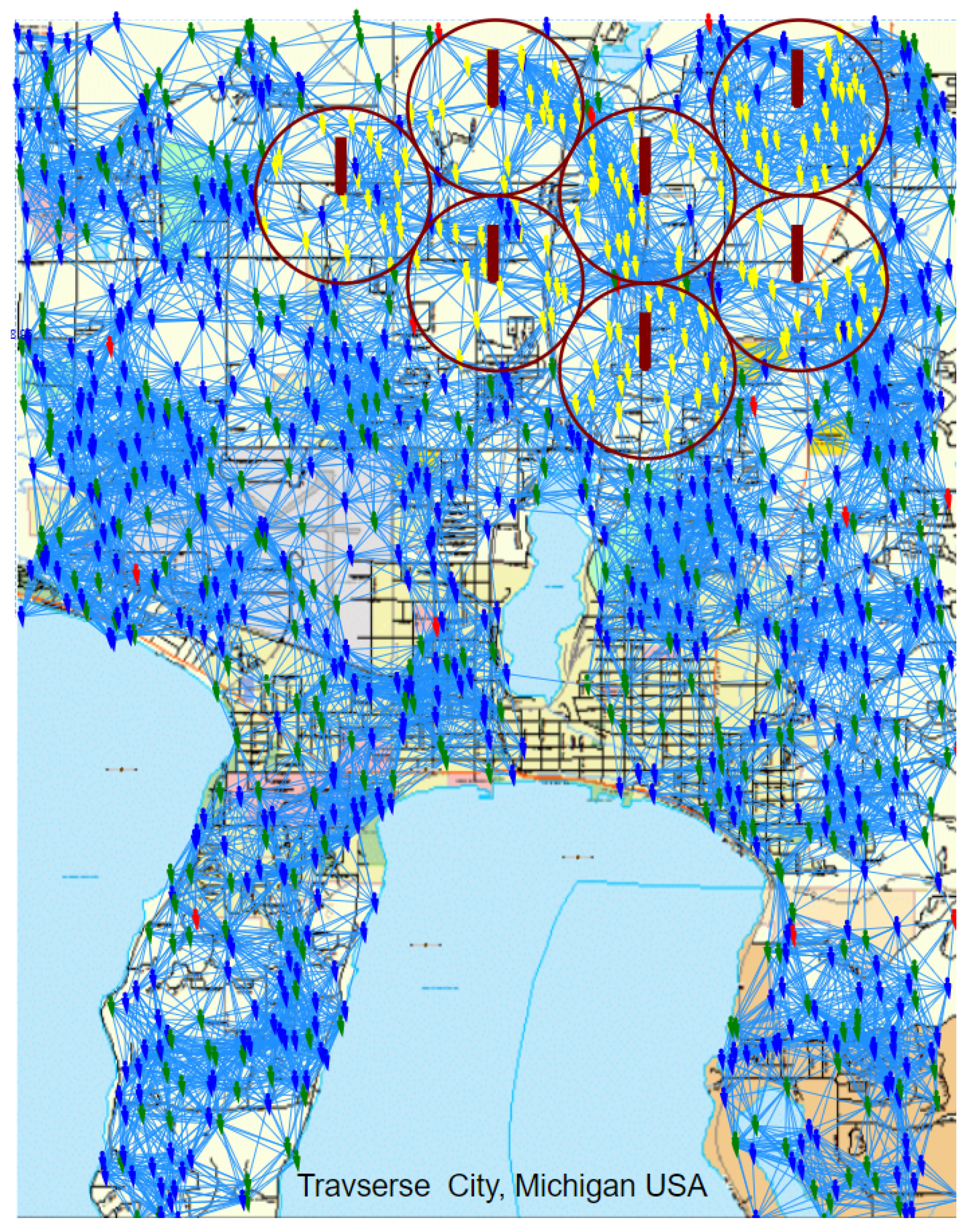
Studied scenario of the Traverse city in Michigan, USA, with 7 gNBs and 15,000 randomly distributed UEs in the AnyLogic® software. Linked UEs (resp. UE-to-gNB links) represent D2D (resp. traditional) communication possibilities. Dark Red circles represent the gNBs’ covering areas in which the gNBs are at the center. Victim (emergency) devices, relay devices, in-coverage devices, and idle devices are represented respectively by the colors, red, green, yellow, and blue.
Figure 6.
Studied scenario of the Traverse city in Michigan, USA, with 7 gNBs and 15,000 randomly distributed UEs in the AnyLogic® software. Linked UEs (resp. UE-to-gNB links) represent D2D (resp. traditional) communication possibilities. Dark Red circles represent the gNBs’ covering areas in which the gNBs are at the center. Victim (emergency) devices, relay devices, in-coverage devices, and idle devices are represented respectively by the colors, red, green, yellow, and blue.
Figure 7.
Variation of under three ranges of . (a) Variation of against and , when the observed in the neighborhood is between 0 and 10. (b) Variation of against and , when the observed in the neighborhood is between 10 and 200. (c) Variation of against and , when the observed in the neighborhood is above 200.
Figure 7.
Variation of under three ranges of . (a) Variation of against and , when the observed in the neighborhood is between 0 and 10. (b) Variation of against and , when the observed in the neighborhood is between 10 and 200. (c) Variation of against and , when the observed in the neighborhood is above 200.
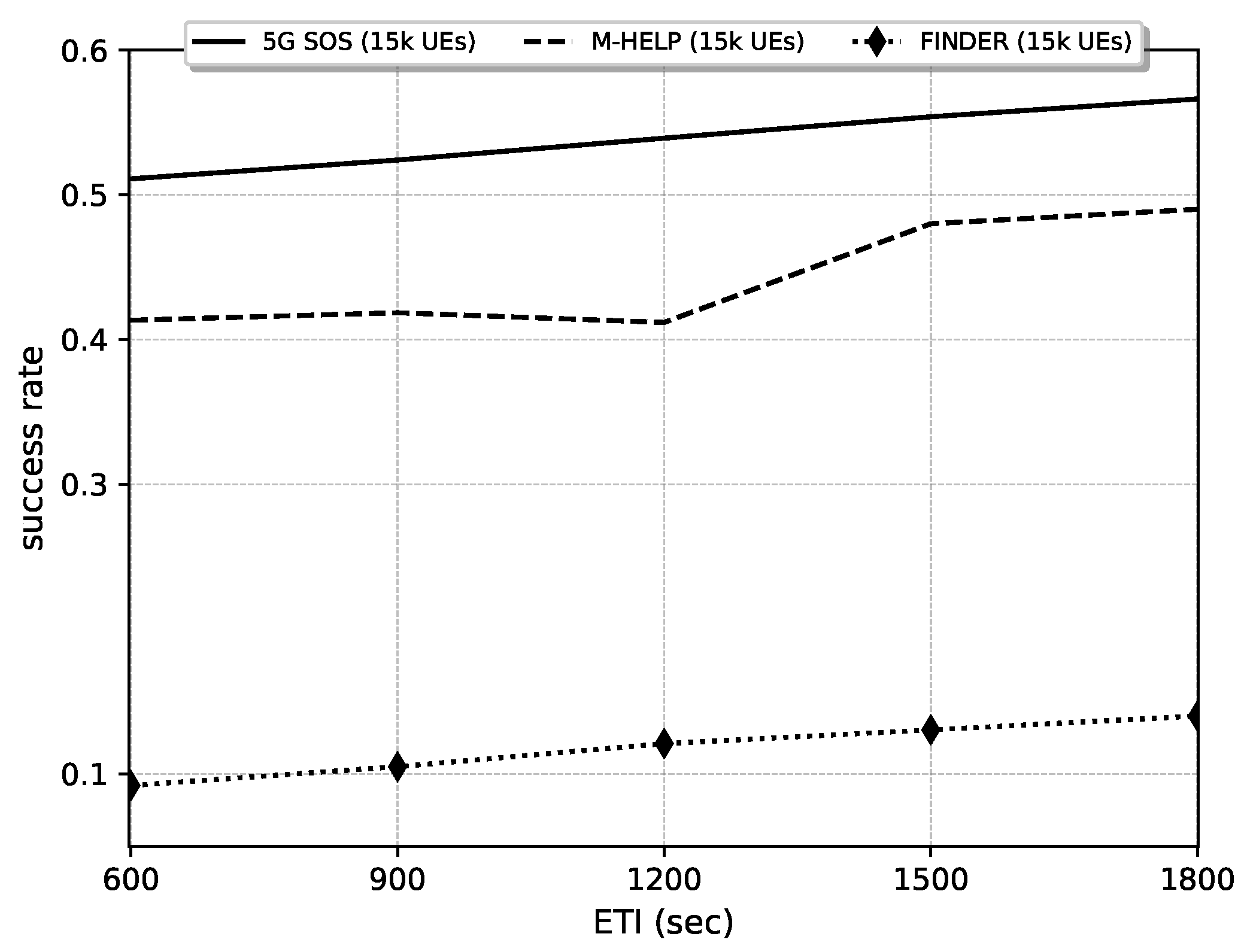
Figure 8.
Comparison of successful rate against emergency time interval (ETI) under 5G-SOS, M-HELP, and FINDER. Parameters: ETI: 600–1800 s, NoU: 15,000, NEC: 5000.
Figure 8.
Comparison of successful rate against emergency time interval (ETI) under 5G-SOS, M-HELP, and FINDER. Parameters: ETI: 600–1800 s, NoU: 15,000, NEC: 5000.
Figure 9.
Comparison of end–end latency against ETI under 5G-SOS, M-HELP, and FINDER. Parameters: ETI: 600–1800 s, NoU: 15,000, NEC: 5000.
Figure 9.
Comparison of end–end latency against ETI under 5G-SOS, M-HELP, and FINDER. Parameters: ETI: 600–1800 s, NoU: 15,000, NEC: 5000.
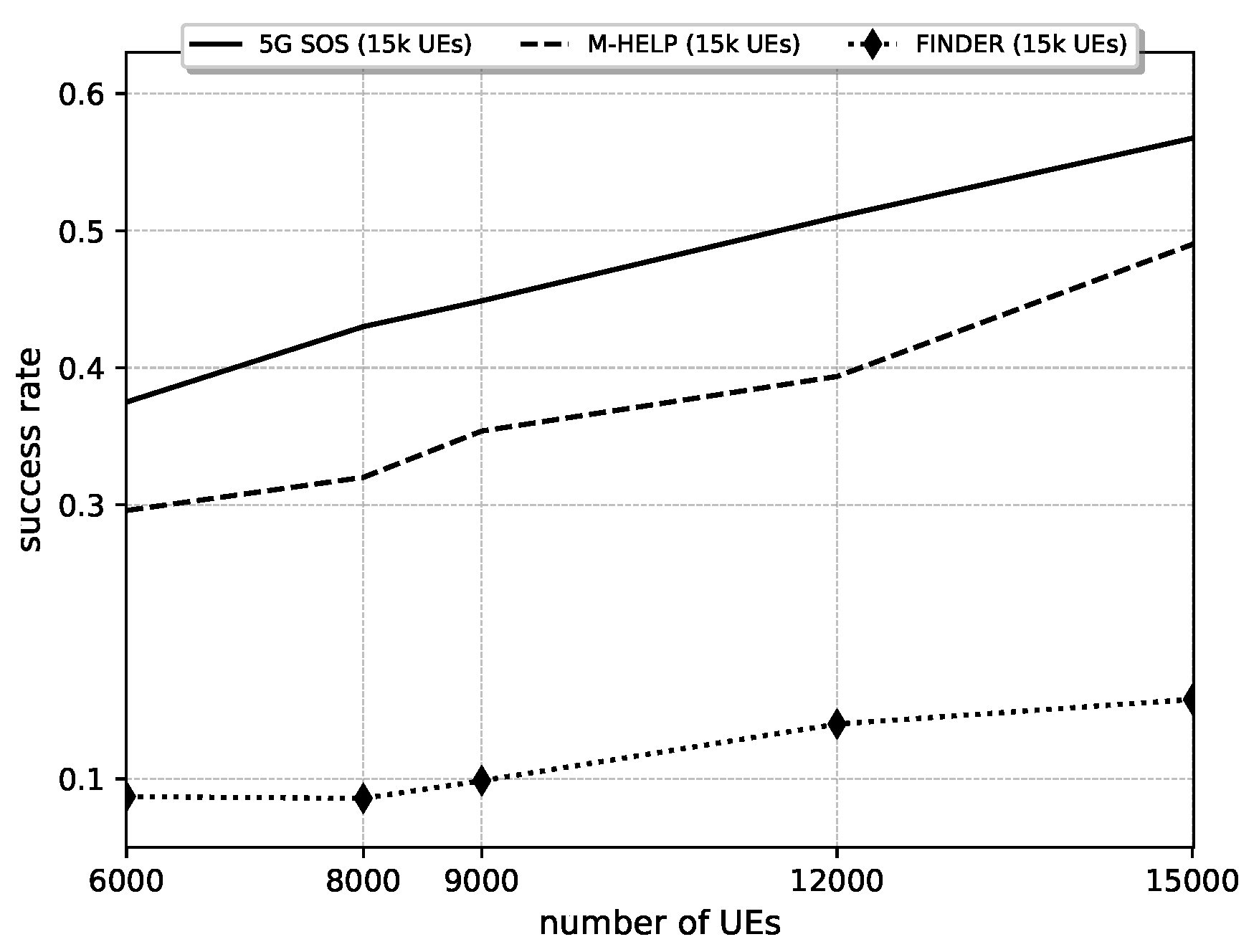
Figure 10.
Comparison of successful rate against number of UEs (NoU) under 5G-SOS, M-HELP, and FINDER. Parameters: NoU: 6000 to 15,000, NEC: 5000, ETI: 1800 s (30 min).
Figure 10.
Comparison of successful rate against number of UEs (NoU) under 5G-SOS, M-HELP, and FINDER. Parameters: NoU: 6000 to 15,000, NEC: 5000, ETI: 1800 s (30 min).
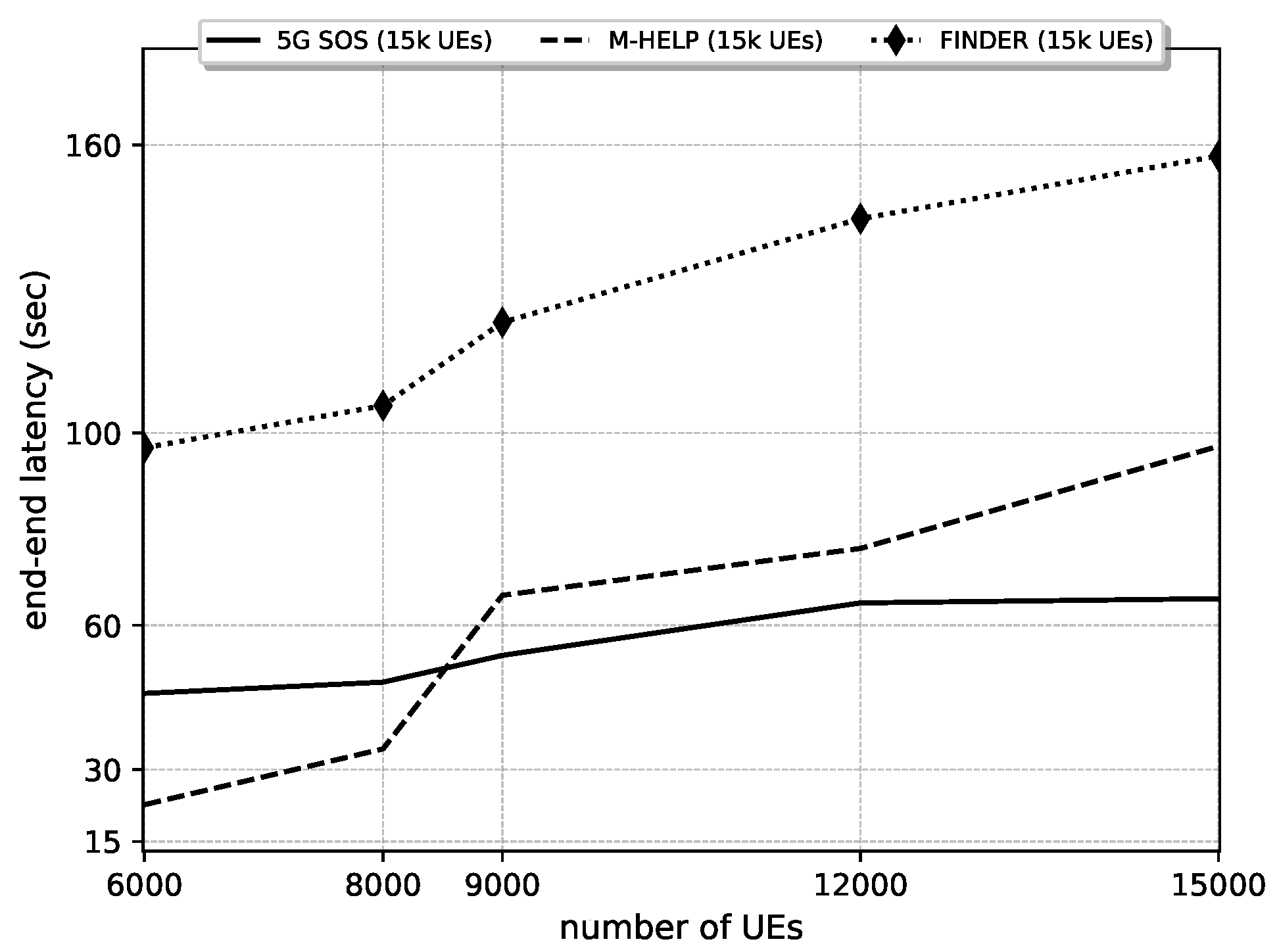
Figure 11.
Comparison of end–end latency against NoU under 5G-SOS, M-HELP, and FINDER. Parameters: NoU: 6000 to 15,000, NEC: 5000, ETI: 1800 s (30 min).
Figure 11.
Comparison of end–end latency against NoU under 5G-SOS, M-HELP, and FINDER. Parameters: NoU: 6000 to 15,000, NEC: 5000, ETI: 1800 s (30 min).
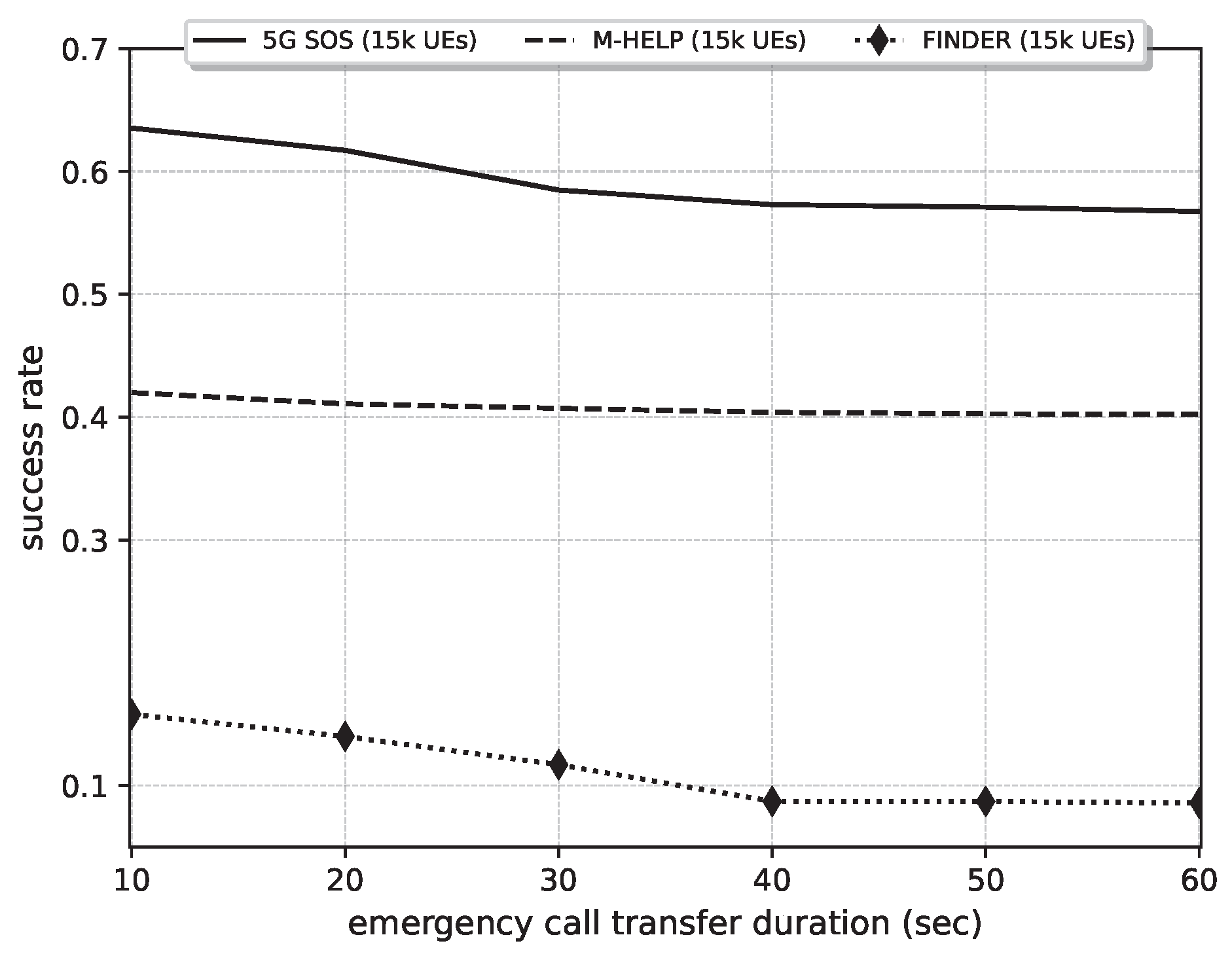
Figure 12.
Comparison of successful rate against emergency call transfer duration under 5G-SOS, M-HELP, and FINDER. Parameters: NoU: 15,000, NEC: 5000, ETI: 1800 s (30 min).
Figure 12.
Comparison of successful rate against emergency call transfer duration under 5G-SOS, M-HELP, and FINDER. Parameters: NoU: 15,000, NEC: 5000, ETI: 1800 s (30 min).
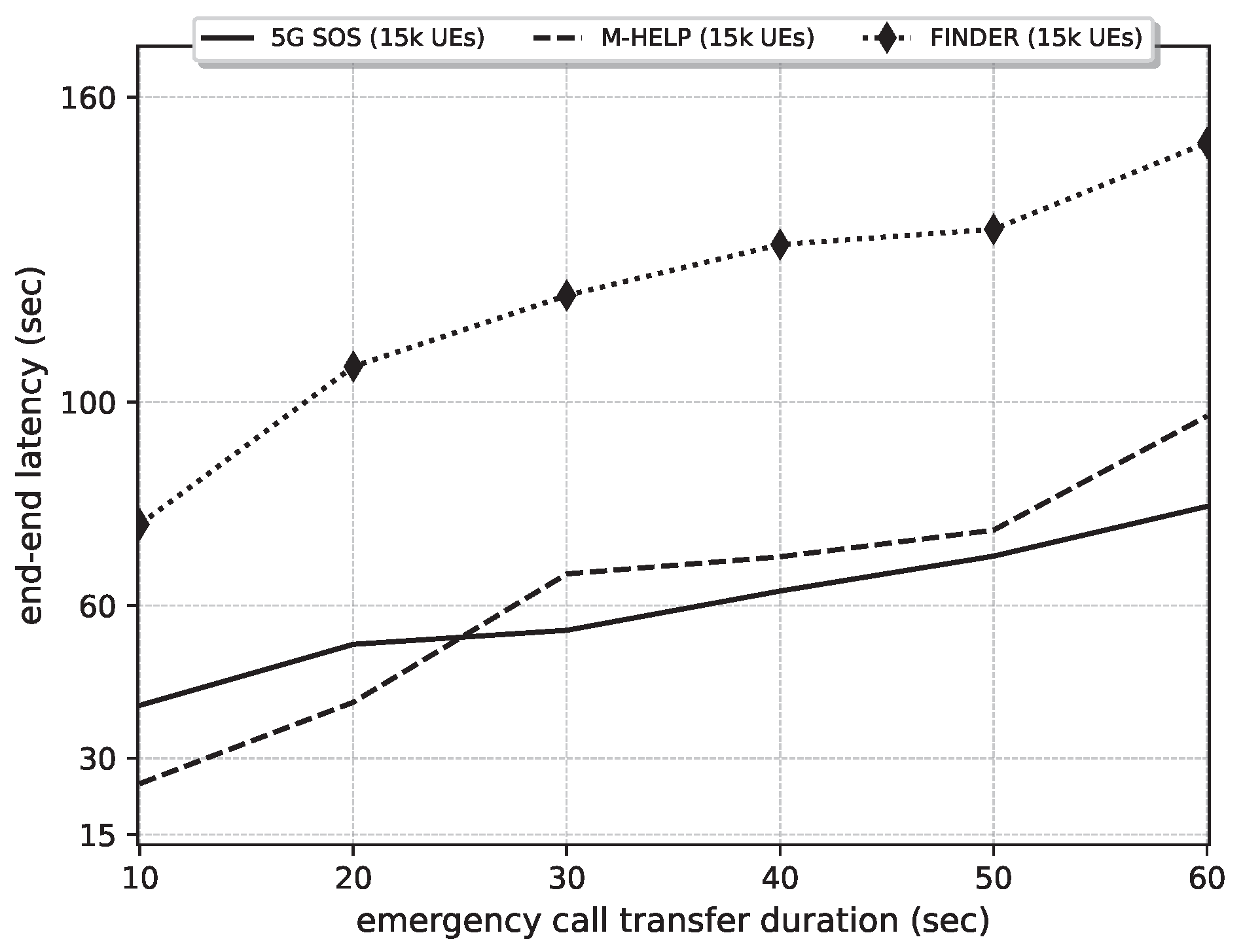
Figure 13.
Comparison of end–end latency against emergency call transfer duration under 5G-SOS, M-HELP, and FINDER. Parameters: NoU: 15,000, NEC: 5000, ETI: 1800 s (30 min).
Figure 13.
Comparison of end–end latency against emergency call transfer duration under 5G-SOS, M-HELP, and FINDER. Parameters: NoU: 15,000, NEC: 5000, ETI: 1800 s (30 min).
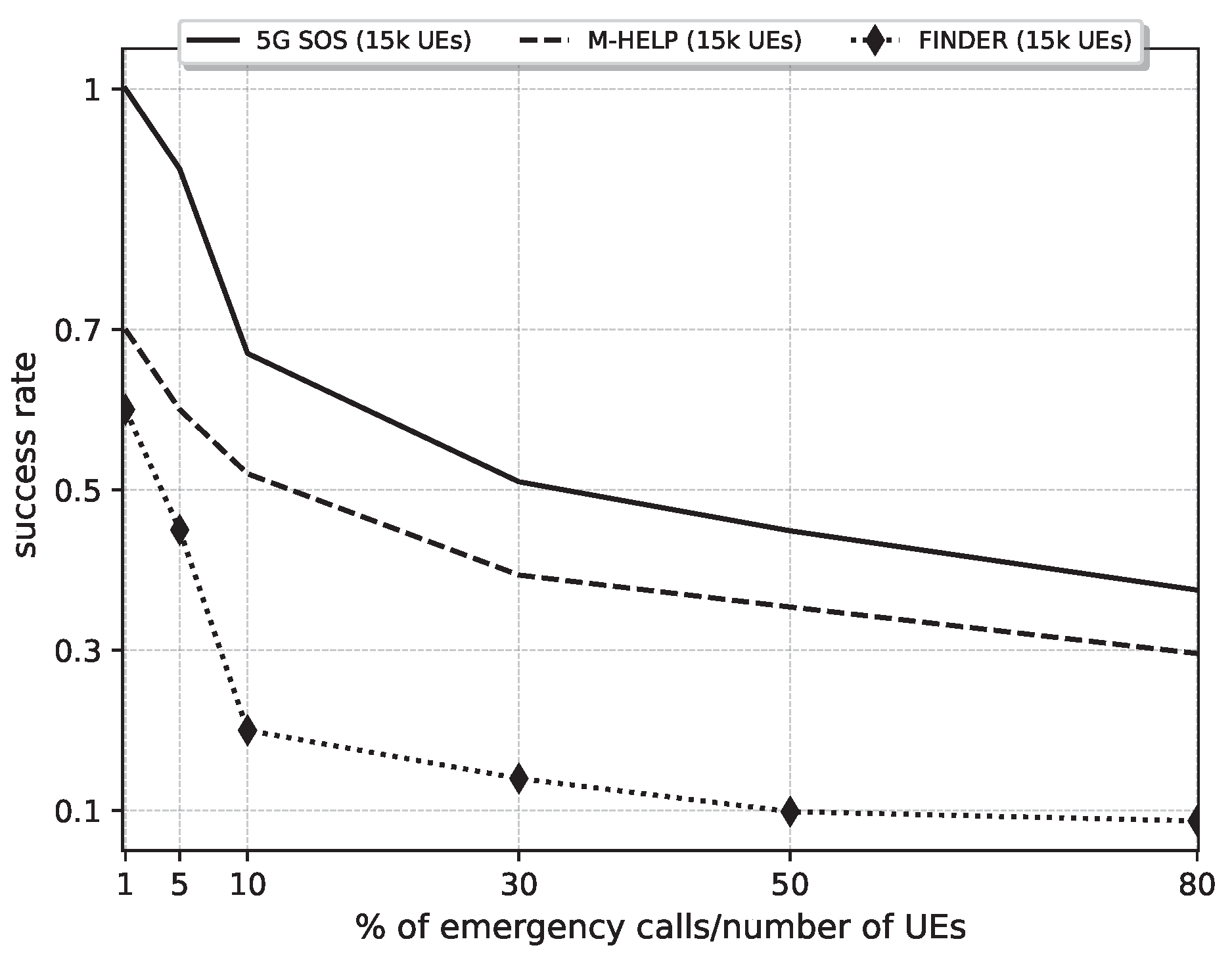
Figure 14.
Comparison of the success rate against the ratio of the number of emergency calls (NEC) to the number of UEs (NoU) under 5G-SOS, M-HELP, and FINDER. Parameters: NoU: NEC: 1% of NoU to 80% of NoU, NoU: 15,000 UEs, ETI: 1800 s (30 min).
Figure 14.
Comparison of the success rate against the ratio of the number of emergency calls (NEC) to the number of UEs (NoU) under 5G-SOS, M-HELP, and FINDER. Parameters: NoU: NEC: 1% of NoU to 80% of NoU, NoU: 15,000 UEs, ETI: 1800 s (30 min).
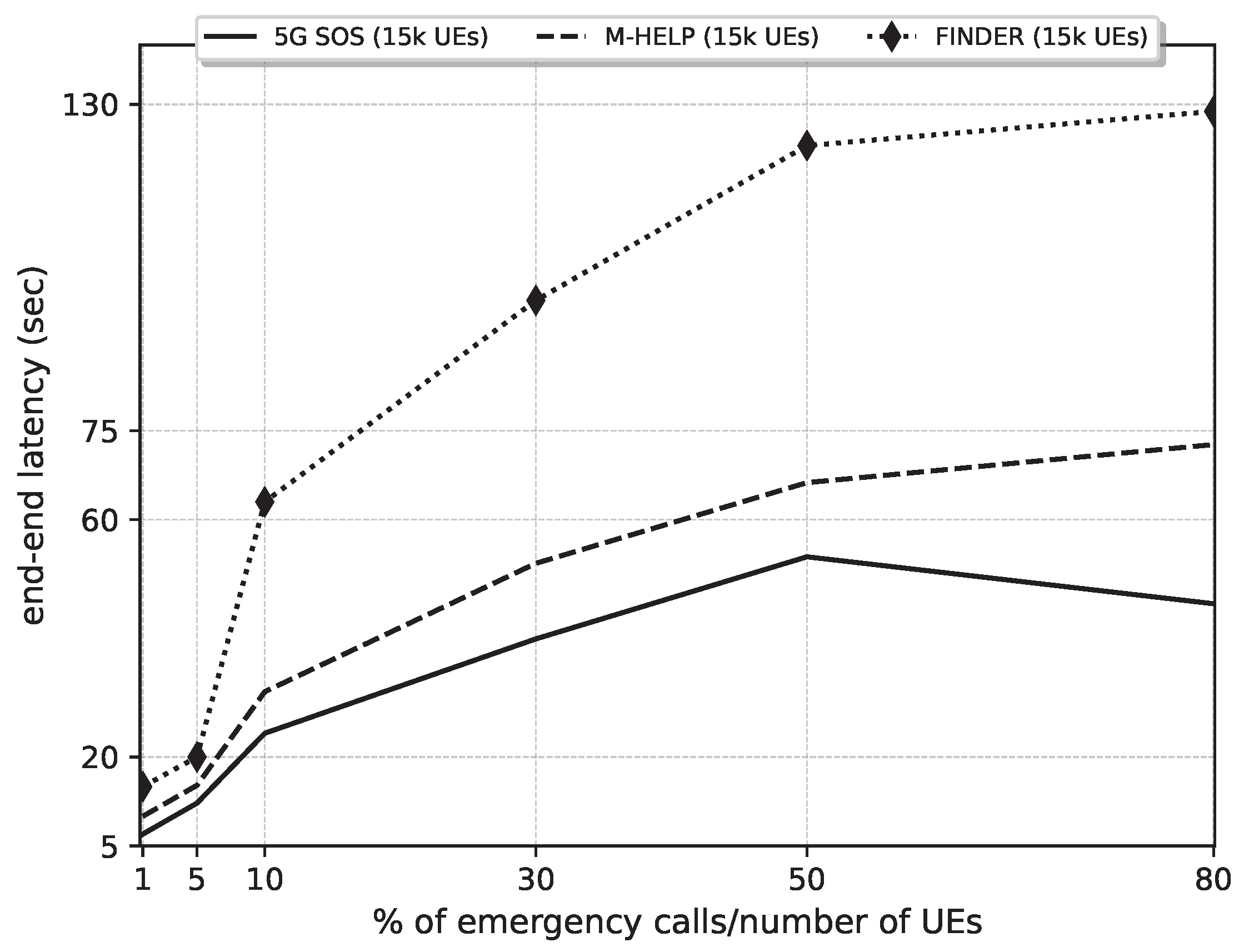
Figure 15.
Comparison of end–end latency against the ratio of the number of emergency calls (NEC) to the number of UEs (NoU) under 5G-SOS, M-HELP, and FINDER. Parameters: NEC: 1% of NoU to 80% of NoU, NoU: 15,000 UEs, ETI: 1800 s (30 min).
Figure 15.
Comparison of end–end latency against the ratio of the number of emergency calls (NEC) to the number of UEs (NoU) under 5G-SOS, M-HELP, and FINDER. Parameters: NEC: 1% of NoU to 80% of NoU, NoU: 15,000 UEs, ETI: 1800 s (30 min).
Figure 16.
Comparison of the number of messages per node against the ratio of the number of emergency calls (NEC) to the number of UEs (NoU) under 5G-SOS, M-HELP, and FINDER. Parameters: NoU: NEC: 1% of NoU to 80% of NoU, NoU: 15,000 UEs, ETI: 1800 s (30 min).
Figure 16.
Comparison of the number of messages per node against the ratio of the number of emergency calls (NEC) to the number of UEs (NoU) under 5G-SOS, M-HELP, and FINDER. Parameters: NoU: NEC: 1% of NoU to 80% of NoU, NoU: 15,000 UEs, ETI: 1800 s (30 min).
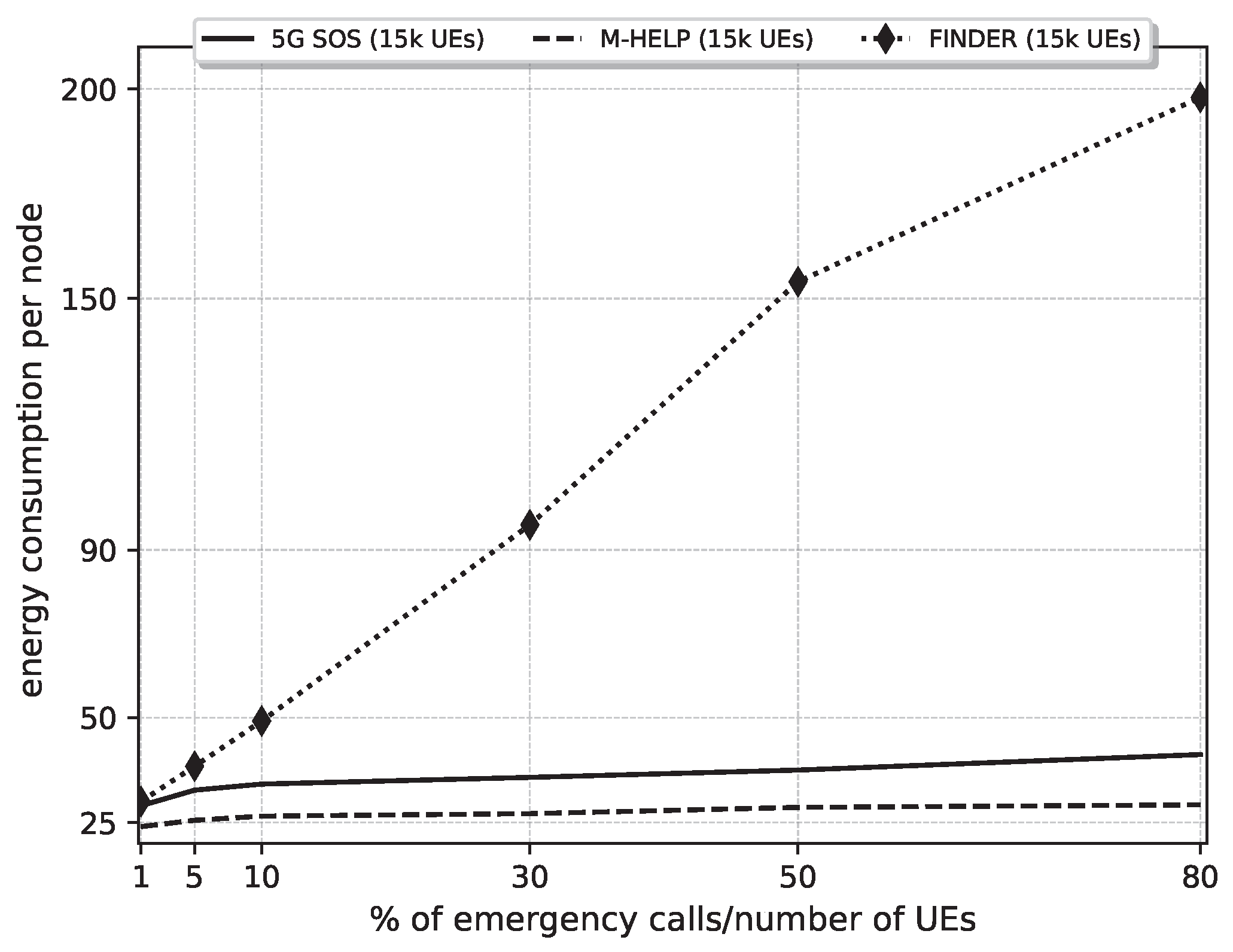
Figure 17.
Comparison of the energy consumption per node against the ratio of the number of emergency calls (NEC) to the number of UEs (NoU) under 5G-SOS, M-HELP, and FINDER. Parameters: NoU: NEC: 1% of NoU to 80% of NoU, NoU: 15,000 UEs, ETI: 1800 s (30 min).
Figure 17.
Comparison of the energy consumption per node against the ratio of the number of emergency calls (NEC) to the number of UEs (NoU) under 5G-SOS, M-HELP, and FINDER. Parameters: NoU: NEC: 1% of NoU to 80% of NoU, NoU: 15,000 UEs, ETI: 1800 s (30 min).
Table 1.
Existing works in the literature on wireless network recovery.
Table 1.
Existing works in the literature on wireless network recovery.
| Related Work | External Architecture | Resilient Architecture | Resilient Application | Resilient Protocol | 3GPP Compatible | Out-of-Coverage |
|---|
| UAV-Assisted Attack Prevention, Detection, and Recovery of 5G Networks [19] | x | | | | | x |
| Post-Disaster 4G/5G Network Rehabilitation Using Drones: Solving Battery and Backhaul Issues [20] | x | | | | | x |
| Integration of satellite and LTE for disaster recovery [18] | x | | | | | x |
| UAV-Empowered Disaster-Resilient Edge Architecture for Delay-Sensitive Communication [21] | x | | | | | x |
| On the Disaster Resiliency within the Context of 5G Networks: The RECODIS Experience [16] | | x | | | x | |
| Enabling Disaster Resilient 4G Mobile Communication Networks [23] | | x | | | x | |
| Terrestrial Trunked Radio-Tetra: A Global Security Tool [24] | | | x | | x | |
| Towards Failure Resiliency in 5G: Service Shifting [25] | | | x | | x | |
| Ad-hoc network recovery after severe disaster [26] | | | | x | | x |
| A mobile ad-hoc network multi-path routing protocol based on biological attractor selection for disaster recovery communication [27] | | | | x | | x |
| D2D Multihop Energy-Efficient Routing and OFDMA Resource Allocation in 5G Networks [28] | | | | x | x | |
| Assisted Routing Algorithm for D2D Communication in 5G Wireless Networks [29] | | | | x | x | |
| FINDER: A D2D based critical communications framework for disaster management in 5G [10] | | | | x | x | x |
| M-HELP-Multi-Hop Emergency Call Protocol in 5G [9] | | | | x | x | x |
Table 2.
Notations used in Algorithms 1–3.
Table 2.
Notations used in Algorithms 1–3.
| Notation | Description |
|---|
| FIFO list of calls in the buffer to be relayed |
| List of calls already received and processed in the past |
| DATA | Emergency call |
| srcID | Identifier of the source device |
| callID | Identifier of the emergency call |
| callIDGenerator | Function used by each UE to generate unique call IDs |
| waitingCall | A call stored in |
| deadline | latest time by which a waitingCall is transmitted |
| nbAttempts | Count that DATA was trasnmitted or relayed |
| relay | relay device information content in DATA |
Table 3.
Expected behavior of with and .
Table 3.
Expected behavior of with and .
Table 4.
Adaptive model parameters.
Table 4.
Adaptive model parameters.
| Limits | a | b |
|---|
| 1 | 0.5 |
| 1 | 0.2 |
| 1 | 0.1 |
Table 5.
Traverse city area emergency simulation parameters.
Table 5.
Traverse city area emergency simulation parameters.
| Parameter | Value |
|---|
| Total network area | 16.2 × |
| Amount of working gNBs | 7 |
| Total UE spread | RAND (16.2,21) |
| Initial | 120 s |
| Initial | 120 s |
| UE’s GPS localization accuracy | RAND (0.001,1) |
| Initial UE’s SoC | RAND (0,100) J |
| BS/gNB Link distance (d) | 1.5 km |
| D2D link connection range | 1.5 km |
| Data transfer delay by D2D mode, | 10 s |
| Data transfer delay by classical PUSCH mode | 1 s |
| Maximum limit for , | 5 |
| Upper bound of waiting time, | 120 s |
| Upper limit of re-transmissions, | 4 |
| Maximum number of messages in | 3 |
| Transmit power of gNB, () | 300.0 dBm |
| Signal transmission frequency of gNBs (f) | 885 MHz |
| BS/gNB antenna effective height () | 100 m |
| UE antenna effective height () | 1.5 m |
| Constant offset of Cost231 Hata model () | 0 dB |
| Number of UEs, NoU | variable |
| Number of emergency calls, NEC | variable |
| Emergency calls occurring interval, ETI | variable |
| Energy to transmit | 0.08 mJ [10] |
| Energy to receive | 0.05 mJ [10] |
| Total Simulation running time | 30 min |
Table 6.
Summary of performance analysis.
Table 6.
Summary of performance analysis.
| Parameter | Gain in 5G-SOS vs. M-HELP | Gain in 5G-SOS vs. FINDER | Comparison |
|---|
| Success rate | | | > |
| | | | > |
| | | << |
| | | << |
| | | << |