Aerial Bombing Crater Identification: Exploitation of Precise Digital Terrain Models
Abstract
1. Introduction
2. Study Area and Historical Context
3. Materials and Methods
3.1. LiDAR Data Acquisition and Processing
3.2. Visualization Power
3.3. PyCDA Algorithm
3.4. Edge Detectors
3.5. Mask Region Based Convolutional Neural Networks (Mask RCNN) Method
3.6. Validation of Method Performance
4. Results
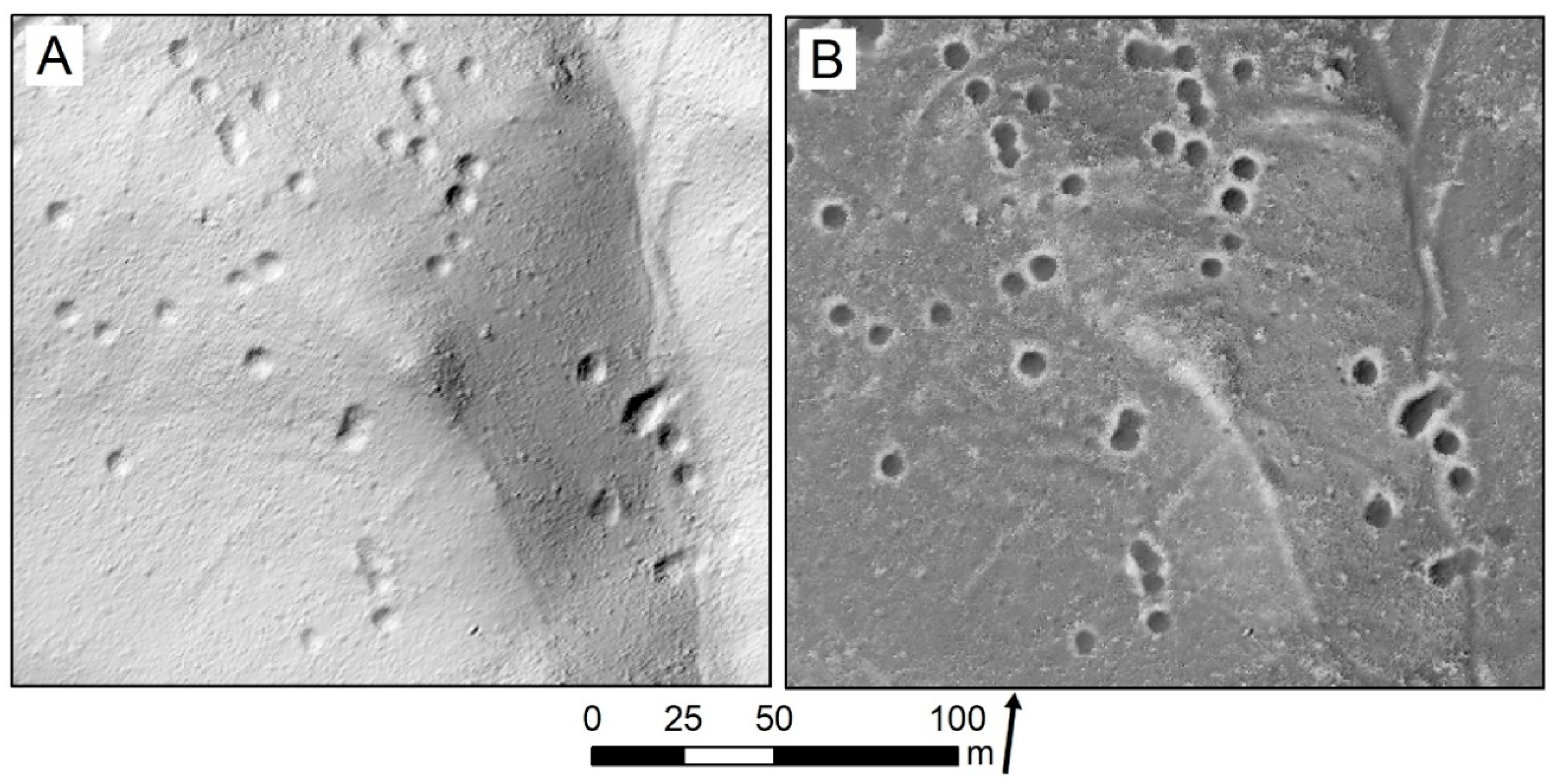
4.1. Point Cloud Data Processing and Aerial Bombing Crater Identification
4.2. Preliminary Identification and Comparison of Methods
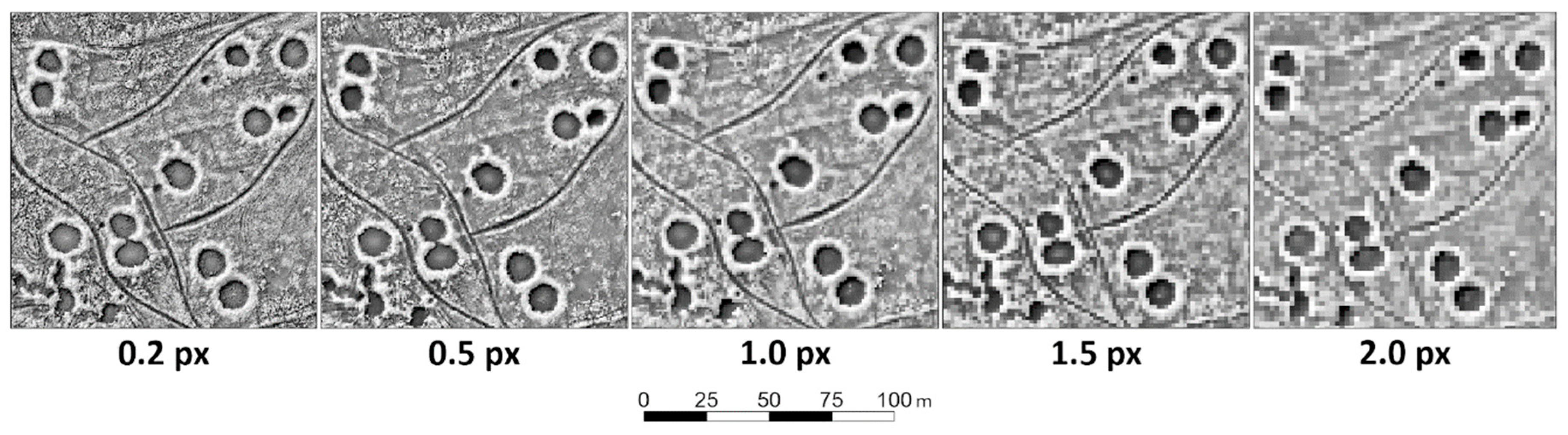
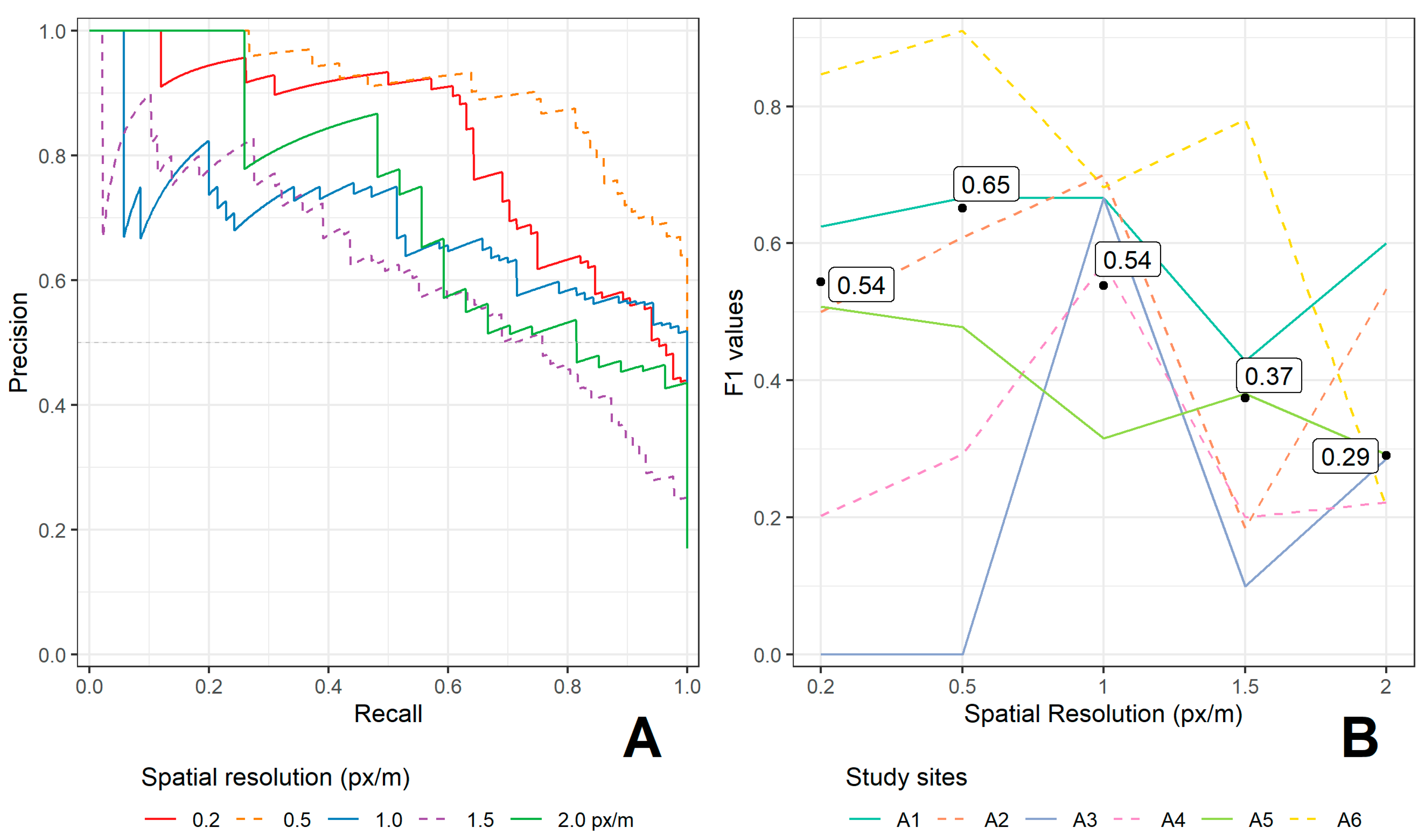
4.3. Effect of the Spatial Resolution of Input Raster—Mask RCNN
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Passmore, D.G.; Harrison, S.; Tunwell, D.C. Second World War conflict archaeology in the forests of north-west Europe. Antiquity 2014, 88, 1275–1290. [Google Scholar] [CrossRef][Green Version]
- Capps Tunwell, D.; Passmore, D.G.; Harrison, S. A witness in the landscape: The bombing of the Forêt domaniale des Andaines and the Normandy Campaign, NW France, 1944. War Hist. 2018, 25, 69–102. [Google Scholar] [CrossRef]
- Furlanello, C.; Merler, S.; Menegon, S.; Paoli, E.; Fontanari, S. Mapping the Risk of Unexploded Bombs from World War Two; TC-IRST: Trento, Italy, 2003. [Google Scholar]
- Macdonald, J.A.; Small, M.J. Assessing Sites Contaminated with Unexploded Ordnance: Statistical Modeling of Ordnance Spatial Distribution. Environ. Sci. Technol. 2006, 40, 931–938. [Google Scholar] [CrossRef] [PubMed]
- Dolejš, M.; Samek, V.; Veselý, M.; Elznicová, J. Detecting World War II bombing relics in markedly transformed landscapes (city of Most, Czechia). Appl. Geogr. 2020, 119, 102225. [Google Scholar] [CrossRef]
- Lacroix, V.; Vanhuysse, S. Crater Detection using CGC—A New Circle Detection Method. In Proceedings of the International Conference on Pattern Recognition Applications and Methods, Lisbon, Portugal, 10–12 January 2015; SCITEPRESS—Science and and Technology Publications: Setúbal, Portugal, 2015; Volume 1, pp. 320–327. [Google Scholar]
- Gheyle, W.; Stichelbaut, B.; Saey, T.; Note, N.; Van den Berghe, H.; Van Eetvelde, V.; Van Meirvenne, M.; Bourgeois, J. Scratching the surface of war. Airborne laser scans of the Great War conflict landscape in Flanders (Belgium). Appl. Geogr. 2018, 90, 55–68. [Google Scholar] [CrossRef]
- Matos-Machado, R.; Toumazet, J.; Bergès, J.; Amat, J.; Arnaud-Fassetta, G.; Bétard, F.; Bilodeau, C.; Hupy, J.P.; Jacquemot, S. War landform mapping and classification on the Verdun battlefield (France) using airborne LiDAR and multivariate analysis. Earth Surf. Process. Landf. 2019, 44, 1430–1448. [Google Scholar] [CrossRef]
- Hesse, R. Geomorphological traces of conflict in high-resolution elevation models. Appl. Geogr. 2014, 46, 11–20. [Google Scholar] [CrossRef]
- van der Schriek, M.; Beex, W. The application of LiDAR-based DEMs on WWII conflict sites in the Netherlands. J. Confl. Archaeol. 2017, 12, 94–114. [Google Scholar] [CrossRef]
- Chen, G.; Weng, Q.; Hay, G.J.; He, Y. Geographic object-based image analysis (GEOBIA): Emerging trends and future opportunities. GISci. Remote Sens. 2018, 55, 159–182. [Google Scholar] [CrossRef]
- Davis, D.S. Object-based image analysis: A review of developments and future directions of automated feature detection in landscape archaeology. Archaeol. Prospect. 2019, 26, 155–163. [Google Scholar] [CrossRef]
- Witharana, C.; Ouimet, W.B.; Johnson, K.M. Using LiDAR and GEOBIA for automated extraction of eighteenth–late nineteenth century relict charcoal hearths in southern New England. GISci. Remote Sens. 2018, 55, 183–204. [Google Scholar] [CrossRef]
- Lin, E.; Qin, R.; Edgerton, J.; Kong, D. Crater detection from commercial satellite imagery to estimate unexploded ordnance in Cambodian agricultural land. PLoS ONE 2020, 15, e0229826. [Google Scholar] [CrossRef] [PubMed]
- Magnini, L.; Bettineschi, C.; De Guio, A. Object-based Shell Craters Classification from LiDAR-derived Sky-view Factor. Archaeol. Prospect. 2017, 24, 211–223. [Google Scholar] [CrossRef]
- Traviglia, A.; Torsello, A. Landscape Pattern Detection in Archaeological Remote Sensing. Geosciences 2017, 7, 128. [Google Scholar] [CrossRef]
- Dhillon, A.; Verma, G.K. Convolutional neural network: A review of models, methodologies and applications to object detection. Prog. Artif. Intell. 2020, 9, 85–112. [Google Scholar] [CrossRef]
- Huang, J.; Rathod, V.; Sun, C.; Zhu, M.; Korattikara, A.; Fathi, A.; Fischer, I.; Wojna, Z.; Song, Y.; Guadarrama, S.; et al. Speed/Accuracy Trade-Offs for Modern Convolutional Object Detectors. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3296–3297. [Google Scholar]
- Verschoof-van der Vaart, W.B.; Lambers, K. Learning to Look at LiDAR: The Use of R-CNN in the Automated Detection of Archaeological Objects in LiDAR Data from the Netherlands. J. Comput. Appl. Archaeol. 2019, 2, 31–40. [Google Scholar] [CrossRef]
- Trier, Ø.D.; Cowley, D.C.; Waldeland, A.U. Using deep neural networks on airborne laser scanning data: Results from a case study of semi-automatic mapping of archaeological topography on Arran, Scotland. Archaeol. Prospect. 2019, 26, 165–175. [Google Scholar] [CrossRef]
- Caspari, G.; Crespo, P. Convolutional neural networks for archaeological site detection—Finding “princely” tombs. J. Archaeol. Sci. 2019, 110, 104998. [Google Scholar] [CrossRef]
- Silburt, A.; Ali-Dib, M.; Zhu, C.; Jackson, A.; Valencia, D.; Kissin, Y.; Tamayo, D.; Menou, K. Lunar crater identification via deep learning. Icarus 2019, 317, 27–38. [Google Scholar] [CrossRef]
- Klear, M.R. PyCDA: An Open-Source Library for Automated Crater Detection. In Proceedings of the 9th Planetary Crater Consort, Boulder, CO, USA, 8–10 August 2018. [Google Scholar]
- Lee, C. Automated crater detection on Mars using deep learning. Planet. Space Sci. 2019, 170, 16–28. [Google Scholar] [CrossRef]
- Benedix, G.K.; Norman, C.J.; Bland, P.A.; Towner, M.C.; Paxman, J.; Tan, T. Automated Detection of Martian Craters Using a Convolutional Neural Network. In Proceedings of the 49th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 19–23 March 2018. Contribution no. 2022. [Google Scholar]
- Brenner, S.; Zambanini, S.; Sablatnig, R. Detection of Bomb Craters in WWII Aerial Images. In Proceedings of the OAGM Workshop, Hall/Tyrol, Austria, 15–16 May 2018; pp. 94–97. [Google Scholar]
- Jones, B.; Bickler, S.H. Multi-Scalar and Semi-Automatic Approaches to Detect Archaeological Features in NZ Using Airborne LiDAR Data. Archaeol. N. Z. 2019, 62, 10–24. [Google Scholar]
- Gauss, C.F. Disquisitiones Generales Circa Superficies Curvas; Typis Ditericianis: Göttingen, Germany, 1828. [Google Scholar]
- Brändli, M. Hierarchical Models for the Definition and Extraction of Terrain Features. In Geographic Objects with Indeterminate Boundaries; Burrough, P.A., Frank, A.U., Eds.; Taylor & Francis: Bristol, PA, USA; London, UK, 1996; ISBN 978-0-7484-0387-5. [Google Scholar]
- Waters, R.S. Morphological mapping. Geography 1958, 43, 10–17. [Google Scholar]
- Young, A.; Clayton, K.M. Slopes; Longman: London, UK, 1972. [Google Scholar]
- Minár, J.; Evans, I.S. Elementary forms for land surface segmentation: The theoretical basis of terrain analysis and geomorphological mapping. Geomorphology 2008, 95, 236–259. [Google Scholar] [CrossRef]
- Troeh, F.R. Landform equations fitted to contour maps. Am. J. Sci. 1965, 263, 616–627. [Google Scholar] [CrossRef]
- Minár, J.; Jenčo, M.; Evans, I.S.; Minár, J.; Kadlec, M.; Krcho, J.; Pacina, J.; Burian, L.; Benová, A. Third-order geomorphometric variables (derivatives): Definition, computation and utilization of changes of curvatures. Int. J. Geogr. Inf. Sci. 2013, 27, 1381–1402. [Google Scholar] [CrossRef]
- Jenčo, M.; Pacina, J.; Shary, P.A. Terrain skeleton and local morphometric variables: Geosciences and computer vision technique. In Proceedings of the Advances in Geoinformation Technologies, Ostrava, Czech Republic, 21–23 January 1993; Volume 8, pp. 57–76. [Google Scholar]
- Pacina, J.; Lenďáková, Z.; Štojdl, J.; Matys Grygar, T.; Dolejš, M. Dynamics of Sediments in Reservoir Inflows: A Case Study of the Skalka and Nechranice Reservoirs, Czech Republic. ISPRS Int. J. Geo-Inf. 2020, 9, 258. [Google Scholar] [CrossRef]
- Malina, O. The search for the invisible. Plow relics of extinct medieval villages and possibilities of their detection and interpretation using the LiDAR data [in Czech]. Zpr. Památ. Péče 2015, 75, 516. [Google Scholar]
- Davis, O. Processing and Working with LiDAR Data in ArcGIS: A Practical Guide for Archaeologists. R. Comm. Anc. Hist. Monum. Wales 2012, 1–23. [Google Scholar]
- Yuen, H.; Princen, J.; Illingworth, J.; Kittler, J. Comparative study of Hough Transform methods for circle finding. Image Vis. Comput. 1990, 8, 71–77. [Google Scholar] [CrossRef]
- Saito, T.; Rehmsmeier, M. Precrec: Fast and accurate precision-recall and ROC curve calculations in R. Bioinformatics 2017, 33, 145–147. [Google Scholar] [CrossRef]
- Capps Tunwell, D.; Passmore, D.G.; Harrison, S. Second World War bomb craters and the archaeology of Allied air attacks in the forests of the Normandie-Maine National Park, NW France. J. Field Archaeol. 2016, 41, 312–330. [Google Scholar] [CrossRef]
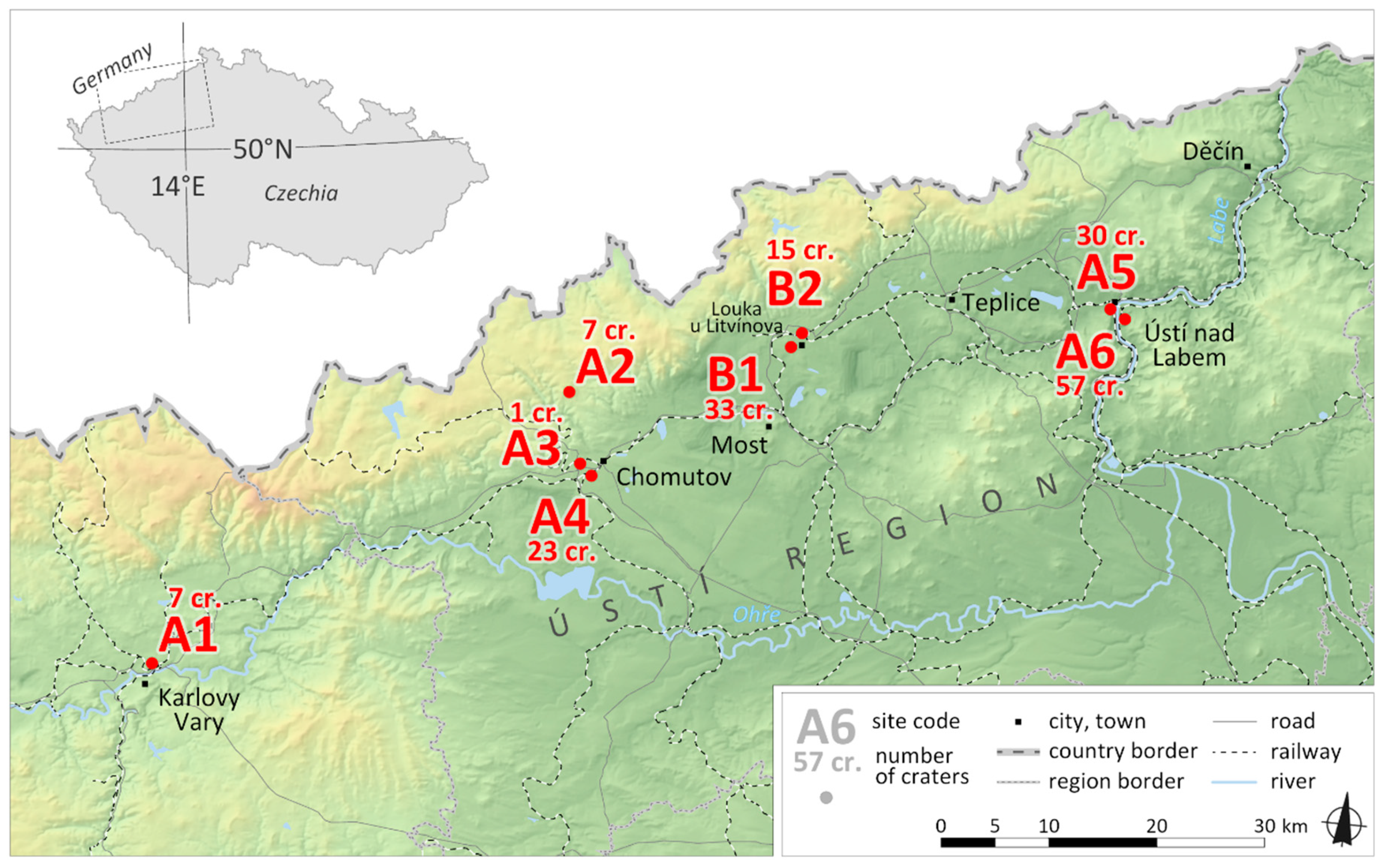
| Study Site | Municipality | Mean Altitude (m asl) | Avg. Point Density (m2) | Soil Type | Dominant Land Use (Current) | National Archive London Collection (AIR) no. |
|---|---|---|---|---|---|---|
| A1 | Karlovy Vary | 432 | 12 | pseudogley | forest | 9/406, 29/407. |
| A2 | Blatno | 728 | 29.6 | cambisol | forest/meadows | 9/407. |
| A3 | Chomutov | 352 | 16 | pseudogley | forest | 9/407. |
| A4 | Chomutov | 352 | 19.2 | cambisol | forest | 29/407. |
| A5 | Ústí nad Labem | 251 | 21.4 | cambisol | forest | 29/407, 40/845, 40/846, 40/847. |
| A6 | Ústí nad Labem | 290 | 29.9 | cambisol | forest | 29/407, 40/845, 40/846, 40/847. |
| B1 | Litvínov | 300 | 22.7 | anthrosol | forest | 29/399, 29/386, 29/382, 40/626. |
| B2 | Litvínov | 300 | 14.8 | cambisol | forest/arable | 29/399, 29/386, 29/382, 40/626. |
| Model | Spatial Resolution (m/px) | Recall | Precision | F1 Score |
|---|---|---|---|---|
| PyCDA | 0.5 | 0.07 | 0.03 | 0.05 |
| Edge Detection | 0.5 | 0.23 | 0.17 | 0.19 |
| Mask RCNN | 0.5 | 0.74 | 0.58 | 0.65 |
| Spatial Resolution (m/px) | Recall | Precision | F1 Score | AUC |
|---|---|---|---|---|
| 0.2 | 0.71 | 0.44 | 0.54 | 0.82 |
| 0.5 | 0.74 | 0.58 | 0.65 | 0.91 |
| 1 | 0.57 | 0.51 | 0.54 | 0.69 |
| 1.5 | 0.74 | 0.25 | 0.37 | 0.62 |
| 2 | 0.22 | 0.42 | 0.29 | 0.73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dolejš, M.; Pacina, J.; Veselý, M.; Brétt, D. Aerial Bombing Crater Identification: Exploitation of Precise Digital Terrain Models. ISPRS Int. J. Geo-Inf. 2020, 9, 713. https://doi.org/10.3390/ijgi9120713
Dolejš M, Pacina J, Veselý M, Brétt D. Aerial Bombing Crater Identification: Exploitation of Precise Digital Terrain Models. ISPRS International Journal of Geo-Information. 2020; 9(12):713. https://doi.org/10.3390/ijgi9120713
Chicago/Turabian StyleDolejš, Martin, Jan Pacina, Martin Veselý, and Dominik Brétt. 2020. "Aerial Bombing Crater Identification: Exploitation of Precise Digital Terrain Models" ISPRS International Journal of Geo-Information 9, no. 12: 713. https://doi.org/10.3390/ijgi9120713
APA StyleDolejš, M., Pacina, J., Veselý, M., & Brétt, D. (2020). Aerial Bombing Crater Identification: Exploitation of Precise Digital Terrain Models. ISPRS International Journal of Geo-Information, 9(12), 713. https://doi.org/10.3390/ijgi9120713





