Application of Ordinary Kriging and Regression Kriging Method for Soil Properties Mapping in Hilly Region of Central Vietnam
Abstract
1. Introduction
2. Materials and Methods
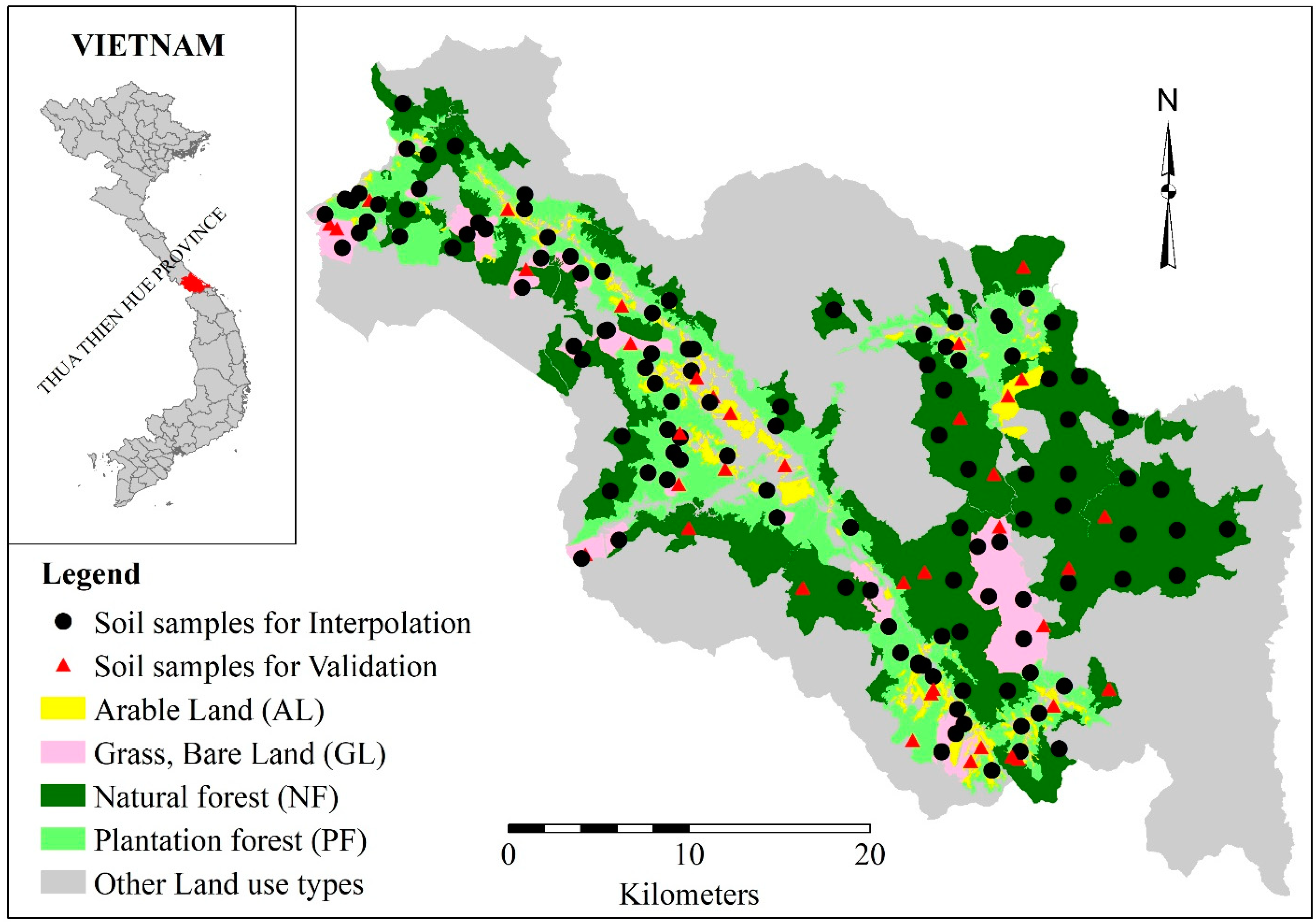
2.1. Research Area
2.2. Remote Sensing Data
2.3. Field Survey and Soil Quality Analysis
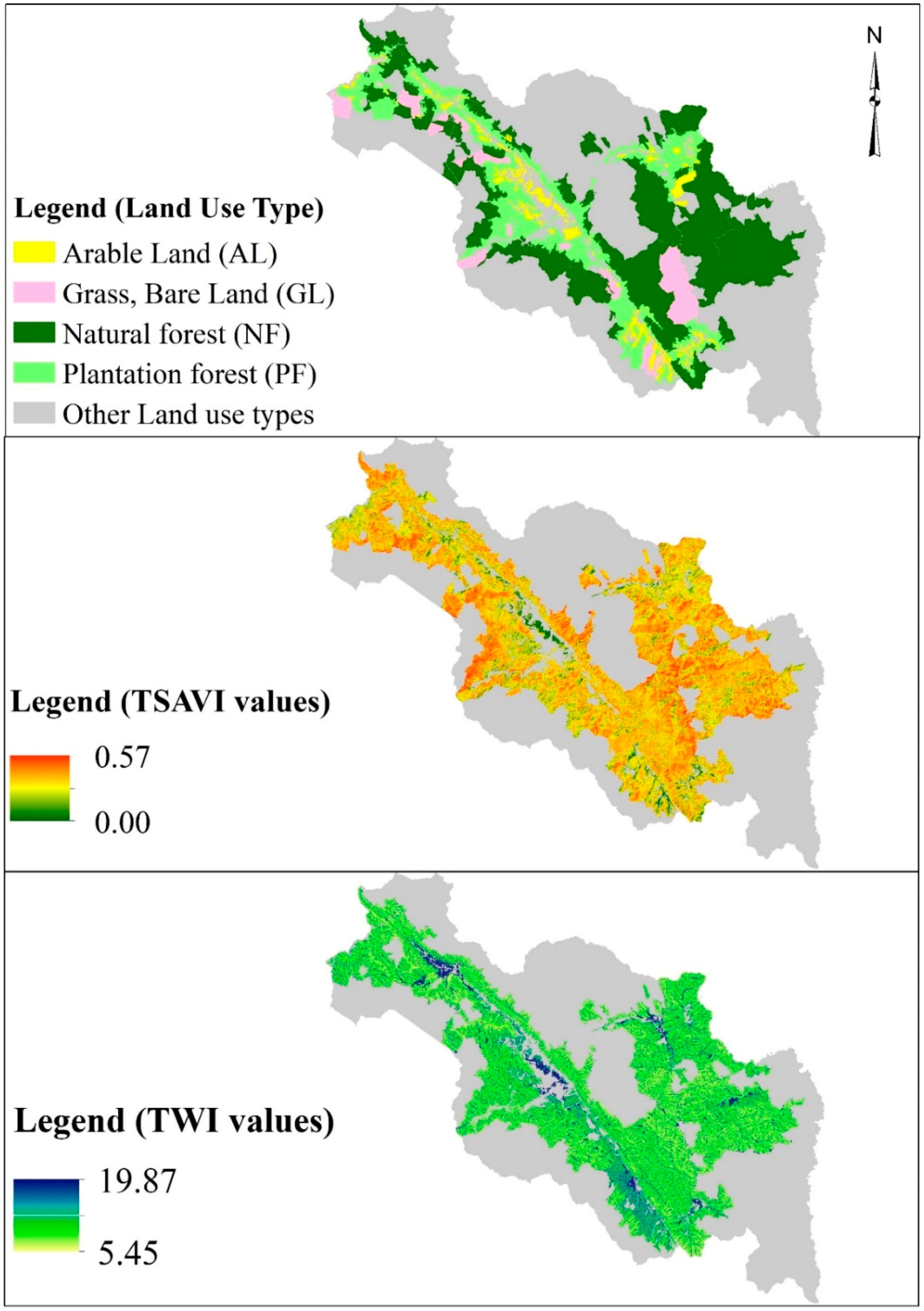
2.4. Environmental Variables Data
2.4.1. Transformed Soil Adjusted Vegetation Index (TSAVI)
2.4.2. Topographic Wetness Index (TWI)
2.5. Spatial Interpolation
2.5.1. Ordinary Kriging
2.5.2. Regression Kriging
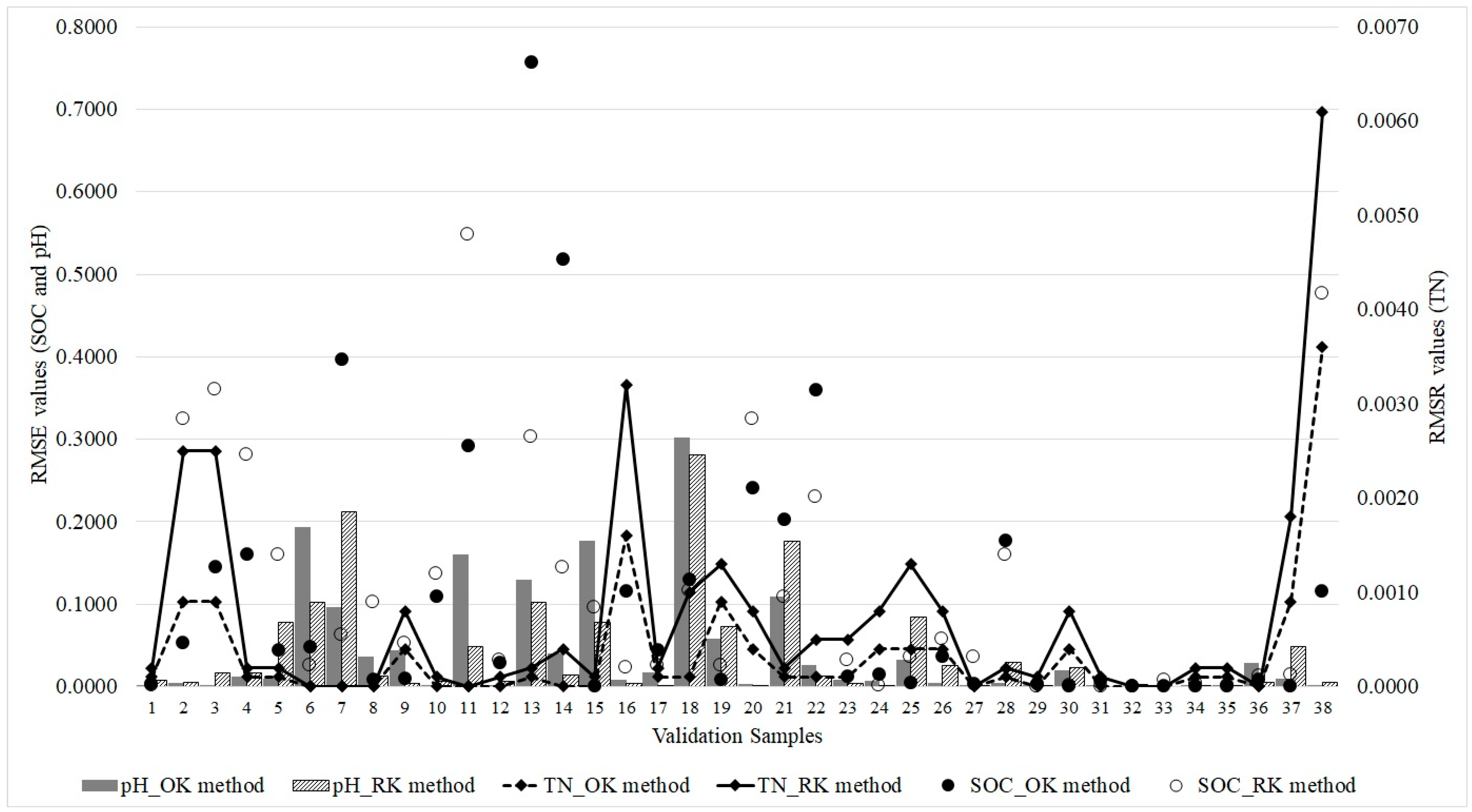
2.6. Validation
3. Results
3.1. Soil Samples Data Descriptions
3.2. Regression Model for Soil Characteristics Mapping
3.2.1. Environmental Variables Calculation
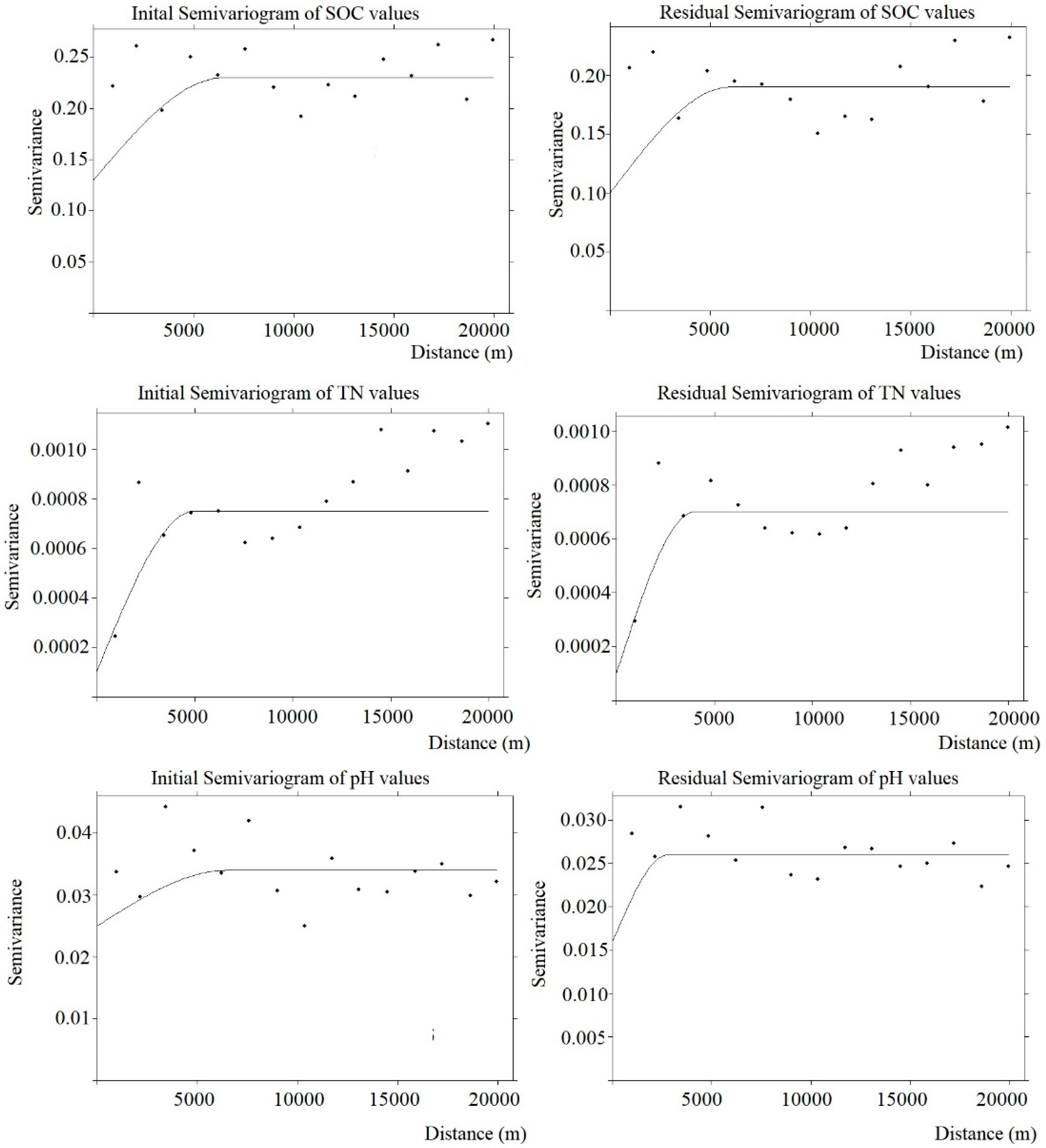
3.2.2. Model for Regression Kriging
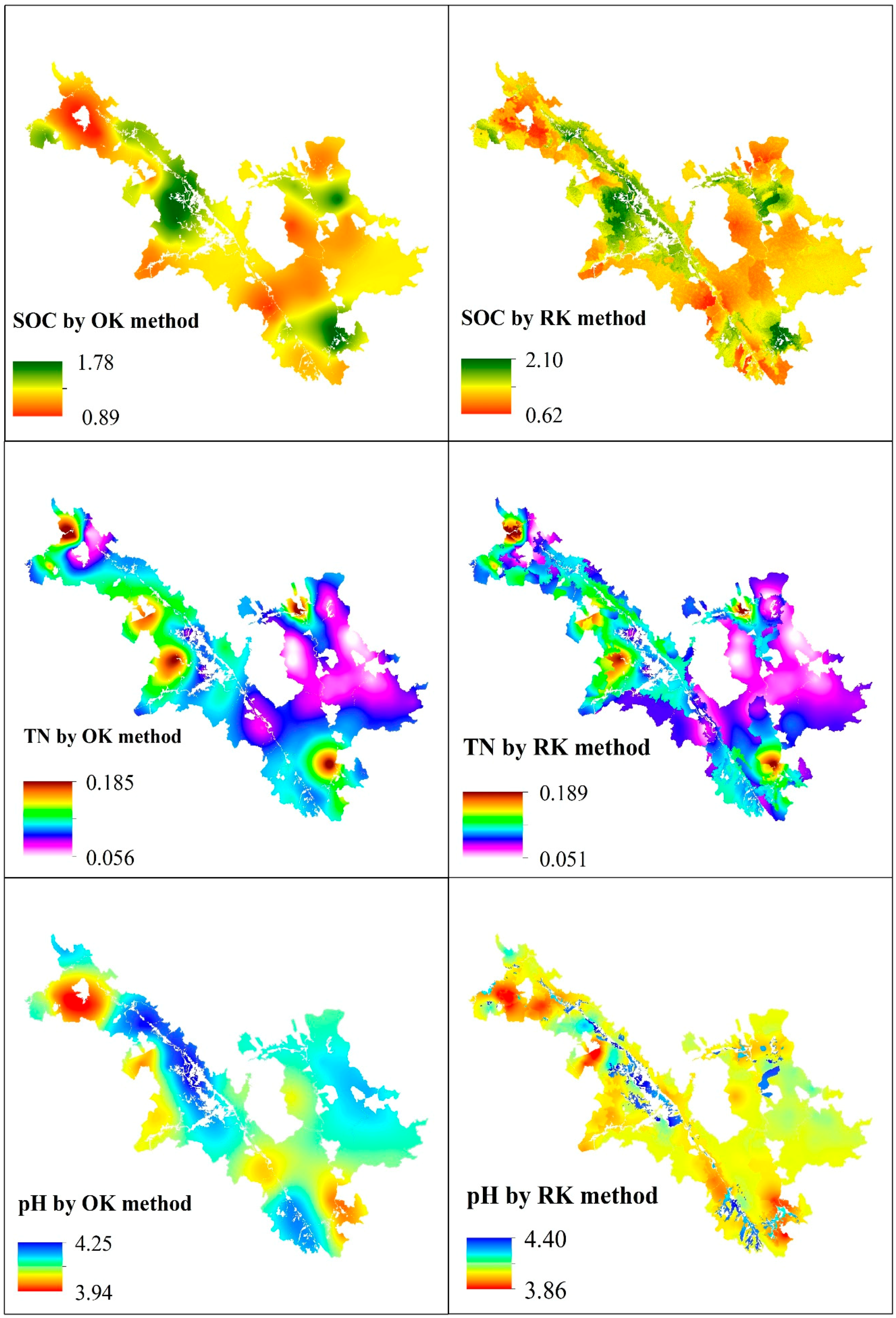
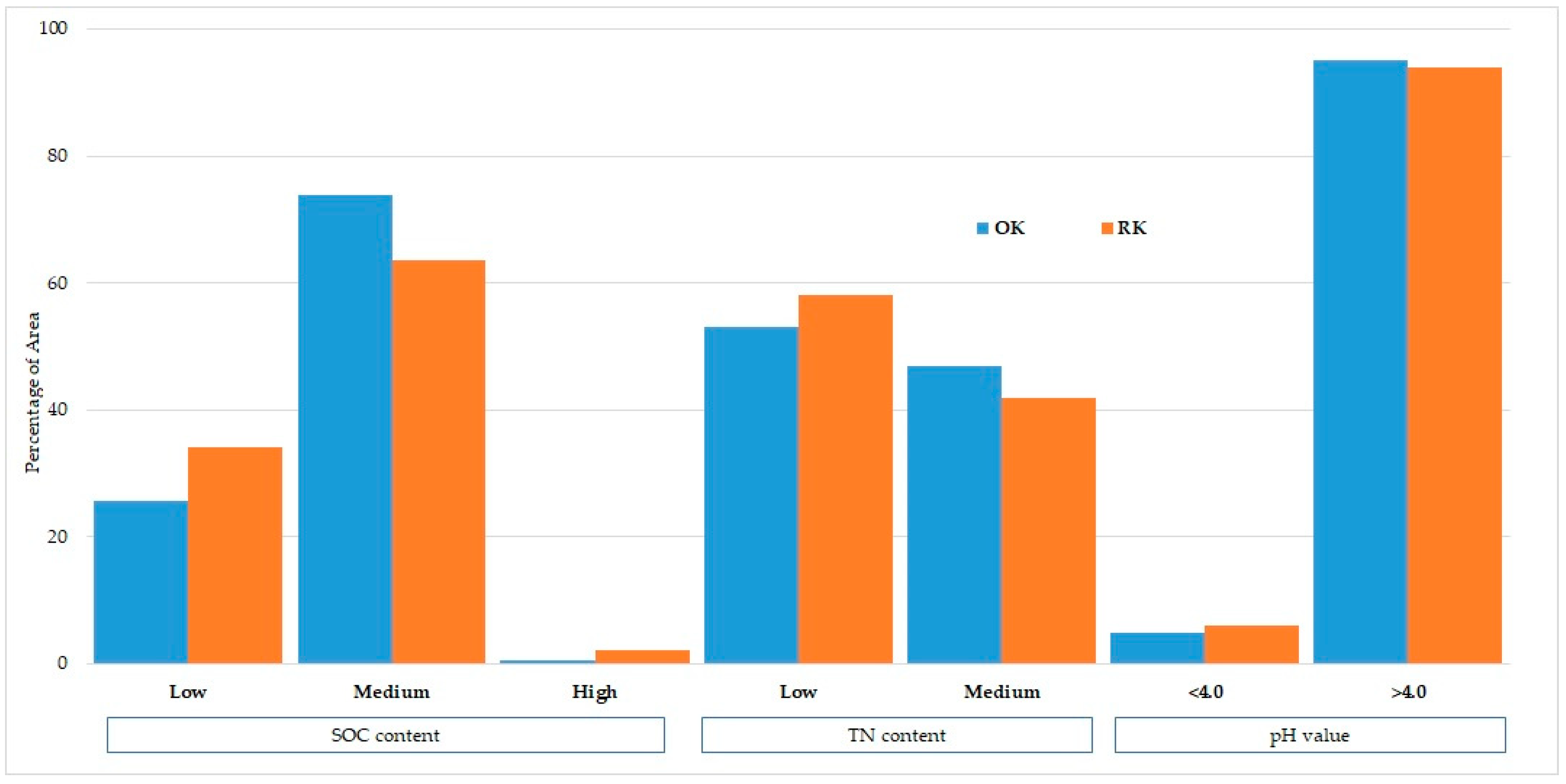
3.3. Spatial Interpolation
4. Discussion
4.1. The Impact of Environmental Variables on SOC, TN, and Soil pH
4.2. Comparison between OK and RK
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, E.M.; Griffiths, J.S. The importance of pedological soil survey in land use planning, resource assessment and site investigation. Geol. Soc. Lond. Eng. Geol. Spec. Publ. 1987, 4, 453–466. [Google Scholar] [CrossRef]
- Seyed, A.; Gilkes, R.J.; Andrews, S.S. A minimum data set for assessing soil quality in rangelands. Geoderma 2006, 136, 229–234. [Google Scholar] [CrossRef]
- Yevheniya, V.; Jenny, N.; Lars, R.; Norberg, T. A minimum data set for evaluating the ecological soil functions in remediation projects. J. Soils Sediments 2014, 14, 1850–1860. [Google Scholar] [CrossRef]
- Reeves, D.W. The role of soil organic matter in maintaining soil quality in continuous cropping systems. Soil Tillage Res. 1997, 43, 131–167. [Google Scholar] [CrossRef]
- Gentili, R.; Ambrosini, R.; Montagnani, C.; Caronni, S.; Citterio, S. Effect of Soil pH on the Growth, Reproductive Investment and Pollen Allergenicity of Ambrosia artemisiifolia L. Front. Plant Sci. 2018, 9, 1335. [Google Scholar] [CrossRef]
- Liu, C.-W.; Sung, Y.; Chen, B.-C.; Lai, H.-Y. Effects of Nitrogen Fertilizers on the Growth and Nitrate Content of Lettuce (Lactuca sativa L.). Int. J. Environ. Res. Public Health 2014, 11, 4427–4440. [Google Scholar] [CrossRef] [PubMed]
- McBratney, A.B.; Mendonça Santos, M.L.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Sumfleth, K.; Duttmann, R. Prediction of soil property distribution in paddy soil landscapes using terrain data and satellite information as indicators. Ecol. Indic. 2008, 8, 485–501. [Google Scholar] [CrossRef]
- Uygur, V.; Irvem, A.; Karanlik, S.; Akis, R. Mapping of total nitrogen, available phosphorous and potassium in Amik Plain, Turkey. Environ. Earth Sci 2010, 59, 1129–1138. [Google Scholar] [CrossRef]
- Shit, P.K.; Bhunia, G.S.; Maiti, R. Spatial analysis of soil properties using GIS based geostatistics models. Model. Earth Syst. Environ. 2016, 2, 495. [Google Scholar] [CrossRef]
- Göl, C.; Bulut, S.; Bolat, F. Comparison of different interpolation methods for spatial distribution of soil organic carbon and some soil properties in the Black Sea backward region of Turkey. J. Afr. Earth Sci. 2017, 134, 85–91. [Google Scholar] [CrossRef]
- Tang, X.; Xia, M.; Pérez-Cruzado, C.; Guan, F.; Fan, S. Spatial distribution of soil organic carbon stock in Moso bamboo forests in subtropical China. Sci. Rep. 2017, 7, 81. [Google Scholar] [CrossRef]
- Conforti, M.; Matteucci, G.; Buttafuoco, G. Organic carbon and total nitrogen topsoil stocks, biogenetic natural reserve ‘Marchesale’ (Calabria region, southern Italy). J. Maps 2017, 13, 91–99. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Stein, A. A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma 2004, 120, 75–93. [Google Scholar] [CrossRef]
- Kumar, S.; Lal, R.; Liu, D. A geographically weighted regression kriging approach for mapping soil organic carbon stock. Geoderma 2012, 189–190, 627–634. [Google Scholar] [CrossRef]
- Peng, G.; Bing, W.; Guangpo, G.; Guangcan, Z. Spatial Distribution of Soil Organic Carbon and Total Nitrogen Based on GIS and Geostatistics in a Small Watershed in a Hilly Area of Northern China. PLoS ONE 2013, 8, e83592. [Google Scholar] [CrossRef]
- Kumar, P.; Pandey, P.C.; Singh, B.K.; Katiyar, S.; Mandal, V.P.; Rani, M.; Tomar, V.; Patairiya, S. Estimation of accumulated soil organic carbon stock in tropical forest using geospatial strategy. Egypt. J. Remote Sens. Space Sci. 2016, 19, 109–123. [Google Scholar] [CrossRef]
- Bhunia, G.S.; Kumar Shit, P.; Pourghasemi, H.R. Soil organic carbon mapping using remote sensing techniques and multivariate regression model. Geocarto Int. 2017, 56, 1–12. [Google Scholar] [CrossRef]
- Mondal, A.; Khare, D.; Kundu, S.; Mondal, S.; Mukherjee, S.; Mukhopadhyay, A. Spatial soil organic carbon (SOC) prediction by regression kriging using remote sensing data. Egypt. J. Remote Sens. Space Sci. 2017, 20, 61–70. [Google Scholar] [CrossRef]
- Gamble, J.D.; Feyereisen, G.W.; Papiernik, S.K.; Wente, C.; Baker, J. Regression-Kriged Soil Organic Carbon Stock Changes in Manured Corn Silage–Alfalfa Production Systems. Soil Sci. Soc. Am. J. 2017, 81, 1557. [Google Scholar] [CrossRef]
- Wang, S.; Zhuang, Q.; Jia, S.; Jin, X.; Wang, Q. Spatial variations of soil organic carbon stocks in a coastal hilly area of China. Geoderma 2018, 314, 8–19. [Google Scholar] [CrossRef]
- Meng, Q. Regression Kriging versus Geographically Weighted Regression Kriging versus Geographically Weighted Regression for Spatial Interpolation. Int. J. Adv. Remote Sens. GIS 2014, 3, 606–615. [Google Scholar]
- Lefohn, A.S.; Knudsen, H.P.; Shadwick, D.S. Using Ordinary Kriging to Estimate the Seasonal W126, and N100 24h-Concentrations for the Year 2000 and 2003. 2005. Available online: https://webcam.srs.fs.fed.us/impacts/ozone/spatial/2000/contractor_2000_2003.pdf (accessed on 4 March 2019).
- Wackernagel, H. Multivariate Geostatistic. An Introduction with Applications; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Sarmadian, F.; Keshavarzi, A.; Rooien, A.; Iqbal, M.; Zahedi, G.; Javadikia, H. Digital mapping of soil phosphorus using multivariate geostatistics and topographic information. Aust. J. Crop Sci. 2014, 8, 1216–1223. [Google Scholar]
- Sun, W.; Minasny, B.; McBratney, A. Analysis and prediction of soil properties using local regression-kriging. Geoderma 2012, 171–172, 16–23. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, C.; Li, W. Predictive mapping of soil total nitrogen at a regional scale: A comparison between geographically weighted regression and cokriging. Appl. Geogr. 2013, 42, 73–85. [Google Scholar] [CrossRef]
- Xu, Y.; Smith, S.E.; Grunwald, S.; Abd-Elrahman, A.; Wani, S.P.; Nair, V.D. Estimating soil total nitrogen in smallholder farm settings using remote sensing spectral indices and regression kriging. CATENA 2018, 163, 111–122. [Google Scholar] [CrossRef]
- Pei, T.; Qin, C.-Z.; Zhu, A.-X.; Yang, L.; Luo, M.; Li, B.; Zhou, C. Mapping soil organic matter using the topographic wetness index: A comparative study based on different flow-direction algorithms and kriging methods. Ecol. Indic. 2010, 10, 610–619. [Google Scholar] [CrossRef]
- Obu, J.; Lantuit, H.; Myers-Smith, I.; Heim, B.; Wolter, J.; Fritz, M. Effect of Terrain Characteristics on Soil Organic Carbon and Total Nitrogen Stocks in Soils of Herschel Island, Western Canadian Arctic. Permafr. Periglac. Process. 2017, 28, 92–107. [Google Scholar] [CrossRef]
- Wang, S.; Zhuang, Q.; Wang, Q.; Jin, X.; Han, C. Mapping stocks of soil organic carbon and soil total nitrogen in Liaoning Province of China. Geoderma 2017, 305, 250–263. [Google Scholar] [CrossRef]
- Fabiyi, O.O.; Ige-Olumide, O.; Fabiyi, A.O. Spatial analysis of soil fertility estimates and NDVI in south-western Nigeria: A new paradigm for routine soil fertility mapping. Res. J. Agric. Environ. Manag. 2013, 2, 403–411. [Google Scholar]
- Bernardi, A.C.d.C.; Grego, C.R.; Andrade, R.G.; Rabello, L.M.; Inamasu, R.Y. Spatial variability of vegetation index and soil properties in an integrated crop-livestock system. Rev. Bras. Eng. Agríc. Ambient. 2017, 21, 513–518. [Google Scholar] [CrossRef]
- Huete, A.R.; Jackson, R.D. Soil and atmosphere influences on the spectra of partial canopies. Remote Sens. Environ. 1988, 25, 89–105. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant Remote Sensing Vegetation Indices: A Review of Developments and Applications. J. Sens. 2017, 2017, 1–17. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G.; Major, D.J. TSAVI: A Vegetation Index Which Minimizes Soil Brightness Effects on LAI and APAR Estimation. In Proceedings of the 12th Canadian Symposium on Remote Sensing Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 10–14 July 1989; Volume 2, pp. 1355–1358. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Chen, Y.; Lian, J.; Luo, Y.; Niu, Y.; Gong, X. Spatial pattern of soil organic carbon and total nitrogen, and analysis of related factors in an agro-pastoral zone in Northern China. PLoS ONE 2018, 13, e0197451. [Google Scholar] [CrossRef]
- Bai, L.; Wang, C.; Zang, S.; Zhang, Y.; Hao, Q.; Wu, Y. Remote Sensing of Soil Alkalinity and Salinity in the Wuyu’er-Shuangyang River Basin, Northeast China. Remote Sens. 2016, 8, 163. [Google Scholar] [CrossRef]
- Pham, T.G.; Nguyen, H.T.; Kappas, M. Assessment of soil quality indicators under different agricultural land uses and topographic aspects in Central Vietnam. Int. Soil Water Conserv. Res. 2018, 6, 280–288. [Google Scholar] [CrossRef]
- Bautista, R.M. Agriculture—Based Development: A SAM Perspective on Central Vietnam; International Food Policy Research Institute: Seoul, Korea, 1999. [Google Scholar]
- Vietnam General Statistics Office. Statistical Yearbook of Vietnam; Statistical Publisher of Vietnam: Hanoi, Vietnam, 2014.
- Huynh, V.C. Multi-Criteria Land Suitability Evaluation for Selected Fruit Crops in Hilly Region of Central Vietnam. with Case Studies in Thua Thien Hue Province; Shaker Verlag: Achen, Germany, 2008. [Google Scholar]
- People’s Committee of A Luoi District. Statistical Year Book: 2005–2015; People’s Committee of A Luoi District: Thua Thien Hue, Vietnam, 2015. [Google Scholar]
- National Institute of Agricultural Planning and Projection of Vietnam. Soil Map of Thua Thien Hue Province (1/100000); National Institute of Agricultural Planning and Projection of Vietnam: Hanoi, Vietnam, 2005. [Google Scholar]
- Natural Resources and Environment Department of A Luoi District. Land Use Map of A Luoi District, Thua Thien Hue province, (1/50000); Natural Resources and Environment Department of A Luoi District: Thua Thien Hue, Vietnam, 2015. [Google Scholar]
- QGIS Development Team. QGIS Geographic Information System. Open Source Geospatial Foundation Project; QGIS Development Team: Grüt, Switzerland, 2018. [Google Scholar]
- Greg, S.; Wu, Y.H. Accuracy and Effort of Interpolation and Sampling: Can GIS Help Lower Field Costs? ISPRS Int. J. Geo-Inf. 2014, 3, 1317–1333. [Google Scholar] [CrossRef]
- Nussbaum, M.; Walthert, L.; Fraefel, M.; Greiner, L.; Papritz, A. Mapping of soil properties at high resolution in Switzerland using boosted geoadditive models. Soil 2017, 3, 191–210. [Google Scholar] [CrossRef]
- Song, X.-D.; Zhang, G.-L.; Liu, F. Predictive Mapping of Soil Organic Matter at a Regional Scale Using Local Topographic Variables: A comparison of Different Polynomial Models. In Digital Soil Mapping Across Paradigms, Scale and Boundaries, 1st ed.; Zhang, G.-L., Brus, D., Liu, F., Song, X.-D., Lagacherie, P., Eds.; Springer: New York, NY, USA, 2016; pp. 219–233. [Google Scholar]
- Walkley, A.; Black, I.S. An examination of the degtjareff method for determining soil organic mater, and a proposed modification of the chromic acid titration method. Soil Sci. 1934, 37, 29–38. [Google Scholar] [CrossRef]
- Bremner, J.M. Determination of nitrogen in soil by the Kjeldahl method. J. Agric. Sci. 1960, 55, 11. [Google Scholar] [CrossRef]
- He, X.T.; Mulvaney, R.L.; Banwart, W.L. A Rapid Method for Total Nitrogen Analysis Using Microwave Digestion. Soil Sci. Soc. Am. J. 1990, 54, 1625–1629. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of The United. Guidelines for Soil Description, 4th ed.; Food and Agriculture Organization of The United: Rome, Italy, 2006. [Google Scholar]
- Xu, D.; Guo, X. A Study of Soil Line Simulation from Landsat Images in Mixed Grassland. Remote Sens. 2013, 5, 4533–4550. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ. 1991, 35, 161–173. [Google Scholar] [CrossRef]
- Richardson, A.J.; Wiegand, C.L. Distinguishing Vegetation from Soil Background Information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
- Fox, G.A.; Sabbagh, G.J.; Searcy, S.W.; Yang, C. An Automated Soil Line Identification Routine for Remotely Sensed Images. Soil Sci. Soc. Am. J. 2004, 68, 1326–1331. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Isaaks, E.H.; Mohan Srivastava, R. An Introduction to Applied Geostatistics; Oxford Unviversity Press: New York, NY, USA, 1989. [Google Scholar]
- Cressie, N.A.C. Statistics for Spatial Data, Revised Edition; John Wiley & Sons, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Hengl, T. A Practical Guide to Geostatistical Mapping, 2nd ed.; Hengl: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Omuto, C.T.; Vargas, R.R. Re-tooling of regression kriging in R for improved digital mapping of soil properties. Geosci. J. 2015, 19, 157–165. [Google Scholar] [CrossRef]
- Odeh, I.O.A.; McBratney, A.B.; Chittleborough, D.J. Further results on prediction of soil properties from terrain attributes: Heterotopic cokriging and regression-kriging. Geoderma 1995, 67, 215–226. [Google Scholar] [CrossRef]
- Edzer Pebesma, B.G. Spatial and Spatio-Temporal Geostatistical Modelling, Prediction and Simulation; R Packages: Münster, Germany, 2018. [Google Scholar]
- Hiemstra, P. Automatic Interpolation Package; R Packages: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Bivand, R.; Keitt, T.; Rowlingson, B.; Pebesma, E.; Sumner, M.; Hijmans, R.; Rouault, E. RGDAL: Bindings for the Geospatial Data Abstraction Library; R Packages: Bergen, Norway, 2017. [Google Scholar]
- Dang, N.T.; Klinnert, C. Problems with and local solutions for organic matter management in Vietnam. Nutr. Cycl. Agroecosyst. J. 2001, 61, 89–97. [Google Scholar] [CrossRef]
- Sam, D.D.; Binh, N.N. Assessment of Productivity of Forest Land in Vietnam; Vietnam Statistical Publishing House: Hanoi, Vietnam, 2001. [Google Scholar]
- Guo, P.-T.; Wu, W.; Liu, H.-B.; Li, M.-F. Effects of land use and topographical attributes on soil properties in an agricultural landscape. Soil Res. 2011, 49, 606. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, G.-L.; Sun, Y.-J.; Zhao, Y.-G.; Li, D.-C. Mapping the Three-Dimensional Distribution of Soil Organic Matter across a Subtropical Hilly Landscape. Soil Sci. Soc. Am. J. 2013, 77, 1241. [Google Scholar] [CrossRef]
- Chen, C.; Hu, K.; Li, H.; Yun, A.; Li, B. Three-Dimensional Mapping of Soil Organic Carbon by Combining Kriging Method with Profile Depth Function. PLoS ONE 2015, 10, e0129038. [Google Scholar] [CrossRef]
- Liu, S.; An, N.; Yang, J.; Dong, S.; Wang, C.; Yin, Y. Prediction of soil organic matter variability associated with different land use types in mountainous landscape in southwestern Yunnan province, China. Catena 2015, 133, 137–144. [Google Scholar] [CrossRef]
- Shi, W.; Liu, J.; Du, Z.; Stein, A.; Yue, T. Surface modelling of soil properties based on land use information. Geoderma 2011, 162, 347–357. [Google Scholar] [CrossRef]
- Radim, V.; Pavlů, L.; Borůvka, L.; Drábek, O. Mapping the Topsoil pH and Humus Quality of Forest Soils in the North Bohemian Jizerské hory Mts. Region with Ordinary, Universal, and Regression Kriging: Cross-Validation Comparison. Soil Water Res. 2013, 8, 97–104. [Google Scholar] [CrossRef]
- Ließ, M.; Schmidt, J.; Glaser, B. Improving the Spatial Prediction of Soil Organic Carbon Stocks in a Complex Tropical Mountain Landscape by Methodological Specifications in Machine Learning Approaches. PLoS ONE 2016, 11, e0153673. [Google Scholar] [CrossRef] [PubMed]
- Ranjan, R.; Ankita, J.; Ramu, N.; Nain, A.S. Soil Organic Carbon Estimation Using Remote Sensing in Tarai Region of Uttarakhand. Ann. Plant Soil Res. 2015, 17, 361–364. [Google Scholar]
- Wu, L.; Li, L.; Yao, Y.; Qin, F.; Guo, Y.; Gao, Y.; Zhang, M. Spatial distribution of soil organic carbon and its influencing factors at different soil depths in a semiarid region of China. Environ. Earth Sci. 2017, 76. [Google Scholar] [CrossRef]
- West, H.; Quinn, N.; Horswell, M.; White, P. Assessing Vegetation Response to Soil Moisture Fluctuation under Extreme Drought Using Sentinel-2. Water 2018, 10, 838. [Google Scholar] [CrossRef]
- Misra, A.; Germund, T. Influence of Soil Moisture on Soil Solution Chemistry and Concentrations of Minerals in the Calcicoles Phleum phleoides and Veronica spicata Grown on a Limestone Soil. Ann. Bot. 1999, 84, 401–410. [Google Scholar] [CrossRef]
- Zhu, H.; Bi, R.; Duan, Y.; Xu, Z. Scale-location specific relations between soil nutrients and topographic factors in the Fen River Basin, Chinese Loess Plateau. Front. Earth Sci. 2017, 11, 397–406. [Google Scholar] [CrossRef]
- Kumar, N.; Velmurugan, A.; Hamm, N.A.S.; Dadhwal, V.K. Geospatial Mapping of Soil Organic Carbon Using Regression Kriging and Remote Sensing. J. Indian Soc. Remote Sens. 2018, 46, 705–716. [Google Scholar] [CrossRef]
- She, D.; Xuemei, G.; Jingru, S.; Timm, L.C.; Hu, W. Soil organic carbon estimation with topographic properties in artificial grassland using a state-space modeling approach. Can. J. Soil. Sci. 2014, 94, 503–514. [Google Scholar] [CrossRef]
- Wiesmeier, M.; Prietzel, J.; Barthold, F.; Spörlein, P.; Geuß, U.; Hangen, E.; Reischl, A.; Schilling, B.; von Lützow, M.; Kögel-Knabner, I. Storage and drivers of organic carbon in forest soils of southeast Germany (Bavaria)—Implications for carbon sequestration. For. Ecol. Manag. 2013, 295, 162–172. [Google Scholar] [CrossRef]
- Yang, R.; Rossiter, D.G.; Liu, F.; Lu, Y.; Yang, F.; Yang, F.; Zhao, Y.; Li, D.; Zhang, G. Predictive Mapping of Topsoil Organic Carbon in an Alpine Environment Aided by Landsat TM. PLoS ONE 2015, 10, e0139042. [Google Scholar] [CrossRef]
- Seibert, J.; Stendahl, J.; Sørensen, R. Topographical influences on soil properties in boreal forests. Geoderma 2007, 141, 139–148. [Google Scholar] [CrossRef]
- Huang, H.-H.; Adamchuk, V.; Biswas, A.; Ji, W.; Lauzon, S. Analysis of Soil Properties Predictability Using Different On-the-Go Soil Mapping Systems. In Proceedings of the 14th International Conference on Precision, Montreal, QC, Canada, 24–27 June 2018. [Google Scholar]
- Hjerdt, K.N.; McDonnell, J.J.; Seibert, J.; Rodhe, A. A new topographic index to quantify downslope controls on local drainage. Water Resour. Res. 2004, 40, 2135. [Google Scholar] [CrossRef]
- Li, X.; McCarty, G.W.; Lang, M.; Ducey, T.; Hunt, P.; Miller, J. Topographic and physicochemical controls on soil denitrification in prior converted croplands located on the Delmarva Peninsula, USA. Geoderma 2018, 309, 41–49. [Google Scholar] [CrossRef]
- Zhu, Q.; Lin, H.S. Comparing Ordinary Kriging and Regression Kriging for Soil Properties in Contrasting Landscapes. Pedosphere 2010, 20, 594–606. [Google Scholar] [CrossRef]
- Herbst, M.; Diekkrüger, B.; Vereecken, H. Geostatistical co-regionalization of soil hydraulic properties in a micro-scale catchment using terrain attributes. Geoderma 2006, 132, 206–221. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, C.; Li, W. Comparison of Geographically Weighted Regression and Regression Kriging for Estimating the Spatial Distribution of Soil Organic Matter. Gisci. Remote Sens. 2012, 49, 915–932. [Google Scholar] [CrossRef]
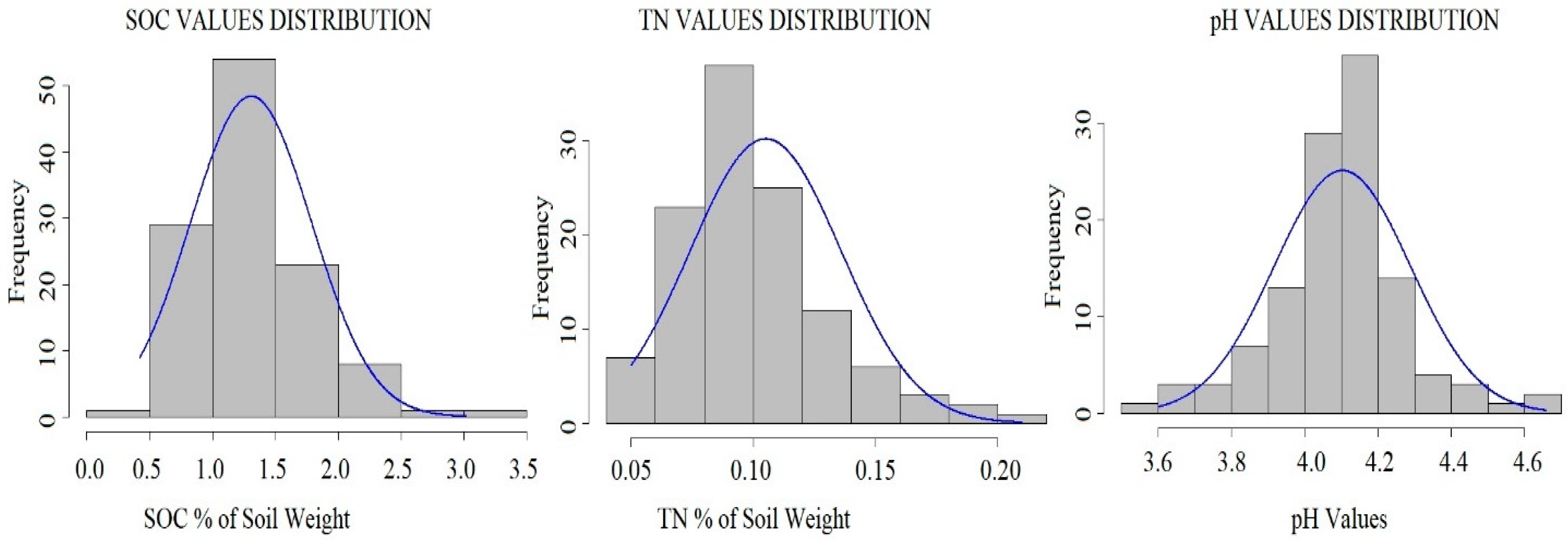
| Soil Indicator | Mean | Median | Min | Max | Std. Deviation | Skewness |
|---|---|---|---|---|---|---|
| SOC | 1.31 | 1.29 | 0.42 | 3.02 | 0.48 | 0.90 |
| TN | 0.11 | 0.10 | 0.05 | 0.21 | 0.03 | 0.82 |
| pH | 4.10 | 4.11 | 3.60 | 4.68 | 0.19 | 0.02 |
| Predictive Model | Variance Explanation (%) | ||
|---|---|---|---|
| SOC | TN | pH | |
| y = f(TSAVI) | 2.08 | 0.01 | 4.03 |
| y = f(TWI) | 7.19 | 0.01 | 4.59 |
| y = f(LUT) | 14.52 | 7.00 | 18.40 |
| y = f(TSAVI, TWI, LUT) | 14.51 | 5.60 | 17.15 |
| y = f(TWI, LUT) | 14.98 | 6.30 | 17.77 |
| y = f(TSAVI, LUT) | 13.91 | 6.25 | 17.71 |
| y = f(TSAVI, TWI) | 7.00 | 0.01 | 5.90 |
| Soil Property | Model | Initial Semivariogram | Residual Semivariogram | Nugget/Sill (Initial Data) | ||||
|---|---|---|---|---|---|---|---|---|
| Range (m) | Sill | Nugget | Range (m) | Sill | Nugget | |||
| SOC | Spherical | 6500 | 0.23 | 0.13 | 3800 | 0.19 | 0.09 | 0.56 |
| TN | Spherical | 5000 | 7.5 × 10−4 | 10−4 | 4000 | 7.5 × 10−4 | 10−4 | 0.13 |
| pH | Spherical | 6500 | 0.029 | 0.025 | 2800 | 0.026 | 0.016 | 0.86 |
| SOC | TN | pH | ||||
|---|---|---|---|---|---|---|
| OK | RK | OK | RK | OK | RK | |
| ME | −0.034 | −0.041 | −0.008 | −0.008 | 0.001 | −0.019 |
| RMSE | 0.327 | 0.337 | 0.018 | 0.020 | 0.202 | 0.198 |
| RI | −3.33% | −10.00% | 1.81% | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gia Pham, T.; Kappas, M.; Van Huynh, C.; Hoang Khanh Nguyen, L. Application of Ordinary Kriging and Regression Kriging Method for Soil Properties Mapping in Hilly Region of Central Vietnam. ISPRS Int. J. Geo-Inf. 2019, 8, 147. https://doi.org/10.3390/ijgi8030147
Gia Pham T, Kappas M, Van Huynh C, Hoang Khanh Nguyen L. Application of Ordinary Kriging and Regression Kriging Method for Soil Properties Mapping in Hilly Region of Central Vietnam. ISPRS International Journal of Geo-Information. 2019; 8(3):147. https://doi.org/10.3390/ijgi8030147
Chicago/Turabian StyleGia Pham, Tung, Martin Kappas, Chuong Van Huynh, and Linh Hoang Khanh Nguyen. 2019. "Application of Ordinary Kriging and Regression Kriging Method for Soil Properties Mapping in Hilly Region of Central Vietnam" ISPRS International Journal of Geo-Information 8, no. 3: 147. https://doi.org/10.3390/ijgi8030147
APA StyleGia Pham, T., Kappas, M., Van Huynh, C., & Hoang Khanh Nguyen, L. (2019). Application of Ordinary Kriging and Regression Kriging Method for Soil Properties Mapping in Hilly Region of Central Vietnam. ISPRS International Journal of Geo-Information, 8(3), 147. https://doi.org/10.3390/ijgi8030147







