A Universal Generating Algorithm of the Polyhedral Discrete Grid Based on Unit Duplication
Abstract
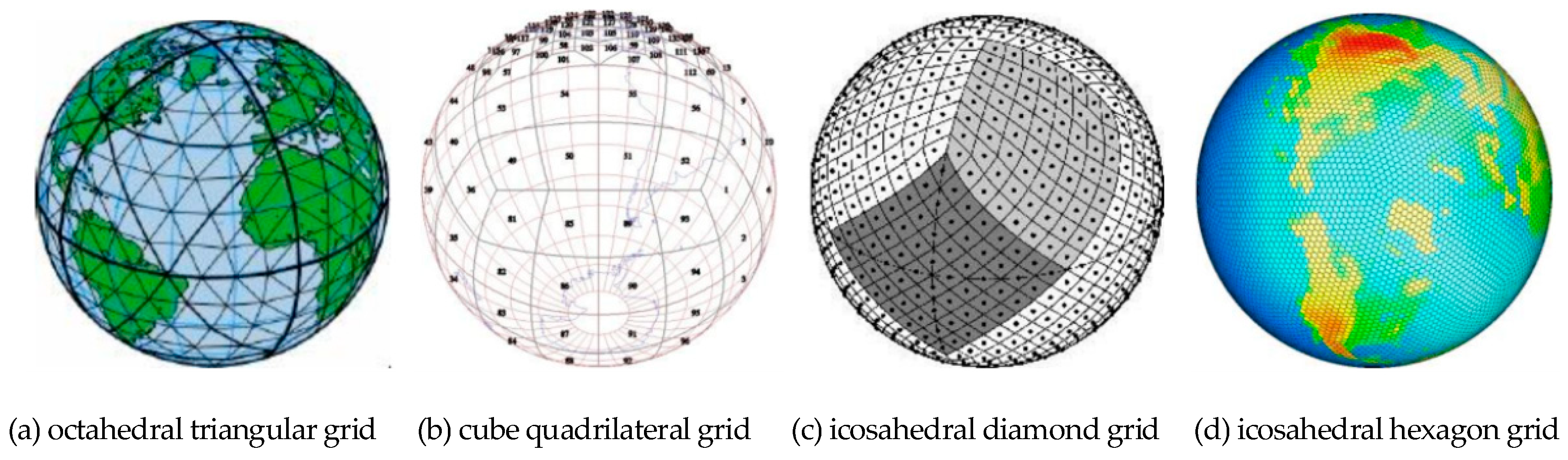
1. Introduction
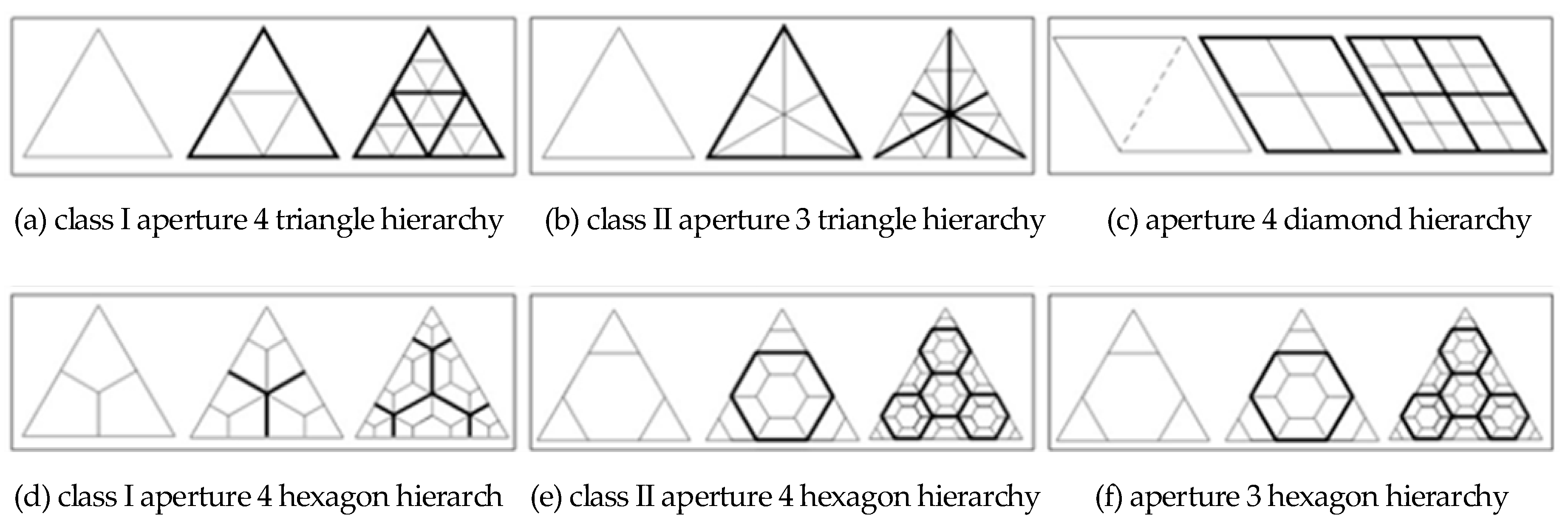
- It is necessary to customize the corresponding grid generation algorithm according to the shape (triangle, quadrilateral, or hexagon) of the target grid, the aperture (3 or 4 aperture) [9], the prime factor, the duality, the centricity of the subdivision frequency [1], and other factors [8]. The recursive subdivision methods of different partition topologies are shown in Figure 2.
- In the process of the recursion grid generation method, an effective distributed algorithm with high algorithmic complexity needs to be designed for the generation of high-level grids.
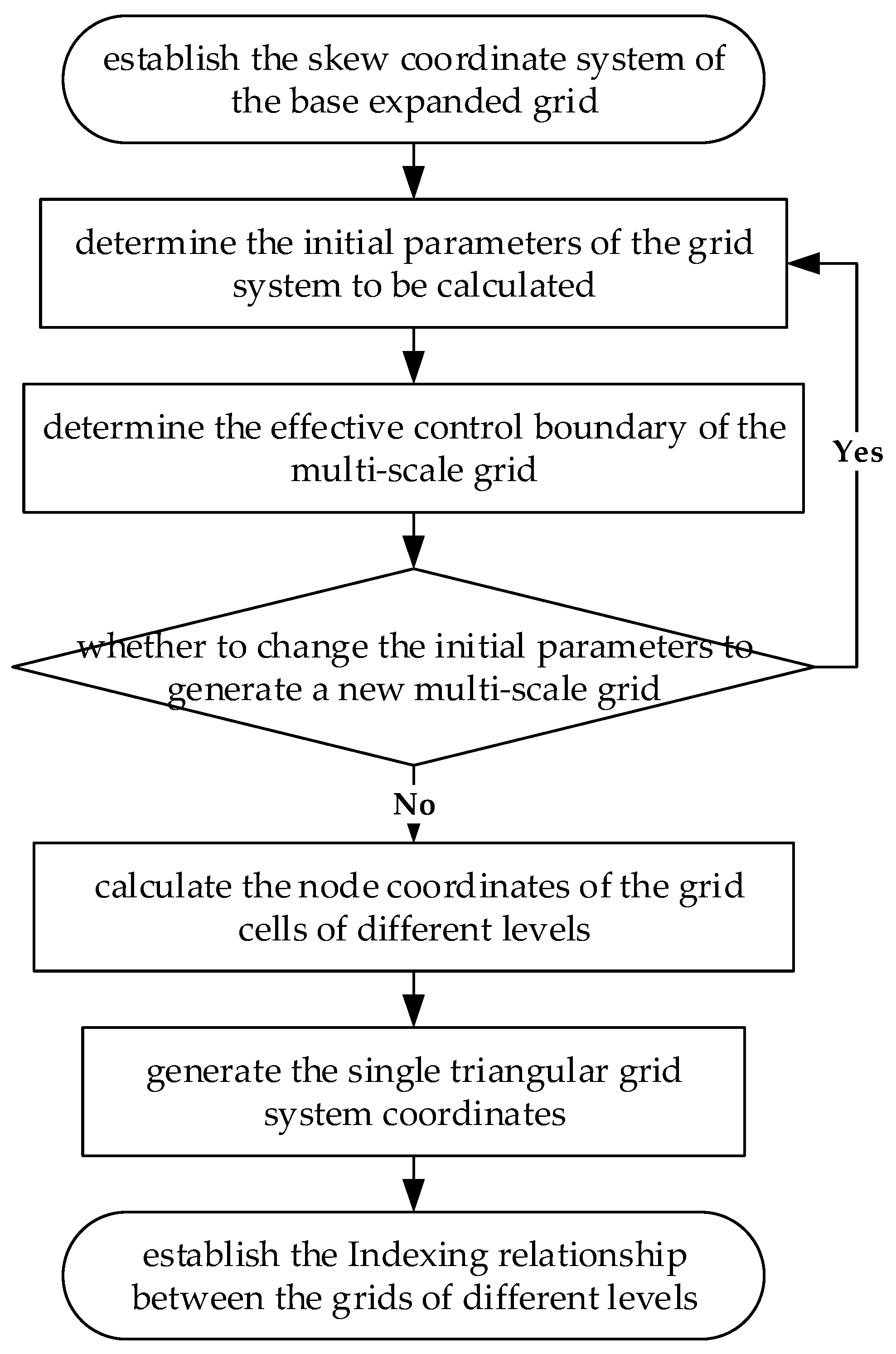
2. Algorithm Thoughts
- (1)
- establish the skew coordinate system of the base expanded grid,
- (2)
- determine the type of the grid system to be calculated,
- (3)
- determine the effective control boundaries of the grids of different levels,
- (4)
- calculate the node coordinates of the grid cells of different levels,
- (5)
- generate the single triangular grid system coordinates,
- (6)
- establish the indexing relationship between the grids of different levels.
3. Methodology
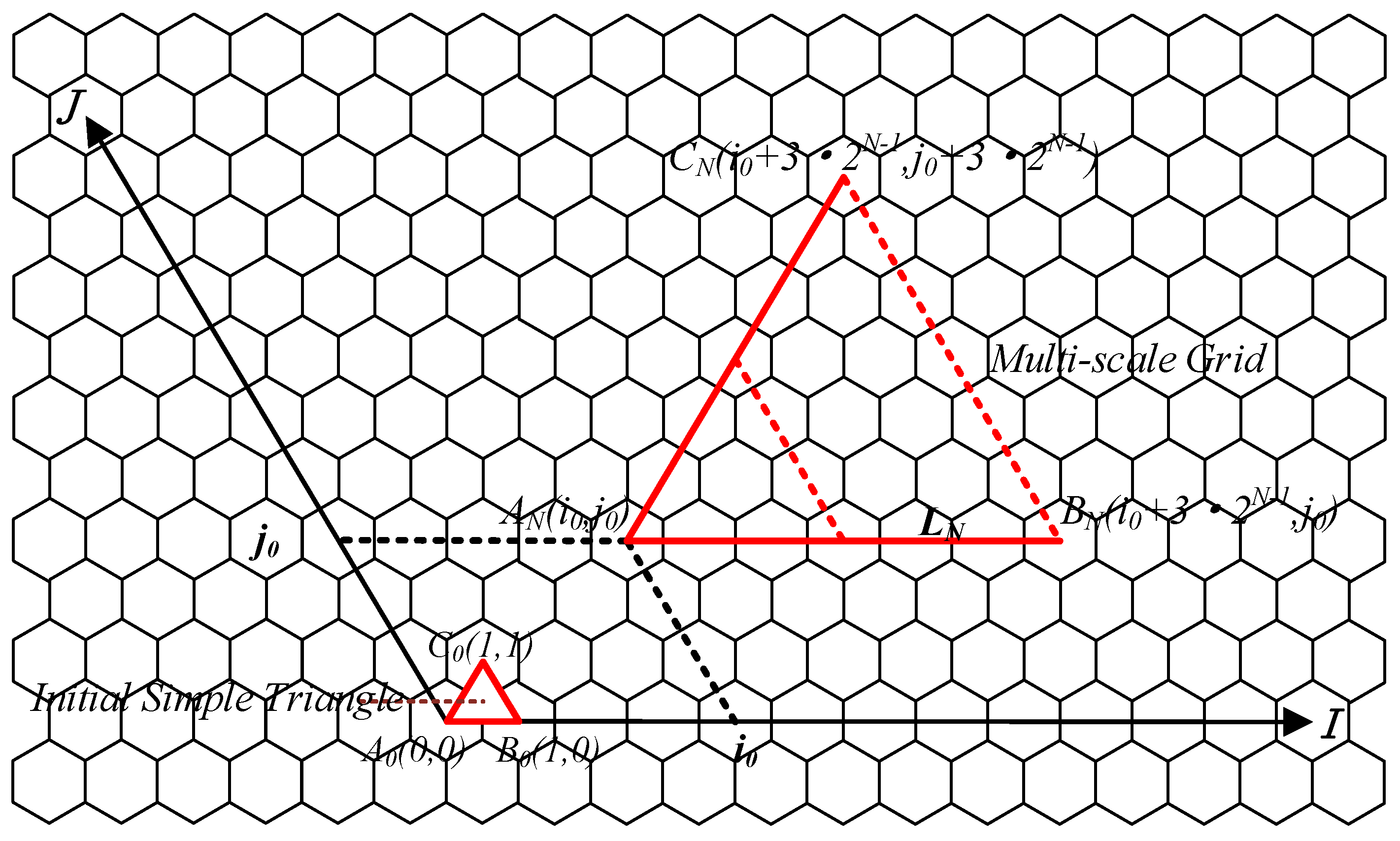
3.1. Establishment of the Skew Coordinate System of the Base Expanded Grid
3.2. Determination the Type of the Grid System to Be Calculated
3.3. Determination of the Effective Control Boundary of the Grids of Different Levels
3.4. Calculation of the Node Coordinates of Grid Cells of Different Levels
3.5. Generation of the Single Triangular Grid System Coordinates
- When , there is a only single triangular grid system unit (plane) and H is a two-dimensional rotation matrix.
- When , a transformation from the initial single triangular face (plane) to the spatial triangular face is required, through which the grid of the icosahedral surface can be directly generated.
3.6. Establishment of the Relationship between the Grids of Different Levels
3.7. Some Key Parameters
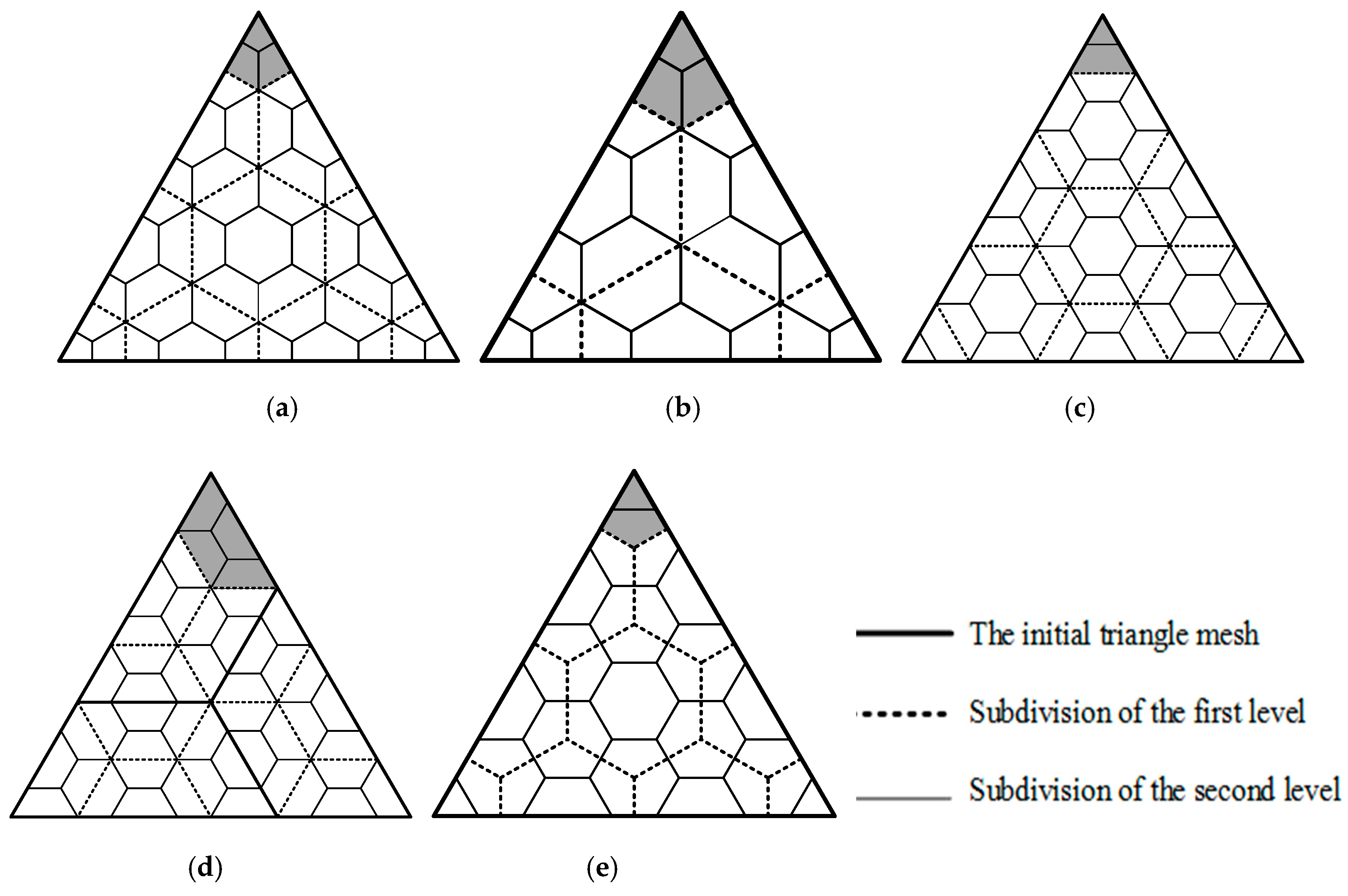
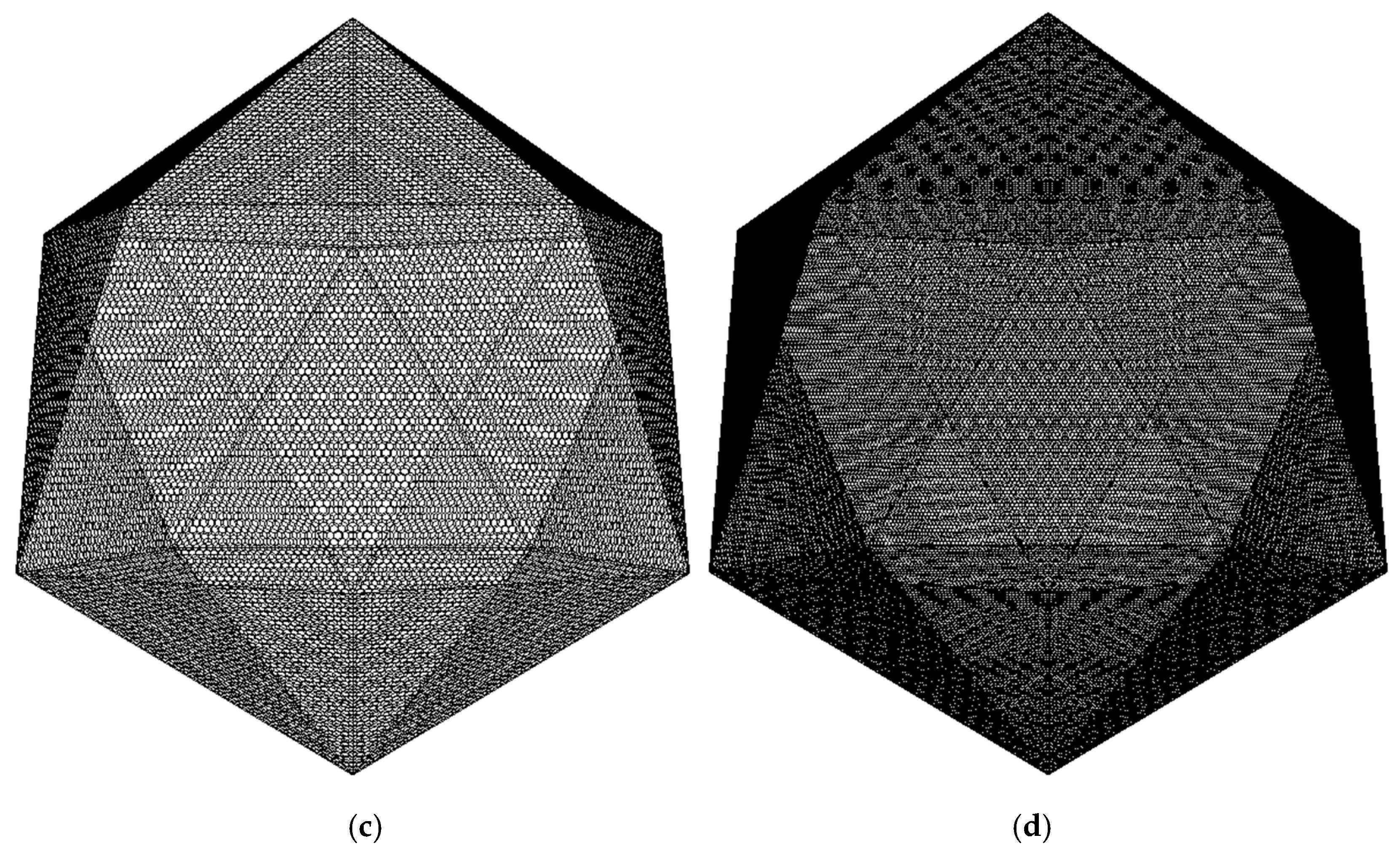
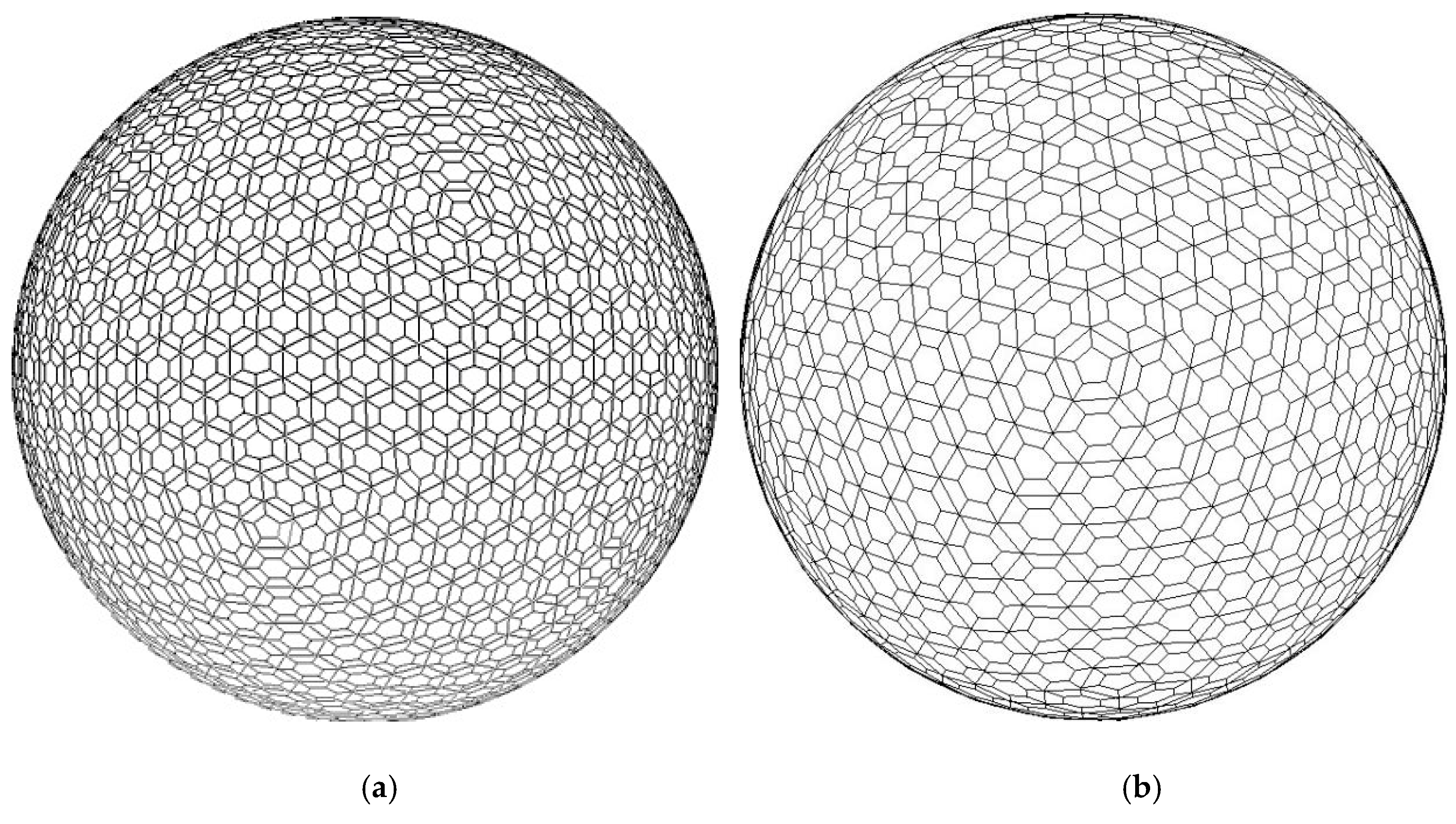
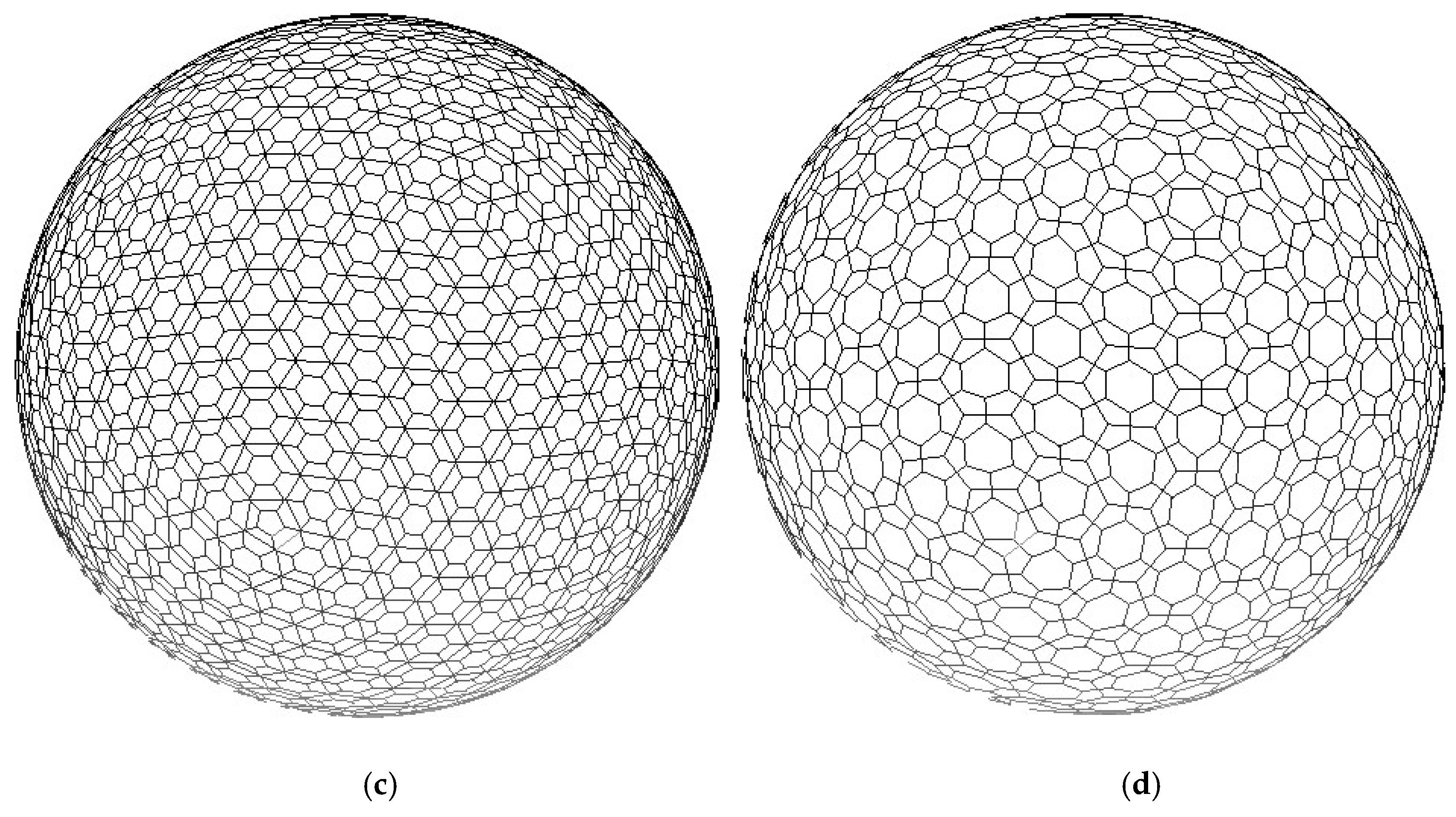
4. Experiments and Discussion
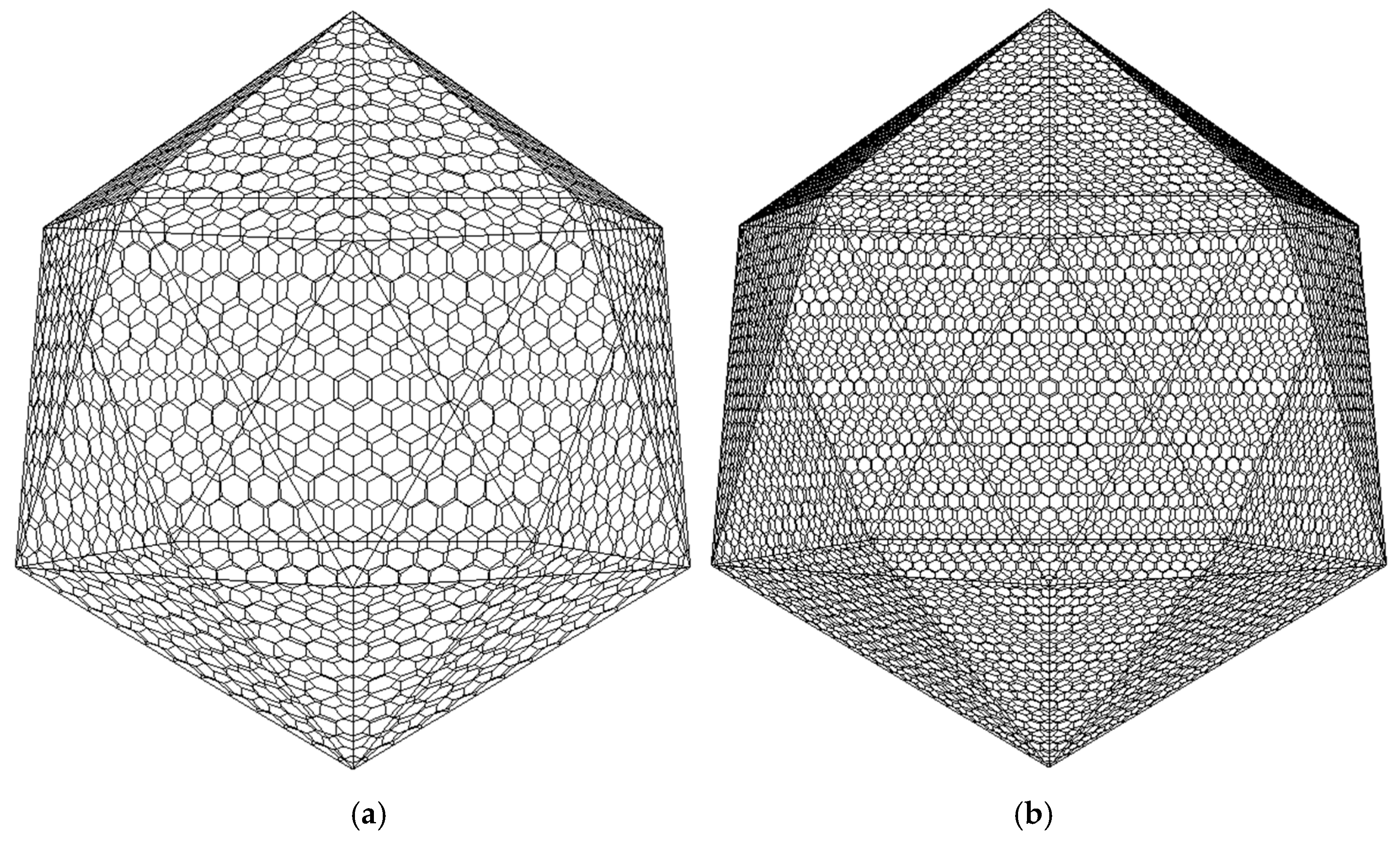
4.1. Experiments
4.2. Discussion
- (1)
- Compared with the existing hierarchical recursive subdivision, it is not necessary to customize the exclusive generation algorithm for a specific aperture, subdivision frequency, and eccentricity, which provides convenience for different split type grid generation algorithms. Furthermore, it highlights the potential links between the various types of grids and strengthens the theoretical research on the communication, sharing and interoperability among the global discrete grid systems.
- (2)
- Compared with hierarchical recursive subdivision, in the process of high-level grid generation, it is not necessary to design an effective distributed algorithm, which reduces the complexity of the algorithm.
- (3)
- In fact, the algorithm is also applicable to the generation of triangular and quadrilateral global grid systems. It only needs to change the basic shape of the mesh in the base extended grid coordinate system. In essence, the algorithm truly achieves the generalized generation of multiscale meshes of each split type.
- (4)
- Compared with the current single-level grid generation method, the algorithm is more concise, more flexible and more operable.
- (1)
- The algorithm only considers one triangle of a regular polyhedron and does not involve the processing of boundary trans-plane elements in terms of the global grid elements.
- (2)
- There is a problem of repeated rendering at the triangle boundary and the vertex of a boundary grid, which affects the efficiency of the global grid generation to some extent.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Y.; Benjin, T.X. Spherical Discrete Grid of Geospatial Information: Theory, Algorithms and Applications; Science Press: Beijing, China, 2007. [Google Scholar]
- Zhang, Y.; Benjin, T.X. Spatial information processing method based on spherical hexagonal grid system. J. Surv. Mapp. Sci. Technol. 2006, 23, 110–114. [Google Scholar]
- Dutton, G. Geodesic modelling of planetary relief. Cartographica 1984, 21, 188–207. [Google Scholar] [CrossRef]
- Dutton, G. Modeling locational uncertainty via hierarchical tessellation. In Accuracy of Spatial Database; Tayor and Francis: London, UK, 1989; pp. 125–140. [Google Scholar]
- Goodchild, M.; Yang, S. A hierarchical spatial data structure for global geographic information systems. Graph. Models Image Process. 1992, 54, 31–44. [Google Scholar] [CrossRef]
- Szalay, A.S.; Gray, J.; Fekete, G.; Kunszt, P.Z.; Kukol, P.; Thakar, A. Indexing the Sphere with the Hierarchical Triangular Mesh; Technical Report; Microsoft Research: Redmond, WA, USA, 2005. [Google Scholar]
- Alborzi, H.; Samet, H. Augmenting SAND with a spherical data model. In Proceedings of the International Conference on Discrete Global Grids, Santa Barbara, CA, USA, 26–28 March 2000. [Google Scholar]
- White, D. Global grids from recursive diamond subdivisions of the surface of an octahedron or icosahedron. Environ. Monit. Assess. 2000, 64, 93–103. [Google Scholar] [CrossRef]
- Sahr, K.; White, D.; Kimerling, A.J. Geodesic Discrete Global Grid Systems. Cartogr. Geogr. Inf. Sci. 2003, 30, 121–134. [Google Scholar] [CrossRef]
- Peterson, P. Closed-Packed Uniformly Adjacent, Multi-Resolutional Overlapping Spatial Data Ordering. U.S. Patent #0,8018,458, 13 September 2011. [Google Scholar]
- Vince, A. Indexing the aperture 3 hexagonal discrete global grid. J. Vis. Commun. Image Represent. 2006, 17, 1227–1236. [Google Scholar] [CrossRef]
- Zheng, X. Efficient Fourier Transforms on Hexagonal Arrays; University of Florida: Gainesville, FL, USA, 2007. [Google Scholar]
- Tong, X.; Ben, J.; Liu, Y.; Zhang, Y. Modeling and Expression of Vector Data in the Hexagonal Discrete Global Grid System. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-4/W2, 15–25. [Google Scholar] [CrossRef]
- Lin, B.; Zhou, L.; Xu, D.; Zhu, A.X.; Lu, G. A discrete global grid system for earth system modeling. Int. J. Geogr. Inf. Sci. 2018, 32, 711–737. [Google Scholar] [CrossRef]
- Mostafavi, M.A.; Gold, C.M. A global kinetic spatial data structure for a marine simulation. Int. J. Geogr. Inf. Sci. 2004, 18, 211–227. [Google Scholar] [CrossRef]
- Ottoson, P.; Hauska, H. Ellipsoidal quadtrees for indexing of global geographical data. Int. J. Geogr. Inf. Sci. 2002, 16, 213–226. [Google Scholar] [CrossRef]
- Bartholdi, J.J.; Goldsman, P. Continuous indexing of hierarchical subdivisions of the globe. Int. J. Geogr. Inf. Sci. 2001, 15, 489–522. [Google Scholar] [CrossRef]
- Amiri, A.M.; Samavati, F.; Peterson, P. Categorization and Conversions for Indexing Methods of Discrete Global Grid Systems. ISPRS Int. J. Geo-Inf. 2015, 4, 320–336. [Google Scholar] [CrossRef]
- Olsen, A.R.; Stevens, D.L.; White, D. Application of global grids in environmental sampling. Computing 1998, 30, 279–284. [Google Scholar]
- Randall, D.A.; Ringler, T.D.; Heikes, R.P.; Jones, P.; Baumgardner, J. Climate modeling with spherical geodesic grids. Comput. Sci. Eng. 2002, 4, 32–41. [Google Scholar] [CrossRef]
- Lee, M.; Samet, H. Navigating through triangle meshes implemented as linear quadtrees. ACM Trans. Graph. 2000, 19, 79–121. [Google Scholar] [CrossRef]
- Tsatcha, D.; Saux, É.; Claramunt, C. A bidirectional path-finding algorithm and data structure for maritime routing. Int. J. Geogr. Inf. Sci. 2014, 28, 1355–1377. [Google Scholar] [CrossRef]
- Stefanakis, E.; Kavouras, M. On the determination of the optimum path in space. Genesis 1995. [Google Scholar] [CrossRef]
- Kiester, A.R.; Sahr, K. Planar and spherical hierarchical, multi-resolution cellular automata. Comput. Environ. Urban Syst. 2008, 32, 204–213. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, L.; Wang, H. Modeling methods and basic problems of global discrete grid. Geogr. Geogr. Inf. Sci. 2012, 28, 29–34. [Google Scholar]
- Zhao, X.; Yuan, Z.; Zhao, L.; Zhu, S. An improved approximate equal-area QTM partition model. J. Surv. Mapp. 2016, 45, 112–118. [Google Scholar]
- Zhao, X.; Bai, J. Global discrete grid hierarchical modeling based on diamond block. J. Chin. Univ. Min. Technol. 2007, 36, 397–401. [Google Scholar]
- Ben, J.; Tong, X.; Zhou, C.; Zhang, K. Hexagonal discrete grid system generation algorithm for octahedron. J. Geo-Inf. Sci. 2015, 17, 789–797. [Google Scholar]

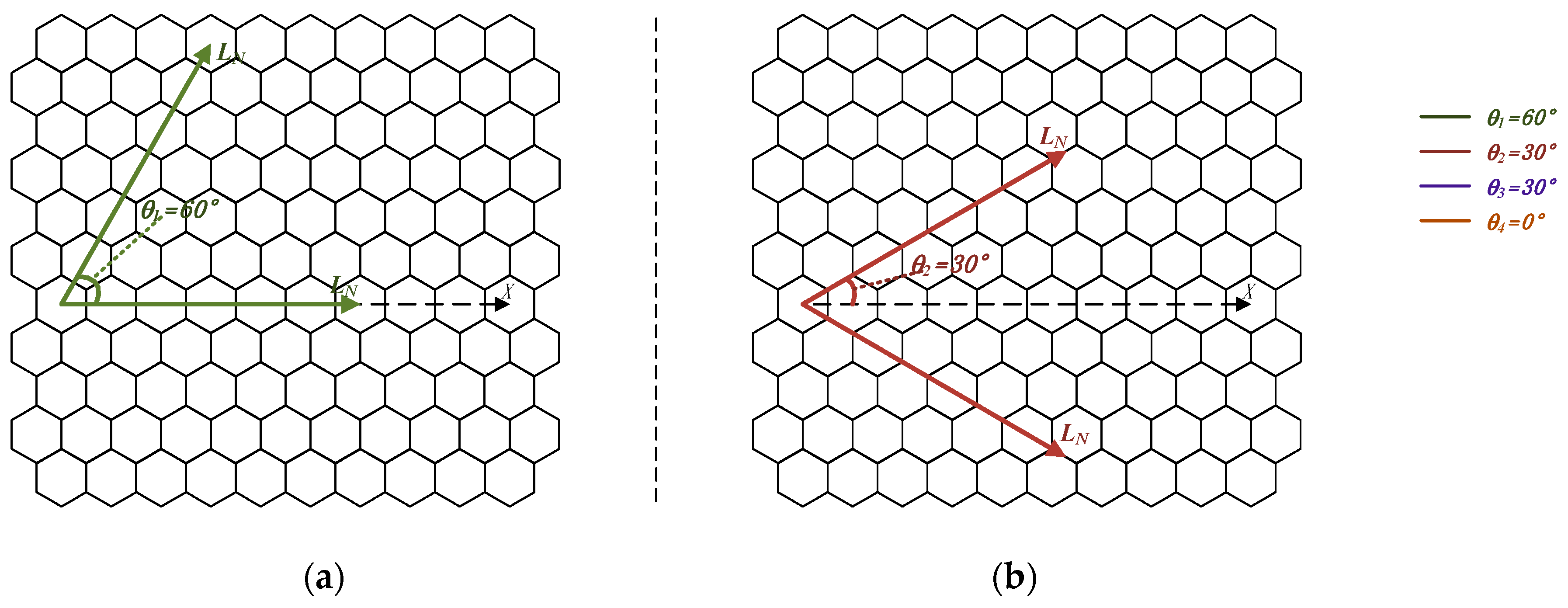
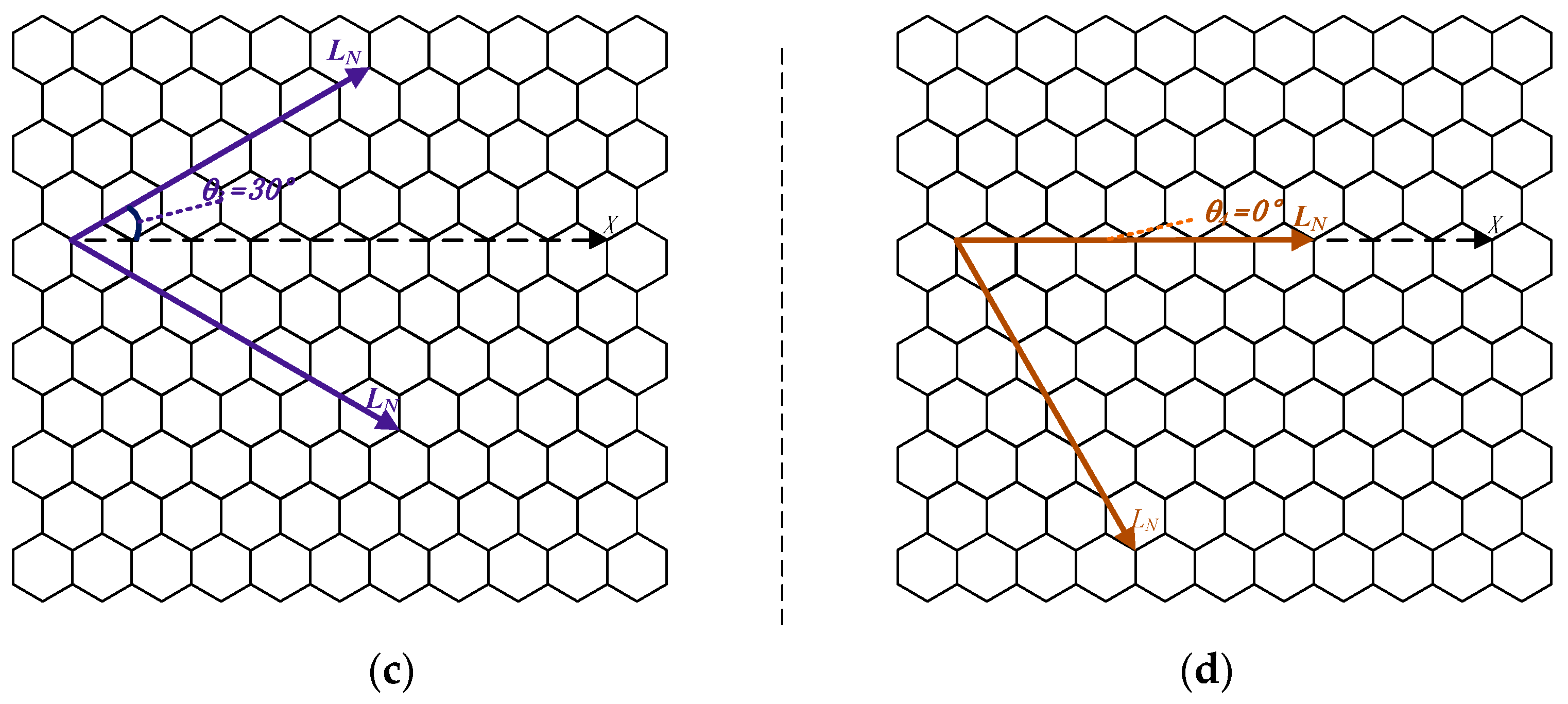
| Grid parameter | Grid Type | Starting Position | Grid Node Coordinates of the Nth Level | Grid Coordinate Range of the Nth Level | Rectangular Coordinates of Unit Nodes in the Single Triangular Grid System | |||
|---|---|---|---|---|---|---|---|---|
| Grid Shape at Triangular Boundaries | ||||||||
 | class I aperture 4 grid | Formula (5) | ||||||
| class II aperture 4 grid | Formula (7) | |||||||
| aperture 3 even grid | Formula (8) | |||||||
 | aperture 3 odd grid | Formula (9) | ||||||
| class III aperture 4 grid | Formula (10) | |||||||
 | class IV aperture 4 grid | Formula (11) | ||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, L.; Tong, X.; Fan, S.; Cheng, C.; Chen, B.; Yang, W.; Hou, K. A Universal Generating Algorithm of the Polyhedral Discrete Grid Based on Unit Duplication. ISPRS Int. J. Geo-Inf. 2019, 8, 146. https://doi.org/10.3390/ijgi8030146
Meng L, Tong X, Fan S, Cheng C, Chen B, Yang W, Hou K. A Universal Generating Algorithm of the Polyhedral Discrete Grid Based on Unit Duplication. ISPRS International Journal of Geo-Information. 2019; 8(3):146. https://doi.org/10.3390/ijgi8030146
Chicago/Turabian StyleMeng, Li, Xiaochong Tong, Shuaibo Fan, Chengqi Cheng, Bo Chen, Weiming Yang, and Kaihua Hou. 2019. "A Universal Generating Algorithm of the Polyhedral Discrete Grid Based on Unit Duplication" ISPRS International Journal of Geo-Information 8, no. 3: 146. https://doi.org/10.3390/ijgi8030146
APA StyleMeng, L., Tong, X., Fan, S., Cheng, C., Chen, B., Yang, W., & Hou, K. (2019). A Universal Generating Algorithm of the Polyhedral Discrete Grid Based on Unit Duplication. ISPRS International Journal of Geo-Information, 8(3), 146. https://doi.org/10.3390/ijgi8030146






