Abstract
A contextual effects model, built based on Bayesian spatial modeling strategy, was used to investigate contextual effects on neighborhood burglary risks in Wuhan, China. The contextual effects denote the impact of the upper-level area on the lower-level units of analysis. These effects are often neglected in Bayesian spatial crime analysis. The contextual effects model accounts for the effects of independent variables, overdispersion, spatial autocorrelation, and contextual effects. Both the contextual effects model and the conventional Bayesian spatial model were fitted to our data. Results showed the two models had almost the same deviance information criterion (DIC). Furthermore, they identified the same set of significant independent variables and gave very similar estimates for burglary risks. Nonetheless, the contextual effects model was preferred in the sense that it provides insights into contextual effects on crime risks. Based on the contextual effects model and the map decomposition technique, we identified, worked out, and mapped the relative contribution of the neighborhood characteristics and contextual effects on the overall burglary risks. The research contributes to the increasing literature on modeling crime data by Bayesian spatial approaches.
1. Introduction
Geographers and criminologists have had an everlasting interest in the geography of crime [1]. An empirical study of crime can investigate the geographical variations of crime risks and potential risk factors underling those variations. Clearly, a comprehensive understanding of this relationship contributes to better-informed crime intervention and prevention efforts. From the existing literature, researchers have adopted non-spatial regression models in ecological studies of crime [2]. These models are not adequate to analyze crime at a small-area scale, as they do not take into account any spatial relationships between units of analysis. In practice, however, small-area crime data are usually spatially auto-correlated. Neglecting this spatial autocorrelation can result in biased inference [3].
Methodologically, spatial autocorrelation has been accounted for by frequentist spatial statistical models. For instance, Morenoff et al. [4] employed a spatial lag model to probe into the association between neighborhood-level characteristics and violent crime. Andresen [5] employed a spatial error model to investigate the impact of socioeconomic features on crime rates at the census tract level. However, these frequentist statistical models have shortcomings. They cannot handle the small number problem [6], possibly leading to unstable risk estimates and underestimated standard errors [7]. Another methodological problem difficult to solve by frequentist statistical models is overdispersion in count data. It has been recognized as a particular problem in generalized linear modeling for the analysis of grouped data [8]. Accounting for overdispersion is essential as it has an impact on the estimates for regression parameters [9].
In addition to frequentist approaches, Bayesian methods have also been applied in spatial data analysis. The Bayesian approach, differing from the frequentist approach, views a parameter as a random variable with a probability distribution. Its basic principle is that prior knowledge is combined with data to produce posterior distributions of parameters on which the posterior estimates are based. Implementation of the Markov chain Monte Carlo (MCMC) simulations makes Bayesian statistics and modeling fashionable in a wide range of scientific research [10]. By MCMC, it is feasible to fit complex models computationally intractable by frequentist statistics. In parallel, the rapid evolution of software such as WinBUGS has further promoted the popularity of Bayesian methods.
Bayesian approaches in spatial data analysis have grown rapidly since the 1990s. They have advantages in fitting complex spatial models and can overcome shortcomings of frequentist approaches. Through random effects terms, Bayesian models account for overdispersion and spatial autocorrelation. They can provide more stable risk estimates than comparable frequentist methods. In spite of these advantages, their application in small-area crime analysis is still not common. Nonetheless, there is a growing awareness of the strengths of the Bayesian spatial modeling approaches. An increasing number of studies have used Bayesian models. Specifically, the influence of socioeconomic variables on property crime [11,12,13], suicide [14], juvenile offenders [15], and violent crime [16], and the spatio-temporal patterns of crime [17,18] have been investigated. Bayesian spatial modeling approaches have gradually gained popularity among researches of crime analysis. Despite the growing awareness of and the increased literature on Bayesian spatial modeling, little work has focused on contextual effects in crime analysis.
Contextual effects generally denote the impact of the upper-level area on the lower-level units of analysis. Take the neighborhood and sub-district in China as an example to illustrate the contextual effects. The neighborhood set is a unique subdivision of the sub-district set in China. Each neighborhood falls uniquely within a sub-district and each sub-district consists of several neighborhoods. Neighborhoods are clustered within sub-districts. It is therefore likely that additional clustering of high (or low) crime risks common to neighborhoods falling within the same sub-district may exist due to urban construction, planning policy, urban administration, and public social control. Some grouping effect based on sub-district could be found for neighborhoods lying within a given sub-district. Specifically, the sub-district level should have a contribution from effects at the neighborhood level. As a consequence, there is multiscale information theoretically in the sense that the lower-level neighborhood units fall completely and uniquely within the upper-level sub-district units. Due to this clustered and hierarchical structure of data, local crime pattern is simultaneously affected by characteristics of the environment at multiple spatial scales [19,20]. It results from the joint effects of different layers of crime potential [21]. Furthermore, the influence of crime risk factors is potentially conditional on context and can operate across multiple scales. Neglecting these information can lead to incorrect inferences on risk factors [22]. One natural way using the multiscale information is to take into account the contextual effects. From the practical perspective, crime risks are influenced by both neighborhood characteristics themselves and contextual effects. Disentangling and identifying the contribution of the two sources of variation on risks are valuable for crime prevention and control. If most of the variation in crime risks is due to neighborhood characteristics, attention should be given to neighborhood-level factors. In contrast, if contextual effects account for most of the variation, a focus on upper-level sub-districts can contribute to a more effective crime prevention strategy.
Contextual effects have been examined in past studies by hierarchical linear models. For example, Johnson and Bowers [23] focused on the relationship between permeability of a street network and burglary risk while taking account of the nesting in the data. Davies and Johnson [24] examined the role of road structure (betweenness and linearity) on the spatial variability of burglary risks by a quantitative network analysis. Steenbeek and Weisburd [25] examined variability of crime for street segments, neighborhoods, and districts in Hague city. Deryol et al. [26] illustrated the effects of nodes, paths, and the macro-environmental context on the formation and development of crime hotspots. Schnell et al. [27] explored the impact of street segments, neighborhood clusters, and community areas on the distribution of violent crime in Chicago. The models these researchers adopted accounted for the hierarchical structure of the data and were fitted by frequentist approaches. More recently, Quick [28] applied a Bayesian cross-classified multilevel modeling approach, accommodating the influence of non-hierarchical upper-level units, to analyze the spatiotemporal patterns of crime in the Region of Waterloo.
In the current research, we aim to shed light on contextual effects on burglary risks. We adopt a contextual effects model to investigate contextual effects on burglary risks. The model is built based on Bayesian spatial modeling strategy and accounts for the hierarchical structure of data. The research contributes to the increasing literature on modeling crime data by Bayesian spatial approaches, as contextual effects are generally overlooked.
The remainder of this paper consists of five parts. Following an introduction, the study area and data are briefly described. Then, we thoroughly introduce the research methodology. Subsequently, results of our analysis are provided. Afterwards, we discuss the results. Finally, we conclude our study.
2. Materials
2.1. Study Area
Our research focused on Jianghan District, located in Wuhan City of Hubei Province, China. Wuhan is the political, economic, educational, and transportation center of Central China. The Jianghan District is one of the most prosperous urban districts of Wuhan, consisting of 13 sub-districts and 116 neighborhoods (Figure 1). The neighborhoods’ area ranges between 0.024 and 5.753 square kilometers, with a mean of 0.320 square kilometers. The sub-districts’ area ranges from 0.406 to 11.028 square kilometers, with a mean of 2.852 square kilometers. In Jianghan, each neighborhood falls uniquely and completely within one sub-district and each sub-district is composed of several neighborhoods. Consequently, some contextual effects based on sub-district could be found for neighborhoods lying within a given sub-district. We aim to investigate these contextual effects on burglary risks while controlling for neighborhood characteristics. Two neighborhoods were not included in our research due to lack of data, resulting in a data set of 114 neighborhoods.
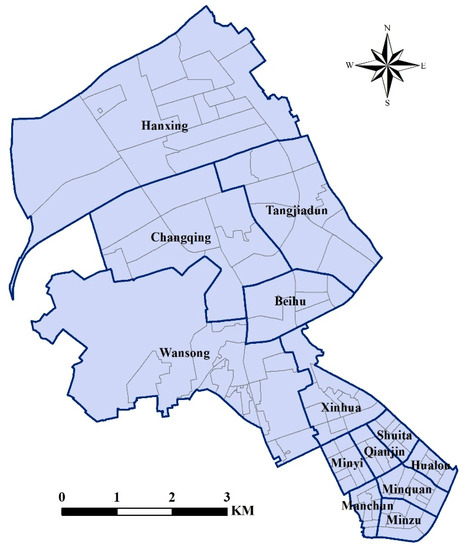
Figure 1.
The sub-districts and neighborhoods in Jianghan.
2.2. Dependent Variables
Burglary data, including the residential and commercial burglaries, were provided by the city’s police department. They were retrieved from the city’s 110-reporting system, a major source of official crimes in China. We used four years of burglary data from 1 January 2012 to 31 December 2015 to minimize the influence of annual fluctuations and get reliable risk estimates for neighborhoods. During the period, 8589 burglaries were recorded. The reported burglary incidents were aggregated to neighborhoods. The neighborhoods range in total burglaries from one to 1457; the mean is 75.34 and the standard deviation is 148.74. We took these burglary data as dependent variables.
2.3. Independent Variables
Two common but predominant theories related to the geography of crime are the social disorganization theory [29] and the routine activity theory [30]. The first theory indicates that crime is strongly related to social disorganization, and characteristics of a neighborhood, including demographic, economic, and other factors, can account for variations in crime [31]. Low socioeconomic status can disrupt social control, which in turn can increase crime rates [32]. The second theory associates occurrence of a crime with people’s daily activities [30]. This theory highlights that the convergence of motivated offenders and suitable targets in situations where capable guardians are absent is a prerequisite for a crime to occur [33]. The routine activity and social disorganization theories are frequently used in spatial analysis of crime [5]. Thus, based on these two theories, a list of seven variables representing neighborhood characteristics were considered to be potential risk factors.
Population density referred to the resident population of each neighborhood divided by its area in square kilometers. We included this variable to allow for differences in population and neighborhood size. The variable has been used in previous studies of crime [34,35]. Young males was measured by the percentage of men aged 15–24. Age and gender are factors often related to offenders and victims [12,36]. Researchers have discovered that criminal behaviors are overrepresented in young males [37]. The population density and percentage of young males are two demographic variables.
High education was the percentage of residents with a high school degree or more over 20 years of age. Unemployment was the percentage of unemployed people aged 18–60 in labor force. These two variables are often selected and used as indicators of neighborhood socioeconomic status [2,5,15].
Bar density was the quantity of bars per 10,000 residents. The presence of particular land use has long been of interest to researchers [38]. Past studies have examined the effects of bars [39] and alcohol outlets [40] on crime. In the current research, apart from bars, we also explored the influence of department stores on variations of urban crime.
Policing was the sum of police rooms and monitoring rooms per 10,000 population. The local police station sets up and maintains these rooms to preserve the public safety and provide services for residents. A police room is usually staffed by several policemen. Policing should prevent crime and enhance the perception of safety. However, a greater policing existence might be a response to higher crime areas. Its relationship with crime has been investigated in previous research [16,34].
We used these seven variables as potential risk factors. Multi-collinearity should be diagnosed before running regressions. As can be seen from the correlation matrix (Table 1), the absolute value of the correlation coefficient between population density and unemployment was largest, reaching 0.42. This indicates that the correlation between this variable pair was moderate according to Evans [41]. The rest values imply a weak or very weak correlation. Besides, the determinant of the matrix was 0.44, not close to 0, suggesting collinearity is not high [42]. As a consequence, we no longer consider the multi-collinearity problem.

Table 1.
Correlation matrix of the seven variables 1.
3. Methodology
3.1. Modeling Strategy
The dependent variable was modeled as a random variable following a Poisson distribution:
where represents counts of burglaries occurred in neighborhood i, signifies counts of burglaries expected, and denotes the relative burglary risk. To investigate the influence of independent variables and contextual effects, we decomposed the expectation of the Poisson distribution by a log—link function:
where is an offset term, is the intercept, , , represent observations of independent variables, , , are regression coefficients. and are two random effects terms, one unstructured and the other structured, to capture overdispersion and spatial autocorrelation at the neighborhood level, respectively. represents the sub-district neighborhood i falling within. refers to the unstructured contextual effects term not accounting for spatial autocorrelation at the sub-district level. measures the spatially-correlated contextual effects that take into account spatial autocorrelation at the sub-district level.
The form of the commonly used conventional Bayesian spatial model is:
This model does not account for the contextual effects as it only contains and . Our contextual effects model extends the conventional model by including another two random effects terms.
3.2. Prior Specification
The Bayesian modeling approach uses the Bayes theorem to combine data and prior distributions to obtain posterior distributions of parameters. Thus, the priors specified for model parameters are import in Bayesian modeling. We chose a uniform prior dflat() for the intercept term [43]. As to the regression coefficients, we specified a vague normal distribution in the absence of a clear knowledge about the impacts of independent variables [11]. A vague prior provides little information, allowing the data to speak for themselves and dominate posterior distributions [44]. and were assigned a normal distribution with mean both zero and variance , respectively. Priors for and were determined by an intrinsic conditional autoregressive (ICAR) distribution that has been adopted extensively in Bayesian spatial data analysis [45]. Specifically, all the model parameters were specified as follows:
where (M) denotes counts of neighborhoods (sub-districts). is the spatial adjacency matrix of neighborhoods with size , where if neighborhoods i and j are adjoining and , otherwise. is the spatial adjacency matrix of sub-districts defined in the same way as . and are the variance parameters of the ICAR distribution.
As for ICAR, it specifies that the structured random effects term given is normally distributed:
where represents the number of the neighbors of neighborhood i. To be specific, the mean and variance of given are and , respectively. The same principle applies to .
With regard to hyperparameters , , and , the precision parameters of the four were determined through the commonly used vague Gamma hyperprior distribution [46]:
An analysis with a uniform prior dunif(0,100) for the standard deviation parameters of the random effects terms was undertaken to assess the sensitivity of choice for hyperparameters [47].
3.3. Model Implementation
To fully demonstrate the contextual model (Equation (2)), we also fitted the commonly used conventional Bayesian spatial model (Equation (3)) by the MCMC method in WinBUGS 1.4.3 and contrasted their results.
Independent variables are often measured on different scales. These scale differences may bring computational problems within sampling algorithms. To speed convergence, independent variables were standardized in advance before models were fitted [48].
Both models were run with three chains. We assessed the convergence by checking the history plot and the Gelman-Rubin statistic plot [49]. After convergence, each chain was run further to produce samples used for posterior inference.
3.4. Model Assessment
The deviance information criterion (DIC) [50] was adopted to evaluate the performance of the contextual effects and the conventional Bayesian spatial models. It is defined as:
where and are the posterior mean deviance and the number of effective model parameters, respectively.
As a Bayesian measure of model adequacy, DIC balances model fit (measured by ) and model complexity (represented by ) [50]. Low-value DICs indicate better-fitted models.
4. Results
4.1. Deviance Summaries of the Models
Table 2 reports the deviance summaries of the conventional Bayesian spatial model and the contextual effects model. In addition to independent variables, the conventional Bayesian spatial model includes only two random effects terms, one unstructured and the other structured. It does not consider the contextual effects. The contextual effects model, on the basis of the conventional model, contains another two random effects term at the sub-district level, accounting for the contextual effects.

Table 2.
Deviance summaries of the conventional and the contextual effects models.
The two models were nearly indistinguishable in terms of DIC (841.059 versus 840.974). On the one hand, the for the conventional Bayesian spatial model and the contextual effects model were 733.509 and 733.606, respectively. This indicated the fit of the two models was nearly equal. On the other hand, the two models had an almost identical (107.550 versus 107.368), despite the additional two random effects terms in the contextual effects model. The sensitivity testing suggested that results were robust to the selection of different hyperprior distributions. DIC had a difference of 1.175 (841.059 versus 839.884) and 1.088 (840.974 versus 839.886), respectively, for the conventional and the contextual effects models.
To summarize, the conventional Bayesian spatial model and the contextual effects model had almost the same DIC. With a difference of only 0.085 (840.974 versus 841.059) in DIC values, the contextual effects model could not be considered better than the conventional Bayesian spatial model. Nonetheless, it was preferred in the sense that it can provide insights into contextual effects on crime risks.
4.2. Analysis of Independent Variables and Variance Parameters
Table 3 represents the intercept term, regression coefficients, and variance parameters estimated by the conventional Bayesian spatial model and the contextual effects model. As can be seen from the table, three independent variables (population density and the two land-use variables) were significant at the 95% credible interval (CI) in both models. These variables had a definite correlation with burglary risks. The other four independent variables were not significant in both models and their signs in the regression estimates given by the two models were also the same. The percentage of young males and unemployment were positively related to burglary risks. High education was negatively associated with burglary risks. Although these three independent variables did not have a strong effect on burglary risks, the directions of the effects were expected. The association between policing and burglary risks was also unclear.

Table 3.
The intercept term, regression coefficients, and variance parameters estimated by the two models.
Regarding the significant independent variables, population density was negatively while bar and department store densities were positively related to burglary risks. In addition to identifying the same set of significant independent variables, the conventional and the contextual effects models made similar estimates for the regression coefficients of the three significant independent variables. The posterior mean regression coefficients for the three variables estimated by the conventional Bayesian model were −0.3597, 0.3617, and 0.1858, respectively. The corresponding estimates given by the contextual effects model were −0.3639, 0.3636, and 0.1830, respectively.
The variance parameters of the random effects terms were also reported in Table 3. Both the conventional Bayesian spatial and the contextual effects models suggested that risk variation due to neighborhood heterogeneity is greater than that due to spatial autocorrelation . Results of the contextual effects model further indicated that variation due to local random effects is greater than that due to contextual effects. After accounting for contextual effects, the posterior mean of increased from 0.6251 to 0.6501, while the mean of decreased from 0.3041 to 0.1422.
4.3. Mapping the Risks
The posterior mean burglary risks given by the conventional model and the contextual effects model are demonstrated in Figure 2. The risks shown in Figure 2a accounted for the impacts of independent variables, overdispersion, and spatial autocorrelation. The risks shown in Figure 2b further considered the contextual effects. All neighborhoods in Figure 2a,b had a burglary risk greater than zero. In addition, each neighborhood had the same relative risk magnitude as it fell into the same interval in Figure 2a,b. Actually, the conventional Bayesian spatial model and the contextual effects model gave a very similar estimate of burglary risk for each neighborhood. The difference between the estimates for any neighborhood given by the two models was not greater than 0.02.
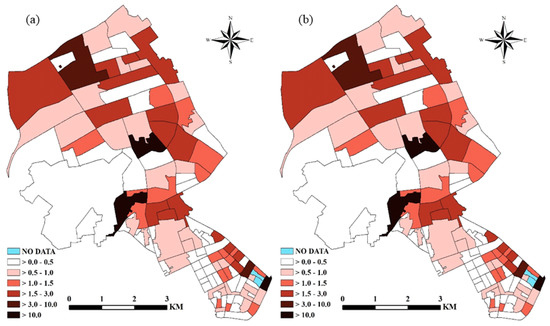
Figure 2.
Burglary risks given by (a) the conventional Bayesian spatial model and (b) the contextual effect model.
The mapped burglary risk for each neighborhood in Figure 2 represents the risk value relative to the average for the whole Jianghan District. Figure 2a,b both suggest that 38 neighborhoods had a value larger than 1.0. Specifically, 21 neighborhoods had a value greater than 1.5, five neighborhoods greater than 3.0, and three neighborhoods greater than 10.0. When making efforts on the prevention and control of burglaries, more attention should be paid to these neighborhoods.
4.4. Identifying and Mapping the Relative Contribution
We adopted the map decomposition strategy [3] to investigate the influence of independent variables and contextual effects on burglary risks. Based on Equation (2), the relative burglary risk can be formulated as:
where is the critical value, since if each component on the right-hand side of Equation (16) is 1.0, equals 1.0. The effects of independent variables on burglary risks can be deduced by , while the magnitude of contextual effects can be deduced by and .
Figure 3 displays the distribution of deduced by the posterior means of corresponding parameters. It indicates the relative burglary risk due to independent variables. Figure 4a,b demonstrate the maps of and , respectively. Figure 4 suggests the relative burglary risk due to contextual effects. Figure 3 and Figure 4 together demonstrate the relative contribution of neighborhood characteristics (represented by the independent variables) and contextual effects (represented by and ) on the overall burglary risks (Figure 2b).
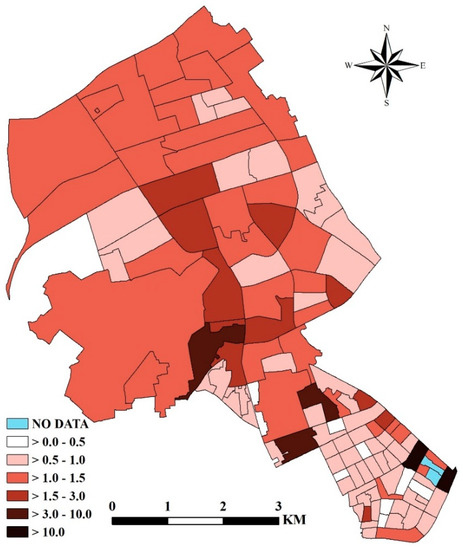
Figure 3.
Burglary risks due to independent variables.
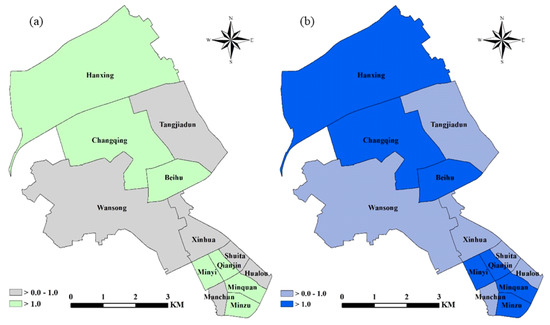
Figure 4.
Burglary risks due to (a) unstructured contextual effects and (b) spatially structured contextual effects.
Regarding the contextual effects, Figure 4a,b show that seven sub-districts, i.e., Hanxing, Changqing, Beihu, Minyi, Qinjin, Minquan, and Minzu, had both and greater than 1.0. These sub-districts have positive impacts on the rise of burglary risks for neighborhoods lying within them. The other six sub-districts, i.e., Tangjiadun, Wansong, Xinhua, Shuita, Hualou, and Manchun, had values of and , both smaller than 1.0. These sub-districts had negative impacts on the rise of burglary risks for neighborhoods falling within them.
Figure 5 further demonstrates the posterior probabilities of the contextual effects having positive impacts on neighborhood burglary risks. In contrast to values shown in Figure 4, posterior probabilities consider the variance of (). They express the strength () is greater than 1.0. In disease-mapping studies, Richardson et al. [51] proposed to use a value around 0.7 to 0.8 as the threshold on posterior probabilities to detect increased-risk areas. Figure 5 indicates that all the values of the posterior probabilities were smaller than 0.7. Nonetheless, the dark color in Figure 5 indicates the strong probability that the sub-district has a positive impact on burglary risks for neighborhoods falling within it.
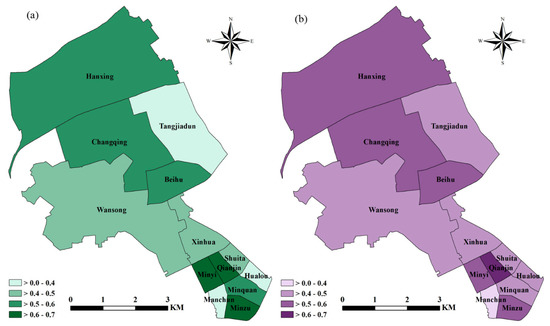
Figure 5.
Posterior probabilities of (a) unstructured contextual effects and (b) spatially structured contextual effects having positive impacts on neighborhood burglary risks.
5. Discussion
This article applied a contextual effects model to investigate contextual effects on burglary risks in Wuhan, China. The model was built based on Bayesian spatial modeling strategy. Crime risks are possibly due to a combination of both individual and its upper-level factors. To disentangle the impacts of the two factors on the overall crime risks, the conventional Bayesian spatial modeling approach should be adapted to suit the clustered and hierarchical structure of data. In our research, each neighborhood falls uniquely within a sub-district and each sub-district consists of several neighborhoods. Neighborhoods are clustered within sub-districts. This suggests that neighborhoods from within the same cluster have characteristics in common and may be more alike because of their shared environment. The sub-district level should have a contribution from effects at the neighborhood level. One way of identifying this contribution is to account for the contextual effects of sub-districts on neighborhoods.
We extended the conventional Bayesian spatial model by adding two random effects terms to account for contextual effects (Equation (2)). Both the conventional Bayesian model (Equation (3)) and the contextual effects model (Equation (2)) were used to fit the data. Our analyses showed the two models were nearly indistinguishable in terms of DIC (Table 2). They had almost the same and values. Although the contextual effects model could not be considered superior to the conventional Bayesian spatial model based on their DICs, it was preferred in the sense that it provides insights into contextual effects on crime risks and can work out the relevant contribution.
The results of the study suggested that the conventional and the contextual effects models identified the same set of significant independent variables (Table 3). To be specific, density of population, bar and department store had a strong association with burglary risks. Population density was inversely related to burglary risks. This is consistent with past research finding that the variable had a negative impact on crime rate [2,5,34,35]. This may be due to the fact that the Jianghan District is the most populous district of Wuhan and thus there are more opportunities for visual surveillance exit. The two land-use variables, i.e., bar density and department store density, both had a significant positive correlation with burglary risks. Our findings are in line with other studies suggesting that bars [39] and alcohol outlets [40] have strong positive impacts on crime. In addition to identifying the same set of significant independent variables, the conventional and the contextual effects models gave similar estimates for their regression coefficients.
The rest of the independent variables, i.e., young males, unemployment, high education and policing, were not significant in both the conventional and the contextual effects models (Table 3). Their signs in the regression estimates given by the two models were all about the same. Specifically, the percentage of young males did not clearly have a positive effect on burglary risk. This is in accordance with prior study indicating that the variable virtually has no effect on crime [38]. High education and unemployment were negatively and positively correlated with burglary risks, respectively. This is somewhat contradictory to previous studies founding that unemployment had a significant positive [5] and the percentage of residents that were well-educated had a significant negative impact on crime [35]. One possible reason why they were not significant in our analyses may be that our measure of socioeconomic status using only these two variables was not adequate. In addition, issues surrounding the ecological fallacy [52] are also worthy of attention. Although the magnitude was not significant, the direction of the effects of these two socioeconomic variables was expected. The positive coefficient for policing was not entirely unanticipated. Policing can prevent crime and enhance the perception of safety. However, a greater policing may also be a natural reaction to higher crime rates in the region. Gracia et al. [16] also found that policing activity had a positive effect on intimate partner violence.
We reported the variance parameters of the random effects terms (Table 3). Results suggested that risk variation due to neighborhood heterogeneity is greater than that due to spatial autocorrelation . The contextual effects model further indicated variation due to local random effects is greater than that due to contextual effects.
We mapped the posterior means of burglary risks estimated the conventional and the contextual effects models (Figure 2). The values demonstrated in Figure 2a took account of the effects of the independent variables, overdispersion, and spatial autocorrelation. The risks shown in Figure 2b further considered the contextual effects. It was implemented by extending the conventional Bayesian spatial model to include another two random effects term at the sub-district level. The conventional Bayesian spatial model and the contextual effects model gave almost the same estimate of burglary risk for each neighborhood, with a biggest difference of only 0.02. Both models indicated that there were 38 neighborhoods having a risk value lager than 1.0. Specifically, 21 neighborhoods had a value greater than 1.5, five neighborhoods greater than 3.0, and three neighborhoods greater than 10.0. By illustrating the spatial distribution of burglary risks, the maps demonstrated in Figure 2 laid a foundation for crime prevention programs.
We adopted the map decomposition technique to work out the contribution of both neighborhood characteristics and contextual effects on burglary risks (Equation (16)). Map decomposition is particularly helpful in visualization and indicative analysis of individual area. It can disentangle the influence of neighborhood characteristics and contextual effects on crime risks. Based on Figure 2b, by identifying and mapping the relative contribution of neighborhood characteristics (Figure 3) and contextual effects (Figure 4), and further demonstrating the posterior probabilities of contextual effects having positive impacts on crime risks (Figure 5), crime prevention practitioners and police officers can assess their crime reduction measures.
6. Conclusions
This study demonstrated a contextual effects model to investigate contextual effects on crime risks. Contextual effects generally denote the impact of the upper-level area on the lower-level units of analysis. Research focusing on crime patterns is often conducted at one spatial scale or at different scales by separate models. Such studies neglect contextual effects and the complex spatial structure of the urban environment [53]. They do not realize that local crime patterns result from the joint effects of different layers of crime potential [21] and is simultaneously affected by characteristics of the environment at multiple spatial levels [19,20]. Due to the clustered and hierarchical structure of spatial data, crime risks are possibly due to a combination of both individual and its upper-level factors. The influence of crime risk factors is potentially conditional on context and can operate across multiple spatial levels [22]. Lower-level crime patterns may vary with the characteristics of the upper-level spatial unit they fall within. The variation, to some degree, can be accounted for by including the upper-level factors. However, for some reason, these factors may be unavailable, leading their effects not be captured specifically.
To work out the contribution of the lower-level and upper-level factors on the overall crime risks, conventional regression approaches must be adapted. Our contextual effects model was built based on Bayesian spatial modeling strategy. It was implemented by extending the conventional Bayesian spatial model (Equation (3)) to include two random effects terms at the upper-level area (Equation (2)). The upper-level random effects terms are used to capture the effects of the upper-level factors. The contextual effects model accounts for the effects of independent variables, overdispersion, spatial autocorrelation, and contextual effects. By the model, we can not only identify the relative contribution of the lower-level independent variables and contextual effects on crime risks, but can also obtain the probabilities of contextual effects having positive impacts on lower-level crime risks. Our research contributes to the increasing literature on modeling crime data by Bayesian spatial approaches, as contextual effects are generally neglected.
The analyses presented in this paper have theoretical and practical implications. Theoretically, data are often clustered among hierarchies. This can lead to the emergence of clusters. In our research, neighborhoods are clustered within sub-districts. Neighborhoods within the same sub-district may share the environment and thus have characteristics in common. It is possible that some grouping effect based on sub-district could be found for neighborhoods lying within a certain sub-district. Therefore, the sub-district level should have a contribution from effects at the neighborhood level. The neighborhood’s crime risk may be pulled towards the sub-district level expected risk. Analyzing crime patterns while accounting for contextual effects provides insight regarding the crime-generating process arising across multiple spatial scales and facilitates the identification of the role of each spatial scale on the variation of crime risks. From the practical perspective, police focusing on burglaries in Jianghan ought to focus on neighborhoods having a high bar or department store density. Furthermore, careful thought must be given to neighborhoods having a high burglary risk. An in-depth investigation to identify the distinctive local characteristics of these neighborhoods is necessary. In addition, by illustrating the spatial distribution of neighborhood burglary risks (Figure 2b), the relative contribution of neighborhood characteristics (Figure 3) and contextual effects on the risks (Figure 4), and the posterior probabilities of contextual effects having positive impacts on burglary risks (Figure 5), our analyses provide the evidential base essential to underpin the decision making process. It can facilitate practitioners, such as police managers and crime analysts, to evaluate crime intervention and prevention efforts that could be strategically targeted towards the characteristics of the problem.
There are also several limitations to our research. The first limitation concerns the contextual effects model itself. As our main aim was to present and illustrate a contextual effects model, we gave the full form of the model but did not further discuss the necessity of incorporating both the two contextual effects terms in the model. Future researchers can specify their contextual effects model according to specific objectives and the actual situation based on our work. The second limitation regards the crime data used in the study. Our burglary data was from the city’s 110-reporting system. Such data could suffer from the problems of entry error and underreporting [54], and may not accurately reflect the scope of victimization [55]. The third limitation of the paper involves the independent variables. We used the residential population instead of other measures of population, such as the ambient population [56] and the commuting population [57]. This may influence the results of our analyses [56,57]. In addition, variables acting as proxies for socioeconomic status, i.e., high education and unemployment, are not comprehensive and adequate. Other commonly used variables, including immigration [12] and the percentage of families receiving public assistance [58], were not incorporated into our model due to the unavailability of data. Further, we did not assess how the processes hypothesized by social disorganization and routine activity theories to be applied in multiple spatial scales as data at the sub-district level were not available. The fourth limitation relates to the measure of model complexity. We used to capture model complexity in our research and did not consider the complexity of the geographical space examined. However, the wide range of spatial and functional complexities involved in studying geographical problems can affect the complexity of the Bayesian models [59], which in turn has an impact on the computational performance of the models themselves, particularly when used in networks [60] or trees [61]. Another limitation concerns the modifiable areal unit problem (MAUP) [62]. Our data were aggregated to neighborhoods and the results of our analysis might have been influenced by the MAUP.
This research could be expanded in the near future in several ways. First, the applicability of the contextual effects model should be further validated. Further application of the model at other spatial scales with other types of crime is recommended. Second, the contextual effects model can be utilized for a joint analysis at multiple spatial scales. If data are available at different aggregation levels, the model can be used to model them jointly within an analysis. This joint multiscale analysis is worth conducting. Third, through a spatio-temporal analysis, future studies should investigate the temporal dynamics of crime patterns as they change over time [63].
Author Contributions
Conceptualization, Hongqiang Liu; Methodology, Hongqiang Liu; Software, Hongqiang Liu; Validation, Hongqiang Liu; Formal Analysis, Hongqiang Liu; Investigation, Hongqiang Liu and Xinyan Zhu; Resources, Xinyan Zhu; Data Curation, Xinyan Zhu; Writing—Original Draft Preparation, Hongqiang Liu; Writing—Review & Editing, Dongying Zhang and Zhen Liu; Visualization, Hongqiang Liu; Supervision, Hongqiang Liu and Xinyan Zhu; Project Administration, Xinyan Zhu; Funding Acquisition, Hongqiang Liu and Xinyan Zhu.
Funding
This research was funded by the National Key R&D Program of China, grant number 2018YFB0505500 and 2018YFB0505503; the National Natural Science Foundation of China, grant number 41830645; LIESMARS (State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University) Special Research Funding; and Open Research Fund of State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, grant number 18I03.
Acknowledgments
The authors greatly appreciate the valuable comments from anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Weisburd, D.; McEwen, T. Crime Mapping and Crime Prevention; Criminal Justice Press: Monsey, NY, USA, 1997. [Google Scholar]
- Zhang, H.; Peterson, M.P. A spatial analysis of neighbourhood crime in Omaha, Nebraska using alternative measures of crime rates. Internet J. Criminol. 2007, 31, 1–31. [Google Scholar]
- Law, J.; Haining, R. A Bayesian Approach to Modeling Binary Data: The Case of High-Intensity Crime Areas. Geogr. Anal. 2004, 36, 197–216. [Google Scholar] [CrossRef]
- Morenoff, J.D.; Sampson, R.J.; Raudenbush, S.W. Neighborhood inequality, collective efficacy, and the spatial dynamics of urban violence. Criminology 2001, 39, 517–558. [Google Scholar] [CrossRef]
- Andresen, M.A. A spatial analysis of crime in Vancouver, British Columbia: A synthesis of social disorganization and routine activity theory. Can. Geogr. 2006, 50, 487–502. [Google Scholar] [CrossRef]
- Gelman, A.; Price, P.N. All maps of parameter estimates are misleading. Stat. Med. 1999, 18, 3221–3234. [Google Scholar] [CrossRef]
- Aguero-Valverde, J.; Jovanis, P.P. Spatial analysis of fatal and injury crashes in Pennsylvania. Accid. Anal. Prev. 2006, 38, 618–625. [Google Scholar] [CrossRef]
- McCullagh, P.; Nelder, J.A. Generalized Linear Models, 2nd ed.; Chapman and Hall: London, UK, 1989. [Google Scholar]
- Haining, R.; Law, J.; Griffith, D. Modelling small area counts in the presence of overdispersion and spatial autocorrelation. Comput. Stat. Data Anal. 2009, 53, 2923–2937. [Google Scholar] [CrossRef]
- Carlin, B.P.; Louis, T.A. Bayes and Empirical Bayes Methods for Data Analysis, 2nd ed.; Chapman and Hall: London, UK, 2000. [Google Scholar]
- Law, J.; Chan, P.W. Bayesian spatial random effect modelling for analysing burglary risks controlling for offender, socioeconomic, and unknown risk factors. Appl. Spat. Anal. Policy 2012, 5, 73–96. [Google Scholar] [CrossRef]
- Matthews, S.A.; Yang, T.-C.; Hayslett-McCall, K.L.; Ruback, R.B. Built environment and property crime in Seattle, 1998–2000: A Bayesian analysis. Environ. Plan. A 2010, 42, 1403. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, X. Joint Modeling of Multiple Crimes: A Bayesian Spatial Approach. Int. J. Geo-Inf. 2017, 6, 16. [Google Scholar] [CrossRef]
- Congdon, P. Bayesian models for spatial incidence: A case study of suicide using the BUGS program. Health Place 1997, 3, 229–247. [Google Scholar] [CrossRef]
- Law, J.; Quick, M. Exploring links between juvenile offenders and social disorganization at a large map scale: A Bayesian spatial modeling approach. J. Geogr. Syst. 2013, 15, 89–113. [Google Scholar] [CrossRef]
- Gracia, E.; López-Quílez, A.; Marco, M.; Lladosa, S.; Lila, M. Exploring neighborhood influences on small-area variations in intimate partner violence risk: A Bayesian random-effects modeling approach. Int. J. Environ. Res. Public Health 2014, 11, 866–882. [Google Scholar] [CrossRef] [PubMed]
- Law, J.; Quick, M.; Chan, P.W. Analyzing Hotspots of Crime Using a Bayesian Spatiotemporal Modeling Approach: A Case Study of Violent Crime in the Greater Toronto Area. Geogr. Anal. 2015, 47, 1–19. [Google Scholar] [CrossRef]
- Li, G.; Haining, R.; Richardson, S.; Best, N. Space–time variability in burglary risk: A Bayesian spatio-temporal modelling approach. Spat. Stat. 2014, 9, 180–191. [Google Scholar] [CrossRef]
- Ouimet, M. Aggregation bias in ecological research: How social disorganization and criminal opportunities shape the spatial distribution of juvenile delinquency in Montreal. Can. J. Criminol. Rev. Can. De Criminol. 2000, 42, 135–156. [Google Scholar] [CrossRef]
- Wooldredge, J. Examining the (ir)relevance of aggregation bias for multilevel studies of neighborhoods and crime with an example comparing census tracts to official neighborhoods in Cincinnati. Criminology 2010, 40, 681–710. [Google Scholar] [CrossRef]
- Brantingham, P.L.; Brantingham, P.J. Nodes, paths and edges: Considerations on the complexity of crime and the physical environment. J. Environ. Psychol. 1993, 13, 3–28. [Google Scholar] [CrossRef]
- Cullen, F.T.; Wilcox, P. The Oxford Handbook of Criminological Theory; Oxford University Press: New York, NY, USA, 2015. [Google Scholar]
- Johnson, S.D.; Bowers, K.J. Permeability and Burglary Risk: Are Cul-de-Sacs Safer? J. Quant. Criminol. 2010, 26, 89–111. [Google Scholar] [CrossRef]
- Davies, T.; Johnson, S.D. Examining the Relationship Between Road Structure and Burglary Risk Via Quantitative Network Analysis. J. Quant. Criminol. 2015, 31, 481–507. [Google Scholar] [CrossRef]
- Steenbeek, W.; Weisburd, D. Where the action is in crime? An examination of variability of crime across different spatial units in The Hague, 2001–2009. J. Quant. Criminol. 2016, 32, 1–21. [Google Scholar] [CrossRef]
- Deryol, R.; Wilcox, P.; Logan, M.; Wooldredge, J. Crime Places in Context: An Illustration of the Multilevel Nature of Hot Spot Development. J. Quant. Criminol. 2016, 32, 305–325. [Google Scholar] [CrossRef]
- Schnell, C.; Braga, A.A.; Piza, E.L. The influence of community areas, neighborhood clusters, and street segments on the spatial variability of violent crime in Chicago. J. Quant. Criminol. 2017, 33, 1–28. [Google Scholar] [CrossRef]
- Quick, M. Multiscale spatiotemporal patterns of crime: A Bayesian cross-classified multilevel modelling approach. J. Geogr. Syst. 2019, 21, 339–365. [Google Scholar] [CrossRef]
- Shaw, C.R.; McKay, H.D. Juvenile Delinquency and Urban Areas; University of Chicago Press: Chicago, IL, USA, 1942. [Google Scholar]
- Cohen, L.E.; Felson, M. Social change and crime rate trends: A routine activity approach. Am. Sociol. Rev. 1979, 44, 588–608. [Google Scholar] [CrossRef]
- Sampson, R.J.; Groves, W.B. Community Structure and Crime: Testing Social-Disorganization Theory. Am. J. Sociol. 1989, 94, 774–802. [Google Scholar] [CrossRef]
- Bursik, R.J. Social disorganization and theories of crime and delinquency: Problems and prospects. Criminology 1988, 26, 519–552. [Google Scholar] [CrossRef]
- Felson, M.; Cohen, L.E. Human ecology and crime: A routine activity approach. Hum. Ecol. 1980, 8, 389–406. [Google Scholar] [CrossRef]
- Faria, J.R.; Ogura, L.M.; Sachsida, A. Crime in a planned city: The case of Brasília. Cities 2013, 32, 80–87. [Google Scholar] [CrossRef]
- Mulligan, G.F. The Determinants of Crime in Tucson, Arizona. Urban Geogr. 2003, 24, 582–610. [Google Scholar]
- Darrell, S.; Cathy, S. Age, Gender, and Crime Across Three Historical Periods: 1935, 1960, and 1985. Soc. Forces 1991, 69, 869. [Google Scholar]
- Krivo, L.J.; Peterson, R.D. Extremely Disadvantaged Neighborhoods and Urban Crime. Soc. Forces 1996, 75, 619–648. [Google Scholar] [CrossRef]
- Roncek, D.W. Dangerous places: Crime and residential environment. Soc. Forces 1981, 60, 74–96. [Google Scholar] [CrossRef]
- Roncek, D.W.; Bell, R. Bars, blocks, and crimes. J. Environ. Syst. 1981, 11, 35–47. [Google Scholar] [CrossRef]
- Britt, H.R.; Carlin, B.P.; Toomey, T.L.; Wagenaar, A.C. Neighborhood Level Spatial Analysis of the Relationship Between Alcohol Outlet Density and Criminal Violence. Environ. Ecol. Stat. 2005, 12, 411–426. [Google Scholar] [CrossRef]
- Evans, J.D. Straightforward Statistics for the Behavioral Sciences; Brooks/Cole Publishing: Pacific Grove, CA, USA, 1996. [Google Scholar]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Thomas, A.; Best, N.; Lunn, D.; Arnold, R.; Spiegelhalter, D. GeoBugs User Manual; Medical Research Council Biostatistics Unit: Cambridge, UK, 2004. [Google Scholar]
- Toomey, T.L.; Erickson, D.J.; Carlin, B.P.; Lenk, K.M.; Quick, H.S.; Jones, A.M.; Harwood, E.M. The association between density of alcohol establishments and violent crime within urban neighborhoods. Alcohol. Clin. Exp. Res. 2012, 36, 1468–1473. [Google Scholar] [CrossRef]
- Besag, J.; York, J.; Mollié, A. Bayesian image restoration, with two applications in spatial statistics. Ann. Inst. Stat. Math. 1991, 43, 1–20. [Google Scholar] [CrossRef]
- Wakefield, J.; Best, N.; Waller, L. Bayesian Approaches to Disease Mapping on Spatial Epidemiology: Methods and Applications; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Gelman, A. Prior distributions for variance parameters in hierarchical models. Bayesian Anal. 2006, 1, 515–534. [Google Scholar] [CrossRef]
- Banerjee, S.; Carlin, B.P.; Gelfand, A.E. Hierarchical Modeling and Analysis for Spatial Data; Chapman and Hall/CRC: New York, NY, USA, 2014. [Google Scholar]
- Gelman, A.; Rubin, D.B. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; Van Der Linde, A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2002, 64, 583–639. [Google Scholar] [CrossRef]
- Richardson, S.; Thomson, A.; Best, N.; Elliott, P. Interpreting posterior relative risk estimates in disease-mapping studies. Environ. Health Perspect. 2004, 112, 1016–1025. [Google Scholar] [CrossRef] [PubMed]
- Robinson, W.S. Ecological correlations and the behavior of individuals. Int. J. Epidemiol. 1950, 15, 351–357. [Google Scholar] [CrossRef]
- Sampson, R.J. The place of context: A theory and strategy for criminology’s hard problems. Criminology 2013, 51, 1–31. [Google Scholar] [CrossRef]
- Groff, E.R.; La Vigne, N.G. Mapping an opportunity surface of residential burglary. J. Res. Crime Delinq. 2001, 38, 257–278. [Google Scholar] [CrossRef]
- Biderman, A.D.; Reiss, A.J. On Exploring the “Dark Figure” of Crime. Ann. Am. Acad. Political Soc. Sci. 1967, 374, 1–15. [Google Scholar] [CrossRef]
- Mburu, L.W.; Helbich, M. Crime Risk Estimation with a Commuter-Harmonized Ambient Population. Ann. Am. Assoc. Geogr. 2016, 106, 804–818. [Google Scholar] [CrossRef]
- Stults, B.J.; Hasbrouck, M. The effect of commuting on city-level crime rates. J. Quant. Criminol. 2015, 31, 331–350. [Google Scholar] [CrossRef]
- Zhu, L.; Gorman, D.M.; Horel, S. Hierarchical Bayesian spatial models for alcohol availability, drug “hot spots” and violent crime. Int. J. Health Geogr. 2006, 5, 54. [Google Scholar] [CrossRef]
- Papadimitriou, F. Mathematical modelling of land use and landscape complexity with ultrametric topology. J. Land Use Sci. 2013, 8, 234–254. [Google Scholar] [CrossRef]
- Campos, C.P.D.; Cozman, F.G. The inferential complexity of Bayesian and credal networks. In Proceedings of the International Joint Conference on Ijcai, Macao, China, 10–16 August 2019. [Google Scholar]
- Kłopotek, M.A. A new Bayesian tree learning method with reduced time and space complexity. Fundam. Inform. 2002, 49, 349–367. [Google Scholar]
- Openshaw, S. The Modifiable Areal Unit Problem; Geo Books: Norwich, UK, 1984. [Google Scholar]
- Helbich, M.; Arsanjani, J.J. Spatial eigenvector filtering for spatiotemporal crime mapping and spatial crime analysis. Am. Cartogr. 2015, 42, 134–148. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).