Exploring the Characteristics of an Intra-Urban Bus Service Network: A Case Study of Shenzhen, China
Abstract
1. Introduction
2. Study Area and Dataset
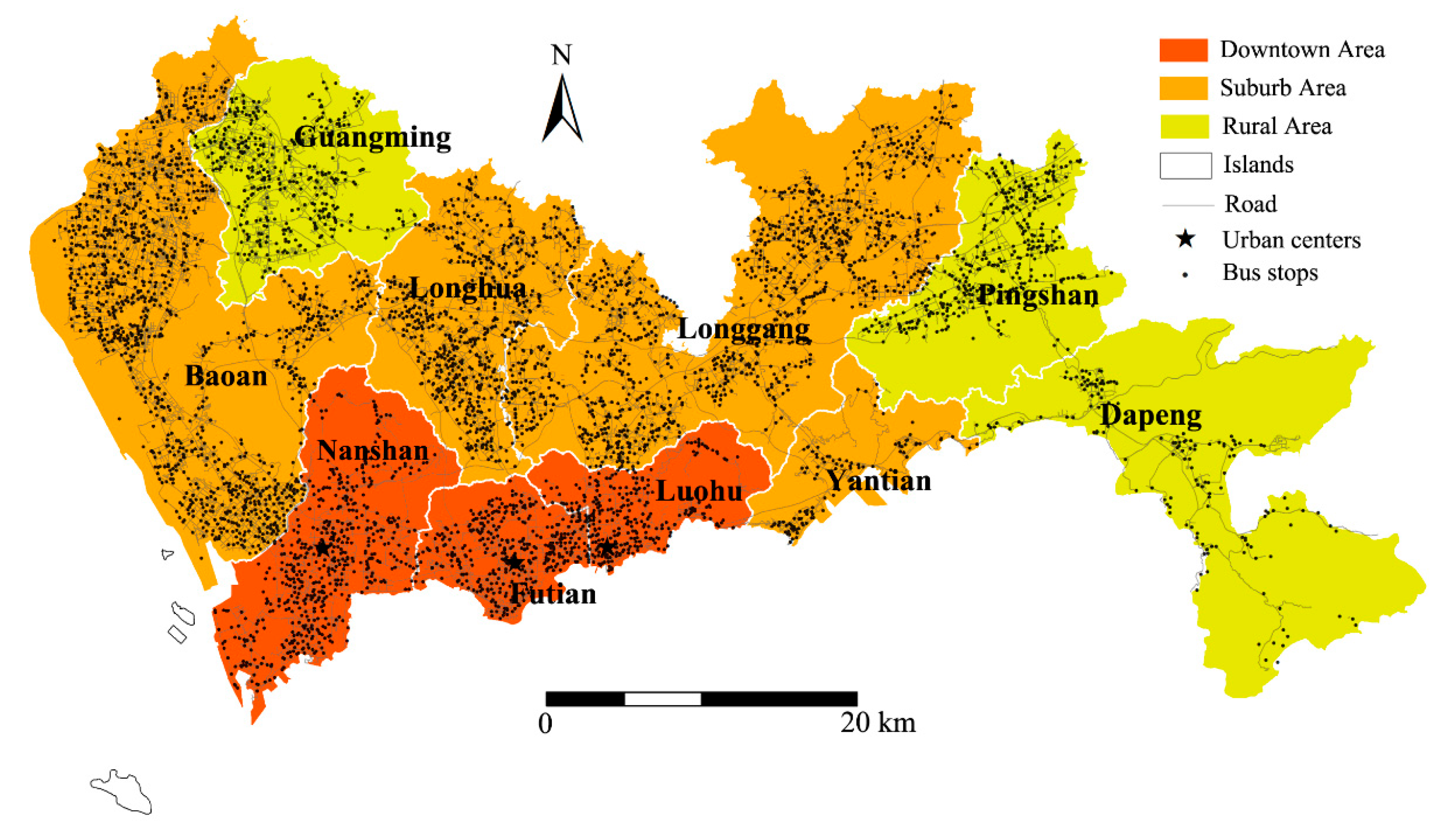
2.1. Study Area
2.2. Dataset Collection
3. Complex Network Analysis
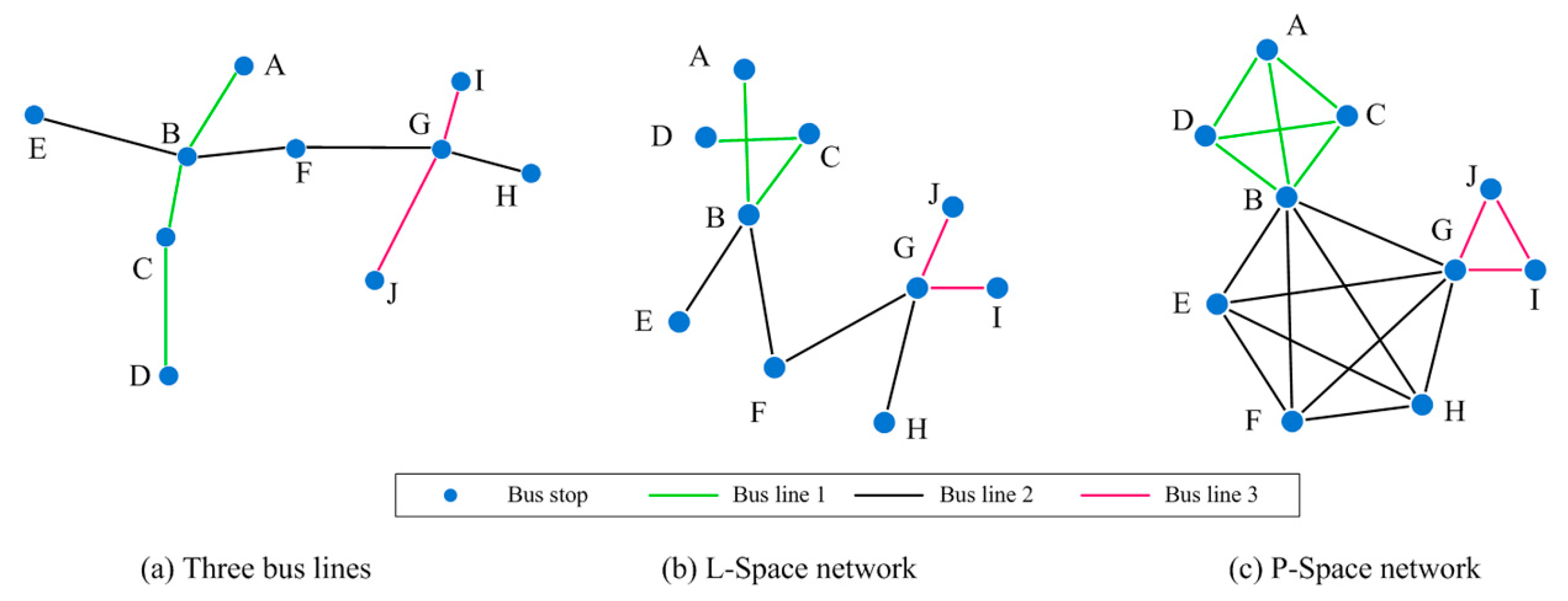
3.1. Network Construction
3.2. Topological Analysis of the Bus Service Network Structure
3.3. Nodes’ Centrality Measurement of the Weighted Bus Network Structure
4. Result and Discussion
4.1. Statistical Characteristic of the Bus Service Network
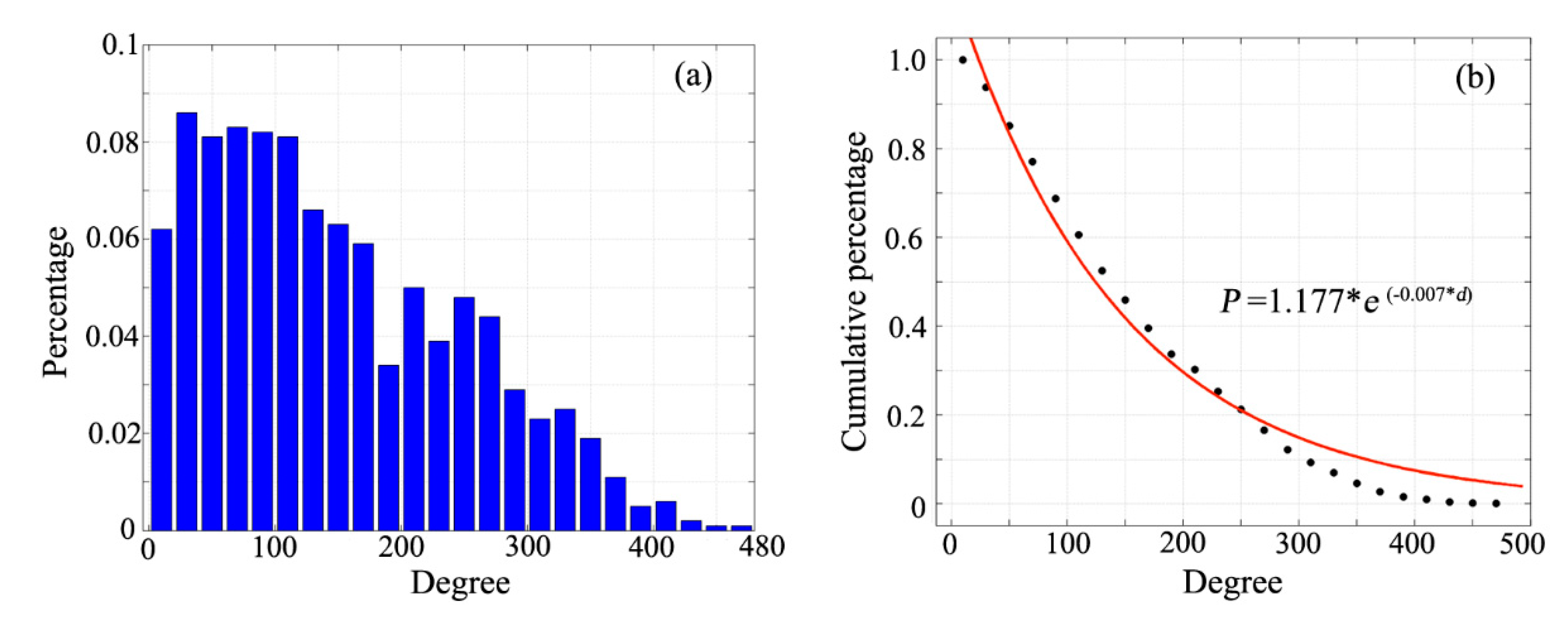
4.1.1. Degree Distribution
4.1.2. Small-World Property
4.2. Spatial Characteristic of the Bus Service Network
4.2.1. Charactering Edge Weight of Bus Service Network
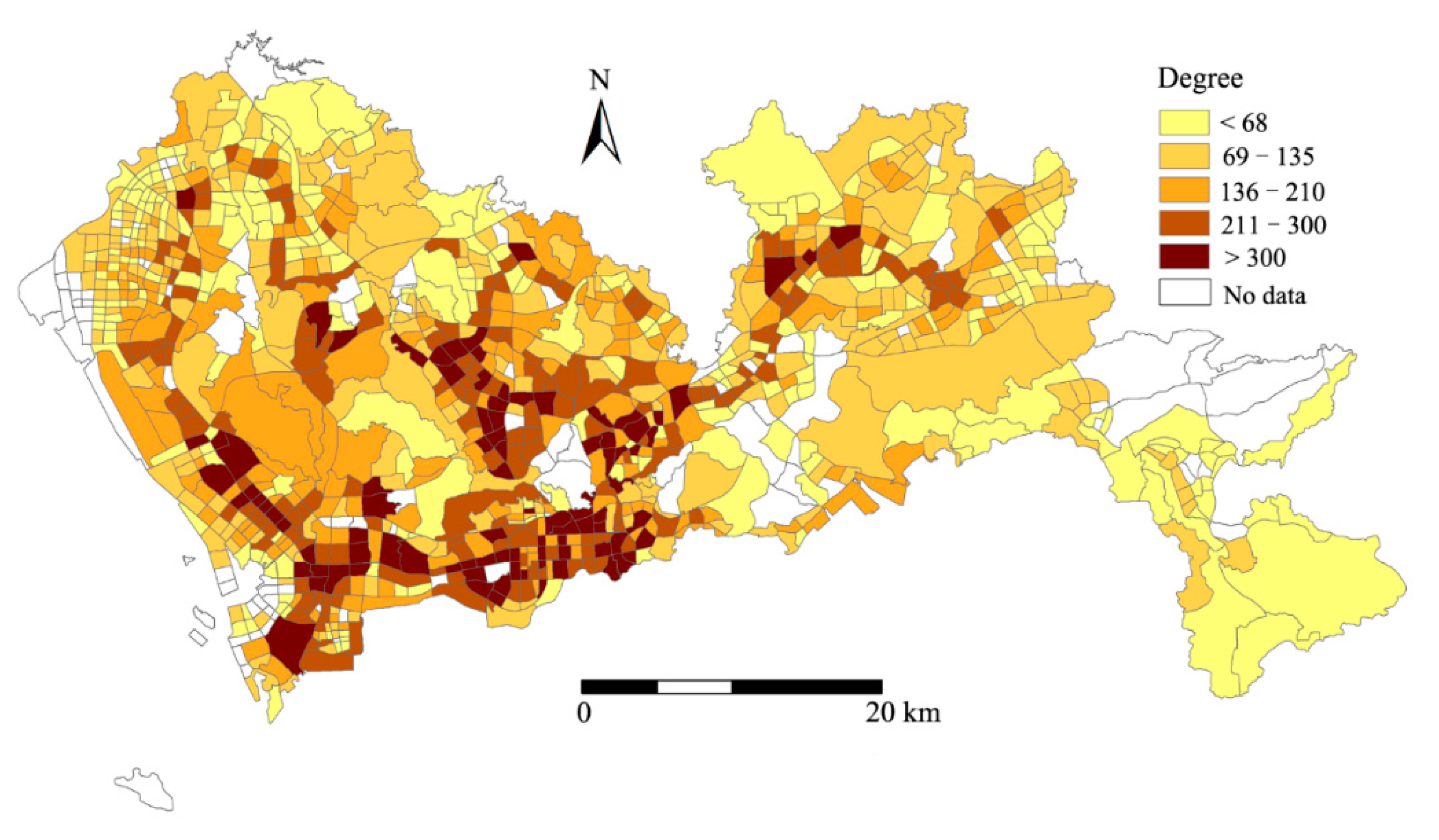
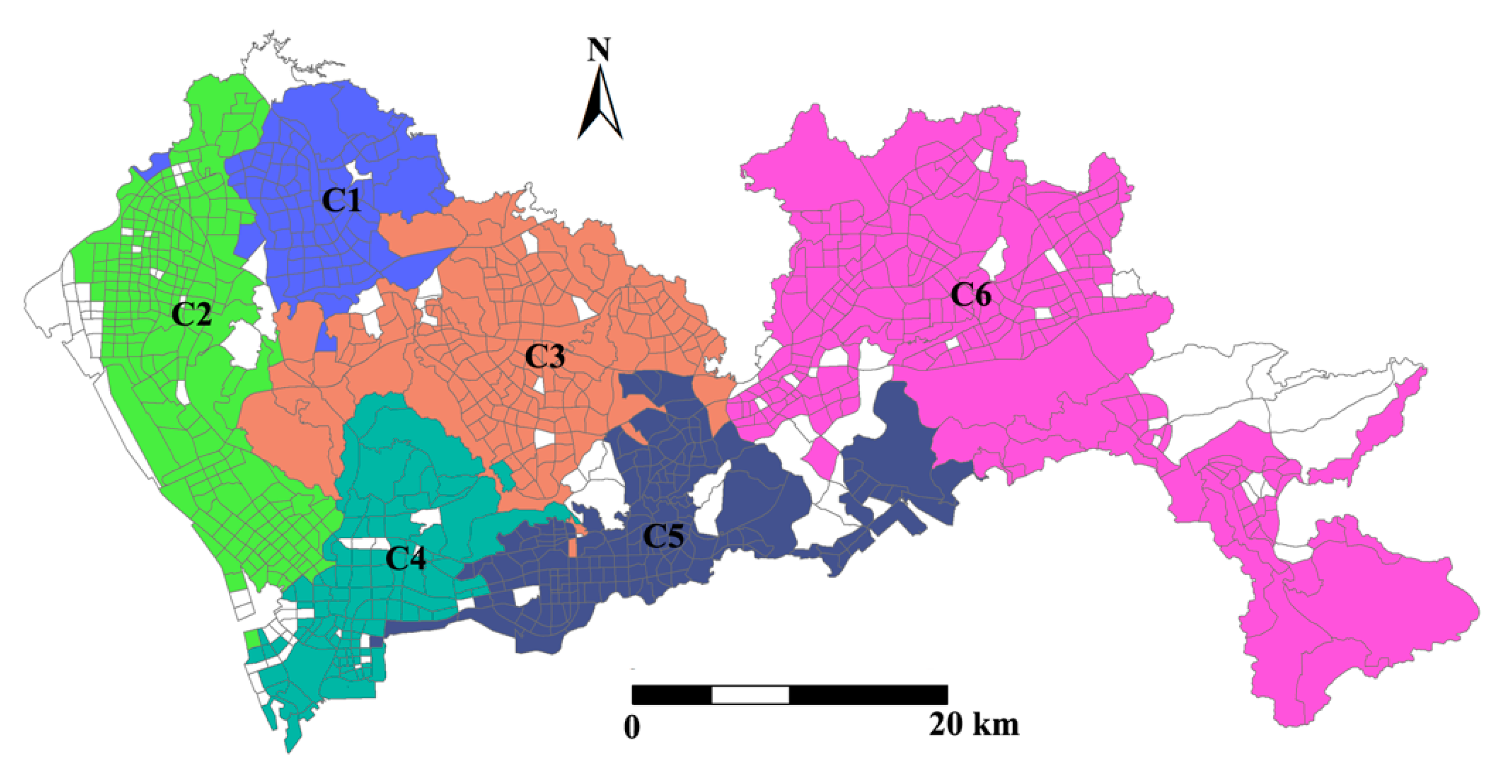
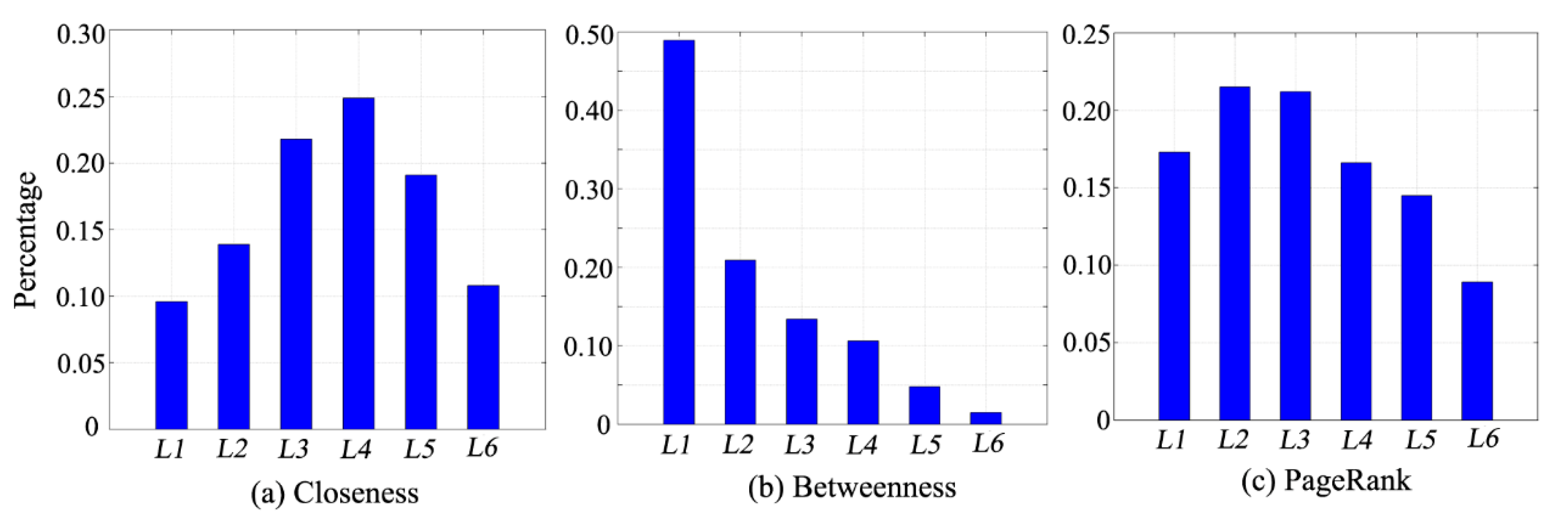
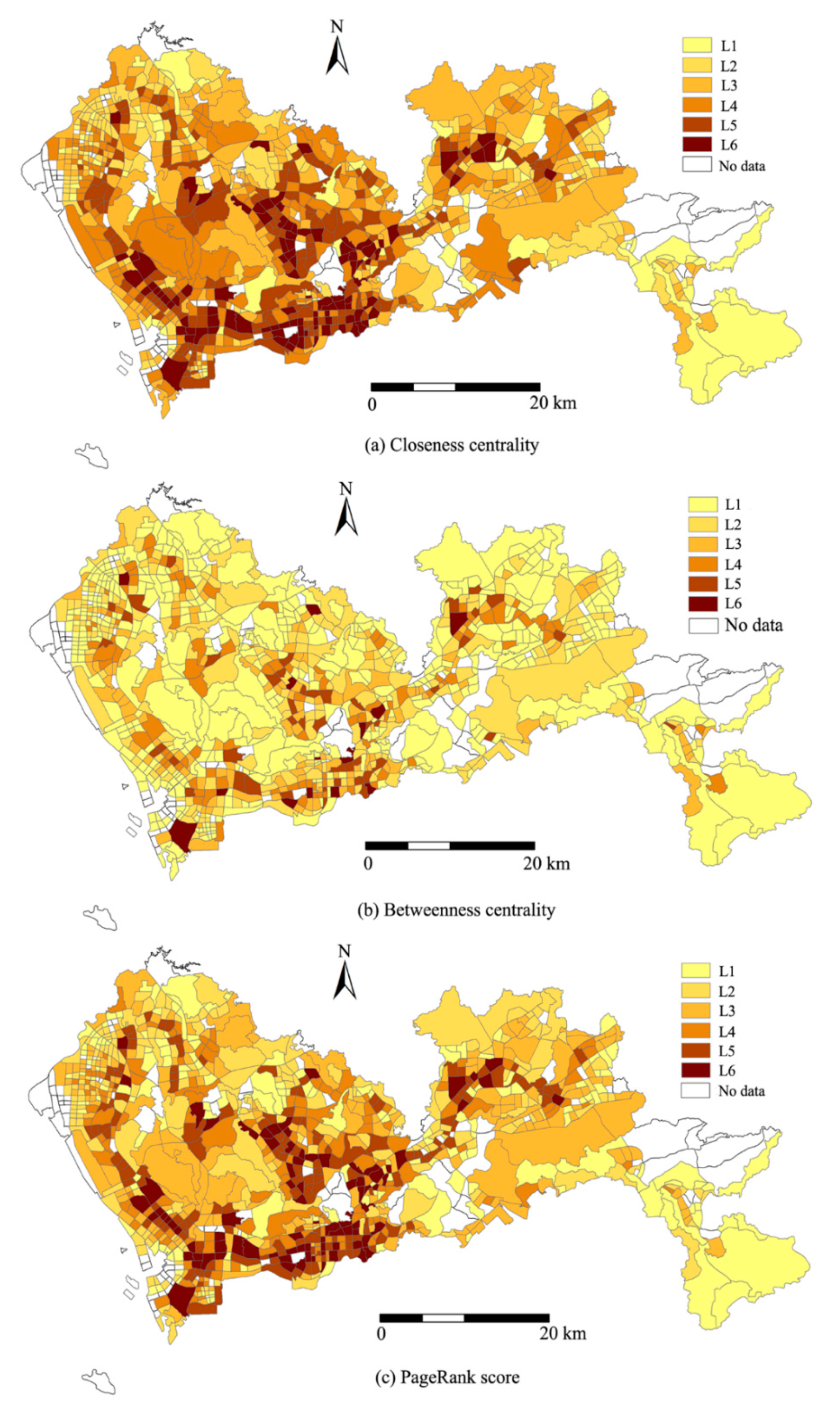
4.2.2. Charactering Centrality of Traffic Analysis Zones in Bus Service Network
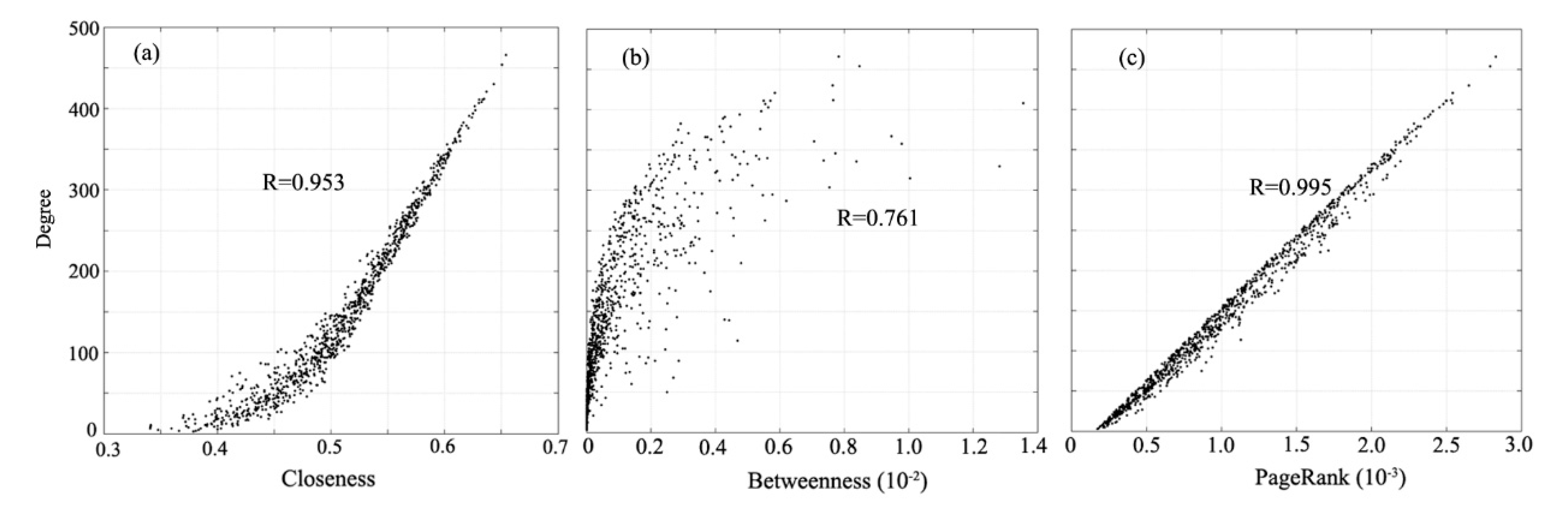
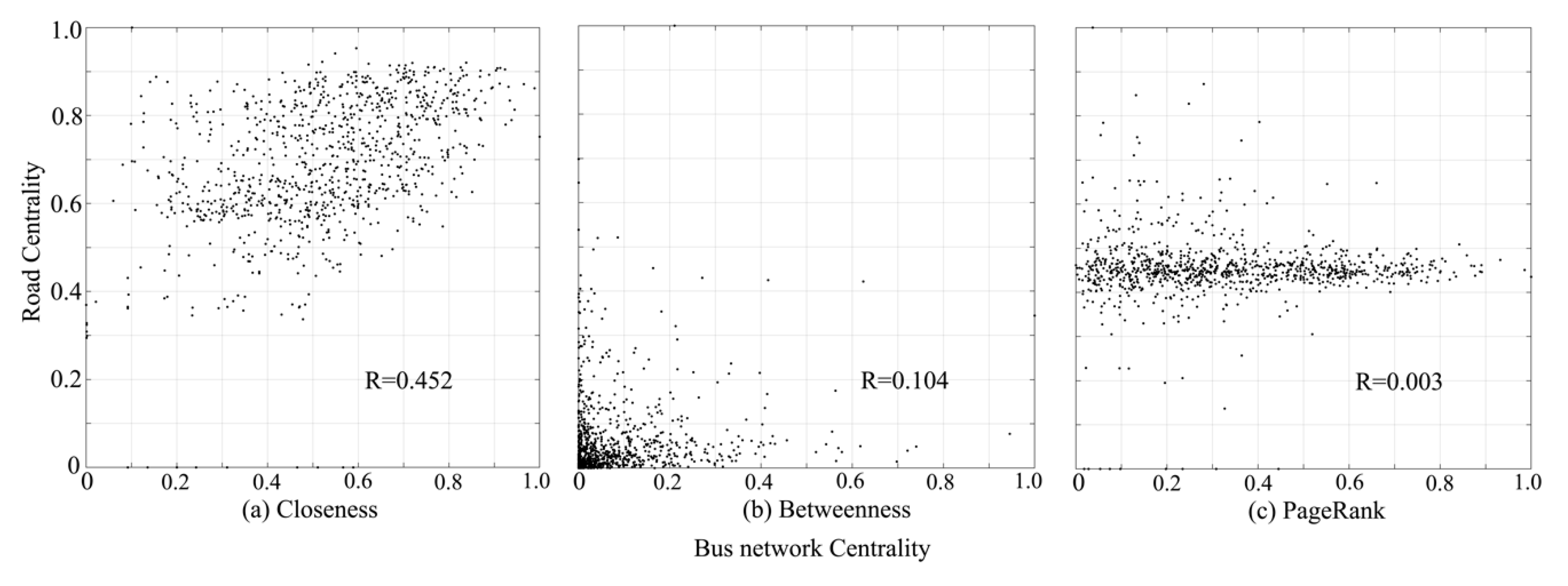
4.2.3. Correlation of Centrality between Bus Network and Road Network
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Pittschieler, K. Performance improvement of urban bus system: Issues and solution. Int. J. Eng. Sci. Technol. 2010, 2, 21–23. [Google Scholar]
- Wang, M.; Hu, B.-Q.; Wu, X.; Niu, Y.-Q. The topological and statistical analysis of public transport network based on fuzzy clustering. In Fuzzy Information and Engineering; Cao, B., Li, T.-F., Zhang, C.-Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2, pp. 1183–1191. [Google Scholar]
- Wu, X.; Dong, H.; Chi, K.T.; Ho, I.W.H.; Lau, F.C.M. Analysis of metro network performance from a complex network perspective. Phys. A Stat. Mech. Appl. 2017, 492, 553–563. [Google Scholar] [CrossRef]
- Lin, J. Network analysis of China’s aviation system, statistical and spatial structure. J. Transp. Geogr. 2012, 22, 109–117. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, M.; Liu, H.; Xu, X. Networked characteristics of the urban rail transit networks. Phys. A Stat. Mech. Appl. 2013, 392, 1538–1546. [Google Scholar] [CrossRef]
- Zhang, J.; Cao, X.B.; Du, W.B.; Cai, K.Q. Evolution of Chinese airport network. Phys. A Stat. Mech. Appl. 2011, 389, 3922–3931. [Google Scholar] [CrossRef]
- Wang, C.; Wang, J. Spatial pattern of the global shipping network and its hub-and-spoke system. Res. Transp. Econ. 2012, 32, 54–63. [Google Scholar] [CrossRef]
- Wang, J.; Mo, H.; Wang, F.; Jin, F. Exploring the network structure and nodal centrality of China’s air transport network: A complex network approach. J. Transp. Geogr. 2011, 19, 712–721. [Google Scholar] [CrossRef]
- Lin, J.; Ban, Y. Complex network topology of transportation systems. Transp. Rev. 2013, 33, 658–685. [Google Scholar] [CrossRef]
- Roth, C.; Kang, S.M.; Batty, M.; Barthélemy, M. Structure of urban movements: Polycentric activity and entangled hierarchical flows. PLoS ONE 2011, 6, e15923. [Google Scholar] [CrossRef]
- Liu, X.; Gong, L.; Gong, Y.; Liu, Y. Revealing travel patterns and city structure with taxi trip data. J. Transp. Geogr. 2015, 43, 78–90. [Google Scholar] [CrossRef]
- Zhong, C.; Arisona, S.M.; Huang, X.; Batty, M.; Schmitt, G. Detecting the dynamics of urban structure through spatial network analysis. Int. J. Geogr. Inf. Sci. 2014, 28, 2178–2199. [Google Scholar] [CrossRef]
- Patuelli, R.; Reggiani, A.; Gorman, S.P.; Nijkamp, P.; Bade, F.J. Network analysis of commuting flows: A comparative static approach to German data. Netw. Spat. Econ. 2007, 7, 315–331. [Google Scholar] [CrossRef]
- Zhu, G.; Corcoran, J.; Shyy, P.; Pileggi, S.F.; Hunter, J. Analysing journey-to-work data using complex networks. J. Transp. Geogr. 2018, 66, 65–79. [Google Scholar] [CrossRef]
- Yang, X.; Fang, Z.; Yin, L.; Li, J.; Zhou, Y.; Lu, S. Understanding the spatial structure of urban commuting using mobile phone location data: A case study of Shenzhen, China. Sustainability 2018, 10, 1435. [Google Scholar] [CrossRef]
- Gonzalez, M.C.; Hidalgo, C.A.; Barabasi, A. Understanding individual human mobility patterns. Nature 2008, 453, 779–782. [Google Scholar] [CrossRef] [PubMed]
- Li, M.X.; Jiang, Z.Q.; Xie, W.J.; Miccichè, S.; Tumminello, M.; Zhou, W.X.; Mantegna, R.N. A comparative analysis of the statistical properties of large mobile phone calling networks. Sci. Rep. 2014, 4, 5132. [Google Scholar] [CrossRef] [PubMed]
- Demsar, U.; Spatenkova, O.; Virrantaus, K. Identifying critical locations in a spatial network with graph theory. Trans. GIS 2008, 12, 61–82. [Google Scholar] [CrossRef]
- Rui, Y.; Ban, Y. Exploring the relationship between street centrality and land use in Stockholm. Int. J. Geogr. Inf. Sci. 2014, 28, 1425–1438. [Google Scholar] [CrossRef]
- Dai, L.; Derudder, B.; Liu, X.; Witlox, F. Transport network backbone extraction: A comparison of techniques. J. Transp. Geogr. 2018, 69, 271–281. [Google Scholar] [CrossRef]
- Jiang, B.; Claramunt, C. Topological analysis of urban street networks. Environ. Plan. B Abstr. 2003, 31, 151–162. [Google Scholar] [CrossRef]
- Sun, D.; Zhao, Y.; Lu, Q.C. Vulnerability analysis of urban rail transit networks: A case study of Shanghai, China. Sustainability 2015, 7, 6919–6936. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, S.; Wang, X. Comparison analysis on vulnerability of metro networks based on complex network. Phys. A Stat. Mech. Appl. 2018, 496, 72–78. [Google Scholar] [CrossRef]
- Soh, H.; Lim, S.; Zhang, T.; Fu, X.; Lee, G.K.K.; Hung, T.G.G.; Di, P.; Prakasam, S.; Wong, L. Weighted complex network analysis of travel routes on the Singapore public transportation system. Phys. A Stat. Mech. Appl. 2010, 389, 5852–5863. [Google Scholar] [CrossRef]
- Chen, Y.Z.; Li, N.; He, D.R. A study on some urban bus transport networks. Phys. A Stat. Mech. Appl. 2007, 376, 747–754. [Google Scholar] [CrossRef]
- Rodrigue, J.P.; Comtois, C.; Slack, B. The geography of transport systems. J. Urban. Technol. 2013, 18, 127. [Google Scholar]
- Feng, S.; Hu, B.; Nie, C.; Shen, X. Empirical study on a directed and weighted bus transport network in china. Phys. A Stat. Mech. Appl. 2016, 441, 85–92. [Google Scholar] [CrossRef]
- Sienkiewicz, J.; Hołyst, J.A. Statistical analysis of 22 public transport networks in Poland. Phys. Rev. 2005, 72, 046127. [Google Scholar] [CrossRef]
- Háznagy, A.; Fi, I.; London, A.; Nemeth, T. Complex network analysis of public transportation networks: A comprehensive study. In Proceedings of the 2015 International Conference on MODELS and Technologies for Intelligent Transportation Systems, Budapest, Hungary, 3–5 June 2015; pp. 371–378. [Google Scholar]
- Tanuja, S.; Ho, I.W.H.; Chi, K.T. Spatial analysis of bus transport networks using network theory. Phys. A Stat. Mech. Appl. 2018, 502, 295–314. [Google Scholar]
- Barabasi, A.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Xu, X.; Hu, J.; Liu, F.; Liu, L. Scaling and correlations in 3 bus-transport networks of China. Phys. A Stat. Mech. Appl. 2007, 374, 441–448. [Google Scholar] [CrossRef]
- Chatterjee, A.; Ramadurai, G. Scaling laws in Chennai bus network. In Proceedings of the International Conference on Complex Systems and Applications ICCSA 2014, Le Havre, France, 23–26 June 2014. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Latora, V.; Marchiori, M. Efficient behavior of small-world networks. Phys. Rev. Lett. 2001, 87, 198701. [Google Scholar] [CrossRef] [PubMed]
- Barthelemy, M. Spatial networks. Phys. Rep. 2010, 499, 1–101. [Google Scholar] [CrossRef]
- Yang, X.-H.; Chen, G.; Chen, S.-Y.; Wang, W.-L.; Wang, L. Study on some bus transport networks in China with considering spatial characteristics. Transp. Res. Part A Policy Pract. 2014, 69, 1–10. [Google Scholar] [CrossRef]
- Fang, Z.; Yang, X.; Xu, Y.; Shaw, S.; Yin, L. Spatiotemporal model for assessing the stability of urban human convergence and divergence patterns. Int. J. Geogr. Inf. Sci. 2017, 31, 2119–2141. [Google Scholar] [CrossRef]
- Amap Platform. Available online: https://www.amap.com/ (accessed on 29 October 2019).
- Sen, P.; Dasgupta, S.; Chatterjee, A.; Sreeram, P.A.; Mukherjee, G.; Manna, S.S. Small-world properties of the Indian railway network. Phys. Rev. E 2003, 67, 036106. [Google Scholar] [CrossRef]
- You, J.; Nedović-Budić, Z.; Kim, T.J. A GIS-based traffic analysis zone design: Technique. Transp. Plan. Technol. 1998, 21, 45–68. [Google Scholar] [CrossRef]
- Dong, H.; Wu, M.; Ding, X.; Chu, L.; Jia, L.; Qin, Y.; Zhou, X. Traffic zone division based on big data from mobile phone base stations. Transp. Res. Part. C Emerg. Technol. 2015, 58, 278–291. [Google Scholar] [CrossRef]
- Amaral, L.A.; Scala, A.; Barthelemy, M.; Stanley, H.E. Classes of small-world networks. Proc. Natl. Acad. Sci. USA 2000, 97, 11149–11152. [Google Scholar] [CrossRef]
- Sabidussi, G. The centrality index of a graph. Psychometrika 1996, 31, 581–603. [Google Scholar] [CrossRef]
- Freeman, L.C. A set of measures of centrality based upon betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual web search engine. Comput. Netw. ISDN Syst. 1998, 30, 107–117. [Google Scholar] [CrossRef]
- Liu, L.; Li, R.; Shao, F.; Sun, R. Complexity analysis of Qingdao’s public transport network. In Proceedings of the International Symposium on Intelligent Information Systems and Applications (IISA 2009), Nanchang, China, 21–22 November 2009; pp. 300–303. [Google Scholar]
- Ferber, C.V.; Holovatch, T.; Holovatch, Y.; Palchykov, V. Network harness: Metropolis public transport. Phys. A Stat. Mech. Appl. 2007, 380, 585–591. [Google Scholar] [CrossRef]
- Huang, Y.; Lu, S.; Yang, X.; Zhao, Z. Exploring railway network dynamics in China from 2008 to 2017. ISPRS Int. J. Geo Inf. 2018, 7, 320. [Google Scholar] [CrossRef]
- Clauset, A.; Newman, M.E.J.; Moore, C. Finding community structure in very large networks. Phys. Rev. E 2004, 70, 066111. [Google Scholar] [CrossRef] [PubMed]
- Jenks, G.F. The data model concept in statistical mapping. Int. Yearb. Cartogr. 1967, 7, 186–190. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Lu, S.; Zhao, W.; Zhao, Z. Exploring the Characteristics of an Intra-Urban Bus Service Network: A Case Study of Shenzhen, China. ISPRS Int. J. Geo-Inf. 2019, 8, 486. https://doi.org/10.3390/ijgi8110486
Yang X, Lu S, Zhao W, Zhao Z. Exploring the Characteristics of an Intra-Urban Bus Service Network: A Case Study of Shenzhen, China. ISPRS International Journal of Geo-Information. 2019; 8(11):486. https://doi.org/10.3390/ijgi8110486
Chicago/Turabian StyleYang, Xiping, Shiwei Lu, Weifeng Zhao, and Zhiyuan Zhao. 2019. "Exploring the Characteristics of an Intra-Urban Bus Service Network: A Case Study of Shenzhen, China" ISPRS International Journal of Geo-Information 8, no. 11: 486. https://doi.org/10.3390/ijgi8110486
APA StyleYang, X., Lu, S., Zhao, W., & Zhao, Z. (2019). Exploring the Characteristics of an Intra-Urban Bus Service Network: A Case Study of Shenzhen, China. ISPRS International Journal of Geo-Information, 8(11), 486. https://doi.org/10.3390/ijgi8110486




