Estimation of Origin-Destination Flows of Passenger Cars in 1925 in Old Tokyo City, Japan
Abstract
1. Introduction
2. Materials and Methods
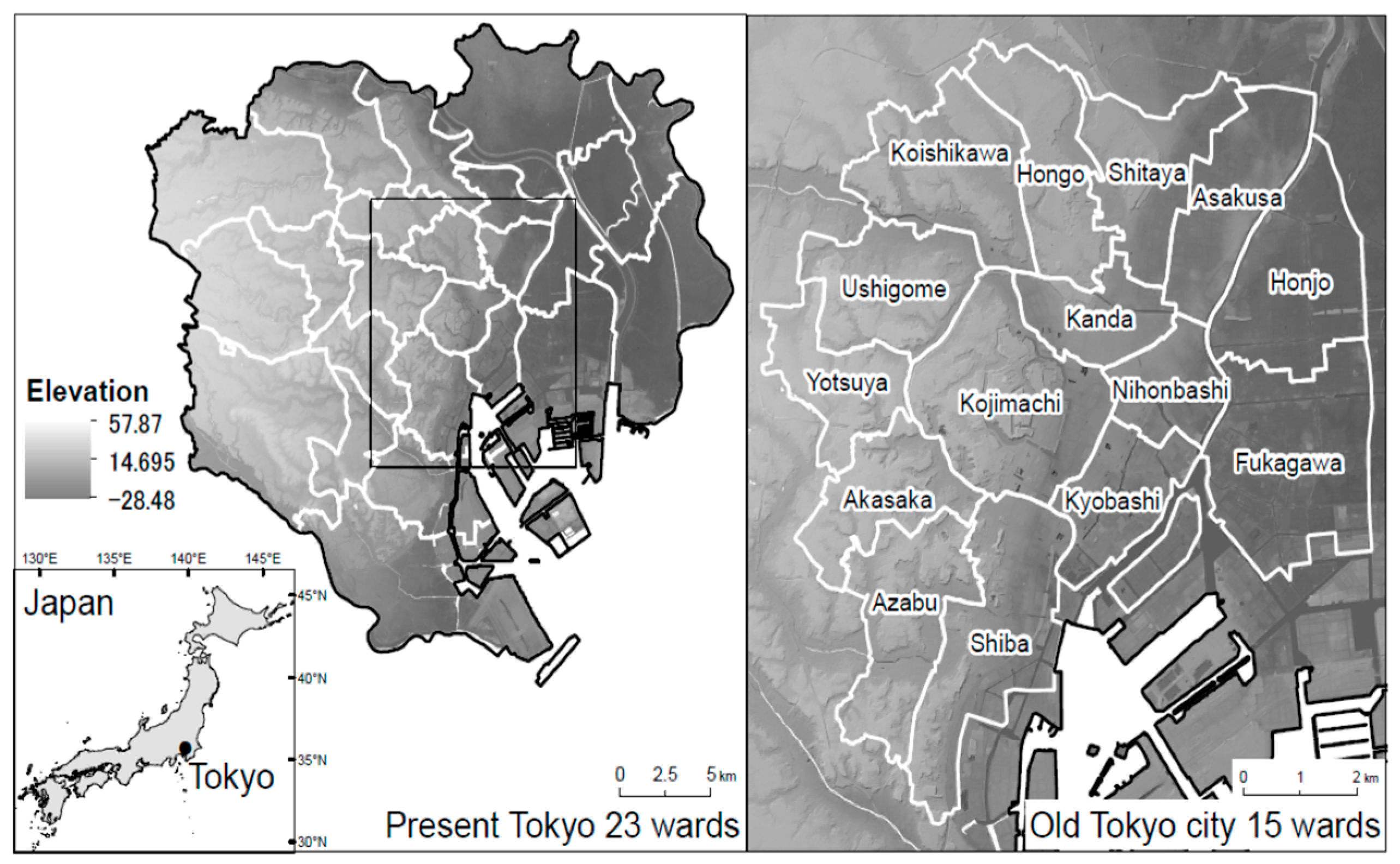
2.1. Study Area
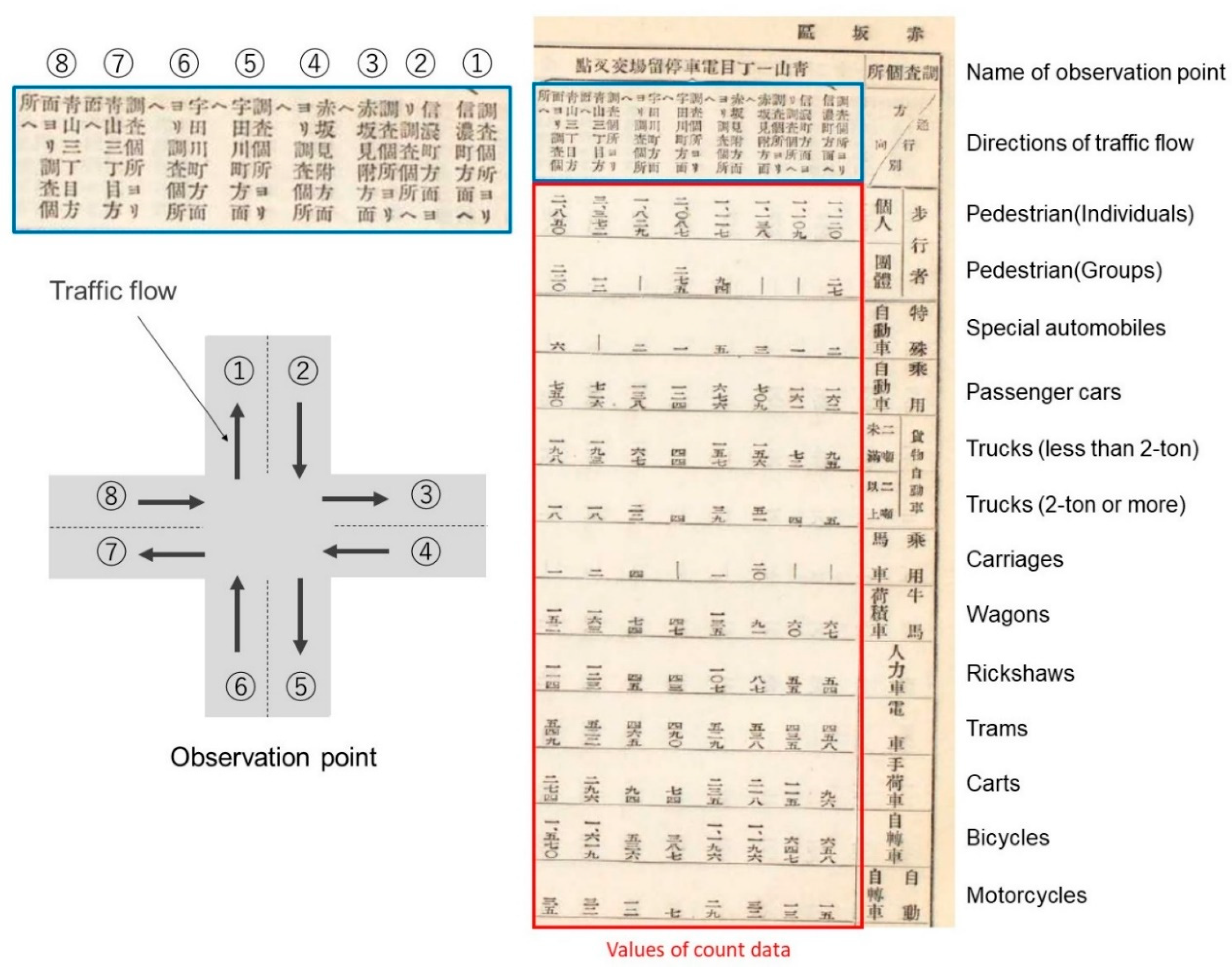
2.2. Data
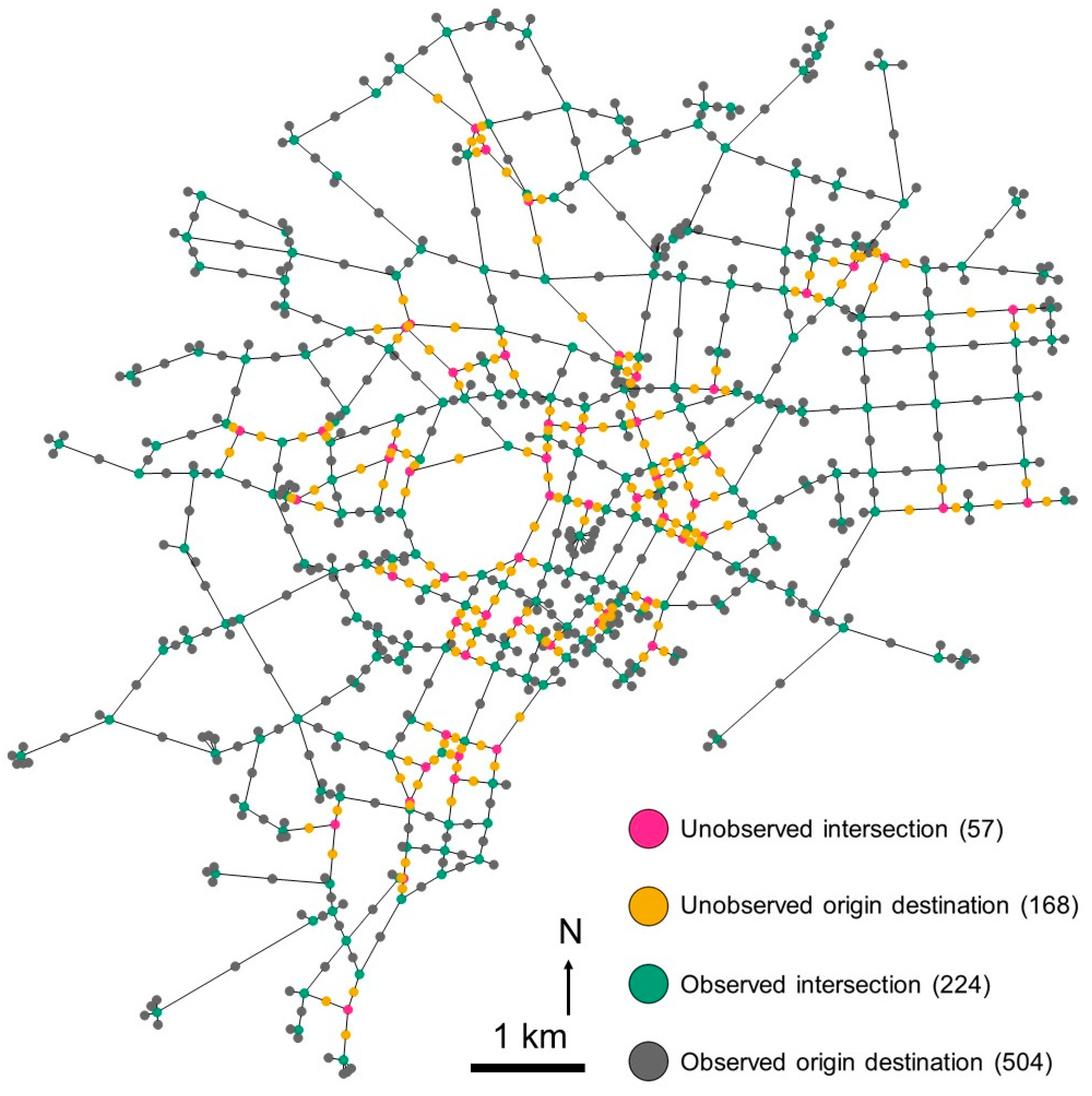
2.3. Road Graph
2.4. OD Flows Estimation by Absorbing Markov Chain Model
2.4.1. Overview of Absorbing Markov Chain Model
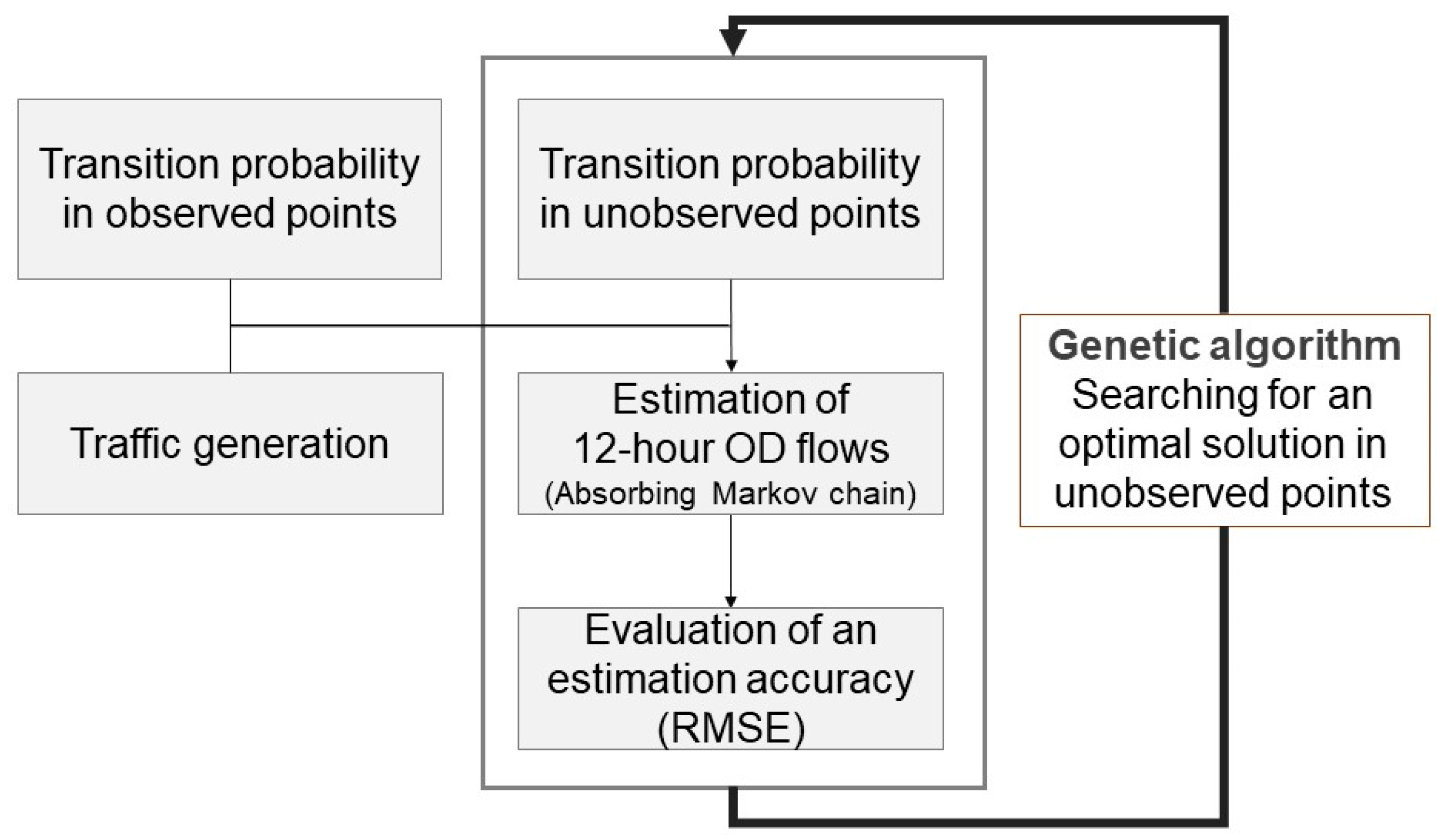
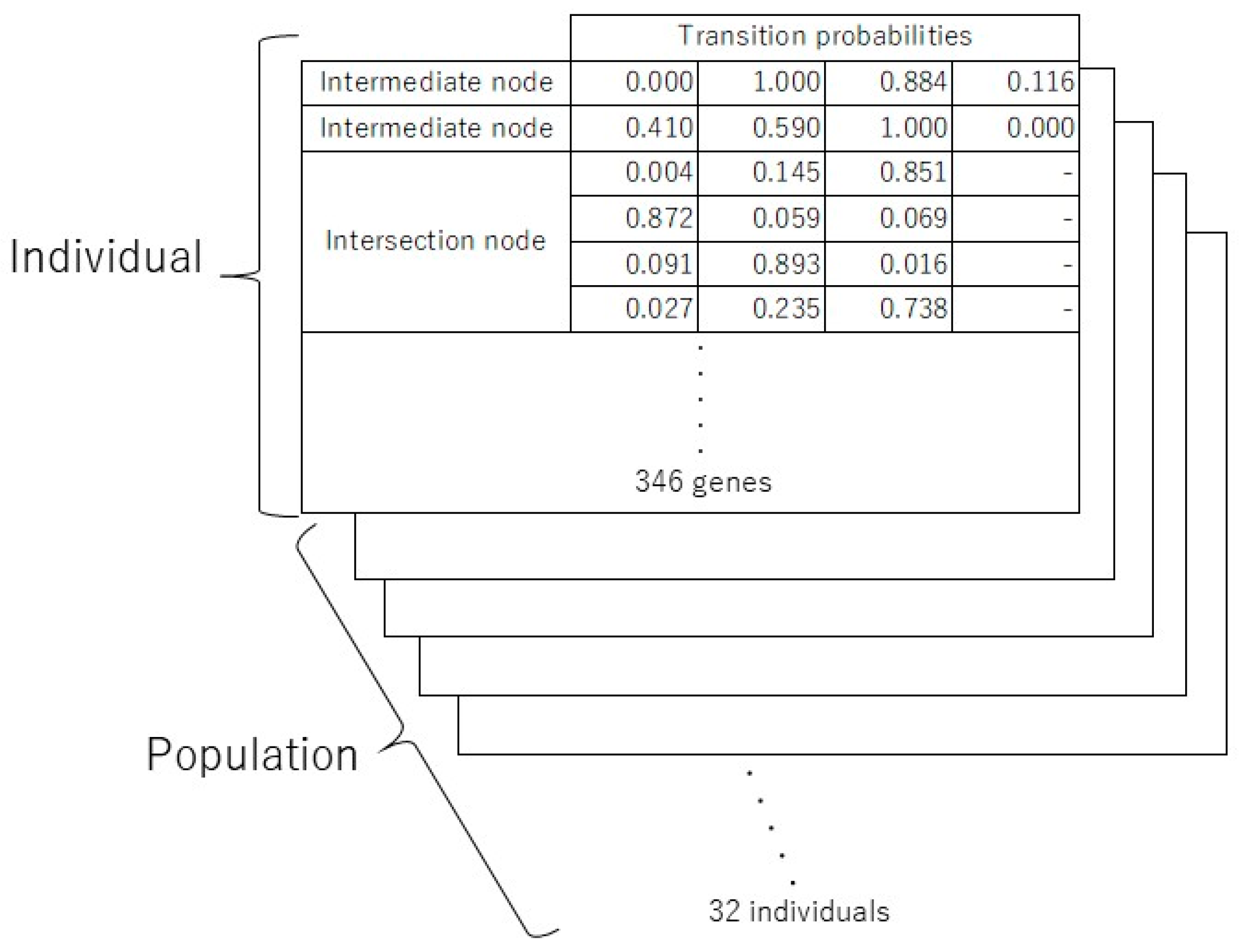
2.4.2. Estimation Procedure of OD Flows
2.5. Estimation of Transition Probabilities on the Unobserved Nodes Using a Genetic Algorithm
2.5.1. Overview of the Genetic Algorithm
2.5.2. Initialization
2.5.3. Evaluation and Convergence Conditions
2.5.4. Selection
2.5.5. Crossover and Mutation
3. Results and Discussions
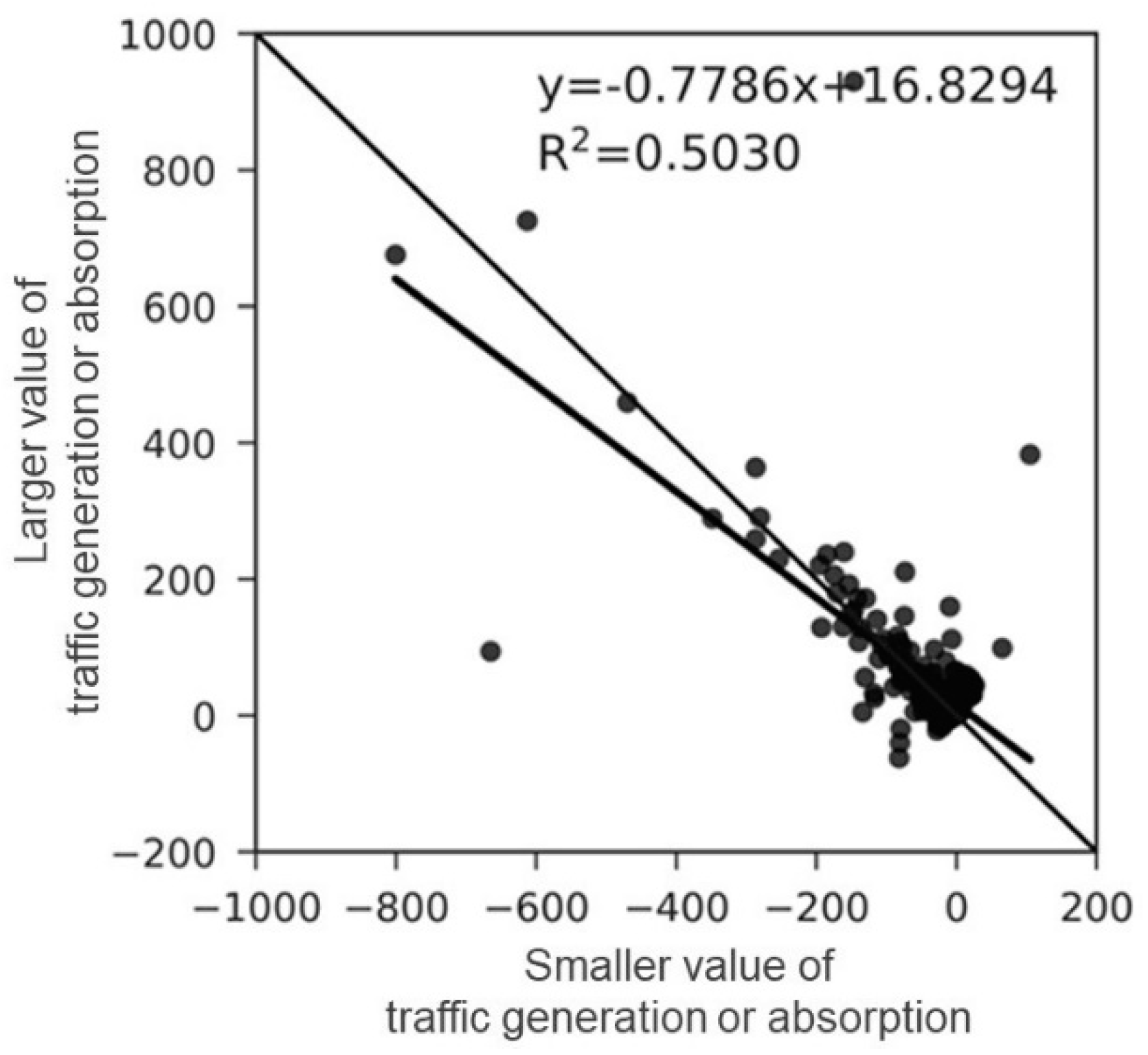
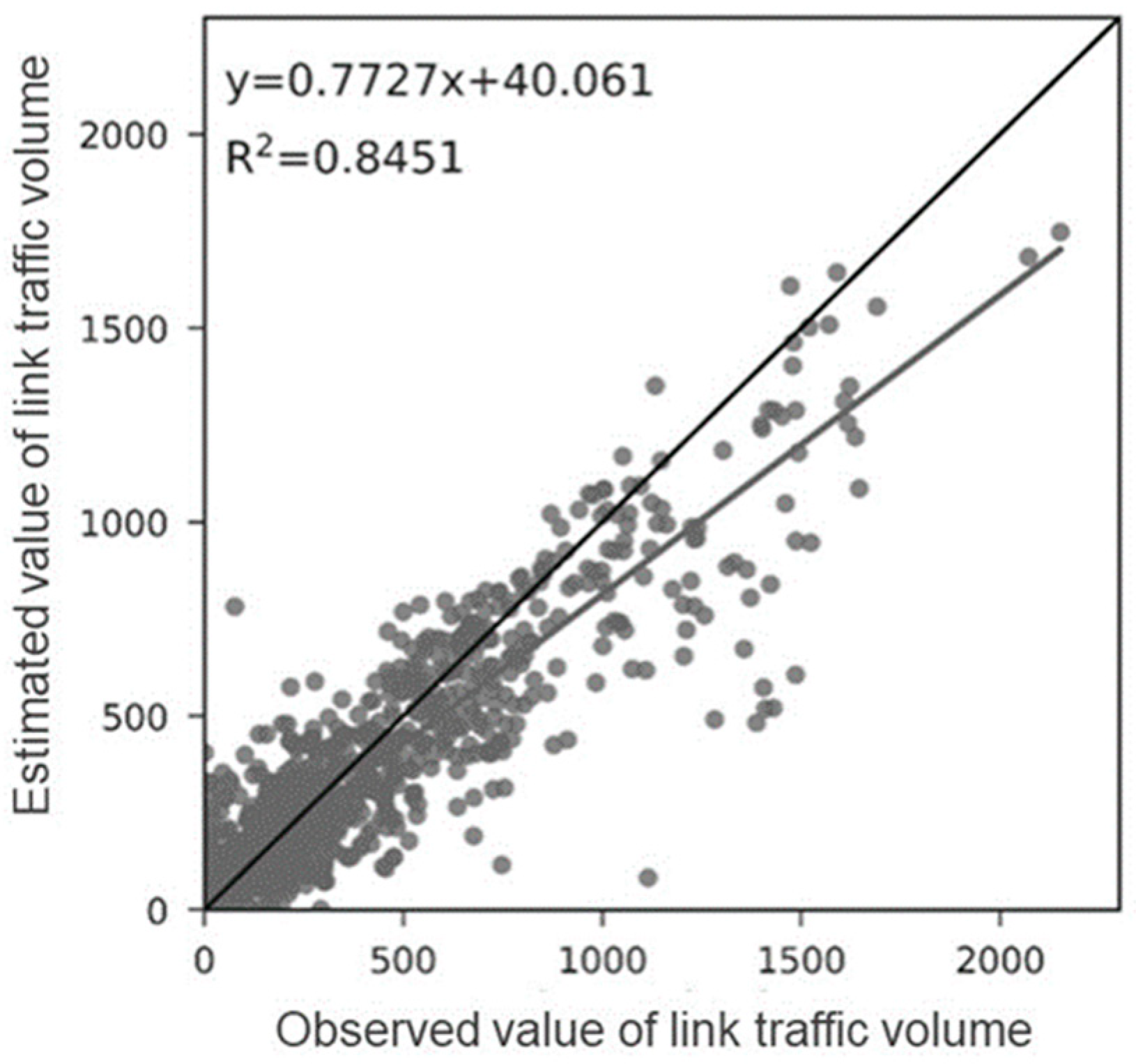
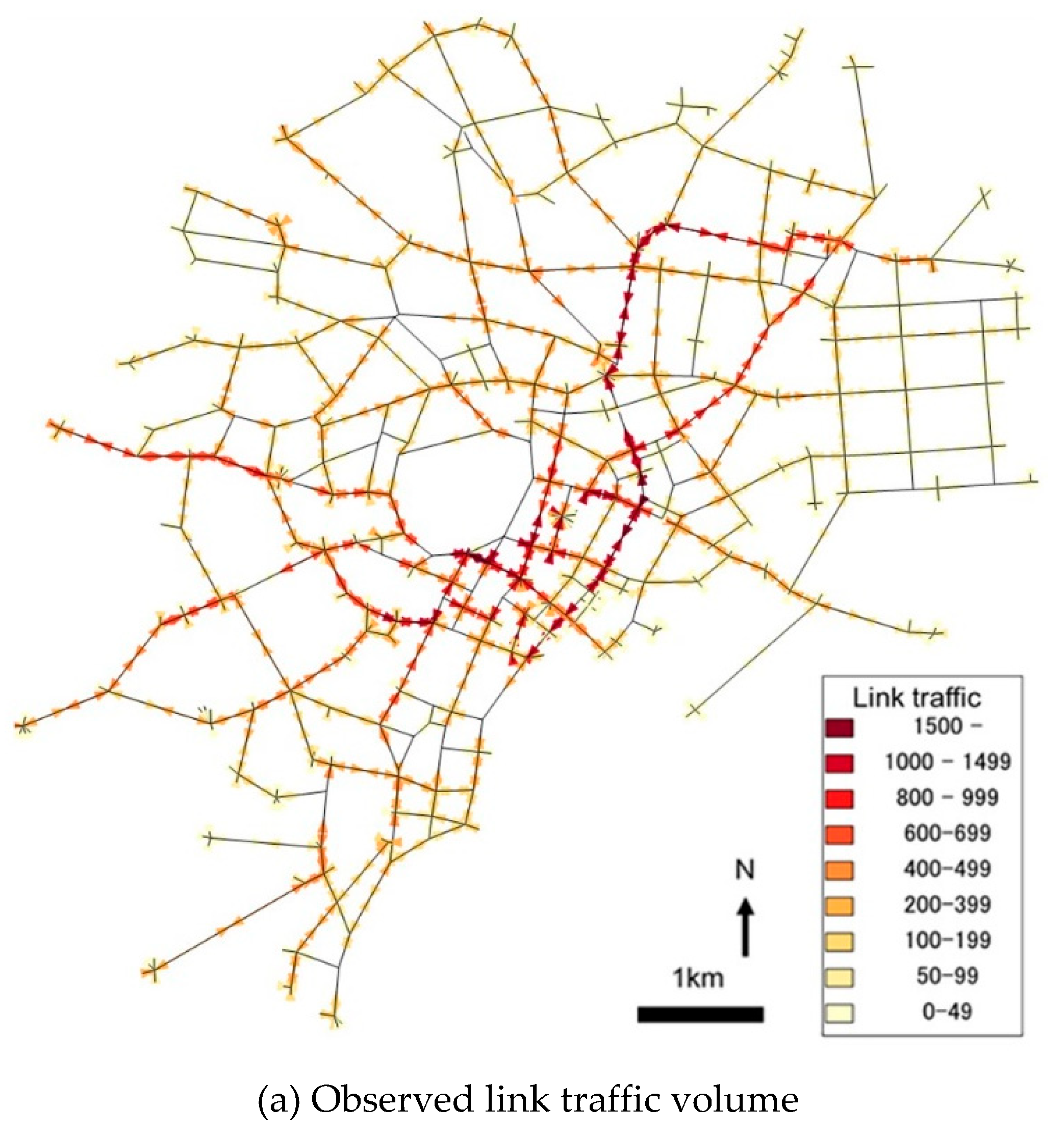
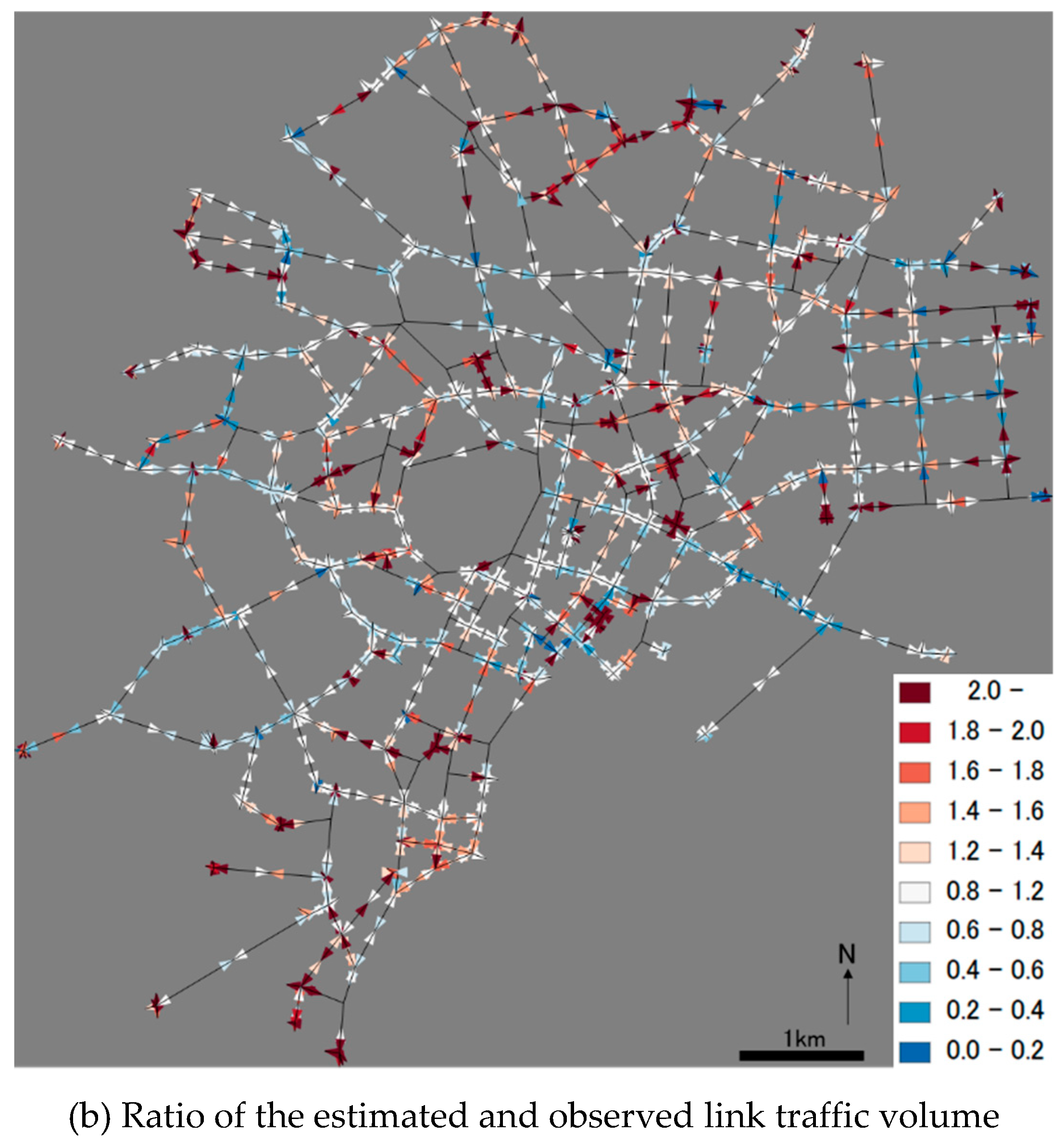
3.1. Evaluation of the GA Model by Comparison of Estimated and Observed Link Traffic
3.2. Estimated OD Flows
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jahanshahi, K.; Jin, Y.; Williams, I. Direct and indirect influences on employed adults’ travel in the UK: New insights from the National Travel Survey data 2002–2010. Transp. Res. Part A Policy Pract. 2015, 80, 288–306. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, X. Explore the relationship between online shopping and shopping trips: An analysis with the 2009 NHTS data. Transp. Res. Part A Policy Pract. 2014, 70, 1–9. [Google Scholar] [CrossRef]
- Giesel, F.; Köhler, K. How poverty restricts elderly Germans’ everyday travel. Eur. Transp. Res. Rev. 2015, 7, 15. [Google Scholar] [CrossRef]
- MLIT What is PT Survey? Available online: http://www.mlit.go.jp/crd/tosiko/pt.html (accessed on 25 April 2019).
- Yamamoto, T. Comparative analysis of household car, motorcycle and bicycle ownership between Osaka metropolitan area, Japan and Kuala Lumpur, Malaysia. Transportation 2009, 36, 351–366. [Google Scholar] [CrossRef]
- Lwin, K.K.; Sugiura, K.; Zettsu, K. Space–time multiple regression model for grid-based population estimation in urban areas. Int. J. Geogr. Inf. Sci. 2016, 30, 1579–1593. [Google Scholar] [CrossRef]
- Sekimoto, Y.; Shibasaki, R.; Kanasugi, H.; Usui, T.; Shimazaki, Y. PFlow: Reconstruction of people flow by recycling large-scale fragmentary social survey data. IEEE Pervasive Comput. 2011, 10, 27–35. [Google Scholar] [CrossRef]
- Osaragi, T. Modeling a spatiotemporal distribution of stranded people returning home on foot in the aftermath of a large-scale earthquake. Nat. Hazards 2013, 68, 1385–1398. [Google Scholar] [CrossRef]
- MLIT OD Survey. Available online: http://www.mlit.go.jp/road/h27road-od/index.html (accessed on 25 January 2019).
- Kohira, H.; Hibino, N.; Morichi, S. Time-series analysis of tourists’ behavior using car based on individual data of both tourism statistic and traffic census. J. Japan Soc. Civ. Eng. Ser. D3 2014, 70, I_423–I_432. [Google Scholar]
- Fujita, M.; Watanabe, K.; Yamada, S. Hourly OD flow estimation from observed traffic flows based on time coefficient of daily OD flow. JSTE J. Traffic Eng. 2016, 2, 11–20. [Google Scholar]
- Iqbal, M.S.; Choudhury, C.F.; Wang, P.; González, M.C. Development of origin-destination matrices using mobile phone call data. Transp. Res. Part C Emerg. Technol. 2014, 40, 63–74. [Google Scholar] [CrossRef]
- Larijani, A.N.; Olteanu-Raimond, A.-M.; Perret, J.; Brédif, M.; Ziemlicki, C. Investigating the Mobile Phone Data to Estimate the Origin Destination Flow and Analysis; Case Study: Paris Region. Transp. Res. Procedia 2015, 6, 64–78. [Google Scholar] [CrossRef]
- Long, Y.; Thill, J.C. Combining smart card data and household travel survey to analyze jobs-housing relationships in Beijing. Comput. Environ. Urban Syst. 2015, 53, 19–35. [Google Scholar] [CrossRef]
- Ma, X.; Liu, C.; Wen, H.; Wang, Y.; Wu, Y.J. Understanding commuting patterns using transit smart card data. J. Transp. Geogr. 2017, 58, 135–145. [Google Scholar] [CrossRef]
- Yue, Y.; Lan, T.; Yeh, A.G.O.; Li, Q.-Q. Zooming into individuals to understand the collective: A review of trajectory-based travel behaviour studies. Travel Behav. Soc. 2014, 1, 69–78. [Google Scholar] [CrossRef]
- Zambrano-Martinez, J.L.; Calafate, C.T.; Soler, D.; Cano, J.C.; Manzoni, P. Modeling and characterization of traffic flows in urban environments. Sensors 2018, 18, 2020. [Google Scholar] [CrossRef]
- Nguyen, T.V.; Krajzewicz, D.; Fullerton, M.; Nicolay, E. DFROUTER—Estimation of Vehicle Routes from Cross-Section Measurements. Lect. Notes Control Inf. Sci. 2015, 13, 3–23. [Google Scholar]
- Konagaya, K. The recent developmant of geography of urban transportation travel demand studies. Jpn. J. Hum. Geogr. 1990, 42, 25–49. [Google Scholar] [CrossRef]
- Gregory, I.N. Different Places, Different Stories: Infant Mortality Decline in England and Wales, 1851–1911. Ann. Assoc. Am. Geogr. 2008, 98, 773–794. [Google Scholar] [CrossRef]
- Tucci, M.; Giordano, A.; Ronza, R.W. Using Spatial Analysis and Geovisualization to Reveal Urban Changes: Milan, Italy, 1737–2005. Cartogr. Int. J. Geogr. Inf. Geovis. 2010, 45, 47–63. [Google Scholar] [CrossRef]
- Pindozzi, S.; Cervelli, E.; Capolupo, A.; Okello, C.; Boccia, L. Using historical maps to analyze two hundred years of land cover changes: Case study of Sorrento peninsula (South Italy). Cartogr. Geogr. Inf. Sci. 2016, 43, 250–265. [Google Scholar] [CrossRef]
- Edelson, S.M.; Ferster, B. MapScholar: A Web Tool for Publishing Interactive Cartographic Collections. J. Map Geogr. Libr. 2013, 9, 81–107. [Google Scholar] [CrossRef]
- Santos, J.; Anastácio, I.; Martins, B. Using machine learning methods for disambiguating place references in textual documents. GeoJournal 2015, 80, 375–392. [Google Scholar] [CrossRef]
- Offen, K. Historical geography II. Prog. Hum. Geogr. 2013, 37, 564–577. [Google Scholar] [CrossRef]
- Brotton, J. Maps online: Digital historical geographies. J. Hist. Geogr. 2014, 43, 169–174. [Google Scholar] [CrossRef]
- Inoue, M. Kyoto’s Daily Rhythm as Seen from Traffic Flow in the Prewar Showa Period. In Historical GIS of Kyoto; Yano, K., Nakaya, T., Kawasumi, T., Tanaka, S., Eds.; Nakanishiya Shuppan: Kyoto, Japan, 2011; pp. 263–272. ISBN 4779505429. [Google Scholar]
- Hayashi, N. Regional Theory of Urban Transportation; Harashobou: Tokyo, Japan, 2007; ISBN 4562091150. [Google Scholar]
- Hoogendoorn, S.P.; Bovy, P.H.L. State-of-the-art of vehicular traffic flow modelling. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2001, 215, 283–303. [Google Scholar] [CrossRef]
- Li, B. Bayesian Inference for Origin-Destination Matrices of Transport Networks Using the EM Algorithm. Technometrics 2005, 47, 399–408. [Google Scholar] [CrossRef]
- Perrakis, K.; Karlis, D.; Cools, M.; Janssens, D.; Vanhoof, K.; Wets, G. A Bayesian approach for modeling origin–destination matrices. Transp. Res. Part A Policy Pract. 2012, 46, 200–212. [Google Scholar] [CrossRef]
- Castillo, E.; Jiménez, P.; Menéndez, J.M.; Nogal, M. A Bayesian method for estimating traffic flows based on plate scanning. Transportation 2013, 40, 173–201. [Google Scholar] [CrossRef]
- Wang, J.; Deng, W.; Guo, Y. New Bayesian combination method for short-term traffic flow forecasting. Transp. Res. Part C Emerg. Technol. 2014, 43, 79–94. [Google Scholar] [CrossRef]
- Ren, Y.; Ercsey-Ravasz, M.; Wang, P.; González, M.C.; Toroczkai, Z. Predicting commuter flows in spatial networks using a radiation model based on temporal ranges. Nat. Commun. 2014, 5, 5347. [Google Scholar] [CrossRef]
- Zhou, H.; Tan, L.; Ge, F.; Chan, S. Traffic matrix estimation: Advanced-Tomogravity method based on a precise gravity models. Int. J. Commun. Syst. 2015, 28, 1709–1728. [Google Scholar] [CrossRef]
- Talebian, A.; Shafahi, Y. The treatment of uncertainty in the dynamic origin–destination estimation problem using a fuzzy approach. Transp. Plan. Technol. 2015, 38, 795–815. [Google Scholar] [CrossRef]
- Willumsen, L. Estimation of an O-D Matrix from Traffic Counts-A Review; Working Paper; Institute of Transport Studies, University of Leeds: Leeds, UK, 1978. [Google Scholar]
- Robillard, P. Estimating the O-D matrix from observed link volumes. Transp. Res. 1975, 9, 123–128. [Google Scholar] [CrossRef]
- Tokyo city Tokyo-Shi Shisei Toukei Genpyou (Munisipal Census of Tokyo City); Tokyo city: Tokyo, Japan. 1927. Available online: http://dl.ndl.go.jp/info:ndljp/pid/1466016 (accessed on 22 October 2019).
- Tokyo city Dai 23 kai Tokyo-Shi Toukei Nenpyou (23th Annual Report of Statistics in Tokyo City); Tokyo city: Tokyo, Japan. 1927. Available online: http://dl.ndl.go.jp/info:ndljp/pid/1448282 (accessed on 22 October 2019).
- Masai, Y.; Hong, C. “Restored land use map of pre-earthquake Tokyo” and its making process. Map J. Japan Cartogr. Assoc. 1993, 31, 35–39. [Google Scholar]
- Hong, C. Urban land use in Tokyo in the early twentieth century: A comparison with Edo. Geogr. Rev. Japan Ser. A 1993, 66, 540–554. [Google Scholar] [CrossRef]
- Sasaki, T. Theory of traffic assignment thorough absorbing markov process. Trans. Japan Soc. Civ. Eng. 1965, 1965, 28–32. [Google Scholar]
- Itoh, S.; Hato, E. Absorbing Markov Chain Traffic Flow Assignment Using a Dynamic Route Choice Model. J. City Plan. Inst. Japan 2013, 48, 447–452. [Google Scholar]
- Tesselkin, A.; Khabarov, V. Estimation of Origin-Destination Matrices Based on Markov Chains. Procedia Eng. 2017, 178, 107–116. [Google Scholar] [CrossRef]
- Takayama, J.; Sugiyama, T. A study on O-D estimation model by observed link flows using absorbing markov chain. Doboku Gakkai Ronbunshu 1997, 1997, 75–84. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992; ISBN 0262581116. [Google Scholar]
- Kim, H.; Baek, S.; Lim, Y. Origin-destination matrices estimated with a genetic algorithm from link traffic counts. Transp. Res. Rec. J. Transp. Res. Board 2001, 1771, 156–163. [Google Scholar] [CrossRef]
- Wood, J.; Dykes, J.; Slingsby, A. Visualization of Origins, Destinations and Flows with OD Maps. Cartogr. J. 2010, 47, 117–129. [Google Scholar] [CrossRef]
- Nakama, T. Nihon chiri fuzoku taikei 2: Dai Tokyo hen (Outline of Tokyo Cultural Geography); Shinkosha: Tokyo, Japan, 1931; p. 409. [Google Scholar]
- Ueno, K. Residential structure of Tokyo during the Taisho era (1920)—a factorial ecological study of the socio-economic characteristics of residential population. Jpn. J. Hum. Geogr. 1981, 33, 385–404. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishikawa, K.; Nakayama, D. Estimation of Origin-Destination Flows of Passenger Cars in 1925 in Old Tokyo City, Japan. ISPRS Int. J. Geo-Inf. 2019, 8, 472. https://doi.org/10.3390/ijgi8110472
Ishikawa K, Nakayama D. Estimation of Origin-Destination Flows of Passenger Cars in 1925 in Old Tokyo City, Japan. ISPRS International Journal of Geo-Information. 2019; 8(11):472. https://doi.org/10.3390/ijgi8110472
Chicago/Turabian StyleIshikawa, Kazuki, and Daichi Nakayama. 2019. "Estimation of Origin-Destination Flows of Passenger Cars in 1925 in Old Tokyo City, Japan" ISPRS International Journal of Geo-Information 8, no. 11: 472. https://doi.org/10.3390/ijgi8110472
APA StyleIshikawa, K., & Nakayama, D. (2019). Estimation of Origin-Destination Flows of Passenger Cars in 1925 in Old Tokyo City, Japan. ISPRS International Journal of Geo-Information, 8(11), 472. https://doi.org/10.3390/ijgi8110472




