Mobile Phone Indicators and Their Relation to the Socioeconomic Organisation of Cities
Abstract
1. Introduction
1.1. The Single-City Focus of Urban Sensing
1.2. Mobile Phone Indicators
1.3. Sensitivity of Urban Scaling Laws to City Definitions
1.4. Research Question and Relevance
2. Data
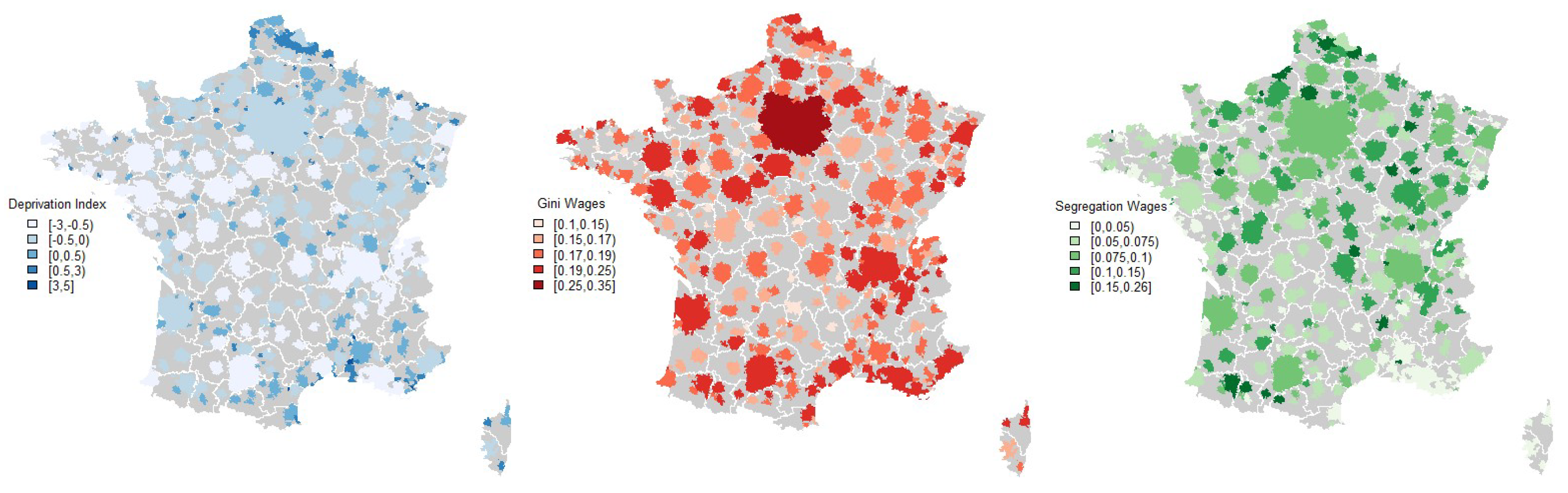
2.1. Census Data on Segregation, Inequality, and Deprivation
2.2. Constructing Indicators from the French Mobile Phone Data
3. Methods
3.1. Aggregation: From Cell Towers to Commune to City
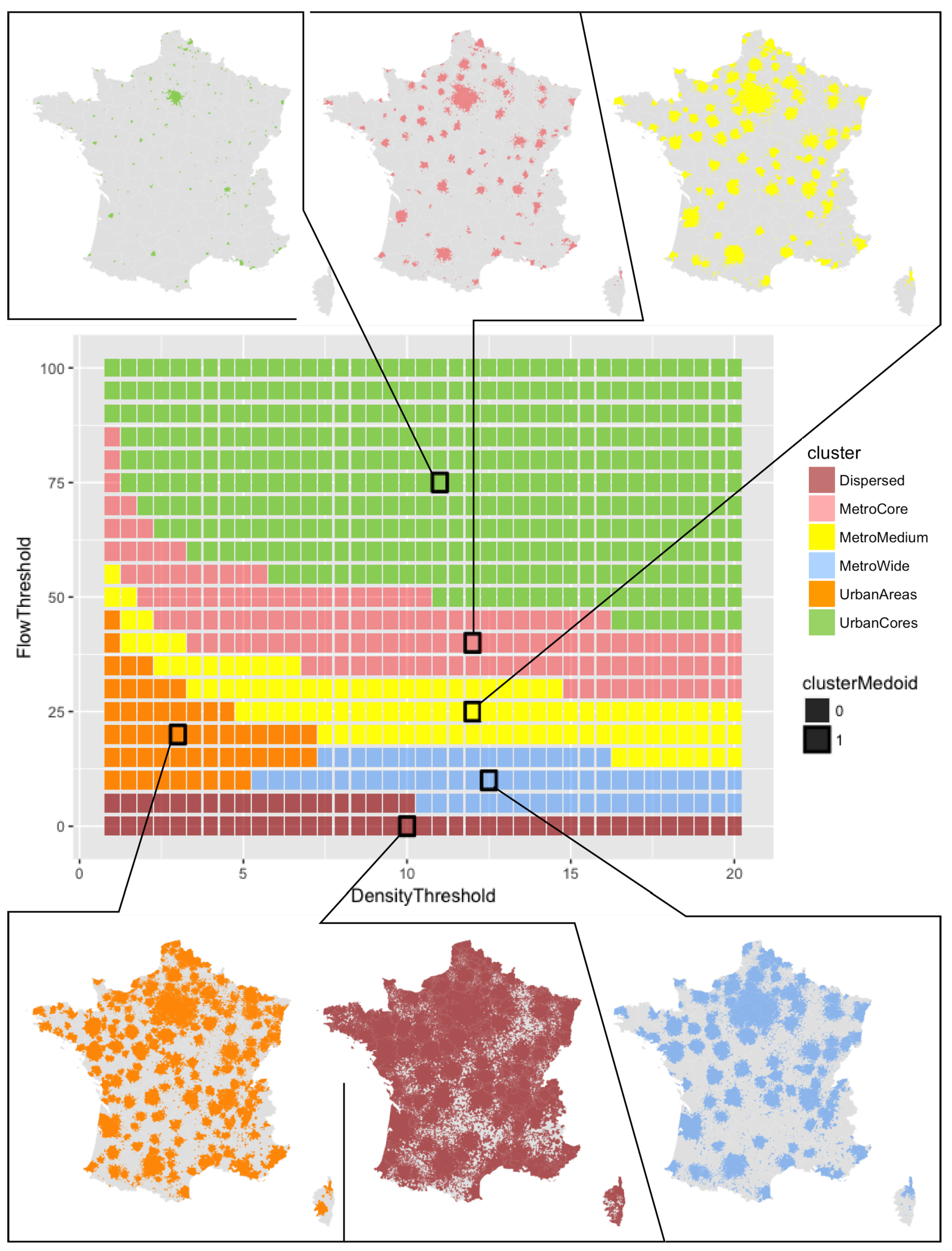
3.2. Simulating City Definitions
3.3. Correlations between Mobile Phone Indicators and Census Data
3.4. Representing Results for All 4914 City Definitions
3.5. Clustering City Definitions into 6 Classes
4. Results
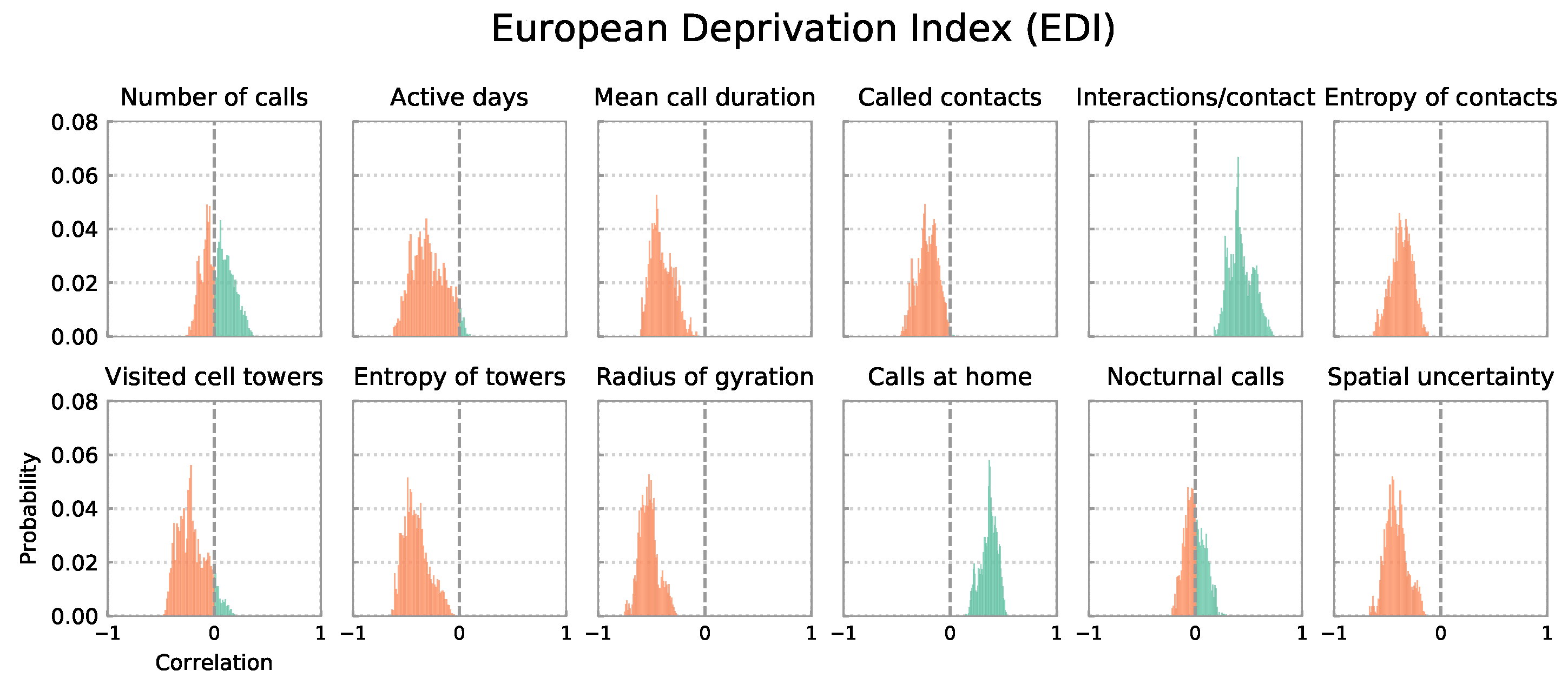
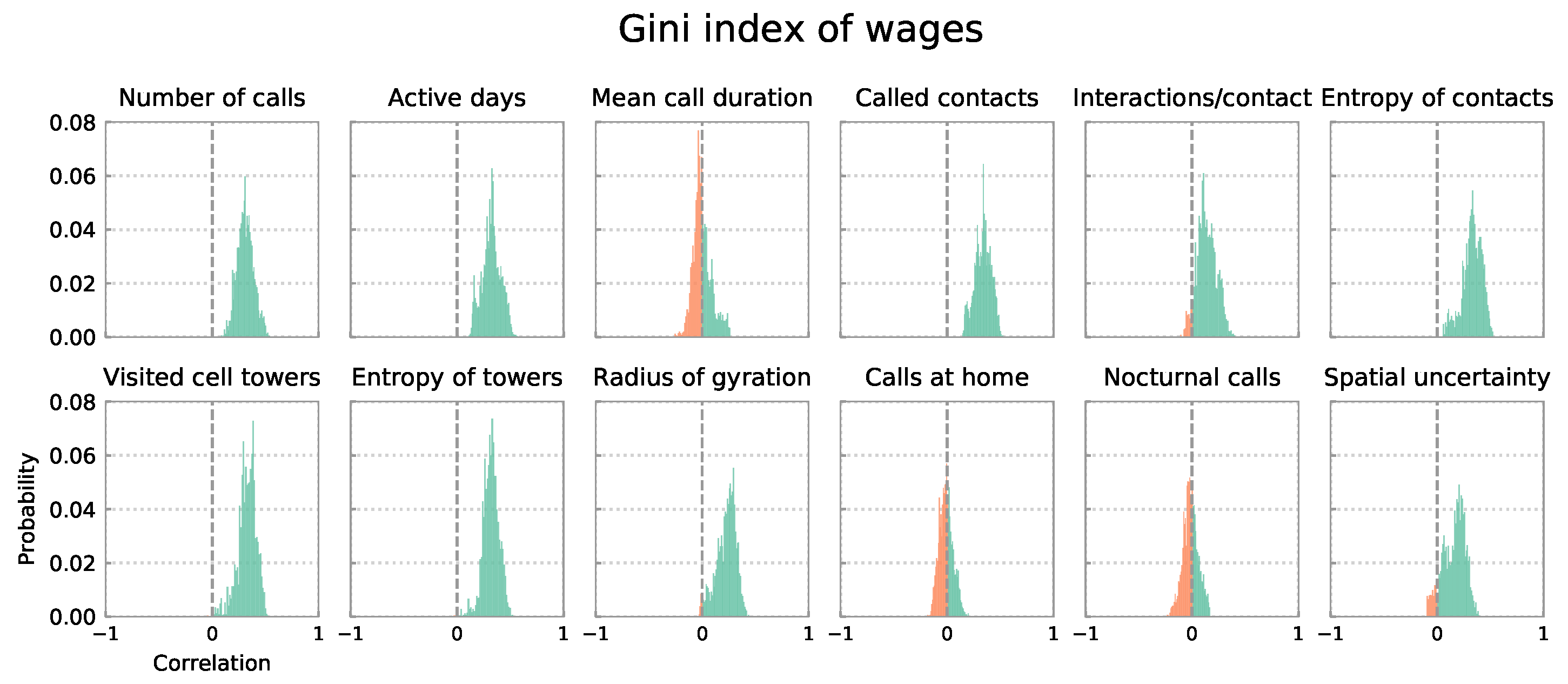
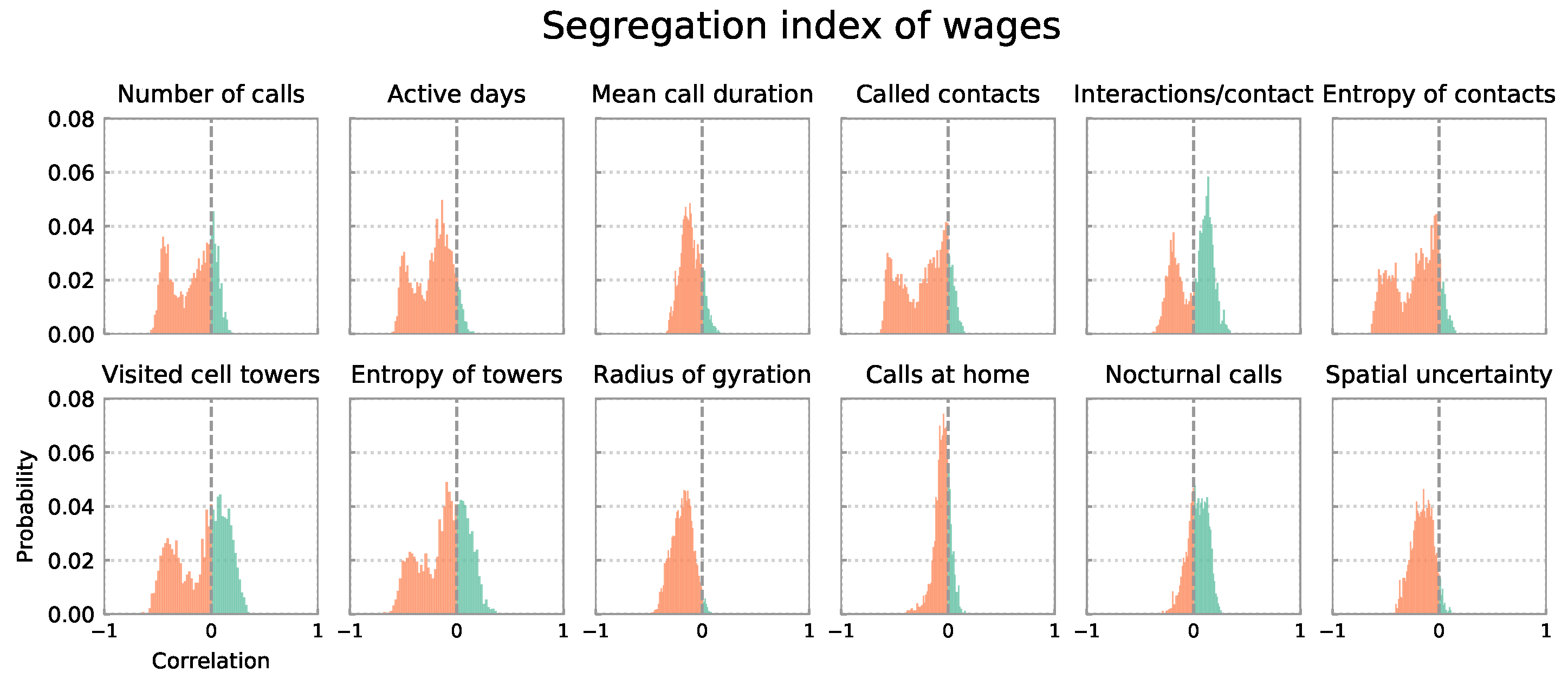
4.1. Distributions of Correlation Coefficients for All 4914 City Definitions
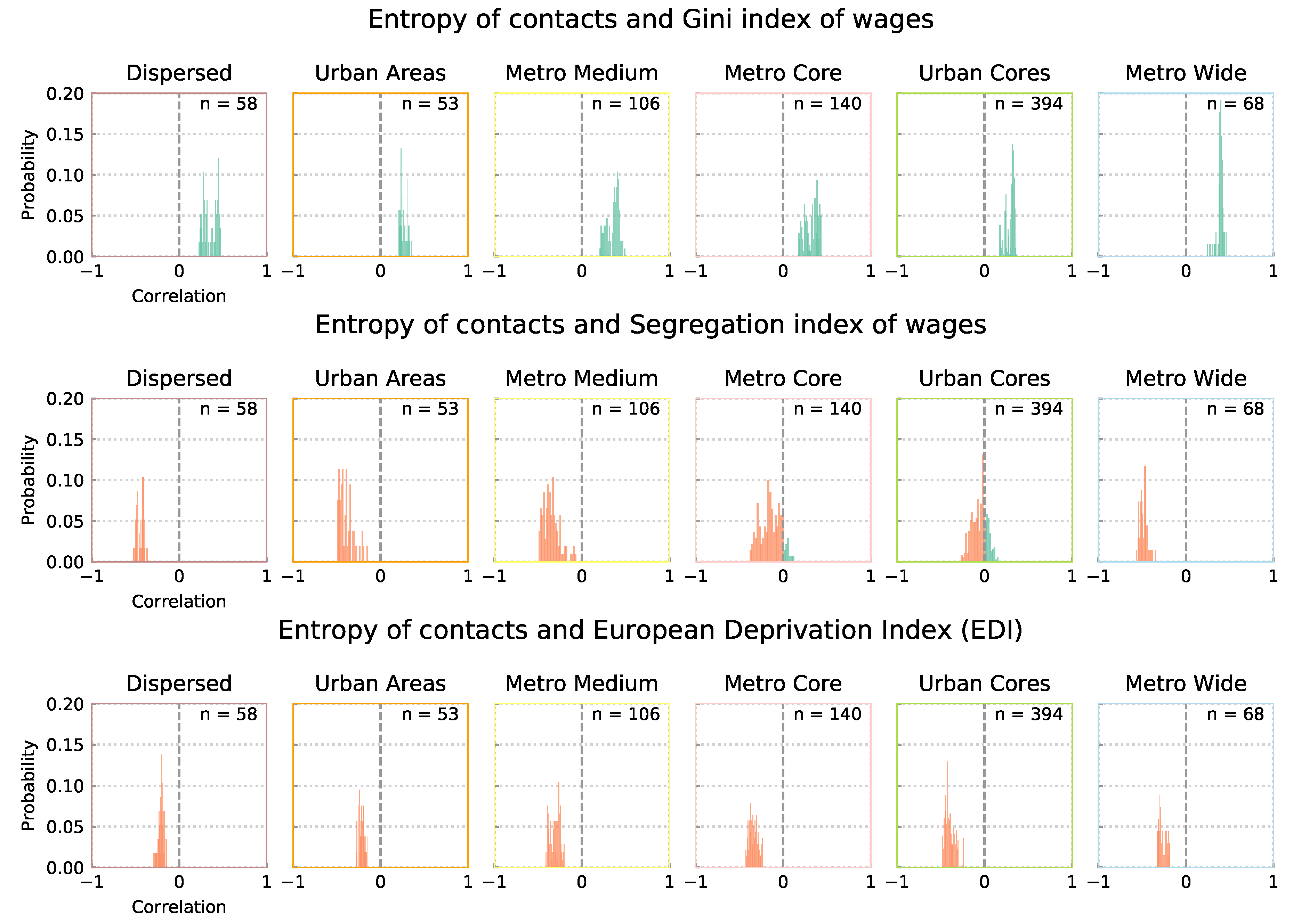
4.2. Distributions of Correlation Coefficients by Definition Cluster
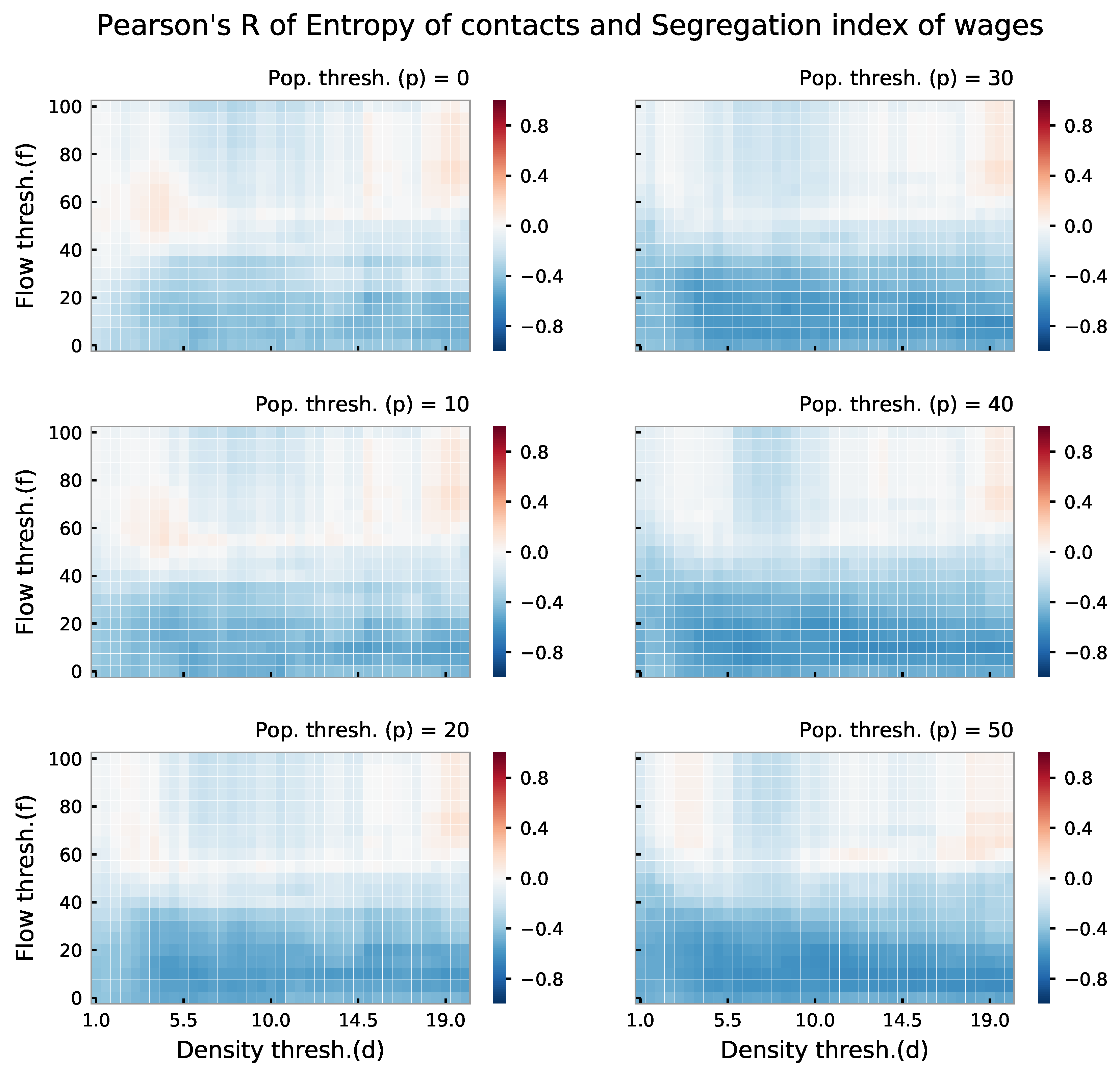
4.3. Heatmaps of Correlations
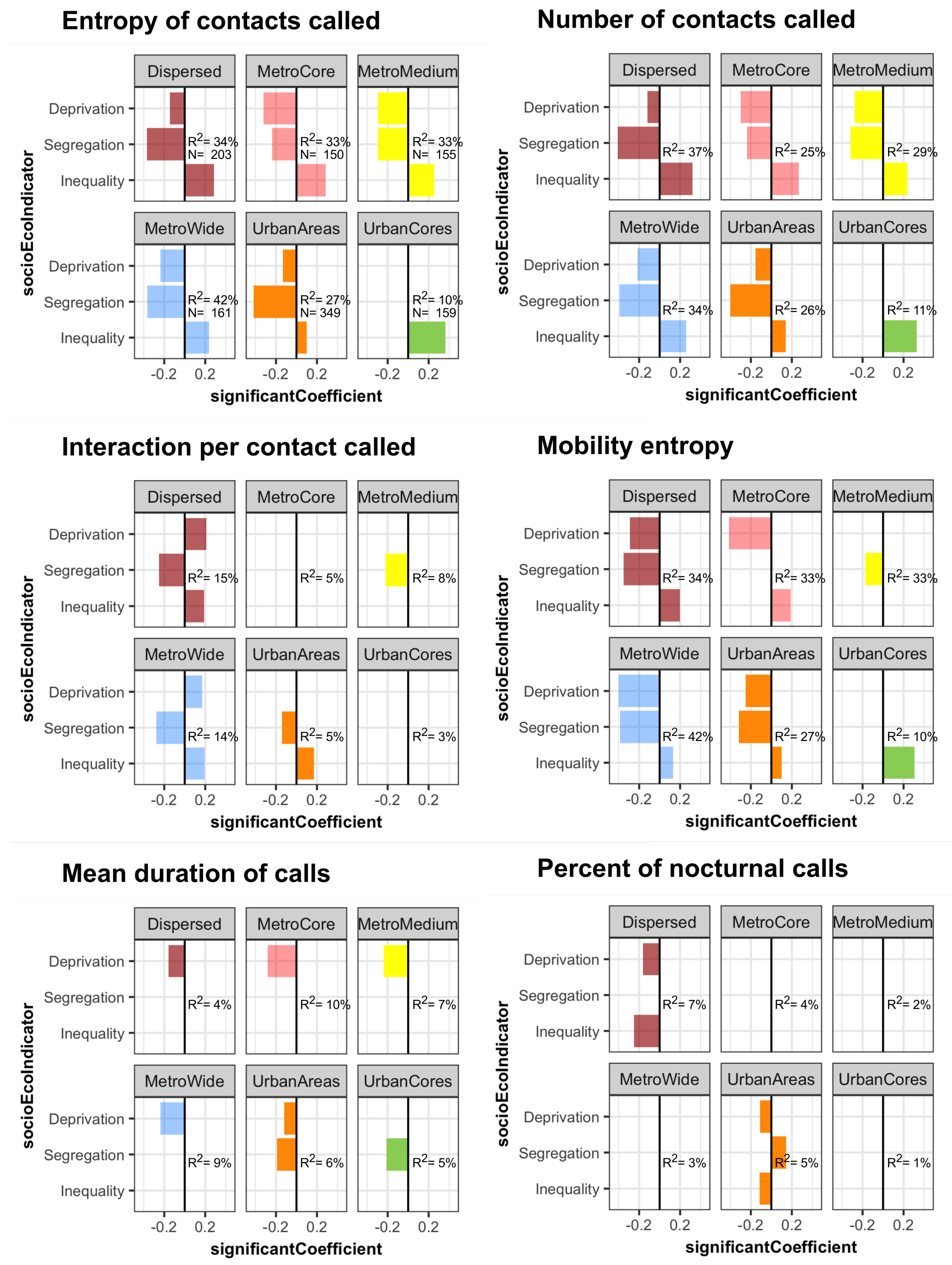
4.4. Multiple Regression of Mobile Phone Indices with Socioeconomic Indicators
5. Discussion & Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gonzalez, M.C.; Hidalgo, C.A.; Barabasi, A.L. Understanding individual human mobility patterns. Nature 2008, 453, 779–782. [Google Scholar] [CrossRef] [PubMed]
- Zhong, C.; Batty, M.; Manley, E.; Wang, J.; Wang, Z.; Chen, F.; Schmitt, G. Variability in regularity: Mining temporal mobility patterns in London, Singapore and Beijing using smart-card data. PLoS ONE 2016, 11, e0149222. [Google Scholar] [CrossRef] [PubMed]
- Lenormand, M.; Louail, T.; Cantú-Ros, O.G.; Picornell, M.; Herranz, R.; Arias, J.M.; Barthelemy, M.; San Miguel, M.; Ramasco, J.J. Influence of sociodemographic characteristics on human mobility. Sci. Rep. 2015, 5, 10075. [Google Scholar] [CrossRef] [PubMed]
- De Montjoye, Y.A.; Radaelli, L.; Singh, V.K. Unique in the shopping mall: On the reidentifiability of credit card metadata. Science 2015, 347, 536–539. [Google Scholar] [CrossRef] [PubMed]
- Alessandretti, L.; Sapiezynski, P.; Sekara, V.; Lehmann, S.; Baronchelli, A. Evidence for a conserved quantity in human mobility. Nat. Hum. Behav. 2018, 2, 485–491. [Google Scholar] [CrossRef]
- Pappalardo, L.; Simini, F.; Rinzivillo, S.; Pedreschi, D.; Giannotti, F.; Barabási, A.L. Returners and explorers dichotomy in human mobility. Nat. Commun. 2015, 6, 8166. [Google Scholar] [CrossRef] [PubMed]
- Batran, M.; Mejia, M.; Kanasugi, H.; Sekimoto, Y.; Shibasaki, R. Inferencing Human Spatiotemporal Mobility in Greater Maputo via Mobile Phone Big Data Mining. ISPRS Int. J. Geo-Inf. 2018, 7, 259. [Google Scholar] [CrossRef]
- Lu, S.; Fang, Z.; Zhang, X.; Shaw, S.L.; Yin, L.; Zhao, Z.; Yang, X. Understanding the representativeness of mobile phone location data in characterizing human mobility indicators. ISPRS Int. J. Geo-Inf. 2017, 6, 7. [Google Scholar] [CrossRef]
- Vanhoof, M.; Reis, F.; Ploetz, T.; Smoreda, Z. Assessing the quality of home detection from mobile phone data for official statistics. J. Off. Stat. 2018, 34, 935–960. [Google Scholar] [CrossRef]
- Longley, P.A.; Adnan, M.; Lansley, G. The geotemporal demographics of Twitter usage. Environ. Plan. A 2015, 47, 465–484. [Google Scholar] [CrossRef]
- Arai, A.; Fan, Z.; Matekenya, D.; Shibasaki, R. Comparative perspective of human behavior patterns to uncover ownership bias among mobile phone users. ISPRS Int. J. Geo-Inf. 2016, 5, 85. [Google Scholar] [CrossRef]
- Schneider, C.M.; Belik, V.; Couronné, T.; Smoreda, Z.; González, M.C. Unravelling daily human mobility motifs. J. R. Soc. Interface 2013, 10, 20130246. [Google Scholar] [CrossRef] [PubMed]
- Dannamann, T.; Sotomayor-Gómez, B.; Samaniego, H. The time geography of segregation during working hours. arXiv, 2018; arXiv:1802.00117. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Belyi, A.; Bojic, I.; Ratti, C. Human mobility and socioeconomic status: Analysis of Singapore and Boston. Comput. Environ. Urban Syst. 2018, 72, 51–67. [Google Scholar] [CrossRef]
- Vanhoof, M.; Schoors, W.; Van Rompaey, A.; Ploetz, T.; Smoreda, Z. Comparing Regional Patterns of Individual Movement Using Corrected Mobility Entropy. J. Urban Technol. 2018, 25, 27–61. [Google Scholar] [CrossRef]
- Vanhoof, M.; Lee, C.; Smoreda, Z. Performance and sensitivities of home detection from mobile phone data. arXiv, 2018; arXiv:1809.09911. [Google Scholar]
- Pappalardo, L.; Vanhoof, M.; Gabrielli, L.; Smoreda, Z.; Pedreschi, D.; Giannotti, F. An analytical framework to nowcast well-being using mobile phone data. Int. J. Data Sci. Anal. 2016, 2, 75–92. [Google Scholar] [CrossRef]
- Eagle, N.; Macy, M.; Claxton, R. Network diversity and economic development. Science 2010, 328, 1029–1031. [Google Scholar] [CrossRef]
- Decuyper, A.; Rutherford, A.; Wadhwa, A.; Bauer, J.M.; Krings, G.; Gutierrez, T.; Blondel, V.D.; Luengo-Oroz, M.A. Estimating food consumption and poverty indices with mobile phone data. arXiv, 2014; arXiv:1412.2595. [Google Scholar]
- Frias-martinez, V.; Soto, V.; Virseda, J.; Frias-martinez, E. Can cell phone traces measure social development. In Third Conference on the Analysis of Mobile Phone datasets, NetMob; Blondel, V., Decuyper, A., Deville, P., De Montjoye, Y.-A., Toole, J., Traag, V., Wang, D., Eds.; MIT Media Lab: Cambridge, MA, USA, 2013; pp. 62–65. [Google Scholar]
- Arcaute, E.; Hatna, E.; Ferguson, P.; Youn, H.; Johansson, A.; Batty, M. Constructing cities, deconstructing scaling laws. J. R. Soc. Interface 2015, 12, 20140745. [Google Scholar] [CrossRef]
- Veneri, P. City size distribution across the OECD: Does the definition of cities matter? Comput. Environ. Urban Syst. 2016, 59, 86–94. [Google Scholar] [CrossRef]
- Cottineau, C.; Hatna, E.; Arcaute, E.; Batty, M. Diverse cities or the systematic paradox of Urban Scaling Laws. Comput. Environ. Urban Syst. 2017, 63, 80–94. [Google Scholar] [CrossRef]
- Louail, T.; Lenormand, M.; Arias, J.M.; Ramasco, J.J. Crowdsourcing the Robin Hood effect in cities. Appl. Netw. Sci. 2017, 2, 11. [Google Scholar] [CrossRef] [PubMed]
- Shelton, T.; Poorthuis, A.; Zook, M. Social media and the city: Rethinking urban socio-spatial inequality using user-generated geographic information. Landsc. Urban Plan. 2015, 142, 198–211. [Google Scholar] [CrossRef]
- Pornet, C.; Delpierre, C.; Dejardin, O.; Grosclaude, P.; Launay, L.; Guittet, L.; Lang, T.; Launoy, G. Construction of an adaptable European transnational ecological deprivation index: The French version. J. Epidemiol. Commun. Health 2012, 66, 982–989. [Google Scholar] [CrossRef] [PubMed]
- Cottineau, C.; Finance, O.; Hatna, E.; Arcaute, E.; Batty, M. Defining urban clusters to detect agglomeration economies. Environ. Plan. B Urban Anal. City Sci. 2018. [Google Scholar] [CrossRef]
- Fuller, M. The estimation of Gini coefficients from grouped data: Upper and Lower Bounds. Econ. Lett. 1979, 3, 187–192. [Google Scholar] [CrossRef]
- Reardon, S.F. Measures of ordinal segregation. In Occupational and Residential Segregation; Research on Economic Inequality; Flückiger, Y., Reardon, S.F., Silber, J., Eds.; Emerald Group Publishing Limited: Bingley, UK, 2009; pp. 129–155. [Google Scholar]
- Grauwin, S.; Szell, M.; Sobolevsky, S.; Hövel, P.; Simini, F.; Vanhoof, M.; Smoreda, Z.; Barabási, A.L.; Ratti, C. Identifying and modeling the structural discontinuities of human interactions. Sci. Rep. 2017, 7, 46677. [Google Scholar] [CrossRef] [PubMed]
- Vanhoof, M.; Hendrickx, L.; Puussaar, A.; Verstraeten, G.; Ploetz, T.; Smoreda, Z. Exploring the use of mobile phones during domestic tourism trips. Netcom 2017, 31, 335–372. [Google Scholar] [CrossRef]
- Vanhoof, M.; Combes, S.; De Bellefon, M.P. Mining mobile phone data to detect urban areas. In Statistics and Data Science: New Challenges, New Generations, SIS 2017; Petrucci, A., Verde, R., Eds.; Firenze University Press: Firenze, Italy, 2017; pp. 1005–1012. [Google Scholar]
- De Montjoye, Y.A.; Rocher, L.; Pentland, A.S. Bandicoot: A python toolbox for mobile phone metadata. J. Mach. Learn. Res. 2016, 17, 6100–6104. [Google Scholar]
- Vanhoof, M.; Reis, F.; Smoreda, Z.; Plötz, T. Detecting home locations from CDR data: Introducing spatial uncertainty to the state-of-the-art. arXiv, 2018; arXiv:1808.06398. [Google Scholar]
- Cottineau, C. MetaZipf. A dynamic meta-analysis of city size distributions. PLoS ONE 2017, 12, e0183919. [Google Scholar] [CrossRef]
- Gower, J.C. A general coefficient of similarity and some of its properties. Biometrics 1971, 27, 857–871. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P. Clustering by Means of Medoids; Faculty of Mathematics and Informatics: Sofia, Bulgaria, 1987. [Google Scholar]
- Cattell, V. Poor people, poor places, and poor health: The mediating role of social networks and social capital. Soc. Sci. Med. 2001, 52, 1501–1516. [Google Scholar] [CrossRef]
- Granovetter, M. The strength of weak ties: A network theory revisited. Sociol. Theory 1983, 1, 201–233. [Google Scholar] [CrossRef]
- Eeckhout, J.; Pinheiro, R.; Schmidheiny, K. Spatial sorting. J. Polit. Econ. 2014, 122, 554–620. [Google Scholar] [CrossRef]
- Sarkar, S. Urban scaling and the geographic concentration of inequalities by city size. Environ. Plan. B Urban Anal. City Sci. 2018. [Google Scholar] [CrossRef]
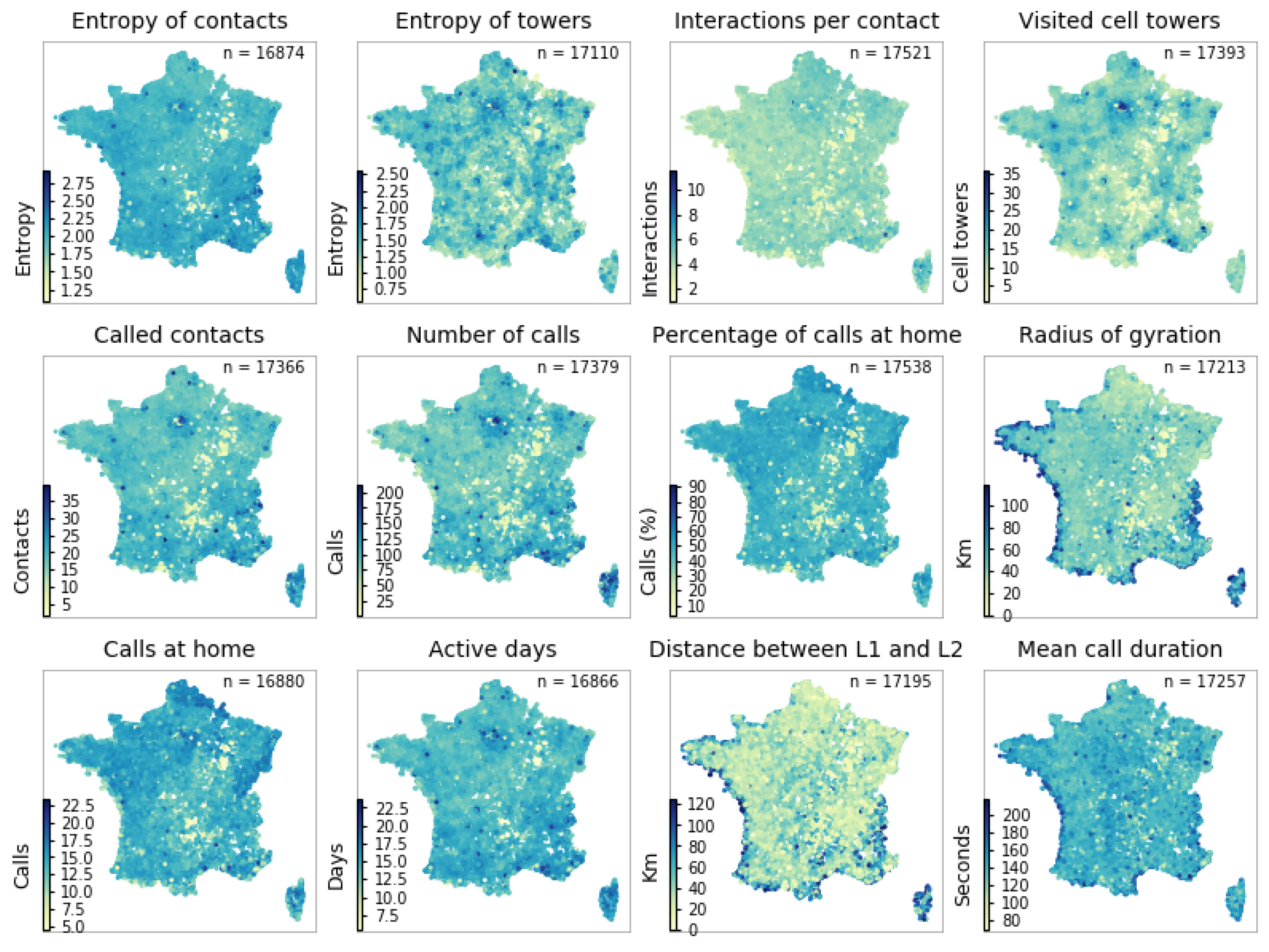
| Mobile Phone Indicator | Description |
|---|---|
| Number of calls | Number of calls made or received |
| Active days | Number of active distinct days |
| Percentage nocturnal calls | Percentage of calls made between 7 p.m. and 9 a.m. |
| Duration of calls | Mean duration of all calls |
| Inter-event time | Mean duration between consecutive calls |
| Number of contacts | Number of contacts interacted with |
| Interaction per contact | Mean amount of interactions per contact |
| Entropy of contacts * (Equation (3)) | Entropy measure of calls to contacts |
| Number of visited cell towers | Number of cell towers used to make calls |
| Radius of gyration * (Equation (1)) | Radius of gyration of movement patterns based on visited cell towers |
| Entropy of visited cell towers * (Equation (2)) | Entropy measure of visited cell towers |
| Distance between l1 and l2 | Distance between most plausible and second most plausible ’home’ cell tower given a home detection algorithm |
| Spatial uncertainty | Uncertainty measure of the detection of the most plausible home location |
| Calls at home | Number of calls made at the presumed home cell tower |
| Percentage calls at home | Percentage of calls made at the presumed home cell tower |
| Deprivation–Inequality | Inequality–Segregation | Segregation–Deprivation | |
|---|---|---|---|
| UrbanAreas | 0.060 | −0.082 | −0.028 |
| Dispersed | 0.062 | −0.252 | −0.144 |
| UrbanCores | −0.044 | 0.192 | 0.186 |
| MetroMedium | −0.059 | −0.047 | −0.156 |
| MetroCore | −0.072 | 0.119 | −0.131 |
| MetroWide | −0.041 | −0.156 | −0.069 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cottineau, C.; Vanhoof, M. Mobile Phone Indicators and Their Relation to the Socioeconomic Organisation of Cities. ISPRS Int. J. Geo-Inf. 2019, 8, 19. https://doi.org/10.3390/ijgi8010019
Cottineau C, Vanhoof M. Mobile Phone Indicators and Their Relation to the Socioeconomic Organisation of Cities. ISPRS International Journal of Geo-Information. 2019; 8(1):19. https://doi.org/10.3390/ijgi8010019
Chicago/Turabian StyleCottineau, Clémentine, and Maarten Vanhoof. 2019. "Mobile Phone Indicators and Their Relation to the Socioeconomic Organisation of Cities" ISPRS International Journal of Geo-Information 8, no. 1: 19. https://doi.org/10.3390/ijgi8010019
APA StyleCottineau, C., & Vanhoof, M. (2019). Mobile Phone Indicators and Their Relation to the Socioeconomic Organisation of Cities. ISPRS International Journal of Geo-Information, 8(1), 19. https://doi.org/10.3390/ijgi8010019




