An Assessment of Spatial Pattern Characterization of Air Pollution: A Case Study of CO and PM2.5 in Tehran, Iran
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sources
2.3. Spatial Autocorrelation Methods
2.3.1. Global Spatial Correlation of Contaminants
2.3.2. Local Spatial Autocorrelation of Pollutants
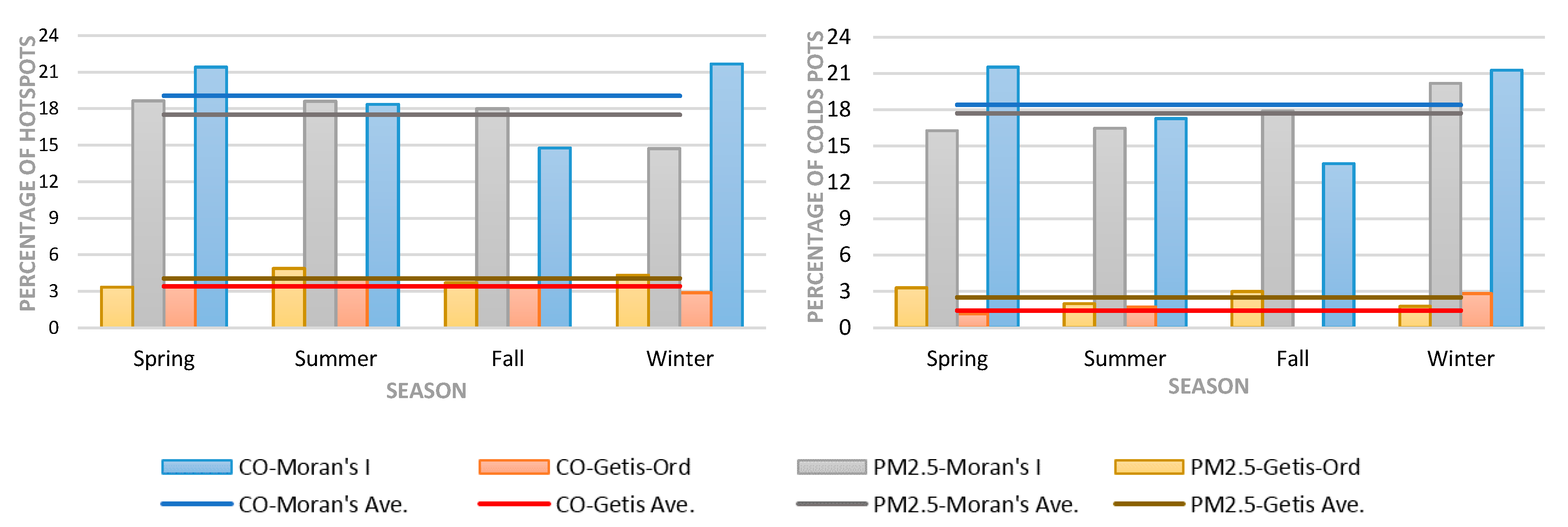
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, L.; Qian, J.; Ou, C.-Q.; Zhou, Y.-X.; Guo, C.; Guo, Y. Spatial and temporal analysis of air pollution index and its timescale-dependent relationship with meteorological factors in guangzhou, china, 2001–2011. Environ. Pollut. 2014, 190, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Alesheikh, A.A.; Oskouei, A.; Atabi, F.; Helali, H. Providing interoperability for air quality in-situ sensors observations using gml technology. Int. J. Environ. Sci. Technol. 2005, 2, 133–140. [Google Scholar] [CrossRef]
- Dix-Cooper, L.; Eskenazi, B.; Romero, C.; Balmes, J.; Smith, K.R. Neurodevelopmental performance among school age children in rural guatemala is associated with prenatal and postnatal exposure to carbon monoxide, a marker for exposure to woodsmoke. Neurotoxicology 2012, 33, 246–254. [Google Scholar] [CrossRef] [PubMed]
- Correia, A.W.; Pope, C.A., III; Dockery, D.W.; Wang, Y.; Ezzati, M.; Dominici, F. The effect of air pollution control on life expectancy in the united states: An analysis of 545 us counties for the period 2000 to 2007. Epidemiology 2013, 24, 23. [Google Scholar] [CrossRef] [PubMed]
- Weichenthal, S.; Villeneuve, P.J.; Burnett, R.T.; van Donkelaar, A.; Martin, R.V.; Jones, R.R.; DellaValle, C.T.; Sandler, D.P.; Ward, M.H.; Hoppin, J.A. Long-term exposure to fine particulate matter: Association with nonaccidental and cardiovascular mortality in the agricultural health study cohort. Environ. Health Perspect. 2014, 122, 609. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.-H.; Kabir, E.; Kabir, S. A review on the human health impact of airborne particulate matter. Environ. Int. 2015, 74, 136–143. [Google Scholar] [CrossRef] [PubMed]
- Wong, C.-S.; Lin, Y.-C.; Hong, L.-Y.; Chen, T.-T.; Ma, H.-P.; Hsu, Y.-H.; Tsai, S.-H.; Lin, Y.-F.; Wu, M.-Y. Increased long-term risk of dementia in patients with carbon monoxide poisoning: A population-based study. Medicine 2016, 95, e2549. [Google Scholar] [CrossRef] [PubMed]
- Ma, T.; Zhou, C.; Pei, T.; Haynie, S.; Fan, J. Quantitative estimation of urbanization dynamics using time series of dmsp/ols nighttime light data: A comparative case study from china’s cities. Remote Sens. Environ. 2012, 124, 99–107. [Google Scholar] [CrossRef]
- Mohammadi, H.; Cohen, D.; Babazadeh, M.; Rokni, L. The effects of atmospheric processes on tehran smog forming. Iran. J. Public Health 2012, 41, 1. [Google Scholar] [PubMed]
- Vafa-Arani, H.; Jahani, S.; Dashti, H.; Heydari, J.; Moazen, S. A system dynamics modeling for urban air pollution: A case study of tehran, iran. Transp. Res. Part D 2014, 31, 21–36. [Google Scholar] [CrossRef]
- Tashayo, B.; Alimohammadi, A.; Sharif, M. A hybrid fuzzy inference system based on dispersion model for quantitative environmental health impact assessment of urban transportation planning. Sustainability 2017, 9, 134. [Google Scholar] [CrossRef]
- Amini, H.; Taghavi-Shahri, S.M.; Henderson, S.B.; Naddafi, K.; Nabizadeh, R.; Yunesian, M. Land use regression models to estimate the annual and seasonal spatial variability of sulfur dioxide and particulate matter in tehran, iran. Sci. Total Environ. 2014, 488, 343–353. [Google Scholar] [CrossRef] [PubMed]
- O’Sullivan, D.; Unwin, D. Geographic Information Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Li, W.; Xu, B.; Song, Q.; Liu, X.; Xu, J.; Brookes, P.C. The identification of ‘hotspots’ of heavy metal pollution in soil–rice systems at a regional scale in eastern china. Sci. Total Environ. 2014, 472, 407–420. [Google Scholar] [CrossRef] [PubMed]
- Mohammadinia, A.; Alimohammadi, A.; Habibi, R.; Shirzadi, M.R. Spatial and statistical analysis of leptospirosis in Guilan province, Iran. Int. Arch. Photogramm., Remote Sens. Spa. Inf. Sci. 2015, 40, 497–502. [Google Scholar] [CrossRef]
- Blazquez, C.A.; Celis, M.S. A spatial and temporal analysis of child pedestrian crashes in santiago, chile. Accid. Anal. Prev. 2013, 50, 304–311. [Google Scholar] [CrossRef] [PubMed]
- Fan, C.; Myint, S. A comparison of spatial autocorrelation indices and landscape metrics in measuring urban landscape fragmentation. Landsc. Urban Plan. 2014, 121, 117–128. [Google Scholar] [CrossRef]
- Lee, Y.; Kwon, P.; Yu, K.; Park, W. Method for determining appropriate clustering criteria of location-sensing data. ISPRS Int. J. Geo-Inf. 2016, 5, 151. [Google Scholar] [CrossRef]
- Zhao, K.; Fu, W.; Liu, X.; Huang, D.; Zhang, C.; Ye, Z.; Xu, J. Spatial variations of concentrations of copper and its speciation in the soil-rice system in wenling of southeastern china. Environ. Sci. Pollut. Res. 2014, 21, 7165–7176. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Luo, L.; Xu, W.; Ledwith, V. Use of local moran’s i and gis to identify pollution hotspots of pb in urban soils of galway, ireland. Sci. Total Environ. 2008, 398, 212–221. [Google Scholar] [CrossRef] [PubMed]
- Fang, C.; Liu, H.; Li, G.; Sun, D.; Miao, Z. Estimating the impact of urbanization on air quality in china using spatial regression models. Sustainability 2015, 7, 15570–15592. [Google Scholar] [CrossRef]
- Pu, H.; Luo, K.; Wang, P.; Wang, S.; Kang, S. Spatial variation of air quality index and urban driving factors linkages: Evidence from chinese cities. Environ. Sci. Pollut. Res. 2017, 24, 4457–4468. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Bi, R.; Wang, S.; Li, F.; Guo, G. The use of spatial autocorrelation analysis to identify pahs pollution hotspots at an industrially contaminated site. Environ. Monit. Assess. 2013, 185, 9549–9558. [Google Scholar] [CrossRef] [PubMed]
- Alqadi, K.A.; Kumar, L.; Khormi, H.M. Mapping hotspots of underground water quality based on the variation of chemical concentration in amman, zarqa and balqa regions, jordan. Environ. Earth Sci. 2014, 71, 2309–2317. [Google Scholar] [CrossRef]
- Réquia, W.J.; Koutrakis, P.; Roig, H.L. Spatial distribution of vehicle emission inventories in the federal district, brazil. Atmos. Environ. 2015, 112, 32–39. [Google Scholar] [CrossRef]
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 23rd ACM National Conference, Las Vegas, NV, USA, 27–29 August 1968; pp. 517–524. [Google Scholar]
- Atabi, F.; Moattar, F.; Mansouri, N.; Alesheikh, A.; Mirzahosseini, S. Assessment of variations in benzene concentration produced from vehicles and gas stations in tehran using gis. Int. J. Environ. Sci. Technol. 2013, 10, 283–294. [Google Scholar] [CrossRef]
- SCI. Census Results of 2016. Available online: www.amar.org.ir (accessed on 25 April 2017).
- Shaffer, M.J.; Bishop, J.A. Predicting and preventing elephant poaching incidents through statistical analysis, gis-based risk analysis, and aerial surveillance flight path modeling. Trop. Conserv. Sci. 2016, 9, 525–548. [Google Scholar] [CrossRef]
- Baller, R.D.; Richardson, K.K. Social integration, imitation, and the geographic patterning of suicide. Am. Soc. Rev. 2002, 67, 873–888. [Google Scholar] [CrossRef]
- Mitchell, A. The Esri Guide to Gis Analysis, Volume 2: Spatial Measurements and Statistics; Esri Press: Redlands, CA, USA, 2005. [Google Scholar]
- Anselin, L. Local indicators of spatial association—Lisa. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. Local Spatial Statistics: An Overview; John Wiley and Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Renzi, M.; Stafoggia, M.; Faustini, A.; Cesaroni, G.; Agabiti, N.; Forastiere, F. Health effects of air pollution in rome in december 2015. Epidemiol. Prev. 2016, 40, 29–32. [Google Scholar] [PubMed]
- Hu, D.; Wu, J.; Tian, K.; Liao, L.; Xu, M.; Du, Y. Urban air quality, meteorology and traffic linkages: Evidence from a sixteen-day particulate matter pollution event in december 2015, beijing. J. Environ. Sci. 2017. [Google Scholar] [CrossRef]
- Rashki, A.; deW Rautenbach, C.; Eriksson, P.G.; Kaskaoutis, D.G.; Gupta, P. Temporal changes of particulate concentration in the ambient air over the city of zahedan, iran. Air Qual. Atmos. Health 2013, 6, 123–135. [Google Scholar] [CrossRef]
- Hassani, A.; Hosseini, V. An assessment of gasoline motorcycle emissions performance and understanding their contribution to tehran air pollution. Transp. Res. Part D 2016, 47, 1–12. [Google Scholar] [CrossRef]
- Yazdi, M.N.; Delavarrafiee, M.; Arhami, M. Evaluating near highway air pollutant levels and estimating emission factors: Case study of tehran, iran. Sci. Total Environ. 2015, 538, 375–384. [Google Scholar] [CrossRef] [PubMed]
- Asghari, M.; Nematzadeh, H. Predicting air pollution in tehran: Genetic algorithm and back propagation neural network. J. AI Data Min. 2016, 4, 49–54. [Google Scholar]
- Akbari, M.; Samadzadegan, F.; Weibel, R. A generic regional spatio-temporal co-occurrence pattern mining model: A case study for air pollution. J. Geogr. Syst. 2015, 17, 249–274. [Google Scholar] [CrossRef]
| District | CO (ppb) | PM2.5 (μg/m3) | District | CO (ppb) | PM2.5 (μg/m3) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min. | Max. | Ave. | Std. | Min. | Max. | Ave. | Std. | Min. | Max. | Ave. | Std. | Min. | Max. | Ave. | Std. | ||
| 1 | 2.87 | 3.69 | 3.26 | 0.25 | 17.33 | 40.19 | 28.45 | 6.00 | 12 | 2.58 | 3.27 | 2.85 | 0.42 | 16.70 | 41.61 | 32.63 | 6.70 |
| 2 | 1.70 | 3.40 | 2.39 | 0.50 | 15.78 | 38.54 | 28.01 | 5.78 | 13 | 1.73 | 3.10 | 2.29 | 0.41 | 13.51 | 35.66 | 23.02 | 5.98 |
| 3 | 2.23 | 3.43 | 2.66 | 0.34 | 18.23 | 54.35 | 32.43 | 8.74 | 14 | 2.29 | 4.19 | 2.69 | 0.49 | 15.44 | 45.65 | 31.76 | 7.97 |
| 4 | 2.35 | 3.42 | 2.68 | 0.36 | 19.32 | 39.19 | 31.64 | 5.28 | 15 | 1.78 | 4.08 | 2.91 | 0.74 | 15.39 | 52.80 | 31.10 | 10.10 |
| 5 | 2.05 | 3.51 | 2.54 | 0.39 | 17.24 | 39.55 | 28.80 | 5.74 | 16 | 2.66 | 6.16 | 3.25 | 0.91 | 17.13 | 59.01 | 36.89 | 11.41 |
| 6 | 2.36 | 4.25 | 2.88 | 0.51 | 15.20 | 41.53 | 27.28 | 6.64 | 17 | 2.55 | 3.88 | 2.98 | 0.38 | 19.81 | 55.79 | 38.60 | 9.91 |
| 7 | 2.23 | 3.84 | 2.88 | 0.50 | 18.83 | 41.94 | 32.32 | 6.43 | 18 | 1.76 | 2.92 | 2.10 | 0.30 | 21.43 | 51.56 | 35.56 | 8.29 |
| 8 | 2.21 | 3.24 | 2.53 | 0.35 | 17.35 | 36.83 | 29.15 | 5.03 | 19 | 2.30 | 5.50 | 3.41 | 0.98 | 18.00 | 52.34 | 35.52 | 8.20 |
| 9 | 1.74 | 3.78 | 2.58 | 0.55 | 20.80 | 50.85 | 35.33 | 7.71 | 20 | 1.89 | 2.99 | 2.30 | 0.35 | 23.79 | 55.70 | 41.47 | 9.80 |
| 10 | 2.48 | 4.50 | 3.10 | 0.55 | 18.17 | 45.26 | 33.68 | 7.00 | 21 | 1.71 | 4.17 | 2.37 | 0.61 | 19.25 | 47.92 | 31.95 | 7.36 |
| 11 | 2.72 | 5.17 | 3.18 | 0.63 | 19.25 | 44.71 | 34.74 | 7.16 | 22 | 2.03 | 3.15 | 2.41 | 0.33 | 18.83 | 43.37 | 31.16 | 6.55 |
| Time Interval | PM2.5 | CO | |||||
|---|---|---|---|---|---|---|---|
| Getis | Moran’s I | Getis | Moran’s I | ||||
| Z-Score | Index Value | Z-Score | Z-Score | Index Value | Z-Score | ||
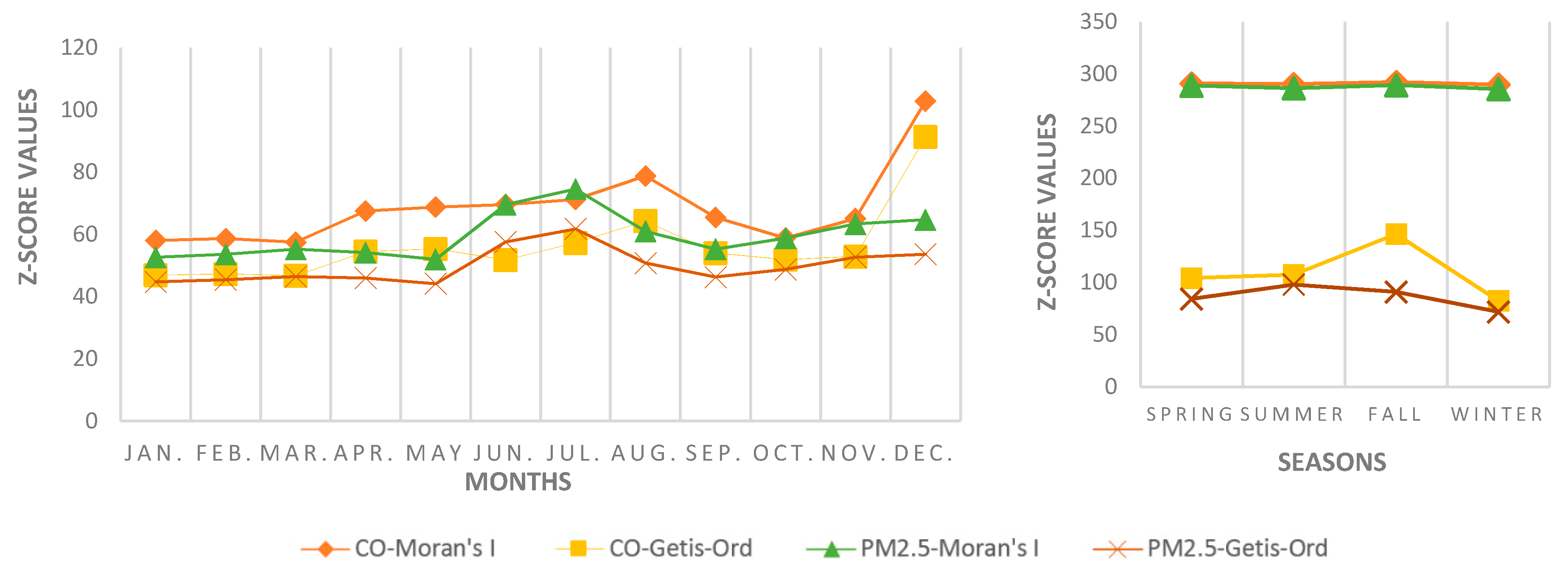
| Season | Spring | 84.38 | 0.994 | 288.87 | 104.37 | 1.000 | 290.96 |
| Summer | 98.08 | 0.985 | 286.31 | 107.62 | 0.998 | 290.28 | |
| Fall | 91.06 | 0.995 | 289.25 | 146.52 | 1.004 | 292.24 | |
| Winter | 72.00 | 0.982 | 285.54 | 82.70 | 0.996 | 289.75 | |
| Month | Jan. | 44.76 | 0.445 | 52.7 | 46.92 | 0.491 | 58.11 |
| Feb. | 45.47 | 0.453 | 53.64 | 47.34 | 0.496 | 58.69 | |
| Mar. | 46.48 | 0.467 | 55.26 | 46.78 | 0.486 | 57.52 | |
| Apr. | 46.03 | 0.458 | 54.22 | 54.5 | 0.571 | 67.55 | |
| May | 44.18 | 0.44 | 52.02 | 55.34 | 0.582 | 68.81 | |
| June | 57.63 | 0.589 | 69.63 | 51.79 | 0.589 | 69.63 | |
| July | 61.79 | 0.631 | 74.61 | 57.31 | 0.603 | 71.28 | |
| Aug. | 50.85 | 0.516 | 61.04 | 64.34 | 0.666 | 78.81 | |
| Sep. | 46.34 | 0.467 | 55.29 | 54.06 | 0.554 | 65.52 | |
| Oct. | 48.80 | 0.497 | 58.84 | 51.90 | 0.497 | 58.84 | |
| Nov. | 52.7 | 0.536 | 63.38 | 52.96 | 0.550 | 65.12 | |
| Dec. | 53.66 | 0.547 | 64.77 | 91.33 | 0.868 | 102.85 | |
| Time Interval | PM2.5 | CO | |||
|---|---|---|---|---|---|
| Getis-Ord | Moran’s I | Getis-Ord | Moran’s I | ||
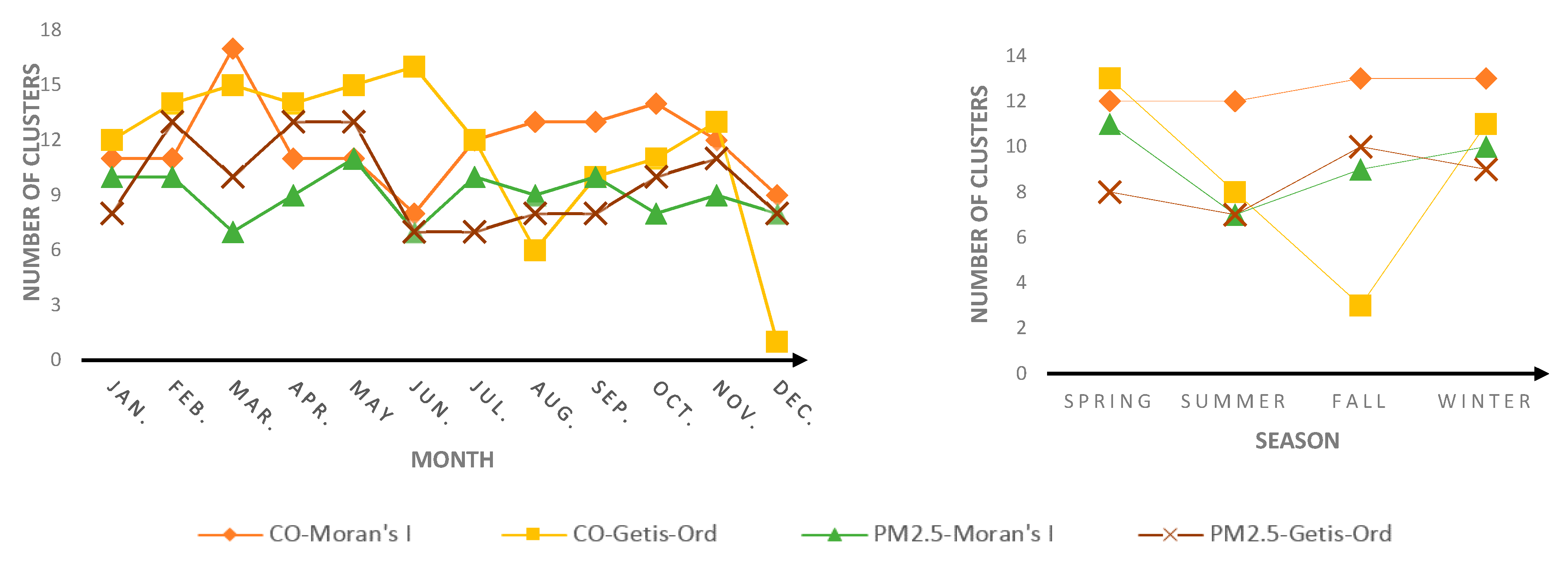
| Seasons | Spring | 1.012 | 1.145 | 2.961 | 0.995 |
| Summer | 2.452 | 1.129 | 2.358 | 1.062 | |
| Fall | 1.231 | 1.006 | - | 1.09 | |
| Winter | 2.422 | 0.73 | 1.02 | 1.019 | |
| Months | Jan. | 2.033 | 0.823 | 0.949 | 0.906 |
| Feb. | 2.237 | 0.693 | 0.908 | 1.043 | |
| Mar. | 1.1 | 0.797 | 1.15 | 1.137 | |
| Apr. | 1.816 | 0.639 | 3.288 | 0.888 | |
| May | 0.76 | 0.933 | 2.99 | 1.239 | |
| June | 1.934 | 1.217 | 1.554 | 1.028 | |
| July | 4.459 | 1.102 | 7.182 | 0.916 | |
| Aug. | 1.062 | 0.958 | 11.177 | 1.099 | |
| Sep. | 0.935 | 1.067 | 2.722 | 0.887 | |
| Oct. | 1.117 | 1.071 | 2.419 | 0.955 | |
| Nov. | 1.548 | 1.122 | 2.406 | 0.975 | |
| Dec. | 0.942 | 1.156 | - | 2.039 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Habibi, R.; Alesheikh, A.A.; Mohammadinia, A.; Sharif, M. An Assessment of Spatial Pattern Characterization of Air Pollution: A Case Study of CO and PM2.5 in Tehran, Iran. ISPRS Int. J. Geo-Inf. 2017, 6, 270. https://doi.org/10.3390/ijgi6090270
Habibi R, Alesheikh AA, Mohammadinia A, Sharif M. An Assessment of Spatial Pattern Characterization of Air Pollution: A Case Study of CO and PM2.5 in Tehran, Iran. ISPRS International Journal of Geo-Information. 2017; 6(9):270. https://doi.org/10.3390/ijgi6090270
Chicago/Turabian StyleHabibi, Roya, Ali Asghar Alesheikh, Ali Mohammadinia, and Mohammad Sharif. 2017. "An Assessment of Spatial Pattern Characterization of Air Pollution: A Case Study of CO and PM2.5 in Tehran, Iran" ISPRS International Journal of Geo-Information 6, no. 9: 270. https://doi.org/10.3390/ijgi6090270
APA StyleHabibi, R., Alesheikh, A. A., Mohammadinia, A., & Sharif, M. (2017). An Assessment of Spatial Pattern Characterization of Air Pollution: A Case Study of CO and PM2.5 in Tehran, Iran. ISPRS International Journal of Geo-Information, 6(9), 270. https://doi.org/10.3390/ijgi6090270






