Evaluating the Impact of Meteorological Factors on Water Demand in the Las Vegas Valley Using Time-Series Analysis: 1990–2014
Abstract
:1. Introduction
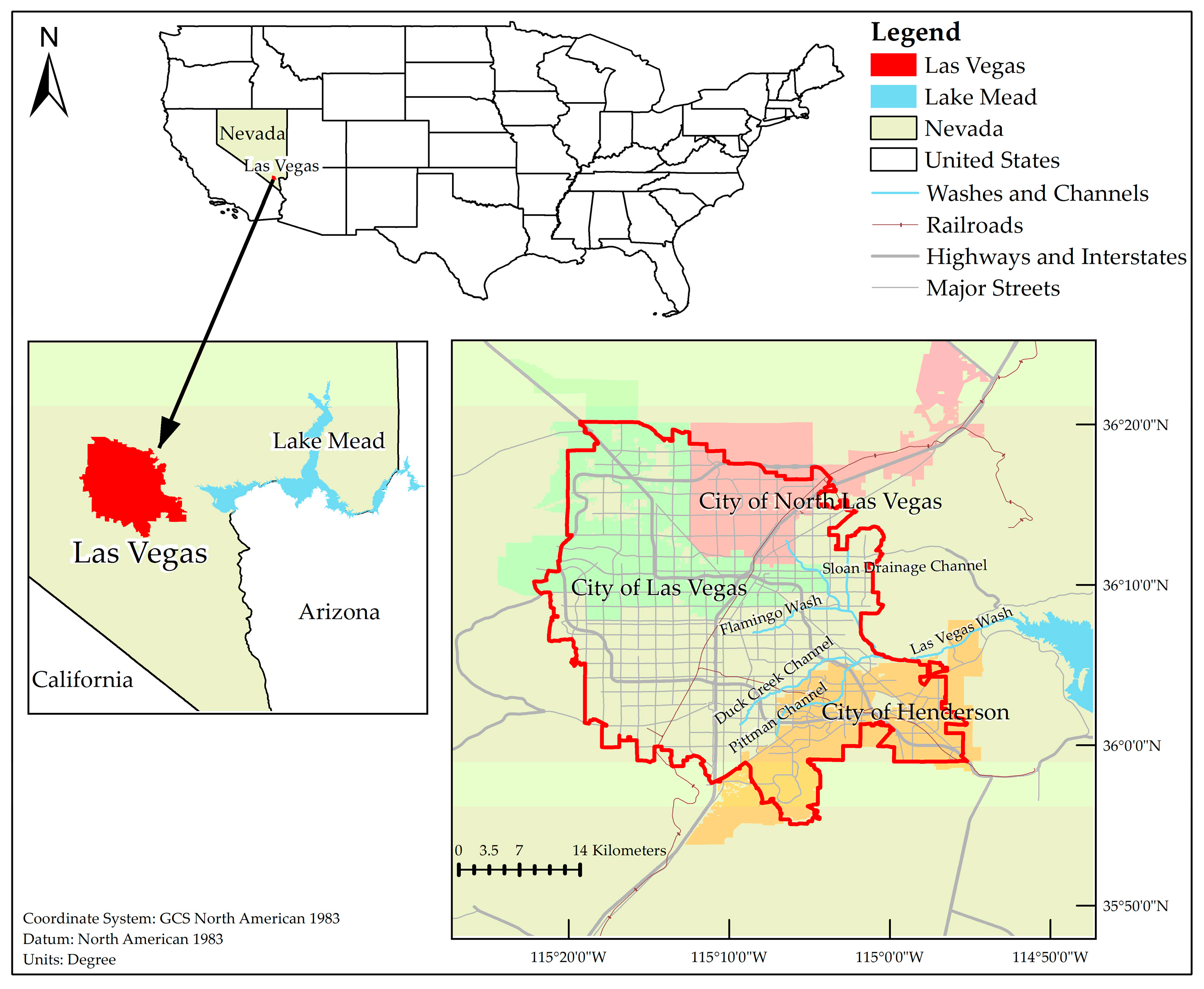
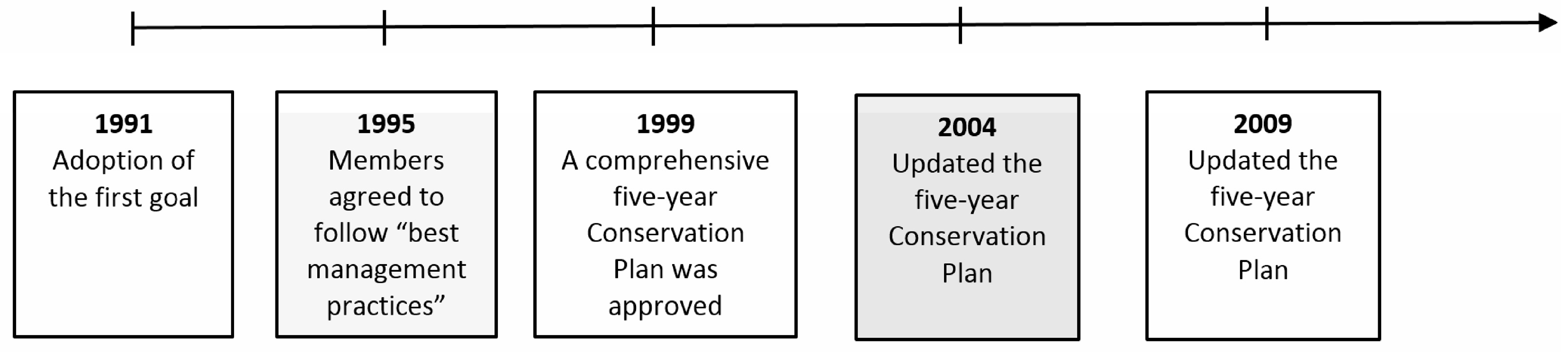
2. Study Area
3. Data and Methodology
3.1. Data Sources
3.2. Data Analysis and Data Transformation
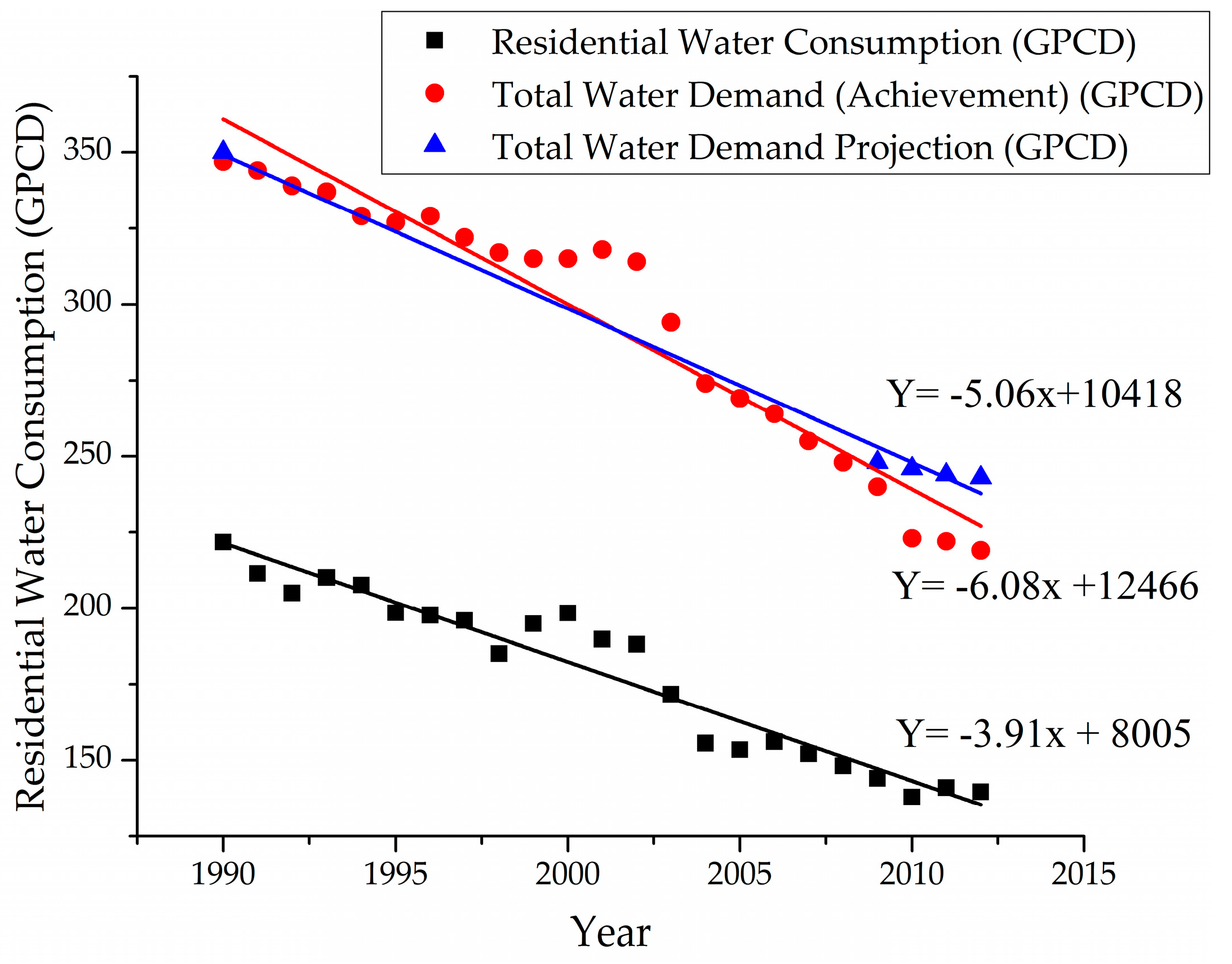
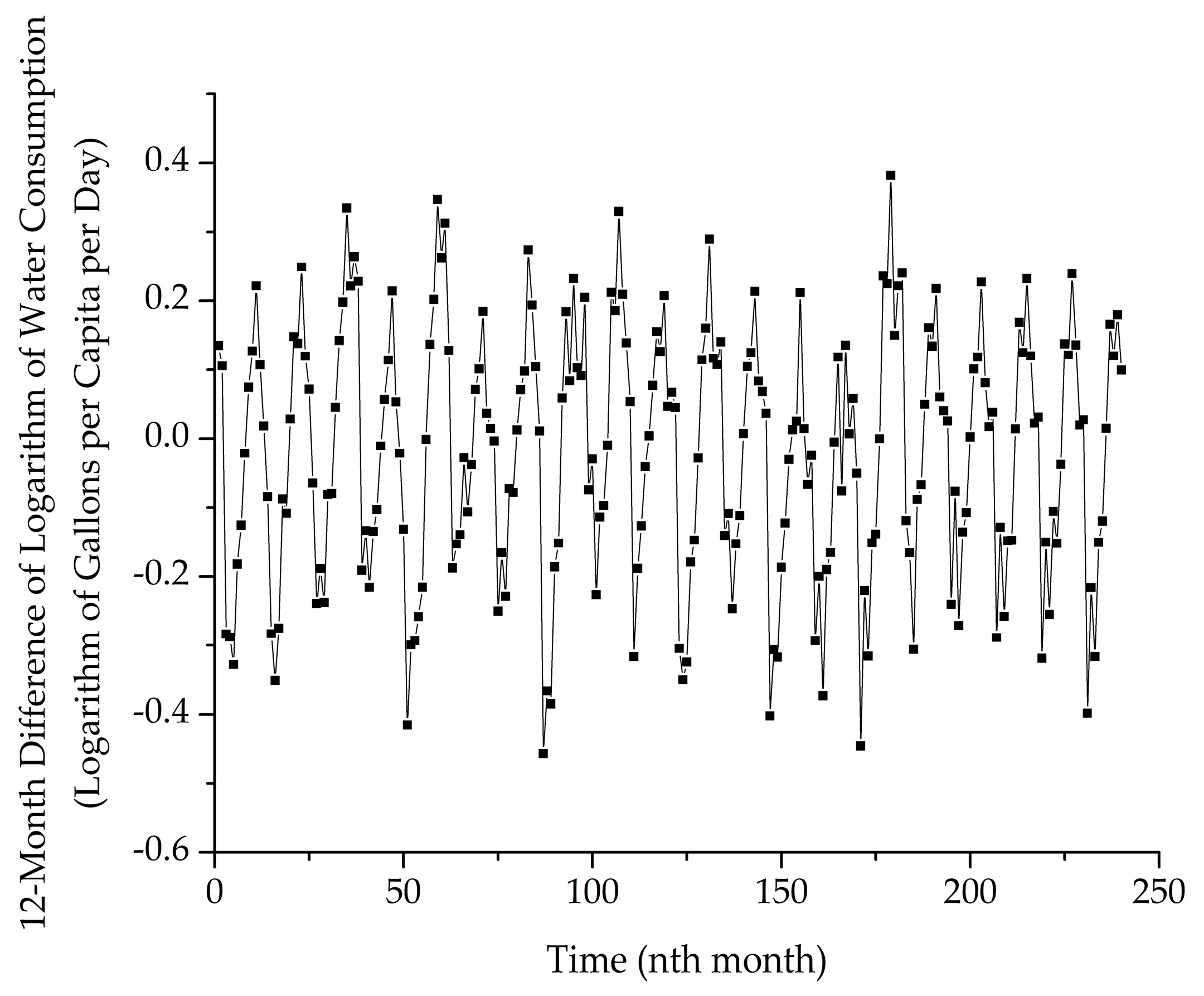
3.2.1. Trend Analysis
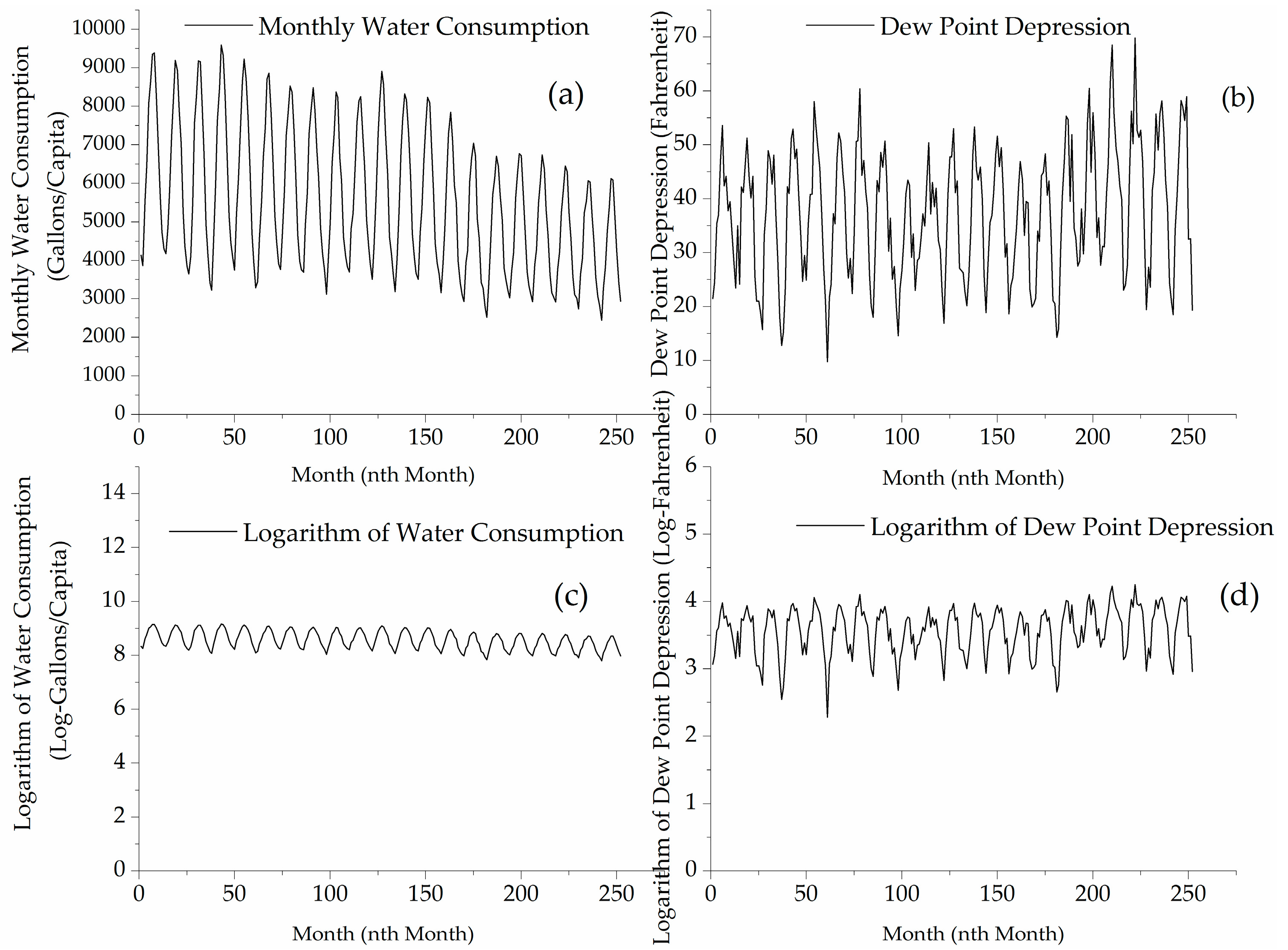
3.2.2. Data Transformation
3.3. Methodology
3.3.1. Time-Series Analysis: Model Description and Assumptions
3.3.2. Differencing for Removing Trend and Seasonality
3.3.3. Model Development: Transfer Function-Noise Model (ARIMAX)
3.3.4. Model Selection
4. Results
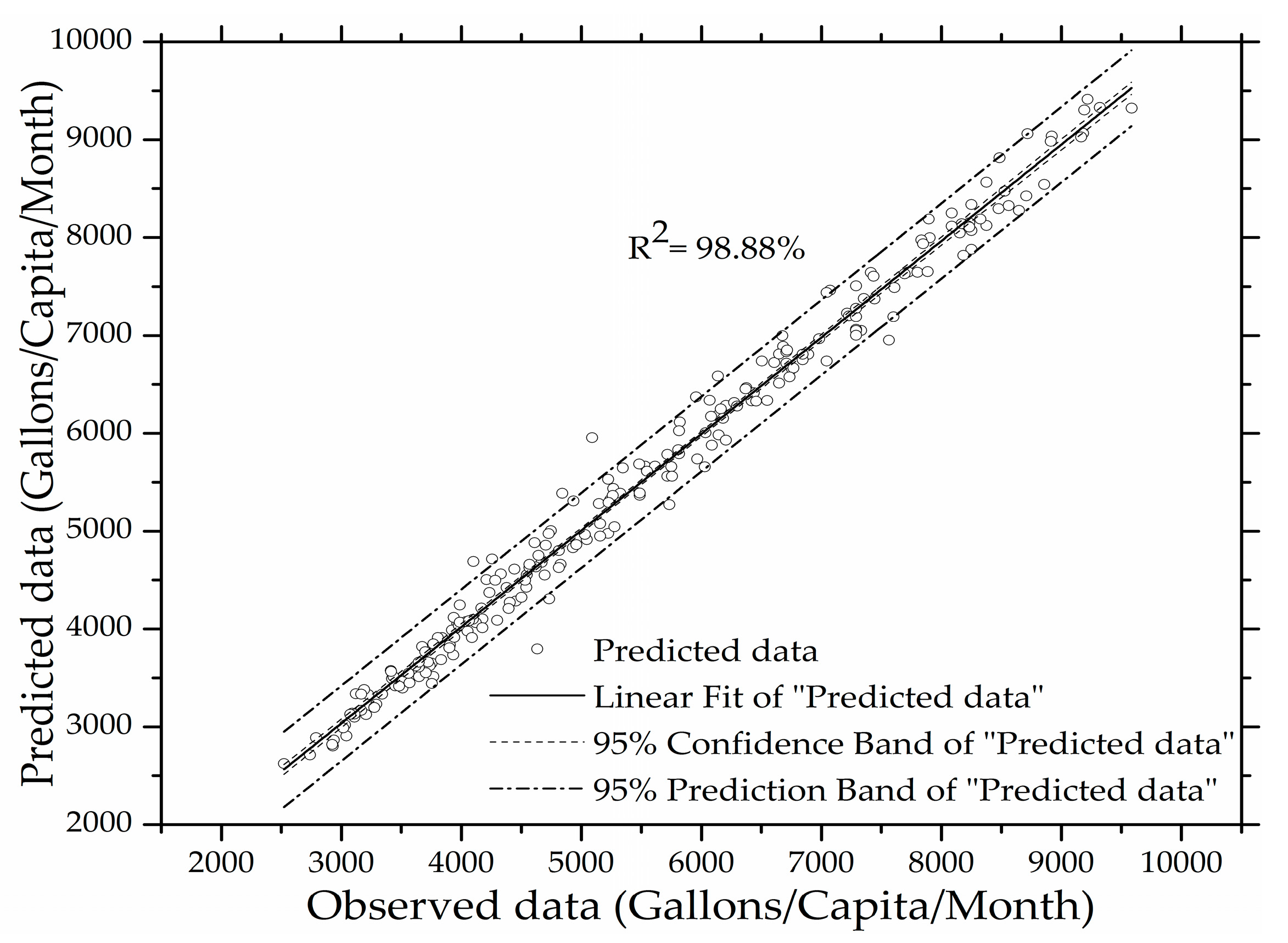
4.1. Model Development Results
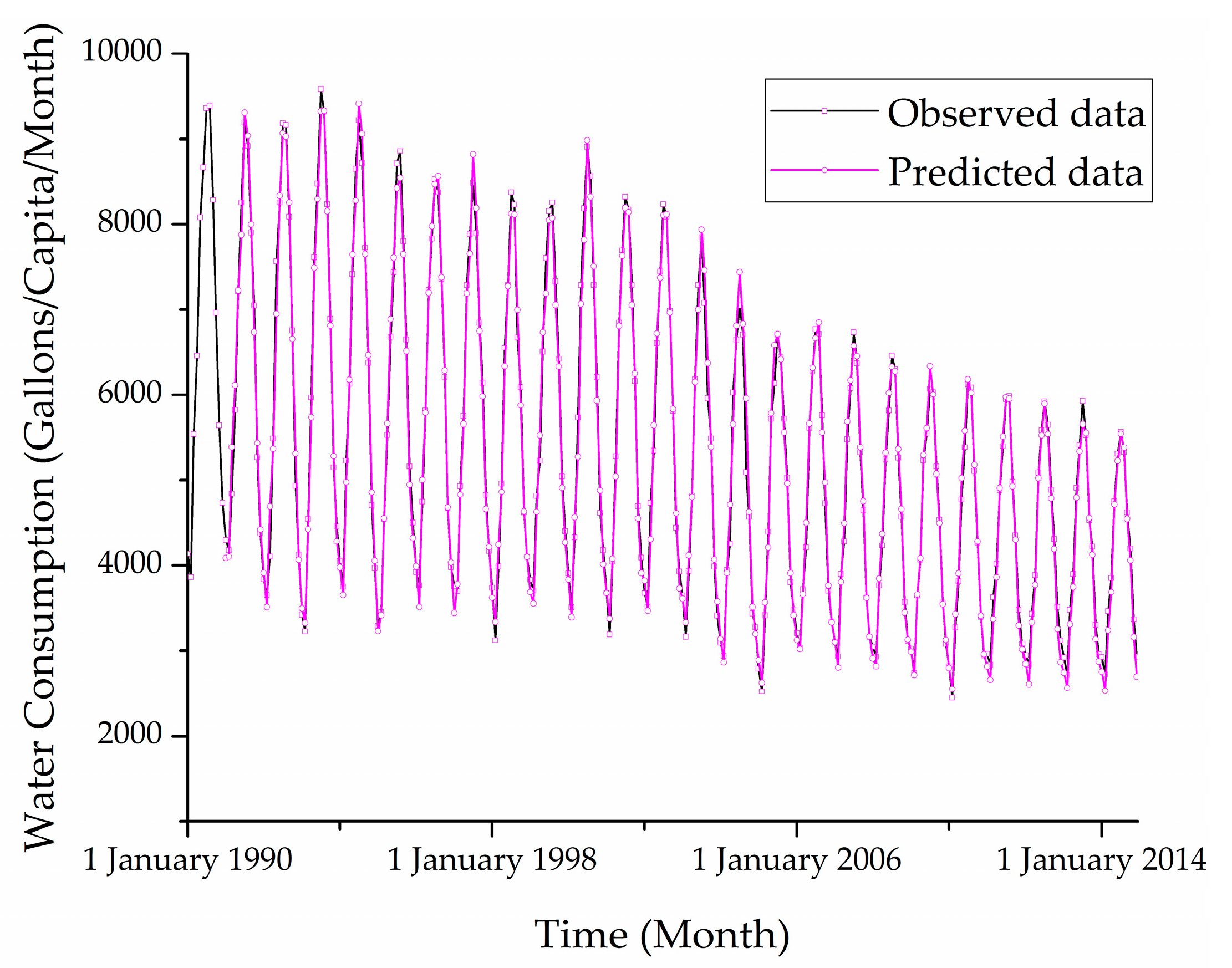
4.2. Forecasting Results
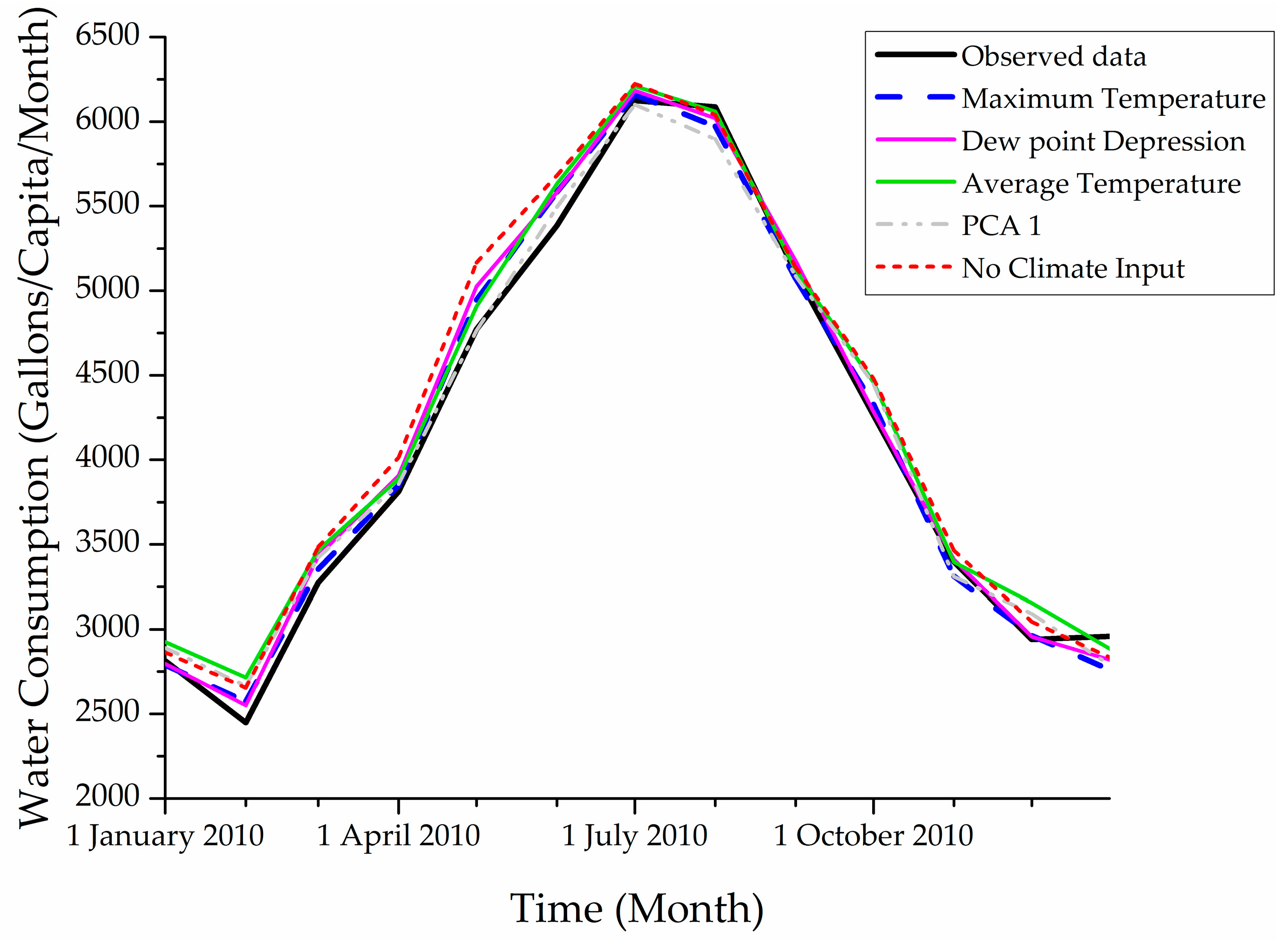
4.3. Sensitivity Analysis Results
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Southern Nevada Water Authority (SNWA). Water Resource Plan 2015. Available online: https://www.snwa.com/assets/pdf/wr_plan.pdf (accessed on 17 July 2017).
- National Park Service (NPS) U.S. Department of Interior. Lake Mead: Low Lake Levels. Available online: https://www.nps.gov/lake/learn/nature/lowwater.htm (accessed on 15 July 2016).
- Southern Nevada Water Authority (SNWA). Water Conservation Plan: 2014–2018. Available online: https://www.snwa.com/assets/pdf/about_reports_conservation_plan.pdf (accessed on 15 July 2016).
- Maidment, D.R.; Parzen, E. Cascade model monthly municipal water use. Water Resour. Res. 1984, 20, 15–23. [Google Scholar] [CrossRef]
- Zhou, S.L.; McMahon, T.A.; Walton, A. Lewis, daily urban water demand: A case study of Melbourne. J. Hydrol. 2000, 36, 153–164. [Google Scholar] [CrossRef]
- Guhathakurta, S.; Gober, P. The impact of the Phoenix urban heat island on residential water use. J. Am. Plan. Assoc. 2007, 73, 317–329. [Google Scholar] [CrossRef]
- Kenney, D.S.; Goemans, C.; Klein, R.; Lowrey, J.; Reidy, K. Residential water demand management: Lessons from Aurora, Colorado. J. Am. Water Resour. Assoc. 2008, 44, 192–207. [Google Scholar] [CrossRef]
- Praskievicz, S.; Chang, H. Identifying the relationships between urban water consumption and weather variable in Seoul, Korea. Phys. Geogr. 2009, 30, 324–337. [Google Scholar] [CrossRef]
- Haque, M.M.; Rahman, A.; Hagare, D.; Kibria, G. Principal component regression analysis in water demand forecasting: An application to the Blue Mountains, NSW, Australia. J. Hydrol. Environ. Res. 2013, 1, 49–59. [Google Scholar]
- Haque, M.M.; Rahman, A.; Hagare, D.; Kibria, G. Probabilistic water demand forecasting using projected climatic data for Blue Mountains water supply system in Australia. Water Resour. Manag. 2014, 28, 1959–1971. [Google Scholar] [CrossRef]
- Haque, M.M.; Prasanna, E.; Rahman, A.; Goonetilleke, A. Assessing the significance of climate and community factors on urban water demand. Int. J. Sustain. Built Environ. 2015, 4, 222–230. [Google Scholar] [CrossRef]
- Parandvash, G.H.; Chang, H. Analysis of long-term climate change on per capita water demand in urban versus suburban areas in the Portland metropolitan area, USA. J. Hydrol. 2016, 538, 574–586. [Google Scholar] [CrossRef]
- Trabia, S.H. Water Use on the Las Vegas Strip: Assessment and Suggestions for Conservation. Master’s Thesis, University of Nevada, Las Vegas, NV, USA, April 2014. [Google Scholar]
- Brelsford, C.; Abbott, J. Growing into water conservation? Decomposing the drivers of reduced water consumption in Las Vegas, NV. Ecol. Econ. 2017, 133, 99–110. [Google Scholar] [CrossRef]
- Tchigriaeva, E.; Lott, C.; Rollins, K. Modeling effects of multiple conservation policy instruments and exogenous factors on urban residential water demand through household heterogeneity. In Proceedings of the Agricultural & Applied Economics Association’s 2014, Minneapolis, MN, USA, 27–29 July 2014; Available online: http://ageconsearch.umn.edu/bitstream/170605/2/AAEA_2014_final_wcover.pdf (accessed on 17 July 2017).
- Boulos, P.F.; Jacobsen, L.B.; Heath, J.E.; Kamojjala, S. Real-time modeling of water distribution systems: A case study. J. Am. Water Works Assoc. 2014, 106, 119–120. [Google Scholar] [CrossRef]
- Lott, C.; Tchigriaeva, E.; Rollins, K. The effects of climate change on residential municipal water demand in Nevada. In Established Program to Stimulate Competitive Research (EPSCoR); University of Nevada: Reno, Nevada, 2013; Available online: https://www.unr.edu/Documents/business/esnr/Technical_report_nov_08_ET.pdf (accessed on 17 July 2017).
- Roderick, M.L.; Farquhar, G.D. The cause of decreased pan evaporation over the past 50 years. Science 2002, 298, 1410–1411. [Google Scholar] [PubMed]
- Xu, C.Y.; Gong, L.; Jiang, T.; Chen, L.; Singh, V.P. Analysis of spatial distribution and temporal trend of reference evapotranspiration and pan evaporation in Changjiang (Yangtze River) catchment. J. Hydrol. 2006, 327, 81–93. [Google Scholar] [CrossRef]
- Tiwari, M.K.; Adamowski, J. Urban water demand forecasting and uncertainty assessment using ensemble wavelet-bootstrap-neural network models. Water Resour. Res. 2013, 49, 6486–6507. [Google Scholar] [CrossRef]
- Caiado, J. Performance of combined double seasonal univariate time series models for forecasting water demand. J. Hydrol. Eng. 2010, 15, 215–222. [Google Scholar] [CrossRef]
- Bakker, M.; Duist, H.V.; Schagen, K.V.; Vreeburg, J.; Rietveld, L. Improving the performance of water demand forecasting models by using weather input. Procedia Eng. 2014, 70, 93–102. [Google Scholar] [CrossRef]
- The United States Census Bureau 2010: State and County Quickfacts. Available online: http://quickfacts.census.gov/qfd/states/32/32003.html (accessed on 10 April 2011).
- Stave, K.A. A system dynamics model to facilitate public understanding of water management options in Las Vegas, Nevada. J. Environ. Manag. 2003, 67, 303–313. [Google Scholar] [CrossRef]
- Tabachnick, B.G.; Fidell, L.S. Time-Series Analysis. In Using Multivariate Statistics, 4th ed.; Allyn and Bacon: Boston, MA, USA, 2001; pp. 837–900. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Transfer function models. In Time Series Analysis Forecasting and Control, 4th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2008; pp. 437–472. [Google Scholar]
- Maidment, D.R.; Miaou, S.P.; Crawford, M.M. Transfer function models of daily urban water use. Water Resour. Res. 1985, 21, 425–432. [Google Scholar] [CrossRef]
- Pankratz, A. Building Dynamic Regression Models: Model Identification. In Forecasting with Dynamic Regressions Models, 3rd ed.; John Wiley and Sons: New York, NY, USA, 1991; pp. 202–252. [Google Scholar]
- House-Peters, L.A.; Chang, H. Urban water demand modeling: Review of concepts, methods, and organizing principles. Water Resour. Res. 2011, 47, W05401. [Google Scholar] [CrossRef]
- Ashoori, N. Forecasting the Effects of Climate, Population, Price, and Conservation Behavior on Water Use in Los Angeles, California. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 29 September 2015. [Google Scholar]
- NSW Office of Water: Climate Change and Its Impacts on Water Supply and Demand in Sydney. Available online: https://www.metrowater.nsw.gov.au/sites/default/files/publication-documents/climatechange_impact_watersupply_summary.pdf (accessed on 1 May 2017).
| Meteorological Parameter | Pearson Correlation (r) |
|---|---|
| Maximum Temperature | 0.369 ** |
| Minimum Temperature | −0.024 |
| Average Temperature | 0.397 ** |
| Dew Point Depression | 0.734 ** |
| Diurnal Temperature | 0.638 ** |
| Precipitation | −0.550 ** |
| Wind Speed | −0.031 |
| Wind Direction | 0.054 |
| Percent of Calm Wind | 0.059 |
| Parameter | AIC | R-Squared (%) |
|---|---|---|
| ARIMAX with log dew point depression | −856.58 | 98.88 |
| ARIMAX with log average temperature | −824.76 | 98.72 |
| ARIMAX with log diurnal temperature | −818.45 | 98.67 |
| ARIMAX with PCA1 *,b | −818.13 | 98.68 |
| ARIMAX with log precipitation | −799.63 | 98.55 |
| ARIMAX with PCA2 **,b | −785.64 | 98.46 |
| ARIMAX with log maximum temperature | −785.30 | 98.48 |
| ARIMAX with log minimum temperature | −775.06 | 98.40 |
| ARIMAX with log wind speed | −773.63 | 98.47 |
| ARIMA (No climate factor) | −769.60 | 98.34 |
| ARIMAX with log wind direction | −765.16 | 98.44 |
| ARIMAX with log percent of calm wind | −713.95 | 98.44 |
| Input | b | µ | ω0 | δ1 | δ9 | ϕ1 | ϕ2 | ϕ12 | θ2 | θ10 | θ24 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| No Input (ARIMA) | −0.021 | 0.755 | −0.727 | 0.606 | |||||||
| (0.003) | (0.044) | (0.059) | (0.070) | ||||||||
| Dew Point Depression | −0.022 | 0.124 | 0.744 | −0.663 | −0.115 | 0.481 | |||||
| (0.004) | (0.012) | (0.046) | (0.063) | (0.060) | (0.075) | ||||||
| Average Temperature | −0.022 | 0.346 | 0.854 | −0.731 | 0.231 | 0.484 | |||||
| (0.003) | (0.042) | (0.039) | (0.058) | (0.063) | (0.074) | ||||||
| Diurnal Teperature | −0.020 | 0.182 | 0.740 | −0.681 | 0.538 | ||||||
| (0.003) | (0.024) | (0.046) | (0.061) | (0.073) | |||||||
| Maximum Temperature | −0.021 | 0.211 | 0.757 | −0.729 | 0.585 | ||||||
| (0.003) | (0.050) | (0.044) | (0.058) | (0.072) | |||||||
| Minimum Temperature | −0.022 | 0.040 | 0.813 | −0.707 | 0.163 | 0.586 | |||||
| (0.003) | (0.018) | (0.043) | (0.059) | (0.060) | (0.069) | ||||||
| PCA1 | −0.022 | 0.064 | 0.827 | −0.197 | −0.694 | 0.496 | |||||
| (0.004) | (0.008) | (0.042) | (0.072) | (0.061) | (0.076) | ||||||
| PCA2 | −0.019 | −0.018 | 0.748 | −0.692 | 0.601 | ||||||
| (0.003) | (0.004) | (0.045) | (0.060) | (0.070) | |||||||
| Percent Calm Wind | 6 | −0.022 | 0.013 | 0.490 | −0.543 | 0.746 | −0.654 | 0.404 | |||
| (0.005) | (0.006) | (0.055) | (0.062) | (0.047) | (0.065) | (0.080) | |||||
| Precipitation | −0.021 | −0.017 | 0.754 | −0.715 | 0.609 | ||||||
| (0.003) | (0.004) | (0.044) | (0.059) | (0.070) | |||||||
| Wind Direction | 4 | −0.023 | −0.104 | 0.772 | −0.736 | 0.544 | |||||
| (0.004) | (0.048) | (0.043) | (0.060) | (0.075) | |||||||
| Wind Speed | 3 | −0.022 | 0.058 | 0.773 | −0.734 | 0.539 | |||||
| (0.004) | (0.023) | (0.043) | (0.059) | (0.075) |
| Parameter | R-Squared (%) | MAPE (%) | RRMSE (%) | ARE (%) |
|---|---|---|---|---|
| ARIMAX with log maximum temperature | 99.33 | 1.97 (48.2) | 2.38 (58.4) | 2.05 (53.7) |
| ARIMAX with log dew point depression | 99.12 | 2.10 (44.7) | 2.75 (48.7) | 2.14 (51.3) |
| ARIMAX with PCA1 | 98.95 | 2.49 (34.5) | 3.00 (42.1) | 2.95 (30.0) |
| ARIMAX with log average temperature | 98.35 | 3.10 (18.4) | 3.75 (22.4) | 3.68 (10.8) |
| ARIMAX with log wind speed | 98.05 | 3.48 (8.4) | 4.08 (13.7) | 3.85 (6.3) |
| ARIMAX with log wind direction | 97.80 | 3.77 (0.8) | 4.33 (7.1) | 3.87 (5.8) |
| ARIMAX with log percent of calm wind | 97.59 | 3.56 (6.3) | 4.53 (1.8) | 3.95 (3.7) |
| ARIMA (no climate factor) | 97.52 | 3.80 | 4.60 | 4.09 |
| ARIMAX with log minimum temperature | 97.51 | 4.00 | 4.60 | 4.44 |
| ARIMA with log diurnal temperature | 95.09 | 5.65 | 6.47 | 5.97 |
| ARIMAX with log PCA2 | 93.77 | 6.22 | 7.28 | 6.13 |
| ARIMAX with log precipitation | 74.12 | 11.28 | 14.85 | 9.85 |
| Input 1 | Forecasting Period (nth Month) 2 | Mean (%) | Standard Deviation (%) | Minimum (%) | Maximum (%) |
|---|---|---|---|---|---|
| No Input (ARIMA) | 1–12 | 3.80 | 2.70 | 0.70 | 9.40 |
| 13–24 | 2.85 | 1.59 | 0.31 | 4.62 | |
| 25–36 | 2.87 | 1.88 | 0.44 | 6.35 | |
| 37–48 | 3.08 | 1.97 | 0.69 | 7.02 | |
| 49–60 | 3.93 | 2.05 | 0.22 | 6.62 | |
| Dew Point Depression | 1–12 | 2.10 | 1.85 | 0.29 | 6.03 |
| 13–24 | 2.49 | 1.75 | 0.56 | 5.93 | |
| 25–36 | 2.96 | 1.82 | 0.57 | 6.01 | |
| 37–48 | 3.02 | 1.67 | 0.57 | 6.48 | |
| 49–60 | 3.21 | 1.84 | 0.48 | 5.57 | |
| Average Temperature | 1–12 | 3.10 | 2.20 | 0.02 | 6.37 |
| 13–24 | 2.27 | 1.41 | 0.10 | 5.00 | |
| 25–36 | 2.55 | 1.66 | 0.00 | 4.96 | |
| 37–48 | 3.03 | 1.46 | 0.89 | 5.61 | |
| 49–60 | 2.95 | 1.41 | 0.26 | 4.63 | |
| Diurnal Temperature | 1–12 | 5.65 | 3.28 | 1.78 | 12.65 |
| 13–24 | 3.47 | 2.96 | 0.58 | 8.75 | |
| 25–36 | 2.60 | 1.54 | 0.67 | 5.27 | |
| 37–48 | 2.87 | 2.66 | 0.25 | 8.81 | |
| 49–60 | 3.39 | 2.56 | 0.69 | 9.13 | |
| Maximum Temperature | 1–12 | 1.97 | 1.40 | 0.52 | 4.69 |
| 13–24 | 3.67 | 2.40 | 0.66 | 6.98 | |
| 25–36 | 4.37 | 2.29 | 1.02 | 7.99 | |
| 37–48 | 4.64 | 1.67 | 1.49 | 7.53 | |
| 49–60 | 4.75 | 2.41 | 0.51 | 7.82 | |
| Minimum Temperature | 1–12 | 4.00 | 2.37 | 0.42 | 7.81 |
| 13–24 | 2.73 | 1.54 | 1.01 | 5.40 | |
| 25–36 | 2.64 | 1.56 | 0.50 | 5.48 | |
| 37–48 | 2.66 | 2.44 | 0.30 | 8.21 | |
| 49–60 | 3.51 | 2.09 | 0.28 | 6.71 | |
| PCA1 | 1–12 | 2.49 | 1.73 | 0.18 | 5.19 |
| 13–24 | 3.38 | 2.39 | 0.02 | 7.22 | |
| 25–36 | 4.52 | 2.74 | 0.08 | 8.20 | |
| 37–48 | 4.70 | 1.93 | 1.16 | 7.74 | |
| 49–60 | 5.84 | 2.14 | 2.55 | 8.91 | |
| PCA2 | 1–12 | 6.22 | 3.95 | 0.24 | 15.6 |
| 13–24 | 3.63 | 2.91 | 0.32 | 9.63 | |
| 25–36 | 2.48 | 1.64 | 0.17 | 4.94 | |
| 37–48 | 3.18 | 2.77 | 0.13 | 9.42 | |
| 49–60 | 4.38 | 3.13 | 0.01 | 10.11 | |
| Percent Calm Wind | 1–12 | 3.56 | 2.92 | 0.14 | 8.78 |
| 13–24 | 3.26 | 1.87 | 1.18 | 5.89 | |
| 25–36 | 3.57 | 2.56 | 0.02 | 7.71 | |
| 37–48 | 4.04 | 2.18 | 0.07 | 6.89 | |
| 49–60 | 4.87 | 2.29 | 0.11 | 8.02 | |
| Precipitation | 1–12 | 11.28 | 10.08 | 1.35 | 25.91 |
| 13–24 | 5.59 | 6.57 | 0.35 | 22.71 | |
| 25–36 | 5.23 | 4.43 | 0.33 | 14.98 | |
| 37–48 | 6.50 | 5.80 | 0.08 | 16.75 | |
| 49–60 | 7.47 | 5.22 | 0.96 | 16.25 | |
| Wind Direction | 1–12 | 3.77 | 2.22 | 0.13 | 6.66 |
| 13–24 | 4.00 | 2.11 | 0.60 | 6.78 | |
| 25–36 | 5.09 | 2.24 | 1.32 | 7.71 | |
| 37–48 | 5.09 | 1.57 | 2.49 | 6.91 | |
| 49–60 | 5.72 | 2.78 | 0.16 | 9.29 | |
| Wind Speed | 1–12 | 3.48 | 2.22 | 0.28 | 6.59 |
| 13–24 | 2.94 | 1.51 | 0.08 | 4.73 | |
| 25–36 | 3.26 | 1.87 | 0.38 | 6.13 | |
| 37–48 | 3.80 | 1.67 | 1.11 | 7.24 | |
| 49–60 | 4.53 | 1.90 | 1.99 | 7.12 |
| Climatic Scenarios | Dew point Depression 1 (Fahrenheit) | Demand Change | Predicted Water Demand 1 (GPC) 2 | Average Temperature 1 (Fahrenheit) | Demand Change | Predicted Water Demand 1 (GPC) 2 |
|---|---|---|---|---|---|---|
| Base value | 21.1 | Base value | 2797.5 | 48.7 | Base value | 2925.1 |
| 1% increase | 21.3 | 0.12% increase | 2800.9 | 49.2 | 0.35% increase | 2935.2 |
| 1% decrease | 20.9 | 0.12% decrease | 2794.0 | 48.2 | 0.35% decrease | 2915.0 |
| 10% increase | 23.2 | 1.19% increase | 2830.7 | 53.6 | 3.35% increase | 3023.2 |
| 10% decrease | 19.0 | 1.30% decrease | 2761.2 | 43.8 | 3.58% decrease | 2820.3 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huntra, P.; Keener, T.C. Evaluating the Impact of Meteorological Factors on Water Demand in the Las Vegas Valley Using Time-Series Analysis: 1990–2014. ISPRS Int. J. Geo-Inf. 2017, 6, 249. https://doi.org/10.3390/ijgi6080249
Huntra P, Keener TC. Evaluating the Impact of Meteorological Factors on Water Demand in the Las Vegas Valley Using Time-Series Analysis: 1990–2014. ISPRS International Journal of Geo-Information. 2017; 6(8):249. https://doi.org/10.3390/ijgi6080249
Chicago/Turabian StyleHuntra, Patcha, and Tim C. Keener. 2017. "Evaluating the Impact of Meteorological Factors on Water Demand in the Las Vegas Valley Using Time-Series Analysis: 1990–2014" ISPRS International Journal of Geo-Information 6, no. 8: 249. https://doi.org/10.3390/ijgi6080249
APA StyleHuntra, P., & Keener, T. C. (2017). Evaluating the Impact of Meteorological Factors on Water Demand in the Las Vegas Valley Using Time-Series Analysis: 1990–2014. ISPRS International Journal of Geo-Information, 6(8), 249. https://doi.org/10.3390/ijgi6080249





