Assessing Essential Qualities of Urban Space with Emotional and Visual Data Based on GIS Technique
Abstract
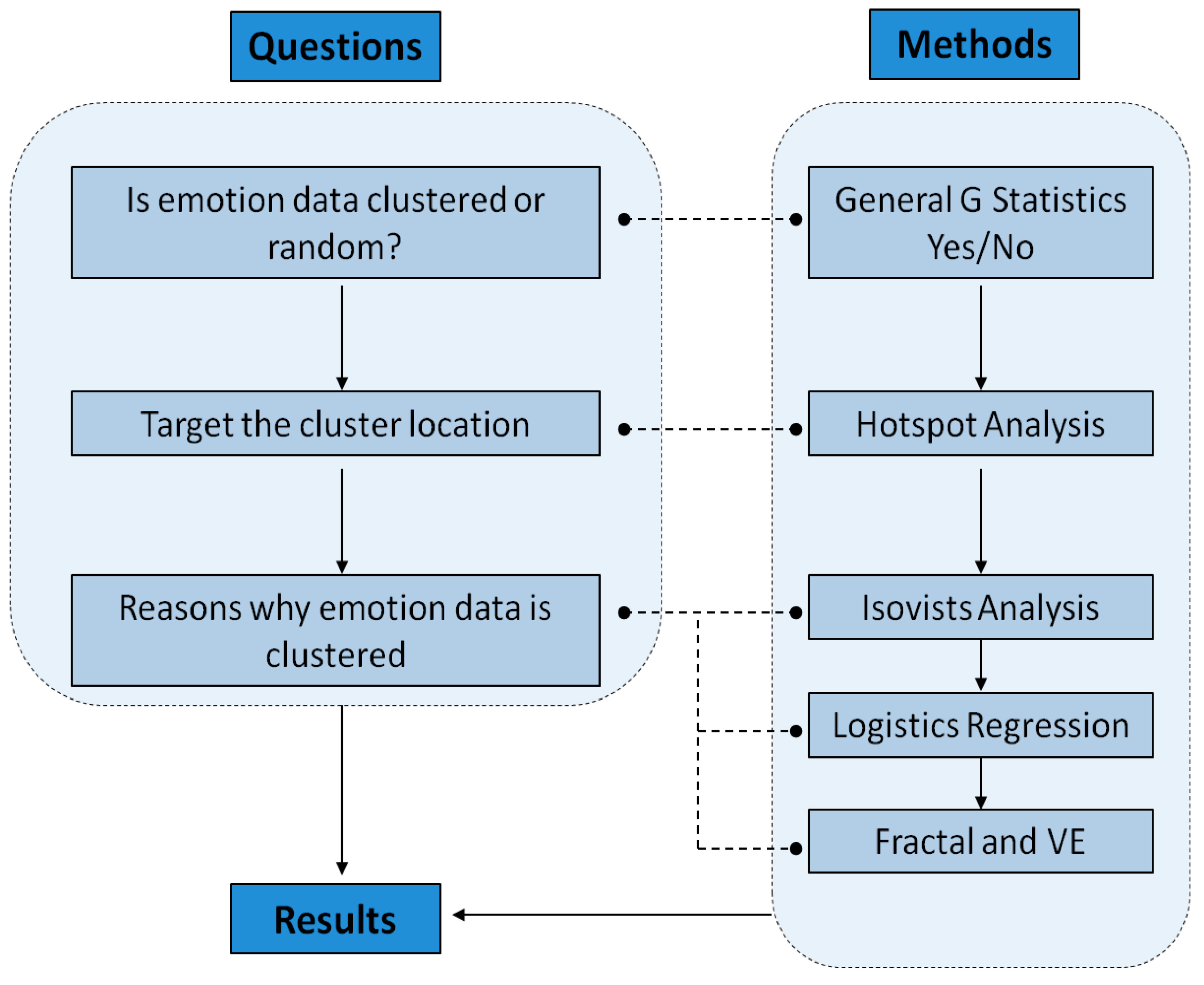
:1. Introduction
2. State of the Art
3. Emotion Data Collection
3.1. Physiological Basis
3.2. Preparation of Experiment
3.3. Emotion Data Preprocessing
4. Spatial Analysis
4.1. Influence from Building Texture
4.2. Isovist Analysis
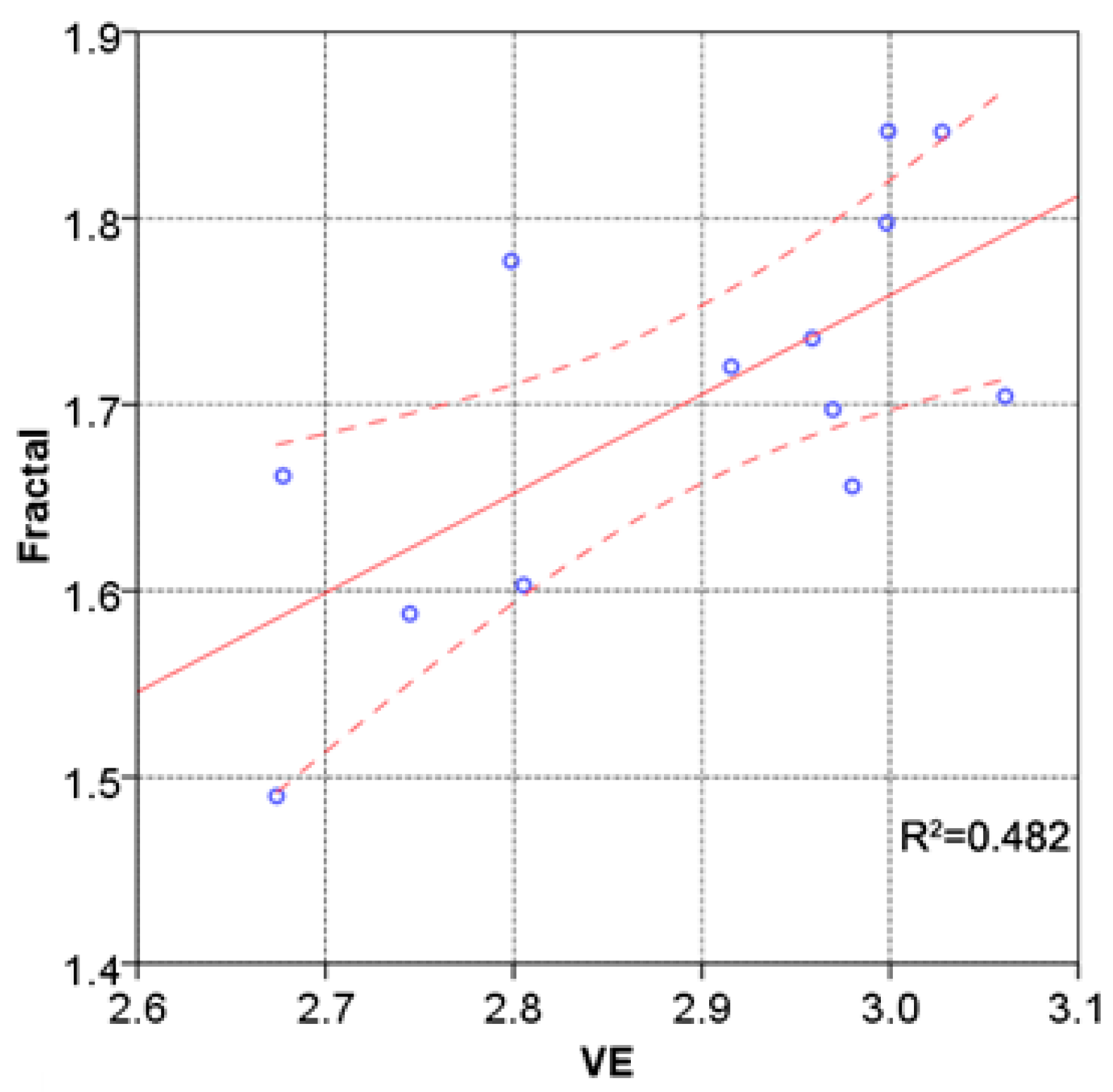
4.3. Analysis of Visual Entropy and Fractals
5. Discussion and Conclusion
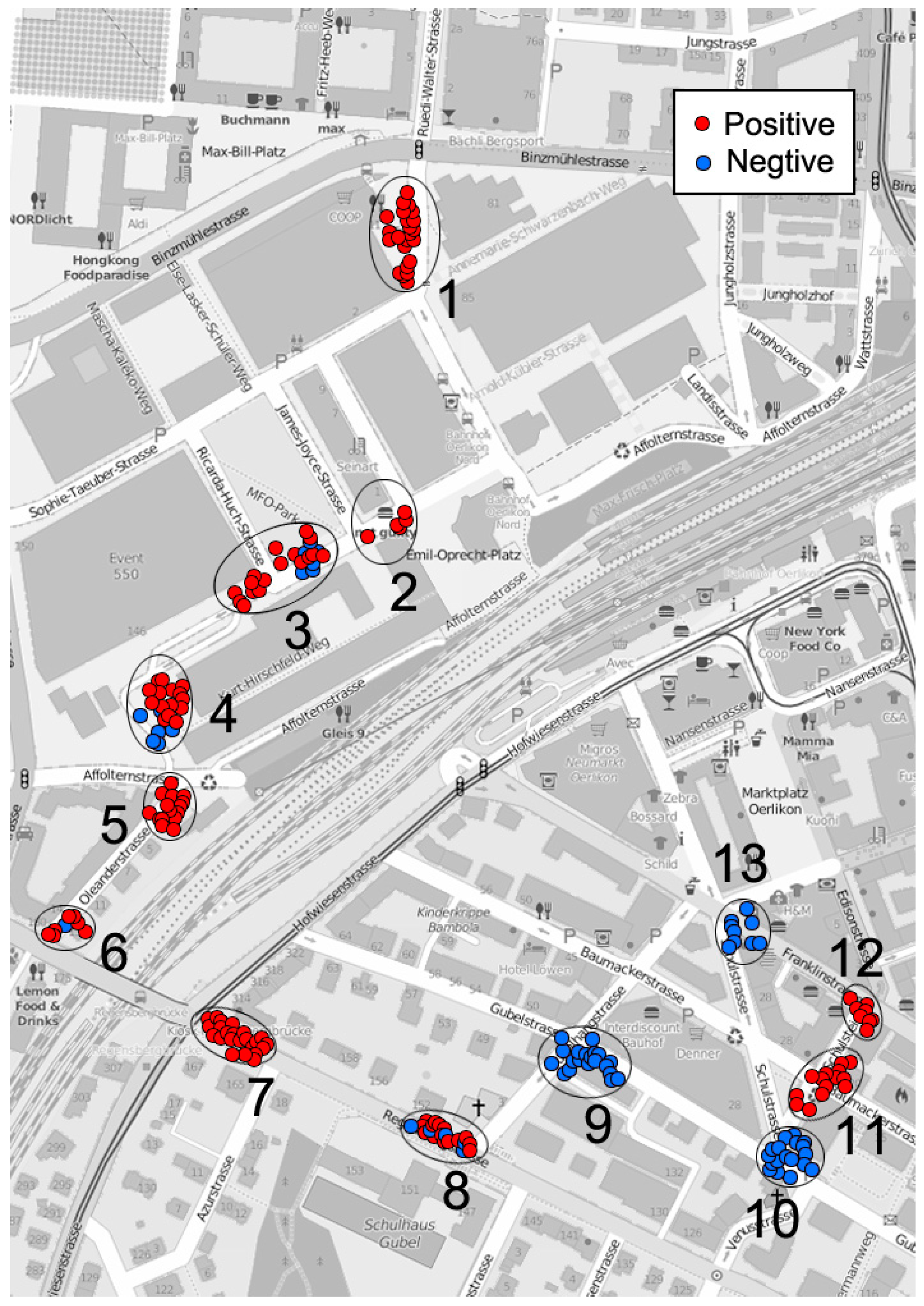
- People’s emotions are affected by different building layouts—in particular, how people perceive the spaces between buildings. Among those factors, isovist scope and relevant attributes are important ways for people to obtain visual information during their urban experience. Pedestrians activities in urban spaces are not simply restricted to any single isovist parameter but to the comprehensive impact of several isovist parameters, of which compactness, occlusivity, and maximum visibility are comparatively dominant. Among the three, higher compactness and greater visibility within a space seem to be advantageous in causing positive emotions, indicating that people may prefer spaces with good vistas within a suitable distance and clearer boundaries. However, this does not mean that people prefer an unlimited field of view. Large unending avenues might be monotonous and boring. A threshold effect may occur, and that is the question our future research will seek to answer.
- Spatial attributes are not merely reflected in planar isovist form; the richness and complexity of three-dimensional space are also important reasons affecting the spatial experience of pedestrians. Visual information analysis can help designers effectively interpret the qualities of an urban space. According to this research, enclosed urban spaces are very important in fostering a sense of security in pedestrians. During the process of urban planning and design, specific entity borders, neat and compact isovist forms, a rich landscape hierarchy and greenery are easy ways to create urban spaces with a sense of place. Some man-made obstacles can seriously weaken the qualities of the spatial environment. Only by strengthening management and daily maintenance is it possible to ensure the design achievements, which are hard to obtain, and maintain a spatial environment with positive qualities.
- Human perception of urban space tends to focus on important spatial nodes; therefore, we cannot neglect changes in the spatial sequence or the design treatment of spatial nodes. These should strengthen the systematic construction of urban spatial nodes, including public squares, street greening, and street corners. The integration of points, lines and networks—especially those that reinforce the continuity and network of pedestrian space—should give full weight to the way in which the scenes of these spatial nodes switch and cultivate urban spatial sequences with special meanings that reinforce positive images during urban movement.
Acknowledgment
Author Contributions
Conflicts of Interest
References
- Alexander, E.R.; Reed, K.D.; Murphy, P. Density Measures and Their Relation to Urban Form: Center for Architecture and Urban Planning Research; University of Wisconsin: Milwaukee, MI, USA, 1988. [Google Scholar]
- Herrera-Yagüe, C.; Schneider, C.M.; Couronne, T.; Smoreda, Z.; Benito, R.M.; Zufiria, P.J.; González, M.C. The anatomy of urban social networks and its implications in the searchability problem. Sci. Rep. 2015. [Google Scholar] [CrossRef] [PubMed]
- Lang, J. Urban Design: The American Experience; John Wiley & Sons: New York, NY, USA, 1994. [Google Scholar]
- Trancik, R. Finding Lost Space: Theories of Urban Design; John Wiley & Sons: New York, NY, USA, 1986. [Google Scholar]
- Noulas, A.; Scellato, S.; Lambiotte, R.; Pontil, M.; Mascolo, C. A tale of many cities: Universal patterns in human urban mobility. PLoS ONE 2012, 7, e37027. [Google Scholar] [CrossRef]
- Polsky, C.; Grove, J.M.; Knudson, C.; Groffman, P.M.; Bettez, N.; Cavender-Bares, J.; Larson, K.L. Assessing the homogenization of urban land management with an application to US residential lawn care. Proc. Natl. Acad. Sci. USA 2014, 111, 4432–4437. [Google Scholar] [CrossRef] [PubMed]
- Expert, P.; Evans, T.S.; Blondel, V.D.; Lambiotte, R. Uncovering space-independent communities in spatial networks. Proc. Natl. Acad. Sci. USA 2011, 108, 7663–7668. [Google Scholar] [CrossRef] [PubMed]
- Franck, K.; Stevens, Q. Loose Space: Possibility and Diversity in Urban Life; Routledge: New York, NY, USA, 2013. [Google Scholar]
- Gehl, J. Life between Buildings: Using Public Space; Island Press: Washington, DC, USA, 2011. [Google Scholar]
- Gospodini, A. Urban design, urban space morphology, urban tourism: An emerging new paradigm concerning their relationship. Eur. Plan. Stud. 2001, 9, 925–934. [Google Scholar] [CrossRef]
- Sun, L.; Axhausen, K.W.; Lee, D.H.; Huang, X. Understanding metropolitan patterns of daily encounters. Proc. Natl. Acad. Sci. USA 2013, 110, 13774–13779. [Google Scholar] [CrossRef] [PubMed]
- Hillier, B.; Iida, S. Network and psychological effects in urban movement. In Spatial Information Theory; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; pp. 475–490. [Google Scholar]
- Hillier, B. Space is the Machine: A Configurational Theory of Architecture; Cambridge University Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Clifford, C.W.G.; Rhodes, G. Fitting the Mind to the World: Adaptation and After-Effects in High-Level Vision; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Stamps, A.E. Advances in visual diversity and entropy. Environ. Plan. B Plan. Des. 2003, 30, 449–463. [Google Scholar] [CrossRef]
- Dalton, R.C. The secret is to follow your nose route path selection and angularity. Environ. Behav. 2003, 35, 107–131. [Google Scholar] [CrossRef]
- Wiener, J.M.; Hölscher, C.; Büchner, S.; Konieczny, L. Gaze behaviour during space perception and spatial decision making. Psychol. Res. 2012, 76, 713–729. [Google Scholar] [CrossRef] [PubMed]
- Franz, G.; Wiener, J.M. From space syntax to space semantics: A behaviorally and perceptually oriented methodology for the efficient description of the geometry and topology of environments. Environ. Plan. B Plan. Des. 2008, 35, 574–592. [Google Scholar] [CrossRef]
- Ewing, R.; Handy, S. Measuring the unmeasurable: Urban design qualities related to walkability. J. Urban Des. 2009, 14, 65–84. [Google Scholar] [CrossRef]
- Handy, S.L.; Boarnet, M.G.; Ewing, R.; Killingsworth, R.E. How the built environment affects physical activity: Views from urban planning. Am. J. Prev. Med. 2002, 23, 64–73. [Google Scholar] [CrossRef]
- Morello, E.; Ratti, C. A digital image of the city: 3D isovists in Lynch’s urban analysis. Environ. Plan. B Plan. Des. 2009, 36, 837–853. [Google Scholar] [CrossRef]
- Batty, M. Agents, cells, and cities: New representational models for simulating multiscale urban dynamics. Environ. Plan. A 2005, 37, 1373–1394. [Google Scholar] [CrossRef]
- Seto, K.C.; Reenberg, A.; Boone, C.G.; Fragkias, M.; Haase, D.; Langanke, T.; Simon, D. Urban land teleconnections and sustainability. Proc. Natl. Acad. Sci. USA 2012, 109, 7687–7692. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Jelinski, D.E.; Luck, M.; Tueller, P.T. Multiscale analysis of landscape heterogeneity: Scale variance and pattern metrics. Geogr. Inf. Sci. 2000, 6, 6–19. [Google Scholar] [CrossRef] [PubMed]
- Rattenbury, T.; Naaman, M. Methods for extracting place semantics from Flickr tags. ACM Trans. Web 2009, 3, 1139–1141. [Google Scholar] [CrossRef]
- Wakamiya, S.; Belouaer, L.; Brosset, D.; Lee, R.; Kawai, Y.; Sumiya, K.; Claramunt, C. Measuring crowd mood in city space through twitter. In Web and Wireless Geographical Information Systems; Springer International Publishing: Cham, Switzerland, 2015; pp. 37–49. [Google Scholar]
- Resch, B.; Summa, A.; Zeile, P.; Strube, M. Citizen-centric urban planning through extracting emotion information from twitter in an interdisciplinary space-time-linguistics algorithm. Urban Plan. 2016, 1, 114–127. [Google Scholar] [CrossRef]
- Resch, B.; Sudmanns, M.; Sagl, G.; Summa, A.; Zeile, P.; Exner, J.P. Crowdsourcing physiological conditions and subjective emotions by coupling technical and human mobile sensors. GIForum J. Geogr. Inf. Sci. 2015, 1, 514–524. [Google Scholar] [CrossRef]
- Academy of Neuroscience for Architecture. 2013. Available online: http://www.anfarch.org/ (accessed on 20 October 2016).
- Peters, D.; Richter, K. Taking off to the third dimension: Schematization of virtual environments. Int. J. Spat. Data Inf. Res. 2008, 3, 20–37. [Google Scholar]
- Russell, J.A. A circumplex model of affect. J. Personal. Soc. Psychol. 1980, 39, 1161–1178. [Google Scholar] [CrossRef]
- Emotions of the Urban Pedestrian: Sensory Mapping. Available online: http://www.walkeurope.org/uploads/File/publications/PQN%20Final%20Report%20part%20B4.pdf#page=32 (accessed on 20 October 2016).
- Bergner, B.S.; Exner, J.P.; Memmel, M.; Raslan, R.; Dina-Taha, D.; Talal, M.; Zeile, P. Human sensory assessment methods in urban planning: A case study in Alexandria. Proc. REAL CORP 2013, 1, 407–417. [Google Scholar]
- Mavros, P.; Coyne, R.; Roe, J.; Aspinall, P. Engaging the brain: Implications of mobile EEG for spatial representation. In Proceedings of the 30th International Conference on Education and Research in Computer Aided Architectural Design in Europe, Prague, Czech Republic, 12–14 September 2012.
- Camras, L.A.; Meng, Z.L.; Ujiie, T.; Dharamsi, S.; Miyake, K.; Oster, H.; Campos, J. Observing emotion in infants: Facial expression, body behavior, and rater judgments of responses to an expectancy-violating event. Emotion 2002, 2, 179–193. [Google Scholar] [CrossRef] [PubMed]
- Solomon, R.C. Back to basics: On the very idea of “basic emotions”. J. Theory Soc. Behav. 2002, 32, 115–144. [Google Scholar] [CrossRef]
- Fabrikant, S.I.; Christophe, S.; Papastefanou, G.; Maggi, S.; Fabrikant, S.I.; Maggi, S. Emotional response to map design aesthetics. In Proceedings of the GIScience Conference 2012, Columbus, OH, USA, 18–21 September 2012.
- Bodymonitor. Available online: http://www.bodymonitor.de/ (accessed on 20 October 2016).
- Papastefanou, J. Experimentelle Validierung eines Sensorarmbandes zur mobilen Messung physiologischer Stressreaktionen. GESIS-Tech. Rep. 2013, 7, 1–14. [Google Scholar]
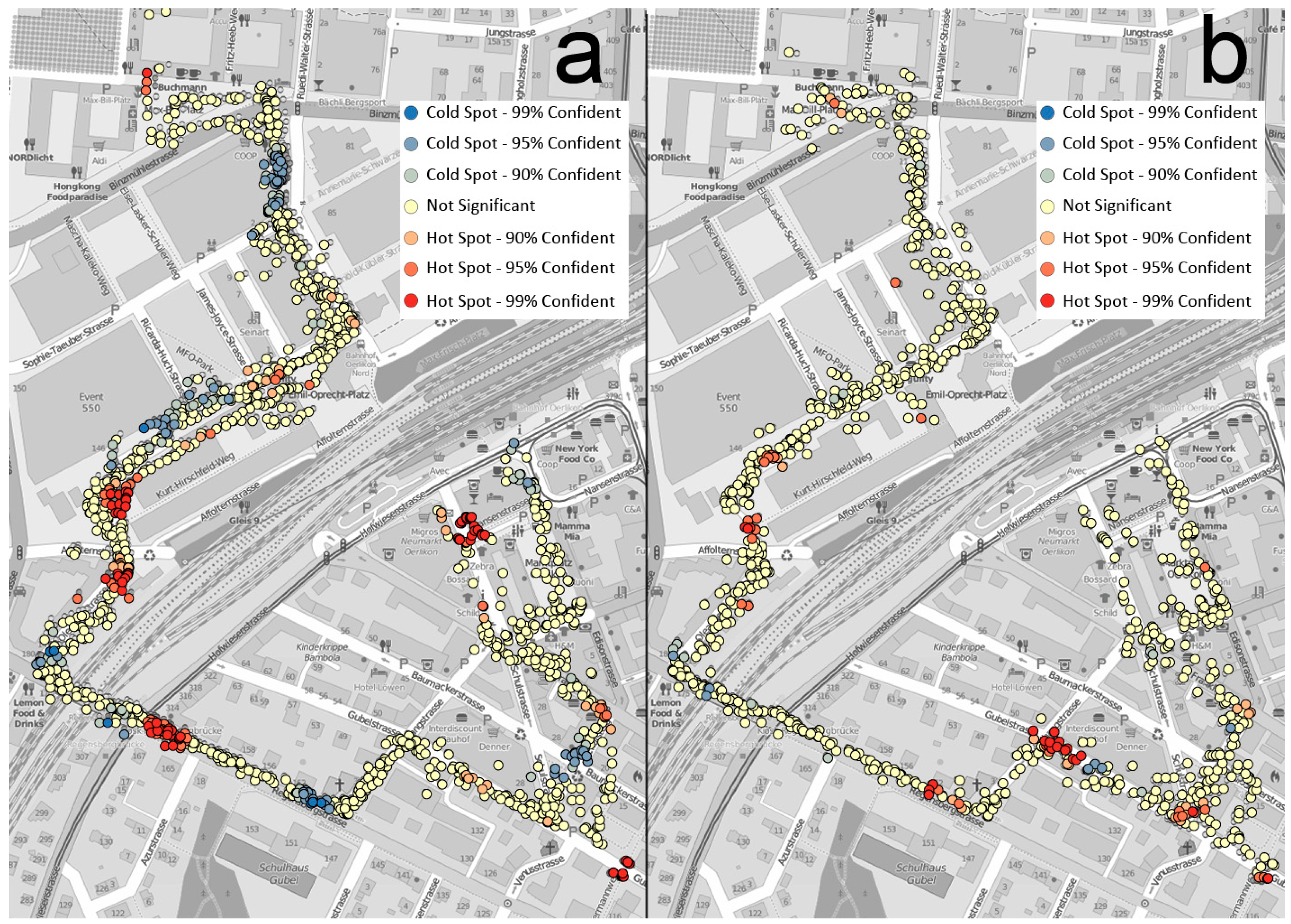
- Zhang, S.L.; Zhang, K. Comparison between General Moran’s index and Getis-Ord General G of spatial autocorrelation. Acta Sci. Nat. Univ. Sunyatseni 2007, 46, 93–97. [Google Scholar]
- Getis, A.; Ord, J.K. The analysis of spatial association by use of distance statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Ord, J.K.; Getis, A. Local spatial autocorrelation statistics—Distributional issues and an application. Geogr. Anal. 1995, 27, 286–306. [Google Scholar] [CrossRef]
- Benedikt, M.L. To take hold of space—Isovists and isovist fields. Environ. Plan. B Plan. Des. 1979, 6, 47–65. [Google Scholar] [CrossRef]
- Davis, L.S.; Benedikt, M.L. Computational models of space: Isovists and isovist fields. Comput. Graph. Image Proc. 2003, 11, 49–72. [Google Scholar] [CrossRef]
- Forman, R.T.T.; Godron, M. Landscape Ecology; John Wiley & Sons: New York, NY, USA, 1986. [Google Scholar]
- Harrell, F.E.X. Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis; Springer Science Business Media: Berlin, Germany, 2013. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recogn. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Segal, I.E. A note on the concept of entropy. J. Math. Mech. 1960, 9, 623–629. [Google Scholar] [CrossRef]
- Berlyne, D.E.; Madsen, K.B. Pleasure, Reward, Preference: Their Nature, Determinants, and Role in Behavior; Academic Press: New York, NY, USA, 2013. [Google Scholar]
- Cooper, J.; Oskrochi, R. Fractal analysis of street vistas: A potential tool for assessing levels of visual variety in everyday street scenes. Environ. Plan. B Plan. Des. 2008, 35, 349–363. [Google Scholar] [CrossRef]
- Stamps, A.E. Entropy, visual diversity, and preference. J. Gen. Psychol. 2002, 129, 300–320. [Google Scholar] [CrossRef] [PubMed]
- Stamps, A.E. On shape and spaciousness. Environ. Behav. 2008, 41, 526–548. [Google Scholar] [CrossRef]
- Sato, T.; Matsuoka, M.; Takayasu, H. Fractal image analysis of natural scenes and medical images. Fractals Int. J. Complex Geom. Nat. 1996, 4, 463–468. [Google Scholar] [CrossRef]
- Jiang, B.; Sui, D.Z. A new kind of beauty out of the underlying scaling of geographic space. Prof. Geogr. 2014, 66, 676–686. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals—Form, Chance, and Dimension; W.H.Freeman & Company: New York, NY, USA, 1977. [Google Scholar]
- Li, J.; Du, Q.; Sun, C.X. An improved box-counting method for image fractal dimension estimation. Pattern Recognit. 2009, 42, 2460–2469. [Google Scholar] [CrossRef]


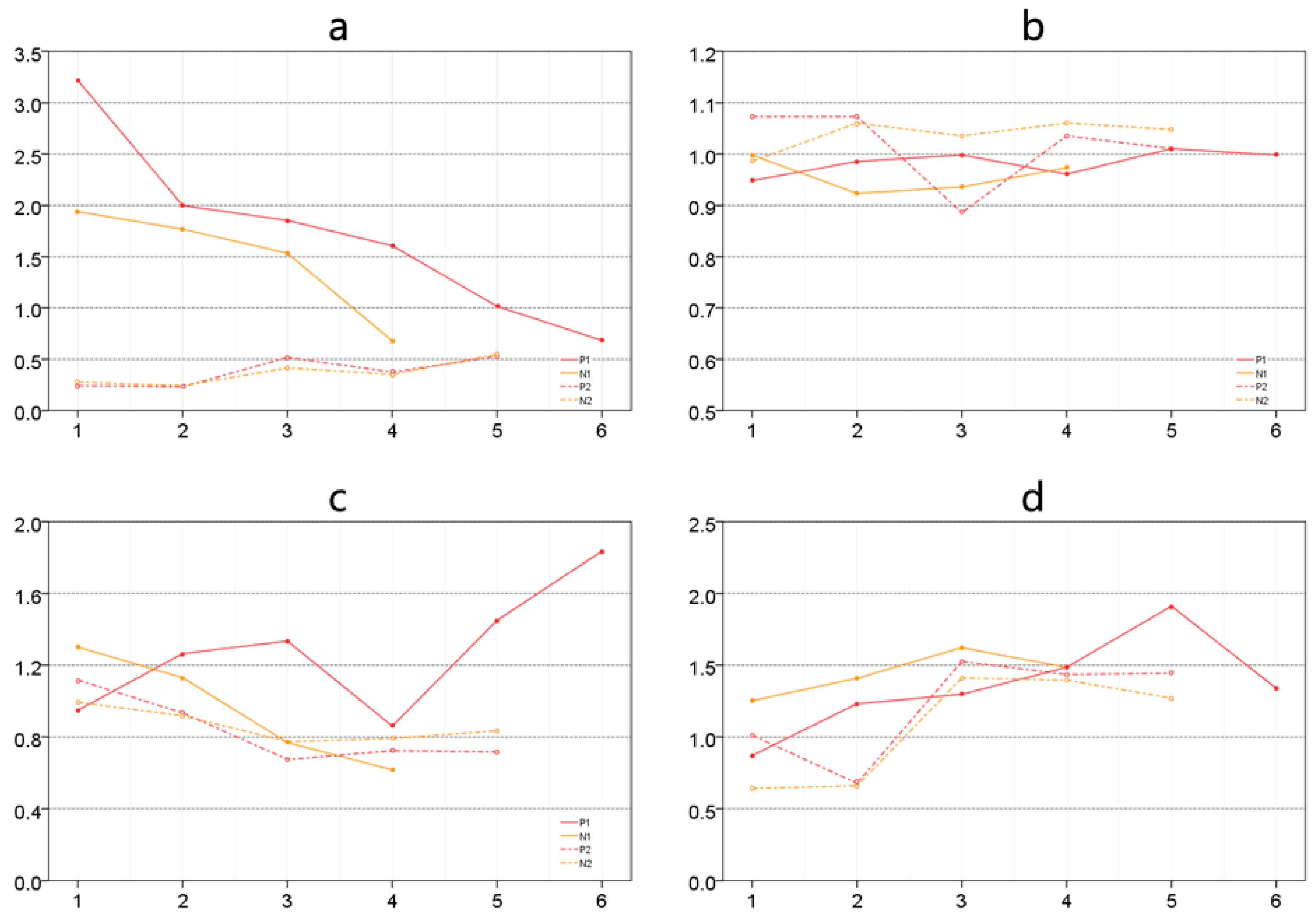


| Sampling Group | Mean Area | Area Dispersion | Average Distance | Degree of Fragmentation |
|---|---|---|---|---|
| P collection (S1) | 1.728 | 1.356 | 1.283 | 0.984 |
| N collection (S1) | 1.478 | 1.443 | 0.955 | 0.958 |
| P collection (S2) | 0.378 | 1.220 | 0.834 | 1.016 |
| N collection (S2) | 0.366 | 1.076 | 0.863 | 1.038 |
| Inspection Coefficient | Inspection Result | Prediction Coefficient | Estimated Coefficient | p-Value | Wals Value |
|---|---|---|---|---|---|
| Cox & Snell R2 | 0.302 | X1 | 1.03 | 0.000 | 36.549 |
| Nagelkerke R2 | 0.438 | X2 | 0.10 | 0.032 | 4.611 |
| Hosmer-Lemeshow | 0.128 | X3 | 0.70 | 0.000 | 14.709 |
| Location No. | Fractal | Visual Entropy | Comprehensive Visual Index | Predicted Value | Observed Value | Inspection Result |
|---|---|---|---|---|---|---|
| 1 | 1.6616 | 2.677428 | 4.339028 | 1 | 1 | √ |
| 2 | 1.7354 | 2.958627 | 4.694027 | 1 | 1 | √ |
| 3 | 1.7770 | 2.798628 | 4.575628 | 0 | 0 | √ |
| 4 | 1.5876 | 2.744836 | 4.332436 | 0 | 0 | √ |
| 5 | 1.4898 | 2.674102 | 4.163902 | 0 | 1 | × |
| 6 | 1.6030 | 2.805265 | 4.408265 | 1 | 0 | × |
| 7 | 1.8466 | 2.999055 | 4.845655 | 1 | 1 | √ |
| 8 | 1.6561 | 2.979993 | 4.636093 | 0 | 0 | √ |
| 9 | 1.7202 | 2.915624 | 4.635824 | 0 | 0 | √ |
| 10 | 1.7974 | 2.998140 | 4.79554 | 1 | 0 | × |
| 11 | 1.8463 | 3.027640 | 4.87394 | 1 | 1 | √ |
| 12 | 1.7044 | 3.061204 | 4.765604 | 0 | 1 | × |
| 13 | 1.6973 | 2.969658 | 4.666958 | 0 | 0 | √ |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Hijazi, I.; Koenig, R.; Lv, Z.; Zhong, C.; Schmitt, G. Assessing Essential Qualities of Urban Space with Emotional and Visual Data Based on GIS Technique. ISPRS Int. J. Geo-Inf. 2016, 5, 218. https://doi.org/10.3390/ijgi5110218
Li X, Hijazi I, Koenig R, Lv Z, Zhong C, Schmitt G. Assessing Essential Qualities of Urban Space with Emotional and Visual Data Based on GIS Technique. ISPRS International Journal of Geo-Information. 2016; 5(11):218. https://doi.org/10.3390/ijgi5110218
Chicago/Turabian StyleLi, Xin, Ihab Hijazi, Reinhard Koenig, Zhihan Lv, Chen Zhong, and Gerhard Schmitt. 2016. "Assessing Essential Qualities of Urban Space with Emotional and Visual Data Based on GIS Technique" ISPRS International Journal of Geo-Information 5, no. 11: 218. https://doi.org/10.3390/ijgi5110218
APA StyleLi, X., Hijazi, I., Koenig, R., Lv, Z., Zhong, C., & Schmitt, G. (2016). Assessing Essential Qualities of Urban Space with Emotional and Visual Data Based on GIS Technique. ISPRS International Journal of Geo-Information, 5(11), 218. https://doi.org/10.3390/ijgi5110218






