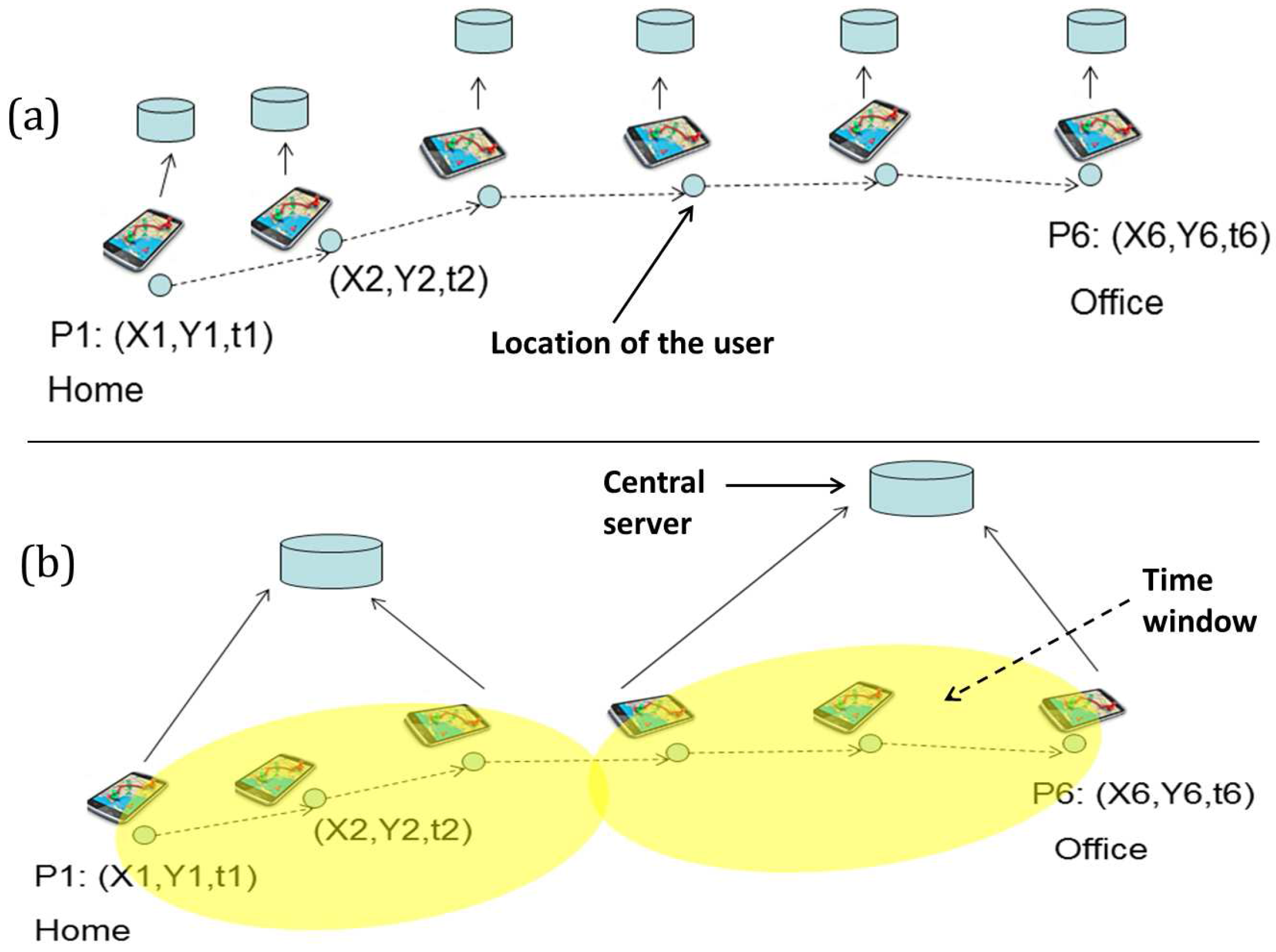
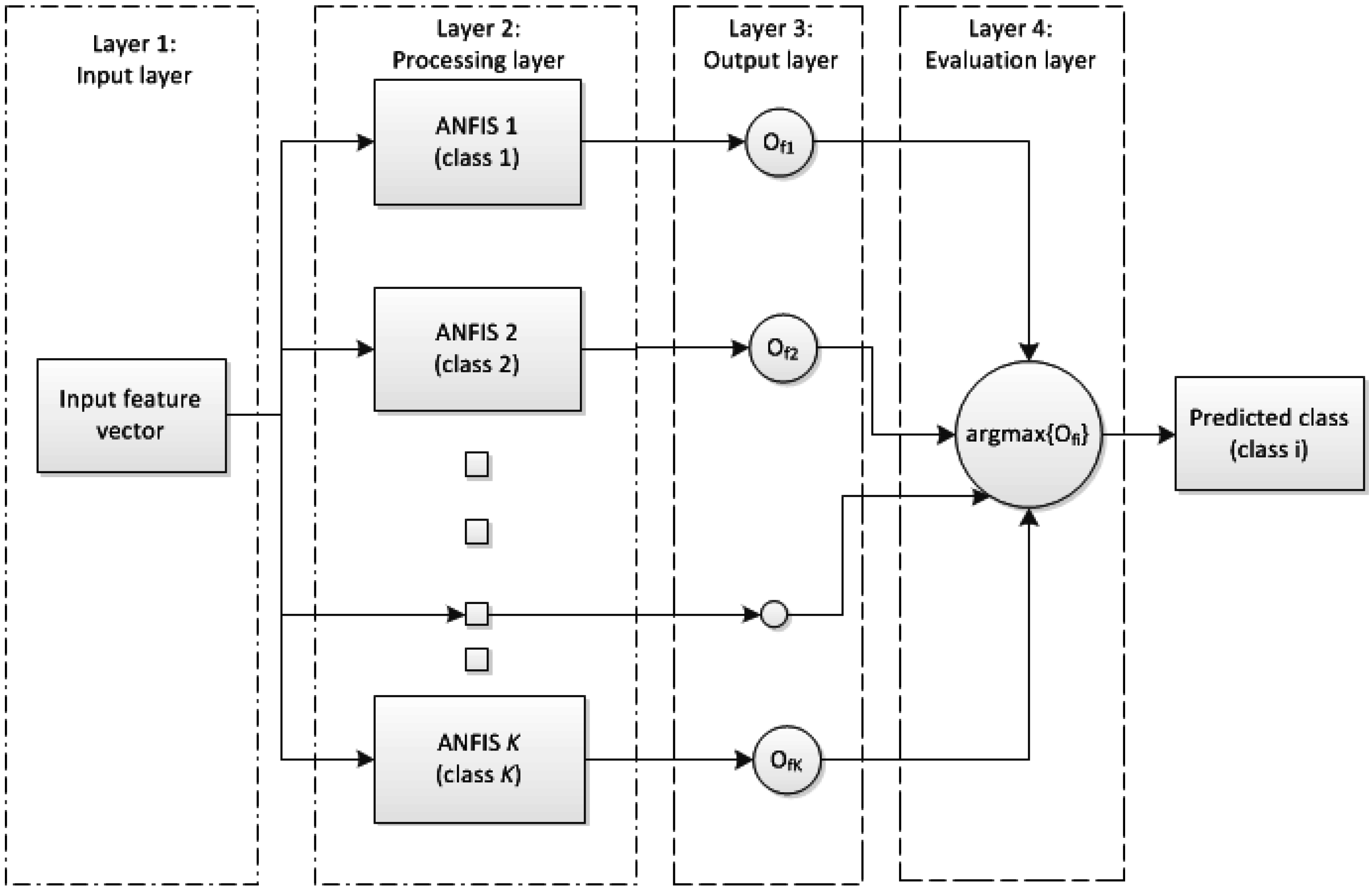
5.3. Experiment
Five sets of experimental setups are designed based on growing time window size starting from 30 s, 40 s, 50 s, 60 s and 120 s. In order to compare the performance of the proposed framework (MLANFIS) a number of machine learning models are also developed based on a multi-layered perceptron neural network (MLP), a radial basis function-based neural network (RBF), a decision tree (DT), K-nearest neighbor (KNN), and a naive Bayes (NB). The result shows at a 60-s and a 120-s time window that MLANFIS yields significant accuracy for detecting different transport modes in near-real time.
In order to evaluate, the same training and testing data have been used for the MLANFIS model and all of the machine learning models. Since MFIS does not require to be trained, hence an MFIS model evaluated using only a testing dataset, which has been used to test the predictive ability of MLANFIS and the machine learning models. A checking dataset is used while building the MLANFIS model in order to make sure the model does not get over-fitted.
Table 2 shows the number of features used as training, checking and testing datasets for different models.
Figure 7 shows how checking error and training error vary with the number of iterations (epochs). A total of 200 iterations are performed for each MLANFIS modal block building. A training error shows a gradual decrease in magnitude over 200 iterations. On the other hand, the checking error shows a gradual decrease in magnitude up to a certain epoch followed by a sudden increase in magnitude. That critical epoch point indicates the moment when the model starts getting over fitted. The membership function parameters are selected at that particular given epoch before the checking error gets increased.
In order to measure the accuracy of the models, precision accuracy, and recall accuracy are used, which are based on true positives (
), false positives (
), true negatives (
), and false negatives (
). The formula for precision and recall accuracy are provided as follows:
Table 3 and
Table 4 show recall and precision accuracy of seven different predictive models, including an MLANFIS and MFIS at 60-s time window. In terms of recall accuracy, MLANFIS outperforms the MFIS model and performs on par with the machine learning models for
walk, train, tram mode. However, MLANFIS works poor in terms of recall accuracy for
bus when compared to the machine learning models. On the other hand, the MFIS model performs better than MLANFIS and other machine learning models in terms of precision accuracy, particularly for
train (96.86%) and
tram (87.91%). MLANFIS works best and very close to an RBF model in terms of precision accuracy for
bus (92.19%). This suggests the rules generated for bus ANFIS block in MLANFIS model are properly tuned and thus giving rise to less Type I error for
bus when evaluated by a MLANFIS. However the rules in the
bus ANFIS block are not sufficient enough to capture all of the kinematic behaviour and signal quality during a bus ride, and hence, although MLANFIS generates less Type I error, but higher Type II error for
bus, that led to low recall accuracy for
bus mode, when compared with the machine learning models. Since different predictive models perform differently for different modes in terms of precision and recall, hence in order evaluate the overall performance of the models, an F1-score (
F) is considered, which combines the precision and recall together.
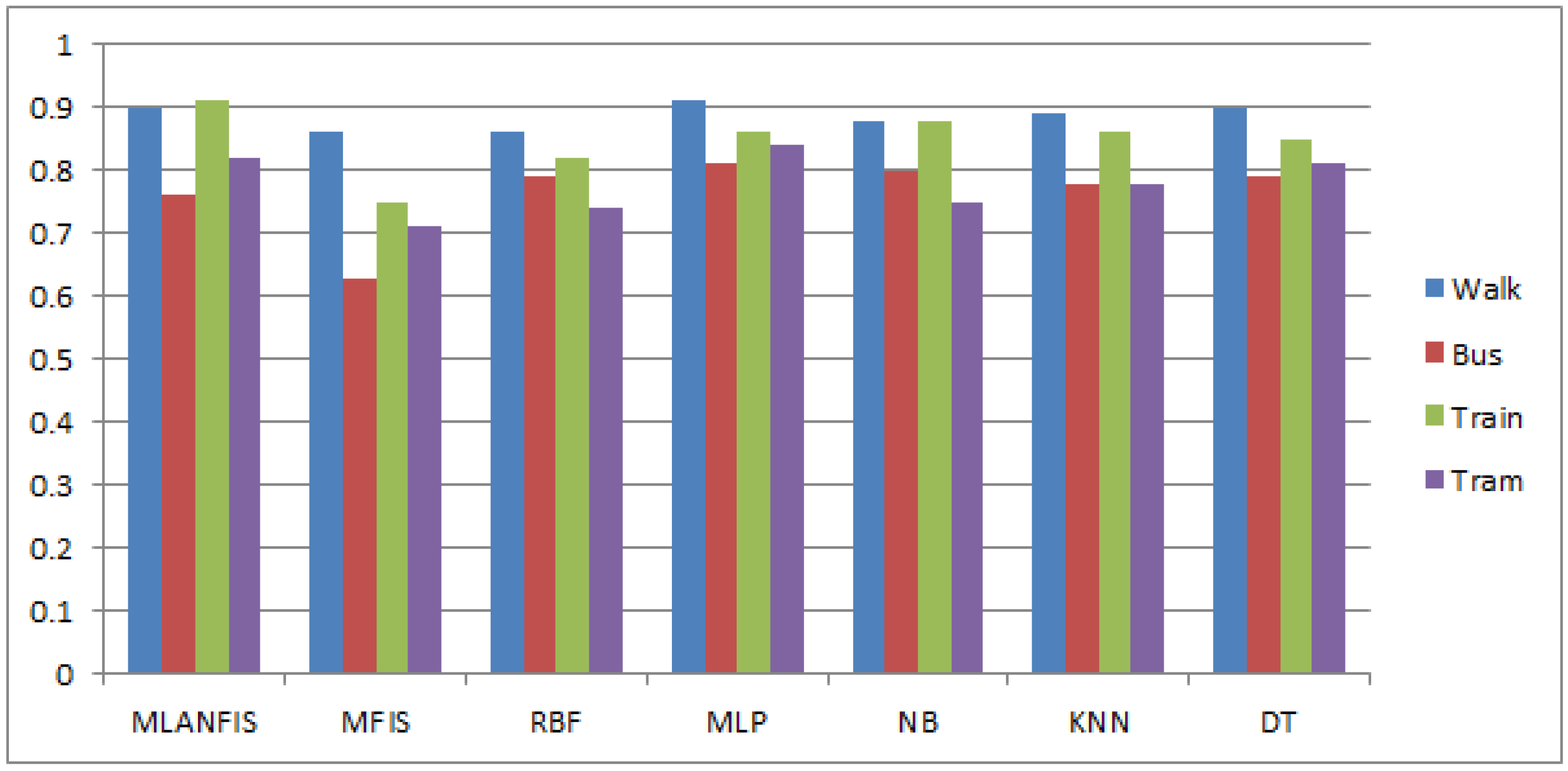
In terms of F1-score, MLANFIS performs similarly as MLP and DT for walk mode detection and outperforms a MFIS and all other machine learning models (
Figure 8). MLANFIS outperforms all other models for train mode detection. For train mode detection, MLANFIS yields 0.91 F1-score followed by 0.88 by MLP, which is the highest F1-score generated by any machine learning model. For tram mode, MLANFIS yields 0.82, which is very close to MLP, which yields 0.84, and a DT model, which generates a 0.81 F1-score. However, for bus mode detection, MLANFIS generates 0.76 F1-score, which is less than the machine learning models, but higher than the MFIS model (
Figure 8).
When evaluated within a 120-s time window, MLANFIS shows the same pattern in terms of recall and precision accuracy, as well as the F1-score. MLANFIS yields the highest recall accuracy for
walk mode, which is 92.87%, seconded by MFIS and DT, which are approximately 91.4%. For
train mode detection, RBF yields the highest recall accuracy, which is 99.10%, whereas an MLANFIS generates 94.31% accuracy. However, an MFIS generates 74.40% accuracy for
train mode detection showing worse performance than MLANFIS and the machine learning models. MFIS also performs poor compared to MLANFIS and the machine learning models in terms of recall accuracy for
bus and
tram mode detection. In terms of precision accuracy for
train, MFIS works best, generating 94.57% accuracy, followed by MLANFIS, which generates 89.23% accuracy, whereas the highest precision accuracy was generated by the machine learning model (NB in this case), which is 87.70% (
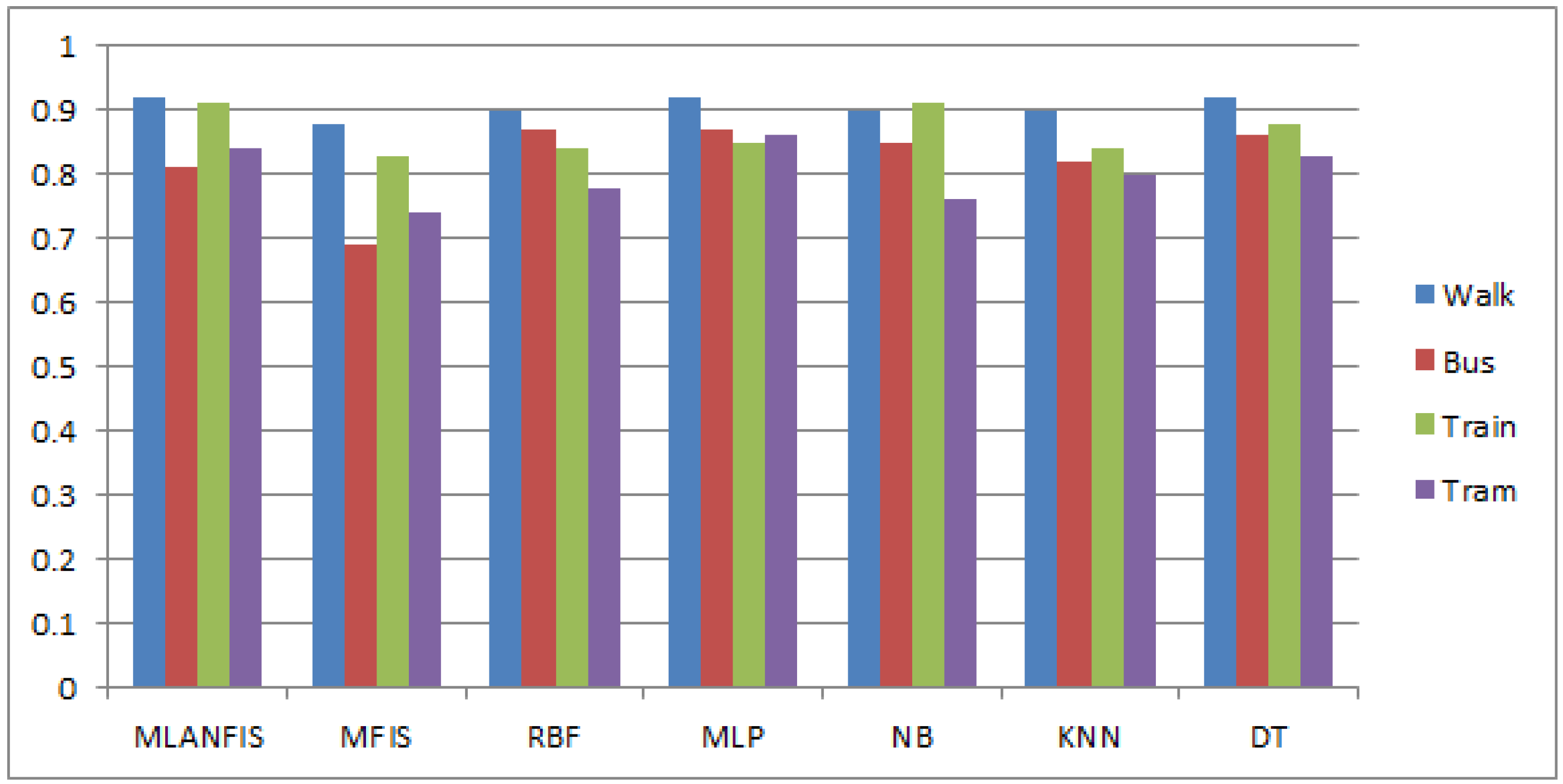
Table 5). However, in terms of F1-score, MLANFIS outperforms all of the predictive models for
train mode detection, whereas it works on par with the machine learning models (and outperforming a MFIS) for
walk mode, detection (
Figure 9). For
tram mode MLANFIS yields 0.84, which is very close to MLP (0.86) and DT (0.83) and outperforms MFIS (0.74), RBF (0.78), NB (0.76) and KNN (0.80).
When a comparison is made only between two different types of knowledge driven models (e.g., MLANFIS and MFIS), the results suggests MLANFIS performs better than MFIS (
Figure 8 and
Figure 9). For a 60-s time window MFIS generates high Type II error for
bus, train and
tram mode compared to a MLANFIS. Thus a MFIS shows a drop in recall accuracy for different public transport modes except
walk (
Table 3). However a MFIS model yields higher precision accuracy for
train and
tram mode (
Table 4) than that of the MLANFIS model, whereas MFIS performs worse compared to MLANFIS in terms of
bus and
walk mode detection. This can be justified as due to the particularities in rule base to capture the different kinematic behaviour in the MFIS model typically at a low speed condition, and
near to
moderate proximity to the tram network or train network, some portion of the actual tram or train trip is detected as
walk. However, most of the retrieved
tram and
train instances are correctly detected owing to high precision accuracy in
train and
tram mode detection. The MFIS rule also does not work well when there is an overlap between tram network and a bus network. A MLANFIS can typically work better than the MFIS model in such ambiguous situations and shows an overall better performance than that of the MFIS model (
Figure 8). Some of the fuzzy rules (out of 243) generated by the MLANFIS bus modal block are as follows:
R1: IF avgSpeed is low AND maxSpeed is low AND avgBusProx is low AND avgTrainProx is low AND avgTramProx is low, Then CF for Bus is out1mf1;
R2: IF avgSpeed is low AND maxSpeed is low AND avgBusProx is low AND avgTrainProx is low AND avgTramProx is moderate, THEN CF for Bus is out1mf2;
Where outimfjis the CF value for the consequent part for fuzzy rule.
Table 6 shows a confusion matrix for MLANFIS at a 60-s time window. The confusion matrix illustrates that most of the Type II error for non-walk modes are misclassified as
walk, and that happened during signal loss or typically at a low speed condition. This suggests a more rigorous rule formation by incorporating more sensor information, such as an accelerometer.
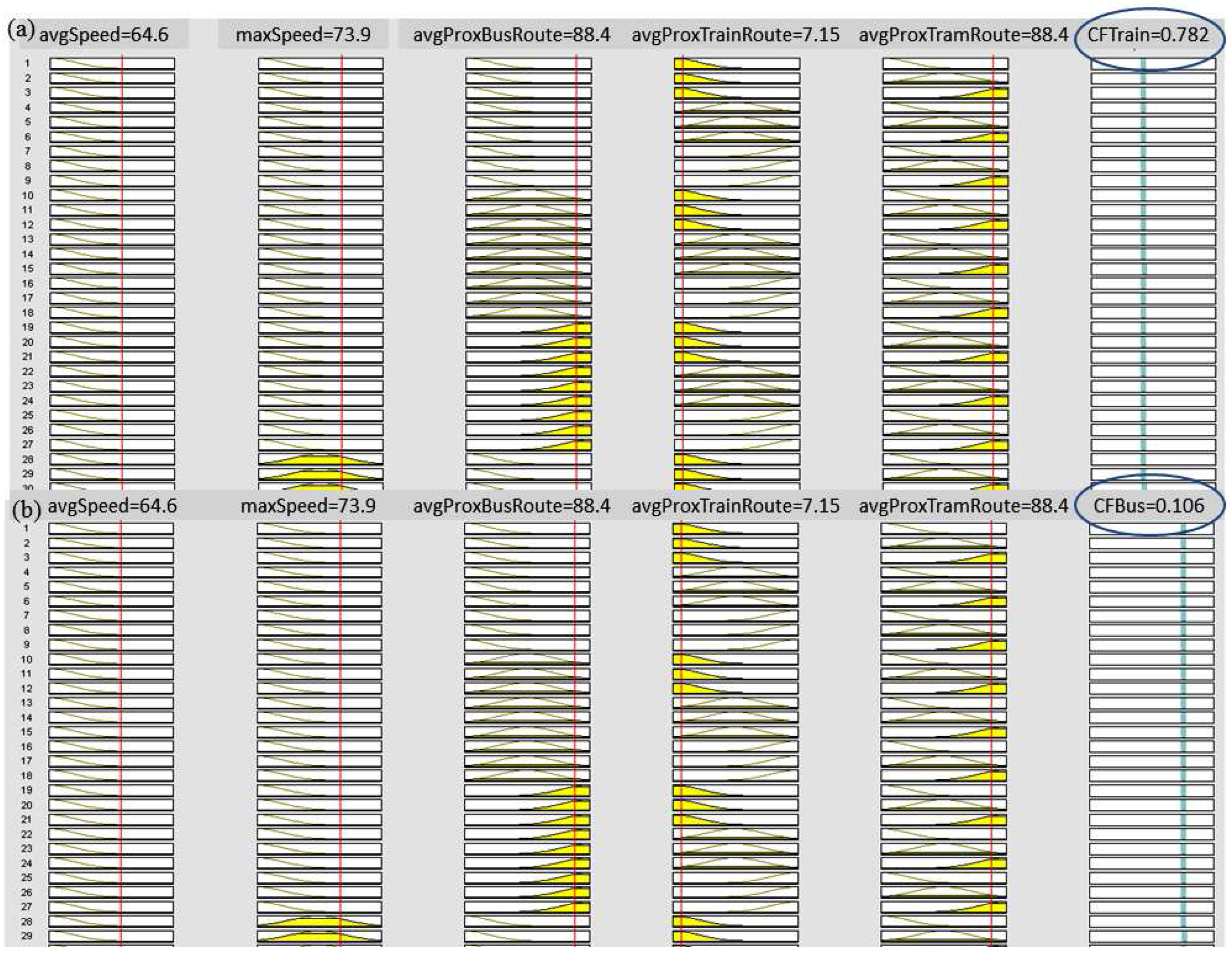
The MLANFIS framework developed in this paper can also produce alternate solutions with varied degrees of confidence. For a given feature vector where the average speed is 64.6 km/h, the maximum speed is 73.9 km/h, the average proximity to bus network is 88.4 m, the average proximity to train network is 7.15 m, and average proximity to the tram network is 88.4 m, MLANFIS produced a certainty factor for being a
train as 0.782 (
Figure 10a) and for being a
bus as 0.106 (
Figure 10b). Due to the space limitations,
Figure 10 shows only 29 rules out of 243 rules for each
train and
bus ANFIS modal block. This also explains the explanatory power and multiple output possibility from the proposed MLANFIS framework, which is missing in machine learning models.
Since choosing the appropriate membership function is important while developing a knowledge driven model, hence two different fuzzy membership functions such as a Trapezoidal function and a Gaussian function are tested while developing MLANFIS and MFIS models. However due to crisp geometrical nature of Trapezoidal function, there are cases when an input feature may fall outside a given range of fuzzy membership function and thus may bear a zero membership value owing to low performance in its predictive process. On the other hand since a Gaussian function is asymptotic in nature, it guarantees to generate a certain membership value
μ always in the range of [
m, 1] where
. A trapezoidal membership function is characterized by four characteristic points (upper left, upper right, lower left and lower right), whereas a Gaussian membership function is characterized by only two characteristic parameters such as the center (c) and the width (
σ).
Table 7 shows different parameters for MLANFIS which are selected automatically based on a hybrid learning involving a gradient descent and least square estimation whereas the parameters for MFIS chosen manually resulting higher ambiguity and low performance in near-real time scenario.
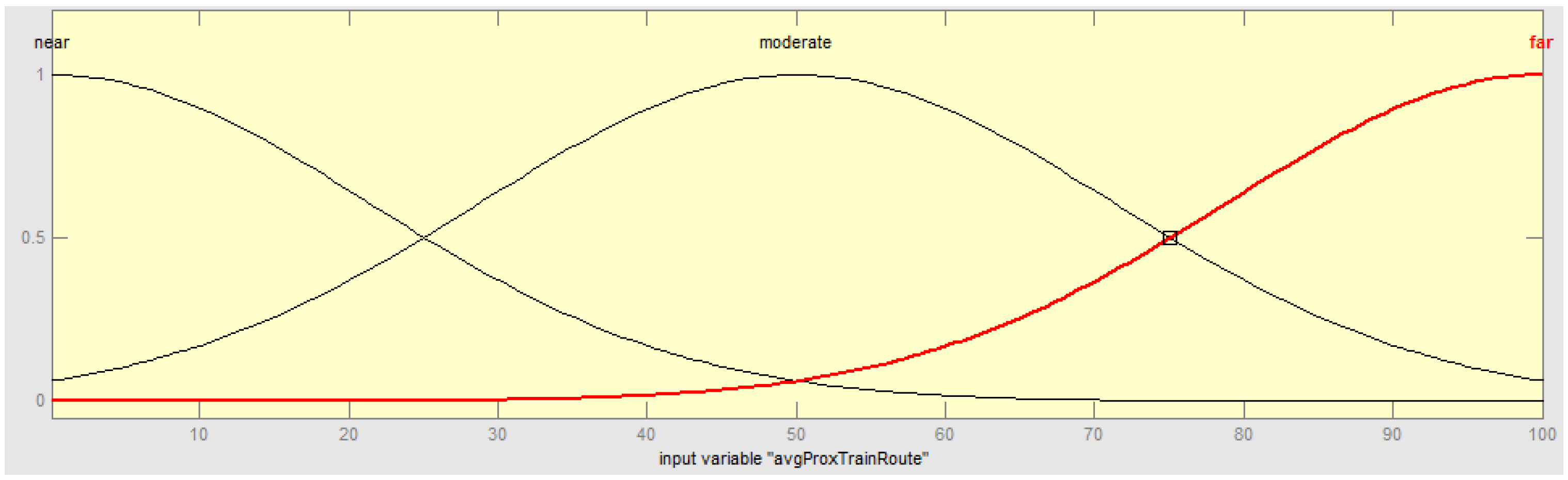
Figure 11 and
Figure 12 show two sets of three different Gaussian membership functions for average proximity to the train network in MLANFIS and MFIS respectively.
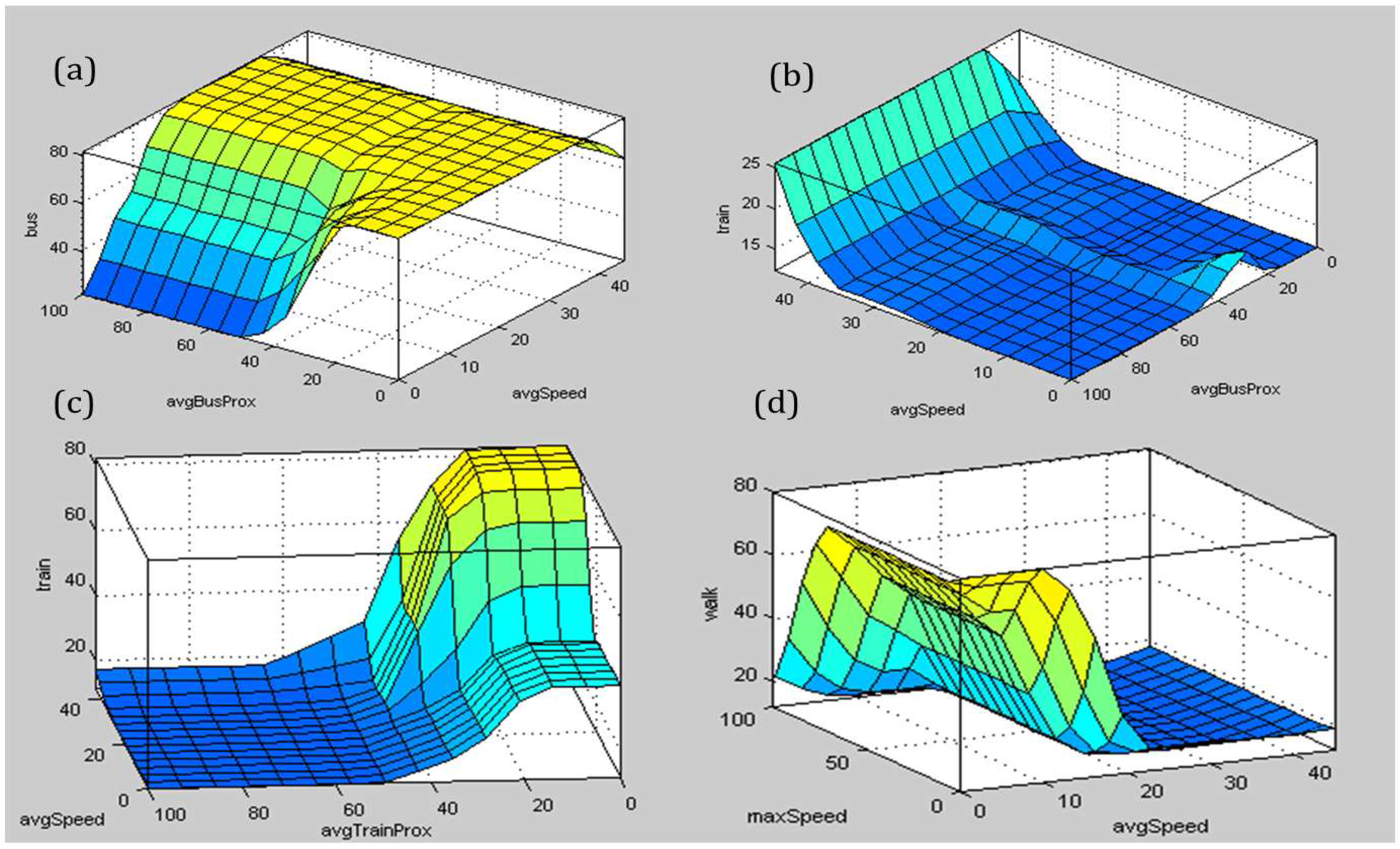
Figure 13 shows how the certainty factor changes with two different fuzzy variables. The figure shows a prominent contrast between change in CF for a
bus and
train when considering the same fuzzy variables such as average proximity to the bus network and average speed (
Figure 13a,b). Since walking can take place anywhere hence in this research nearness to the street network is not used as the streets in Melbourne show a significant overlap with the tram and bus network. Thus in order to detect the walking mainly a low speed behavior is considered (
Figure 13d).
For trapezoidal membership function, the recall accuracy at the 60-s time window for MLANFIS and MFIS drops significantly. For MLANFIS, for
walk, recall accuracy drops from 92.58% down to 89.31%, for
bus accuracy, drops from 65.21% down to 57.52%; for train, from 93.33% down to 88%; for tram accuracy; down from 88.94% down to 85.42%. For MFIS, the drop is more prominent. For MFIS, recall accuracy for
bus drops from 61.20% down to 51.67%; for
train, it drops from 61.77% down to 40.22%, and for
tram the accuracy drops from 60.06% down to 35.74%. Thus, the result suggests that a Gaussian function is better than a trapezoidal membership function for near-real time mode detection using fuzzy logic-based knowledge-driven models. The results also suggest a hybrid neuro-fuzzy (MLANFIS) works better than a purely knowledge-driven fuzzy logic-based MFIS model and performs on par with some of the state of the art machine learning models, and even sometimes outperforms them for many places (
Figure 8).