Abstract
Accurate forecasting of city-level large-scale traffic flow is crucial for efficient traffic management and effective transport planning. However, previously proposed traffic flow prediction methods model dynamic spatial correlations across entire traffic networks, leading to high computational complexity, elevated memory usage, and model overfitting. Therefore, a novel grid partition-based dynamic spatial–temporal graph convolutional network was developed in this study to capture correlations within a large-scale traffic network. It includes the following: a dynamic graph convolution module to divide the traffic network into grid regions and thereby effectively capture the local spatial dependencies inherent in large-scale traffic topologies, an attention-based dynamic graph convolutional network to capture the local spatial correlations within each region, a global spatial dependency aggregation module to model inter-regional correlation weights using sequence similarity methods and comprehensively reflect the overall state of the traffic network, and multi-scale gated convolutions to capture both long- and short-term temporal correlations across varying time ranges. The performance of the proposed model was compared with that of different baseline models using two large-scale real-world datasets; the proposed model significantly outperformed the baseline models, demonstrating its potential effectiveness in managing large-scale traffic networks.
1. Introduction
Rapidly developing social economies and urbanisation have explosively increased the number of motor vehicles using roads, leading to traffic congestion, traffic accidents, and other transportation issues [1]. Therefore, intelligent transportation systems (ITSs) have been developed by integrating sensing, communication, decision-making, and control capabilities utilising advanced technologies to effectively address conflicts between people, vehicles, and roads [2]. Accurate traffic flow forecasting based on historical and current spatial–temporal traffic flow data is critical for traffic control, guidance, and route planning within an ITS [3]. However, traffic flow forecasting remains challenging because of the complex dynamic spatial and temporal correlations and network topologies associated with traffic data. Therefore, the dynamic spatial–temporal relationships in traffic data must be accurately captured to ensure accurate real-time traffic flow forecasting [4].
Traffic flow data typically exhibit dynamic temporal correlations and periodic patterns such as daily and weekly variations [5]. Indeed, the traffic flow at the current time point is often closely related to the flow at a previous or several earlier time points and changes with peak and off-peak hours following regular patterns. Researchers have analysed the temporal patterns and dependencies between adjacent points of time-series traffic flow data using statistical methods [6,7]. However, statistical methods cannot capture the nonlinearity and uncertainty of traffic data. Deep learning methods, such as using the recurrent neural networks (RNNs) and their variants, like long short-term memory (LSTM) networks and gated recurrent units (GRUs), have also been applied to timeseries forecasting [8,9,10,11,12] because they can process and identify patterns in sequential historical data while effectively capturing temporal information within. However, RNNs are prone to vanishing and exploding gradients [13], which make them less effective in handling long sequences. In contrast to RNN-based models, which struggle with parallelism, temporal convolutional networks (TCNs) use causal and dilated convolutions to process long sequences in parallel [14].
Traffic flow data also exhibit spatial correlations as the traffic conditions in different roads or areas can influence each other [15]. Congestion in one road segment can affect the traffic flow in adjacent segments. As shown in Figure 1, the traffic flow at point 5275 is strongly correlated with that at the major downstream point 5274, whereas it is not correlated with that at the minor downstream points 4280 or 4248, indicating that the traffic flow to each branch dynamically changes over time. Graph convolutional networks (GCN) learn from complex network topologies by generating convolutional kernels based on static road networks and employing aggregation functions to capture the local spatial dependencies on neighbouring nodes [16]. Therefore, GCN have emerged as an effective solution for capturing the spatial dependencies in traffic networks and have been widely applied to improve the efficiency of traffic flow prediction [13,17,18].
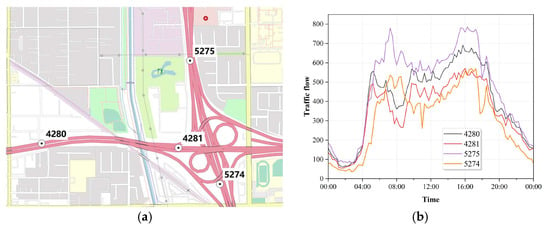
Figure 1.
(a) Adjacency of four sensor points along three branches at the intersection of two highways. (b) Traffic flow captured by these sensors throughout the day.
Given the strong spatial and temporal dynamics of traffic flow, the correlations between different locations in a traffic network, as well as their impacts on future conditions, change over time. Generally, research on dynamic correlations can be categorised into two approaches: calculating dynamic correlations during data preprocessing and computing correlations within the model. Based on the previous methods, such as using dynamic time warping (DTW) to construct the semantic time series similarity [19,20] and applying the Wasserstein distance to measure differences in probability distributions to quantify semantic similarity [18], these methods require less memory. However, the drawback is that the determined correlation is still static and cannot truly reflect the dynamic spatial correlation. Based on the latter methods, such as using attention mechanisms to focus on dynamic correlations at different time points [17,21], constructing dynamic graph generators [22], and developing adaptive adjacency graphs to mine latent spatial correlations in data [23,24,25], they typically provide higher prediction accuracy, thus making them more common. Current research focuses on the correlations of the entire graph, requiring fine-grained attention to all sensors in the traffic network, and shows good performance. The traffic graph of the current research is of a small scale. However, urban traffic networks often have a high degree of complexity and are of large scale. Therefore, when applied to large-scale traffic networks, this approach can face challenges, such as increased computational complexity, higher memory consumption, and degraded prediction accuracy, potentially leading to model failure [26].
Moreover, traffic flow models must consider not only short-range spatial interactions but also long-range spatial dependencies in which distant regions influence each other. This combination of global and local features enhances the capture of spatial–temporal variations across regions. Recent studies [27] have combined street-view visual features with road network topology to model intra-street spatial correlations, while also utilising check-in data to construct inter-street interaction relationships.
To address these issues, a grid partition-based dynamic spatial–temporal graph convolutional network (GPDSTGCN) is proposed in this study that employs the attention mechanism, GCN, and TCN methods to capture both global and local dynamic spatial–temporal correlations in large-scale traffic networks. A grid-based graph partitioning approach is introduced to divide the traffic graph into multiple local subgraph regions. Within each region, a fine-grained attention method is applied to extract the local spatial correlations for each node while avoiding computation on irrelevant nodes, and a coarse-grained attention method is employed to capture the global spatial correlations for nodes outside the considered region. The proposed model was demonstrated in this study using data from the LargeST dataset, its functionality was explored through ablation experiments, and its superior performance was confirmed through comparison with that of previously proposed models.
2. Basic Definitions
2.1. Traffic Network Modelling
In this study, the traffic graph network is represented as , where denotes the set of road sensors, represents a set of connected edges between sensors. The adjacency matrix is defined as a binarised matrix (where is the number of sensors) representing the undirected adjacency relationships in the traffic graph. In this study, the geographical feature data of the sensors were utilised to partition the traffic graph into regions based on a latitude and longitude grid.
2.2. Traffic Flow Forecasting
The graph signal of sensor at time is represented as , where is the feature dimension. This signal comprises the traffic flow at sensor , the index of time within one day (i.e., out of 1440 min) (), and the index of time within one week (i.e., out of 7 d) (). The traffic from the entire network at time is represented as , where the traffic features are denoted as , the daily index is denoted as and the weekly index is denoted as . The predicted traffic condition in the entire network at a future time is represented as , and traffic flow is predicted for the next time steps as based on the historical multidimensional traffic feature data (where T is the number of historical time steps), , and using network model as follows:
3. Proposed Forecasting Methodology
The proposed GPDSTGCN model, shown in Figure 2, comprises three primary components: a data embedding module, spatial–temporal feature module, and a traffic flow prediction module. First, the feature, daily, and weekly traffic flow data are introduced into the data embedding module. Next, stacked layers in the spatial–temporal feature module are used to capture the dynamic spatial and temporal features of the embedded traffic flow data. Finally, the prediction module aggregates the spatial–temporal features to produce the final multistep traffic flow forecast.
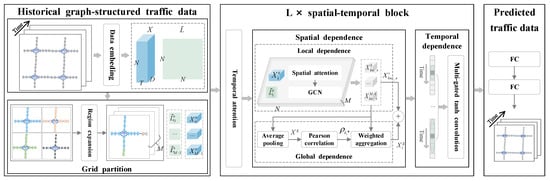
Figure 2.
Overall framework of the proposed GPDSTGCN model: N is the number of nodes in the traffic graph, T is the length of historical time steps, D is the dimension of the embedded data, and M is the number of regions in the partitioned graph.
3.1. Subsection Data Embedding Module
The data embedding module represents the traffic flow using high-dimension features to facilitate the capture of underlying patterns, thereby fusing the periodic features in the data. This module includes traffic flow data feature and periodicity embeddings.
First, the traffic flow data features are embedded by transforming them into high-dimension features. These data are converted from to , where is the embedding dimension. Furthermore, traffic flow exhibits regular changes over time with flow peaks and troughs influenced by daily commuting activity in the mornings and evenings on weekdays and by weekend travel with later peaks, as shown in Figure 3. Therefore, data embedding methods are applied to model the periodicity of traffic flow by dividing a day into 1440 min and a week into 7 d to construct periodic indices. Next, D-dimensional data embedding is performed on these indices to transform the daily index from to and the weekly index from to . Finally, the data feature and periodicity embeddings are aggregated to obtain the final embedding result as follows:
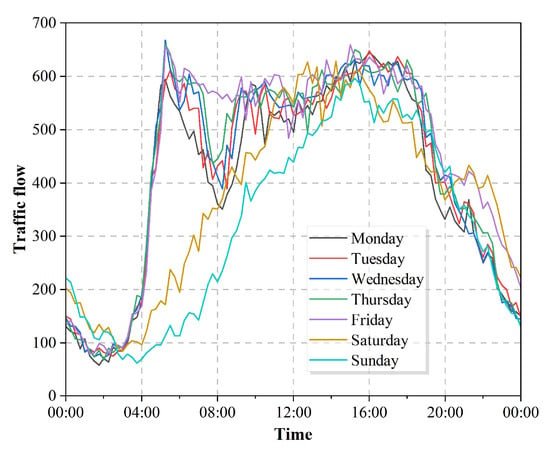
Figure 3.
One week of traffic flow in LargeST.
3.2. Spatial–Temporal Feature Module
A dynamic spatial–temporal feature module is proposed to capture both the global and local dynamic features of traffic flow data utilising the attention mechanism, grid partitioning, local GCN, serial correlation, and gated convolution methods. First, dynamic spatial–temporal correlations are calculated using an attention mechanism. Next, spatial dependencies are extracted by partitioning the traffic graph into regions based on a latitude and longitude grid, then employing a fine-grained dynamic GCN to capture the local spatial dependencies within. These local dependencies are aggregated to generate global dependencies, which reflect coarse-grained spatial correlations between regions through weighting. Subsequently, a multiscale gated temporal convolution layer is applied to capture both short- and long-term temporal correlations. Finally, residual learning units and regularisation techniques are employed to combine multiple spatial–temporal feature modules capturing the underlying dynamic features.
3.2.1. Dynamic Spatial–Temporal Attention Layer
Static adjacency relationships cannot capture the dynamic effects of traffic flow propagation between sensors. Therefore, a spatial–temporal attention layer is employed to capture the dynamic spatial–temporal correlations between sensors by separately applying an attention mechanism to the temporal and spatial dimensions of the historical data.
In the spatial dimension, the correlation strength between nodes changes dynamically over time; therefore, static adjacency relationships are insufficient. An attention mechanism [17,28,29] is applied to aggregate features at different time points by calculating the dynamic spatial correlation strength between the source node and target node as follows:
which is converted into attention weights between nodes i and j using the softmax method as follows:
where represents the traffic flow data after embedding; , , , , and are learnable parameters; and is the sigmoid activation function.
In the temporal dimension, the influences of travel demand and traffic conditions dynamically vary the strength of the correlation between different periods. Therefore, an attention mechanism is applied to capture the dynamic temporal correlation strength between the source time point and target time point as
which is converted into attention weights for each period as follows:
where represents the transposed embedded feature data and , , , , and are learnable parameters.
3.2.2. Spatial Dependency Layer
The spatial dependency layer captures the spatial dependencies at different locations within the transportation network. As traffic data adhere to Tobler’s First Law of Geography, which states that ‘everything is related to everything else, but near things are more related to each other’, the spatial correlations of these data cannot be sufficiently constructed using only adjacent regions; traffic conditions in more distant regions must be considered as well. Existing methods for doing so employ multigraph structures to capture local and global spatial dependencies by first using a static adjacency graph to obtain the former, then using methods such as DTW, Wasserstein distance, adaptive adjacency graph, or graph generation module to construct semantic adjacency relationships that reflect the latter.
However, current methods for constructing spatial dependencies perform fine-grained calculations across the entire traffic graph which is effective for small-scale graphs but leads to substantial complexity and memory requirements for large-scale traffic networks. This makes capturing the dynamic spatial correlations in large-scale traffic networks quite challenging. Therefore, a grid partitioning-based graph convolution module is proposed. Following grid partitioning, an attention mechanism-based GCN is applied to the nodes within adjacent regions to focus on fine-grained local spatial dependencies. Next, coarse-grained focus is applied to nodes farther away to capture the global spatial dependencies by aggregating the node features within each region into global dependencies, then weighting them by calculating the correlations between regions. This approach allows the model to capture both local and global dependencies while limiting memory consumption, thereby enabling its application to large-scale traffic networks.
Thus, the spatial dependency extraction layer comprises three components: grid partitioning, identification of local spatial dependencies, and aggregation of global spatial dependencies.
- 1.
- Grid Partitioning
Considering the First Law of Geography, a target sensor in a large-scale traffic network will have significantly fewer sensors with adjacency relationships than without. Figure 4 shows the spatial distribution of sensors in the LargeST GLA dataset [26], in which the red points represent the target sensor, blue points represent sensors with strong correlations to the target, and green points represent sensors with weak or no correlations to the target. Using a dynamic GCN based on this entire traffic network to calculate the spatial correlation for each sensor will involve many sensors that are unrelated to the considered sensor, leading to unnecessary computation and significant memory usage. Therefore, the grid partitioning module is used to partition the entire traffic graph into regions, preserving the local adjacency relationships between sensors while reducing the number of nodes in the graph convolution network, enhancing the ability of the model to handle large-scale traffic networks. This module divides the minimum bounding rectangle of geographical feature into regular regions. Based on their spatial coordinates, road segments are assigned to the corresponding grids. Within each subgraph, the local traffic network is constructed by extracting the connectivity information among road segments from the global adjacency topology.
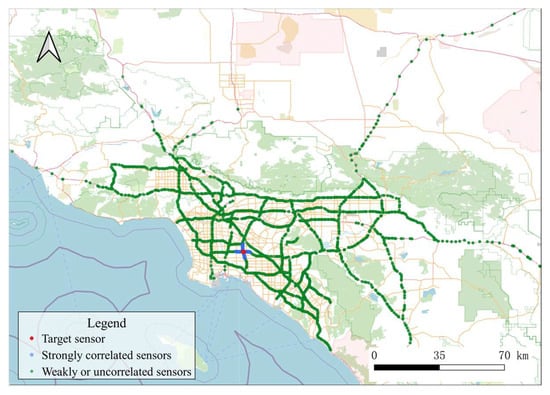
Figure 4.
GLA dataset sensor distribution diagram.
Each grid region contains sensors that form the traffic network graph for that region. The number of sensors in the -th region, , is considerably smaller than , where . As dynamic spatial correlation calculations are performed separately on each subgraph , the parameter count is significantly reduced from to , where . Thus, the computational complexity and memory usage of the proposed model is reduced by excluding sensors unrelated to the current region. Figure 5a shows the grid partitioning results for the LargeST dataset.
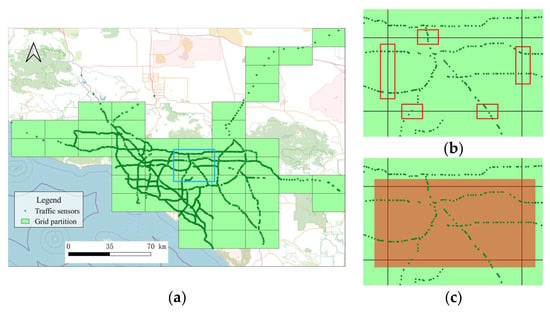
Figure 5.
(a) Grid partitioning applied to the GLA dataset. (b) Magnified view of the blue box in (a), with the red boxes indicating adjacent nodes along the partition edges. (c) The region in (b) expanded by 1/10.
Note that latitude- and longitude-based grid partitioning can result in adjacent sensors being placed in different regions, an issue that becomes more pronounced near region boundaries. For example, in Figure 5b, the sensors within the red boxes are upstream and downstream of the region border, placing them in separate regions. To address this issue, each grid region is extended by a certain ratio to form a larger region—the red region in Figure 5c is expanded by 1/10 of the original region size—effectively mitigating incomplete adjacency relationships at the partition edges. By constructing adjacency subgraphs using the sensors within each expanded region, the number of sensors in the -th expanded region is defined as , where . This improves the accuracy with which spatial dependencies are captured.
To determine the optimal grid partitioning strategy, this study systematically evaluates the impact of different partition counts and region expansion ratios on model performance. Partition counts ranging from 7 × 7 to 21 × 21 are examined. As shown in Figure 6a,b, the experimental results indicate that as the partitioning granularity increases, the number of nodes within each region tends to decrease, significantly reducing the model’s memory overhead, computational load, and parameter size. However, training time exhibits a non-monotonic trend—first decreasing and then increasing—owing to the trade-off between region traversal frequency and subgraph scale.
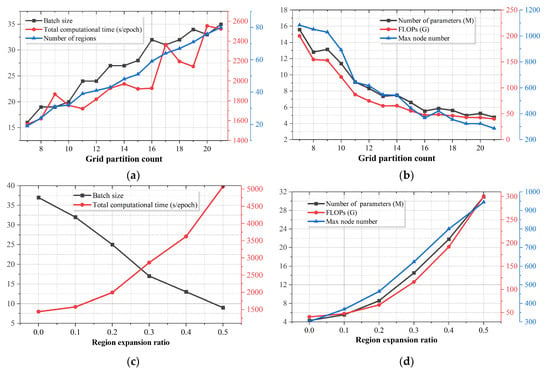
Figure 6.
Sensitivity analysis of partition parameters. (a,b) Analysis of the impact of partition parameter settings; (c,d) Analysis of the impact of partition expansion ratio. Subfigures (a,c) present batch size, total computation time, and number of partitions; (b,d) show the number of parameters, FLOPs, and the maximum number of nodes within a partition.
Multiple tests are conducted for the region expansion ratio using values ranging from 0.0 to 0.5. As illustrated in Figure 6c,d, the results indicate that increasing the expansion ratio effectively enhances boundary information fusion and perceptual range through the region expansion mechanism. After comprehensively considering computational efficiency, memory usage, and prediction accuracy, the final grid partitioning and expansion ratio are selected.
The current regular grid partitioning method exhibits certain limitations when applied to traffic networks with highly uneven sensor distributions. In some regions, sensor nodes may be overly dense, while in others, they may be sparse. This distribution imbalance affects the uniformity of regional feature representation.
- 2.
- Identification of Local Spatial Dependencies
The GCN can effectively leverage the topological structure of the network to aggregate features from the considered node as well as neighbouring nodes. When multiple layers are stacked in a GCN, the network can extract multi-level spatial dependencies. The GCN uses the Laplacian matrix to represent the adjacency relationship graph, transforming graph signals and convolution kernels into the spectral domain using Fourier transforms to capture the spatial correlations between nodes as follows:
where represents the convolution kernel in the Fourier-transformed space, in which is the basis for the Fourier transform constructed using .
However, as constructing requires performing eigendecomposition on (a computationally complex process), -th order Chebyshev polynomials are applied to approximate the convolution kernel and thereby capture the spatial dependency of -th order neighbours (ChebNet) [30]. The dynamic nature of spatial correlations is considered by incorporating a dynamic spatial–temporal attention layer to enhance the adjacency relationship dynamics as follows:
where represents the learnable parameters for the -th order feature transformation, in which is the dimension of the embedded data and is the dimension of the GCN output; denotes the -th order Chebyshev polynomial, in which is the scaled , is the largest eigenvalue of , and is the identity matrix. Figure A1 illustrates a numerical example of the graph convolutional network, demonstrating the feature update process influenced by the adjacency matrix.
A GCN is constructed in each region to capture the fine-grained local spatial dependencies among the sensors within. Following regional partitioning, a region expansion mechanism is designed to prevent information fragmentation caused by boundary divisions. Specifically, when constructing the adjacency matrix for each region, nodes from neighbouring boundary regions are included in addition to those within the region itself, thereby enhancing spatial correlations across regions. As shown in the adjacency subgraph A of Figure 7, the original nodes in Region A are expanded to include adjacent nodes (e.g., Nodes 6 and 7), enabling cross-region information flow during graph convolution computation. To support efficient graph convolution computation and feature mapping, we employ three multi-dimensional lists to record the index mappings within the graph structure: , , and . Specifically, represents the node indices in the original subgraph, records all node indices contained within the expanded region, and indicates the relative position indices of the nodes from within . Considering subgraph D in Figure 7 as an example, the corresponding indices are: = [9, 11, 12], = [7, 8, 9, 11, 12], and = [3, 4, 5]. During the model’s forward pass, we first iterate over to perform graph convolution operations within the expanded region, extracting spatial features. Subsequently, we use to retrieve feature representations corresponding to the original region’s nodes and map them back to the positions specified by , completing the spatial feature update for the original subgraph. This process enables the model to effectively capture spatial dependencies across regional boundaries during both training and inference phases. First, the dynamic correlation matrix between the sensors within each region are calculated, then the GCN is applied to obtain the local dynamic spatial dependencies. The local GCN in the -th region is given by
and the data from each region are concatenated (using the method) to obtain the local spatial dependencies for all sensors, represented by , as follows:
where represents the learnable parameters of the Chebyshev polynomial convolution kernel for the -th region, is the dynamic spatial attention for the -th region, is the scaled for the -th region, and denotes the traffic features for the -th region.
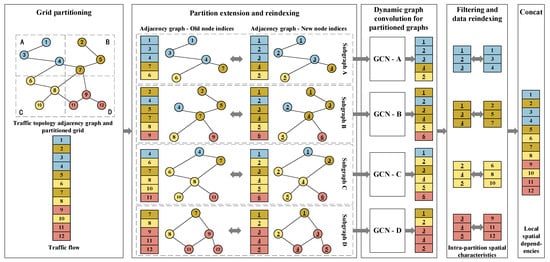
Figure 7.
Schematic diagram of the local spatial dependency module’s computational workflow. Numeric labels represent node indices, where i represents a node’s new index within the subgraph. The different colors represent the original partitions to which each node belongs prior to subgraph extraction. This coloring highlights how nodes from multiple partitions contribute to the local computation.
When extending the local region based on the original grid partitioning, the local GCN computation for the -th region is updated as follows:
and the local spatial dependency for all sensors is subsequently computed as using
where the method extracts the local spatial dependencies from the extended region corresponding to the dependencies before extension, represents the traffic features for the -th region after extension, denotes the scaled for the -th region after extension, and is the dynamic spatial attention of the -th region after extension.
- 3.
- Aggregation of Global Spatial Dependencies
The grid partitioning-based graph convolution method focuses only on the traffic conditions within a specific region and cannot account for global traffic conditions. Performing fine-grained global graph convolution on a large-scale graph is also challenging. Therefore, a coarse-grained approach is used to capture global spatial dependencies. Figure 8 illustrates the architecture and information aggregation process of the global-local feature fusion module.
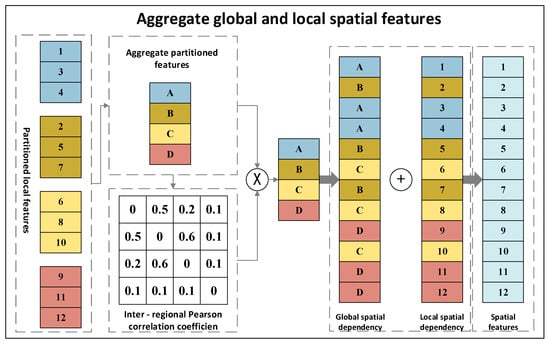
Figure 8.
Structural diagram of the global-local feature fusion module. Numeric labels indicate node indices. Distinct colours represent different original partitions. Lettered regions denote the aggregated features of each partition after region-level fusion, distinguishing them from the individual node representations.
First, average pooling is applied to aggregate the features within each region, representing the global dependencies for that region. The global dependencies for the -th region are denoted by , and the global dependencies for all regions are denoted by . Next, the correlations between the global dependencies of different regions are calculated in terms of Pearson’s correlation coefficient. The correlation between regions and is denoted by , which is calculated as follows:
Finally, the global spatial dependencies are weighted based on the regional correlations. Defining the global-local spatial dependencies of the sensors in region as , the aggregation of global dependencies can be accomplished by
and the global-local spatial dependencies for all sensors can be obtained by concatenating the dependencies from all regions, represented by , as follows:
where represents the learnable parameters used to enhance the ability of the model to capture dynamic global correlations, denotes the number of regions, and represents element-wise multiplication. These elements are used in the model to effectively aggregate and weight the global spatial dependencies.
3.2.3. Temporal Dependency Layer
The TCN is used to capture the potential temporal correlations in traffic flow data because it offers better parallel processing capabilities than the RNN. The TCN updates the features at the current time step by focusing on those of adjacent time steps. The ability of the model to learn dynamic temporal changes is enhanced by providing gated tanh units (GTUs) on top of the TCN to control the flow of signals and better capture long-term dependencies in the time series.
A one-dimensional (1D) convolution is applied to the output data from the spatial dependency layer along the time dimension to obtain the temporal dependency , as follows:
where represents the learnable parameters for the 1D convolution.
Subsequently, GTU activation produces the temporal dependency output, , calculated according to
where the convolution kernel is , in which controls the temporal neighbourhood of each time step, and are the results of slicing along the time dimension.
Temporal information with different receptive fields is captured by stacking using convolutional kernels of various sizes, forming a multi-gated tanh convolution [18] with the architecture shown in Figure 9. Figure 10 illustrates the architecture of the multi-scale gated temporal convolution module. A total of different kernel sizes are set and the GTU output for a kernel size of is denoted as . The temporal dependencies across multiple scales are aggregated using the Cat method, then passed through the rectified linear unit () activation function to obtain the multi-scale temporal dependencies, denoted as , as follows:
where denotes the fully connected layer, and using different convolutional kernels allows to incorporate features from various time ranges, enhancing the ability of the model to learn and predict short-, medium-, and long-term temporal sequences.
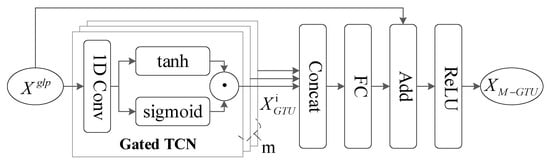
Figure 9.
Architecture of multi-gated tanh convolution module.
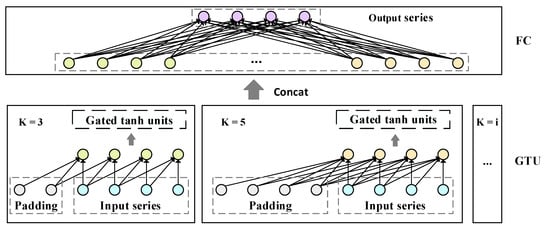
Figure 10.
Multi-scale gated temporal convolution module. Blue circles indicate the input sequence; gray circles represent padding time steps in the TCN; green and yellow circles show outputs from different convolutional kernels within the TCN; and purple circles represent the final aggregated output after multi-level GTU.
3.3. Prediction Module
After the spatial–temporal feature module has extracted the dynamic spatial–temporal dependencies, the prediction module aggregates these dependencies through two fully connected layers to forecast the future traffic flow.
4. Experimental Means and Methods
4.1. Datasets
The performance of the proposed GPDSTGCN traffic flow prediction model was evaluated using the publicly available LargeST dataset [26], a large-scale benchmark dataset for traffic flow forecasting that contains traffic flow data collected every 5 min from 8600 sensors across California over a five-year period from 2017 to 2021. The number of sensors included in the four sub-datasets within LargeST increases from SD (716) to GBA (2352), GLA (3834), and CA (8600). In this study, the larger GLA and CA datasets were selected to validate the ability of the proposed model to handle large-scale traffic networks. The 5 min interval traffic flow data from 2019 was aggregated into 15 min intervals, resulting in 35,040 time steps. These data exhibited seasonal variations over the full year. Therefore, the dynamic spatial–temporal correlations across different seasons were captured by first concatenating the dataset into sequential samples, randomly shuffling the sample order, then splitting the data into training, validation, and test sets in a 6:6:2 ratio, thereby ensuring that each set included data from all seasons.
4.2. Evaluated Models
A comparative study was conducted to validate the effectiveness of the proposed GPDSTGCN traffic flow prediction model. Many existing prediction models have complex structures designed to capture the intricate dynamic correlations in traffic flows. However, these models are often challenged by large-scale traffic networks owing to their high computational complexity and memory usage, which limit their ability to predict such graphs. Therefore, the following most efficient models running on an RTX 4090 graphics processing unit (GPU) were also applied using the GLA and CA datasets for comparison:
- STGCN [14], which combines graph convolution with gated causal convolution to extract spatial–temporal features.
- DCRNN [31], which uses diffusion graph convolution to improve the GRU module, providing strong interpretability for dynamic spatial dependency and employs an encoder–decoder architecture to capture the spatial–temporal correlations in timeseries traffic data.
- GWNET [25], which utilises an adaptive adjacency matrix to represent adjacency relationships, combines a GCN with diffusion convolution to aggregate the transformed feature information from different neighbourhood orders, and captures temporal dependencies using gated dilated causal convolution.
- ASTGCN [17], which employs attention mechanisms to capture dynamic temporal and spatial correlations and combines the GCN and TCN to effectively capture dynamic spatial–temporal dependencies.
- AGCRN [23], which explores the parameters of spatial graph convolution using an adaptive adjacency matrix, learns a parameter space for each node, and integrates adaptive graph convolution into a GRU network to capture spatial–temporal dependencies.
- STGODE [19], which constructs a semantic similarity matrix using DTW and combines it with an original adjacency matrix, employs a continuous graph neural network to address GCN over-smoothing and capture dynamic spatial relationships, and uses a TCN to capture temporal dependencies.
- STWave [32], which employs a novel disentangled fusion framework that decomposes complex traffic data into stable trends and fluctuating events and introduces a new query sampling strategy and graph wavelet-based positional encoding to capture dynamic spatial dependencies effectively.
- HGCN [33] applies spectral clustering to aggregate node-level information at the region level and uses spatial gated convolution to capture hierarchical features. A region-to-node information transfer module facilitates cross-level fusion, and both node- and region-level features are jointly used for traffic prediction.
- HSTGODE [34], which builds on a hierarchical modelling framework similar to HGCN, introduces a spatiotemporal ODE module for continuous hierarchical representation learning. It also adopts attention mechanisms and skip connections to facilitate iterative and effective cross-level feature fusion.
Furthermore, the effectiveness of each component of the proposed GPDSTGCN model was evaluated by conducting the following ablation experiments using the GLA dataset:
- RemEmb, in which the day and week data embedding was removed.
- RemExt, in which the region expansion module was removed, leading to incomplete adjacency relationships for the sensors at the partition edges.
- RemPart, in which the partitioning was removed and a dynamic GCN was applied to the entire traffic graph.
- RemGlo, in which the global dependency module was removed, leaving only the local spatial dependencies.
- GPMK-M, in which the grid partitioning method was replaced with K-means clustering based on the spatial location.
- RemMGTU, in which the multi-scale gated temporal convolution module was replaced with a single-layer TCN.
4.3. Experiment Settings
The experiments used historical data of 12 historical timesteps to predict the traffic flow for the next 12 timesteps. These experiments were conducted on a CentOS server equipped with an NVIDIA GeForce RTX 4090 GPU and 128 GB of memory.
Based on a comparison and analysis of preliminary experimental results, the following hyperparameters were set for the model:
The data embedding and feature output dimensions for the time and space modules were set to 64. The -th order Chebyshev polynomial, which specifies the number of neighbouring levels to be considered, was set to 2. To determine the optimal grid partition count and region expansion ratio, this study employed systematic parameter testing and comparative analysis. In the parameter sensitivity analysis, prediction accuracy metrics were newly incorporated in addition to previously examined effects of partition count and expansion ratio on computational efficiency and memory consumption. Experimental results demonstrate that for both GLA and CA datasets, the model achieves an optimal balance among these three critical metrics—prediction accuracy, computational efficiency, and memory consumption—when partition counts are set to 16 × 16 and 36 × 36, respectively, with a unified expansion ratio of 0.1. The number of spatial–temporal feature layers was set to two. The expansion ratio for each region was set to 0.1. As data partitioning is primarily influenced by the distribution of the road network and number of sensors, the CA dataset was divided into 36 partitions along both the x- and y-axes and the GLA dataset into 16 partitions along both axes. Learning rates of 0.001 and 0.002 were set for the CA and GLA datasets, respectively, to account for their different batch sizes. The maximum number of training epochs was set to 100.
The performance of each baseline and ablation study model was evaluated using the mean absolute error (MAE), root mean square error (RMSE), and mean absolute percentage error (MAPE) between the predicted and measured traffic flow conditions.
5. Experiment Results and Discussion
5.1. Predictive Accuracy
Table 1 compares the multistep traffic flow predicted by each evaluated model using the GLA and CA datasets. Note that AGCRN and ASTGCN failed to perform effectively on the CA dataset owing to the high computational complexity of these models and the large-scale traffic graph of this dataset.

Table 1.
Performance of different models on the GLA and CA datasets.
The use of causal convolutions allows STGCN to exhibit suitable performance in medium-to long-term forecasting, but its effectiveness in this study was limited by its use of static adjacency matrices that struggle to capture dynamic adjacency relationships. Though ASTGCN enhances ChebNet with spatial–temporal attention mechanisms, the accompanying increase in model parameters made model convergence difficult, resulting in poorer performance. Note that DCRNN employs bidirectional random walks to capture spatial dependency but fails to account for dynamic spatial adjacency, which led to sub-optimal prediction results. Both GWNET and AGCRN utilise adaptive adjacency graphs instead of predefined adjacency matrices, allowing them to adaptively discover hidden spatial dependencies. Though GWNET uses diffusion graph convolutions, it suffered from over-smoothing of the adaptive adjacency relationships, resulting in poor performance. By replacing the multilayer perceptron element of the GRU with graph convolutions and performing multiple adaptive adjacency computations per time step, AGCRN provides a strong ability to capture spatial–temporal dependencies. As a result, it performed well on the GLA dataset at the cost of significantly increased computational complexity and memory usage, which led to its failure on the larger CA dataset. Finally, STGODE builds on static adjacency relationships and uses DTW to construct semantic correlations across spaces, and provided suitable prediction performance accordingly. Both HGCN and HSTGODE construct region-level hierarchical structures using spectral clustering; however, their clustering methods exhibit varying adaptability across different traffic networks, which affects prediction performance. Compared with HGCN, both our method and HSTGODE incorporate attention mechanisms to enhance the modelling of dynamic dependencies among nodes, thereby improving prediction accuracy at the cost of additional computational overhead.
The proposed GPDSTGCN model demonstrated superior performance on both datasets, highlighting the effectiveness of this approach. It particularly excelled in medium-to long-term forecasting, indicating its ability to capture dynamic spatial–temporal correlations between sensors. This success can be attributed to the enhancement of the local spatial dependencies with global spatial correlations across regions. Compared with models using a full-graph GCN approach, the grid partitioning method incorporated in GPDSTGCN effectively captured the complete adjacency relationships between sensors, confirming the feasibility of dividing a large-scale traffic network into multiple smaller graphs. Therefore, the proposed method can not only alleviate the potential overfitting and high memory consumption issues associated with dynamic correlation models but also improve predictive accuracy.
To validate the model’s effectiveness in long-term forecasting tasks, paired t-tests were employed to statistically compare prediction errors with the strongest baseline model across multiple prediction steps. The results demonstrate consistent outperformance of the proposed model over the baseline at all forecasting horizons (Table 2). The improvements are particularly significant for long-term predictions (≥2 h), with most p-values below 0.01.

Table 2.
Paired t-test results comparing prediction errors (MAE) with baseline models across different forecasting horizons.
In this study, roads are classified based on functional categories (Interstate highways, US highways, and state highways) and number of lanes (small, medium, large, and extra-large roads). We analyse the MAE across each category. Table 3 presents the comparison of the MAE across different road types and lane sizes. The results demonstrate that the proposed method, GPDSTGCN, consistently outperforms the baseline methods across all road categories and scales. Overall, state highways exhibit the lowest prediction error, while US highways show higher errors, likely because of their serve more diverse traffic functions, resulting in more complex traffic state variations. Small roads have the lowest prediction error, and the error increases significantly with road size. This suggests that large and extra-large trunk roads, owing to their complex flow patterns and strong regional connectivity, pose greater challenges for prediction. Further comparisons reveal that after removing the global dependency modelling, the RemGlo model shows higher errors on large and extra-large roads compared to GPDSTGCN. This validates that global dependency modelling enhances the model’s ability to capture cross-regional flow patterns, thereby effectively improving prediction accuracy for large-scale roads. Overall, the analysis demonstrates that the proposed method has strong generalisation ability across different road levels and functional categories, although further optimisation is required when handling the complex flow characteristics of major trunk roads.

Table 3.
MAE comparison for different road types and lanes.
5.2. Ablation Study
Figure 11 shows the multistep traffic flow forecasts obtained in each ablation experiment. The RemEmb results indicated that the traffic data exhibited strong periodicity; encoding these periodic features significantly enhanced the accuracy of traffic flow forecasting by better capturing the cyclical nature of traffic patterns. The RemExt results indicated that directly partitioning grids based on latitude and longitude resulted in incomplete sensor adjacency at the region edges, leading to poor prediction performance; expanding the regions ensured the completeness of the local node adjacency relationships. The RemPart results demonstrated that applying a dynamic GCN to an entire traffic graph can lead to overfitting, prevent convergence, and even cause model failure when dealing with large-scale graphs; partitioning the traffic graph helped to alleviate these issues, confirming that nodes exhibiting strong correlations with the central node require fine-grained dynamic graph convolution, whereas nodes exhibiting weaker correlations require only coarse-grained regional correlation computation.
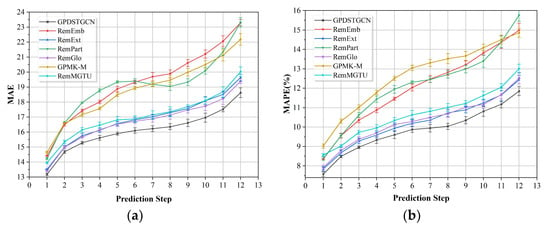
Figure 11.
Ablation study results for (a) MAE and (b) MAPE for each prediction step.
The RemGlo results confirmed that solely focusing on local spatial dependencies is insufficient to adequately reflect the overall traffic conditions; the global spatial dependency module captured potential long-distance spatial correlations, and that focusing on global information improved the accuracy of traffic flow forecasting. Finally, the GPMK-M results showed that partitioning using K-means clustering based on spatial location disrupted the local adjacency relationships in the traffic network, reducing prediction accuracy; the incorporation of region expansion into the grid partitioning process effectively mitigated this issue. The RemMGTU experimental results demonstrate the superior performance of multi-scale gated temporal convolution in modelling complex temporal dependencies. By simultaneously extracting historical features across multiple time scales, this module effectively captures both short-term variations and long-term trends, thereby enhancing prediction accuracy in multi-step forecasting tasks. These findings confirm that the multi-scale temporal perception mechanism significantly improves the model’s adaptability to temporal dynamics.
5.3. Efficiency
The efficiency of the proposed GPDSTGCN model was evaluated by comparing its computational costs with those of baseline models when using the GLA and CA datasets. All models were run using a maximum batch size (BS) of 64 and a minimum BS equal to the largest size allowed by the GPU. Table 4 reports the BS for each model along with the associated training and inference times.

Table 4.
Comparison of computational costs when using the GLA and CA datasets.
Because the STGCN model does not account for dynamic spatial–temporal correlations, it exhibited the fastest training and inference times. Both GWNET and STGODE constructed potential spatial correlations, which can increase the computational load and thereby require more processing time. However, as the correlations in STGODE were precomputed, the required training time was relatively low. HGCN uses a multi-level spatiotemporal graph structure to model static spatial correlations, achieving high computational efficiency but failing to capture dynamic spatial dependencies. Conversely, HSTGODE, ASTGCN, and RemPart employ full-graph attention mechanisms, leading to excessively high computational complexity. The proposed GPDSTGCN innovatively introduces a grid-partitioned attention mechanism, demonstrating notable advantages through localised spatial correlation computation: (1) a 90×, 100×, and 70× reduction in computational complexity compared to HSTGODE, ASTGCN, and RemPart, respectively; (2) a memory consumption reduction to one-third, one-fourth, and one-eighth of the baseline models, respectively. However, the complexity of the proposed model increased owing to its use of a loop-based structure to compute the spatial correlations for each region. Despite this increase, its relatively lower memory requirements make the proposed model well-suited to large-scale traffic networks.
To further quantify the computational efficiency and scalability of our model, this study analyses two dimensions: model parameter count and computational FLOPs. By employing the regional partitioning strategy that divides the complete traffic graph into smaller subgraphs, where the node count of each subgraph is significantly smaller than the full graph’s node count , the computational complexity is substantially reduced.
The computational complexity of full-graph attention (Equation (3)) is given by . Through graph partitioning, this complexity is optimised to . Given that , the computational load is substantially decreased. Experimental results demonstrate that on the GLA dataset, the proposed strategy reduces computation by approximately 70 times and decreases model parameters to 10% of the original method, effectively alleviating resource consumption and overfitting issues during training. Even greater optimisation results are observed on the CA dataset, validating the proposed method’s superior scalability when handling larger-scale graph data.
5.4. Visualisation
The errors between the predicted and actual traffic flows were determined to compare the accuracy of the proposed GPDSTGCN model with that of the well-performing STGCN and AGCRN models. Figure 12 shows the 15 min traffic flow forecasts versus the actual values from sensors located within and at the edges of regions. The results confirm that the partition-based approach ensured complete local adjacency relationships: the proposed model achieved a predictive accuracy comparable to that of STGCN and AGCRN, which utilise the entire graph GCN. However, STGCN does not account for dynamic spatial–temporal correlations, leading to a poorer predictive performance; in contrast, the proposed model includes a dynamic correlation module that better captured dynamic changes in traffic flow.
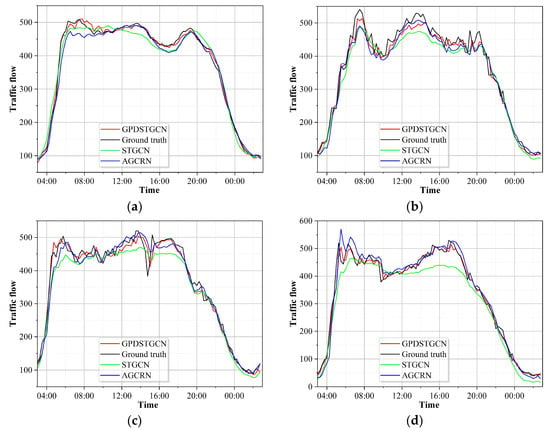
Figure 12.
Comparison of 15 min traffic flow predictions with the actual values at nodes (a) 1099, (b) 593, (c) 660, and (d) 1842 in the GLA dataset.
Figure 13 compares the multistep traffic flow forecast results obtained by each model, indicating that the proposed model performed well in medium- to long-term forecasting and demonstrating its ability to capture long-term spatial–temporal traffic flow patterns. Finally, the ability of the proposed model to capture global dependencies was intuitively demonstrated by visualising the correlations between different regions in the GLA dataset.
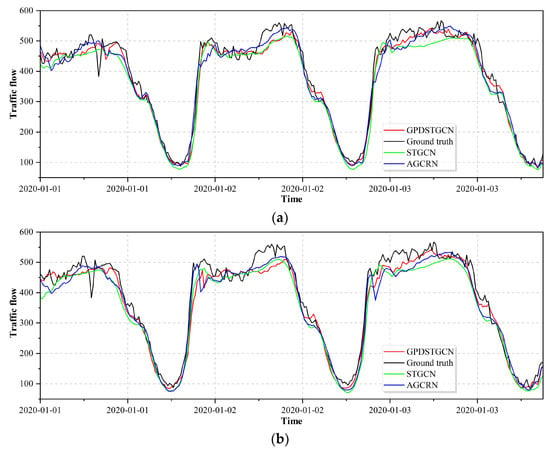
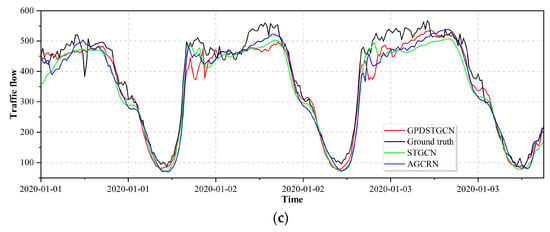
Figure 13.
Comparison of (a) 1 h, (b) 2 h, and (c) 3 h multistep traffic flow forecasts with actual values at node 660 in the GLA dataset.
Experimental results reveal the model’s effectiveness in capturing traffic flow dynamics at various sensor locations:
Intra-partition sensors (e.g., Nodes 1099 and 1842) accurately reflect dynamic traffic volume variations, with predictions showing high consistency against ground truth, confirming the model’s strong local prediction capability. Boundary sensors (e.g., Nodes 593 and 660) capture flow trends accurately but exhibit systematic underestimation and lag effects during peak-flow predictions. Further analysis reveals that although the model demonstrates strong performance in fitting periodic traffic patterns during 3 h long-term forecasting, its precision declines for abrupt peak flows.
These limitations are likely caused by the current model’s exclusive reliance on spatiotemporal features without incorporating external sudden factors (e.g., weather, accidents). Future work will focus on integrating multimodal data to enhance anomaly event modelling, thereby improving adaptability and prediction accuracy for sudden scenarios.
Figure 14a shows the spatial distributions of regions and sensors, and Figure 14b provides the Pearson correlation strengths between regions. The proposed model determined that region 10 exhibited strong correlations with adjacent regions 4 and 11 as well as with non-adjacent regions 16 and 17 owing to the structural similarities of the traffic networks in these areas. This confirms that the proposed model can effectively capture close correlations between adjacent regions while recognising potential connections between nonadjacent regions, thereby achieving a comprehensive understanding of both global and local spatial dependencies. Indeed, this capability significantly enhanced the generalisation ability of the model, mitigated overfitting issues, and improved the traffic flow forecasting accuracy.
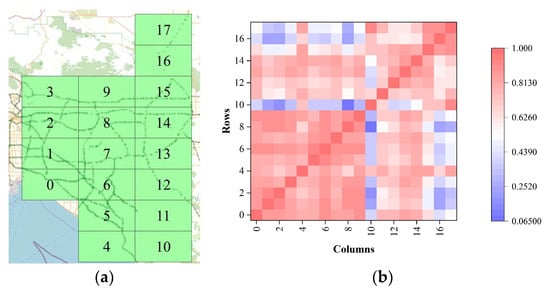
Figure 14.
(a) Distribution of regions in the GLA dataset. (b) Pearson correlation strength between these regions. Rows and columns represent the number of regions.
Furthermore, to rigorously validate the effectiveness of the global dependency module, the Pearson correlation coefficient was computed between the total global feature weight received by each region and its corresponding error improvement magnitude . Specifically, the prediction error (MAE) for each region was first calculated after removing the global module, and the error difference () was then determined between this ablated model and the complete model. Subsequently, the weighted sum of global features () received by each region from all other regions was computed, serving as a measure of its dependency on global information. Finally, Pearson correlation analysis was employed to examine the relationship between and . The results reveal a statistically significant positive correlation , providing strong evidence that the model effectively identifies and utilises global information from highly dependent regions to enhance performance.
Figure 15 illustrates the MAE differences between road segments under conditions with and without global dependency modelling. After incorporating regional global spatial dependencies, prediction accuracy improves in most areas, indicating that traffic flows exhibit correlated influences across different regions and validating the effectiveness of our module. However, a small number of nodes show increased prediction errors after introducing global dependencies. A potential explanation is that these roads are primarily dominated by local traffic variations, where the introduction of regional global features may introduce noise interference.
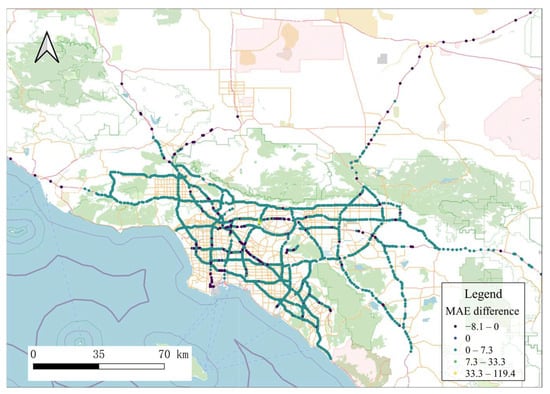
Figure 15.
MAE differences between RemGlo and GPDSTGCN (RemGlo−GPDSTGCN).
6. Conclusions
This study proposes a large-scale traffic flow prediction method based on the GPDSTGCN, exploring a new pathway for multi-level traffic network modelling. The method efficiently captures both fine-grained local and coarse-grained global spatial dependencies. Compared to existing approaches, this study’s main innovations include: an innovative grid-based partitioning strategy is designed to preserve complete road topology while efficiently capturing dynamic spatiotemporal dependencies, significantly reducing computational costs during dynamic modelling. Specifically, on the GLA dataset, memory usage is reduced by six times and computational load by 70% compared to non-partitioned models. Additionally, a global spatial dependency aggregation module is introduced, leveraging a region correlation-based weighting mechanism to dynamically capture coarse-grained global spatial features, thereby enhancing the model’s spatiotemporal perception capabilities. This design notably improves traffic flow prediction, particularly for trunk roads supporting inter-district mobility. Comparative experiments on two real-world large-scale traffic datasets demonstrate that GPDSTGCN consistently outperforms baseline models in prediction accuracy, fully validating its effectiveness.
Future work will focus on enhancing the model’s generalisability, efficiency, and robustness. To address the sensitivity of fixed grid partitioning to traffic network structures, we will explore adaptive partitioning methods based on node distribution and regional functionality and validate them using multi-city datasets. Specifically, to enhance partitioning’s semantic rationality, we will systematically incorporate both road hierarchy and functional types into our framework. To enhance computational efficiency, parallel optimisation of the partitioned graph convolution module will be implemented to resolve the bottleneck introduced by the current iterative processing design. Furthermore, considering both the similarity of traffic patterns across regions during specific periods and the impact of external factors such as weather and accidents, we will further explore semantic relationships among sensors to improve prediction accuracy, while strengthening the model’s capability to incorporate external factors for effective adaptation to abnormal traffic conditions.
Author Contributions
Conceptualisation, Agen Qiu; methodology, Lifeng Gao, Agen Qiu, Jianlong Wang and Cai Chen; validation, Lifeng Gao and Qinglian Wang; formal analysis, Lifeng Gao; investigation, Liujia Chen; resources, Geli Ou’er; writing—original draft preparation, Lifeng Gao; writing—review and editing, Agen Qiu, Jianlong Wang and Cai Chen; supervision, Fuhao Zhang. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Chinese Academy of Surveying and Mapping Basic Research Fund Program [grant number AR2204], Basic Research Program of Qinghai Province [grant number 2024-ZJ-927].
Data Availability Statement
The publicly available data used in this study are accessible at https://www.kaggle.com/datasets/liuxu77/largest (accessed on 12 April 2024).
Conflicts of Interest
No potential conflict of interest was reported by the author(s).
Appendix A
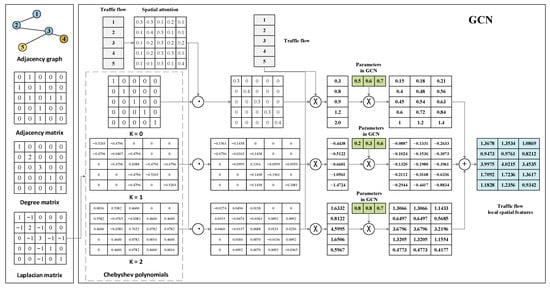
Figure A1.
Numerical example of graph convolution computation.
References
- Zhao, D.; Dai, Y.; Zhang, Z. Computational intelligence in urban traffic signal control: A survey. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2011, 42, 485–494. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, F.-Y.; Wang, K.; Lin, W.-H.; Xu, X.; Chen, C. Data-driven intelligent transportation systems: A survey. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1624–1639. [Google Scholar] [CrossRef]
- Yin, X.; Wu, G.; Wei, J.; Shen, Y.; Qi, H.; Yin, B. Deep learning on traffic prediction: Methods, analysis, and future directions. IEEE Trans. Intell. Transp. Syst. 2021, 23, 4927–4943. [Google Scholar] [CrossRef]
- Duan, Y.; Chen, N.; Shen, S.; Zhang, P.; Qu, Y.; Yu, S. FDSA-STG: Fully dynamic self-attention spatio-temporal graph networks for intelligent traffic flow prediction. IEEE Trans. Veh. Technol. 2022, 71, 9250–9260. [Google Scholar] [CrossRef]
- Ma, C.; Dai, G.; Zhou, J. Short-term traffic flow prediction for urban road sections based on time series analysis and LSTM_BILSTM method. IEEE Trans. Intell. Transp. Syst. 2021, 23, 5615–5624. [Google Scholar] [CrossRef]
- Williams, B.M.; Hoel, L.A. Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: Theoretical basis and empirical results. J. Transp. Eng. 2003, 129, 664–672. [Google Scholar] [CrossRef]
- Liu, J.; Guan, W. A summary of traffic flow forecasting methods. J. Highw. Transp. Res. Dev. 2004, 21, 82–85. [Google Scholar]
- Lingras, P.; Sharma, S.; Zhong, M. Prediction of recreational travel using genetically designed regression and time-delay neural network models. Transp. Res. Rec. 2002, 1805, 16–24. [Google Scholar] [CrossRef]
- Ma, X.; Tao, Z.; Wang, Y.; Yu, H.; Wang, Y. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data. Transp. Res. Part C Emerg. Technol. 2015, 54, 187–197. [Google Scholar] [CrossRef]
- Yao, H.; Tang, X.; Wei, H.; Zheng, G.; Li, Z. Revisiting spatial-temporal similarity: A deep learning framework for traffic prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 5668–5675. [Google Scholar]
- Guo, K.; Hu, Y.; Qian, Z.; Sun, Y.; Gao, J.; Yin, B. Dynamic graph convolution network for traffic forecasting based on latent network of Laplace matrix estimation. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1009–1018. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, F.; Cui, Z.; Guo, Y.; Zhu, Y. Deep learning architecture for short-term passenger flow forecasting in urban rail transit. IEEE Trans. Intell. Transp. Syst. 2020, 22, 7004–7014. [Google Scholar] [CrossRef]
- Geng, X.; Li, Y.; Wang, L.; Zhang, L.; Yang, Q.; Ye, J.; Liu, Y. Spatiotemporal multi-graph convolution network for ride-hailing demand forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 3656–3663. [Google Scholar]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. arXiv 2017, arXiv:1709.04875. [Google Scholar]
- Tedjopurnomo, D.A.; Bao, Z.; Zheng, B.; Choudhury, F.M.; Qin, A.K. A survey on modern deep neural network for traffic prediction: Trends, methods and challenges. IEEE Trans. Knowl. Data Eng. 2020, 34, 1544–1561. [Google Scholar] [CrossRef]
- Yao, H.; Tang, X.; Wei, H.; Zheng, G.; Yu, Y.; Li, Z. Modeling spatial-temporal dynamics for traffic prediction. arXiv 2018, arXiv:1803.01254. [Google Scholar]
- Guo, S.; Lin, Y.; Feng, N.; Song, C.; Wan, H. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 922–929. [Google Scholar]
- Lan, S.; Ma, Y.; Huang, W.; Wang, W.; Yang, H.; Li, P. Dstagnn: Dynamic spatial-temporal aware graph neural network for traffic flow forecasting. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; pp. 11906–11917. [Google Scholar]
- Fang, Z.; Long, Q.; Song, G.; Xie, K. Spatial-temporal graph ode networks for traffic flow forecasting. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtual Event, 14–18 August 2021; pp. 364–373. [Google Scholar]
- Jiang, J.; Han, C.; Zhao, W.X.; Wang, J. Pdformer: Propagation delay-aware dynamic long-range transformer for traffic flow prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; pp. 4365–4373. [Google Scholar]
- Zheng, C.; Fan, X.; Wang, C.; Qi, J. Gman: A graph multi-attention network for traffic prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 1234–1241. [Google Scholar]
- Li, F.; Feng, J.; Yan, H.; Jin, G.; Yang, F.; Sun, F.; Jin, D.; Li, Y. Dynamic graph convolutional recurrent network for traffic prediction: Benchmark and solution. ACM Trans. Knowl. Discov. Data 2023, 17, 1–21. [Google Scholar] [CrossRef]
- Bai, L.; Yao, L.; Li, C.; Wang, X.; Wang, C. Adaptive graph convolutional recurrent network for traffic forecasting. Adv. Neural Inf. Process. Syst. 2020, 33, 17804–17815. [Google Scholar]
- Shao, Z.; Zhang, Z.; Wei, W.; Wang, F.; Xu, Y.; Cao, X.; Jensen, C.S. Decoupled dynamic spatial-temporal graph neural network for traffic forecasting. arXiv 2022, arXiv:2206.09112. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Zhang, C. Graph wavenet for deep spatial-temporal graph modeling. arXiv 2019, arXiv:1906.00121. [Google Scholar]
- Liu, X.; Xia, Y.; Liang, Y.; Hu, J.; Wang, Y.; Bai, L.; Huang, C.; Liu, Z.; Hooi, B.; Zimmermann, R. Largest: A benchmark dataset for large-scale traffic forecasting. Adv. Neural Inf. Process. Syst. 2024, 36, 75354–75371. [Google Scholar]
- Zhang, Y.; Li, Y.; Zhang, F. Multi-level urban street representation with street-view imagery and hybrid semantic graph. ISPRS J. Photogramm. Remote Sens. 2024, 218, 19–32. [Google Scholar] [CrossRef]
- Feng, X.; Guo, J.; Qin, B.; Liu, T.; Liu, Y. Effective Deep Memory Networks for Distant Supervised Relation Extraction. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence (IJCAI-17), Melbourne, Australia, 19–25 August 2017; pp. 1–7. [Google Scholar]
- Zhang, T.; Wang, J.; Liu, J. A gated generative adversarial imputation approach for signalized road networks. IEEE Trans. Intell. Transp. Syst. 2021, 23, 12144–12160. [Google Scholar] [CrossRef]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. Adv. Neural Inf. Process. Syst. 2016, 29, 3844–3852. [Google Scholar]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting. arXiv 2017, arXiv:1707.01926. [Google Scholar]
- Fang, Y.; Qin, Y.; Luo, H.; Zhao, F.; Xu, B.; Zeng, L.; Wang, C. When spatio-temporal meet wavelets: Disentangled traffic forecasting via efficient spectral graph attention networks. In Proceedings of the 2023 IEEE 39th International Conference on Data Engineering (ICDE), Anaheim, CA, USA, 3–7 April 2023; pp. 517–529. [Google Scholar]
- Guo, K.; Hu, Y.; Sun, Y.; Qian, S.; Gao, J.; Yin, B. Hierarchical graph convolution network for traffic forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtul, 19–21 May 2021; pp. 151–159. [Google Scholar]
- Xu, T.; Deng, J.; Ma, R.; Zhang, Z.; Zhao, Y.; Zhao, Z.; Zhang, J. Hierarchical spatio-temporal graph ODE networks for traffic forecasting. Inf. Fusion 2025, 113, 102614. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).