Explainable Spatio-Temporal Inference Network for Car-Sharing Demand Prediction
Abstract
1. Introduction
2. Literature Review
2.1. Benefits of Accurate Demand Prediction
2.2. Feature Extraction and Selection in Demand Prediction Models
2.3. The eX–STIN Model: Origin and Development
2.4. Explainability in Predictive Models
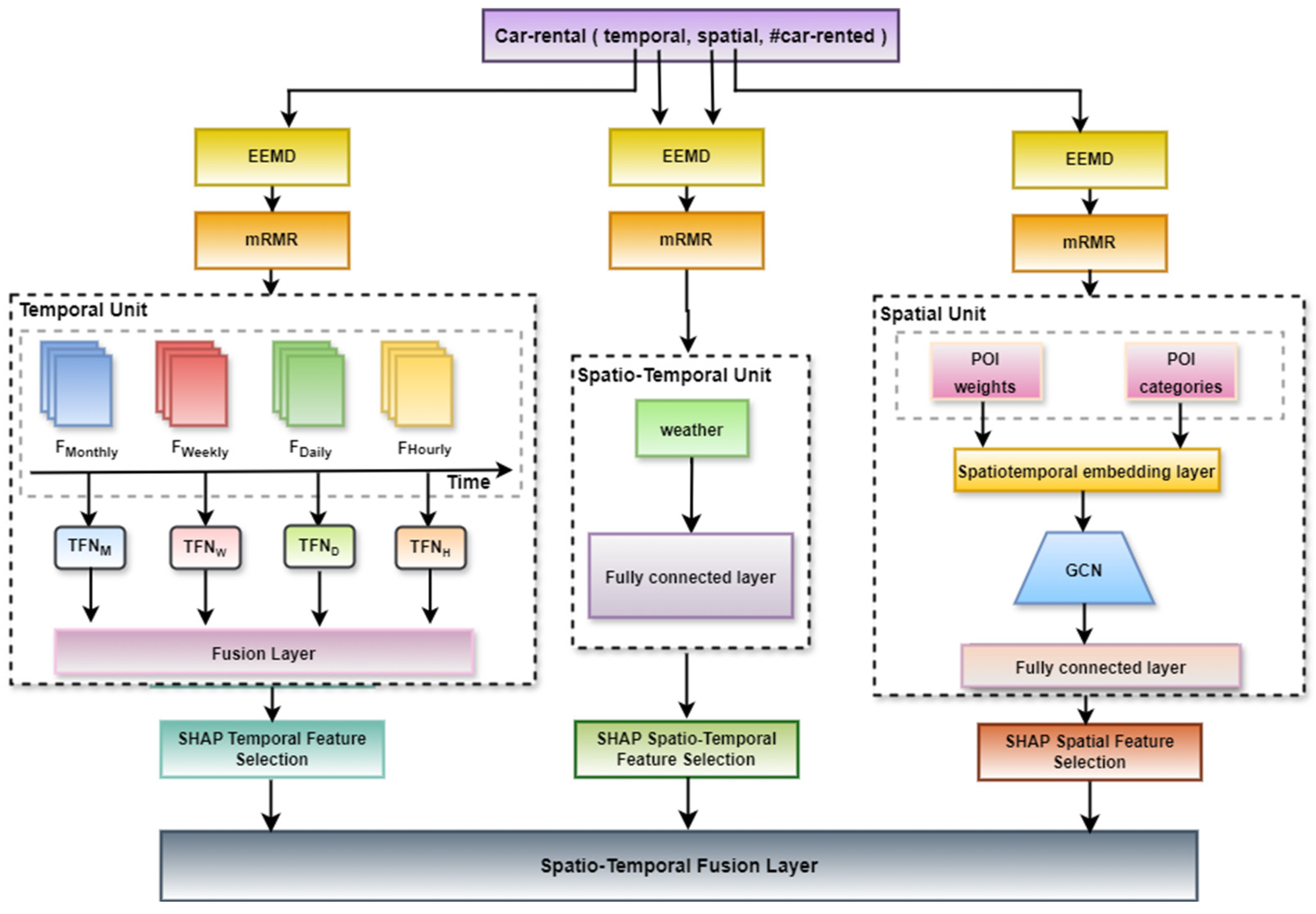
3. Methodology
3.1. Feature Extraction
3.1.1. Temporal Feature Extraction
- : IMFs from temporal data, with as the IMF index and as the trial index.
- : residual pattern after decomposing .
3.1.2. Spatial Feature Extraction
- : IMFs from the spatial data.
- : residual pattern left after decomposing .
3.1.3. Spatio-Temporal Feature Extraction
- : IMFs from spatio-temporal data.
- : residual pattern after decomposing .
3.2. Mutual Information
- : the probability mass function of .
- : the joint probability mass function of and .
- : the conditional probability mass function of given .
3.3. Feature Selection
3.3.1. Temporal Feature Selection
- : the subset of selected features from .
- : the features within the subset .
- : the mutual information entropy between features and .
- : mutual information between feature and target variable .
3.3.2. Spatial Feature Selection
- : the subset of selected features from .
- : the features within the subset .
- : the mutual information entropy between features and .
- : mutual information between feature and target variable .
3.3.3. Spatio-Temporal Feature Selection
- : the subset of selected features from .
- : the features within the subset .
- : the mutual information entropy between features and .
- : mutual information between feature and target variable .
3.4. Predictive Model
3.4.1. Temporal Feature Unit
- Encoder: temporal convolutional network (TCN)
- : the output of the TCN.
- : the weight matrix of the convolutional filter.
- : the bias term.
- : the convolution operation.
- : batch-normalized output at a specific time step .
- : mean and variance computed over the batch.
- : learnable parameters specific to each feature dimension.
- : small constant added for numerical stability.
- 2.
- Attention mechanism layer
- : the number of attentional correlations from moment to moment .
- : the attentional weight.
- : the current time step in the decoder.
- : the time steps in the encoder’s output.
- : the total number of time steps in the encoder output.
- : an iterator in the normalization sum.
- 3.
- Decoder: long short-term memory layer (LSTM)
- : weight matrices for input gate, forget gate, output gate, and candidate cell state, respectively.
- bias terms for input gate, forget gate, output gate, and candidate cell state, respectively.
- : the current cell state.
- : the cell state from the previous time step.
- : the current hidden state.
- : sigmoid activation function.
- element-wise multiplication.
- : represents the concatenated outputs from the LSTM decoders at four different time scales (daily, weekly, monthly, and yearly).
- : the weight matrix of the fully connected layer.
- : the bias of the dense fully connected layer.
3.4.2. Spatial Feature Unit
- Spatial density calculation
- 2.
- Regression model
- 3.
- Spatio-temporal embedding layer
- 4.
- Graph convolutional network layer (GCN)
- 5.
- Fully connected layer
- : weight of the fully connected layer.
- : bias of the fully connected layer.
3.4.3. Spatio-Temporal Feature Unit
- : weight of the fully connected layer.
- : bias of the fully connected layer.
3.4.4. Shapley Additive Explanation Analysis and Model Training
- : the normalized SHAP output from the temporal feature unit.
- : the normalized SHAP output from the spatial feature unit.
- : the normalized SHAP output from the spatio-temporal feature unit.
- , , and : the weight matrices.
- : the bias.
- : the weight matrix that maps the final integrated feature representation to the predicted car demand.
4. Experimental Section
4.1. Data Description
4.2. Experimental Setting
4.3. Baseline Models’ Configuration
4.4. Model Configuration
4.5. Evaluation Metrics
4.5.1. Mean Absolute Error (MAE)
4.5.2. Mean Square Error (MSE)
4.5.3. Root Mean Square Error (RMSE)
4.5.4. Mean Absolute Percentage Error (MAPE)
- : the actual value.
- : the forecast value.
- : the number of fitted points.
5. Discussion
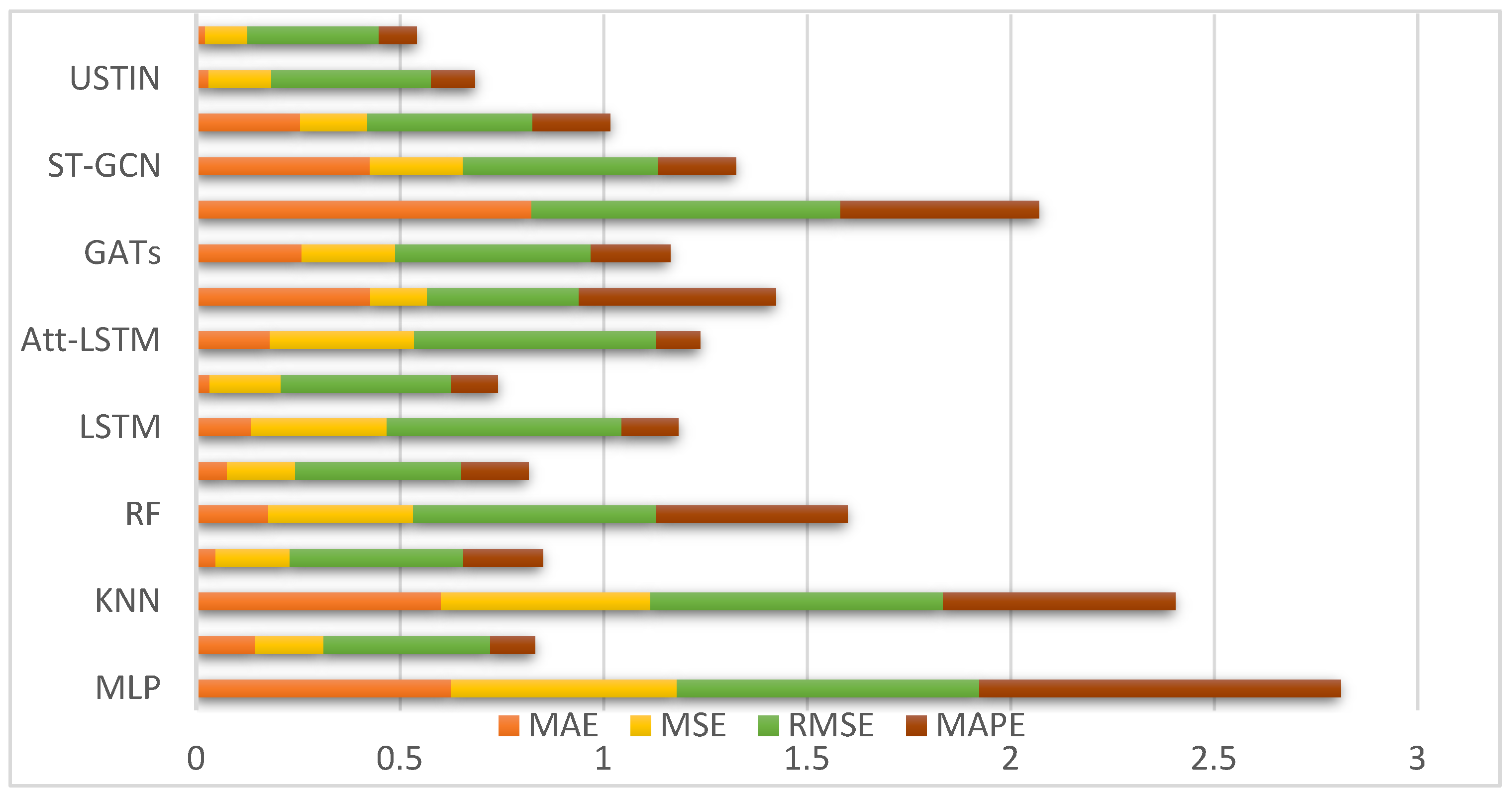
5.1. Evaluation of eX-STIN for Car-Sharing Demand Prediction
5.2. Prediction Results and Interpretability Analysis
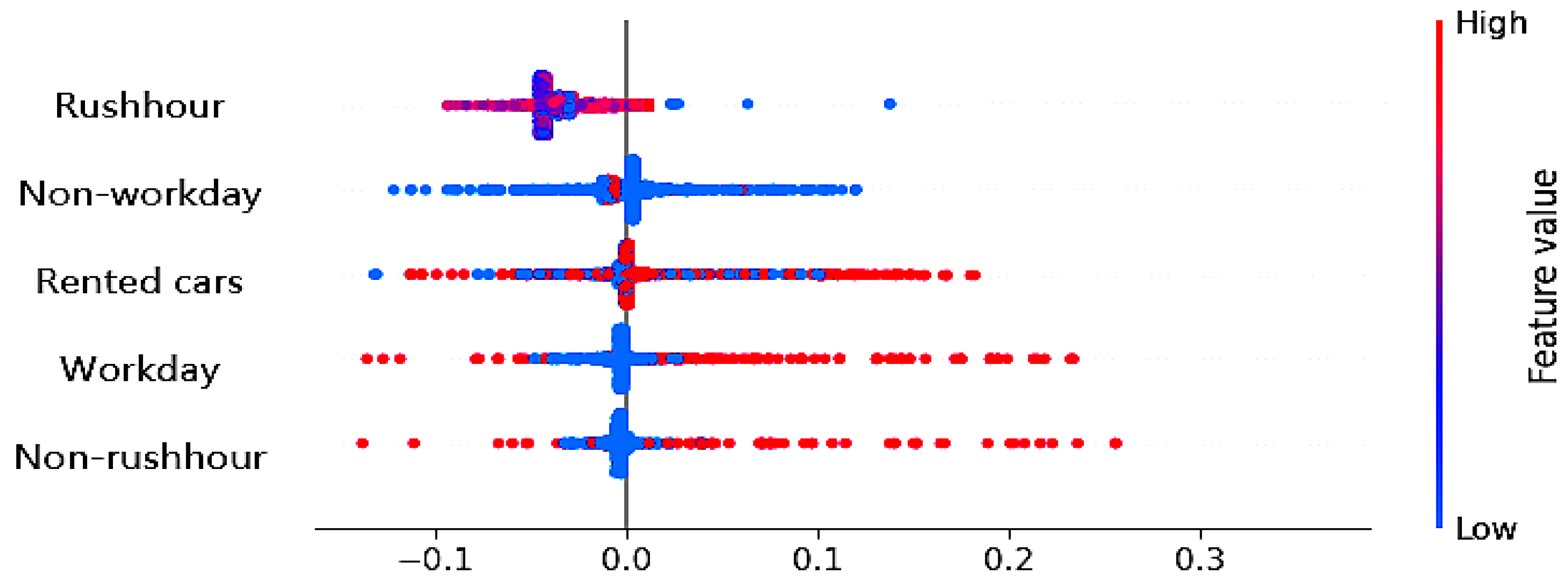
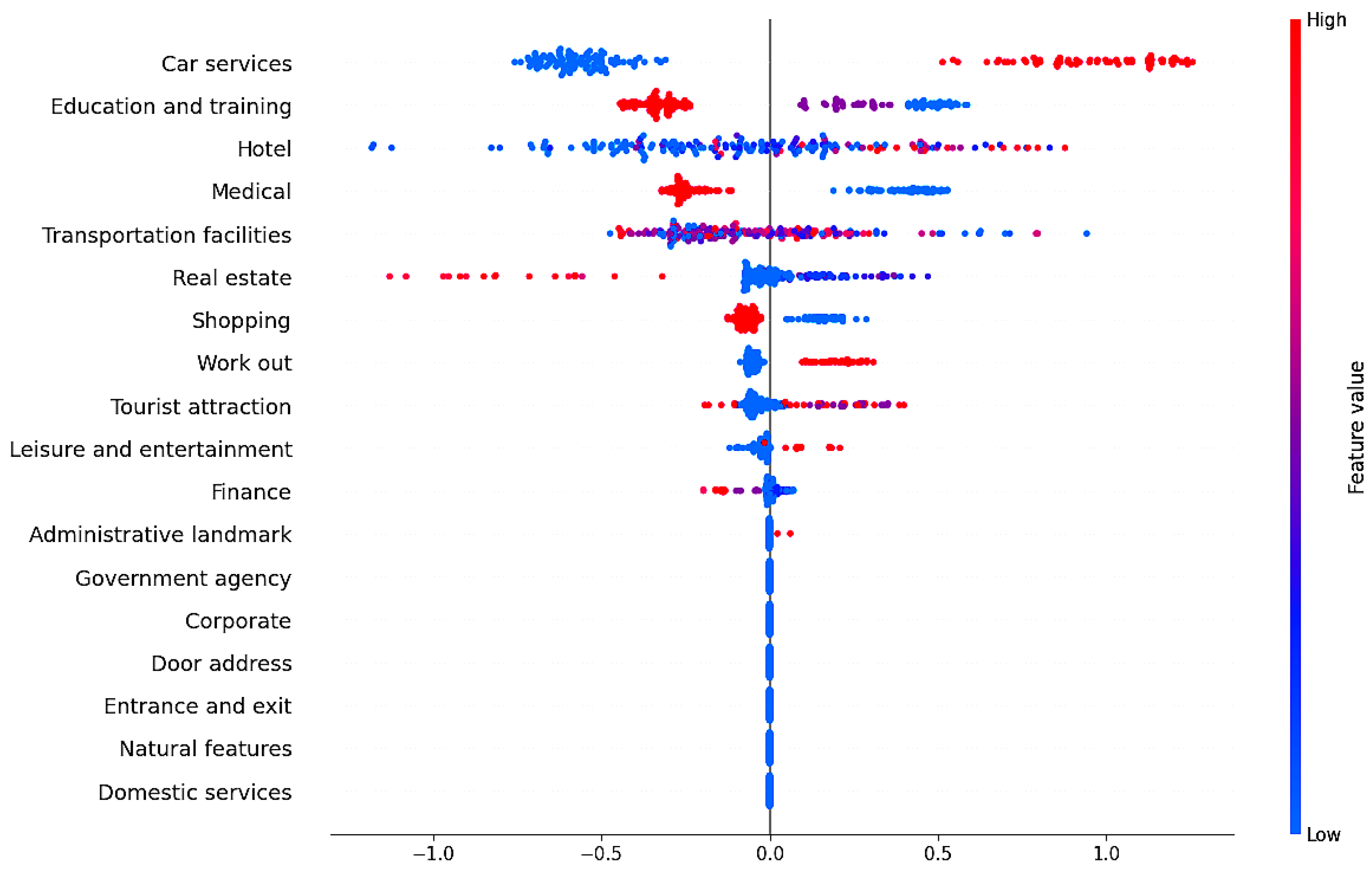
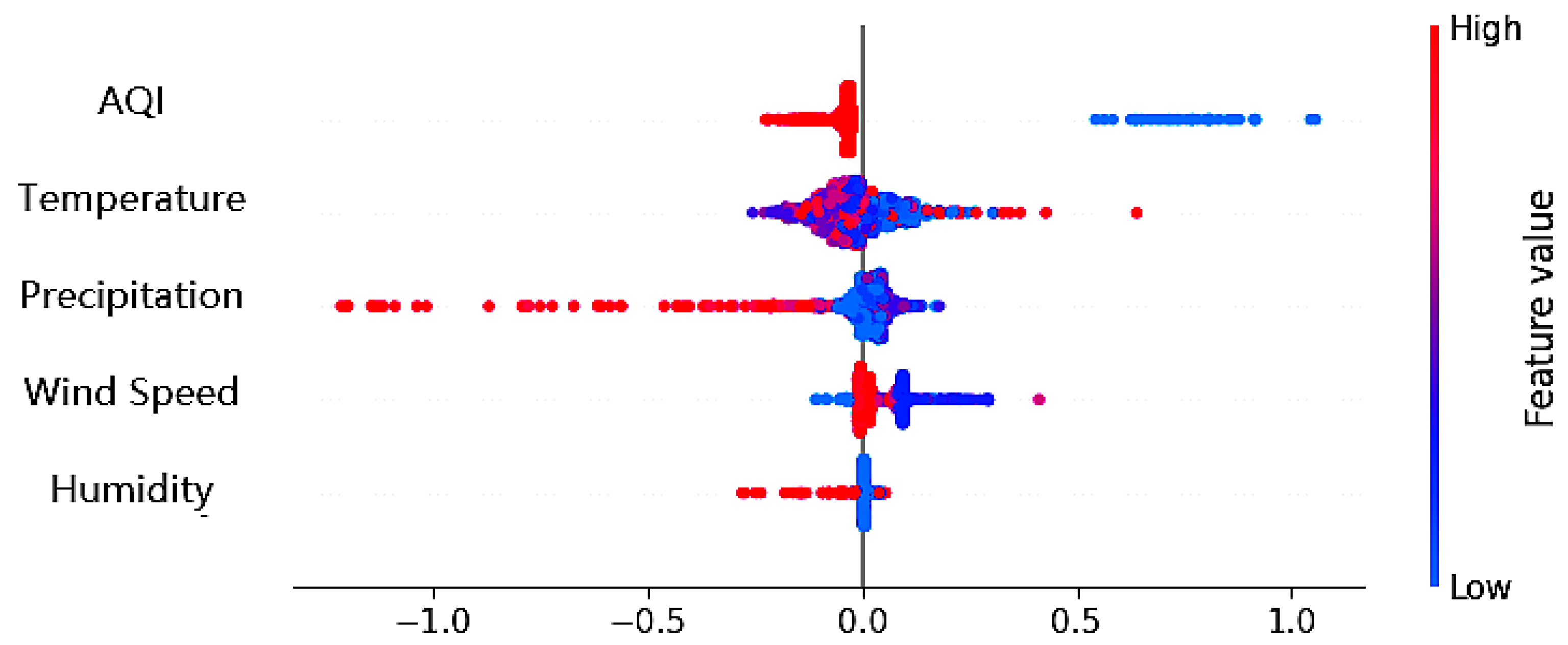
5.3. Features Impact on the Unit’s Output
5.3.1. Temporal Unit
5.3.2. Spatial Unit
5.3.3. Spatio-Temporal Unit
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qian, X.; Guo, S.; Aggarwal, V. DROP: Deep relocating option policy for optimal ride-hailing vehicle repositioning. Transp. Res. Part C Emerg. Technol. 2022, 145, 103923. [Google Scholar] [CrossRef]
- Brahimi, N.; Zhang, H.; Dai, L.; Zhang, J.; Benito, R.M. Modelling on Car-Sharing Serial Prediction Based on Machine Learning and Deep Learning. Complexity 2022, 2022, 8843000. [Google Scholar] [CrossRef]
- Brahimi, N.; Zhang, H.; Zaidi, S.D.A.; Dai, L. A Unified Spatio-Temporal Inference Network for Car-Sharing Serial Prediction. Sensors 2024, 24, 1266. [Google Scholar] [CrossRef] [PubMed]
- Ke, J.; Zheng, H.; Yang, H.; Chen, X. (Michael) Short-term forecasting of passenger demand under on-demand ride services: A spatio-temporal deep learning approach. Transp. Res. Part C Emerg. Technol. 2017, 85, 591–608. [Google Scholar] [CrossRef]
- Ströhle, P.; Flath, C.M.; Gärttner, J. Leveraging Customer Flexibility for Car-Sharing Fleet Optimization. Transp. Sci. 2018, 53, 42–61. [Google Scholar] [CrossRef]
- Moein, E.; Awasthi, A. Carsharing customer demand forecasting using causal, time series and neural network methods: A case study. Int. J. Serv. Oper. Manag. 2020, 35, 36–57. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, Y.; Yang, X.T.; Zhao, T.; Liu, Y. Deep Q learning-based traffic signal control algorithms: Model development and evaluation with field data. J. Intell. Transp. Syst. 2023, 27, 314–334. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Allen, P.G.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. Adv. Neural Inf. Process. Syst. 2017, 30. Available online: https://github.com/slundberg/shap (accessed on 25 April 2024).
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should i trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar] [CrossRef]
- Samek, W.; Montavon, G.; Vedaldi, A.; Hansen, L.K.; Müller, K.-R. Explainable AI: Interpreting, Explaining and Visualizing Deep Learning; Springer: Berlin, Germany, 2019; Volume 11700. [Google Scholar] [CrossRef]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Wang, S.; Cao, J.; Yu, P.S. Deep Learning for Spatio-Temporal Data Mining: A Survey. IEEE Trans. Knowl. Data Eng. 2022, 34, 3681–3700. [Google Scholar] [CrossRef]
- Firnkorn, J.; Müller, M. Selling Mobility instead of Cars: New Business Strategies of Automakers and the Impact on Private Vehicle Holding. Bus. Strateg. Environ. 2012, 21, 264–280. [Google Scholar] [CrossRef]
- Becker, H.; Ciari, F.; Axhausen, K.W. Comparing car-sharing schemes in Switzerland: User groups and usage patterns. Transp. Res. Part A Policy Pract. 2017, 97, 17–29. [Google Scholar] [CrossRef]
- Nair, R.; Miller-Hooks, E. Fleet Management for Vehicle Sharing Operations. Transp. Sci. 2010, 45, 524–540. [Google Scholar] [CrossRef]
- Müller, J.; Homem de Almeida Correia, G.; Bogenberger, K. An explanatory model approach for the spatial distribution of free-floating carsharing bookings: A case-study of German cities. Sustainability 2017, 9, 1290. [Google Scholar] [CrossRef]
- Cheng, Y. Optimizing Location of Car-Sharing Stations Based on Potential Travel Demand and Present Operation Characteristics: The Case of Chengdu. J. Adv. Transp. 2019, 2019, 7546303. [Google Scholar] [CrossRef]
- Boyaci, B.; Zografos, K.G.; Geroliminis, N. An optimization framework for the development of efficient one-way car-sharing systems. Eur. J. Oper. Res. 2015, 240, 718–733. [Google Scholar] [CrossRef]
- Hua, Y.; Zhao, D.; Wang, X.; Li, X. Joint infrastructure planning and fleet management for one-way electric car sharing under time-varying uncertain demand. Transp. Res. Part B Methodol. 2019, 128, 185–206. [Google Scholar] [CrossRef]
- Deza, A.; Huang, K.; Metel, M.R. Charging station optimization for balanced electric car sharing. Discret. Appl. Math. 2022, 308, 187–197. [Google Scholar] [CrossRef]
- Atter, G.B.; Leitner, M.; Ljubi, I. Location of Charging Stations in Electric Car Sharing Systems. Transp. Sci. 2020, 54, 1408–1438. [Google Scholar] [CrossRef]
- Kuwahara, M.; Yoshioka, A.; Uno, N. Practical Searching Optimal One-Way Carsharing Stations to Be Equipped with Additional Chargers for Preventing Opportunity Loss Caused by Low SoC. Int. J. Intell. Transp. Syst. Res. 2021, 19, 12–21. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, Q.; Peng, Z.; Shao, Z.; Song, H.; Wang, W. Charging and relocating optimization for electric vehicle car-sharing: An event-based strategy improvement approach. Energy 2020, 207, 118285. [Google Scholar] [CrossRef]
- Alencar, V.A.; Rooke, F.; Cocca, M.; Vassio, L.; Almeida, J.; Vieira, A.B. Characterizing client usage patterns and service demand for car-sharing systems. Inf. Syst. 2021, 98, 101448. [Google Scholar] [CrossRef]
- Hu, S.; Chen, P.; Lin, H.; Xie, C.; Chen, X. Promoting carsharing attractiveness and efficiency: An exploratory analysis. Transp. Res. Part D Transp. Environ. 2018, 65, 229–243. [Google Scholar] [CrossRef]
- Di Febbraro, A.; Sacco, N.; Saeednia, M. One-Way Car-Sharing Profit Maximization by Means of User-Based Vehicle Relocation. IEEE Trans. Intell. Transp. Syst. 2019, 20, 628–641. [Google Scholar] [CrossRef]
- Deveci, M.; Canıtez, F.; Gökaşar, I. WASPAS and TOPSIS based interval type-2 fuzzy MCDM method for a selection of a car sharing station. Sustain. Cities Soc. 2018, 41, 777–791. [Google Scholar] [CrossRef]
- Zhao, L.; Zhou, Y.; Lu, H.; Fujita, H. Parallel computing method of deep belief networks and its application to traffic flow prediction. Knowl.-Based Syst. 2019, 163, 972–987. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, M.L.; Qu, W.; Long, S.R.; Shen, S.S.P. Applications of Hilbert-Huang transform to non-stationary financial time series analysis. Appl. Stoch. Model. Bus. Ind. 2003, 19, 245–268. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Snin, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hubert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Hamad, K.; Shourijeh, M.T.; Lee, E.; Faghri, A. Near-term travel speed prediction utilizing Hilbert-Huang transform. Comput.-Aided Civ. Infrastruct. Eng. 2009, 24, 551–576. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, M.C. Forecasting the short-term metro passenger flow with empirical mode decomposition and neural networks. Transp. Res. Part C Emerg. Technol. 2012, 21, 148–162. [Google Scholar] [CrossRef]
- Sun, W.; Ren, C. Short-term prediction of carbon emissions based on the EEMD-PSOBP model. Environ. Sci. Pollut. Res. 2021, 28, 56580–56594. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Xu, C. Carbon price prediction based on modified wavelet least square support vector machine. Sci. Total Environ. 2021, 754, 142052. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Deng, D.; Zhao, J.; Cai, D.; Hu, W.; Zhang, M.; Huang, Q. A Novel Hybrid Short-Term Load Forecasting Method of Smart Grid Using MLR and LSTM Neural Network. IEEE Trans. Ind. Inform. 2021, 17, 2443–2452. [Google Scholar] [CrossRef]
- Pandey, P.; Bokde, N.D.; Dongre, S.; Gupta, R. Hybrid Models for Water Demand Forecasting. J. Water Resour. Plan. Manag. 2020, 147, 04020106. [Google Scholar] [CrossRef]
- Gu, X.; Guo, J.; Xiao, L.; Ming, T.; Li, C. A Feature Selection Algorithm Based on Equal Interval Division and Minimal-Redundancy–Maximal-Relevance. Neural Process. Lett. 2020, 51, 1237–1263. [Google Scholar] [CrossRef]
- Gu, X.; Guo, J.; Xiao, L.; Li, C. Conditional mutual information-based feature selection algorithm for maximal relevance minimal redundancy. Appl. Intell. 2021, 52, 1436–1447. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, R.; Zhou, J.; Xu, W. DeepTransport: Learning Spatial-Temporal Dependency for Traffic Condition Forecasting. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 1–8 July 2018. [Google Scholar] [CrossRef]
- Yang, X.; Tang, K.; Yao, X. The minimum redundancy-maximum relevance approach to building sparse support vector machines. In Proceedings of the Intelligent Data Engineering and Automated Learning-IDEAL 2009: 10th International Conference, Burgos, Spain, 23–26 September 2009; Volume 5788 LNCS, pp. 184–190. [Google Scholar] [CrossRef]
- Nanayakkara, S.; Fogarty, S.; Tremeer, M.; Ross, K.; Richards, B.; Bergmeir, C.; Xu, S.; Stub, D.; Smith, K.; Tacey, M.; et al. Characterising risk of in-hospital mortality following cardiac arrest using machine learning: A retrospective international registry study. PLoS Med. 2018, 15, e1002709. [Google Scholar] [CrossRef]
- Parmar, J.; Das, P.; Dave, S.M. A machine learning approach for modelling parking duration in urban land-use. Phys. A Stat. Mech. Its Appl. 2021, 572, 125873. [Google Scholar] [CrossRef]
- Shams Amiri, S.; Mottahedi, S.; Lee, E.R.; Hoque, S. Peeking inside the black-box: Explainable machine learning applied to household transportation energy consumption. Comput. Environ. Urban Syst. 2021, 88, 101647. [Google Scholar] [CrossRef]
- Shapley, L. A Value for n-Person Games. In Contributions to the Theory of Games II; Kuhn, H., Tucker, A., Eds.; Princeton University Press: Princeton, NJ, USA, 1953; pp. 307–317. [Google Scholar] [CrossRef]
- Štrumbelj, E.; Kononenko, I. Explaining prediction models and individual predictions with feature contributions. Knowl. Inf. Syst. 2014, 41, 647–665. [Google Scholar] [CrossRef]
- Datta, A.; Sen, S.; Zick, Y. Algorithmic Transparency via Quantitative Input Influence. In Proceedings of the 2016 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2016; pp. 598–617. [Google Scholar] [CrossRef]
- Lipovetsky, S.; Conklin, M. Analysis of regression in game theory approach. Appl. Stoch. Models Bus. Ind. 2001, 330, 319–330. [Google Scholar] [CrossRef]
- Max-dependency, C. Feature Selection Based on Mutual Information. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- Deep Learning—Ian Goodfellow, Yoshua Bengio, Aaron Courville—Google Livres. Available online: https://books.google.com/books?hl=fr&lr=&id=omivDQAAQBAJ&oi=fnd&pg=PR5&dq=Goodfellow,+I.,+Bengio,+Y.,+Courville,+A.+(2016).+%22Deep+Learning.%22&ots=MON2arpCTY&sig=_MYlqTHO7Xe9VyfN-eNh7q_b-Ns#v=onepage&q=Goodfellow%2C I.%2CBengio%2C Y.%2C Courville%2C A.(2016).%22Deep Learning.%22&f=false (accessed on 26 April 2024).
- Mao, X.; Yang, A.C.; Peng, C.K.; Shang, P. Analysis of economic growth fluctuations based on EEMD and causal decomposition. Phys. A Stat. Mech. Its Appl. 2020, 553, 124661. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, Y.; Hu, C.; Peng, Z. Recent progress on decoupling diagnosis of hybrid failures in gear transmission systems using vibration sensor signal: A review. Meas. J. Int. Meas. Confed. 2016, 90, 4–19. [Google Scholar] [CrossRef]
- Villaverde, A.F.; Ross, J.; Morán, F.; Banga, J.R. MIDER: Network inference with mutual information distance and entropy reduction. PLoS ONE 2014, 9, e96732. [Google Scholar] [CrossRef]
- Zhang, Y.; Ding, C.; Li, T. Gene selection algorithm by combining reliefF and mRMR. BMC Genom. 2008, 9 (Suppl. 2), S27. [Google Scholar] [CrossRef]
- Ardiles, L.G.; Tadano, Y.S.; Costa, S.; Urbina, V.; Capucim, M.N.; da Silva, I.; Braga, A.; Martins, J.A.; Martins, L.D. Negative Binomial regression model for analysis of the relationship between hospitalization and air pollution. Atmos. Pollut. Res. 2018, 9, 333–341. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, Y.; Wang, M. A Unified Approach to Interpreting Model Predictions Scott. Nips 2012, 16, 426–430. [Google Scholar]
- Ahmed, S.F.; Alam MS, B.; Hassan, M.; Rozbu, M.R.; Ishtiak, T.; Rafa, N.; Gandomi, A.H. Deep Learning Modelling Techniques: Current Progress, Applications, Advantages, and Challenges; Springer: Dordrecht, The Netherlands, 2023; Volume 56, ISBN 0123456789. [Google Scholar]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A survey of methods for explaining black box models. ACM Comput. Surv. 2018, 51, 1–42. [Google Scholar] [CrossRef]
- Simp, A.X.V.I.; Remoto, S. PM2.5 Prediction Based on Random Forest, XGBoost, and Deep Learning Using Multisource Remote Sensing Data Mehdi. Atmosphere 2019, 10, 373. [Google Scholar] [CrossRef]
- Zhang, P.; Li, X.; Chen, J. Prediction Method for Mine Earthquake in Time Sequence Based on Clustering Analysis. Appl. Sci. 2022, 12, 11101. [Google Scholar] [CrossRef]
- Tandon, S.; Tripathi, S.; Saraswat, P.; Dabas, C. Bitcoin Price Forecasting using LSTM and 10-Fold Cross validation. In Proceedings of the 2019 International Conference on Signal Processing and Communication (ICSC), Noida, India, 7–9 March 2019; pp. 323–328. [Google Scholar] [CrossRef]
- Chen, C.; Twycross, J.; Garibaldi, J.M. A new accuracy measure based on bounded relative error for time series forecasting. PLoS ONE 2017, 12, e0174202. [Google Scholar] [CrossRef] [PubMed]
- Dashdorj, Z.; Jargalsaikhan, Z.; Grigorev, S.; Trufanov, A.; Kang, T.K.; Altangerel, E. Learning Medical Subject Headings in PubMed Articles to Enhance Deep Predictions. In Proceedings of the 2024 IEEE 11th International Conference on Computational Cybernetics and Cyber-Medical Systems (ICCC), Hanoi, Vietnam, 4–6 April 2024; pp. 371–374. [Google Scholar] [CrossRef]
- Troiano, L.; Mejuto, E.; Kriplani, P. On Feature Reduction using Deep Learning for Trend Prediction in Finance. arXiv 2017, arXiv:1704.03205. [Google Scholar]
- Marey, N.; Ganna, M. Integrating Deep Learning and Explainable Artificial Intelligence Techniques for Stock Price Predictions: An Empirical Study Based on Time Series Big Data. Int. J. Account. Manag. Sci. 2024, 3, 479–504. [Google Scholar] [CrossRef]
- Khan, M.A.; Park, H. Exploring Explainable Artificial Intelligence Techniques for Interpretable Neural Networks in Traffic Sign Recognition Systems. Electronics 2024, 13, 306. [Google Scholar] [CrossRef]


| First-Level Indicator | Second-Level Indicator |
|---|---|
| Usage feature | rented cars |
| Temporal features | workday (1 for yes and 0 for no); rush hour (1 for yes and 0 for no) |
| Weather conditions | temperature (°C), precipitation (1 for yes and 0 for no), and AQI (Air Quality Index) |
| Building land attribute | hotel, shopping, domestic services, beauty, tourist attractions, leisure and entertainment, work out, education and training, culture media, medical, car services, transportation facilities, finance, real estate, corporate, government agency, entrance and exit, natural features, administrative landmark, and door address |
| Model | Hyperparameters |
|---|---|
| MLP | 2 fully connected layers, 20 and 15 hidden units |
| XGBoost | N_estimators: 25 Max_depth: 5 |
| KNN | N_neighbours: 5 Weights: “uniform” |
| RF | N_estimators: 100 Max_depth: 5 Min_samples_split: 15 |
| LSTM | Hidden layers: 2 Hidden units: 25, 15 neurons Learning rate: 0.01 Drop out: 0.5 Optimizer: Adam Epochs: 80 |
| CNN-LSTM | CNN layers: 2 LSTM layers: 2 Filters: 64 Kernel size: 3 LSTM units: 50 Dropout: 0.3 Optimizer: Adam |
| Att-LSTM | Layers: 5 Units: 50 Attention type: Bahdanau Dropout: 0.4 Optimizer: Adam |
| ConvLSTM | Layers: 2 Filters: 64 Kernel size: 3 × 3 Dropout: 0.3 Optimizer: Adam |
| GATs | Number of attention heads: 4 Hidden units: 20 Learning rate: 0.01 Dropout: 0.6 Optimizer: Adam |
| Transformer | Heads: 4 Layers: 3 Size: 128 Feedforward size: 512 Dropout: 0.1 Optimizer: Adam |
| ST-GCN | Spatial graph convolutional layers: 3 Hidden units: 64 Kernel size: 5 Dropout: 0.2 Optimizer: Adam |
| DCN | Cross layers: 3 Deep layers: 2 Hidden units deep layer: 32 Dropout: 0.2 Optimizer: Adam |
| Model | Hyperparameters |
|---|---|
| TCN | Hidden layers: 3 Kernel size: 3 Dilations: [1, 2, 4, 8, 16, 32, 64] Number filters: 64 Learning rate: 0.01 Drop out: 0.2 Optimizer: Adam Epochs: 80 |
| LSTM | Hidden layers: 2 Hidden units: 25, 15 neurons Learning rate: 0.01 Drop out: 0.3 Optimizer: Adam Epochs: 100 |
| GCN | Hidden layers: 2 (32, 64 neurons) Hidden units: 32, 64 neurons Learning rate: 0.01 Epochs: 80 |
| MAE | MSE | RMSE | MAPE | |
|---|---|---|---|---|
| MLP | 0.626 | 0.554 | 0.744 | 0.887 |
| TCN | 0.145 | 0.168 | 0.410 | 0.109 |
| KNN | 0.601 | 0.515 | 0.718 | 0.571 |
| GCN | 0.048 | 0.182 | 0.427 | 0.195 |
| RF | 0.177 | 0.356 | 0.597 | 0.469 |
| XGBoost | 0.076 | 0.167 | 0.409 | 0.164 |
| LSTM | 0.135 | 0.333 | 0.577 | 0.139 |
| CNN-LSTM | 0.033 | 0.175 | 0.418 | 0.115 |
| Att-LSTM | 0.181 | 0.354 | 0.595 | 0.108 |
| ConvLSTM | 0.428 | 0.139 | 0.373 | 0.484 |
| GATs | 0.259 | 0.230 | 0.480 | 0.195 |
| Transformer | 0.824 | 0. 575 | 0.758 | 0.488 |
| ST-GCN | 0.426 | 0.229 | 0.479 | 0.192 |
| DCN | 0.255 | 0.165 | 0.406 | 0.191 |
| USTIN | 0.031 | 0.154 | 0.392 | 0.108 |
| Our(eX-STIN) | 0.022 | 0.104 | 0.322 | 0.094 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brahimi, N.; Zhang, H.; Razzaq, Z. Explainable Spatio-Temporal Inference Network for Car-Sharing Demand Prediction. ISPRS Int. J. Geo-Inf. 2025, 14, 163. https://doi.org/10.3390/ijgi14040163
Brahimi N, Zhang H, Razzaq Z. Explainable Spatio-Temporal Inference Network for Car-Sharing Demand Prediction. ISPRS International Journal of Geo-Information. 2025; 14(4):163. https://doi.org/10.3390/ijgi14040163
Chicago/Turabian StyleBrahimi, Nihad, Huaping Zhang, and Zahid Razzaq. 2025. "Explainable Spatio-Temporal Inference Network for Car-Sharing Demand Prediction" ISPRS International Journal of Geo-Information 14, no. 4: 163. https://doi.org/10.3390/ijgi14040163
APA StyleBrahimi, N., Zhang, H., & Razzaq, Z. (2025). Explainable Spatio-Temporal Inference Network for Car-Sharing Demand Prediction. ISPRS International Journal of Geo-Information, 14(4), 163. https://doi.org/10.3390/ijgi14040163








