A New Derivation of the Formula for the Length of a Loxodrome Arc on a Sphere Using Cylindrical Projections

Abstract

If we take a distance from a map without considering the distortion, we will not get the correct value. We will get the correct value if we take the distortion into account, that is, if we use an expression for distance that does not contain distortion. The article shows how to determine the distance measured along a loxodrome between two points on a sphere if we have an image of the loxodrome in a cylindrical projection. Using the examples of Mercator, equidistant and equal-area projections, a formula was derived that does not depend on the map projection used. This was done with the aim of achieving two goals. The first was that when calculating the distance between two places shown on a map, the distortion inherent in the map due to the applied map projection should be considered. The second goal was to show how, using the theory of map projections, a formula can be derived that does not depend on the applied map projection.

1. Introduction

A map is the result of mapping data usually from the Earth, a celestial body, or an imaginary world into a planar representation on a piece of paper or on a digital screen such as a computer monitor. Maps are usually created by transforming the data first onto a spherical or ellipsoidal surface and then into a plane. Mapping a curved surface into a plane is known as map projection and can take different forms [1].

Since no map projection is isometric, i.e., it does not preserve the correct scale throughout, it is important to be aware of its variation on the map. On a world map, distortion is obvious to the eye familiar with maps. It is usually noted to what extent land masses are of inappropriate size or altered shape, and to what extent meridians and parallels do not intersect at right angles or are not evenly spaced. On maps of countries or even continents, distortion may not be visible to the eye but becomes apparent after careful measurement and analysis [2].

All map projections introduce distortion of area, angles and/or distances. Some types of distortions can be controlled to preserve specific characteristics, but map projections must distort other characteristics of the depicted object. The main problem in cartography is that it is not possible to map a spherical or ellipsoidal surface into a plane without distortion. Euler was the first to prove in 1772 that a sphere cannot be mapped into a plane with distortion equal to zero [3,4].

At the beginning, we notice that every map projection introduces certain distortions. The local length scale factor c serves as a measure of length distortion, which we define as follows for a sphere of radius R [2,5,6]:

$$c^2={\displaystyle \frac{d{s^{\prime }}^2}{d{s}^2}}={\displaystyle \frac{E{d\phi }^2+2Fd\phi d\lambda +G{d\lambda }^2}{{R^{2}d\phi }^2+R^2{\mathrm{c}\mathrm{o}\mathrm{s}}^2\phi {d\lambda }^2}}.$$

(1)

where ds is the differential of the arc on the surface being mapped, and ds^′ is the corresponding differential of the arc in the projection plane, E, F and G are coefficients defined in this way:

$$E={\left({\displaystyle \frac{\partial x}{\partial \phi }}\right)}^2+{\left({\displaystyle \frac{\partial y}{\partial \phi }}\right)}^2, F={\displaystyle \frac{\partial x}{\partial \phi }}{\displaystyle \frac{\partial x}{\partial \lambda }}+{\displaystyle \frac{\partial y}{\partial \phi }}{\displaystyle \frac{\partial y}{\partial \lambda }}, G={\left({\displaystyle \frac{\partial x}{\partial \lambda }}\right)}^2+{\left({\displaystyle \frac{\partial y}{\partial \lambda }}\right)}^2,$$

(2)

where $\phi$ and $\lambda$ are latitude and longitude, respectively, $\phi \in \left[-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}}\right]$, $\lambda \in \left[-\pi ,\pi \right]$.

$$x=x\left(\phi ,\lambda \right), y=y\left(\phi ,\lambda \right).$$

(3)

are equations of map projection, or in our case formulas by which a sphere of radius R is mapped, and x and y are the coordinates of a point in a rectangular (mathematical, right-handed) coordinate system in the plane. We will assume that (3) defines a regular mapping, except perhaps at the edges of the interval, i.e., for $\phi \in \left\{-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}}\right\}$ and $\lambda \in \left\{-\pi ,\pi \right\}$.

The formula $c={\displaystyle \frac{ds\prime }{ds}}$ is usually used to determine the local linear scale factor c, but it can also be used to calculate the arc length of a curve in a projection $\left(d{s}^{\prime }=c ds\right)$ or to calculate the arc length of a curve on a sphere $\left(ds={\displaystyle \frac{ds\prime }{c}}\right)$. In this article, we will demonstrate this using examples of normal aspect cylindrical projections and loxodromes.

For normal aspect cylindrical projections, Equation (3) is simplified to [2,5,6]

$$x=K\lambda , y=y\left(\phi \right),$$

(4)

and then the expression for the square of the local linear scale factor is simpler

$$c^2={\displaystyle \frac{h^2{d\phi }^2+k^2{{\mathrm{c}\mathrm{o}\mathrm{s}}^2\phi d\lambda }^2}{{d\phi }^2+{\mathrm{c}\mathrm{o}\mathrm{s}}^2\phi {d\lambda }^2}},$$

(5)

where h and k are the factors of local length scales in the direction of the meridians and parallels, respectively.

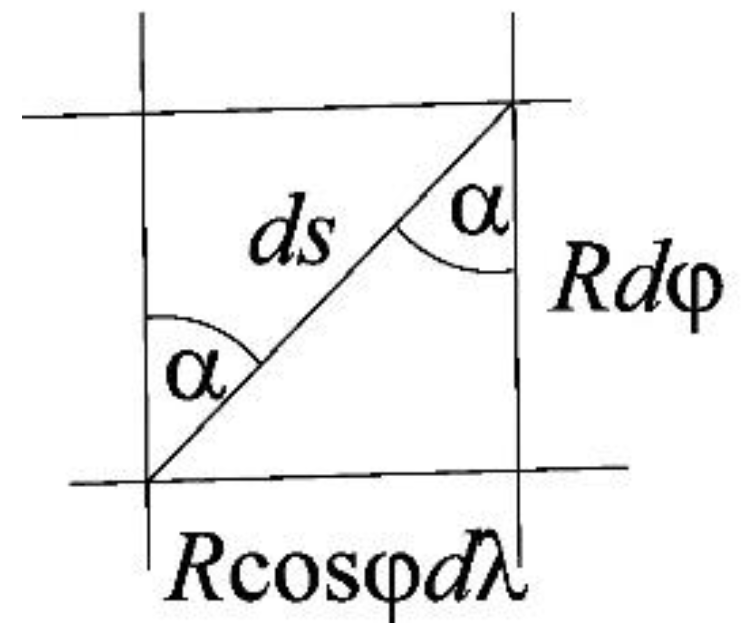
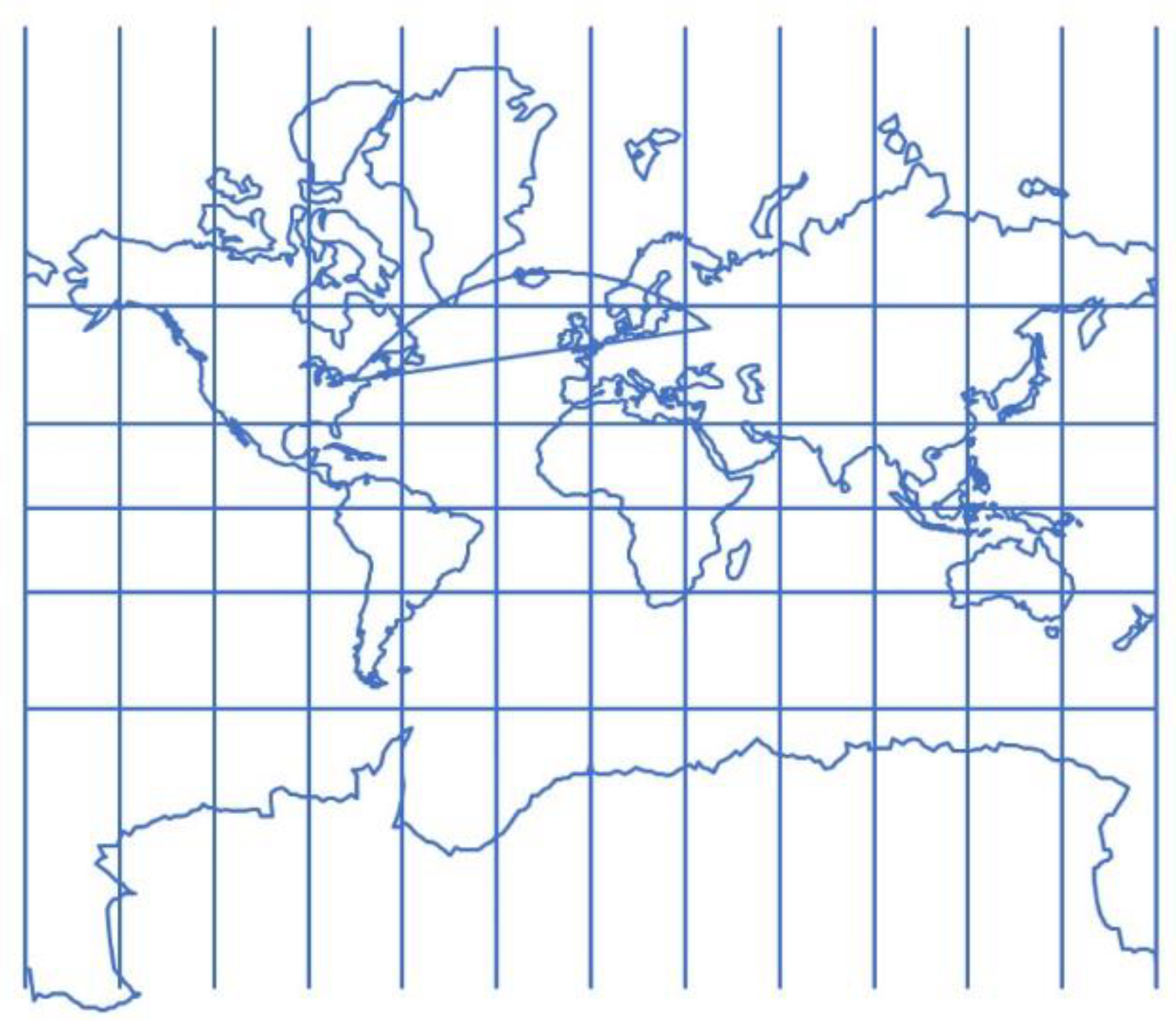
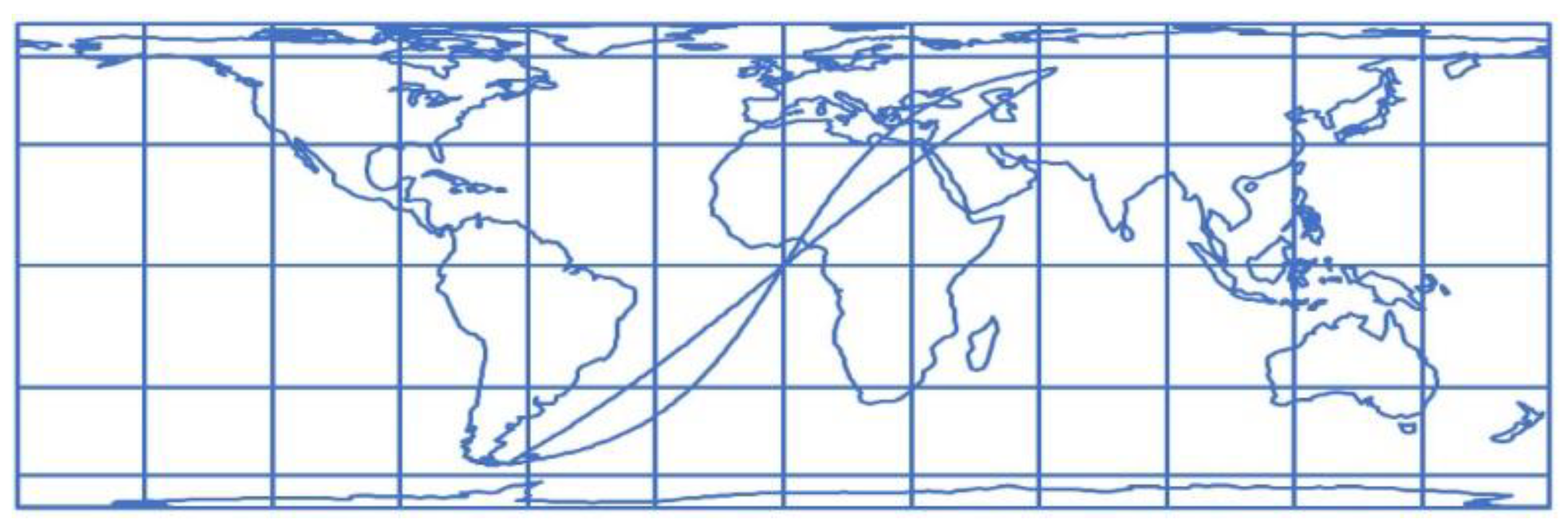
2. Loxodrome

Let a sphere of radius R centred at the origin of the coordinate system be defined by the geographic parameterization

$$X=R\cos \phi \cos \lambda , y=R\cos \phi \sin \lambda , Z=R\sin \phi ,$$

(6)

where $\phi$ and $\lambda$ are latitude and longitude, $\phi \in \left[-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}}\right]$, $\lambda \in \left[-\pi ,\pi \right]$. An infinitesimal triangle on a sphere is shown in Figure 1. The arc length differential of a curve is ds, the meridian arc length differential is $Rd\phi$, and the parallel arc length differential is $R\cos \phi d\lambda$.

For any curve on a sphere we can write (see Figure 1):

$$\tan \alpha ={\displaystyle \frac{R\cos \phi d\lambda }{Rd\phi }}$$

(7)

and from there

$$d\lambda =\tan \alpha {\displaystyle \frac{d\phi }{\cos \phi }}$$

(8)

If we assume that $\alpha =const$., i.e., that it is a loxodrome, by integrating expression (8) we will obtain the equation of the loxodrome in the form

$$\lambda =a\ln \tan \left({\displaystyle \frac{\pi }{4}}+{\displaystyle \frac{\phi }{2}}\right)+\beta ,$$

(9)

where $a=\tan \alpha$ and $\beta$ are constants. For simplicity and brevity, we will introduce the isometric width, or the function $q=q\left(\phi \right)$ as follows [5,6]

$$q\left(\phi \right)=\ln \tan \left({\displaystyle \frac{\pi }{4}}+{\displaystyle \frac{\phi }{2}}\right)={\displaystyle \frac{1}{2}}\ln {\displaystyle \frac{1+\sin \phi }{1-\sin \phi }}={\tanh }^{-1}\left(\sin \phi \right)$$

(10)

and from there

$$dq={\displaystyle \frac{d\phi }{\cos \phi }}.$$

(11)

Now we can write the equation of the loxodrome (9) in the form

$$\lambda =aq\left(\phi \right)+\beta .$$

(12)

Furthermore, from (10) and (12) for $a\ne 0$ it follows

$$\sin \phi =\tanh q\left(\phi \right)=\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}{\displaystyle \frac{\lambda -\beta }{a}},$$

(13)

and then

$$\phi ={\sin }^{-1}\left(\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}{\displaystyle \frac{\lambda -\beta }{a}}\right)=2{\tan }^{-1}\left(e^{{\displaystyle \frac{\lambda -\beta }{a}}}\right)-{\displaystyle \frac{\pi }{2}}.$$

(14)

If the loxodrome passes through the points with coordinates $\left({\phi }_1,{\lambda }_1\right)$ and $\left({\phi }_2,{\lambda }_2\right)$ then

$$a=\tan \alpha ={\displaystyle \frac{{\lambda }_2-{\lambda }_1}{q\left({\phi }_2\right)-q\left({\phi }_1\right)}},$$

(15)

$$\beta ={\lambda }_1-aq\left({\phi }_1\right)={\lambda }_2-aq\left({\phi }_2\right)={\displaystyle \frac{{\lambda }_{2}q\left({\phi }_1\right)-{\lambda }_{1}q\left({\phi }_2\right)}{q\left({\phi }_2\right)-q\left({\phi }_1\right)}}.$$

(16)

3. Loxodrome in Some Cylindrical Projections

3.1. Loxodrome in the Mercator Projection of the Sphere

The equations of the normal aspect Mercator projection of the sphere are:

$$x=K\lambda , y=K\ln \tan \left({\displaystyle \frac{\pi }{4}}+{\displaystyle \frac{\phi }{2}}\right).$$

(17)

where $K>0$ is a constant [2,5,6]. Given (10), we can write these equations in the form

$$x=K\lambda , y=Kq\left(\phi \right).$$

(18)

If we substitute the expression for $\lambda$ from (12) into (18), we will obtain the equation of the loxodrome in that projection

$$x=K\left[aq\left(\phi \right)+\beta \right], y=Kq\left(\phi \right),$$

(19)

where it can be easily obtained

$$x=ay+K\beta .$$

(20)

Since $K,a, \beta$ are constants, (20) represents a linear relationship between x and y, so the graphical representation of relation (20) is a straight line in the projection plane. In other words, the loxodrome image on a map made in the normal aspect Mercator projection is a straight line. If that line passes through two points with coordinates $\left(x_1,y_1\right)$ and $\left(x_2,y_2\right)$, then the distance d between those two points in the projection plane is equal to

$$d=\sqrt{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2}.$$

(21)

Due to the distortions that are present in every map projection, we doubt that formula (21) is the true length of the loxodrome on the sphere. If we do not know the formula for calculating the length of the loxodrome on the sphere, we will now derive it by using the theory of map projections.

In the normal aspect Mercator projection, the local linear scale factor c is equal to [2,5,6]

$$c=h=k={\displaystyle \frac{1}{\cos \phi }}.$$

(22)

Due to

$$dx=ady=aKdq={\displaystyle \frac{aKd\phi }{\cos \phi }}$$

(23)

according to (1) it is true

$$ds={\displaystyle \frac{ds\prime }{c}}=\cos \phi \sqrt{{dx}^2+{dy}^2}=K\sqrt{1+a^2}d\phi ={\displaystyle \frac{K}{\cos \alpha }}d\phi .$$

(24)

and after integration, with $K=R$ so that the local linear scale factor would be equal to 1 at the equator,

$$s={\displaystyle \frac{R}{\cos \alpha }}{\int }_{{\phi }_1}^{{\phi }_2}d\phi ={\displaystyle \frac{R}{\cos \alpha }}\left({\phi }_2-{\phi }_1\right).$$

(25)

For example, the length of the loxodrome between New York (${\phi }_1=43°{00}^{\prime }N$, ${\lambda }_1=76°{00}^{\prime }W=-76°{00}^{\prime } E$), and Moscow (${\phi }_2=55°{45}^{\prime } N$, ${\lambda }_2=37°{37}^{\prime } E$) with the assumed radius of the Earth’s sphere R = 6370 km is 8283.2 km (Figure 2). The distance d between New York and Moscow on a map drawn in the Mercator projection according to formula (21) is 12,820.7 km. This is the length of the loxodrome image on the map, which is significantly different from the length of the loxodrome on the sphere.

3.2. Loxodrome in the Equidistant Cylindrical Projection of the Sphere

The equations of the normal aspect equidistant cylindrical projection of a sphere of radius R are

$$x=K\lambda , y=R\left({\displaystyle \frac{\pi }{2}}-\phi \right),$$

(26)

where $K>0$ is a constant [2,5,6]. If we substitute the expression for $\lambda$ from (12) into (26), we will obtain the parametric equations of the image of the loxodrome

$$x=K\left[aq\left(\phi \right)+\beta \right], y=R\left({\displaystyle \frac{\pi }{2}}-\phi \right),$$

(27)

from which the equation of the image of a loxodrome can easily be obtained in the form

$$x=K\left[aq\left({\displaystyle \frac{y}{R}}\right)+\beta \right],$$

(28)

or

$$y=R\left[{\displaystyle \frac{\pi }{2}}-{\sin }^{-1}\left(\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}{\displaystyle \frac{\frac{x}{K}-\beta }{a}}\right)\right]=R\left[\pi -2{\tan }^{-1}\left(e^{{\displaystyle \frac{\frac{x}{K}-\beta }{a}}}\right)\right].$$

(29)

Since $R,K, a,\beta$ are constants, (28) or (29) do not represent a linear relationship between x and y, so the graphic representation of the loxodrome image will not be a straight line in the plane of the equidistant cylindrical projection, but some other curve. If the loxodrome passes through points with coordinates $\left({\phi }_1,{\lambda }_1\right)$ and $\left({\phi }_2,{\lambda }_2\right)$ then $a$ and $\beta$ are determined by (10).

The distance between two points on the loxodrome image in that projection cannot be obtained by a simple Formula (21). Assuming that $K=R$ so that at the equator the local linear scale factor is equal to 1, the differential of the arc of the image of the loxodrome in the plane of the equidistant cylindrical projection will be:

$$d{s}^{\prime }=\sqrt{d{x}^2+d{y}^2}=R\sqrt{{\displaystyle \frac{a^2}{{\cos }^2\phi }}+1}d\phi .$$

(30)

Integration gives

$$s^{\prime }=R{\int }_{{\phi }_1}^{{\phi }_2}{\displaystyle \frac{\sqrt{a^2+{\cos }^2\phi }}{\cos \phi }}d\phi .$$

(31)

The value of the integral in (31) can be calculated using some of the numerical integration methods. In addition, it is shown that the solution to this integral can be written using elementary functions as follows:

$$s^{\prime }=R\left[{\sin }^{-1}\left({\displaystyle \frac{\sin \phi }{\sqrt{a^2+1}}}\right)+a{\tanh }^{-1}\left({\displaystyle \frac{a\sin \phi }{\sqrt{a^2+{\cos }^2\phi }}}\right)\right]\begin{array}{c}{\phi }_2\\ \\ {\phi }_1\end{array}.$$

(32)

In this way, we obtained an expression for calculating the length of the arc of the image of a loxodrome in the plane of an equidistant cylindrical projection.

For the normal aspect equidistant cylindrical projection (26) we have [2,5,6]:

$$h=1, k={\displaystyle \frac{K}{R\cos \phi }}.$$

(33)

Assuming that $K=R$

$$c^2={\displaystyle \frac{d{\phi }^2+d{\lambda }^2}{d{\phi }^2+{\cos }^2\phi d{\lambda }^2}}.$$

(34)

and then for points on the loxodrome, taking into account (8)

$$c^2={\displaystyle \frac{1+{\left(\frac{d\lambda }{d\phi }\right)}^2}{1+{\cos }^2\phi {\left(\frac{d\lambda }{d\phi }\right)}^2}}={\displaystyle \frac{1+{\left(\frac{a}{\cos \phi }\right)}^2}{1+a^2}}.$$

(35)

Now we can write

$$ds={\displaystyle \frac{ds\prime }{c}}={\displaystyle \frac{R\sqrt{1+\frac{a^2}{{\cos }^2\phi }}d\phi }{\sqrt{\frac{1+{\left(\frac{a}{\cos \phi }\right)}^2}{1+a^2}}}}=R\sqrt{1+a^2}d\phi ={\displaystyle \frac{R}{\cos \alpha }}d\phi .$$

(36)

After integrating expression (36), we obtain (25), which is the formula for calculating the length of a loxodrome arc on a sphere that is independent of the applied map projection and thus free from the distortions that the projection entails.

Figure 3 shows a world map in a normal aspect equidistant cylindrical projection. The almost straight line connecting the points with the coordinates ${\phi }_1=55°{00}^{\prime } S$, ${\lambda }_1=65°{00}^{\prime } W$ and ${\phi }_2=55°{00}^{\prime } N$, ${\lambda }_2=65°{00}^{\prime }E$ is the image of a loxodrome, and the curve that resembles the letter S, the image of an orthodrome that connects those same two points in the projection. Solving the integral (32) with the radius of the Earth’s sphere R = 6370 km equals 18,994.60 km. It is the length of the loxodrome image on the map, which is significantly different from the length of the loxodrome on the sphere, which according to formula (25) is 17,147.67 km.

3.3. Loxodrome in the Equal-Area Cylindrical Projection of the Sphere

The equations of the normal aspect equal-area cylindrical projection of a sphere of radius R are

$$x=K\lambda , y={\displaystyle \frac{R^2}{K}}\sin \phi ,$$

(37)

where $K>0$ is a constant [2,5,6]. If we substitute the expression for $\lambda$ from (12) into (37), we can obtain the parametric equations of the image of the loxodrome

$$x=K\left[aq\left(\phi \right)+\beta \right], y={\displaystyle \frac{R^2}{K}}\sin \phi ,$$

(38)

from which, assuming that $K=R$, we can obtain the equation of the image of the loxodrome in the form

$$x=R\left(a{\tanh }^{-1}{\displaystyle \frac{y}{R}}+\beta \right),$$

(39)

or

$$y=R\tanh {\displaystyle \frac{1}{a}}\left({\displaystyle \frac{x}{R}}-\beta \right).$$

(40)

Since $R,a, \beta$ are constants, (39) or (40) do not represent a linear relationship between x and y, so the graphic representation of the loxodrome image in the plane of the equal-area cylindrical projection will not be a straight line but some other curve.

Figure 4 shows the world map in a normal aspect equal-area cylindrical projection. The almost straight line connecting the points with the coordinates ${\phi }_1=55°{00}^{\prime }S$, ${\lambda }_1=65°{00}^{\prime }W$ and ${\phi }_2=55°{00}^{\prime }N$, ${\lambda }_2=65°00\prime E$ is the image of a loxodrome, and the curve that resembles the letter S, is the image of an orthodrome that connects those same two points in the projection.

This means that the distance between two points on the image of the loxodrome in that projection cannot be obtained by the simple Formula (21). The differential of the arc of the image of the loxodrome in the plane of the equal-area cylindrical projection will be, assuming that $K=R$

$$d{s}^{\prime }=\sqrt{d{x}^2+d{y}^2}=R\sqrt{{\displaystyle \frac{a^2}{{\cos }^2\phi }}+{\cos }^2\phi }d\phi .$$

(41)

Integration gives

$$s^{\prime }=R{\int }_{{\phi }_1}^{{\phi }_2}{\displaystyle \frac{\sqrt{a^2+{\cos }^4\phi }}{\cos \phi }}d\phi .$$

(42)

It can be shown that the solution of this integral cannot be written using elementary functions. The value of this integral can be calculated using a numerical integration method. It remains to be shown that the formula for the length of an arc of a loxodrome on a sphere can be derived from the relationship between the differential of the arc of the loxodrome image (41) and the factor of the local linear scale.

For the normal aspect equal-area cylindrical projection (37) the following holds [2,5,6]:

$$h={\displaystyle \frac{R\cos \phi }{K}}, k={\displaystyle \frac{K}{R\cos \phi }}.$$

(43)

so for this projection, assuming that $K=R$ according to (5), it holds

$$c^2={\displaystyle \frac{{\cos }^2\phi d{\phi }^2+d{\lambda }^2}{d{\phi }^2+{\cos }^2\phi d{\lambda }^2}},$$

(44)

and then for points on the loxodrome, considering (8)

$$c^2={\displaystyle \frac{{\cos }^2\phi +{\left(\frac{d\lambda }{d\phi }\right)}^2}{1+{\cos }^2\phi {\left(\frac{d\lambda }{d\phi }\right)}^2}}={\displaystyle \frac{{\cos }^2\phi +{\left(\frac{a}{\cos \phi }\right)}^2}{1+a^2}}.$$

(45)

Now we can write

$$ds={\displaystyle \frac{ds\prime }{c}}={\displaystyle \frac{R\sqrt{\frac{a^2}{{\cos }^2\phi }+{\cos }^2\phi }d\phi }{\sqrt{\frac{{\cos }^2\phi +{\left(\frac{a}{\cos \phi }\right)}^2}{1+a^2}}}}=R\sqrt{1+a^2}d\phi ={\displaystyle \frac{R}{\cos \alpha }}d\phi ,$$

(46)

After integrating expression (46), we obtain (25), which is a formula for calculating the length of a loxodrome arc on a sphere that is independent of the applied map projection and thus free from the distortions that the projection entails.

4. Final Considerations

Let the normal aspect cylindrical projection (4) be given. For such a projection,

$$dx=Kd\lambda , dy=y\prime d\phi .$$

(47)

where $y\prime$ denotes the derivative of the function $y$ with respect to $\phi$. Since $d{s}^{\prime }=\sqrt{{dx}^2+{dy}^2}$, it is

$$ds={\displaystyle \frac{ds\prime }{c}}={\displaystyle \frac{1}{c}}\sqrt{{dx}^2+{dy}^2}={\displaystyle \frac{1}{c}}\sqrt{K^2{d\lambda }^2+{y\prime }^2{d\phi }^2}.$$

(48)

Relation (48) is valid for the differential of any curve on the sphere that is represented in a normal aspect cylindrical projection (4). If it is a loxodrome, then (5) due to (8) can be written in the form

$$c^2={\displaystyle \frac{h^2+a^2{k}^2}{1+a^2}}.$$

(49)

so when we substitute this into (48), assuming $K=R$, we get

$$ds=R\sqrt{1+a^2}d\phi ={\displaystyle \frac{R}{\cos \alpha }}d\phi .$$

(50)

Conversely, for the normal aspect cylindrical projection (4), (5) holds. Since $s^{\prime }=c ds$, and $d{s}^2=R^2\left({d\phi }^2+{\mathrm{c}\mathrm{o}\mathrm{s}}^2\phi {d\lambda }^2\right)$, we can write

$$d{s}^{\prime }=R\sqrt{h^2{d\phi }^2+k^2{{\mathrm{c}\mathrm{o}\mathrm{s}}^2\phi d\lambda }^2}=R\sqrt{h^2+k^2{\cos }^2\phi {\left({\displaystyle \frac{d\lambda }{d\phi }}\right)}^2}d\phi .$$

(51)

Relation (51) is valid for the differential of any curve that is mapped from a sphere to the projection plane. If it is a loxodrome, then due to (8) we can write

$$d{s}^{\prime }=R\sqrt{h^2+a^2{k}^2}d\phi .$$

(52)

and depending on the projection, i.e., on the local scales along the meridian h and the parallel k, integrating (52) gives the length of the arc of the loxodrome in the projection. Therefore, the formula $c={\displaystyle \frac{ds\prime }{ds}}$ which we usually use to determine the factor of the local linear scale, can also be used to calculate the length of the arc of a curve in the projection $\left(d{s}^{\prime }=c ds\right)$ or to calculate the length of the arc of a curve on a sphere $\left(ds={\displaystyle \frac{ds\prime }{c}}\right)$. The above is valid for any map projection.

5. Conclusions

Orthodromic navigation, although very promising, is possible only in automatic steering systems where an autopilot (course controller which stabilises the required course) is connected with a track controller, but such systems are very rare in marine navigation. Most common is a separate autopilot and for example a GPS receiver which sometimes can calculate the orthodromic or loxodromic course (mainly on a sphere) and this course must be manually set on an autopilot [7].

Every map projection carries certain distortions with it. To read the message written on a map, we need to know its distortions. For example, we often need the distance between two places. If we measure this distance from the map without taking the distortion into account, we will not get the correct value. We will get the correct value if we eliminate the distortion, that is, if we use expressions that do not contain distortion.

This article presents the problem of determining the distance measured along a loxodrome connecting two points on a sphere, assuming that we have an image of the loxodrome in a normal aspect cylindrical projection. Using the examples of the Mercator, equidistant and equal-area cylindrical projections, a formula has been derived that does not depend on the map projection used. This formula is not new, it is a new derivation using the theory of map projections. This has achieved two goals. The first, more or less known, is that when calculating the distance between two places shown on a map, the distortion inherent in the map due to the applied map projection should be taken into account. The second goal is to show how, using the theory of map projections, a formula can be derived that does not depend on the applied map projection.