A New Derivation of the Formula for the Length of a Loxodrome Arc on a Sphere Using Cylindrical Projections
Abstract
1. Introduction
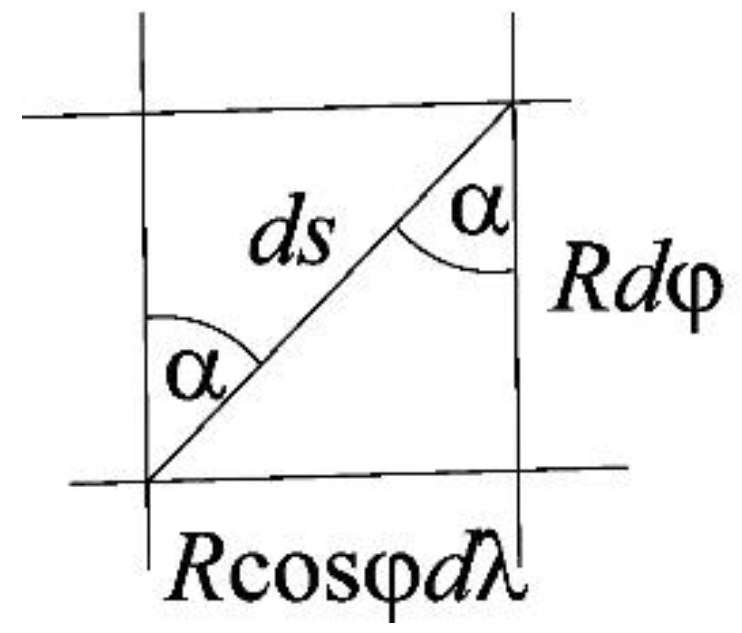
2. Loxodrome
3. Loxodrome in Some Cylindrical Projections
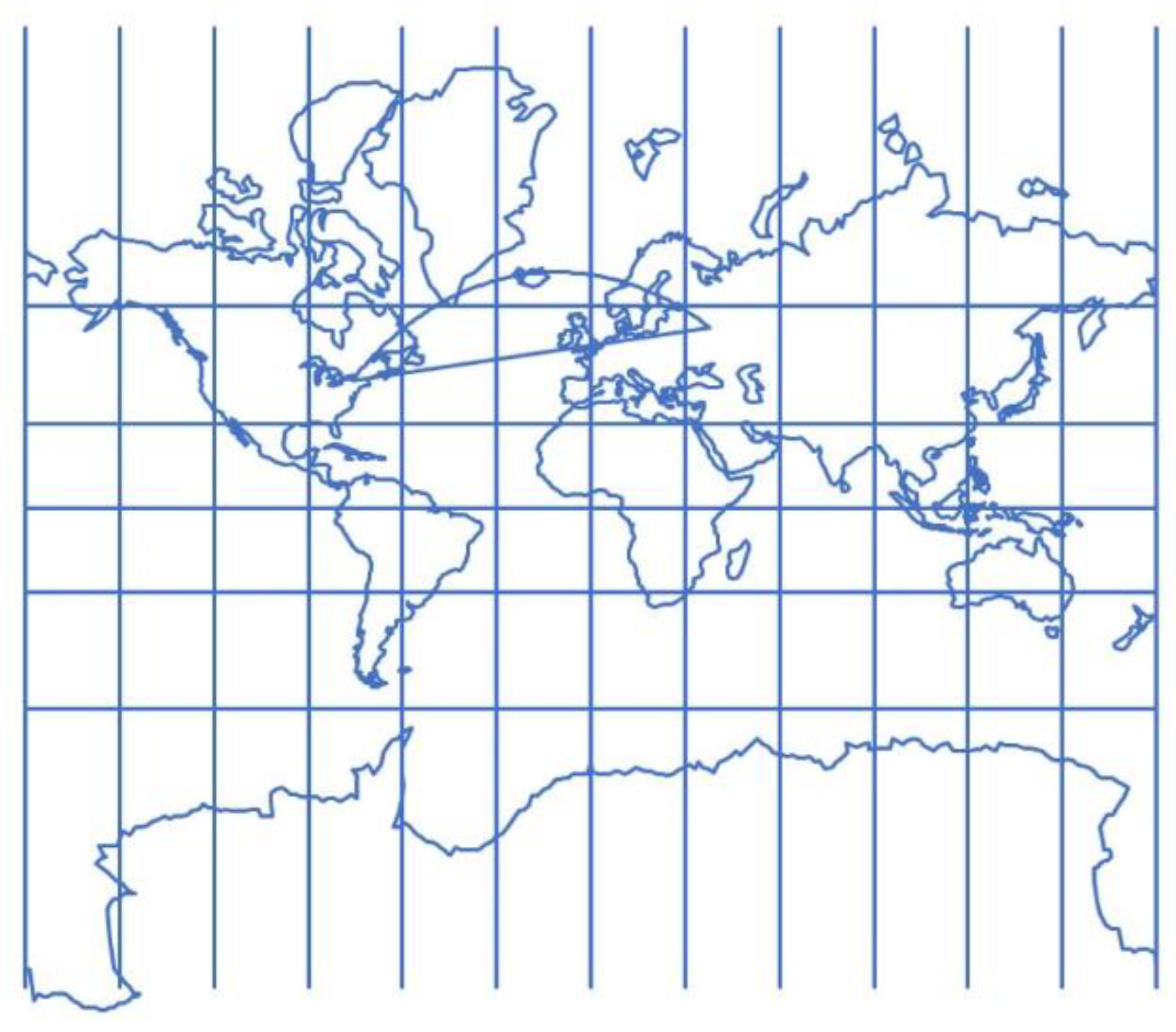
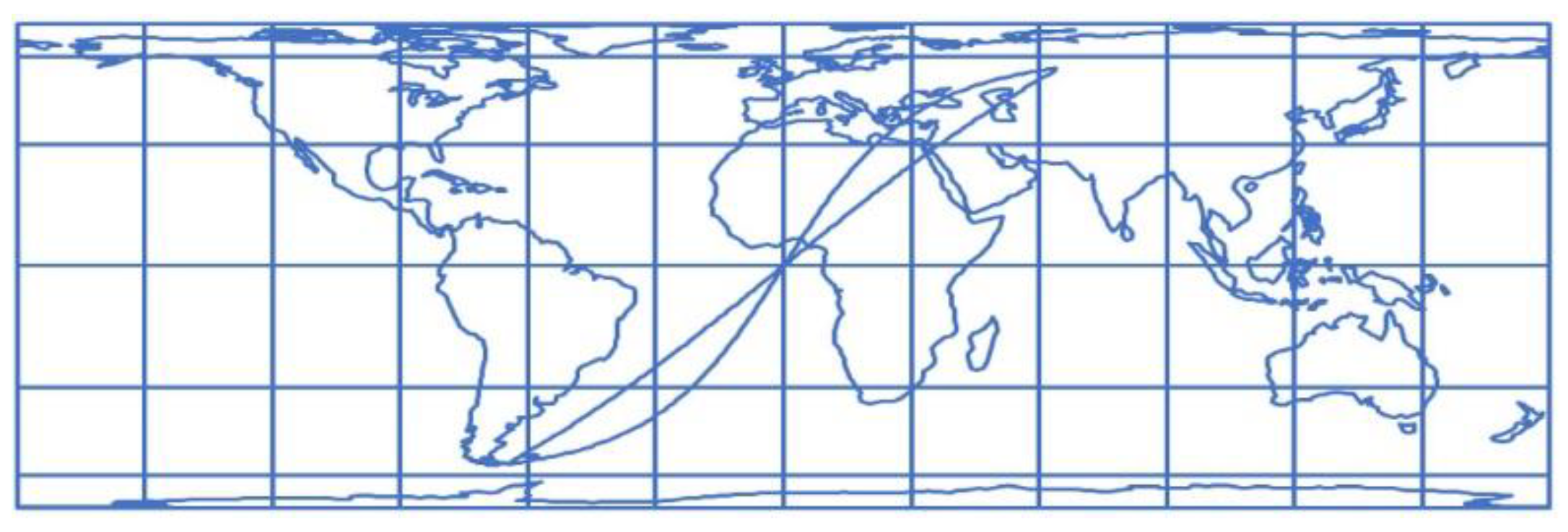
3.1. Loxodrome in the Mercator Projection of the Sphere
3.2. Loxodrome in the Equidistant Cylindrical Projection of the Sphere
3.3. Loxodrome in the Equal-Area Cylindrical Projection of the Sphere
4. Final Considerations
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lapaine, M. Map Projection Article on Wikipedia. Advances in Cartography and GIScience of the International Cartographic Association. In Proceedings of the 29th International Cartographic Conference (ICC 2019), Tokyo, Japan, 15–20 July 2019; Volume 1, pp. 1–8. [Google Scholar] [CrossRef][Green Version]
- Snyder, J.P. Map Projections: A Working Manual; USGS Professional Paper 1395; USGS: Washington, DC, USA, 1987. [Google Scholar]
- Euler, L. De repraesentatione superficiei sphaericae super plano. Acta Acad. Sci. Imp. Petropolitanae 1778, 1777, 107–132. [Google Scholar]
- Biernacki, F. Teoria Odwzorowań Powierzchni dla Geodetów i Kartografów; no. 4. Główny Urząd Pomiarów Kraju, Prace Geodezyjnego Instytutu Naukowo-Badawczego: Warsaw, Poland; 1949. (In Polish); Translated into English as Theory of Representation of Surfaces for Surveyors and Cartographers; U.S. Department of Commerce: Washington, DC, USA, 1965. [Google Scholar]
- Bugayevskiy, L.M.; Snyder, J.P. Map Projections—A Reference Manual; Taylor & Francis: London, UK, 1995. [Google Scholar]
- Frančula, N. Kartografske projekcije; textbook; Geodetski fakultet Sveučilišta u Zagrebu: Zagreb, Croatia, 2004. (In Croatian) [Google Scholar]
- Lenart, A.S. Orthodromes and Loxodromes in Marine Navigation. J. Navig. 2017, 70, 432–439. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lapaine, M. A New Derivation of the Formula for the Length of a Loxodrome Arc on a Sphere Using Cylindrical Projections. ISPRS Int. J. Geo-Inf. 2025, 14, 137. https://doi.org/10.3390/ijgi14040137
Lapaine M. A New Derivation of the Formula for the Length of a Loxodrome Arc on a Sphere Using Cylindrical Projections. ISPRS International Journal of Geo-Information. 2025; 14(4):137. https://doi.org/10.3390/ijgi14040137
Chicago/Turabian StyleLapaine, Miljenko. 2025. "A New Derivation of the Formula for the Length of a Loxodrome Arc on a Sphere Using Cylindrical Projections" ISPRS International Journal of Geo-Information 14, no. 4: 137. https://doi.org/10.3390/ijgi14040137
APA StyleLapaine, M. (2025). A New Derivation of the Formula for the Length of a Loxodrome Arc on a Sphere Using Cylindrical Projections. ISPRS International Journal of Geo-Information, 14(4), 137. https://doi.org/10.3390/ijgi14040137





