Previous Article in Journal
A GIS-Native Framework for Qualitative Place Models: Implementation and Evaluation
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJGI
Volume 14
Issue 12
10.3390/ijgi14120475
ijgi-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Leveraging Explainable Artificial Intelligence for Place-Based and Quantitative Strategies in Urban Pluvial Flooding Management

by
Chaorui Tan
1,2,*,
Entong Ke
3 and
Haochen Shi
4
1
Enshi Tujia Miao Autonomous Prefecture Transportation Planning and Cost Department, Enshi 445000, China
2
Faculty of Engineering, China University of Geosciences, Wuhan 430074, China
3
Beidou Research Institute, South China Normal University, Foshan 528225, China
4
College of Architecture and Urban Planning, Guangzhou University, Guangzhou 510006, China
*
Author to whom correspondence should be addressed.
ISPRS Int. J. Geo-Inf. 2025, 14(12), 475; https://doi.org/10.3390/ijgi14120475 (registering DOI)
Submission received: 20 October 2025 / Revised: 25 November 2025 / Accepted: 29 November 2025 / Published: 1 December 2025
(This article belongs to the Topic Natural Hazards Monitoring, Risk Assessment, Modelling and Management in the Artificial Intelligence Era)
Browse Figures
Versions Notes

Abstract

Reducing urban pluvial flooding susceptibility requires identifying dominant variables in different regions and offering quantitative management strategies, which remains a challenge for existing methodologies. To address this, this study delves into the characteristics of SHAP’s (Shapley Additive exPlanations) local interpretability and proposes a novel and concise framework based on explainable artificial intelligence (ensemble learning-SHAP) and applies it to the central urban area of Guangzhou as a case study. The research findings are as follows: (1) This framework captures the nonlinear and threshold effects of flood drivers, identifying specific inflection points where landscape features shift from mitigating to exacerbating flooding. (2) Anthropogenic variables, specifically impervious surface density (ISD) and vegetation (kNDVI), are identified as the dominant variables driving susceptibility in urban hotspots at the grid scale. (3) The interpretability results demonstrate high stability across model iterations. Finally, based on these findings, this study provides place-based and quantitative pluvial flooding management recommendations: for areas dominated by impervious surfaces and vegetation, maintaining the impervious surface density below 0.8 and the kNDVI above 0.25 can effectively reduce the susceptibility to urban flooding. This study provides a framework for achieving place-based and quantitative flooding management and offers valuable scientific insights for flooding management, urban planning, and sustainable urban development in the central district of Guangzhou, as well as in broader developing regions.

1. Introduction

With the progression of urbanization, areas susceptible to urban pluvial flooding have been rapidly expanding worldwide. Urban pluvial flooding is a result of multiple factors, including intensified urban extreme weather events, expansion of impervious surfaces within cities, and inadequate drainage systems [1,2,3]. Currently, more than 20% of global residential areas are located in regions with moderate to high flooding susceptibility, and this proportion continues to rise [4]. With the emergence of concepts such as low-impact development (LID) [5], urban managers have been dedicated to reducing the urban pluvial flooding susceptibility (UPFS) of cities by modifying the urban environment. To achieve effective management, identifying the primary factors contributing to urban pluvial flooding in different regions and offering quantified management strategies is crucial.
Identification of the dominant variables reflects the heterogeneity inherent in addressing the issue. In existing research, scholars commonly employ spatial statistical models to investigate the impact of flooding-related variables (FRVs) on UPFS across different regions [6,7]. Models exploring spatial heterogeneity are primarily classified into those based on local spatial heterogeneity theory [8,9] and those based on spatial stratified heterogeneity theory [10,11]. Models exploring local heterogeneity are exemplified by geographically weighted regression (GWR). However, though these models address the limitations of traditional models concerning spatiality, they still rely on linear assumptions. Therefore, employing local spatial heterogeneity models falls short in providing quantitative decision support. Models exploring spatial stratified heterogeneity, such as the geo-detector model (GDM), are representative examples. These models possess spatiality while not relying on linear assumptions [12]. However, due to the limitations of spatial stratified heterogeneity theory, GDM and other similar models require discretized data [13]. This limitation still hinders the provision of quantitative recommendations for flooding mitigation based on continuous numerical values.
Quantitative decision support not only relies on quantitative assessment results as references but also demands quantitative improvement guidance for urban pluvial flooding management. While some studies have devised quantitative improvement recommendations through algorithmic designs [14,15,16], they suffer from limitations in comprehensively considering and explaining FRVs related to urban flooding and lack adaptability in practical applications. Conversely, most studies, although yielding quantitative assessment results, only provide qualitative improvement recommendations based on the relationship between FRVs and UPFS. For instance, Sakieh (2017) explored the impact of spatial patterns on UPFS using a multiple linear regression model, and concluded qualitatively that increasing the cohesiveness of urban forest patches can enhance flooding resilience [17]. Similarly, Lin et al. (2021) investigated the influence of three-dimensional building structures on UPFS using random forest regression and provided qualitative recommendations, such as reducing building density, for mitigating flooding [18]. These studies often offer improvement suggestions for FRVs, but fall short in providing quantitative guidance for improvement. The impact of FRVs on UPFS is nonlinear [7], so simply lowering or increasing the values of FRVs is not an effective approach to managing flooding. For addressing the needs of pluvial flooding management, quantitative recommendations specifying the threshold values below or above which FRVs should be adjusted are essential. Fundamentally, the quantification of decision support is limited by the assessment methods for UPFS. Existing assessment methods mainly fall into two categories: statistical models and machine learning models. Statistical models often provide insights into the linear or approximate linear trends of FRVs’ influences on UPFS [19,20,21], but struggle to accurately depict the influence curve of FRVs on UPFS; ML can effectively capture nonlinear relationships [22,23,24], but due to their limited interpretability, they face challenges in providing quantitative decision support.
With the development of explainable artificial intelligence (XAI), particularly interpretable machine learning, developing place-based and quantitative decisions for flooding mitigation becomes feasible. Currently, SHAP (Shapley Additive exPlanations) has emerged as a dominant method due to its basis in game theory and its ability to ensure consistency and local accuracy [25,26]. Recognizing these advantages, a growing number of recent studies have applied SHAP to UPFS modeling [27,28,29]. These studies have successfully improved model transparency by revealing the global importance rankings of FRVs and illustrating the nonlinear relationships between variables and susceptibility [30,31,32]. However, a critical gap remains in the application of these techniques: existing studies predominantly focus on global interpretation while underutilizing the power of SHAP for local interpretation. Global interpretation assumes a uniform driving mechanism across the entire study area, which contradicts the spatial heterogeneity inherent in urban environments. For instance, while impervious surface is frequently identified as the primary flood driver at the city scale [20,33], it may not exert the same dominant influence across all local scenarios. Its role in a highly developed region may differ significantly from that in an urban green space, where other variables might take precedence. Existing SHAP-based flood studies rarely leverage local SHAP values to identify the spatially varying “dominant variables” at the grid scale. Consequently, while they provide a general understanding of flood mechanisms, they fall short of offering place-based guidance, that is, telling planners exactly which variable needs to be adjusted in which specific area.
Place-based and quantitative decision recommendations are essential for pluvial flooding control, yet current research has not elucidated how to provide them. As reviewed earlier, XAI methods offer a promising avenue to address this challenge effectively. Leveraging ensemble learning and the SHAP method enables the capture of complex relationships between UPFS and FRVs while providing both quantitative and local explanations. Therefore, this study aims to: (1) propose a concise and effective framework for decision support in pluvial flooding mitigation; (2) explore the nonlinear influences of FRVs on UPFS; (3) identify the variables that dominate flooding occurrences in different regions; (4) offer quantitative decision support tailored to the dominant variables in distinct regions. This study focuses on the central urban area of Guangzhou, a city that frequently experiences flooding disasters in China. We believe this research will furnish improved decision support for pluvial flooding management in Guangzhou’s central urban area, namely, place-based and quantitative decision support, and offer insights for the sustainable development of more cities.

2. Materials and Methods

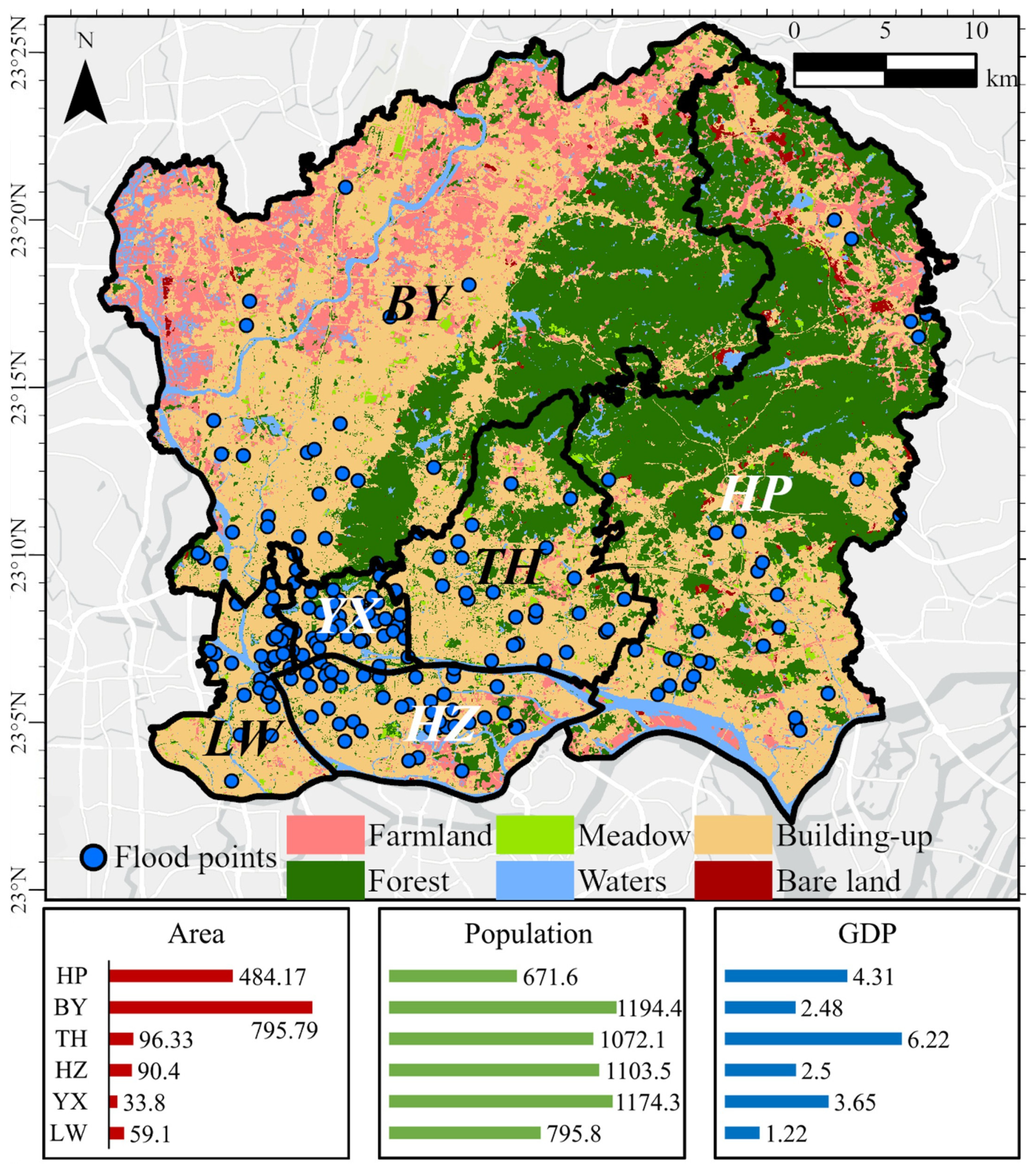
2.1. Research Area

In this research, the study area is the central urban area of Guangzhou, located in Guangdong Province, China. Guangzhou is a megacity and one of the most important economic centers in China, as well as one of the most densely populated cities in the country. However, it is also frequently affected by urban pluvial flooding, which exposes both the city’s functions and the lives and property of its residents to flooding hazards. Situated south of the Tropic of Cancer, Guangzhou’s coastal location makes it particularly prone to heavy rainfall from June to September each year. As a result, Guangzhou, particularly its central urban area, serves as a typical region for studying urban flooding.
The central urban area of Guangzhou includes six administrative districts: Liwan (LW), Yuexiu (YX), Haizhu (HZ), Tianhe (TH), Baiyun (BY), and Huangpu (HP). Based on the historical development and characteristics of these districts [34], this study classifies them into three categories: (1) Old town, including LW, YX, and HZ, which are among the earliest established administrative areas in Guangzhou and the first to undergo urbanization; (2) New town, represented by TH, which has undergone rapid urbanization and has transformed from a suburb area 20 years ago to one of the most prosperous regions in the city; (3) Developing areas, including BY and HP, which cover large areas and are experiencing rapid development. The area, population, and 2023 GDP of these three types of districts are shown in the bar chart in Figure 1.

2.2. Data Sources

Multivariate data are employed in this study, including flood points, satellite imagery, the Digital Elevation Model (DEM), soil texture, land use data, and Building Height (BH). The flood points, which represent high-susceptibility locations derived from historical summaries of flooding in previous years, serve as the labels for the dataset. The remaining data sources are used to extract feature variables. Detailed information is provided in Table 1.

2.3. Selection of FRVs

The variables related to urban pluvial flooding are diverse and complex, necessitating the selection of FRVs from multiple dimensions for UPFS modeling. UPFS refers to the physical environmental characteristics that contribute to the occurrence of pluvial floods [38]. Therefore, in this study, UPFS is represented by the probability of pluvial flood occurrence, which is computed based on the selection of appropriate physical environmental features. In this study, the FRVs are classified into three groups: climate, geography, and surface characteristics.
In terms of climate, heavy rainfall is the primary source of urban flooding. The spatial distribution of rainfall is often consistent with the locations of flooding events [39]. In this study, the average precipitation during the rainy seasons (June, July, and August) from 2020 to 2022 was used to generate the precipitation data (PRE).
Geographical variables affecting flooding include topography and land texture. Topography affects the accumulation of surface water [40], while land texture affects water infiltration [41]. In the UPFS modelling, the DEM and surface slope were utilized as fundamental topographical variables, with slope derived from the DEM. The available water capacity (AWC) is a land texture variable that is directly related to the capacity of infiltration. It was therefore included in the study.
Surface characteristics, such as land use types and spatial patterns, significantly impact UPFS by governing hydrological processes like runoff and infiltration [42,43,44]. Consequently, we selected several variables to represent these characteristics. Impervious Surface Density (ISD) is a primary indicator of urbanization’s hydrological impact; greater surface sealing prevents rainwater infiltration and directly increases the volume and velocity of surface runoff. As a counterpart, the Kernel Normalized Difference Vegetation Index (kNDVI) was used to quantify vegetation cover, which mitigates flooding by enhancing soil infiltration and intercepting rainfall. We also included distance to water (Dis2w) to account for an area’s proximity to natural drainage systems (e.g., rivers and canals) that help discharge stormwater. Additionally, the three-dimensional structure of buildings may influence flooding by affecting local climate conditions [18,27]. Therefore, BH was also included in the UPFS modeling.

2.4. Ensemble Learning Models

Ensemble learning models have demonstrated strong modeling capabilities in UPFS assessment [23,45,46]. Therefore, in this study, ensemble learning models were employed for UPFS modeling. The models utilized in this study include eXtreme Gradient Boosting (XGBoost), Gradient Boosting Decision Tree (GBDT), and Random Forest (RF). Ultimately, we selected the best-performing model for susceptibility mapping and interpretation, while the other models were used for comparing model performance and confirming the stability of interpretation results.
Additionally, in the process of constructing the dataset, we employed the Repeated Random Undersampling (RRU) method to more accurately select negative samples of urban flooding [47]. In this study, when the trained ensemble learning model achieves an area under the curve (AUC) of 0.90 on both the training and testing datasets, it indicates sufficiently good quality of negative samples.

2.5. SHAP Method

SHAP quantifies the impact of different features by estimating the SHAP values for each feature [25]. In this study, SHAP was used to measure the local impact of all FRVs on UPFS. The local dependent variable prediction value can be calculated using the following equation:
y = E ( Y ) + S 1 X 1 + S 2 X 2 + ⋯ + S n X n
where y is the predicted value of the dependent variable for a specific local instance, E ( Y ) is the mean prediction across all local instances (i.e., the base value), and S n X n is the SHAP value of feature n of the local instance. This equation indicates that the more positive a feature’s SHAP value is, the greater its positive contribution to the prediction y ; conversely, the more negative a SHAP value is, the greater its negative contribution. A SHAP value close to zero implies that the feature has little influence on the prediction result y .
Tree SHAP is a method specifically designed for ensemble learning models [26]. Tree SHAP offers high computational efficiency and can calculate interactions between features. Since the ensemble learning algorithms used in this study are all tree-based, the tree SHAP method was applied in this research.

2.5.1. Quantitative Influences of Flooding-Related Variables

SHAP dependence plots are employed to express the quantitative relationship of FRVs. These plots facilitate the understanding of how FRVs affect UPFS across different values. Based on the interpretive outcomes, plotting FRVs along with their corresponding SHAP values as scatter plots provides a quantitative representation of FRVs’ influence on UPFS.

2.5.2. Identification of Dominant Variables in Different Regions

We identify the top three FRVs with the highest SHAP values greater than 0 in each geographic unit (i.e., grid cell) as the dominant variables for urban flooding occurrence. If the maximum SHAP value in a unit is less than 0, it indicates that there are no variables dominating the occurrence of flooding in that location, denoted as “None”. Finally, these results are depicted as three maps showcasing the dominant variables.

2.6. Study Framework

This study establishes a simplified framework for place-based and quantitative decision recommendations, based on ensemble learning and the SHAP method (Figure 2). The framework involves the following steps: (1) variables relevant to UPFS are selected from precipitation, geography and land surface. Flood points are also obtained. (2) after preprocessing the data, it is fed into ensemble learning models to train and obtain the optimal model. (3) the SHAP method is employed for quantitative and local interpretations. By analyzing the interpretations, place-based and quantitative decision recommendations are provided for pluvial flooding mitigation.

3. Results

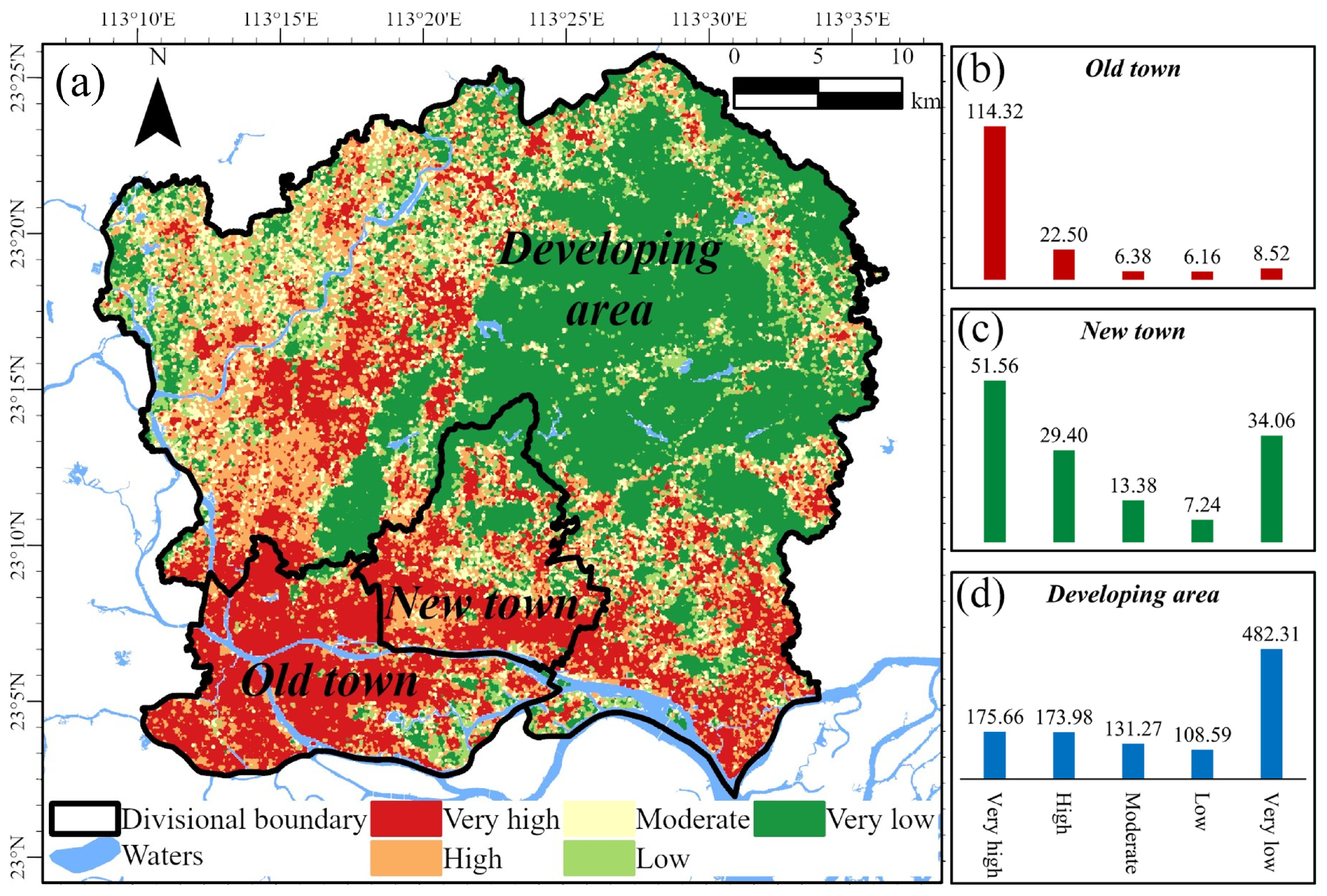
3.1. UPFS Assessment Based on Ensemble Learning

Due to the potential issue of high multicollinearity that can affect the interpretation results of UPFS, it is necessary to conduct a multicollinearity test on the variables before inputting them into the ensemble learning process. Variables with a Variance Inflation Factor (VIF) greater than 10 should be excluded [48,49]. The results of the test are presented in Table 2, indicating that all the selected variables in this study have successfully passed the multicollinearity test.
We employed three models, RF, GBDT, and XGBoost, to model UPFS. The performance of these models is depicted in Table 3, where XGBoost demonstrates superior performance across all performance metrics. Consequently, subsequent UPFS mapping and interpretation are based on the trained XGBoost model.
We generated an UPFS map of the central urban area of Guangzhou using the trained XGBoost model (Figure 3a), categorized into five levels using natural breaks. Within the central urban area of Guangzhou, regions with extremely low susceptibility are predominant, primarily distributed in the central and northeastern parts, accounting for 38.44% of the central urban area. Following are the areas with extremely high and high susceptibility, accounting for 25.02% and 16.54%, respectively, mainly concentrated in the southern and western parts of the central urban area.
Figure 3b–d demonstrates that different types of urban areas emphasize different susceptibility levels. In the historically developed old town, the majority of regions exhibit extremely high susceptibility, covering an area of 114.32 km2, representing 72.41% of the town. The southeastern part of the old town constitutes the remaining “low UPFS island” due to extensive wetlands. In the more modernized new town, most regions exhibit extremely high susceptibility, primarily located in the southern part, covering an area of 51.56 km2, accounting for 38.01% of the new town. Regions with extremely low and high susceptibility also occupy significant proportions, accounting for 25.11% and 21.68%, respectively, of the new town. The central part of the developing area features extensive mountainous terrain, resulting in predominantly extremely low susceptibility regions covering an area of 482.31 km2, representing 45% of the developing area. Following are regions with high and moderate susceptibility, primarily distributed in the southern and eastern parts, accounting for 16.39% and 16.23%, respectively, of the developing area.

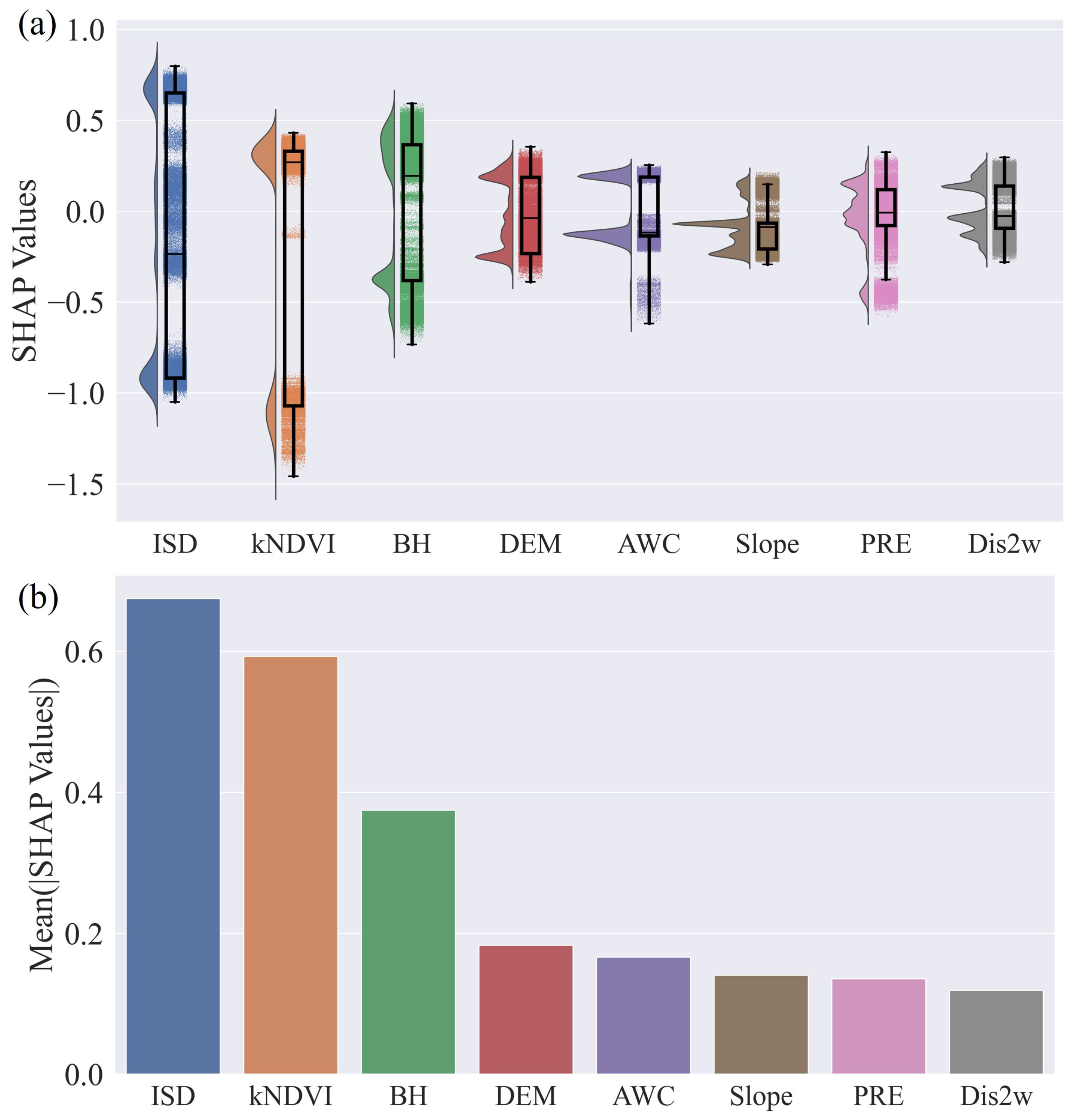
3.2. Quantitative Interpretation of FRVs

Figure 4 illustrates the global importance of FRVs along with their data distributions. The box plot reveals that ISD and kNDVI exhibit the widest range of SHAP values, while slope and PRE have the narrowest range. Additionally, violin plots and scatter plots demonstrate that the SHAP values of ISD and kNDVI are densely distributed near the maximum and minimum values within their respective ranges, whereas the SHAP values of slope and PRE are relatively evenly distributed. Such observations correspond to the mean of the absolute SHAP values of the variables.
The mean of absolute SHAP reflects the extent of influence of each variable on UPFS. The results indicate that ISD, kNDVI, and BH have a strong influence on UPFS, which aligns with the findings of several previous studies [50,51,52]. In contrast, the influence of climate and geography is relatively minor. This can be attributed to the fact that the climate and geographical conditions in the central urban area of Guangzhou are similar, making it challenging for these variables to exert significant spatial variation on UPFS. Overall, in the central urban area, the effects of land surface resulting from human activities (excluding distance to water) have a far greater influence on UPFS than natural variables.
Figure 5a–c illustrates the influence of three categories of variables across different regions. In this study, individuals with SHAP values whose absolute values are less than 0.1 are classified as having low influence, those less than −0.1 are considered to have negative influence, and those greater than 0.1 are considered to have positive influence. As expected, in high susceptibility areas (represented by darker regions on the map), precipitation, geographical variables, and land surface variables all exhibit positive influence, contributing to an increase in susceptibility. The urban heat island effect leads to the formation of an urban rain island [18], resulting in higher rainfall in the urban areas. Additionally, urban areas have flatter terrain, land use, and spatial patterns that facilitate runoff, further contributing to higher susceptibility in these areas.
Figure 5(a1,b1–b3,c1–c4) illustrates the influence of FRVs on UPFS. The influence trends of PRE, DEM, AWC, ISD, and kNDVI are consistent with the mechanisms of urban pluvial flooding as suggested by qualitative prior knowledge. The advantage of SHAP lies in its ability to quantitatively depict the effects of these variables, surpassing the limitations of prior knowledge. Consequently, from the SHAP dependence plots, quantitative recommendations can be derived for variables that are under human control, such as ISD and kNDVI. Figure 5(c1) indicates that when ISD is below 0.3, it has a strong negative influence on UPFS. When ISD is between 0.3 and 0.8, the SHAP values for ISD hover around 0, meaning the influence is reduced. When ISD is greater than 0.8, it has a positive influence on the occurrence of flooding, meaning it promotes flooding. Figure 5(c2) shows that when kNDVI is below 0.25, it has a positive influence on flooding (promoting it); when kNDVI is above 0.25, it has a negative influence (mitigating it). It is noteworthy that the influence of kNDVI is sensitive only to this 0.25 threshold, showing a distinct change without other obvious threshold effects. Therefore, for managing urban flooding, controlling ISD within the range of 0.3 to 0.8 can mitigate its influence on UPFS, while keeping ISD below 0.3 can effectively suppress the occurrence of urban flooding. Similarly, maintaining kNDVI above 0.25 can also effectively inhibit the onset of urban flooding.
Furthermore, the SHAP dependence plots of dis2w, slope, and BH also demonstrate the tremendous potential of SHAP in identifying factors contributing to urban flooding. In Figure 5(c3), as the dis2w increases, the SHAP values initially decrease and then increase, aligning with the viewpoint from other studies that proximity to water facilitates drainage [53]. In Figure 5(b2), the slope also exhibits a pronounced nonlinear influence. Previous studies often obtained a linear conclusion that higher slopes correspond to higher susceptibility [54]. However, the dependence plot of slope reveals that gentle slopes may actually promote the occurrence of urban flooding. As shown in Figure 5(B1,B2), SHAP effectively identifies the presence of overpasses. Due to the distinctive terrain beneath overpasses, they are frequent locations for urban flooding. Previous studies, limited by their interpretive methods, often treated slope and distance to overpasses as two independent variables when inputting them into ML models for interpretation [55]. However, through the utilization of SHAP, distance to overpasses has been incorporated into the interpretation of slope from the perspective of urban flooding mechanisms. The nonlinear influence of BH is evident in Figure 5(c4), where SHAP values first rise and then fall as BH increases. Beyond the established effects of buildings on urban climate, we propose that BH serves as an effective proxy for the characteristics of urban sub-regions. As depicted in Figure 5(C1), developing areas with low-rise buildings often feature a higher density of construction, a greater proportion of impervious surfaces, and possibly outdated drainage systems. In contrast, modern high-rise districts may have better-planned infrastructure (Figure 5(C2)). The SHAP results strongly support this interpretation. Specifically, the model has learned to associate lower BH values with a greater risk of flooding; this is demonstrated by the large, positive SHAP values for instances with low BH, which signify that this feature is a key driver pushing the model’s output towards a higher UPFS prediction. Therefore, this analysis provides a complementary perspective to the climate-centric view, highlighting the role of BH as an indicator of underlying infrastructure vulnerability.

3.3. Identification of Dominant Variables for Pluvial Flooding

We identified the dominant variables by selecting the top three SHAP values for each grid (Section 2.5.2), corresponding to the FRVs, as shown in Figure 6a–c. Figure 6a indicates that in areas with extremely high and high susceptibility, the primary dominant variable is primarily ISD. In contrast, in the mountainous regions and the suburbs in the northern part of the central urban district, the primary variables are often those unrelated to human activity, such as PRE, DEM, and dis2w. Figure 6b demonstrates that in areas with extremely high and high susceptibility, the secondary dominant variables remain related to human activity: in the new and developing areas, BH is most prevalent, while in the old town, kNDVI is predominant. Figure 6c reveals that in areas with extremely high and high susceptibility, the tertiary dominant variables are still largely related to human activity, such as BH and kNDVI. Additionally, several variables unrelated to human activity serve as the tertiary variables in the southwestern, northwestern, and southeastern parts of the centra urban. Notably, most of the mountainous regions lack a tertiary dominant variable.
In the extremely high and high susceptibility areas of the old town, new town, and developing area, we selected representative regions A, B, and C, respectively. The details of the environments in regions A, B, and C are shown in Figure 6A–C. Figure 6(A1–C1) illustrates the impact of FRVs on the respective UPFS in regions A, B, and C, where red indicates a positive influence and blue indicates a negative influence. The predicted value f(x) can be obtained by adding the SHAP values of the FRVs to the base value (which is −0.014 in this study). The probability of pluvial flooding is derived by applying the Softmax function to f(x). Comparing regions A and B, region A shows relatively higher SHAP values for kNDVI and BH. This suggests that the underdeveloped green environment, building patterns, and drainage system capabilities in the old town contribute to a higher flooding susceptibility. Notably, compared to region B, region A’s PRE also contributes to an increase in flooding susceptibility, likely due to the stronger urban heat island effect in the old town [56], which in turn triggers the rain island effect [18]. The UPFS in regions B and C are similar; however, the SHAP values for BH and kNDVI in region C contribute more significantly to the increase in susceptibility, while a relatively lower PRE results in comparable susceptibility levels with region B. This indicates that the green environment, building layout, and drainage system in region C are severely underdeveloped and urgently need improvement.

3.4. Stability and Reliability Validation of Interpretation Results

To ensure consistency and stability in the interpretation results across different models, following the approach outlined by Adnan et al. (2023) [57], we conducted Pearson correlation analysis to examine the mean SHAP values of all features for the three ML models. If the correlation coefficient exceeds 0.85, we consider the interpretation results stable. The correlation coefficients for the interpretation results of RF, GBDT, and XGBoost are 0.91, 0.88, and 1, respectively, with p-values all less than 0.01. This indicates a high level of consistency among the interpretation results across different models, demonstrating the stability of the interpretations. Furthermore, we compared the SHAP-based feature importance with Permutation Importance to validate the findings. Both Pearson and Spearman correlation analyses demonstrated high consistency between the two interpretation methods (Pearson’s r = 0.96, Spearman’s r = 0.86; both p < 0.01), which further corroborates the stability and robustness of our results.
To assess the reliability of the interpretation results, we analyzed the relationship among the most influential variable ISD, its corresponding SHAP values, and the final predicted probability of UPFS (Figure 7). The purpose of this analysis is to demonstrate that the SHAP values provide a transparent and logical explanation of how the model’s predictions are formulated. To objectively identify the key inflection points, we located the extrema of the first derivative of the smoothed SHAP curve. A bootstrap analysis confirmed the stability of these data-driven points at approximately ISD = 0.299 (95% CI: [0.298, 0.299]) and ISD = 0.794 (95% CI: [0.794, 0.794]). The narrowness of these confidence intervals reflects the distinct threshold effect learned by the model. In the low-impact range below this first threshold, the consistently low SHAP values explain the model’s prediction of low probabilities. As ISD increases between the two thresholds, a positive rise in SHAP values directly accounts for the increase in predicted probability, indicating this is a highly sensitive range. Beyond the second threshold, the SHAP values begin to plateau, revealing a saturation effect learned by the model where further increases in ISD contribute little additional susceptibility; this is consistently reflected in the UPFS probabilities stabilizing at a high level. This systematic correspondence between the SHAP values and the UPFS probability confirms the reliability of our interpretation, enhancing confidence that the model has learned a meaningful, nonlinear relationship.

4. Discussions

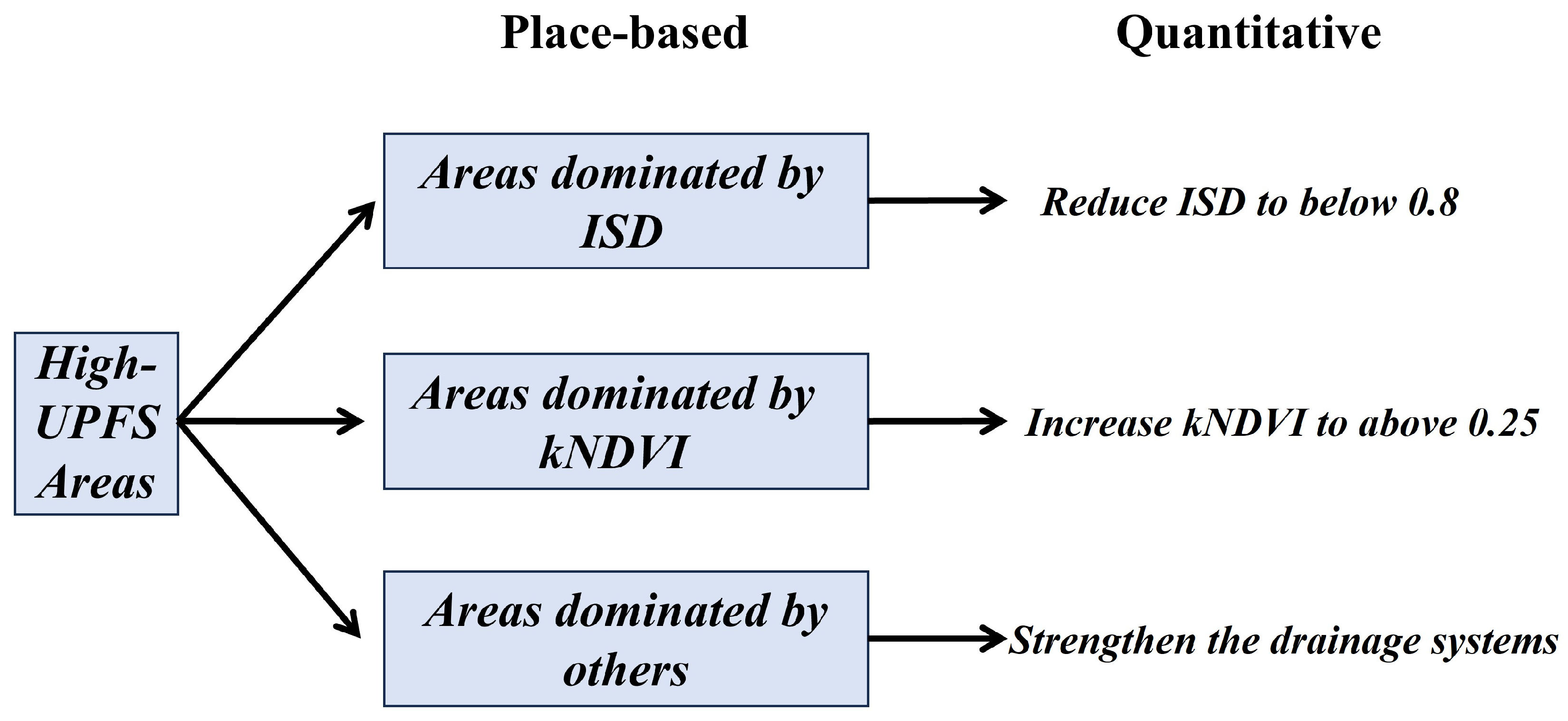
4.1. Place-Based and Quantitative Decision Recommendations

To effectively mitigate urban flooding disasters in the central urban area of Guangzhou, this study provides the following decision support for urban renewal planning based on the analysis results (Figure 8): (1) For areas dominated by ISD, controlling it below 0.8 can effectively alleviate its promoting effect on UPFS. (2) For areas dominated by the kNDVI, maintaining it above 0.25 is necessary to effectively mitigate the occurrence of flooding. (3) For regions dominated by non-human activity-related variables, it is necessary to strengthen the local drainage system. Furthermore, as we believe that BH contains information about the building pattern and drainage system capacity, for areas dominated by BH, it is necessary to appropriately reduce the density of buildings and enhance the capacity of the drainage system. However, due to data limitations, quantitative transformation recommendations for these variables cannot currently be provided.
In addition to decision support, we also provide tailored recommendations for flooding management in the central urban area of Guangzhou based on its current status: (1) For the old town, it is advisable to increase the proportion of pervious surfaces, such as urban green spaces. By breaking the continuity of impervious surfaces and achieving a spatial distribution of “high-low-high” impervious surface density through measures like increasing urban greenery [16], ISD and kNDVI can approach their respective thresholds. Moreover, increasing urban green spaces can regulate local climate, thereby mitigating urban heat islands and rain islands [58]. Additionally, there is a need to develop more robust drainage systems to withstand flooding. (2) Due to its relatively modern nature, only localized renewal is needed in the new town. Therefore, flooding mitigation strategies in the new town can integrate concepts such as LID with localized measures, allowing ISD and kNDVI to approach their thresholds as much as possible. For example, managing rainwater by installing green roofs. (3) During urban renewal in the developing area, it is essential to judiciously re-plan impervious surfaces, urban green spaces, building patterns, and drainage systems. Combining the interpretation results with urban flooding mitigation model can facilitate the optimal spatial distribution of impervious surfaces and drainage systems in urban renewal designs [14]. This approach also partially addresses the limitation of being unable to provide quantitative transformation recommendations for drainage systems.

4.2. Comparison with Existing Studies

The results are highly compatible with existing research. In this study, we assessed UPFS in the central urban area of Guangzhou using ensemble learning. The performance of our model and the flooding susceptibility maps show that, compared to previous studies, we not only achieved better evaluation results but also observed a higher degree of consistency in the flooding susceptibility distribution [59]. Additionally, we utilized the SHAP method to demonstrate the global importance of FRVs. The results indicate that human activity-related variables, such as ISD and kNDVI, have a significant impact on UPFS, which aligns with findings from several studies [33,54,59].
Moreover, this study uncovered the relationship between urban surface structures and urban flooding, which has often been overlooked in previous research, through the nonlinear explanations of variables like slope, dis2w, and BH, as well as the identification of dominant variables. This not only enhances the value of the study but also highlights the potential of interpretable ensemble learning methods.
Furthermore, it is worth noting that tree SHAP is capable of identifying interaction effects between independent variables. However, in the results of this study, no strong interaction effects between FRVs were observed. This contrasts with the findings reported by Zhang et al. (2023) [7], which may be due to their study being conducted at the watershed scale, whereas ours is based on a finer 100 m grid. The difference in scale likely weakens the interaction effects among the FRVs.
Compared to existing research, this study presents the following highlights: (1) Utilizing the local interpretation of SHAP, this study reveals the heterogeneity of the effects of FRVs in different regions and identifies dominant variables. (2) The stability and reliability of the UPFS interpretation results were validated. (3) A simple and effective framework for UPFS assessment and interpretation was proposed, meeting the needs of place-based and quantitative decision making. (4) Tailored quantitative decision recommendations for alleviating urban flooding in the central urban area of Guangzhou were provided based on the dominant variables identified in different regions.

4.3. Limitations

This study has some limitations concerning the spatial database of variables. Some potential variables are challenging to quantify into grid data, making decision support for these variables difficult to provide, such as drainage systems. In future research, we will focus on addressing these issues and incorporating more potential FRVs to gain a more comprehensive understanding of the mechanisms underlying urban flooding, including the use of proxy variables for drainage systems. We look forward to future studies providing more scientific insights for mitigating urban flooding, urban renewal planning, and the sustainable development of cities.
In addition, we acknowledge that the ensemble learning–SHAP approach is merely a method for analyzing associations. Before applying it, domain knowledge is required to understand the relationships between variables and urban pluvial flooding. In this study, BH is an example of a variable that does not have a direct causal relationship with UPFS. In future work, we plan to employ causal models to further explore the relationships between different variables and urban pluvial flooding.
Finally, we acknowledge that the threshold obtained in this study is entirely data-driven. In future work, we will aim to verify its physical significance in real-world settings.

5. Conclusions

This study established a spatially explicit framework integrating XGBoost and SHAP to decipher the complex, nonlinear mechanisms driving urban pluvial flooding. By applying this framework to central Guangzhou, we moved beyond global averaging to reveal how flood drivers vary significantly across local micro-environments. The analysis confirms that anthropogenic variables, specifically impervious surface and vegetation, are not merely correlated with flooding but exhibit distinct nonlinear threshold effects that dictate susceptibility levels in urban hotspots. The high stability of the interpretation results across different model iterations further validates the robustness of this data-driven approach. Crucially, this study translates these diagnostic insights into actionable, place-based management strategies. The results provide place-based and quantitative pluvial flooding management recommendations: for areas dominated by impervious surfaces and vegetation, maintaining the impervious surface density below 0.8 and the kNDVI above 0.25 can effectively reduce the susceptibility to urban flooding. Our framework acts as a tool to advance Sustainable Development Goal (SDG) 11 and SDG 13. The key implementation pathway involves embedding these quantitative thresholds into municipal land use regulations and prioritizing green infrastructure investments in the identified high-susceptibility zones.
Moreover, the proposed framework exhibits strong potential for scalability and broader application. Its reliance on widely available remote sensing data and open-source models means it can be readily adapted to other cities facing similar challenges, provided local flood inventory data is available for model training. We believe this data-driven approach is a crucial step towards proactive and sustainable urban flood management in a changing climate.

Author Contributions

Chaorui Tan: Conceptualization, Methodology, Software, Validation, Writing—original draft, Visualization, Funding acquisition, Investigation, Writing—review and editing. Entong Ke: Conceptualization, Writing—review and editing, Funding acquisition, Supervision, Investigation. Haochen Shi: Conceptualization, Writing—review and editing, Project administration. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Technical Consultation of Housing Integrated Service Station of Hubei Provincial Department of Education (No. BXLBX1136), and the Scientific Research Innovation Project of Graduate School of South China Normal University (No. 2024KYLX100).

Data Availability Statement

Dataset available on request from the authors.

Acknowledgments

We would like to express our gratitude to the editors and the reviewers for their valuable comments and suggestions, which helped to improve the manuscript.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Bera, D.; Kumar, P.; Siddiqui, A.; Majumdar, A. Assessing Impact of Urbanisation on Surface Runoff Using Vegetation-Impervious Surface-Soil (V-I-S) Fraction and NRCS Curve Number (CN) Model. Model. Earth Syst. Environ. 2022, 8, 309–322. [Google Scholar] [CrossRef]
  2. Manawi, S.M.A.; Nasir, K.A.M.; Shiru, M.S.; Hotaki, S.F.; Sediqi, M.N. Urban Flooding in the Northern Part of Kabul City: Causes and Mitigation. Earth Syst. Environ. 2020, 4, 599–610. [Google Scholar] [CrossRef]
  3. Schreider, S.Y.; Smith, D.I.; Jakeman, A.J. Climate Change Impacts on Urban Flooding. Clim. Change 2000, 47, 91–115. [Google Scholar] [CrossRef]
  4. Rentschler, J.; Avner, P.; Marconcini, M.; Su, R.; Strano, E.; Vousdoukas, M.; Hallegatte, S. Global Evidence of Rapid Urban Growth in Flood Zones since 1985. Nature 2023, 622, 87–92. [Google Scholar] [CrossRef]
  5. Davis, A.P. Green Engineering Principles Promote Low-Impact Development. Environ. Sci. Technol. 2005, 39, 338A–344A. [Google Scholar] [CrossRef]
  6. Wu, J.; Sha, W.; Zhang, P.; Wang, Z. The Spatial Non-Stationary Effect of Urban Landscape Pattern on Urban Waterlogging: A Case Study of Shenzhen City. Sci. Rep. 2020, 10, 7369. [Google Scholar] [CrossRef]
  7. Zhang, Q.; Wu, Z.; Cao, Z.; Guo, G.; Zhang, H.; Li, C.; Tarolli, P. How to Develop Site-Specific Waterlogging Mitigation Strategies? Understanding the Spatial Heterogeneous Driving Forces of Urban Waterlogging. J. Clean. Prod. 2023, 422, 138595. [Google Scholar] [CrossRef]
  8. Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically Weighted Regression. J. R. Stat. Soc. Ser. D (Stat.) 1998, 47, 431–443. [Google Scholar] [CrossRef]
  9. Fotheringham, A.S.; Yang, W.; Kang, W. Multiscale Geographically Weighted Regression (MGWR). Ann. Am. Assoc. Geogr. 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
  10. Song, Y.; Wang, J.; Ge, Y.; Xu, C. An Optimal Parameters-Based Geographical Detector Model Enhances Geographic Characteristics of Explanatory Variables for Spatial Heterogeneity Analysis: Cases with Different Types of Spatial Data. GISci. Remote Sens. 2020, 57, 593–610. [Google Scholar] [CrossRef]
  11. Zhang, Z.; Song, Y.; Wu, P. Robust Geographical Detector. Int. J. Appl. Earth Obs. Geoinf. 2022, 109, 102782. [Google Scholar] [CrossRef]
  12. Wang, J.; Li, X.; Christakos, G.; Liao, Y.; Zhang, T.; Gu, X.; Zheng, X. Geographical Detectors-Based Health Risk Assessment and Its Application in the Neural Tube Defects Study of the Heshun Region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
  13. Wang, J.-F.; Zhang, T.-L.; Fu, B.-J. A Measure of Spatial Stratified Heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
  14. Ke, E.; Zhao, J.; Zhao, Y.; Wu, J.; Xu, T. Coupled and Collaborative Optimization Model of Impervious Surfaces and Drainage Systems from the Flooding Mitigation Perspective for Urban Renewal. Sci. Total Environ. 2024, 917, 170202. [Google Scholar] [CrossRef]
  15. Yu, H.; Zhao, Y.; Xu, T.; Li, J.; Tang, X.; Wang, F.; Fu, Y. A High-efficiency Global Model of Optimization Design of Impervious Surfaces for Alleviating Urban Waterlogging in Urban Renewal. Trans. GIS 2021, 25, 1716–1740. [Google Scholar] [CrossRef]
  16. Zhao, J.; Ke, E.; Wang, B.; Zhao, Y. An Optimization Model for the Impervious Surface Spatial Layout Considering Differences in Hydrological Unit Conditions for Urban Waterlogging Prevention in Urban Renewal. Ecol. Indic. 2024, 158, 111546. [Google Scholar] [CrossRef]
  17. Sakieh, Y. Understanding the Effect of Spatial Patterns on the Vulnerability of Urban Areas to Flooding. Int. J. Disaster Risk Reduct. 2017, 25, 125–136. [Google Scholar] [CrossRef]
  18. Lin, J.; He, X.; Lu, S.; Liu, D.; He, P. Investigating the Influence of Three-Dimensional Building Configuration on Urban Pluvial Flooding Using Random Forest Algorithm. Environ. Res. 2021, 196, 110438. [Google Scholar] [CrossRef]
  19. Liu, W.; Zhang, X.; Feng, Q.; Yu, T.; Engel, B.A. Analyzing the Impacts of Topographic Factors and Land Cover Characteristics on Waterlogging Events in Urban Functional Zones. Sci. Total Environ. 2023, 904, 166669. [Google Scholar] [CrossRef]
  20. Sohn, W.; Kim, J.-H.; Li, M.-H.; Brown, R.D.; Jaber, F.H. How Does Increasing Impervious Surfaces Affect Urban Flooding in Response to Climate Variability? Ecol. Indic. 2020, 118, 106774. [Google Scholar] [CrossRef]
  21. Wang, L.; Hou, H.; Li, Y.; Pan, J.; Wang, P.; Wang, B.; Chen, J.; Hu, T. Investigating Relationships between Landscape Patterns and Surface Runoff from a Spatial Distribution and Intensity Perspective. J. Environ. Manag. 2023, 325, 116631. [Google Scholar] [CrossRef]
  22. Motta, M.; de Castro Neto, M.; Sarmento, P. A Mixed Approach for Urban Flood Prediction Using Machine Learning and GIS. Int. J. Disaster Risk Reduct. 2021, 56, 102154. [Google Scholar] [CrossRef]
  23. Tang, X.; Wu, Z.; Liu, W.; Tian, J.; Liu, L. Exploring Effective Ways to Increase Reliable Positive Samples for Machine Learning-Based Urban Waterlogging Susceptibility Assessments. J. Environ. Manag. 2023, 344, 118682. [Google Scholar] [CrossRef]
  24. Tehrany, M.S.; Jones, S.; Shabani, F. Identifying the Essential Flood Conditioning Factors for Flood Prone Area Mapping Using Machine Learning Techniques. Catena 2019, 175, 174–192. [Google Scholar] [CrossRef]
  25. Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 1–10. [Google Scholar]
  26. Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
  27. Wang, M.; Li, Y.; Yuan, H.; Zhou, S.; Wang, Y.; Adnan Ikram, R.M.; Li, J. An XGBoost-SHAP Approach to Quantifying Morphological Impact on Urban Flooding Susceptibility. Ecol. Indic. 2023, 156, 111137. [Google Scholar] [CrossRef]
  28. Tian, J.; Chen, Y.; Yang, L.; Li, D.; Liu, L.; Li, J.; Tang, X. Enhancing Urban Flood Susceptibility Assessment by Capturing the Features of the Urban Environment. Remote Sens. 2025, 17, 1347. [Google Scholar] [CrossRef]
  29. Zerouali, B.; Almaliki, A.H.; Santos, C.A.G. Flood Susceptibility Mapping in Arid Urban Areas Using SHAP-Enhanced Stacked Ensemble Learning: A Case Study of Jeddah. J. Environ. Manag. 2025, 393, 127128. [Google Scholar] [CrossRef]
  30. Li, Z.; Tian, J.; Zhu, Y.; Chen, D.; Ji, Q.; Sun, D. A Study on Flood Susceptibility Mapping in the Poyang Lake Basin Based on Machine Learning Model Comparison and SHapley Additive exPlanations Interpretation. Water 2025, 17, 2955. [Google Scholar] [CrossRef]
  31. Gulshad, K.; Yaseen, A.; Szydłowski, M. From Data to Decision: Interpretable Machine Learning for Predicting Flood Susceptibility in Gdańsk, Poland. Remote Sens. 2024, 16, 3902. [Google Scholar] [CrossRef]
  32. Singha, C.; Chakraborty, N.; Sahoo, S.; Pham, Q.B.; Xuan, Y. A Novel Framework for Flood Susceptibility Assessment Using Hybrid Analytic Hierarchy Process-Based Machine Learning Methods. Nat. Hazards 2025, 121, 13765–13810. [Google Scholar] [CrossRef]
  33. Liu, F.; Liu, X.; Xu, T.; Yang, G.; Zhao, Y. Driving Factors and Risk Assessment of Rainstorm Waterlogging in Urban Agglomeration Areas: A Case Study of the Guangdong-Hong Kong-Macao Greater Bay Area, China. Water 2021, 13, 770. [Google Scholar] [CrossRef]
  34. Ministry of Civil Affairs of the People’s Republic of China. Administrative Divisions of the People’s Republic of China, 1949–1997; China Society Press: Beijing, China, 1998; ISBN 978-7-80146-034-9. [Google Scholar]
  35. Peng, S. 1-Km Monthly Precipitation Dataset for China (1901–2022); National Tibetan Plateau Data Center: Beijing, China, 2020. [Google Scholar]
  36. Li, Z.; He, W.; Cheng, M.; Hu, J.; Yang, G.; Zhang, H. SinoLC-1: The First 1-meter Resolution National-Scale Land-Cover Map of China Created with a Deep Learning Framework and Open-Access Data. Earth Syst. Sci. Data 2023, 15, 4749–4780. [Google Scholar] [CrossRef]
  37. Wu, W.-B.; Ma, J.; Banzhaf, E.; Meadows, M.E.; Yu, Z.-W.; Guo, F.-X.; Sengupta, D.; Cai, X.-X.; Zhao, B. A First Chinese Building Height Estimate at 10 m Resolution (CNBH-10 m) Using Multi-Source Earth Observations and Machine Learning. Remote Sens. Environ. 2023, 291, 113578. [Google Scholar] [CrossRef]
  38. Monte, B.E.O.; Goldenfum, J.A.; Michel, G.P.; de Albuquerque Cavalcanti, J.R. Terminology of Natural Hazards and Disasters: A Review and the Case of Brazil. Int. J. Disaster Risk Reduct. 2021, 52, 101970. [Google Scholar] [CrossRef]
  39. Yan, Z.; Guo, X.; Zhao, Z.; Tang, L. Achieving Fine-Grained Urban Flood Perception and Spatio-Temporal Evolution Analysis Based on Social Media. Sustain. Cities Soc. 2024, 101, 105077. [Google Scholar] [CrossRef]
  40. McGuire, K.J.; McDonnell, J.J.; Weiler, M.; Kendall, C.; McGlynn, B.L.; Welker, J.M.; Seibert, J. The Role of Topography on Catchment-Scale Water Residence Time. Water Resour. Res. 2005, 41, 5002. [Google Scholar] [CrossRef]
  41. Crave, A.; Gascuel-Odoux, C. The Influence of Topography on Time and Space Distribution of Soil Surface Water Content. Hydrol. Process. 1997, 11, 203–210. [Google Scholar] [CrossRef]
  42. Ke, E.; Zhao, J.; Zhao, Y. Investigating the Influence of Nonlinear Spatial Heterogeneity in Urban Flooding Factors Using Geographic Explainable Artificial Intelligence. J. Hydrol. 2025, 648, 132398. [Google Scholar] [CrossRef]
  43. Xu, T.; Zhang, X.; Liu, F.; Zhao, Y.; Ke, E. How Do Social Management Systems and Urbanization Influence the Spatio-Temporal Characteristics of Urban Flood Risk? A Comparison between Guangzhou and Hong Kong, China. J. Hydrol. 2025, 647, 132335. [Google Scholar] [CrossRef]
  44. Zhang, W.; Qiu, S.; Lin, Z.; Chen, Z.; Yang, Y.; Lin, J.; Li, S. Assessing the Influence of Green Space Morphological Spatial Pattern on Urban Waterlogging: A Case Study of a Highly-Urbanized City. Environ. Res. 2025, 266, 120561. [Google Scholar] [CrossRef]
  45. Ma, M.; Zhao, G.; He, B.; Li, Q.; Dong, H.; Wang, S.; Wang, Z. XGBoost-Based Method for Flash Flood Risk Assessment. J. Hydrol. 2021, 598, 126382. [Google Scholar] [CrossRef]
  46. Towfiqul Islam, A.R.M.; Talukdar, S.; Mahato, S.; Kundu, S.; Eibek, K.U.; Pham, Q.B.; Kuriqi, A.; Linh, N.T.T. Flood Susceptibility Modelling Using Advanced Ensemble Machine Learning Models. Geosci. Front. 2021, 12, 101075. [Google Scholar] [CrossRef]
  47. Tang, X.; Hong, H.; Shu, Y.; Tang, H.; Li, J.; Liu, W. Urban Waterlogging Susceptibility Assessment Based on a PSO-SVM Method Using a Novel Repeatedly Random Sampling Idea to Select Negative Samples. J. Hydrol. 2019, 576, 583–595. [Google Scholar] [CrossRef]
  48. Lee, J.-Y.; Kim, J.-S. Detecting Areas Vulnerable to Flooding Using Hydrological-Topographic Factors and Logistic Regression. Appl. Sci. 2021, 11, 5652. [Google Scholar] [CrossRef]
  49. Rana, M.S.; Mahanta, C. Spatial Prediction of Flash Flood Susceptible Areas Using Novel Ensemble of Bivariate Statistics and Machine Learning Techniques for Ungauged Region. Nat. Hazards 2023, 115, 947–969. [Google Scholar] [CrossRef]
  50. Blum, A.G.; Ferraro, P.J.; Archfield, S.A.; Ryberg, K.R. Causal Effect of Impervious Cover on Annual Flood Magnitude for the United States. Geophys. Res. Lett. 2020, 47, e2019GL086480. [Google Scholar] [CrossRef]
  51. Li, Y.; Osei, F.B.; Hu, T.; Stein, A. Urban Flood Susceptibility Mapping Based on Social Media Data in Chengdu City, China. Sustain. Cities Soc. 2023, 88, 104307. [Google Scholar] [CrossRef]
  52. Wang, Y.; Li, C.; Liu, M.; Cui, Q.; Wang, H.; Lv, J.; Li, B.; Xiong, Z.; Hu, Y. Spatial Characteristics and Driving Factors of Urban Flooding in Chinese Megacities. J. Hydrol. 2022, 613, 128464. [Google Scholar] [CrossRef]
  53. Yu, S.; Yuan, M.; Wang, Q.; Corcoran, J.; Xu, Z.; Peng, J. Dealing with Urban Floods within a Resilience Framework Regarding Disaster Stages. Habitat. Int. 2023, 136, 102783. [Google Scholar] [CrossRef]
  54. Zhang, Q.; Wu, Z.; Zhang, H.; Dalla Fontana, G.; Tarolli, P. Identifying Dominant Factors of Waterlogging Events in Metropolitan Coastal Cities: The Case Study of Guangzhou, China. J. Environ. Manag. 2020, 271, 110951. [Google Scholar] [CrossRef] [PubMed]
  55. Li, H.; Wang, Q.; Li, M.; Zang, X.; Wang, Y. Identification of Urban Waterlogging Indicators and Risk Assessment Based on MaxEnt Model: A Case Study of Tianjin Downtown. Ecol. Indic. 2024, 158, 111354. [Google Scholar] [CrossRef]
  56. Chen, G.; Chen, Y.; Tan, X.; Zhao, L.; Cai, Y.; Li, L. Assessing the Urban Heat Island Effect of Different Local Climate Zones in Guangzhou, China. Build. Environ. 2023, 244, 110770. [Google Scholar] [CrossRef]
  57. Adnan, M.S.G.; Siam, Z.S.; Kabir, I.; Kabir, Z.; Ahmed, M.R.; Hassan, Q.K.; Rahman, R.M.; Dewan, A. A Novel Framework for Addressing Uncertainties in Machine Learning-Based Geospatial Approaches for Flood Prediction. J. Environ. Manag. 2023, 326, 116813. [Google Scholar] [CrossRef]
  58. Aflaki, A.; Mirnezhad, M.; Ghaffarianhoseini, A.; Ghaffarianhoseini, A.; Omrany, H.; Wang, Z.-H.; Akbari, H. Urban Heat Island Mitigation Strategies: A State-of-the-Art Review on Kuala Lumpur, Singapore and Hong Kong. Cities 2017, 62, 131–145. [Google Scholar] [CrossRef]
  59. Zhao, J.; Wang, J.; Abbas, Z.; Yang, Y.; Zhao, Y. Ensemble Learning Analysis of Influencing Factors on the Distribution of Urban Flood Risk Points: A Case Study of Guangzhou, China. Front. Earth Sci. 2023, 11, 1042088. [Google Scholar] [CrossRef]
Ijgi 14 00475 g001
Figure 1. The central urban area of Guangzhou, along with its Area (km2), population (in thousands), and 2023 GDP (in trillions of yuan). LW: Liwan District. YX: Yuexiu District. HZ: Haizhu District. TH: Tianhe District. BY: Baiyun District. HP: Huangpu District.
Figure 1. The central urban area of Guangzhou, along with its Area (km2), population (in thousands), and 2023 GDP (in trillions of yuan). LW: Liwan District. YX: Yuexiu District. HZ: Haizhu District. TH: Tianhe District. BY: Baiyun District. HP: Huangpu District.
Ijgi 14 00475 g001
Ijgi 14 00475 g002
Figure 2. Research framework. FRVs: flooding-related variables. UPFS: Urban pluvial flooding susceptibility.
Figure 2. Research framework. FRVs: flooding-related variables. UPFS: Urban pluvial flooding susceptibility.
Ijgi 14 00475 g002
Ijgi 14 00475 g003
Figure 3. (a) UPFS map of the central urban area of Guangzhou; (b–d) area (in square kilometers) of each susceptibility rank in the old town, new town, and developing area.
Figure 3. (a) UPFS map of the central urban area of Guangzhou; (b–d) area (in square kilometers) of each susceptibility rank in the old town, new town, and developing area.
Ijgi 14 00475 g003
Ijgi 14 00475 g004
Figure 4. (a) Distributions of SHAP values for FRVs. (b) Global importance of FRVs for UPFS.
Figure 4. (a) Distributions of SHAP values for FRVs. (b) Global importance of FRVs for UPFS.
Ijgi 14 00475 g004
Ijgi 14 00475 g005
Figure 5. (a–c) binary maps of susceptibility in relation to precipitation, geographical variables, and land surface variables. Darker colors indicate higher susceptibility, with the color spectrum of red, green, and blue representing positive, low, and high influences, respectively. (a1,b1–b3,c1–c4) SHAP dependence plots for FRVs. The low influence intervals are covered in purple. The density of scatter points is quantified based on kernel density estimation (KDE). (B1) enlarged binary map highlights the area around overpasses. (B2) satellite image of the overpass. (C1) low-rise building cluster in the developing area. (C2) high-rise building cluster in the new town.
Figure 5. (a–c) binary maps of susceptibility in relation to precipitation, geographical variables, and land surface variables. Darker colors indicate higher susceptibility, with the color spectrum of red, green, and blue representing positive, low, and high influences, respectively. (a1,b1–b3,c1–c4) SHAP dependence plots for FRVs. The low influence intervals are covered in purple. The density of scatter points is quantified based on kernel density estimation (KDE). (B1) enlarged binary map highlights the area around overpasses. (B2) satellite image of the overpass. (C1) low-rise building cluster in the developing area. (C2) high-rise building cluster in the new town.
Ijgi 14 00475 g005
Ijgi 14 00475 g006
Figure 6. Distribution of dominant variables and local analysis of variables contributions of representative individuals. (a–c) The primary, secondary, and tertiary dominant variables map; (A–C) Regions corresponding to representative individuals A, B, and C (highlighted in red) along with their satellite images; (A1–C1) SHAP values for FRVs in regions A, B, and C. E(f(x)) is the base value of the SHAP values, which is −0.014 in this study.
Figure 6. Distribution of dominant variables and local analysis of variables contributions of representative individuals. (a–c) The primary, secondary, and tertiary dominant variables map; (A–C) Regions corresponding to representative individuals A, B, and C (highlighted in red) along with their satellite images; (A1–C1) SHAP values for FRVs in regions A, B, and C. E(f(x)) is the base value of the SHAP values, which is −0.014 in this study.
Ijgi 14 00475 g006
Ijgi 14 00475 g007
Figure 7. Relationship among ISD, UPFS and SHAP values. Pink points represent the SHAP values for ISD, while the blue scatter points show the predicted UPFS probabilities. The consistent trend between ISD and UPFS indicates that the interpretation results are reliable. The two dashed lines represent the two thresholds, respectively.
Figure 7. Relationship among ISD, UPFS and SHAP values. Pink points represent the SHAP values for ISD, while the blue scatter points show the predicted UPFS probabilities. The consistent trend between ISD and UPFS indicates that the interpretation results are reliable. The two dashed lines represent the two thresholds, respectively.
Ijgi 14 00475 g007
Ijgi 14 00475 g008
Figure 8. A place-based and quantitative decision support framework for high-UPFS areas.
Figure 8. A place-based and quantitative decision support framework for high-UPFS areas.
Ijgi 14 00475 g008
Table 1. Data source.
Table 1. Data source.
DataSourceDescription
Flood pointsGuangzhou Water Affairs BureauShapefile format, published in 2020, representing the complete dataset for Guangzhou
Landsat 8 OLI satellite imageryAI Earth platformTIFF format, 30 m resolution, captured in November 2019
PrecipitationPeng (2020) [35]TIFF format, 1 km resolution
Digital Elevation Model (DEM)ASTGTM V003TIFF format, 30 m resolution
Soil textureHWSD v2.0s databaseTIFF format, 1 km resolution
Land use dataZ. Li et al. (2023) [36]TIFF format, 1 m resolution, 2020
Building Height (BH)Wu et al. (2023) [37]TIFF format, 10 m resolution, 2020
Table 2. Results of the multicollinearity test.
Table 2. Results of the multicollinearity test.
FRVsPREDEMSlopeAWCISDkNDVIDis2wBH
VIF1.0524.9025.5122.575.986.051.2792.034
Table 3. Model performance evaluation.
Table 3. Model performance evaluation.
ModelOverall AccuracyF1 ScoreAUCKappa
RF0.8290.8480.9120.656
GBDT0.8380.8530.9050.674
XGBoost0.8550.8640.9180.709
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Tan, C.; Ke, E.; Shi, H. Leveraging Explainable Artificial Intelligence for Place-Based and Quantitative Strategies in Urban Pluvial Flooding Management. ISPRS Int. J. Geo-Inf. 2025, 14, 475. https://doi.org/10.3390/ijgi14120475

AMA Style

Tan C, Ke E, Shi H. Leveraging Explainable Artificial Intelligence for Place-Based and Quantitative Strategies in Urban Pluvial Flooding Management. ISPRS International Journal of Geo-Information. 2025; 14(12):475. https://doi.org/10.3390/ijgi14120475

Chicago/Turabian Style

Tan, Chaorui, Entong Ke, and Haochen Shi. 2025. "Leveraging Explainable Artificial Intelligence for Place-Based and Quantitative Strategies in Urban Pluvial Flooding Management" ISPRS International Journal of Geo-Information 14, no. 12: 475. https://doi.org/10.3390/ijgi14120475

APA Style

Tan, C., Ke, E., & Shi, H. (2025). Leveraging Explainable Artificial Intelligence for Place-Based and Quantitative Strategies in Urban Pluvial Flooding Management. ISPRS International Journal of Geo-Information, 14(12), 475. https://doi.org/10.3390/ijgi14120475

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop