Abstract
In this paper we describe the potentialities of a tool for the visualization of experimental results directly on a three-dimensional model. The case study concerns the visualization of the results of a dynamic finite element analysis (FEA/FEM) applied to the calculation of seismic risk on works belonging to the Italian infrastructural heritage, specifically bridges, viaducts and overpasses. The project is based on finite element analysis performed on an exemplary set of eight structures located on the Italian territory, performed by means of the open-source software framework OpenSees, according to the guidelines indicated in the Technical Standards for Construction NTC08. The application created for this project is classifiable as a webGIS, since all data are georeferenced and visualized on a map through an application executed through a browser. The graphical interface displays the interested works on the map of the Italian territory and allows to select them by mouse click. Following the selection, a 3D rendering of the model of the work and the surrounding terrain is shown, in which the results of the analysis are represented using color gradients directly on the three-dimensional model. The necessary tools are present for the selection of the type of result and for the animation in real time of the response of the work to the seismic action. The 3D representation is freely navigable by the user due to intuitive tools of panning, rotation and zoom through mouse and keyboard. The application takes advantage of HTML5, CSS and Javascript to show graphical features such as Cartesian diagrams of accelerograms used in modal analysis.
1. Introduction
Italy can count on a rich infrastructural heritage, made up of bridges, viaducts and overpasses on both road and rail networks. Economic development is based on these infrastructures and inevitably relies on the transport sector to move goods and raw materials that are fundamental to all sectors of the economy.
The safety of infrastructural works, of course, is not only important for commercial purposes but it is especially important for the safety of millions of people who travel on them every day; tragedies such as the recent collapse of the Morandi bridge in Genoa have shown that monitoring and complete knowledge of the structural elements of these works is of fundamental importance.
One of the major risks in the country is seismic; Italy is one of the countries with high seismic risk, especially along the Apennines, and this requires extreme caution in the design and maintenance of infrastructure works, which are by their nature vulnerable to ground movements caused by an earthquake. For this reason, in 2008 the Technical Standards for Construction [1] were introduced, then updated in 2018, in which, among other things are defined criteria with which to perform analysis for seismic risk.
Civil and structural engineers who deal with these issues rely on finite state modeling software, or FEA/FEM (finite element analysis/finite element method), to perform the necessary calculations [2]; this software starts from a three-dimensional model of the system to be analyzed, dividing it into small parts for which it is easier to perform the calculations, then arriving at the final result [3,4,5].
The finite element (FE) method is a popular community simulation technique. Since its appearance in the late 1940s as a method for structural analysis, it has continually developed into a sophisticated simulation method with application in many scientific disciplines. As with any numerical technique, there is the drawback that FE simulations produce information that is proportional to the size of the numerical model. For simulations, the time or iterative analyses involve multiple simulation steps with an enormous amount of information produced. As a result, visualization techniques have evolved significantly over the past few decades and have become indispensable for interpreting finite element output data. Most of the current FEM post-processors currently available are still in the local environment due to the limited ability to navigate and interact with the model in open environments, such as the web.
A number of commercial VR-based software packages have recently become available, for example [6,7,8]. These products are, however, proprietary, which eliminates users’ potential and extensions because the source code is not publicly available. For example, users cannot develop new training, research and education tools that rely directly on these platforms.
One such software is OpenSees [9], created by the University of Berkley, which is proposed as an alternative to commercially available software on the market.
OpenSees is a well-known analysis platform in earthquake engineering research because it provides a powerful solver with many standard and constitutive material models, finite element types, boundary conditions, and analysis capabilities. A large number of researchers are actively contributing to its development and innovative features. However, engineers are not interested in using it in their professions because of its lack of a GUI. Visualization through a GUI is important; for these reasons the idea of transforming the models generated in the OpenSees environment and distribute them in a web environment through the browser was born, with the possibility of having a user friendly environment to verify the simulations obtained and disseminate them to a large number of users, professionals and students.
The project described in this paper proposes to be a valid help in the elaboration and visualization of the results of these analyses, presenting them in the form of a color gradient applied directly to a three-dimensional model of the work.
In order to insert the model even better in its natural context, it was decided to add a model of the surrounding terrain, with elevation data taken from the DEM (digital elevation model) TINITALY/01 of INGV [10], and textures obtained from the satellite images [11].
In recent years, there has been a growth in the proposal and use of web platforms, executed by the browsers already installed on the computers. As a consequence, this lead to the significant advantages, such as independence from the operating system and type of hardware, execution of complex calculations on the remote servers and lack of installers that could lead to attacks by malicious software. For this reason it was decided to follow this path, creating a cartographic web application in which data are georeferenced and 3D rendering is carried out client-side through the Three.js Javascript library [12,13,14,15].
2. Materials and Methods
2.1. GIS System
Geographic information systems (GIS) systems are computerized information systems that allow the acquisition, processing and display of georeferenced spatial data. The computer system is therefore able to associate data with their position on the earth’s surface, to allow their processing, aggregation, search and display on a map [16].
The main use of GIS systems is in digital cartography, in the study and representation of natural and human phenomena in relation to the territory.
GIS systems are composed of a hardware part, consisting of processors in which data are stored on file systems or databases, and a software part, which is responsible for acquiring any input data, perform processing and interface with the user through the UI (user interface).
2.2. WebGIS System
In recent years, the internet connection has expanded considerably, and nowadays it is difficult to find a device (PC, tablet, smartphone) that is not connected to the network. For this reason, in addition to desktop GIS applications [17], i.e., installed and executed locally on the device, more and more cartographic applications executed through a browser, the so-called webGIS, have become popular.
WebGIS are based on a client-server architecture: the client, running on a browser, has the task of displaying geographical information and acquiring input data and commands; the server, on the other hand, processes the input data and provides the client with the required data in the form of numerical data, vector or raster geographical data. The web approach has significant advantages:
- There is no need to install software locally, with all the problems of hardware and software incompatibility that this might entail;
- It allows for the development and maintenance of a single version of the software: the browsers on which it runs are an additional level of abstraction, and it is up to them to manage the differences, for example, between Windows, Linux, MacOS environments;
- It has the ability to access the software from any device, anywhere in the world, as long as it has an internet connection: most webGIS offer authentication features, allowing access to personal data and settings once logged in;
- Execution of any processing can be carried out on the server hardware instead of on the user’s device: this allows, especially in case of heavy processing, to launch their execution, disconnect from the application and return to check the status of processing, without keeping local resources busy [18,19].
2.3. Data Types
Working with graphical representations of data, GIS systems must be able to handle various formats in which these may be presented. The two main categories are vector data and raster data.
2.3.1. Vector Data
Vector data consists of vectors containing numerical information about the positioning of the various points that make up the geographic data. These can be point, linear or polygonal data. As seen in Figure 1, Figure 2 and Figure 3. They are usually composed of two parts: the geographic vector itself, used by the GIS system to position the geometry on the map, and a set of attributes associated with the geometry, which can be displayed for example when selecting the point of interest.

Figure 1.
Point-type vector geometry.

Figure 2.
Linear type vector geometry.

Figure 3.
Polygon type vector geometry.
- Punctual: each point is described by 2 or 3 coordinates that represent its position; since they do not have a displayed geometry, they are usually represented by a symbology (circles, colored squares) that indicate their position;
- Linear: each line is represented by a break, in which a series of coordinates indicate the position of its segments; the end point of a segment corresponds with the starting point of the next segment;
- Polygonal: are represented by a series of coordinates, as well as linear geometries; the initial point, however, always corresponds with the end point, so as to obtain a closed polygon; there may be cavities within the polygons, often represented with an inverse order of the vertices with respect to that of the inverse polygon (clockwise/counterclockwise direction).
Vector data have the advantage, being numerical representations, of not undergoing degradation even at high zoom levels of the map, as the geometries are recalculated and re-projected on the screen coordinates (the so-called screen space) in real time.
2.3.2. Raster Data
In raster data, geographic information is saved within the pixels of a bitmap figure, therefore in a grid of fixed dimensions.
The functionalities of the GIS system will then allow, due to the metadata associated with the image, to correctly position it on the map, deforming its vertices so that they correspond to the initial and final coordinates indicated in the metadata.
In Figure 4, the same raster image displayed with two different coordinate reference system (CRS) can be seen. On the left the CRS used corresponds to that of the raster image, while on the right the GIS system had to perform a deformation to adapt the CRS of the image to that of the project [7]. Figure 5 shows the resolution of a raster image.

Figure 4.
Raster image represented by two different CRSs.

Figure 5.
Resolution of a raster image.
Being composed of a limited number of pixels, raster data suffers from resolution loss and grainy effects at high zoom levels; moreover, unlike vector data, they cannot usually have multiple attributes associated with a single pixel. However, they are useful for representing complex phenomena that cannot be represented by point or polygonal geometries [20,21,22].
2.4. Finite Element Analysis
Finite element analysis (FEM, finite elements method, or more properly FEA, finite elements analysis), is a computational technique performed using computers, which allows to study the structural behavior of a system. This tool is commonly used in engineering to study the behavior of mechanical systems.
The analysis consists of creating a three-dimensional model (mesh) of the system to be analyzed and subdividing it into many smaller elements of easy mathematical solution. The total result will be obtained by summing the results obtained on all the elements. A finite element analysis allows you to study how the system reacts to external stresses, recording the displacements, deformations and stresses to which each part is subjected. As shown in Figure 6 and Figure 7.
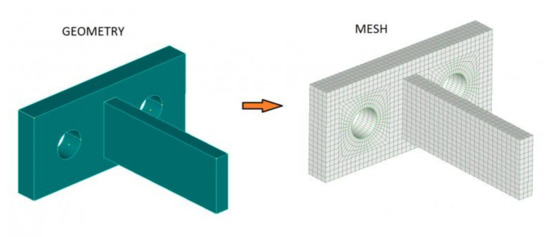
Figure 6.
Generation of a mesh from the geometry.
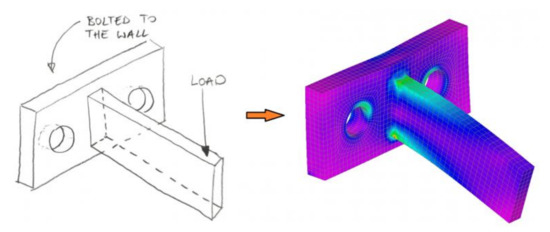
Figure 7.
Mesh deformation after analysis.
2.4.1. Modal Analysis with FEM Method
Modal analysis is the study of the dynamic properties of structures under vibrational excitation. It is performed on the linear elastic model, so elastic elements have also been defined for curves. In structural engineering, modal analysis involves the use of both, a system mass matrix and a system stiffness matrix. The purpose is to estimate the natural frequencies (periods) and corresponding mode shapes associated with the dynamics of the system. These vibration periods are crucial to note in earthquake engineering, since it is desirable that the natural frequency of a structure does not match the frequency of earthquakes expected in the region where the building is to be constructed. If the natural frequency of a structure matches the frequency of an earthquake, the structure could continue to resonate and suffer structural damage.
The goal of modal analysis in structural mechanics is to determine the shapes and frequencies of the natural modes of an object or structure during free vibration. The finite element method (FEM) is used to perform this analysis because, like other calculations using FEM, the object being analyzed can have an arbitrary shape and the results of the calculations are acceptable. The types of equations that arise from modal analysis are those seen in eigensystems. The physical interpretation of the eigenvalues and eigenvectors that arise from solving the system is that they represent frequencies and modes corresponding shapes. Sometimes, the only desired modes are the lowest frequencies because they may be the most important modes in which the object will vibrate, dominating all the higher frequency modes [23,24].
For the most basic problem involving a linear elastic material that obeys Hooke’s Law, the matrix equations take the form of a three-dimensional dynamic mass-spring system. The generalized equation of motion is given as:
where [M] is the mass matrix, [Ű] is the second derivative of displacement [U] (i.e., acceleration), [Ŭ] is the velocity, [C] is a damping matrix, [K] is the stiffness matrix, and [F] is the force vector. The general problem, with non-zero damping, is a quadratic eigenvalue problem. However, for vibrational modal analysis, the damping is generally ignored, leaving only the 1st and 3rd terms on the left-hand side:
[M][Ű] + [C][Ŭ] + [K][U] = [F]
[M][Ű] + [K][U] = [0]
This is the general eigensystem form encountered in structural engineering using FEM. To represent the free vibration solutions of the structure, we assume harmonic motion, so that [Ű] is equal to ω2 [U], where ω2 is an eigenvalue (with squared reciprocal time units, [s -2]), and the equation reduces to:
this eigenvalue problem will provide the natural frequency of the system, through which it will be possible to calculate the eigenvectors, physically represented by the shapes of the modes of the system, as mentioned before. The calculated natural frequencies are derived from the analytical model with the elastic boundary elements located at the ends of the shoulders, and the fixed ends for the columns. The mode shapes corresponding to the calculated natural frequencies of the bridge are plotted for the vertical and transverse directions.
[M][U] ω2 + [K][U] = [0]
2.4.2. Seismic Risk Analysis
Italy is a country characterized by a high seismic risk. The damages, both economic and in terms of human lives, are mostly due to the collapse or serious damage of buildings and infrastructures; for this reason, it is important to carry out careful analysis on the Italian infrastructural heritage, to understand how the thousands of works present on the territory (bridges, viaducts, overpasses) could respond to a possible seismic event commensurate with the seismic hazard of the place where they are located.
An analysis of this type can detect the criticality of the work, possibly also identifying which elements need more monitoring or strengthening interventions.
The first step is to identify what is the seismic hazard at the point where the work rises: for this purpose, the INGV has released a seismic hazard map, which indicates the PGA (peak ground acceleration) expected with a probability of 10% in 50 years shown in Figure 8.
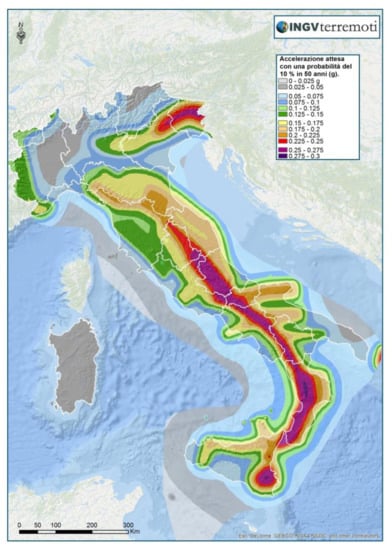
Figure 8.
Italian seismic risk map.
In 2008, the Technical Standards for Construction (NTC) [25] were introduced, which define the methods according to which these analyses must be performed.
First of all, nine return periods are identified, corresponding to 30, 50, 72, 101, 140, 201, 475, 975, 2475 years. A return period indicates the time in which, statistically, an event of a certain magnitude may recur.
Three values are defined for each of these periods:
- Ag (or PGA), maximum horizontal ground acceleration;
- F0, maximum value of the amplification factor of the spectrum in horizontal acceleration;
- T*C, start period of the constant velocity section of the spectrum in o-horizontal acceleration.
These values describe the seismic spectrum, shown in Figure 9, i.e., the time trend of ground acceleration for that given return.
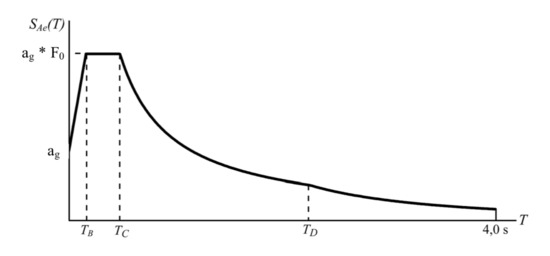
Figure 9.
Seismic spectrum.
On the basis of the seismic spectrum, the accelerograms which will be used in the simulation are generated numerically; these are artificial signals whose deviation must not exceed 10% below and 30% above the starting spectrum [26,27,28].
The results obtained from the dynamic finite element analysis are then summarized in a series of fragility curves associated with the work; these curves indicate the probability of reaching a certain level of damage, which may represent light, moderate, severe or collapse of the infrastructure [29,30].
2.5. OpenSees Software
OpenSees (open system for earthquake engineering simulation) is a software framework for simulating the seismic response of structural and geotechnical systems using finite element simulation.
OpenSees is open-source, and was originally developed as a computational platform for earthquake engineering research at the Pacific Earthquake Engineering Research Center, a research program of Berkley University of California.
The framework has advanced capabilities for modeling and analysis of systems using a wide choice of models, elements, and resolution algorithms. It is also prepared for parallel computing, thus ensuring scalability of simulations, [31,32,33,34] shown in Figure 10.
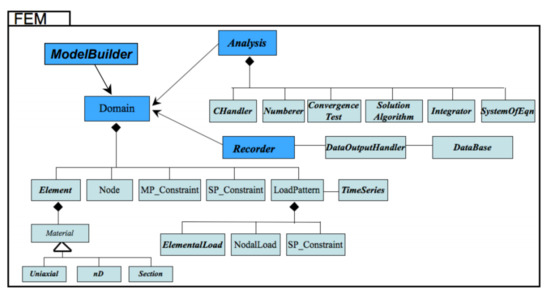
Figure 10.
Logical schema of the OpenSees class hierarchy.
OpenSees uses object-oriented methodologies to offer maximum modularity and extensibility, is written primarily in C++ with numerical libraries in Fortran and C.
The executable is essentially an interpreter based on the TCL scripting language, which is installed together with the framework, and the input files will then be written following the rules of that language.
The execution of a simulation using OpenSees is divided into three basic steps:
- Creation of the model;
- Analysis on the created model;
- Output of the analysis.
2.5.1. Creation of the Model
OpenSees provides beam-column elements and continuum elements to create structural and geotechnical models. A wide variety of uniaxial materials and sections for beam-column elements are also available.
The model creation process consists of generating one or more .xtcl files containing information about the system. In particular, the nodes, materials, sections, elements connecting the nodes, and masses to be applied to the nodes must be defined, as shown in Figure 11.
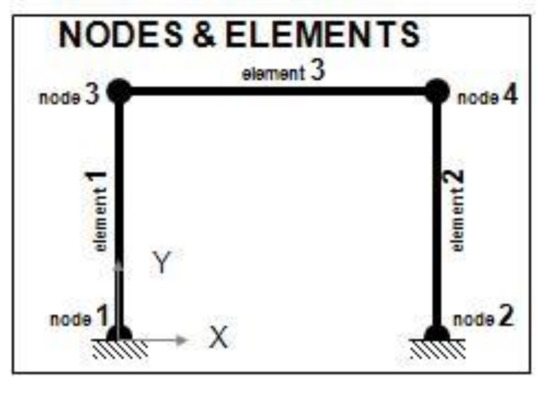
Figure 11.
Representation of the OpenSees model.
This information will be passed to the ModelBuilder module, which will take care of generating a mathematical model of the system to be simulated.
2.5.2. Types of Analysis
Nonlinear analysis requires a variety of algorithms and resolution methods. OpenSees provides both static and dynamic nonlinear methods, equation solvers and methods for the management of constraints.
The dynamic analysis, performed for this project according to the indications of the NTC 2008, foresees the use of 9 return times, fixed at 30, 50, 72, 101, 140, 201, 475, 975 and 2475 years, for each of which are extracted the values ag, f0, T*c according to the local seismic hazard at the site of the work. Starting from these 3 values, the so-called artificial signals are numerically created, i.e., random accelerograms in the X (longitudinal with respect to the work) and Y (transverse) coordinates, which reproduce the pga (peak ground acceleration) typical of an earthquake. Each accelerogram is defined for a minimum duration of 25 s, according to NTC08.
The analysis of the OpenSees software simulates the response of the infrastructure to the seismic action, recording the forces applied to its various elements and the consequent displacements.
2.5.3. Solving Algorithms
The main incremental iterative procedures are available in OpenSees, for nonlinear analysis. The available algorithms are Newton–Raphson, Newton–Raphson with inline search, and Broyden and derivatives. The algorithms are used in the order presented, later in case the convergence of the previous one fails [35,36].
- The Newton–Raphson algorithm is the most widely used and most robust iterative method for re-solving systems of nonlinear algebraic equations. It is also the most demanding in terms of computational effort because the stiffness matrix must be updated at each iteration step.
- The Newton–Raphson algorithm with line search introduces line search to solve the nonlinear residual equation. Line search increases the effectiveness of Newton’s method when convergence is slow due to the roughness of the residual. The stiffness matrix is not updated at each step. This implies reduced computational effort, which is the advantage of this method. The disadvantage of this method is that it requires more iterations than Newton’s method, so convergence is slower.
- Broyden’s algorithm is for general non-symmetric systems. It performs successive rank-one updates of the tangent at the first iteration of the time step. This algorithm is only used in critical cases because the algorithm concentrates iterations at points where the solution has difficulty converging, hence convergence is slower.
2.5.4. Analysis Output
OpenSees allows to decide which quantities will have to be saved on file after the execution of the simulation, through the Recorders. These are listed again in a file .xtcl, in which some parameters are indicated, as for example on which element the Recorder will have to act (Nodes or Elements), the output file in which to save the results, the type of result to save (localForce, basicDeformation, etc.)
The output of the analysis can be found in 3 files with extension .out:
- -
- recorderNodeDisplacements.out
- -
- recorderEleLocalForces.out
- -
- ecorderEleBasicDeformation.out
For the purposes of the case study, the file that will be taken into account will be recorderNodeDisplacements.out, in which there are 6 values for each node of the model: the displacement in the 3 axes X, Y, Z, and its rotation, always in the 3 axes.
It is a textual file, where the first line indicates the initialization of the model and re-ports a series of zeros, while the subsequent lines are the result of 25 s of simulation with steps of 0.01 s, for a total of 2500 lines.
3. Case Study: Visualization of Seismic Risk
The idea at the base of the experimental project is to visualize the results of the simulations carried out using the OpenSees software directly on a three-dimensional model of the infrastructural work, through the use of color gradations to indicate the amplitude of the stresses suffered.
To better place the work within the real environment in which it is located, it was decided to add the three-dimensional model of the surrounding area, obtaining the elevation from the DEM (digital elevation model) on the INGV website, and the texture from satellite maps.
3.1. Implementation Approach
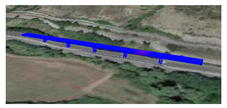
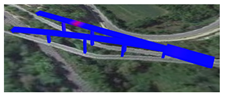
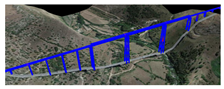
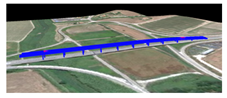
For the purposes of the project, we focused on eight works (bridges, viaducts, flyovers) as examples of the Italian infrastructural heritage, as shown in Table 1. Of these works the model for OpenSees has been created and the dynamic analyses have been performed as per NTC08 standards.

Table 1.
Data of the Analyzed Works.
For the visualization of the simulation results, a GIS application with access from a web browser was chosen. The application interface is composed of two main screens:
- A first screen in which it is visualized a classic two-dimensional map of Italy, in which it is possible to select the infrastructure of which it is wished to visualize the results through, click, as shown in Figure 12;
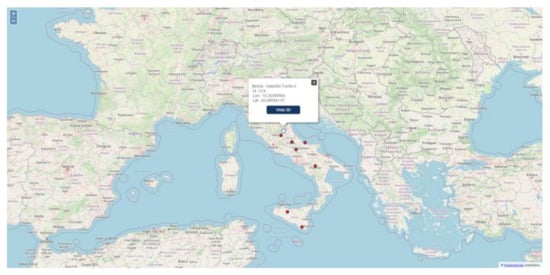 Figure 12. Two-dimensional map.
Figure 12. Two-dimensional map. - a second screen in which, after the selection, the three-dimensional rendering of the work and the surrounding area is executed, as shown in Figure 13.
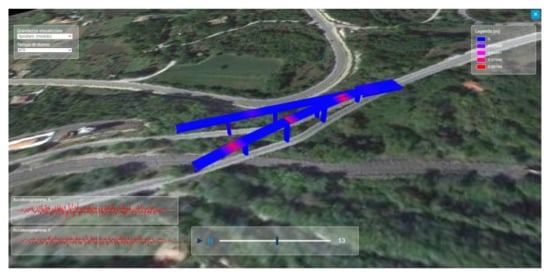 Figure 13. Render three-dimensional map.
Figure 13. Render three-dimensional map.
In this same screen there are tools for selecting the type of result to be shown. Since the NTC08 standards indicate a simulation time of 25 s, in which the stresses undergone as a result of a particular accelerogram are measured it was thought to provide animation features to allow real-time viewing of how the stresses change over time; the accelerograms (on the axes X, longitudinal with respect to the work, and Y, transverse) used as input for the simulation are also displayed.
3.2. Digital Elevation Model
The DEM used is TINITALY/01, downloadable from the INGV website (http://tinitaly.pi.ingv.it/, accessed on 25 June 2021). The model, presented in 2007, is obtained starting from the individual DEMs of the different Italian administrative regions, and has a resolution of 10 m per pixel, as shown in Figure 14; it is available in GeoTIFF format, with UTM WGS84 projection, zone 32.
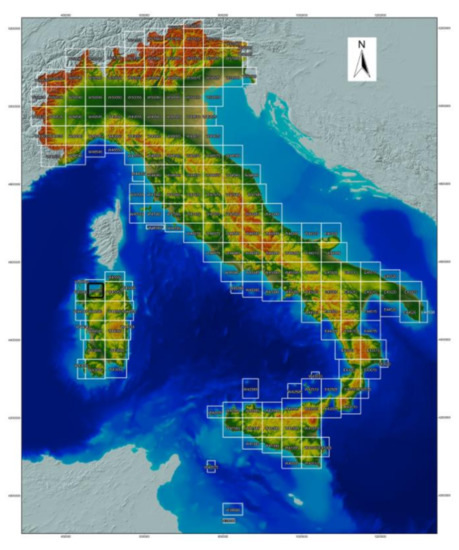
Figure 14.
Digital elevation model TINITALY/01.
All the GeoTIFF related to the position of the works taken into consideration have been downloaded from the INGV website. Since the downloaded tiles cover a very large area, using QGIS software we proceeded to crop the area of interest (area of 1km × 1km having as center the coordinates of the work). The file was then saved in ENVI format, which presents the GeoTIFF data as a simple vector of binary data, ready to be read by the Three.js graphic library used in the front-end for the assignment of elevation to the three-dimensional mesh.
Each pixel is represented within the ENVI format by 4 bytes that make up a floating point (floating point) value with 32 bits of precision. The order of the bytes is LSF (least significant first). The floating point format allows you to use the data directly in Three.js without having to make any kind of conversion, simplifying the process and ensuring an excellent resolution.
Again, through QGIS, the extension of the layer obtained from the DEM was used to save to file the corresponding portion of the satellite map of the area, which will later be used as a texture to be applied to the ground mesh.
3.3. OpenSees: Pre-Processing and Post-Processing
In the phase of pre-processing, the analysis is carried out through the OpenSees framework using the file .tcl that describes all the characteristics of the model. The model changes from the state at time t to the state at time t + dt. This change can be performed by a simple linear static analysis or by a non-linear transient analysis (transient analysis, variable transient analysis). In general terms, the analysis objects are used to solve the following time-dependent equilibrium-equation problem for a transient analysis:
where FI is the acceleration-dependent inertial force vector, FR is the velocity (damping) and displacement-dependent (stiffness) resisting-force vector. P(t) is the external applied-force vector. The acceleration, velocity and displacement vectors are all time-dependent. In OpenSees each analysis object is composed of several components, which define the type of analysis and how the analysis is performed. The .tcl files that describe the model are characterized by a very precise syntax, the geometric parts that interest us are the elements and nodes. The single elements of the system (lines) are associated in their endpoints (nodes). In the phase of post-processing of the model they come generated two essential files that correspond to the elements (file: elements.xtcl) and the endpoints (file: nodes.xtcl), these two files associate all the parameters of the carried out simulations.
FI(Ű) + FR(U, Ŭ) = P(t)
3.4. System Architecture
The workflow of the project involves the use of an off-line component, to be executed once when adding a new work, called “Conversion Tool”. This component allows the OpenSees output files to be adapted into the formats required by the application.
Once the necessary files are created, the web application follows the client-server architecture, with a Java back-end and an HTML/CSS/javascript front-end published via Tomcat application server, as shown in Figure 15.
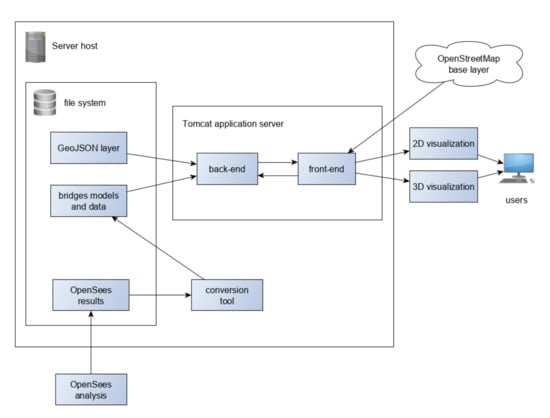
Figure 15.
System architecture.
3.5. Conversion Tool
The conversion tool is built in Java. It is located in the same project as the web application, in a reserved package named “processing”. The processing analysis class takes care of reading some of the OpenSees output files and producing the files needed by the application in .JSON format.
The first operation performed by the tool is the loading in memory of the data contained in the files nodes.xtcl and elements.xtcl through the methods:
| loadFileNodes(String filename) loadFileElements(String filename) |
The data of nodes and model elements are saved in data structures in memory, specifically HashMaps with the node/element id as key, using auxiliary classes node and element:
| public Map<Integer, Node> nodesList; public Map<Integer, Element> elementsList; |
Figure 16 shows the model generated for OpenSees analysis: the white dots represent the nodes, and the green lines the elements that connect them.
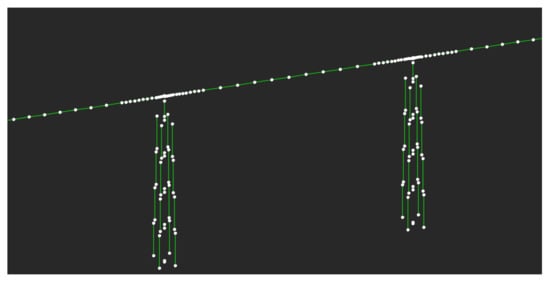
Figure 16.
OpenSees model visualization.
OpenSees associates to each node of the model a section; the extrusion of this section will then represent what will be displayed in the interface, and is saved in the bridge_model.csv file; the next step is then to load the three-dimensional model in memory, and associate to each face the reference node. The same model of Figure 16 can be seen in Figure 17 with the sections associated to each node.
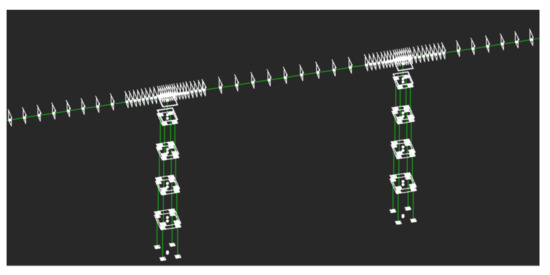
Figure 17.
OpenSees with the sections of each node.
OpenSees saves data sequentially, so it is sufficient to cycle through all elements of the bridge_model.csv file and its elementList elements to have a correct association.
All these operations are carried out from the method
| loadFileModel(String filename) |
After the model has been loaded in memory and saved in the .json file, it remains only to create the files that will serve for the various thematizations. Inside two nested cycles that take into consideration all the return times and the three required output types, the accelerograms files are first read and saved in .json format, through the method:
| creaJsonAccel(String id, String tr, String simul, String dir) subsequently it comes executed the methods loadFileNodeDisplacements(String filename, String result) creaJsonTematization(int t) |
The first takes care of reading the file RecorderNodesDisplacement_[tr]-1 and extracting the required re-sult, while the second will generate, from these results, a json structure in which for each node are listed the RGB values appropriately scaled, and the minimum and maximum values used to populate the legend.
All RecorderNodesDisplacement files are composed of sequences of [number of nodes] * 6 elements, where the 6 values indicate:
- X-axis displacement
- Y-axis displacement
- Z-axis displacement
- X-axis rotation
- Y-axis rotation
- Z-axis rotation
For the purposes of the project are taken into account the first three, since the rotations of the elements are not very significant.
The file records the results on 25 s of simulated shock, with steps of 0.01 s, for a total of 2500 rows; in order to keep the data structures manageable, it was decided to sample the results every second, thus obtaining 25 data sets corresponding to the 25 s of simulation. The data sets are then saved in an array within the json structure.
The files obtained from the procedure can finally be copied into the WebContent/assets/[work id]/folder of the project in order to be served to the front-end at the time of the request.
3.6. Back-End
The back-end is realized in Java and executed through Tomcat application server. It is based on the use of servlets, collected in the appropriate package “servlet” and recalled by URL from the front-end. The necessary servlets are registered in the file WebCon-tent/WEB-INF/web.xml to allow the server to know their location and the URL to which they must respond.
Given the simplicity of the system architecture, the back-end is composed of two main servlets:
The first one is named GetFeatures and it takes care of reading from file system the data related to the points of interest, organizing them in json format and passing them to the front-end, where they will then be displayed as layers on a map. The file in which these data are saved is in .CSV format and is called “opere_feat.csv”. Its location on the file system is configurable through the “config.conf” file.
The second is called GetDatiOpera and provides the front-end, at the time of selection of a work, all the data necessary for its visualization, and then:
- Latitude and longitude of the model;
- Orientation with respect to north and elevation of its lowest foundation;
- Latitude and longitude limits of the terrain mesh (minimum and maximum latitude, minimum and maximum longitude);
- X and Y dimensions of the terrain mesh in meters.
These data are also saved in a .CSV file called “data_opere.csv” in the same folder on file system as the previous file.
3.7. Front-End
The front-end uses some auxiliary libraries for geographic and three-dimensional visualization. The libraries used are listed in Table 2:

Table 2.
Front-end libraries used.
The web application is a so-called single-page application. This means that there is no navigation between various HTML pages as in a common website, but the whole application is loaded in a single HTML page, which is updated and modified if necessary through javascript functions.
The welcome page is index.html, which has a very simple initial structure:
| <body> <div id=“mainDiv”> <div id=‘map’></div> <div id=‘div3d’> <div id=“sliderOuter”> <div id=“sliderDiv”> </div> </div> </div> </div> </body> |
Within a main DIV (“mainDiv”) that occupies the entire screen, the DIVs “map” and “div3d” are created. The latter is initially declared invisible through the CSS directive display: none;
The creation of content is delegated to the functions in the file mainapp.js. In particular:
| window.onload = function(e) { setupMap(); loadBaseLayer(); loadLayerPonti(); } |
The onload function of the window object is automatically called by the browser when all HTML components are loaded, and therefore represents the initialization of our application. In this moment, they recal the specific functions that deal to visualize the map of OpenLayers.
Following are the portions of code significant for the creation of the map:
| olMap = new ol.Map({ layers : [], target : ‘map’, view : new ol.View({ center : ol.proj.fromLonLat(centerCoordDefault), zoom : zoomStartDefault, maxZoom : 19, minZoom : 6 }) }); |
and for loading the OpenStreetMap base layer:
| var newBaseLayer = new ol.layer.Tile({ source : new ol.source.OSM({ url : “https://tile.openstreetmap.org/{z}/{x}/{y}.png”, crossOrigin : null }), id : ‘base_layer’, name : “Base Map” }); olMap.addLayer(newBaseLayer); |
Always using the Openlayers functions, the click selection functionality has been added to the map, which will allow to open the pop-up window.
The 3D visualization is realized using the Three.js library. Starting with version r106, the recommended method of using this library is using modules defined by ECMAscript version 6, often called ES6 modules [38,39]. This modular architecture has been created to insert also in javascript the concept of “class” already present in other languages such as C++ and Java, to allow to import in the project only the required functionalities of a given library, and to limit the scope of the variables reducing the risk of overlapping typical of the use of global variables, and the elasticity of the Javascript language that does not signal as an error the multiple declaration of the same variable.
The concept of an ES6 module is that everything that is declared inside it is not visible to the outside, apart from the methods that are explicitly exported through the instruction
| export {function}; |
From the outside, the necessary functions of the module can be imported via the directive:
| import { funzione } from ‘./modulo.js’; |
In the project, the specially created module page3D.js is presented that exports a single function, render3Dview, which in turn imports the three.js library and performs the rendering of the three-dimensional scene.
The basic operations performed by render3Dview are:
- Initialization of Three.js and creation of the scene
- Loading of all the necessary files (3D model, Digital Elevation Model, textures, tematizations)
- Creation of the elements of the interface
- Render of the scene
To facilitate the generation of the elements of the interface have been created two custom components that exploit the potential of HTML5 canvas:
- slider.js : this is a component that shows two buttons (Play and Stop) and a time slider bar with a slider. When Play is pressed, it creates a setInterval function that executes a callback function specified by the user at each predefined interval; at the same time it advances the slider on the scroll bar, thus creating a real-time animation;
- acceler_graph.js : draws a graph from an array of data, scaling the visualized data based on the height of the DIV in which it was inserted. It allows the setting of a vertical bar, thus realizing the synchrony with the position of the animation slider.
3.8. Three-Dimensional Rendering
The Three.js library provides all the necessary tools to create a 3D scene complete with three-dimensional objects, lights, cameras and effects within a normal web page.
The conceptual diagram of a Three.js scene is represented in Figure 18.
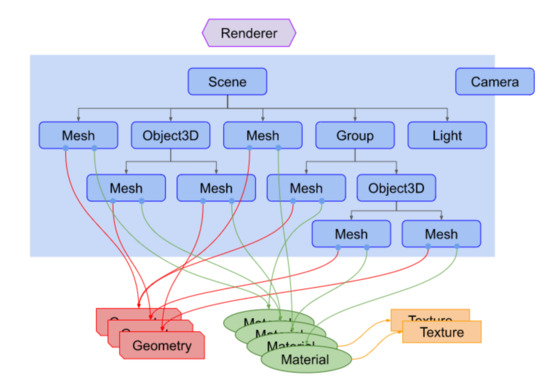
Figure 18.
Diagram of a three.js scene.
The renderer is the object that takes care of representing on screen all that is present in a scene, as if the user were positioned in the point where the camera is present, that is a real camera with a position, an orientation and a field of view (FOV) that frames the scene.
Inside the scene we find all the objects that make up the “set” that we are going to frame: the mesh are the real 3D objects, which in turn are composed of geometry, the polygonal geometries that describe its appearance, and material, the materials that define color, light reflection properties, etc. The materials can refer to textures and raster decals that are applied to the geometries.
The objects that are framed on the camera are displayed on the screen, within the so-called “frustum”. The “frustum” is a truncated pyramid shaped area bounded by the FOV of the camera and the clipping planes near and far.
A representation of the frustum is visible in Figure 19.
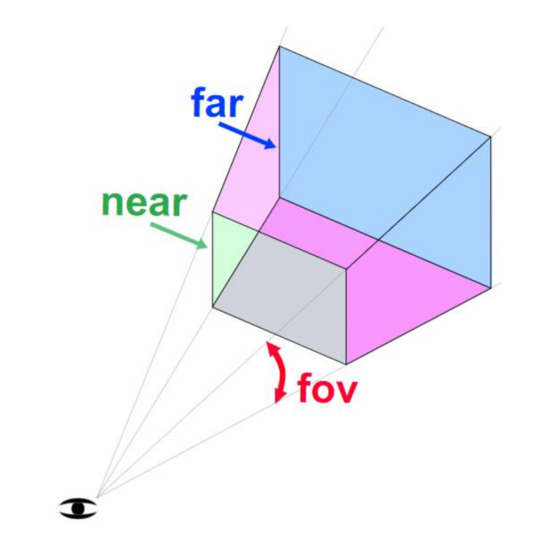
Figure 19.
Representation of “frustum”.
A great importance in any three-dimensional space is the coordinate system: although they are always composed of the three axes X, Y, Z, in some cases we consider the Z as the vertical axis, in others the Y. Three.js uses the latter convention, as shown in Figure 20.
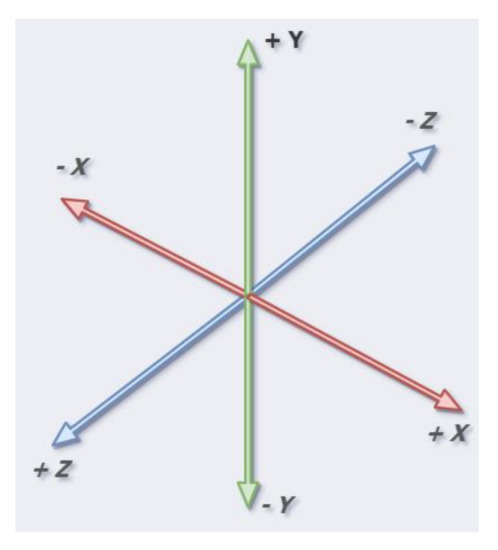
Figure 20.
Coordinate system of Three.js.
Since in geographic systems the values of longitude and latitude are often reported to X and Y coordinates, it would be more convenient to use a reference system in which the Z axis corresponds to the elevation, then the vertical axis; fortunately, the library allows for changing the reference system through a single function:
| THREE.Object3D.DefaultUp = new THREE.Vector3(0, 0, 1); |
This function creates a unit vector in the Z-direction and assigns it to the one that is considered “high” (up); in this way you have returned to the desired condition.
3.8.1. Polygonal Rendering
At the base of the rendering techniques used by three.js is polygonal rendering. This technique consists in approximating any object that is represented in a three-dimensional space to a series of polygons, and in particular everything is represented by triangles, called faces, as visible in Figure 21.

Figure 21.
Polygonal mesh.
The order in which the three vertices of the triangle are listed is important, as they define whether it faces the camera or the other direction, in particular, three.js uses a counterclockwise convention, as shown in Figure 22.
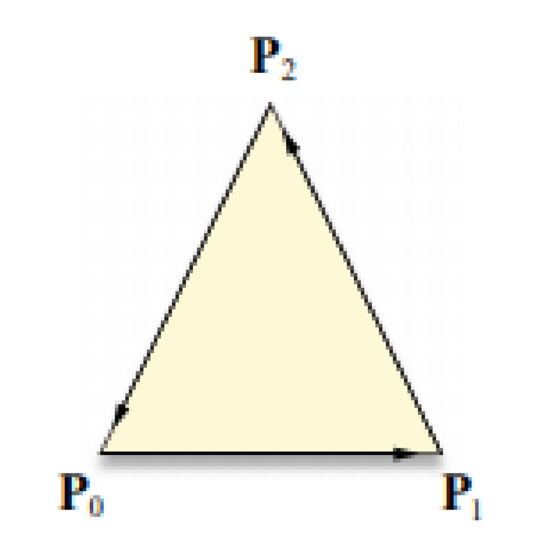
Figure 22.
Orientation of a triangle.
A crucial quantity that must be calculated for each triangle is its normal. This is a unit vector perpendicular to the plane formed by the vertices of the triangle that will allow, compared to the angle of incidence of the light source (or sources in the case of multiple illumination) to determine the degree of illumination of that face.
In the example of Figure 23, N1, N2, N3 and N4 are the normals of the four faces that make up the mesh.
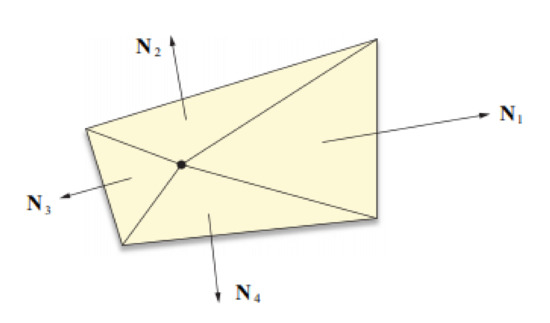
Figure 23.
Normals on a 4-sided mesh.
In the most recent rendering engines, this value is interpolated for each point of the face taking into account the normals of neighboring faces; this technique, which takes the name of Gouraud Shading, allows you to generate more harmonious shapes and not “faceted” as those obtained with a flat lighting for each face (flat shading).
In the Three.js library, the first step in creating a polygonal mesh is to define its geometry. For this purpose you can use the THREE.BufferGeometry object that replaces the previous THREE.Geometry for performance reasons. A BufferGeometry is in fact represented by the one-dimensional arrays in which the X, Y, Z coordinates of each point are listed below, without objects containing them. This approach, although less intuitive for the developer, allows the webGL libraries a significant performance boost.
In the case where many vertices are shared among several faces, as is often the case, you can list them once in the position array and then create a second index array that simply lists references to the vertices of each face.
Once the two arrays are filled with the model data, it is possible to associate them with the Buffer-Geometry through the instruction:
| geometry.setAttribute(‘position’, new THREE.Float32BufferAttribute(vertices, 3)); geometry.setIndex( indices ); |
In which it comes created an appropriate object of Three.js, Float32BufferAttribute, beginning from the vector, and this comes then assigned to the attribute “position” of the buffer geometry.
The array of indices is instead directly set via the set Index function. The coloration of the model in this plan is dependent from a sure value assumed from the vertices (tied up to the nodes of the simulation, v. 4.3.1). It is therefore chosen to use, rather than textures applied to the model, a technique called vertex shading, that allows to assign a color to every vertex of the figure. The rendering engine will then interpolate the colors throughout the surface of the face, as visible in Figure 24.

Figure 24.
Example of vertex shading.
This is possible by setting the vertexColors attribute to true in the material:
and then setting a new attribute (“color”) of the geometry, passing an array containing the R, G, B components normalized between 0.0 and 1.0 of each vertex, geometry.setAttribute(‘color’, new THREE.Float32BufferAttribute(colors, 3));
| const material = new THREE.MeshPhongMaterial ({ ambient: 0x050505, vertexColors: true, specular: 0x5555, shininess: 0 }); |
3.8.2. Elevation Assignment
The mesh representing the portion of land surrounding the work is a simple plane geometry:
| const geometry = new THREE.PlaneGeometry(1000, 1000, 99, 99); |
Since the real dimensions of the area are 1000 × 1000 m, it is convenient to generate the mesh of the same dimensions (parameters 1 and 2). The third and fourth parameters represent the number of subdivisions that the plane must have on the X and Y axes.
Dividing the geometry into 99 sections per side, we will find ourselves with exactly 100 vertices, a number equal to the values we extracted from the DEM.
At this point, after having read the values of the ENVI file that was previously saved in the/assets folder it will be sufficient to save them in an array of type Float32Array and overwrite the Z value of the array “position” of the geometry to include the elevation data in the terrain model, as shown in Figure 25.

Figure 25.
Terrain mesh before and after applying elevation.
3.8.3. Terrain Texture
The texture to be applied to the terrain mesh was obtained through QGIS. In fact, the program allows to add a layer “XYZ Tiles” that accepts custom connections. It will be sufficient to choose a service that offers satellite maps; at this point, through the tool “Convert map to raster”, it is possible to save the desired portion of the map as GeoTIFF on the file system. The extension will be given by the layer that has been previously cropped from the DEM; a tile size of 1000 will be chosen, equal to the meters of the area of interest, and a “Map unit per pixel” equal to 1. In this way, we will have 1 pixel for each meter of land, which guarantees a good quality of texture without too high resolutions that would compromise the performance of the application.
The GeoTIFF format is a lossless format, so there is no quality loss due to compression, but unfortunately it generates large files. Fortunately, GeoTIFF is read by graphics programs as if it were a normal TIFF. This was then converted to JPEG format, which is web-friendly and greatly reduces the size of the generated file.
The result of the conversion was then copied like the other files in the assets/folder and imported into three.js using the instructions:
| const loader = new THREE.TextureLoader(); loader.crossOrigin = ““; const textureTerreno = loader.load(file, callback) |
Next, the texture can be assigned to a new material that, associated with the previously generated geometry, will form the mesh of the terrain (see Figure 26).

Figure 26.
Terrain mesh applying the terrain texture.
3.8.4. Positioning the Model of the Work
Once the terrain mesh has been created and inserted into the scene, the three-dimensional model of the work must be positioned, applying the correct X, Y, Z coordinates and rotation so that it is correctly inserted with respect to the surrounding terrain. Such operations are performed by the function posizionaPonte() of the page3D.js file, of which the meaningful portion is brought back:
| var diffLon = endLon - startLon; var diffLat = endLat - startLat; var x = ((lon - startLon) * dimTerrenoX)/diffLon - (dimTerrenoX/2.0); var y = ((lat - startLat) * dimTerrenoY)/diffLat - (dimTerrenoY/2.0); for (var i = 0; i < bridge.length; i++) { var mesh = bridge[i]; mesh.position.x = x; mesh.position.y = y; mesh.position.z = elev - baseZ; mesh.rotation.set(0,0,degrees_to_radians(rotaz)); } |
The first operation performed is the calculation of the dimensions in WGS84 degrees of the terrain mesh (variables diffLon and diffLat). Using these values, the initial coordinates of the terrain, the coordinates of the bridge and the size in meters of the terrain, through a simple proportion, we obtain the X and Y coordinates of the three-dimensional space in which to place the model.
Since the model is composed of various meshes saved in the bridge array, click on the elements of the bridge array applying to each one the translation through the mesh.position object. For the Z coordinate the elevation of the work is used (elev variable, normalized with respect to the minimum elevation of the baseZ terrain).
The instruction mesh.rotation.set(x, y, z) allows for the rotation angle of a mesh to be set and is used with the value of rotation of the work with respect to north, appropriately transformed in radians from its initial value in degrees.
4. User Interface
The user interface is presented with a main screen where it is possible to select from the map the work of which it is interesting to know the data. After the selection, a second full-screen will open in which the work will be rendered.
4.1. Two-Dimensional Visualization
The initial screen shown when the web page is loaded is dominated by the two-dimensional map centered on Italy, as shown in Figure 27. On the top left are the zoom adjustment keys, and all the mouse commands are active: panning by moving the cursor while pressing the left key, zoom in/out by the central wheel. The outward zoom is limited in order to keep the user’s attention on the area of interest.
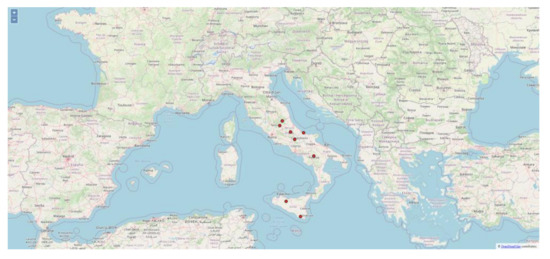
Figure 27.
Two-dimensional display screen.
The base map displayed is that of OpenStreetMap [40]. Above it, there is a layer with point elements, represented by red circles; this layer represents the works of which seismic verifications have been performed using OpenSees.
It is possible to click on one of the points of interest to show a pop-up window containing the basic information of the work: its name, the internal id of the application and its coordinates in the form of longitude and latitude WGS84.
The pop-up can be closed with the “X” button at the top right of the window.
In addition to the summary data of the work, the pop-up also contains the “3D View” button. Pressing the button will take the user to the 3D view of the artwork.
4.2. Three-Dimensional Visualization
Once a work is selected, the main view of the application opens: the 3D render. Once all the necessary files have been loaded (bridge model, thematic, elevation model, terrain textures), the screen will appear as shown in Figure 28:
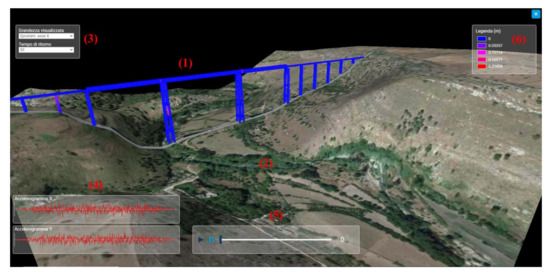
Figure 28.
Three-dimensional display screen.
The main components of the interface are:
- Three-dimensional model of the work
- Ground Mesh
- Selection menu of the quantities to show
- Accelerograms
- Animation toolbar
- Legend
Navigation within the three-dimensional screen can be performed by mouse and keyboard controls: by moving the cursor while pressing the left key, it is possible to rotate the view around the model; by using the central wheel, it is possible to zoom in/out; by pressing the SHIFT key while dragging the mouse it is possible to pan the camera to move within the scene.
Through the selection menu (3), it is possible to select:
(a) The simulated size to show on the model. The three possible choices are:
- X axis displacement. It represents the displacement of the nodes of the model in longitudinal direction with respect to the work.
- Y axis displacement. It represents the displacement of the nodes of the model in transverse direction with respect to the work.
- Displacement (module). It represents the modulus of the vector resulting from the two X and Y displacements. It indicates the generic stress borne by the node, regardless of its direction.
(b) The time of return to show on the model. In this case, there are nine possible choices: 30 years, 50 years, 72 years, 101 years, 140 years, 201 years, 475 years, 975 years and 2475 years.
At each change of selection, the data set for the model is reloaded for all 25 s that make up the simulation; also the legend is repopulated to reflect the new minimum and maximum limits of the data set taken into account.
In case of change of the return time, also the accelerograms are redrawn as these are dependent on the selected return time.
Through the toolbar of animation, is possible to move among the various instants of the simulation, with steps of one second each. The operation is intuitive and resumes one of any player video, as shown in Figure 29.

Figure 29.
Toolbar animation.
The animation can be scrolled in two ways: an automatic mode, activated by the “Play” button, which will scroll the moments in real time. This mode can be stopped by pressing the “Stop” button.
The second mode is manual: in this case you just need to drag the slider on the time bar to move as you like along the 25 s.
On the right of the bar there is a number that indicates the frame (in seconds) displayed at that moment.
At each change of time the coloration of the model is automatically updated, allowing to evaluate which are the points of the work more stressed by the seismic shock. The color gradations can be easily compared with those present in the legend, to have also a numerical indication of the entity of the displacement, as shown Figure 30.

Figure 30.
Differences in coloration in different frames.
The accelerogram graphs have a vertical bar, which automatically moves to follow that of the animation: in this way it is also possible to compare the response of the elements in relation to the input data used by OpenSees at that time.
At any time, the “X” button at the top right of the screen can be pressed to return to the two-dimensional view and select a new work.
5. Conclusions and Future Work
5.1. Conclusions
The project has shown how a rapid visual representation of the numerical results can improve the understanding of the most stressed areas of an infrastructural work subject to seismic movements. It has also allowed for the appreciation of the difference in behavior between works of different types, in particular in the presence of very high piers or particularly long decks.
The platform can be used particularly when it is necessary to divulge the results obtained from analyses carried out on the works, thus allowing even those who do not have specific skills to qualitatively evaluate the effects on the stressed structures, comparing these effects on the basis of different PGA, and therefore of different intensity of the earthquake.
The system allows to choose the direction in which to visualize the shifts both on the longitudinal axis and on the vertical axis of the bridge. In this method, it is easy to see which shifts the elements receive. For example, beams receive displacements in the vertical direction, while vertical elements (pillars) have displacements in the horizontal direction.
The modularity with which the architecture of the system has been designed makes it easy to add new works of which the analyses carried out using the OpenSees software are available: the conversion tool takes care of adapting the format of the output files and performing the calculations necessary to display the results, while the saving of the data of the works on .CSV files guarantees maximum ease in adding new points of interest to the platform.
The product, although designed to show the results of a seismic analysis, can be easily adapted to display any type of stress to which a structure is subjected. For example, again for bridges, it would be possible to perform FEM analysis on the vertical loads to which the decks are subjected; or one could focus on other infrastructural works, such as buildings, retaining walls or tunnels.
The development of this platform has also highlighted how nowadays it is possible to obtain professional results even using open-source software and libraries, and therefore free of charge, thus allowing even small companies to create tools that can be used by professionals to evaluate and disseminate the results of their numerical analysis.
The major difficulties encountered in the creation of the application were in the findings and in interpreting the data for the analysis, which is for competent professionals in the field of structural engineering.
5.2. Future Work
At present, the project requires a series of operations for the addition of new works: in addition to the results of finite element analysis, a basic element to be able to thematize the model, there are several steps to follow, mostly through a special software such as QGIS, to create the elevation files derived from the DEM and the textures to be applied to the terrain model.
An evolution of the platform could, starting from the coordinates of the work to be added, directly query the INGV site to download the portion of DEM desired and obtain from this the area of 1 km × 1 km around the work; in the same way, satellite images of the area could be obtained through the WMS service and saved on the file system, or loaded into the browser at each request.
These operations, addressed to a user with administrator privileges, could be collected in a web editor, together with other operations for fine-tuning the positioning of the work, such as the possibility of modifying the coordinates, the elevation, and the rotation with respect to the north, to ensure that the model is correctly positioned on the ground mesh.
Regarding the types of data displayed on the model, in addition to the displacement values currently displayed, OpenSees also makes available the values related to the forces to which the elements of the work are subjected, which could constitute additional values that can be displayed through color gradations.
Since the displacements of each node in the three directions X, Y, Z are available, a further development could also show the real-time animation with the actual displacement of the vertices of the three-dimensional model, relatively to the values of the reference node.
As for the three-dimensional model, at the moment it is a simplified model generated from nodes, extruding the sections associated with them. For a more accurate representation, the ideal would be to have access to the more detailed model that OpenSees creates within it to perform the analysis; however, this would involve, in addition to research on the actual possibility of exporting this model, also an operation of optimization of the mesh to make it viewable on the browser without overloading the graphics hardware of the computer that runs it.
Author Contributions
Conceptualization, Mauro Mazzei; methodology, Mauro Mazzei; software, Davide Quaroni; validation, Mauro Mazzei, Davide Quaroni; formal analysis, Mauro Mazzei; data curation, Mauro Mazzei and Davide Quaroni; writing—review and editing, Mauro Mazzei and Davide Quaroni; supervision, Mauro Mazzei. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The source of the data of the seismic maps are the INGV Institute (National Institute of Geophysics and Volcanology) that since 2004 releases this map of seismic hazard with which it provides a picture of the most dangerous areas in Italy. (http://zonesismiche.mi.ingv.it, accessed on 25 June 2021).
Acknowledgments
The authors thank Pacific Earthquake Engineering Research Center as a source of documentation necessary for the conduct of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- D.M. 14 Gennaio 2008, Approvazione Delle Nuove Norme Tecniche per le Costruzioni. Available online: https://www.camera.it/cartellecomuni/leg15/RapportoAttivitaCommissioni/commissioni/allegati/08/08_all_dm_2008.pdf (accessed on 25 June 2021).
- Metaingegneria.com. Available online: https://www.metaingegneria.com/cos-e-una-simulazione-fea/ (accessed on 25 June 2021).
- Next Generation Attenuation Database, PEER Ground Motion Database. Available online: http://peer.berkeley.edu/peer_ground_motion_database (accessed on 25 June 2021).
- Coleman, J.; Spacone, E. Localization issues in force-based frame elements. J. Struct. Eng. 2001, 127, 1257–1265. [Google Scholar] [CrossRef]
- Priestley MJ, N.; Seible, F.; Calvi, G.M. Seismic Design and Retrofit of Bridges; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Connell, M.; Tullberg, O. A framework for immersive FEM visualization using transparent object communication in a distributed network environment. Adv. Eng. Softw. 2002, 33, 453–459. [Google Scholar] [CrossRef]
- Rahman, M.M.; Nahar, T.T.; Kim, D. FeView: Finite element model (FEM) visualization and post-processing tool for OpenSees. SoftwareX 2021, 15, 100751. [Google Scholar] [CrossRef]
- Liverani, A.; Kuester, F.; Hamann, B. Towards interactive finite element analysis of shell structures in virtual reality. In Proceedings of the 1999 IEEE International Conference on Information Visualization, London, UK, 14–16 July 1999. [Google Scholar]
- OpenSees User Documentation. Available online: https://opensees.berkeley.edu/wiki/index.php (accessed on 25 June 2021).
- Tarquini, S.; Isola, I.; Favalli, M.; Battistini, A. TINITALY, a Digital Elevation Model of Italy with a 10 Meters Cell Size (Version 1.0) [Data Set]; Istituto Nazionale di Geofisica e Vulcanologia (INGV): Rome, Italy, 2007. [Google Scholar] [CrossRef]
- INGV Terremoti. Available online: https://ingvterremoti.com/la-pericolosita-sismica/ (accessed on 25 June 2021).
- Threejs.org Documentation, Getting Started. Available online: https://threejs.org/docs/index.html#manual/en/introduction/Creating-a-scene (accessed on 25 June 2021).
- Jquery.org, About. Available online: https://learn.jquery.com/about-jquery/ (accessed on 25 June 2021).
- Mozilla Foundation—MDN Web Docs, JavaScript Modules. Available online: https://developer.mozilla.org/en-US/docs/Web/JavaScript/Guide/Modules (accessed on 25 June 2021).
- Three.js Fundamentals. Available online: https://threejsfundamentals.org/threejs/lessons/threejs-fundamentals.html (accessed on 25 June 2021).
- Gomarasca, M.A. Elementi di Geomatica; ASITA: Rome, Italy, 2004. [Google Scholar]
- QGIS Project, QGIS Documentation—Coordinate Reference System. Available online: https://docs.qgis.org/3.16/en/docs/ (accessed on 25 June 2021).
- Mazzei, M.; Palma, A.L. Spatial multicriteria analysis approach for evaluation of mobility demand in urban areas. In Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Auer, M.; Zipf, A. 3D WebGIS: From Visualization to Analysis. An Efficient Browser-Based 3D Line-of-Sight Analysis. ISPRS Int. J. Geo-Inf. 2018, 7, 279. [Google Scholar] [CrossRef] [Green Version]
- Mazzei, M. Software Development for Unsupervised Approach to Identification of a Multi Temporal Spatial Analysis Model. In Proceedings of the 2018 International Conference on Image Processing, Computer Vision, and Pattern Recognition, IPCV 2018, Las Vegas, NV, USA, 30 July–2 August 2018; pp. 85–91. Available online: https://csce.ucmss.com/cr/books/2018/LFS/CSREA2018/IPC3126.pdf (accessed on 25 June 2021).
- Mazzei, M. An Unsupervised Machine Learning Approach for Medical Image Analysis. In Advances in Information and Communication. FICC 2021; Arai, K., Ed.; Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2021; Volume 1364. [Google Scholar] [CrossRef]
- Mazzei, M.; Di Guida, S. Spatial data warehouse and spatial OLAP in indoor/outdoor cultural environments. In Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Mazzei, M.; Palma, A.L. Analysis of Localization and Space Interaction Models. Proposal of very good linked model applied to a study area for the localization of a large shopping mall. Geomedia 2014, 18 (Suppl. S1), 265–275. [Google Scholar]
- Mazzei, M.; Palma, A.L. Spatial Statistical Models for the Evaluation of the Landscape. In Computational Science and Its Applications—ICCSA 2013; Murgante, B., Misra, S., Carlini, M., Torre, C.M., Nguyen, H.-Q., Taniar, D., Apduhan, B.O., Gervasi, O., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2014; Volume 7974. [Google Scholar] [CrossRef]
- Ministero Delle Infrastrurtture e dei Trasporti. Aggiornamento Delle «Norme Tecniche per le Costruzioni». (18A00716); (G.U. n.42 del 20-2-2018—Suppl. Ordinario n. 8); Ministero Delle Infrastrurtture e dei Trasporti: Rome, Italia, 2018. Available online: http://www.labcontrols.it/wp-content/uploads/2018/07/DM-17_01_2018_CAP-11_Prove-materiali.pdf (accessed on 5 June 2021).
- Hale, C.; Abrahamson, N.; Bozorgnia, Y. Probabilistic Seismic Hazard Analysis Code Verification; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2018. [Google Scholar]
- Casarotti, C.; Pinho, R. An Adaptive Capacity Spectrum Method for Assessment of Bridges Subjected to Earthquake Action; Bulletin of Earthquake Engineering; Springer: Berlin/Heidelberg, Germany, 2007; pp. 377–390. [Google Scholar]
- ATC 40. Seismic Evaluation and Retrofit of Concrete Buildings; Applied Technology Council: Redwood City, CA, USA, 1996; Volume 1. [Google Scholar]
- FEMA 273. NEHRP Guidelines for the Seismic Rehabilitation of Buildings; Federal Emergency Management Agency: Washington, DC, USA, 1997. [Google Scholar]
- Caltrans SDC 2010, Caltrans Seismic Design Criteria Version 1.6; California Department of Transportation: Sacramento, CA, USA, 2010.
- Spacone, E.; Filippou, F.C.; Taucer, F.F. Fibre beam-column model for nonlinear analysis of R/C frames: Part I. Formulation. Earthq. Eng. Struct. Dyn. 1996, 25, 711–725. [Google Scholar] [CrossRef]
- California Department of Transportation Division of Maintenance. Structure Maintenance and Investigations; BIRIS, Jamboree Road Overcrossing; California Department of Transportation Division of Maintenance: Sacramento, CA, USA, 2015. [Google Scholar]
- Aviram, A.; Mackie, K.R.; Stojadinovic, B. Effect of abutment modeling on the seismic response of bridge structures. Earthq. Eng. Eng. Vib. 2008, 7, 395–402. [Google Scholar] [CrossRef]
- Aviram, A.; Mackie, K.R.; Stojadinovic, B. Guidelines for Nonlinear Analysis of Bridge Structures in California; PEER Report No. 2008/03; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2008. [Google Scholar]
- Mazzei, M.; Palma, A.L. Comparative Analysis of Models of Location and Spatial Interaction. In Computational Science and Its Applications—ICCSA 2014; Murgante, B., Misra, S., Carlini, M., Torre, C.M., Nguyen, H.-Q., Taniar, D., Apduhan, B.O., Gervasi, O., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2014; Volume 8582. [Google Scholar] [CrossRef]
- Mazzei, M. An Unsupervised Machine Learning Approach in Remote Sensing Data. In Computational Science and Its Applications—ICCSA 2019; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; Volume 11621. [Google Scholar] [CrossRef]
- Openlayers API. Available online: https://openlayers.org/en/latest/apidoc/ (accessed on 25 June 2021).
- Lengyel, E. Mathematics for 3D Game Programming and Computer Graphics, 3rd ed.; Course Technology; Cengage Learning PTR: Farmington Hills, MI, USA, 2012; pp. 175–176. [Google Scholar]
- LearnopenGL.com. Available online: https://learnopengl.com/Getting-started/Shaders (accessed on 25 June 2021).
- OpenStreetMap. Available online: https://www.openstreetmap.org/ (accessed on 25 June 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).