Constrained-Differential-Kinematics-Decomposition-Based NMPC for Online Manipulator Control with Low Computational Costs
Abstract
1. Introduction
2. Modeling and Mathematical Decomposition of the Manipulator
2.1. Analysis of the Inverse Kinematics
2.2. Decomposition of Differential Kinematics
3. Optimal Trajectory Control Using Decomposed Differential Kinematics
3.1. Polynomial Trajectory Planning
3.2. Optimization-Based Translational Trajectory Control
3.3. Jacobian Transpose Controller Achieving Desired Orientation
4. Simulation Results and Evaluation
4.1. Quantitative Analysis of the Computation Times
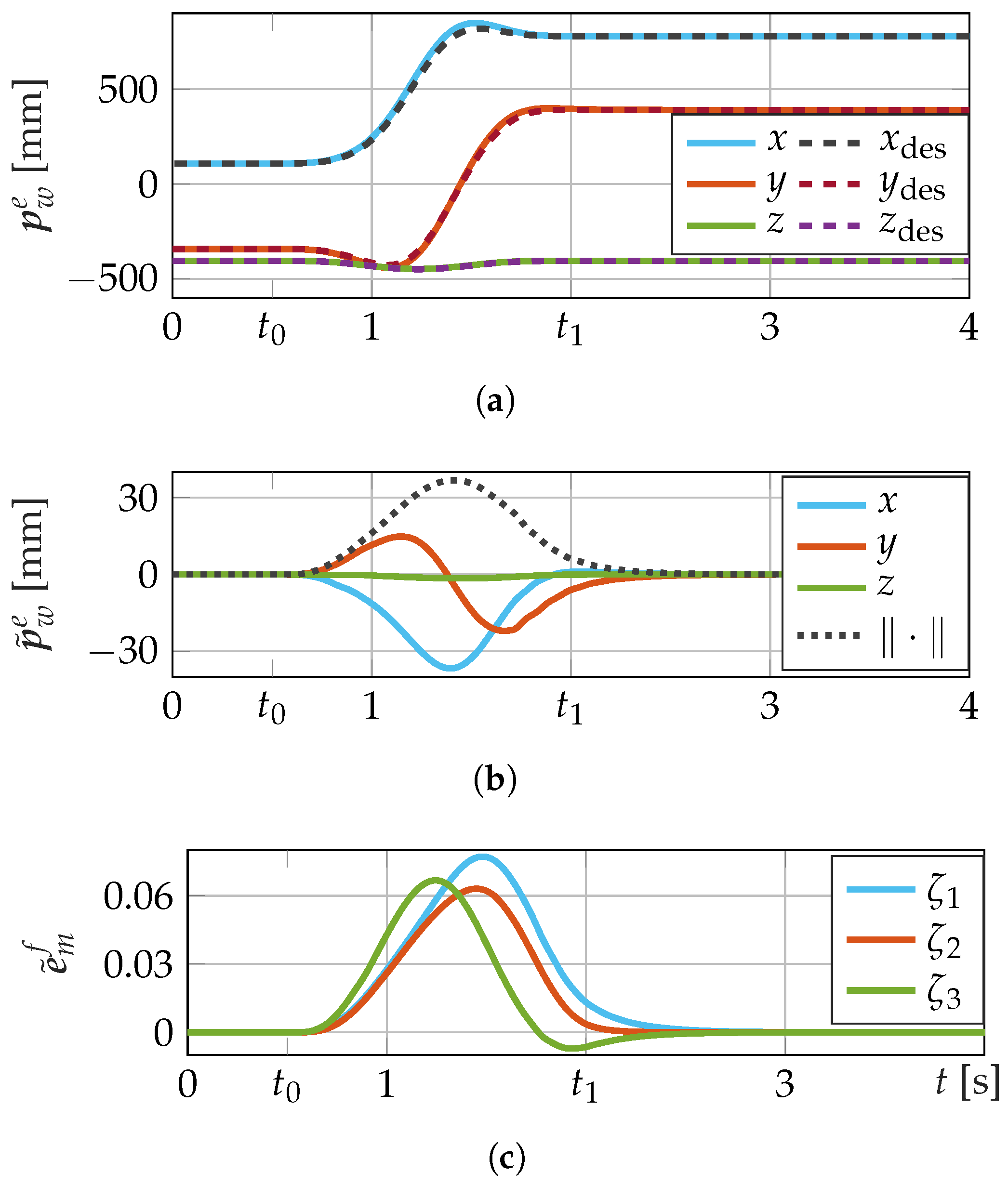
4.2. Trajectory Tracking Accuracy of the Controller
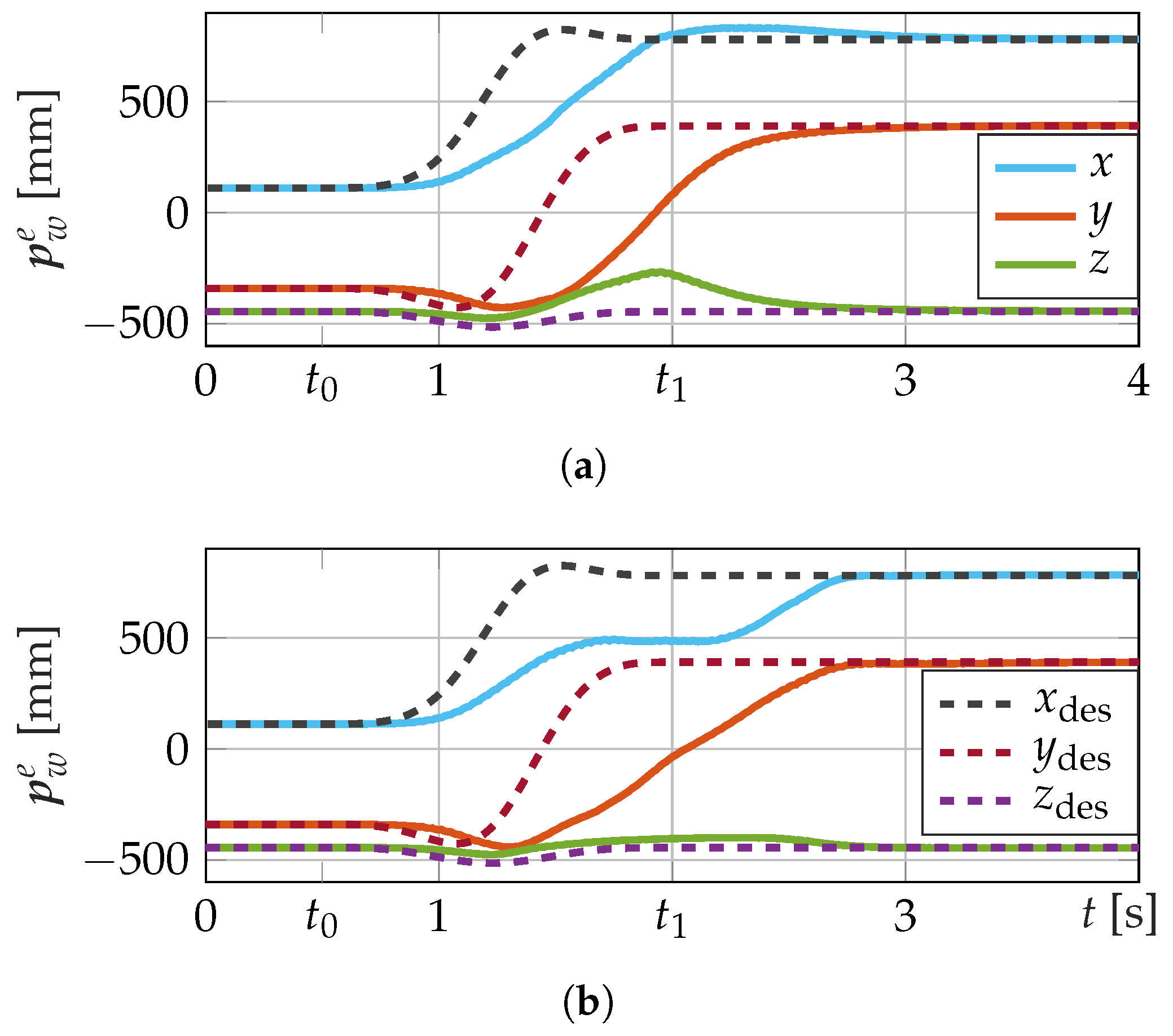
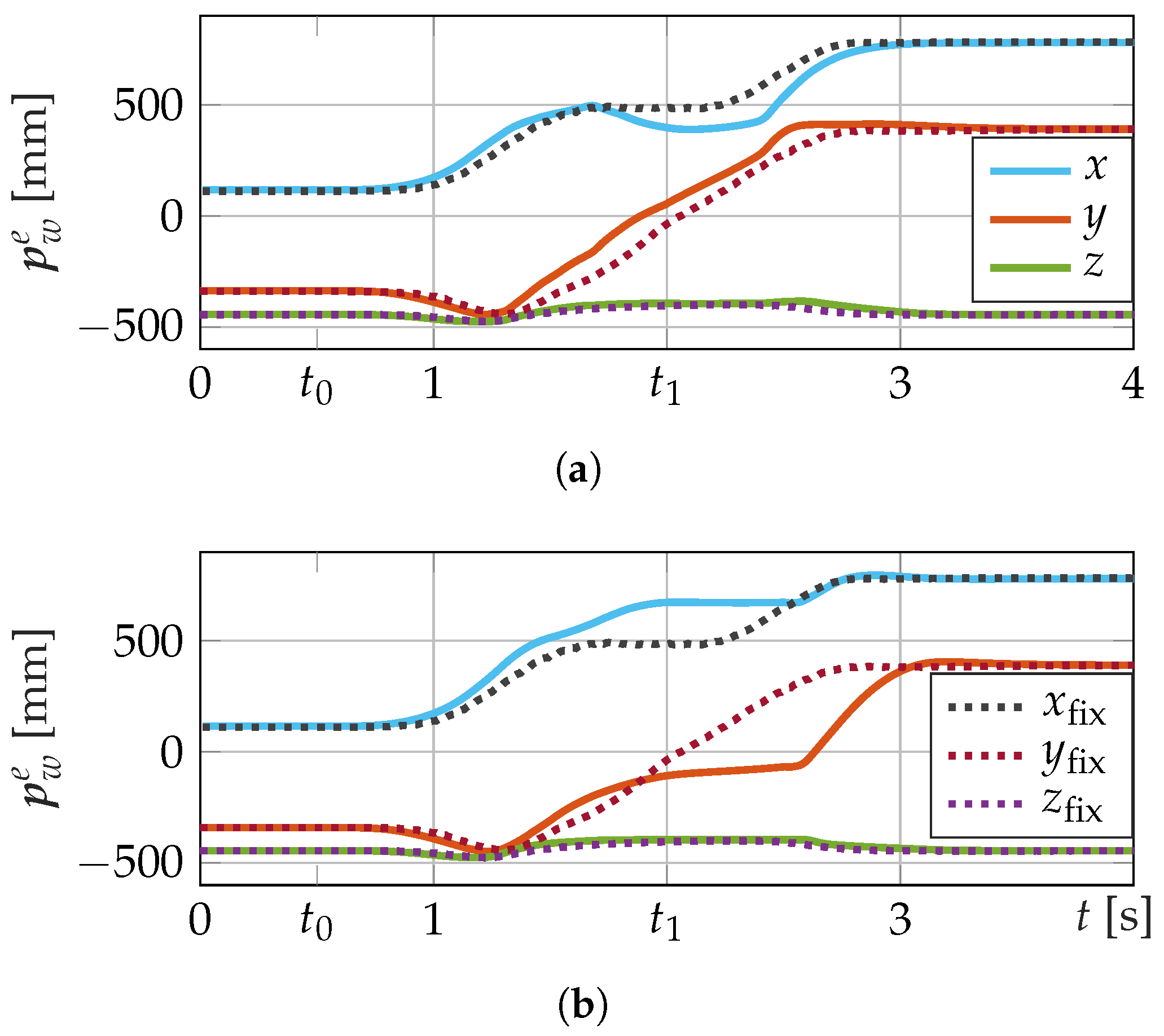
4.3. Trajectory Control in Disturbed Environment with Fixed Obstacles
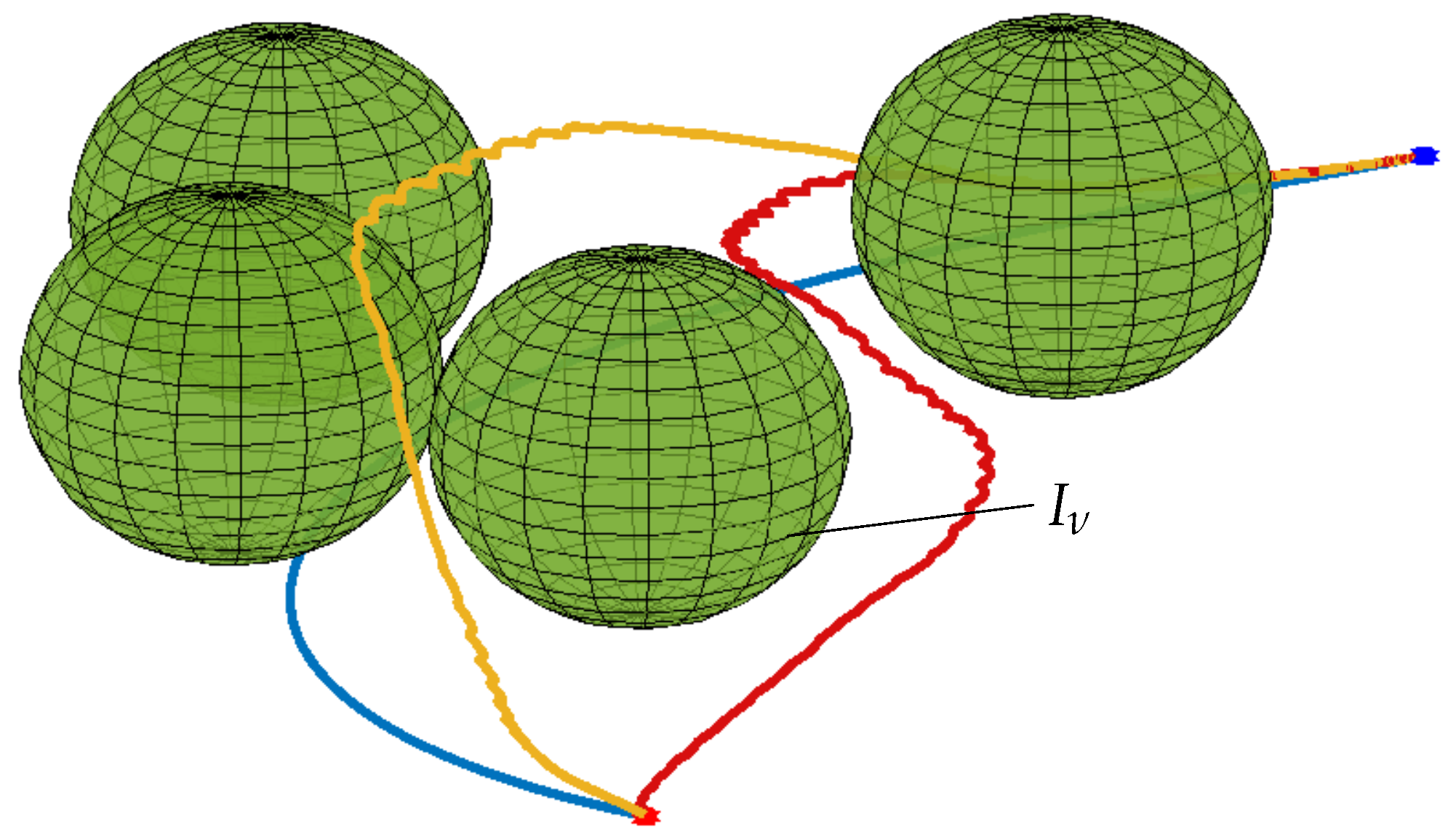
4.4. Trajectory Control in a Varying Environment with Moving Obstacles
5. Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3D | three-dimensional |
| des | desired |
| DH | Denavit–Hartenberg |
| DOF | degree of freedom |
| e.g., | for example |
| Fig. | Figure |
| fix | fixed |
| IPOPT | interior-point |
| NMPC | nonlinear model predictive control |
| OCP | optimal control problem |
| Tab. | Table |
References
- Bootz, J.P.; Michel, S.; Pallud, J.; Monti, R. Possible changes of Industry 4.0 in 2030 in the face of uberization: Results of a participatory and systemic foresight study. Technol. Forecast. Soc. Chang. 2022, 184, 121962. [Google Scholar] [CrossRef]
- Vaisi, B. A review of optimization models and applications in robotic manufacturing systems: Industry 4.0 and beyond. Decis. Anal. J. 2022, 2, 100031. [Google Scholar] [CrossRef]
- Edwards, M. Robots in industry: An overview. Appl. Ergon. 1984, 15, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Singh, J.; Shah, B.; Sehra, S.S.; Ali, F. Augmented Reality and GPS-Based Resource Efficient Navigation System for Outdoor Environments: Integrating Device Camera, Sensors, and Storage. Sustainability 2022, 14, 12720. [Google Scholar] [CrossRef]
- Grau, A.; Indri, M.; Lo Bello, L.; Sauter, T. Robots in Industry: The Past, Present, and Future of a Growing Collaboration with Humans. IEEE Ind. Electron. Mag. 2021, 15, 50–61. [Google Scholar] [CrossRef]
- Liu, F.; Wang, C.; Luo, M.; Zhou, S.; Liu, C. An investigation of the coupling coordination of a regional agricultural economics-ecology-society composite based on a data-driven approach. Ecol. Indic. 2022, 143, 109363. [Google Scholar] [CrossRef]
- Spykman, O.; Emberger-Klein, A.; Gabriel, A.; Gandorfer, M. Autonomous agriculture in public perception-German consumer segments’ view of crop robots. Comput. Electron. Agric. 2022, 202, 107385. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, T.N.; Ngo, B.V. A VGG-19 Model with Transfer Learning and Image Segmentation for Classification of Tomato Leaf Disease. AgriEngineering 2022, 4, 871–887. [Google Scholar] [CrossRef]
- Junior, L.C.M.; Alfredo, C.; Ulson, J. Real Time Weed Detection using Computer Vision and Deep Learning. In Proceedings of the 2021 14th IEEE International Conference on Industry Applications (INDUSCON), São Paulo, Brazil, 15–18 August 2021; pp. 1131–1137. [Google Scholar]
- Wendel, A.; Underwood, J. Self-supervised weed detection in vegetable crops using ground based hyperspectral imaging. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 5128–5135. [Google Scholar]
- Bručienė, I.; Buragienė, S.; Šarauskis, E. Weeding Effectiveness and Changes in Soil Physical Properties Using Inter-Row Hoeing and a Robot. Agronomy 2022, 12, 1514. [Google Scholar] [CrossRef]
- Abdulsalam, M.; Aouf, N. Deep Weed Detector/Classifier Network for Precision Agriculture. In Proceedings of the 2020 28th Mediterranean Conference on Control and Automation (MED), Saint-Raphaël, France, 16–19 June 2020; pp. 1087–1092. [Google Scholar]
- Gasparetto, A.; Boscariol, P.; Lanzutti, A.; Vidoni, R. Path Planning and Trajectory Planning Algorithms: A General Overview. Mech. Mach. Sci. 2015, 29, 3–27. [Google Scholar]
- Gasparetto, A.; Boscariol, P.; Lanzutti, A.; Vidoni, R. Trajectory Planning in Robotics. Math. Comput. Sci. 2012, 6, 269–279. [Google Scholar] [CrossRef]
- Meysami, A.; Cuillière, J.C.; François, V.; Kelouwani, S. Investigating the Impact of Triangle and Quadrangle Mesh Representations on AGV Path Planning for Various Indoor Environments: With or Without Inflation. Robotics 2022, 11, 50. [Google Scholar] [CrossRef]
- Yanbin, L.; Jiang, Y. Robotic Path Planning Based on a Triangular Mesh Map. Int. J. Control. Autom. Syst. 2020, 18, 2658–2666. [Google Scholar]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Elbanhawi, M.; Simic, M. Sampling-Based Robot Motion Planning: A Review. IEEE Access 2014, 2, 56–77. [Google Scholar] [CrossRef]
- Hayat, A.A.; Sadanand, R.O.M.; Saha, S.K. Robot Manipulation through Inverse Kinematics. In Proceedings of the Proceedings of the 2015 Conference on Advances In Robotics, Goa, India, 2–4 July 2015; Association for Computing Machinery: New York, NY, USA, 2015. AIR ’15. [Google Scholar]
- Djojo, M.A.; Karyono, K. Computational load analysis of Dijkstra, A*, and Floyd-Warshall algorithms in mesh network. In Proceedings of the 2013 International Conference on Robotics, Biomimetics, Intelligent Computational Systems, Jogjakarta, Indonesia, 25–27 November 2013; pp. 104–108. [Google Scholar]
- Reinhold, J.; Olschewski, J.; Lippross, S.; Meurer, T. Image-Based Online Command Adaptation and Guidance to Arbitrarily Shaped Objects for Robot-Assisted Medical Procedures. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 9241–9246. [Google Scholar]
- Ratliff, N.; Zucker, M.; Bagnell, J.A.D.; Srinivasa, S. CHOMP: Gradient Optimization Techniques for Efficient Motion Planning. In Proceedings of the Proceedings of (ICRA) International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 489–494. [Google Scholar]
- Kalakrishnan, M.; Chitta, S.; Theodorou, E.; Pastor, P.; Schaal, S. STOMP: Stochastic trajectory optimization for motion planning. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 4569–4574. [Google Scholar]
- Schulman, J.; Duan, Y.; Ho, J.; Lee, A.; Awwal, I.; Bradlow, H.; Pan, J.; Patil, S.; Goldberg, K.; Abbeel, P. Motion planning with sequential convex optimization and convex collision checking. Int. J. Robot. Res. 2014, 33, 1251–1270. [Google Scholar] [CrossRef]
- Hu, S.; Babaians, E.; Karimi, M.; Steinbach, E. NMPC-MP: Real-time Nonlinear Model Predictive Control for Safe Motion Planning in Manipulator Teleoperation. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 8309–8316. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Bristow, D.; Tharayil, M.; Alleyne, A. A survey of iterative learning control. IEEE Control Syst. Mag. 2006, 26, 96–114. [Google Scholar]
- Longman, R.W. Iterative learning control and repetitive control for engineering practice. Int. J. Control 2000, 73, 930–954. [Google Scholar] [CrossRef]
- Cuiyan, L.; Dongchun, Z.; Xianyi, Z. A survey of repetitive control. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No.04CH37566), Sendai, Japan, 28 September–2 October 2004; Volume 2, pp. 1160–1166. [Google Scholar]
- Pane, Y.; Nageshrao, S.; Kober, J.; Babuska, R. Reinforcement learning based compensation methods for robot manipulators. Eng. Appl. Artif. Intell. 2019, 78, 236–247. [Google Scholar] [CrossRef]
- Grüne, L. NMPC without terminal constraints. IFAC Proc. Vol. 2012, 45, 1–13. [Google Scholar] [CrossRef]
- Grüne, L.; Pannek, J.; Seehafer, M.; Worthmann, K. Analysis of Unconstrained Nonlinear MPC Schemes with Time Varying Control Horizon. SIAM J. Control. Optim. 2010, 48, 4938–4962. [Google Scholar] [CrossRef]
- Schwenzer, M.; Ay, M.; Bergs, T.; Abel, D. Review on model predictive control: An engineering perspective. Int. J. Adv. Manuf. Technol. 2021, 117, 1327–1349. [Google Scholar] [CrossRef]
- Drgoňa, J.; Arroyo, J.; Cupeiro Figueroa, I.; Blum, D.; Arendt, K.; Kim, D.; Ollé, E.P.; Oravec, J.; Wetter, M.; Vrabie, D.L.; et al. All you need to know about model predictive control for buildings. Annu. Rev. Control 2020, 50, 190–232. [Google Scholar] [CrossRef]
- Findeisen, R.; Allgöwer, F. An Introduction to Nonlinear Model Predictive Control. In Proceedings of the 21st Benelux Meeting on Systems and Control, Veldhoven, The Netherlands, 19–21 March 2002. [Google Scholar]
- Qin, S.J.; Badgwell, T.A. An Overview of Nonlinear Model Predictive Control Applications. In Proceedings of the Nonlinear Model Predictive Control; Allgöwer, F., Zheng, A., Eds.; Birkhäuser Basel: Basel, Switzerland, 2000; pp. 369–392. [Google Scholar]
- Al Younes, Y.; Barczyk, M. Nonlinear Model Predictive Horizon for Optimal Trajectory Generation. Robotics 2021, 10, 90. [Google Scholar] [CrossRef]
- Arbo, M.H.; Grøtli, E.I.; Gravdahl, J.T. Mid-Level MPC and 6 DOF output path following for robotic manipulators. In Proceedings of the 2017 IEEE Conference on Control Technology and Applications (CCTA), Maui, HI, USA, 27–30 August 2017; pp. 450–456. [Google Scholar]
- Bai, G.; Meng, Y.; Liu, L.; Luo, W.; Gu, Q.; Liu, L. Review and Comparison of Path Tracking Based on Model Predictive Control. Electronics 2019, 8, 1077. [Google Scholar] [CrossRef]
- Ozana, S.; Krupa, F.; Nemcik, J.; Takacs, G.; Mozaryn, J.; Beremlijski, P.; Singh, A.; Kawala-Sterniuk, A. Design and Implementation of Adaptive NMPC in industrial applications: Case study. In Proceedings of the 2022 23rd International Carpathian Control Conference (ICCC), Sinaia, Romania, 29 May–1 June 2022; pp. 12–18. [Google Scholar]
- Leva, A.; Formentin, S.; Seva, S. Overlapping-Horizon MPC: A Novel Approach to Computational Constraints in Real-Time Predictive Control. In Proceedings of the Third Workshop on Next Generation Real-Time Embedded Systems (NG-RES 2022), Budapest, Hungary, 22 June 2022; Bertogna, M., Terraneo, F., Reghenzani, F., Eds.; Schloss Dagstuhl–Leibniz-Zentrum für Informatik: Dagstuhl, Germany, 2022; Volume 98. [Google Scholar]
- Gil, P.; Henriques, J.; Dourado, A.; Duarte-Ramos, H. Non-Linear Predictive Control Based On A Recurrent Neural Network. In Proceedings of the ESIT’99, European Symposium on Intelligent Techniques, Platanias, Greece, 3–4 June 1999; p. 6. [Google Scholar]
- van Duijkeren, G.; Verschueren, R.; Pipeleers, G.; Diehl, M.; Swevers, J. Path-following NMPC for serial-link robot manipulators using a path-parametric system reformulation. In Proceedings of the 2016 European Control Conference (ECC), Aalborg, Denmark, 29 June–1 July 2016; pp. 477–482. [Google Scholar]
- Cisneros, P.G.; Werner, H. Fast Nonlinear MPC for Reference Tracking Subject to Nonlinear Constraints via Quasi-LPV Representations. IFAC-PapersOnLine 2017, 50, 11601–11606. [Google Scholar] [CrossRef]
- Erez, T.; Lowrey, K.; Tassa, Y.; Kumar, V.; Kolev, S.; Todorov, E. An integrated system for real-time model predictive control of humanoid robots. In Proceedings of the 2013 13th IEEE-RAS International Conference on Humanoid Robots (Humanoids), Atlanta, GA, USA, 15–17 October 2013; pp. 292–299. [Google Scholar]
- Nakanishi, J.; Cory, R.; Mistry, M.; Peters, J.; Schaal, S. Operational Space Control: A Theoretical and Empirical Comparison. Int. J. Robot. Res. 2008, 27, 737–757. [Google Scholar] [CrossRef]
- Faulwasser, T.; Kern, B.; Findeisen, R. Model predictive path-following for constrained nonlinear systems. In Proceedings of the Proceedings of the 48h IEEE Conference on Decision and Control (CDC) Held Jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 8642–8647. [Google Scholar]
- Faulwasser, T.; Weber, T.; Zometa, P.; Findeisen, R. Implementation of Nonlinear Model Predictive Path-Following Control for an Industrial Robot. IEEE Trans. Control. Syst. Technol. 2017, 25, 1505–1511. [Google Scholar] [CrossRef]
- Mazdarani, H.; Farrokhi, M. Adaptive neuro-predictive control of robot manipulators in work space. In Proceedings of the 2012 17th International Conference on Methods & Models in Automation & Robotics (MMAR), Miedzyzdroje, Poland, 27–30 August 2012; pp. 349–354. [Google Scholar]
- Zhou, B.; Yang, L.; Wang, C.; Chen, Y.; Chen, K. Inverse Jacobian Adaptive Tracking Control of Robot Manipulators with Kinematic, Dynamic, and Actuator Uncertainties. Complexity 2020, 2020, 5070354. [Google Scholar] [CrossRef]
- Dulęba, I.; Opalka, M. A comparison of Jacobian-based methods of inverse kinematics for serial robot manipulators. Int. J. Appl. Math. Comput. Sci. 2013, 23, 373–382. [Google Scholar] [CrossRef]
- Hu, Y.; Su, H.; Zhang, L.; Miao, S.; Chen, G.; Knoll, A. Nonlinear Model Predictive Control for Mobile Robot Using Varying-Parameter Convergent Differential Neural Network. Robotics 2019, 8, 64. [Google Scholar] [CrossRef]
- Faulwasser, T.; Findeisen, R. Nonlinear Model Predictive Control for Constrained Output Path Following. IEEE Trans. Autom. Control 2016, 61, 1026–1039. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, L.; Li, Y.; Li, D. Model predictive control and its application in agriculture: A review. Comput. Electron. Agric. 2018, 151, 104–117. [Google Scholar] [CrossRef]
- Mavrogiannis, C.I.; Liarokapis, M.V.; Kyriakopoulos, K.J. Quantifying anthropomorphism of robot arms. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 4084–4089. [Google Scholar]
- Jazar, R.N. Inverse Kinematics. In Theory of Applied Robotics: Kinematics, Dynamics, and Control; Springer: Boston, MA, USA, 2007; pp. 263–296. [Google Scholar]
- Taki, S.; Nenchev, D. A novel singularity-consistent inverse kinematics decomposition for S-R-S type manipulators. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 5070–5075. [Google Scholar]
- Moosavian, S.A.A.; Papadopoulos, E. Modified transpose Jacobian control of robotic systems. Automatica 2007, 43, 1226–1233. [Google Scholar] [CrossRef]
- Pires, J.N.; Loureiro, A.; Bölmsjo, G. Welding Robots; Springer: London, UK, 2006. [Google Scholar]
- Maurtua, I.; Ibarguren, A.; Kildal, J.; Susperregi, L.; Sierra, B. Human–robot collaboration in industrial applications: Safety, interaction and trust. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417716010. [Google Scholar] [CrossRef]
- Schmitz, A. Human-Robot Collaboration in Industrial Automation: Sensors and Algorithms. Sensors 2022, 22, 5848. [Google Scholar] [CrossRef] [PubMed]
- Murray, R.M.; Zexiang, L.; Shankar, S. A Mathematical Introduction to Robotic Manipulation; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Stäubli International AG. TX2-90 Industrial Robot Range. Available online: https://www.staubli.com/en/robotics/product-range/industrial-robots/6-axis-robots/tx2-90/ (accessed on 1 January 2021).
- Koenig, N.; Howard, A. Design and use paradigms for Gazebo, an open-source multi-robot simulator. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No.04CH37566), Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2149–2154. [Google Scholar]
- Stanford Artificial Intelligence Laboratory. Robotic Operating System (ROS) Melodic Morenia. Available online: https://www.ros.org (accessed on 1 February 2021).
- Lüling, N.; Reiser, D.; Stana, A.; Griepentrog, H. Using depth information and colour space variations for improving outdoor robustness for instance segmentation of cabbage. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 2331–2336. [Google Scholar]
- Diankov, R. Automated Construction of Robotic Manipulation Programs. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2010. AAI3448143. [Google Scholar]
- Xie, S.; Sun, L.; Wang, Z.; Chen, G. A speedup method for solving the inverse kinematics problem of robotic manipulators. Int. J. Adv. Robot. Syst. 2022, 19, 17298806221104602. [Google Scholar] [CrossRef]
- Siciliano, B.; Sciavicco, L.; Villani, L.; Oriolo, G. Robotics-Modelling, Planning and Control; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Alavala, C. Difference between Denavit-Hartenberg (D-H) Classical and Modified Conventions for Forward Kinematics of Robots with Case Study. In Proceedings of the International Conference on Advanced Materials and manufacturing Technologies, Solo, Indonesia, 16–17 September 2014. [Google Scholar]
- McCarthy, J. Introduction to Theoretical Kinematics; MIT Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Chevallereau, C.; Khalil, W. A new method for the solution of the inverse kinematics of redundant robots. In Proceedings of the Proceedings. 1988 IEEE International Conference on Robotics and Automation, Philadelphia, PA, USA, 24–29 April 1988; Volume 1, pp. 37–42. [Google Scholar]
- Wang, X.; Zhang, D.; Zhao, C. The inverse kinematics of a 7R 6-degree-of-freedom robot with non-spherical wrist. Adv. Mech. Eng. 2017, 9, 1687814017714985. [Google Scholar] [CrossRef]
- Corke, P. Robotics, Vision and Control-Fundamental Algorithms in MATLAB; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Rülling, K.; Schröer, S. Algebraic loop groups. arXiv 2021, arXiv:2109.11364. [Google Scholar]
- Görner, M.; Haschke, R.; Ritter, H.; Zhang, J. MoveIt! Task Constructor for Task-Level Motion Planning. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 190–196. [Google Scholar]
- Ott, C. Cartesian Impedance Control of Redundant and Flexible-Joint Robots, 1st ed.; Springer Publishing Company, Incorporated: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Zube, A. Cartesian nonlinear model predictive control of redundant manipulators considering obstacles. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 137–142. [Google Scholar]
- Zhang, X.; Liniger, A.; Borrelli, F. Optimization-Based Collision Avoidance. IEEE Trans. Control. Syst. Technol. 2020, 29, 972–983. [Google Scholar] [CrossRef]
- Jiménez, P.; Thomas, F.; Torras, C. 3D collision detection: A survey. COmputers Graph. 2001, 25, 269–285. [Google Scholar] [CrossRef]
- Grüne, L.; Pannek, J. Nonlinear Model Predictive Control. Theory and Algorithms; Springer: London, UK, 2011. [Google Scholar]
- Diehl, M.; Bock, H.G.; Diedam, H.; Wieber, P.B. Fast Direct Multiple Shooting Algorithms for Optimal Robot Control. In Proceedings of the Fast Motions in Biomechanics and Robotics; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Sarabandi, S.; Thomas, F. Accurate Computation of Quaternions from Rotation Matrices. In Proceedings of the Advances in Robot Kinematics 2018; University of Bologna, Italy; Lenarcic, J., Parenti-Castelli, V., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 39–46. [Google Scholar]
- Shuster, M.D. The nature of the quaternion. J. Astronaut. Sci. 2008, 56, 359–373. [Google Scholar] [CrossRef]
- Andrle, M.S.; Crassidis, J.L. Geometric Integration of Quaternions. J. Guid. Control Dyn. 2013, 36, 1762–1767. [Google Scholar] [CrossRef]
- Chiaverini, S.; Siciliano, B. The Unit Quaternion: A Useful Tool for Inverse Kinematics of Robot Manipulators. Syst. Anal. Model. Simul. 1999, 35, 45–60. [Google Scholar]
- MATLAB. Version 9.8.0.1323502 (R2020a); The MathWorks Inc.: Natick, MA, USA, 2020. [Google Scholar]
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi—A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- vd. Hoorn, G. (TU Delft Robotics Institute). Staubli_Experimental. Available online: https://wiki.ros.org/staubli_experimental (accessed on 10 September 2020).
- Mavrommati, A.; Osorio, C.; Valenti, R.G.; Rajhans, A.; Mosterman, P.J. An Application of Model Predictive Control to Reactive Motion Planning of Robot Manipulators. In Proceedings of the 2021 IEEE 17th International Conference on Automation Science and Engineering (CASE), Lyon, France, 23–27 August 2021; pp. 915–920. [Google Scholar]
- Reinhold, J.; Baumann, H.; Meurer, T. mdpi-robotics-kard-2022_acon-kiel-janr_nmpc-decomp-robot.mp4. Available online: https://cloud.rz.uni-kiel.de/index.php/s/xJLRyg8WFYTTTDM (accessed on 15 November 2022).
- EtherCAT Technology Group. EtherCAT—The Ethernet Fieldbus. Available online: https://www.ethercat.org/ (accessed on 1 January 2022).
- Reinhold, J.; Elsner, L.; Meurer, T. Force-Based Pick-and-Place Along Curved Surfaces Exploiting Robot Repeatability. In Proceedings of the ISR Europe 2022; 54th International Symposium on Robotics, Munich, Germany, 20–21 June 2022; pp. 1–8. [Google Scholar]
- Verschueren, R.; Frison, G.; Kouzoupis, D.; Frey, J.; van Duijkeren, N.; Zanelli, A.; Novoselnik, B.; Albin, T.; Quirynen, R.; Diehl, M. acados—A modular open-source framework for fast embedded optimal control. Math. Program. Comput. 2021, 14, 147–183. [Google Scholar] [CrossRef]
- Reinhold, J.; Amersdorfer, M.; Meurer, T. A Dynamic Optimization Approach for Sloshing Free Transport of Liquid Filled Containers using an Industrial Robot. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 2336–2341. [Google Scholar]
- Käpernick, B.; Graichen, K. The gradient based nonlinear model predictive control software GRAMPC. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 1170–1175. [Google Scholar]



| Properties | I: Anthropomorphic arm | II: Spherical Wrist |
|---|---|---|
| intended use |
|
|
| constraints |
|
|
| control |
|
|
| singularity avoidance |
|
|
| i | ||||
|---|---|---|---|---|
| w | 0 | 0 | 0 | |
| 1 | 50 | 478 | ||
| 2 | 425 | 0 | 0 | |
| 0 | 50 | |||
| 425 | 0 | 50 | ||
| 4 | 0 | 425 | ||
| 5 | 0 | 0 | ||
| f | 0 | 0 | 100 | |
| e | 0 | 0 | 150 | 0 |
| Point-to-Point Movement | Decomp. System | Full System | |
|---|---|---|---|
| without obstacles | |||
| with obstacle | |||
| with obstacle and height constraints | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reinhold, J.; Baumann, H.; Meurer, T. Constrained-Differential-Kinematics-Decomposition-Based NMPC for Online Manipulator Control with Low Computational Costs. Robotics 2023, 12, 7. https://doi.org/10.3390/robotics12010007
Reinhold J, Baumann H, Meurer T. Constrained-Differential-Kinematics-Decomposition-Based NMPC for Online Manipulator Control with Low Computational Costs. Robotics. 2023; 12(1):7. https://doi.org/10.3390/robotics12010007
Chicago/Turabian StyleReinhold, Jan, Henry Baumann, and Thomas Meurer. 2023. "Constrained-Differential-Kinematics-Decomposition-Based NMPC for Online Manipulator Control with Low Computational Costs" Robotics 12, no. 1: 7. https://doi.org/10.3390/robotics12010007
APA StyleReinhold, J., Baumann, H., & Meurer, T. (2023). Constrained-Differential-Kinematics-Decomposition-Based NMPC for Online Manipulator Control with Low Computational Costs. Robotics, 12(1), 7. https://doi.org/10.3390/robotics12010007







