Design and Construction of Hybrid Autonomous Underwater Glider for Underwater Research

Abstract

The main goal of this paper was to design and construct a hybrid autonomous underwater glider (HAUG) with a torpedo shape, a size of 230 cm in length and 24 cm in diameter. The control, navigation, and guidance system were executed simultaneously using a Udoo X86 minicomputer as the main server and three BeagleBone Black single-board computers as the clients. The simulations showed a controlled horizontal speed of 0.5 m/s in AUV mode and 0.39 to 0.51 m/s in glide mode with a pitch angle between 14.13${}^{\circ }$ and 26.89${}^{\circ }$. In addition, the field experiments under limited space showed the proposed HAUG had comparable results with the simulation, with a horizontal speed in AUV mode of 1 m/s and in glide mode of around 0.2 m/s. Moreover, the energy consumption with an assumption of three cycles of gliding motion per hour was 51.63 watts/h, which enabled the HAUG to perform a mission for 44.74 h. The proposed HAUG was designed to hold pressure up to 200 m under water and to perform underwater applications such as search and rescue, mapping, surveillance, monitoring, and maintenance.

1. Introduction

The tasks of underwater gliders have been performed in fisheries, environment monitoring, and other scientific and defence purposes [1,2,3,4]. Applications of underwater gliders have been conducted in large fisheries using acoustic sensors such as hydrophones for detecting and tracking objects [5,6]; others use hydrophones for tracking mammals [7,8] and vessels [9,10]. In other applications, underwater gliders have helped the researcher to get information on environment monitoring [5,11,12,13]. Moreover, an application of underwater gliders for monitoring and surveillance is reported in [14]. An underwater glider works as an autonomous vehicle that operates with the concept of a buoyancy-driven vehicle and the dynamics of its mechanical design to convert vertical motion to horizontal motion [15]. Most underwater gliders use this principle and produce long-endurance performance and are energy-efficient [16]. Due to the underactuated system, the underwater glider has a limitation in speed and manoeuvrability performance. Moreover, it is difficult to control the underwater glider with a limited propulsion system and limited motion control in underwater environments and disturbance [17]. The universal design of an underwater glider involves a buoyancy control device, a moving-mass engine, and a rudder. The underwater glider moves through the ocean by adjusting the buoyancy with the buoyancy engine and the pitch angle with the moving-mass engine [18]. In terms of controller methods, classical and modern control methods have been used in underwater gliders to control motion. Proportional–integral–derivative (PID) controllers and linear–quadratic regulators (LQR) are commonly used to perform the depth and pitch motion [19,20,21]. Other methods, such as sliding mode control (SMC) and artificial neural network have been used in [17,20,22,23,24,25] for controlling pitch motion and depth. The precise sensing related to navigation [26,27] and control, energy optimization, path planning, and obstacle avoidance has been the major focus of research in hybrid underwater gliders [11,28,29].

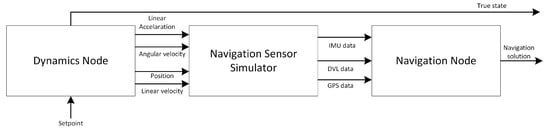
The existing technology, for example, the US3157145A patent [30], which uses a gliding mode system, such as a sea glider [31], blended-wing-body underwater glider (BWUBG) [32], and Petrel [33], utilizing a moving-mass engine and buoyancy engine. However, this type of technology has limitations in speed and manoeuvrability. To maximize speed and manoeuvrability, a hybrid system was developed in this paper. This hybrid system uses the gliding mode and propulsion mode, which is known as the hybrid autonomous underwater glider (HAUG). The HAUG is a category of autonomous underwater vehicle (AUV) that can operate autonomously and has a combination of gliding mode and propulsion mode. The gliding mode takes advantage of a buoyancy engine to perform durability movement to operate in the long term, while the propeller mode takes advantage of propulsion to perform speed and manoeuvrability. The HAUG can be used for various fields such as deep-sea exploration, detecting seabed oil and gas pipelines, underwater object detection, and depth measuring (bathymetry). Knowledge of bathymetry holds the major key to an underwater map. This underwater map provides information on marine transportation navigation (both on the surface and subsurface) that is safe to pass, as well as scientific studies regarding ocean volume, ecology, and circulation related to the Earth’s climate. The HAUG needs a control system, a navigation system, and a guidance system to use the advantages of each mode. The guidance system directs the HAUG’s movement to follow a trajectory based on the input of waypoint points from the user. The control system drives each HAUG’s actuator to follow directions from the guidance system. The navigation system provides position, attitude, and velocity information. In some research, the navigation system is equipped with a gliding map which provide a gliding route with a low sea current [34].

The main contribution of this paper is the design and construction of the mechanical system, electrical system, navigation systems, control system, and communication system of a hybrid autonomous underwater glider for underwater research. The term hybrid in this paper states that there are additional actuators, such as bow, stern, and main thrusters as well as a complete set of control surface: rudder and elevator. This paper also describes the design of the moving-mass engine and the buoyancy engine which are adapted to the modular hull design. In addition, the performance of the mechanical design, electronic systems, communication systems, control and guidance systems, and multisensor navigation systems in dual mode, AUG, and AUV mode, are shown in this paper in the form of simulation results and field experiments.

This paper is organized as follows: Section 2 describes the mechanical design development. Section 3 presents the electrical design. Section 4 presents the control and guidance system design and some experimental results in a real-world underwater environment. Section 5 describes the sensor used for the navigation system. Section 6 expresses the communication design. Finally, Section 7 summarizes the conclusions of the paper.

2. Mechanical Design

The HAUG is designed for two main modes: AUG mode and AUV mode. The AUG mode uses two main actuators: a buoyancy engine and a moving-mass engine. The moving-mass engine is used to control the pitch and the buoyancy engine is used to control the heave motion. Under certain conditions, the two engines produce a longitudinal motion. In AUV mode, the HAUG uses two main actuators: three propulsion-based thrusters (main, bow, and stern thrusters) and surface controls (rudder and elevator). The thrusters control the surge, yaw, and sway motion, while the elevator and rudder control yaw and pitch. Figure 1 shows the HAUG’s mechanical design with a modular design. The modular design consists of four compartments. The first compartment consists of the bow thruster, altimeter sensor, and Doppler velocity log (DVL) sensor. The second compartment consists of a moving-mass engine. The third compartment consists of the battery, wing, and charge sensor (side-scanning sonar sensor). Finally, the last compartment consists of the elevator, rudder, Global Positioning System (GPS) sensor, inertial measurement unit (IMU), stern thruster, and main thruster. Figure 2 shows the given design and Figure 3 shows the underwater prototype HAUG. The HAUG has a combination of glide movement capabilities on the sea glider in glide mode and propeller-based movement (propulsion) in AUV mode. The glide mode utilizes the ability of the buoyancy engine to control the HAUG’s buoyancy for movement, while the AUV mode utilizes propulsion and surface control for manoeuvring and movement.

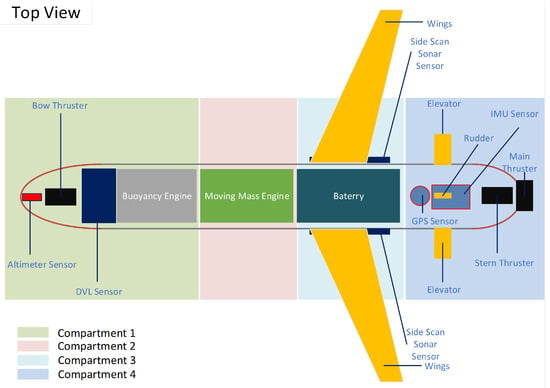
Figure 1. HAUG’s concept design.

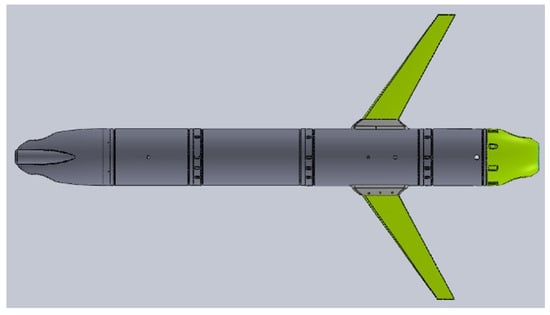
Figure 2. Rendered concept design.

Figure 3. Underwater HAUG prototype.

2.1. Buoyancy Engine Design

A buoyancy engine is an engine that controls the buoyancy of an underwater vehicle by changing the internal bladder volume. One of the buoyancy engines currently available, such as the US7921795B2 patent [35], uses an internal bladder inside a pressure chamber. The internal fluid bag volume is measured by using a pressure sensor on the pressurized chamber. Another buoyancy engine model is the US Patent US8205570B1 [36] on a self-contained underwater vehicle with a piston-based buoyancy engine. Moreover, a similar buoyancy engine model is found in the WIPO Patent WO2013044644A1 [37], where the patented buoyancy engine utilizes the same piston movement. The disadvantage of piston-based buoyancy engine models is the dimensions required to accommodate the pistons which require a large space. Another type of buoyancy engine model is shown in US Patent US8100074B2 [38]. This buoyancy engine works based on the electrolysis system. The disadvantage of this type is the need for adequate material requirements for a chemical reaction to be carried out repeatedly. Moreover, the electrolysis reaction requires a certain reaction area for the buoyancy engine to work quickly. The advantage of the proposed design is that the design is preferable in terms of mechanical systems and simpler on the electronic side. Figure 4 shows the prototype of the buoyancy engine.

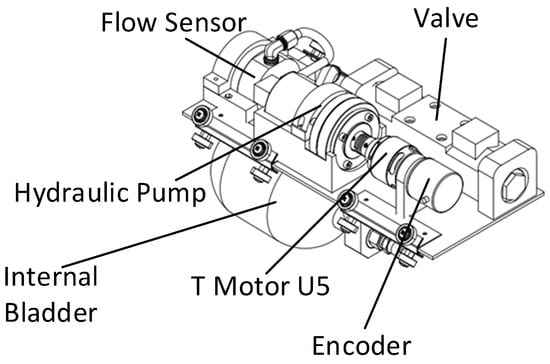
Figure 4. Underwater HAUG’s buoyancy engine prototype.

The block diagram in Figure 5 shows the electronic diagram to control the buoyancy engine. The CX-M9 sensor, a micro flow sensor from Shanghai Cixi Instrument-Shanghai, China, measures the hydraulic oil volume which is pumped from the internal bladder to the external bladder and vice versa. This sensor has a 5 mL/pulse resolution with 6–600 L/h and 0.2% in full-scale accuracy. The LDP3806 sensor is an Optical Rotary Encoder from Domoticx-Mariënheem, Netherlands which is used to measure the rotation per minute of the U5 motor. The U5 motor is a 24 V brushless from T-Motor-Nanchang, China, with a maximum of 7000 rpm at 30 A. The proposed design used a Hydro Leduc PB36.5, a hydraulic pump from Hydro Leduc-Azerailles, France, with a maximum of 6000 rotation per minute and a maximum pressure of 5075 Psi. Moreover, to control the direction of the hydraulic oil flow, the buoyancy engine uses a Yuken DSG-01 hydraulic valve, a 4-way and 3-position valves from Yuken Sea-Bangkok, Thailand.

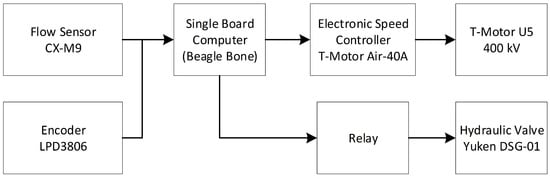
Figure 5. Buoyancy engine block diagram.

The buoyancy engine workflow is shown in Figure 6. The buoyancy engine receives information from the operator or guidance system. The information is in the form of a desired internal bladder volume (X). The BeagleBone Black, a single board computer from BeagleBoard.org-Michigan, USA, evaluates the current volume of the internal bladder (Y) and the difference from the desired internal bladder volume (X). If the internal bladder volume (Y) is more than the desired internal bladder volume (X), the BeagleBone Black commands an action. The action is to run the hydraulic pump motor and relay to open the hydraulic valve according to the flow and desired volume. However, if the desired internal bladder volume (X) is less than the internal bladder volume, the BeagleBone Black gives the same signal with a different flow direction.

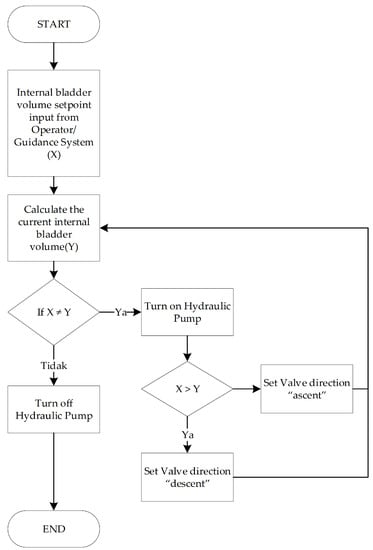
Figure 6. Buoyancy engine workflow.

The rotation speed of the hydraulic pump motor is measured using a motor rotation sensor as feedback to the BeagleBone Black. Subsequently, the speed of the motor controller is determined using the proportional, derivative, and integral control methods. Control of the motor rotation speed is necessary due to the maximum rotational speed limitation of the hydraulic pump, while the rotation speed can be varied depending on the environmental pressure. A fluid displacement rotates the flow sensor that provides pulse signal feedback to calculate the internal bladder volume (Y). Moreover, if the difference between the desired internal bladder volume (X) and the internal bladder volume (Y) is less than the tolerance value, the BeagleBone Black gives a stop signal to the motor and relay.

The buoyancy engine’s hydraulic diagram is shown in Figure 7. This figure shows the buoyancy engine’s hydraulic pump work in a one-way flow direction. Four-way and three-position valves are used to control the hydraulic fluid direction where the valve position is normally closed.

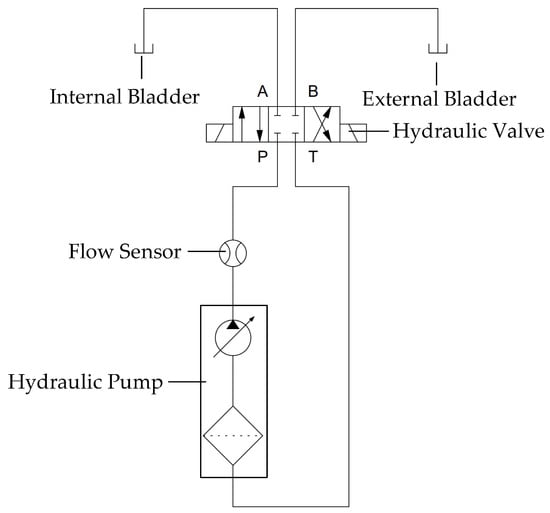
Figure 7. Buoyancy engine’s hydraulic diagram.

2.2. Moving-Mass Engine Design

The design of the moving-mass engine prototype is shown in Figure 8. The workflow of the moving-mass engine is to move a certain mass in an underwater vehicle to produce a displacement of the vehicle’s centre of gravity. This change in the centre of gravity results in a change in the angle of inclination in either the pitch direction or the roll direction.

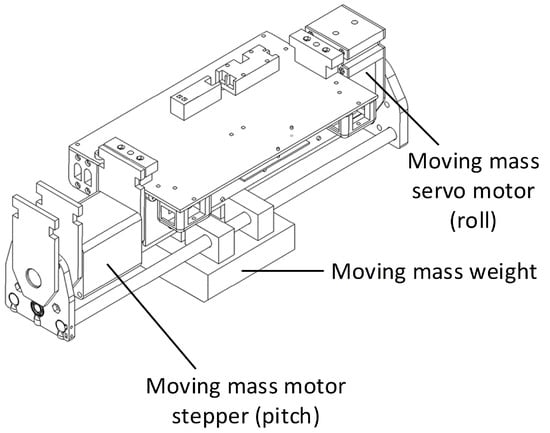
Figure 8. Underwater HAUG’s moving-mass engine prototype.

The design of this moving mass consists of two motors and a single moveable mass that can move linearly and rotate. The first motor uses a NEMA 23, a stepper motor from Soya Motor-Changzhou, China, with a detent torque of 70 mN·m and a holding torque of 1.3 N·m. This motor can move a moveable mass weighing 4 kg in a linear direction. The second motor uses a Dynamixel XM540-W270T, a servo motor from Robotis-Seoul, South Korea, with a stall torque of 10.6 N·m and a resolution of 4096 pulse/rev. This motor can move the moveable mass and all components of the holder weighing 7 kg. In addition, this prototype uses two mechanical switch sensors that are placed at each end of the movement space. The function of this mechanical switch sensor is to mark the limit of the movement of the moving mass. Moreover, this prototype processes information from the mechanical switch sensors and position sensors in the Dynamixel XM540-W270T on the BeagleBone Black to determine the current position and give instruction to move the moveable mass to the desired position. The block diagram in Figure 9 shows the electronic diagram to control the moving-mass engine.

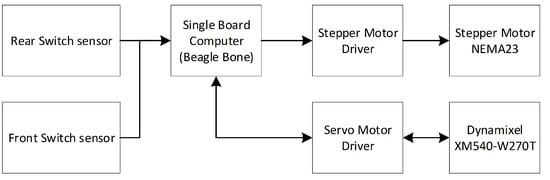
Figure 9. Moving-mass engine block diagram.

The moving-mass engine workflow in the longitudinal axis is shown in Figure 10a. The moving-mass engine receives information from the operator or guidance system. The information is in the form of a desired pitch/roll (A). The BeagleBone Black evaluates the current position of the moveable mass (B) and the difference from the desired position (A). If the difference between the position of the desired moveable mass (A) and the current position of moveable mass (B) is more than the tolerance value, the BeagleBone Black signals a command to turn on the stepper motor. If the position is smaller, then the BeagleBone Black signals to turn on the stepper motor in a “forward” motion. Meanwhile, if the position is greater, then the BeagleBone Black gives a signal to turn on the stepper motor in a “backward” motion. The system calculates the position of the moveable mass by using the number of given signals to the stepper motor.

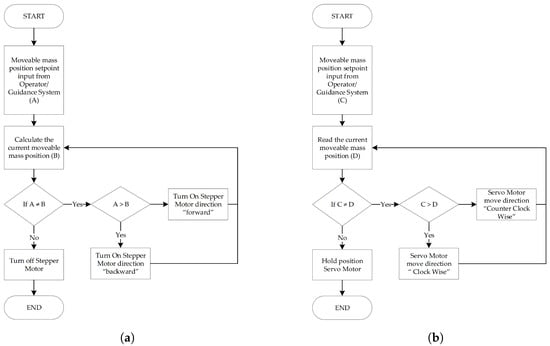
Figure 10. Lateral and longitudinal engine workflow. (a) Moving mass’s pitch; (b) Moving mass’s roll.

In addition, the moving-mass engine workflow in the lateral axis is shown in Figure 10b. The workflow in the lateral axis is the same as the workflow in the longitudinal axis. The motion difference is in the lateral axis; the moving-mass engine uses the servo motor in an anticlockwise motion or clockwise motion depending on the desired position. Furthermore, this prototype uses the encoder inside the servo motor to get the position information in the lateral axis.

2.3. Kinematic Model

The kinematic Model of the HAUG consists of the linear displacement $\eta$ and the velocity V, which is shown in Equations (1) and (2). To define the orientation of the vehicle in terms of Euler angles, the linear displacement describes the three inertial axes and three rotation axes, while the speed is described as the linear and angular speeds in the body-fixed frame. The relation between linear displacement and velocity V is shown in Equations (3) and (4) [39,40].

$$\eta ={\left[\begin{array}{cccccc}(x& y& z& \varphi & \theta & \psi )\end{array}\right]}^T$$

(1)

$$V={\left[\begin{array}{cccccc}u& v& w& p& q& r\end{array}\right]}^T$$

(2)

$$\dot{\eta }=J\left(\eta \right)V$$

(3)

$$J\left(\eta \right)=\left[\begin{array}{cc}{J\left(\eta \right)}_{linear}& 0\\ 0& {J\left(\eta \right)}_{rotational}\end{array}\right]$$

(4)

where x, y, and z defines the vehicle’s position, while $\varphi$, $\theta$, and $\psi$ express the roll, pitch, and yaw in an earth-frame, respectively. A linear movement is expressed in u, v, and w, which describe, respectively, a surge, sway, and heave movement. The rotational movement is represented in p, q, and r, which describe the roll velocity, pitch velocity, and yaw velocity, respectively. J$\left(\eta \right)$ is the linear and rotational transform matrix. To simulate the velocities, orientations, and positions, it is necessary to understand the dynamics of HAUG.

2.4. Dynamic Model

The dynamic model is constructed from [39,41] and is represented in Equations (5)–(8). The general design of the HAUG is considered as a low-speed vehicle and is symmetrical in the x–y plane and x–z plane.

$$M\dot{V}+C\left(V\right)V+D\left(V\right)V+g\left(\eta \right)={\tau }_{Actuator}+{\tau }_{SeaCurrent}$$

(5)

$$M=M_{RB}+M_A$$

(6)

$$C\left(v\right)=C_{RB}\left(V\right)+C_A\left(V\right)$$

(7)

$$D\left(V\right)=D_q\left(V\right)+D_l\left(V\right)$$

(8)

where M is the total mass matrix, $C\left(V\right)$ is the total Coriolis and centripetal matrix, $D\left(V\right)$ is the quadratic and linear hydrodynamic damping matrix, $g\left(\eta \right)$ is the gravitational and restoring force matrix, ${\tau }_{Actuator}$ is the force and moment of the actuator, and ${\tau }_{SeaCurrent}$ is the force and moment of the sea current. The variables of the HAUG’s dynamic model, some determined using computational fluid dynamics, are shown in Table 1.

Table 1. HAUG dynamic variables.

Symbols	Value	Units
Mass (m)	86.5	kg
Gravitational constant (g)	9.8	m/s2
Weight (W)	847.7	N
Buoyancy force (B)	847.7	N
Water density ($\rho$)	1000	kg/m3
Length (L)	2.3	m
Diameter (d)	0.24	m
Centre of gravity (CoG)	$\left(x_G,y_G,z_G\right)=\left(0,0,-0.0113\right)$	m
Centre of buoyancy (CoB)	$\left(x_B,y_B,z_B\right)=\left(0,0,0\right)$	m
KD0 (from CFD)	8.8	-
KD (from CFD)	242	-
KL0 (from CFD)	0	-
KL (from CFD)	395	-

In addition, KD0 defines the drag when there is no angle of attack movement or the HAUG is in a straight motion. This constant needs to be as low as possible to create a high lift constant compared with the drag constant (high L/D); KD describes how much the drag increases as the angle attack increases. This constant needs to be as low as possible to create a high lift constant compared with the drag constant (high L/D); KL0 defines the lift when there is no angle of attack. This constant needs to be near zero, to ensure a symmetrical ascent and descent. KL describes how much the lift increases as the angle of attack increases. This constant needs to be as high as possible (high L/D). In general, a high KL is usually equal to a high KD.

To achieve the proposed design in Table 1, a weight balancing was added to the construction. This weight balancing was made from lead alloy material which was suitable in weight to volume ratio. The weight distribution of the HAUG is shown in Table 2.

Table 2. Weight distribution for the proposed HAUG.

Item	Description	Weight (in kg)
Wings	Composite fibre	2
Compartment 4	Composite fibre, aluminium T6 and component weight	10.7
Compartment 3	Aluminium T6 and component weight	11.1
Compartment 2	Moving mass weight, aluminium T6 and component weight	18.1
Compartment 1	Composite Fibre, aluminium T6 and component weight	22.3
Battery	24 V lithium battery 110 Ah	12.3
Weight balancing	Neutral buoyancy weight distribution	10
	Total weight	86.5

2.5. Glide Motion Simulation of HAUG

As explained previously, to obtain nonimaginary values, we need to have KD and KD0 as low as possible and KL as high as possible. KL0 will usually be overpowered by KD0’s cot terms, and only show the symmetry of the ascent and descent. This relation is determined using Equation (9) to find the ideal angle of attack for each given HAUG variable.

$$\alpha =\frac{K_{L}tan\gamma }{2K_D}\left(-1+\sqrt{1-4\frac{K_D}{K_L^2}cot\gamma \left(K_{D0}cot\gamma +K_{L0}\right)}\right)$$

(9)

Figure 11a shows the gliding angle simulation for a given HAUG variable. This figure shows the ideal pitch angle for a gliding motion is between 14.13${}^{\circ }$ to 26.89${}^{\circ }$ which yields 0.39 m/s to 0.51 m/s of horizontal speed. Figure 11b shows the mechanical energy usage to the given gliding angle. This figure shows that the lowest energy usage is at the lowest gliding angle, which is around 20${}^{\circ }$.

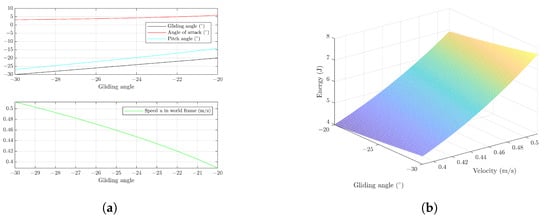
Figure 11. Dynamicmodel simulation. (a) Gliding angle simulation; (b) mechanical energy, gliding angle, and velocity simulation.

After finding the best gliding angle, a motion simulation was conducted by using the finite state machine in Figure 12. This figure shows a gliding motion from the surface to a depth of 200 m and then returning to the surface again. There are five states, initial, descent, neutral, ascend, and surfacing. The initial state describes the moving mass’s position in the neutral position (0 mm) and the buoyancy engine in a neutral buoyancy position (BE = 0 N). The descent state describes a pitch down position with a moving mass moved to 5.6 mm and the buoyancy engine in a submerged position (BE = −5 N). The neutral state describes the same as the initial state, which is used to eliminate the momentum of the previous state. The ascent state describes the opposite of the descent state, where the moving mass’s position is in a pitch up (moved to −5.6 mm) and the buoyancy engine is in a floating position (BE = 5 N). The surfacing state describes the same as the initial state, where the moving mass and buoyancy engine are set to neutral (BE = 0 N and moving mass position = 0).

Figure 12. Finite statemachine for underwater gliding motion.

Figure 13 shows the gliding motion simulation using the finite state machine in Figure 12. The horizontal distance travelled in Figure 13a for 2034 s is 575.92 m with a depth of 199.35 m in Figure 13b. Figure 14a shows the pitch in a gliding motion. The maximum pitch for the descent state is 22.01${}^{\circ }$ with a stabilized pitch at 18.26${}^{\circ }$, while for the ascent state, the maximum pitch is 23.46${}^{\circ }$ and stabilized pitch at 18.23${}^{\circ }$. Figure 14b shows the moving-mass engine and buoyancy engine operation in time.

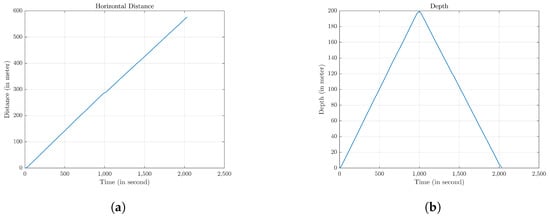
Figure 13. Gliding motion simulation. (a) Simulation gliding motion in the distance axis; (b) simulation gliding motion in the depth axis.

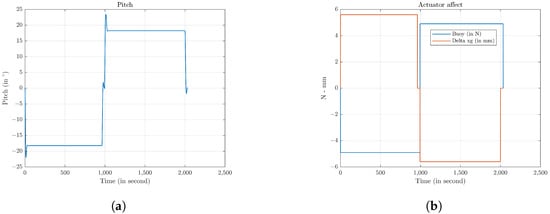
Figure 14. Gliding motion simulation for pitch and actuator. (a) Simulation gliding motion with pitch axis; (b) the actuator motion in a gliding motion.

3. Electrical Design

Figure 15 illustrates the block diagram and electronic components of the entire HAUG system, where the colour determines the voltage used for each component (24 V, 12 V, and 5 V). This system consists of five subsystems: four subsystems are onboard the vehicle, and one subsystem is on the ground control station on the ground. The four subsystems within the vehicle communicate via Ethernet cables, while the vehicle’s subsystem and the ground control station communicate via Ethernet cables wrapped in Kevlar strands for strength and Dacron fibres for buoyancy and space-filling. Communication between the vehicle and the ground control station uses a Fathom-X module, an interface communication module from Bluerobotics-California, USA, that changes the TCP/IP protocol to the RS-485 protocol and vice versa. This module increases communication capabilities from a maximum of 100 m on a TCP/IP-based system to a maximum of 1000 m without repeaters.

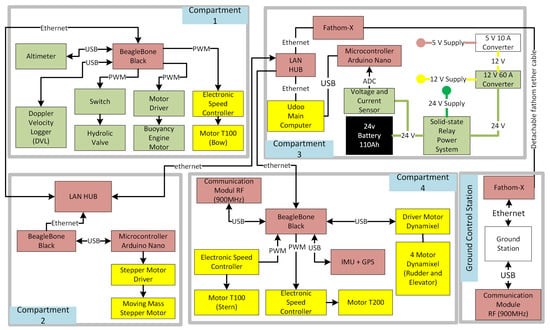
Figure 15. Block diagram and electrical component of the HAUG.

The HAUG’s first subsystem (compartment 1) consists of a single board computer BeagleBone Black, a buoyancy engine motor (T-Motor U5), a DVL sensor, an altimeter sensor, a Yuken DSG-01 hydraulic valve switch, and a T100 motor driver. The BeagleBone Black is responsible for executing parallel tasks in compartment 1, such as (i) data acquisition from the DVL sensors and altimeter sensors; (ii) buoyancy engine motor control in coordination with the guidance and control system; (iii) bow motor control (T100), which also coordinates with the guidance and control system; and (iv) communication between subsystems. The buoyancy engine motor produces 2 Nm and a maximum of 7000 rpm for a hydraulic pump with a displacement of 1800 cm³/min and 300 psi of maximum pressure. Meanwhile, the T100 motor is a brushless motor from Bluerobotics-California, USA, that produces a maximum torque of 1.85 kgf and a 4200 rpm maximum rotation speed.

The second subsystem is compartment 2. This compartment consists of a BeagleBone Black and a moving-mass stepper motor. The BeagleBone Black on this subsystem is responsible for executing parallel tasks in compartment 2, which are (i) controlling the stepper motor for pitch control, which coordinates with the guidance and control system; and (ii) communication between subsystems.

The third subsystem is compartment 3. This compartment consists of a Udoo main computer, voltage and current sensors, voltage converters from 24 V to 12 V and 5 V, and a solid-state relay as the main switch to power the HAUG system. The Udoo, The third subsystem is compartment 3. This compartment consists of a Udoo main computer, voltage and current sensors, voltage converters from 24 V to 12 V and 5 V, and a solid-state relay as the main switch to power the HAUG system. The Udoo, a single board computer with x86 architecture from a startup company in Italy named as Udoo. It has several responsibilities, such as: (i) hosting the main server for the Robot Operating System (ROS) system and any computation requirement during operation; (ii) data acquisition from voltage and current sensors; and (iii) communication between subsystems and the ground control station via a tether cable.

The last subsystem is compartment 4. This compartment consists of a BeagleBone Black, an IMU, a GPS, two Bluerobotic driver motors for controlling the main thruster and stern thruster, and a Dynamixel motor AX-12 for controlling the elevator and rudder. The BeagleBone Black on this subsystem is responsible for (i) data acquisition from the IMU and GPS; (ii) controlling the main thruster and stern thruster; (iii) controlling the rudder and elevator; (iv) communication between subsystems; and (v) communication via the radio frequency module. The power specification of each electrical component used in the HAUG is shown in Table 3.

Table 3. Power specification of each electrical component.

No.	Component	Voltage			Max. Current
		5 V	12 V	24 V
1	DVL			V	3.3 A
	Altimeter		V	V	125 mA
	Bow thruster		V		12.5 A
	BBB	V			2 A
	LED strobe		V		1.25 A
	Motor pump			V	30 A
	Valve			V	3 A
2	BBB	V			2 A
	Arduino	V			280 mA
	Motor’s moving mass		V		3 A
	LAN Hub	V			600 mA
3	UDOO X86		V		3000 mA
	Tether fathom	V	V	V	500 mA
	LAN Hub	V			600 mA
4	BBB	V			2 A
	Rudder		V		1.5 A
	Elevator		V		1.5 A
	Poseidon GPS	V			25 mA
	Spatial Advance IMU	V			100 mA
	RF	V			1 A
	Stern thruster		V		17 A
	Main thruster		V		17 A

The HAUG’s electrical power usage during the hotel load operation is shown in Figure 16. In this figure, there are several spikes appearing in the graph, which indicate when the DVL sensor is being activated. From this figure, the HAUG can operate in standby mode for 47.55 h, with an average hotel load energy consumption of 55.51 watts/h with a 110 Ah 24 V battery at full charge.

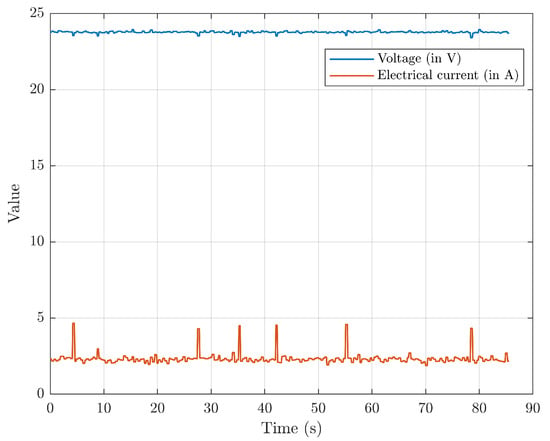
Figure 16. The HAUG’s electrical power usage during the hotel load operation.

4. Control and Guidance

4.1. Control and Guidance Design

In Figure 17, the method for guiding the HAUG’s movement includes the following stages. The HAUG receives information in the form of mission area coordinate points and mission depth from ground stations via cable, radio, and/or satellite communications. The HAUG sends a signal to indicate that the vehicle has successfully received information from the ground station. Then, the HAUG retrieves its current position, attitude, speed, and depth information from the navigation system. The guidance system processes the information to determine the direction so that it can follow a guided path. To follow this guided path, the HAUG uses the line-of-sight (LOS) guidance method. The LOS guidance method uses three reference points to direct the HAUG’s movement: the point of the current position, the point of the destination position, and the point of the reference position that has been passed. The control system determines the magnitude of the action of the buoyancy engine, moving-mass engine, rudder, elevator, and thruster, according to the input from the guidance system. Then, the current HAUG’s state is updated according to the finite state machine.

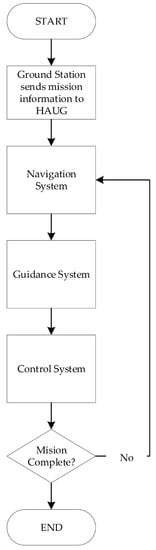
Figure 17. Flowchart diagram of control system and guidance system.

Figure 18 shows the finite state machine in every state. First, in the initial state, the HAUG is lowered into the sea. Then, if condition (a) is met, that is, the HAUG receives input from the ground station, the initial state switches to the gliding mode (descent) state. In this situation, the HAUG uses the LOS method to determine the direction of the movement to follow the guidance path, then the control system uses the proportional, integral, and derivative (PID) method, which is equipped with the gain-scheduling method and the antiwindup method to determine the angle deflection of the rudder. In addition, the control system sends a certain magnitude of action to the buoyancy engine so that the buoyancy engine pushes the fluid into the internal bladder and to the moving-mass engine to move the moveable mass to the front, so it slides down. The HAUG continues to slide down until condition (b) is met, that is, the HAUG is at a certain depth from the seabed. When condition (b) is met, the glide mode (descent) changes to the neutral state. In this state, the control system controls the buoyancy engine to release some of the fluid out to the external bladder. This action alters the HAUG, so it does not move up and does not move down. Moreover, the control system moves the moveable mass to the centre so that the HAUG has a pitch angle near zero degree. Furthermore, if condition (c) is met, that is, the HAUG’s location is outside a certain receiving radius from the destination position, then the neutral state switches to the glide mode (ascend) state. In this state, the control system sends a certain magnitude of action to the buoyancy engine (1) so that the buoyancy engine (1) releases fluid out to the external bladder and to the moving-mass engine to move the moveable mass to the rear position so that the HAUG glides up. The HAUG continues to glide up until condition (d) is met, which is when the HAUG appears on the surface of the sea. If this condition is met, the glide mode (ascent) state changes to the surface state. In this state, the control system controls the moving-mass engine to guide the HAUG to have a pitch angle near zero degree. In addition, on the surface state, the navigation system updates the current HAUG position information by using a GPS sensor. Furthermore, if condition (e) is met, that is, the HAUG’s location is outside a certain receiving radius from the destination position, then the surface state changes to a glide mode (descend) state. If condition (b) is met, the glide mode (descend) state switches back to the neutral state. In addition to the previous condition (b), condition (b) can also be fulfilled if the HAUG is at the depth of the mission and the HAUG’s position is within a certain radius of acceptance (ROA) from the destination. In the glide mode (ascent) state, condition (i) can be met, i.e., the HAUG is at the depth of the mission and the HAUG’s position is within a certain ROA from the destination. If condition (i) is met, the glide mode (ascent) changes to the neutral state. Then, if the HAUG is in a neutral state and condition (f) is met, that is, the current HAUG’s position is in a ROA from the destination, then the neutral state switches to the AUV mode state. In this AUV mode, the control system provides a value for the action of the rudder, elevator, and thrusters in manoeuvring. This AUV mode state works so that the HAUG moves towards the mission area and then carries out missions in that mission area.

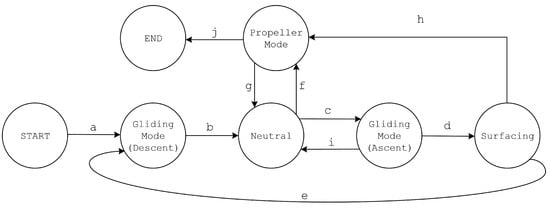
Figure 18. Finite state machine of the HAUG.

In this state, the control system uses the same method as the method of determining the value of the rudder action in the glide mode. Then, if condition (g) is met, i.e., the HAUG has completed the mission, then the AUV mode state switches back to the neutral state. Then, the HAUG repeats the procedure for the glide mode (ascent) state, the surface state, the glide mode (descent) state, and the neutral state until it reaches the point back at the surface state. Then, if condition (h) is met, where the HAUG’s position enters the ROA in the return area, the surface state switches to an AUV mode state to reach the return point. Then, if condition (j) is met, i.e., the HAUG has reached the return point, the AUV mode state moves to the end state. In the final state, the HAUG shuts down all actuator functions, sends a signal containing the coordinates of the current HAUG position via radio and/or satellite communication, and waits to be lifted back from the sea.

4.2. Simulation Experiment

The HAUG’s control and guidance systems were developed in the ROS framework. Based on the derivation of the dynamic model of the HUG GaneshBlue vehicle [42], the controller was divided into three parts, which were based on the direction of movement: surge, pitch, and yaw. The parameters value for each component are shown in Table 4.

Table 4. PID value for each controller.

Parameter	Surge Controller	Yaw Controller	Pitch Controller
Kp	2	0.9	0.9
Ki	0.2	0.2	0.2
Kd	0.1	7	7

Figure 19 shows a simulation scenario in glider mode using the control surface-elevator for controlling the pitch. The current pitch was used as feedback for the PID control. The scenario’s parameters were as follows:

• Pitch desired = ±20${}^{\circ }$;
• Buoyancy engine = ±0.5 L;
• Moving mass = ±15 cm.

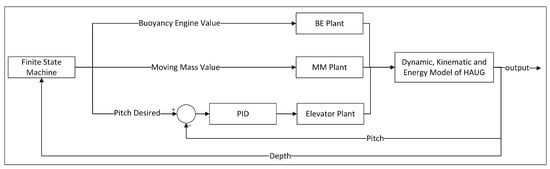
Figure 19. Glide mode simulation scenarios with Buoyancy Engine, Moving Mass, and pitch control.

Figure 20 describes the simulation results of pitch, depth, and energy with reference to the x-earth coordinates in the glider mode. The PID values were: Kp = 0.9, Ki = 0.2, and Kd = 7 with a saturation at a ±45${}^{\circ }$ elevator angle. By controlling the pitch angle, the energy efficiency regarding distance could be improved.

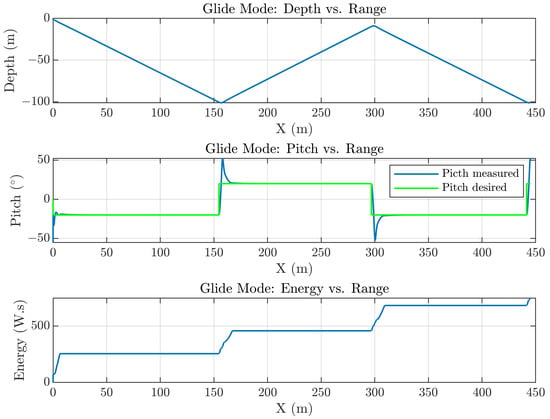
Figure 20. The simulation resultof the buoyancy engine, moving mass, and pitch control.

Figure 21 shows the simulation scenario in the AUV mode using the predefined parameters: desired speed, yaw, and pitch. The scenario’s parameters were as follows:

• Speed desired = 0.5 m/s;
• Pitch desired = 20${}^{\circ }$;
• Yaw desired = 20${}^{\circ }$.

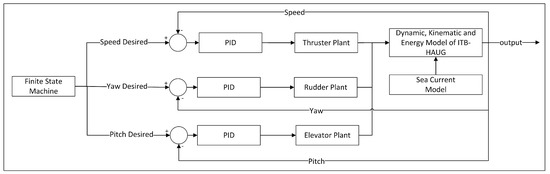
Figure 21. AUV mode simulation scenario with desired speed, yaw angle, and pitch.

Figure 22, Figure 23 and Figure 24 show the simulation results of each PID control. From these figures, the pitch control simulation results produced a better control with the same PID values compared to the yaw control. This occurred due to the differences in fin surface areas for the rudder for the yaw control and the elevator for the pitch control.

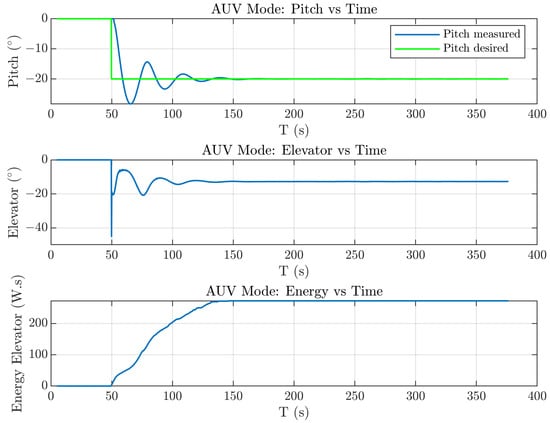
Figure 22. Simulation results in AUV mode with the desired pitch.

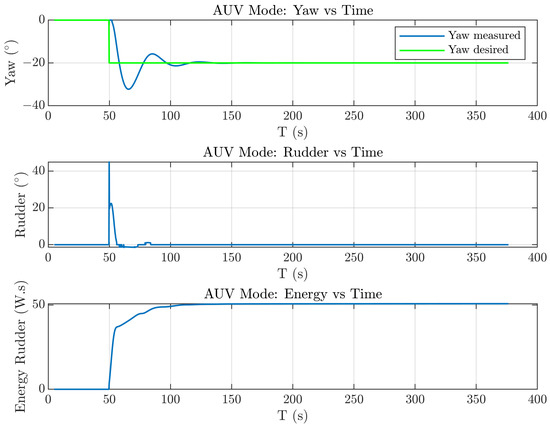
Figure 23. Simulation results of AUV mode with the desired yaw.

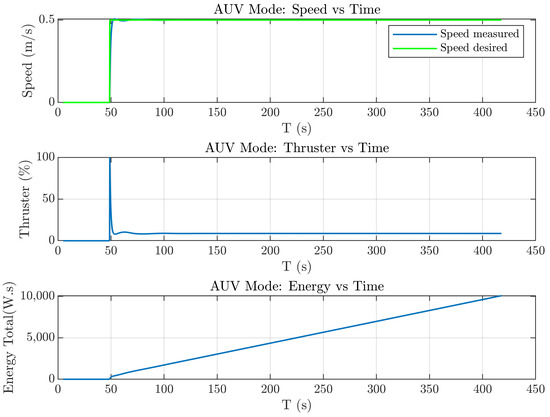
Figure 24. Simulationresults of AUV mode with the desired speed.

Figure 25 describes a simulation scenario in the AUV mode using the parameters: desired depth and speed. The scenario’s parameters were as follows:

• Speed desired = 0.5 m/s;
• Depth desired = 100 m.

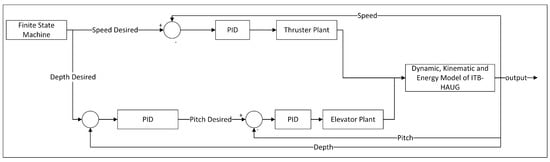
Figure 25. AUV mode simulation scenario with a setpoint of the desired speed and desired depth.

Figure 26 shows the simulation results of the depth control using the elevator. This simulation result shows that the depth control can be accomplished by controlling the elevator. At the beginning of the operation, the control system was not able to provide a good control due to the elevator’s efficient speed of operation. After achieving the operational speed of the elevator, the error value could be fixed by the control system.

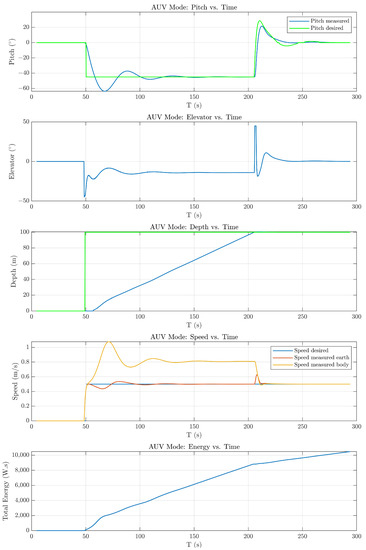
Figure 26. The simulation resultsin AUV mode with desired speed and depth.

4.3. Field Experiment

The HAUG’s in-field experiment was conducted in the Saraga diving pool, Bandung, Indonesia. The objective of the experiment was to demonstrate the basic function of the HAUG. Figure 27 shows the HAUG’s underwater experiment at a 1 m depth.

Figure 27. The HAUG’s underwater experiment.

The first experiment scenario was to perform the simple finite state machine shown in Figure 28. This figure describes the finite state machine in the glider mode, starting from the surface, submerging, and resurfacing for the field experiment. Each state is described as follows:

• Initial:
  In the initial state, the moving mass and engine buoyancy setpoint were set to 0. The value for each setpoint was entered by the guidance system or the operator.
• Descent:
  The operation began by giving a negative pitch. A negative pitch or pitch-down attitude was performed by setting the moving mass’s setpoint to 0.003, which meant shifting the centre of mass by 0.003 m, and the buoyancy engine setpoint to −5 N, which meant moving the oil from the external bladder to the internal bladder. This state submerged the vehicle until the desired glide depth was reached.
• Neutral:
  The HAUG began to neutralize the pitch and made the buoyancy force in the neutral state. This condition was set by adjusting the setpoint value of the moving-mass and buoyancy engine to 0.
• Ascent:
  The operation was to set a positive pitch. This positive pitch meant adjusting the moving mass’s setpoint to −0.003 and the buoyancy engine to 5 N. With this state, the vehicle floated with a pitch-up attitude until the desired depth was reached.
• Surfacing;
  This state is described as the last state after the HAUG finishes a mission. The setpoint values for the moving-mass and buoyancy engine were equal to those of the initial state. The HAUG’s position was on the surface and waiting to be lifted.

Figure 28. Finite state machine in glider mode.

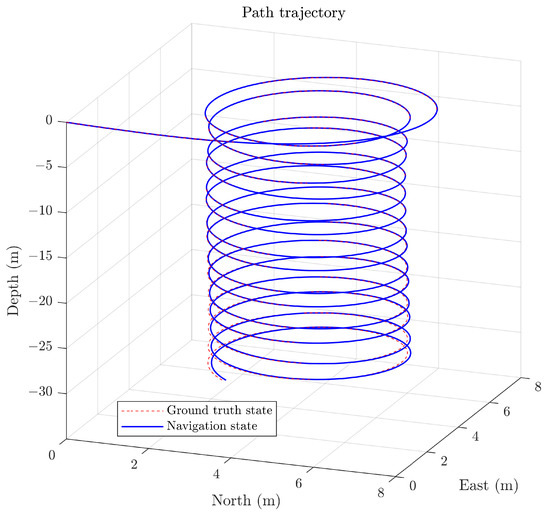
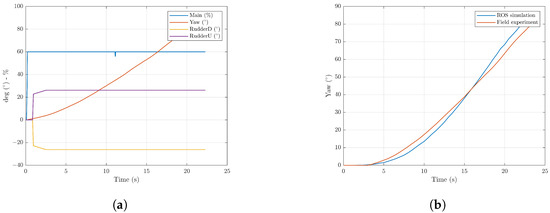
Figure 29 shows the simulation and field experiment using the finite state machine in Figure 28. Figure 29a shows the comparison in pitch measurement under the ROS simulation and field experiment, while Figure 29b shows the comparison with an in-depth measurement. The results show that the field experiment’s result was close to that of the ROS simulation.

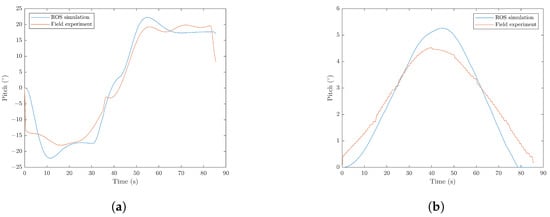
Figure 29. ROS Simulation vs. field experiment result in Saraga’s swimming pool. (a) Pitch experiment; (b) depth experiment.

The second field experiment scenario was to use a control system to control the pitch and depth simultaneously by using a buoyancy engine and a moving-mass engine in the gliding mode. In this scenario, several pitch angles were tested, 10${}^{\circ }$, 15${}^{\circ }$, and 20${}^{\circ }$ in three gliding cycles with target depths between 0.5 m and 3.5 m. Figure 30 shows the performance of the pitch and depth control system to track the desired pitch and depth.

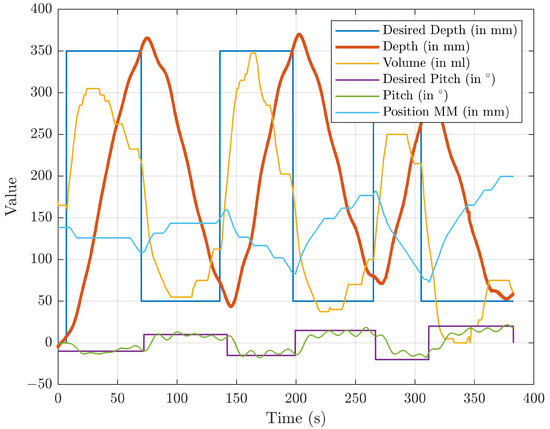
Figure 30. Moving- mass and buoyancy engine performance in gliding mode.

The energy and velocity measurement during three gliding cycles is shown in Figure 31. Figure 31a shows the amount of energy used in three gliding cycles, while Figure 31b shows the resulting surge velocity and heave velocity when running the gliding mode. The maximum horizontal speed (surge velocity) was at around 0.2 m/s and the maximum vertical speed (heave velocity) was at around 0.1 m/s, while the energy consumption in three gliding cycles was 51.63 watts. With an assumption of three cycles of gliding motion per hour using 51.63 watts/h, with a 24 V 110 Ah battery, the HAUG would be able to perform a mission for 44.74 h.

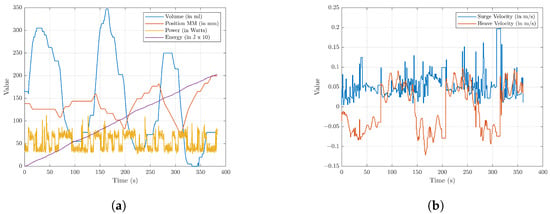
Figure 31. Energy consumption and velocity measurement in 3 gliding cycles. (a) Energy consumption; (b) surge and heave velocity.

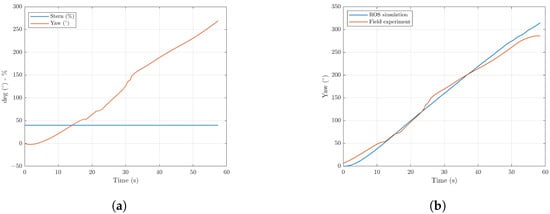
The third field experiment scenario was to use a surge control system in the AUV mode. In this scenario, due to limited space, by using the main thruster, the desired horizontal velocity was set to 1 m/s. Figure 32 shows the performance of the surge control system to track the desired speed. The maximum horizontal speed is 1 m/s and the energy consumption, while the main thruster was active, is 120.32 watts.

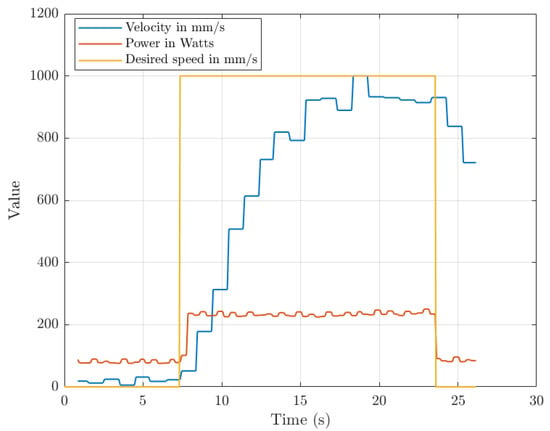
Figure 32. Energy and velocity measurement in AUV mode.

5. Navigation System Design

Almost all AUVs use an inertial navigation system (INS) as their main sensor [43]. An INS is a separate system that can provide navigation data, such as position, speed, and orientation. However, the navigation solution issued by an INS has errors that continue to grow over time. To produce a better solution, data from an INS are usually integrated with other sensors such as a Doppler velocity log (DVL), Global Positioning System (GPS), acoustic-based sensors such as long baseline (Long Baseline) and ultrashort baseline (USBL), or optical-based sensor such as camera [44] and lidar.

There are several ways to estimate the state of a vehicle, such as using a Bayes filter, a Kalman filter, an extended Kalman filter (EKF), and an unscented Kalman filter (UKF). Each of the estimation methods has advantages and disadvantages. A Bayes filter is an optimal state estimation, although it is difficult to control the computation load. The Kalman filter is a state estimation algorithm which assumes that the state has a Gaussian distribution, with a certain mean and covariance, and the system must be linear. An extended Kalman filter is an extension of the Kalman filter, which can accommodate nonlinear model systems. The unscented Kalman filter has a higher computation load; however, it can reduce the error from the linearization in the EKF. Beside using an EKF, some research works propose other methods that can be used for multisensor fusion, that is, using a neural network and the error-state Kalman filter [45].

The navigation system design used the Kalman filter technique, which fuses the INS sensor with supporting sensors such as DVL, GPS, and a depth sensor. The EKF was chosen as the navigation system algorithm because the system model was nonlinear, and the computational load was acceptable. In this construction, the following sensors were used.

5.1. Micro DVL 600 NavQuest

Micro DVL 600 NavQuest is a sonar-based sensor to measure the speed of vehicles underwater. This sensor works by emitting acoustic sound bursts along beams angled downward in various directions. The returned echoes are then calculated as the velocity and the direction of the vehicle. The sensor’s full performance specifications are shown in Table 5.

Table 5. Micro DVL 600 Performance.

Parameter	Performance	Units
Frequency	600	kHz
Accuracy	1	% ±1 mm/s
Maximum altitude	110	m
Minimum altitude	0.3	m
Maximum velocity	±20	knots
Maximum ping rate	5	1/s
Maximum transmit	80	watts
Average power consumption	2–5	watts
Input voltage	24	V ± 2 V

5.2. Advanced Navigation’s Spatial IMU

Advanced Navigation’s Spatial IMU is a sensor to measure the attitude (roll, pitch, and yaw) of the vehicle and to measure the acceleration that affects the vehicle (in the x, y, and z directions). This sensor integrates accelerometers, gyroscopes, magnetometers, and a pressure sensor that are temperature-calibrated and presents highly accurate and reliable position, velocity, acceleration, and orientation for navigation and orientation. The sensor’s performance specifications are shown in Table 6.

Table 6. Spatial Advance Navigation Performance.

Parameter	Performance	Units
Roll and pitch	0.1	${}^{\circ }$
Heading	0.2	${}^{\circ }$
RTK positioning	20	mm
MEMS gyroscope	3	${}^{\circ }$/h
Update rate	1000	Hz
Shock limit	2000	gr

5.3. Valeport’s VA500 Altimeter Sensor

Valeport’s VA500 is an acoustic-based sensor that monitors the presence of an object in front of the vehicle. This sensor uses a 500 kHz transducer and signal processing to detect an underwater object. In addition, this sensor provides a high-accuracy pressure sensor to measure current depth. Table 7 shows the sensor’s performance specifications.

Table 7. VA500 Valeport Performance.

Parameter	Performance	Units
Acoustic frequency	500	kHz
Acoustic range	0.1–100	m
Acoustic resolution	1	mm
Acoustic beam angle	±3	${}^{\circ }$
Pressure range	300	bar
Pressure accuracy	±0.01	% Full-scale
Pressure resolution	0.001	% Full-scale
Type of pressure sensor	Temperature-compensated piezoresistive

5.4. Poseidon GPS Antenna

Poseidon is an add-on subsea antenna for Advanced Navigation’s Spatial IMU to obtain a GNSS fix when surfaced. This GNSS antenna was chosen because it is lightweight, compact, corrosion-resistant, and withstands depths of up to 3000 m. This sensor provides geolocation information and timing information to GPS receivers. Table 8 shows the sensor’s performance specifications.

Table 8. Poseidon GPS antenna performance.

Parameter	Performance	Units
Maximum pressure rating	300	bar
Noise	2	dB
Antenna element gain	4	dBiC
Input voltage	2.5 to 16	V DC

5.5. Sensor Noise

The noise parameters used for the simulation in each sensor are shown in Table 9. These values were measured based on real-world experiments in static motion for each sensor.

Table 9. Sensor noise.

Parameter	Value	Units
Accelerometer noise in 3 axes	$94.354\times {10}^{-8}$,	$\frac{\mathrm{m}}{{\mathrm{s}}^2}\frac{1}{\sqrt{\mathrm{Hz}}}$
	$81.1\times {10}^{-8}$,
	$1.44\times {10}^{-6}$,
Accelerometer bias noise in 3 axes	$6.25\times {10}^{-6}$, $11.56\times {10}^{-6}$, $13.3298\times {10}^{-8}$	$\frac{\mathrm{m}}{{\mathrm{s}}^3}\frac{1}{\sqrt{\mathrm{Hz}}}$
Gyro noise in 3 axes	$1.849\times {10}^{-8}$, $2.106\times {10}^{-8}$, $71\times {10}^{-10}$	$\frac{\mathrm{rad}}{\mathrm{s}}\frac{1}{\sqrt{\mathrm{Hz}}}$
Gyro bias noise	0, 0, 0	$\frac{\mathrm{rad}}{{\mathrm{s}}^2}\frac{1}{\sqrt{\mathrm{Hz}}}$
DVL noise in 3 axes	$65.61\times {10}^{-8}$, $19.8025\times {10}^{-10}$ $2.89\times {10}^{-8}$	$\frac{\mathrm{m}}{\mathrm{s}}\frac{1}{\sqrt{\mathrm{Hz}}}$
GPS noise	${10}^{-4},{10}^{-4}$	$\frac{\mathrm{m}}{\mathrm{Hz}}$
Depth sensor noise	${10}^{-4}$	$\frac{\mathrm{m}}{\mathrm{Hz}}$

The design of the navigation system for simulating the navigation sensor on the HAUG is shown in Figure 33.

Figure 33. The HAUG’s navigation system simulation design.

5.6. Simulation Experiment

For measuring the performance of the navigation based on the sensor noises from Table 9, Equation (1) through Equation (8), and the HAUG’s navigation system, the Robotic Operating System (ROS) was used to simulate the motion. The forces that affected the HAUG were set to a 50% thrust, a 11.5${}^{\circ }$ rudder, and a 5 N buoyancy engine effect. The vehicle was provided with a setpoint control in such a way as to produce a 3D helix motion as shown in Figure 34.

Figure 34. Three-dimensional helix moving simulation.

Figure 35 presents the position error, velocity error, and orientation error produced by the navigation system using the IMU sensor during the 3D helix moving scenario. From this figure, the number of position errors and velocity errors increased with time while using only the IMU sensor; however, the orientation error was still maintained under 0.01${}^{\circ }$.

Figure 35. Three-dimensional Helix motion error. (a) Position error; (b) velocity error; (c) orientation error.

5.7. Field Experiment

To verify the feasibility of the navigation system, a simple experiment within a limited space was conducted to investigate the variation in navigation measurements. Saraga’s ITB diving pool, with a 15 m width, 15 m length, and 5 m depth, was chosen for its accessibility and for being one of the deepest diving pools in Bandung, Indonesia. Figure 36 shows a top-down view of the Saraga’s ITB diving pool while experimenting.

Figure 36. Saraga’s ITB Diving Pool.

Several scenarios were conducted to verify the navigation system. Figure 37 shows the yaw measurement using the IMU compared with the ROS simulation. In this figure, the stern thruster was activated with 50% of power to do a rotational motion, and we measured the yaw value with the IMU sensor.

Figure 37. Rotational motion scenario for the yaw experiment using the stern thruster. (a) Thruster output and IMU sensor; (b) Yaw simulation and field experiment.

Figure 38 shows the rotational motion scenario using the rudder and main thruster. The picture on the left shows the field experimental result, while the picture on the right shows the ROS simulation compared to the field experiment. The experiments in Figure 19 and Figure 20 show that the experimental result is close to the simulation result.

Figure 38. Rotational motion scenario for the yaw experiment based on the IMU using the main thruster and rudder. (a) Thruster–rudder output and IMU sensor; (b) Yaw simulation and field experiment.

Figure 39 shows the scenario of a rectangular motion around the pool using a manual input from the operator. The picture shows the position which was measured using a GPS and the DVL-added IMU. This experiment shows that the navigation sensor could deliver the position information during surfacing and submerging.

Figure 39. Rectangular motion around the pool scenario.

6. Communication Design from HAUG to Ground Control Station

6.1. Design of Communication System

The communication system on the HAUG was designed to use a wireless system using a radiofrequency module (RF) and a wired system using a tethered module as shown in Figure 40. The block diagram in Figure 40a describes the communication system on the HAUG and the ground control station (GCS). The ROS node communication design using a wireless communication module is shown in Figure 40b.

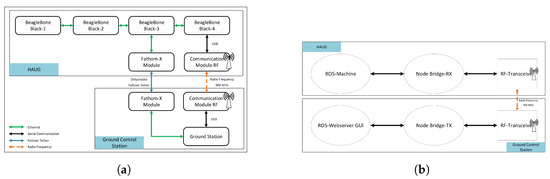
Figure 40. Communication system design. (a) Communication system diagram block; (b) ROS node communication design.

6.2. Data Communication Experiment via RF Module

The data communication experiment objective was to test the functionality of the communication module to send and receive information from the GCS to the HAUG and vice versa, as can be seen in Figure 41. Figure 41a shows the received data streaming and the desired setpoint at the GCS, while Figure 41b shows the experiment with the GCS on the left (orange dotted line rectangle) and the transceiver for the HAUG on the right (blue dotted line rectangle).

Figure 41. Communication system experiment. (a) Graphical user interface in the GCS; (b) Communication system experiment.

7. Conclusions

The design and construction of buoyancy engines, moving-mass engines, dynamic models, kinematic models, energy consumption models, basic control systems, basic navigation systems, and communication systems of underwater hybrid glider systems were introduced. The torpedo-shaped design with a size of 230 cm in length, 24 cm in diameter, and 86.5 kg in weight was developed to hold pressure up to 200 m. The guidance, navigation, and control systems were implemented by using one Udoo X86 as the main server and three BeagleBone Black as the clients in the ROS framework. The simulation results were a controlled horizontal speed of 0.5 m/s in the AUV mode and 0.34 to 0.5 m/s in the glide mode with a pitch angle between 10${}^{\circ }$ to 26${}^{\circ }$. The field experiment under a limited environment showed that the system could obtain a horizontal speed in the glide mode of 0.1 m/s and in the AUV mode of 1 m/s. Moreover, the energy consumption with an assumption of three cycles of gliding motion per hour was 51.63 watts/h, which enabled the HAUG to perform a mission for 44.74 h. This paper, however, is subject to several limitations. There are two major limitations in this study that could be addressed in future research. First, the mechanical design of the moving mass had a limitation in the velocity to move the moving mass weight to reach the desired pitch. Under these conditions, a control design for slow-response actuators and slow-response systems becomes a necessity. Second, the results of the current navigation system design still produced high position and velocity errors. The utilization of several fusion sensors, such as acoustic-based sensors or optical-based sensors, is a necessity to produce a navigation system in both shallow seas and deep seas. Yet, the modular design increases potential applications by enabling payload sensor changes, such as the need for a different sensor for surveillance, monitoring, mapping, search and rescue.