Design of a Mechanism with Embedded Suspension to Reconfigure the Agri_q Locomotion Layout ^†

Abstract

The Agri_q is an electric unmanned ground vehicle specifically designed for precision agriculture applications. Since it is expected to traverse on unstructured terrain, especially uneven terrain, or to climb obstacles or slopes, an eight-wheeled locomotion layout, with each pair of wheels supported by a bogie, has been chosen. The wide contact surface between the vehicle and the ground ensures a convenient weight distribution; furthermore, the bogie acts like a filter with respect to ground irregularities, reducing the transmissibility of the oscillations. Nevertheless, this locomotion layout entails a substantial lateral slithering along curved trajectories, which results in an increase of the needed driving torque. Therefore, reducing the number of ground contact points to compare the torque adsorption in different configurations, namely four, six, or eight wheels, could be of interest. This paper presents a reconfiguration mechanism able to modify the Agri_q locomotion layout by lifting one of the two wheels carried by the bogie and to activate, at the same time, a suspension device. The kinematic synthesis of the mechanism and the dynamic characteristics of the Agri_q suspended front module are presented.

1. Introduction

Precision agriculture is the management of crop inputs, like water, fertilizer, and plant protection products, at the correct time and place to increase productivity and maximize yields, in a sustainable manner. It requires the cooperation between unmanned aerial vehicles (UAV), which monitor the crops, and unmanned ground vehicles (UGV), which perform the intervention function. Focusing on the UGV, the adaption of commercial machinery as mobile platform for autonomous agricultural vehicles is the most common choice [1,2,3,4]. Nevertheless, recently custom mobile robots, which integrate some navigation strategy, have been studied and proposed as universal intelligent platform for various engineering tasks on rough ground [5,6,7,8,9,10]. Since the capability to move over an irregular and loose soil is one of the mandatory requirements, tracked and the multi-wheeled locomotion layouts are preferred. Tracked mobile robots ensure a wide contact surface between the vehicle and the ground, correctly distributing on the soil the static and dynamic forces acting on the vehicle. On the other hand, complexity and a high power-to-weight ratio characterize this kind of vehicles. Multi-wheeled robots tend to reproduce the ground pressure distribution of track-based systems, with a higher efficiency and a simpler mechanical structure than track-based rovers. These intelligent moving platforms are expected to carry sensitive equipment, like sensors and end-effectors for different tasks, on uneven terrain. Therefore, the riding comfort and stability is fundamental and, independently on the chosen locomotion strategy, appropriate suspension systems have to be provided. Some mobile robots adopted the active vibration isolation approach, altering their structures and configurations to change the position of their center of mass when traversing complicated unstructured terrains [11,12,13,14]. Nevertheless, expensive manufacturing costs and energy consumption limited the development and application, and passive suspension devices are preferred. A passive bio-inspired limb-like suspension implemented on a truck-based robot is reported in [15]. Some authors report the use of independent suspensions, made up of adjustable gas spring and oil dampened shock absorber, on wheeled vehicles [16,17]. Passive articulated suspensions, which permit some of the wheels to rise, relative to the chassis, over bumps without changing the weight distribution or changing it as little as possible, are particularly interesting. A notable example is the so-called rocker-bogie suspension [18] that has been successfully demonstrated by NASA’s rovers Spirit and Opportunity for planetary exploration (Maimone et al., 2004) [19].

In [20] the authors report the concept of a novel multi-wheeled electric UGV, named Agri_q, equipped by passive articulated suspensions; each pair of its eight wheels, in fact, is supported by a bogie, which acts like a filter with respect to ground irregularities, reducing the transmissibility of the oscillations. Figure 1 shows the first prototype, characterized by a reconfigurable chassis. The rover, in fact, integrates a positioning mechanism able to compensate longitudinal slopes [21]; this mechanism, together with a motorized roll joint compensating transversal slopes, ensures a horizontal landing surface for drones even when the rover is moving on steep slopes, as shown in Figure 1a. Solar panels cover the landing platform for partial auto recharging of the batteries collection during the passive phases; the previously mentioned positioning mechanism permits to orient the chassis in the most convenient way for solar energy collection. A collaborative robotic arm, exploiting the positioning mechanism to expand its workspace, has been integrated into the rover, to collect ground or leaves samples for lab analysis, as shown in Figure 1b [22].

Preliminary experimental field tests highlighted that, when the rover engages curved trajectories, a substantial lateral slithering, combined to an increase of the needed driving torque, occurs. Therefore, comparing the torque adsorption in the standard eight-wheeled configuration and in a modified six-wheeled configuration (two front wheels, four back wheels, as in Figure 2) could be of interest. In [23] the authors presented a preliminary study of a mechanism able to lift one of the two wheels carried by the rover front bogie. Two possible functional solutions were compared and a kinematic design methodology was presented. Since, in the two front-wheeled configuration, the bogie loses its filter function, the reduction of the vibration transmitted to the sub-chassis was transferred to a commercial suspension system embedded in the reconfiguration mechanism itself, whose dynamics was not yet studied.

This work presents the locomotion layout reconfiguration system in its final version and focuses on the dynamic behavior of the rover in the two front-wheeled configuration. Firstly, a 2DOF model of the rover suspended front box and a linearized analytical model of the system are presented. Then, results coming from the latter model are compared to those obtained with a numerical approach.

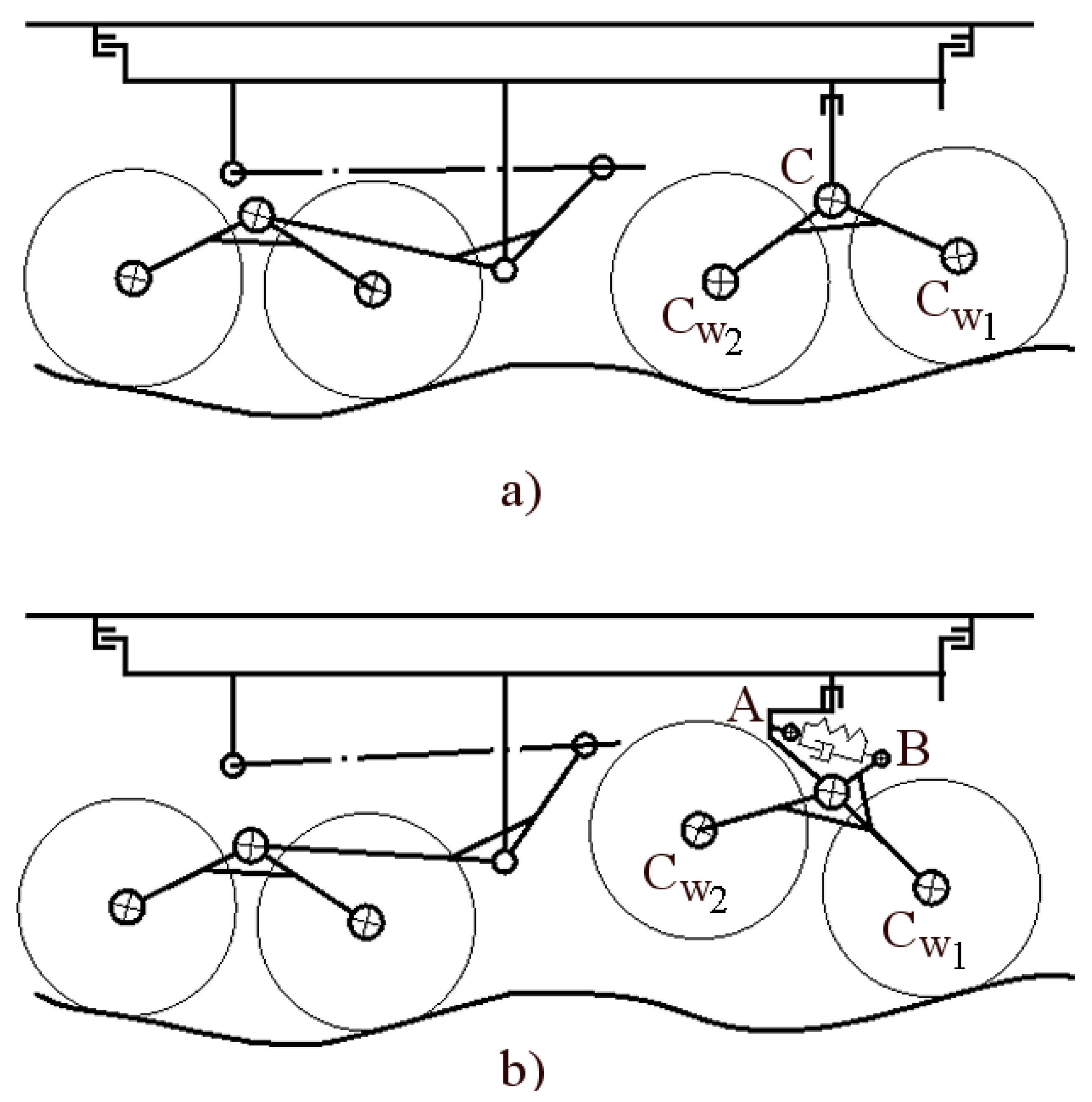
2. The Reconfiguration Mechanism

2.1. Working Principle

A functional sketch of the proposed reconfiguration mechanism is shown in Figure 3. A four bar-linkage DCAB, driven by a linear actuator linked to the first rocker arm DA, controls the position of the UGV bogie CC_w1C_w2 through its second rocker arm CB. The latter, in fact, is integral with the bogie itself and is pivoted about the joint C fixed on the vehicle front box. In the standard four front-wheeled configuration, the actuator reversibility ensures free rotation of the bogie about the pivot joint C; therefore, in the case of a vertical displacement of a single wheel, caused by the contact with an obstacle, a reduced vertical displacement of the whole vehicle is obtained.

Enabling the actuator, the link DA goes beyond a dead point and comes finally in contact with a limit stop fixed on the front box; consequently, the bogie rotates about C and a two-front wheeled configuration is obtained. Since the limit stop prevents further counterclockwise rotations of DA and the force transmitted by the ground ensures a stable configuration of the four-bar linkage, the actuator power supply can be interrupted. Nevertheless, in case of motion over very irregular soil, the link DA could lose its contact with the limit stop; therefore, a brake has to be provided.

In the two front-wheeled configuration, the mechanical filtering of ground irregularities performed by the bogie is lost. Therefore, the coupler link AB of the proposed reconfiguration mechanism embeds a deformable body. Figure 2 highlights that, when the vehicle is in the two-front wheeled configuration, the hinge A of the reconfiguration mechanism acts like a pivot joint fixed on the front box and the coupler link AB works as a suspension. A rear shock absorber for mountain bike (size 210 mm, spring stiffness k = 131,000 N/m, damping coefficient c = 1.7 × 10⁴ N s/m) has been chosen as deformable body.

2.2. Kinematic Requirements

Figure 4 shows some relevant locations taken by the bogie when the rover locomotion layout is changed; the variable angle α is measured from the vertical direction. In the nominal configuration CC_W1_i, corresponding to the four front-wheeled layout, the bogie can freely rotate within a range Δα_i = 26°, to ensure a wide contact surface between the vehicle and the ground even on an irregular terrain.

In order to move to a two front-wheeled layout, the reconfiguration mechanism has to place the unloaded bogie arm at the location CC_{W1_f}, imposing a rotation Δα. Finally, because of the effect of the force transmitted by the ground on the wheel, an additional counterclockwise rotation from α_f to α_s is obtained, which determines the shock absorber preloading. Therefore, at the location CC_{W1_s} the suspension device is active and ready to work, within the range Δα_s = 26°, which permits a wheel hub vertical displacement of 50 mm.

Figure 5 shows the bogie CC_w1C_w2 in the two front-wheeled static configuration, which corresponds to the equilibrium point between the force F_G transmitted from the ground to the wheel, the lifted wheel weight F_w and the suspension preload F_S0. Considering h = 100 mm as a reasonable distance between the soil and the lifted wheel and taking into account the shock absorber stiffness, a rotating angle Δα = 26° has to be imposed by the reconfiguration mechanism.

In the following, the relationship between the desired rotation Δα and the needed stroke of the linear actuator is obtained. The kinematic study was carried out considering the reconfiguration mechanism as made up of rigid bodies. In fact, only when the rocker DA reaches the limit stop, the deformability of the coupler link can be exploited.

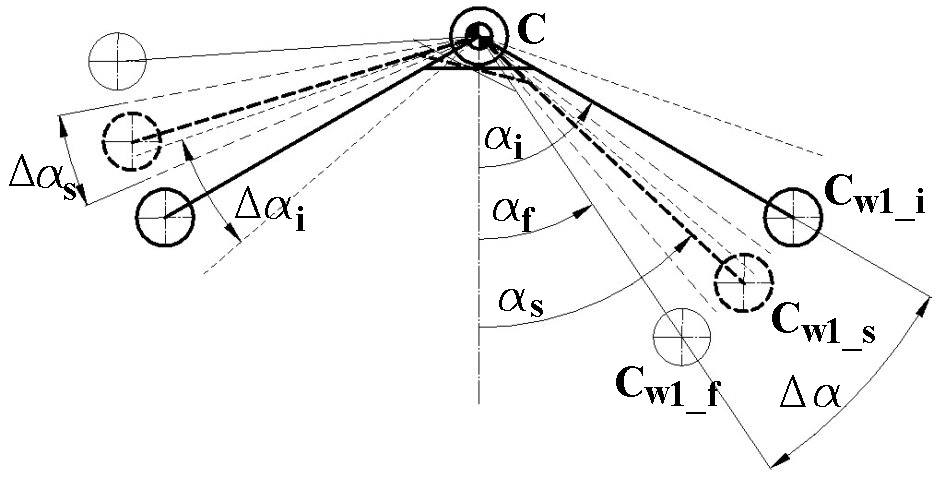
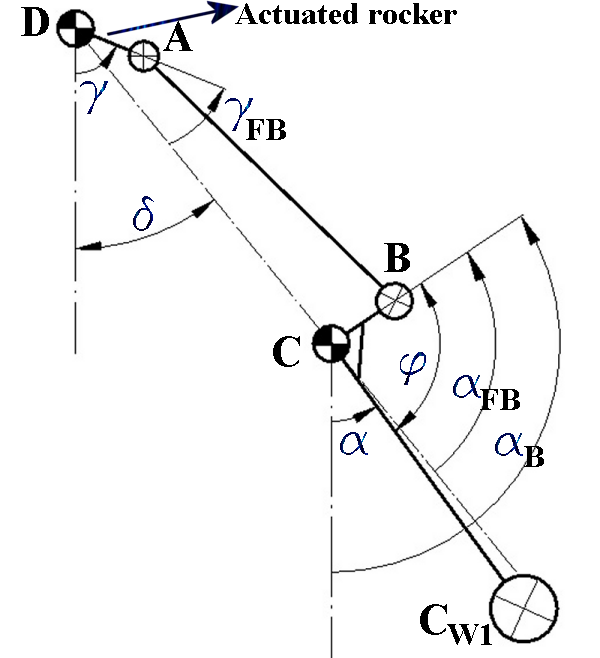
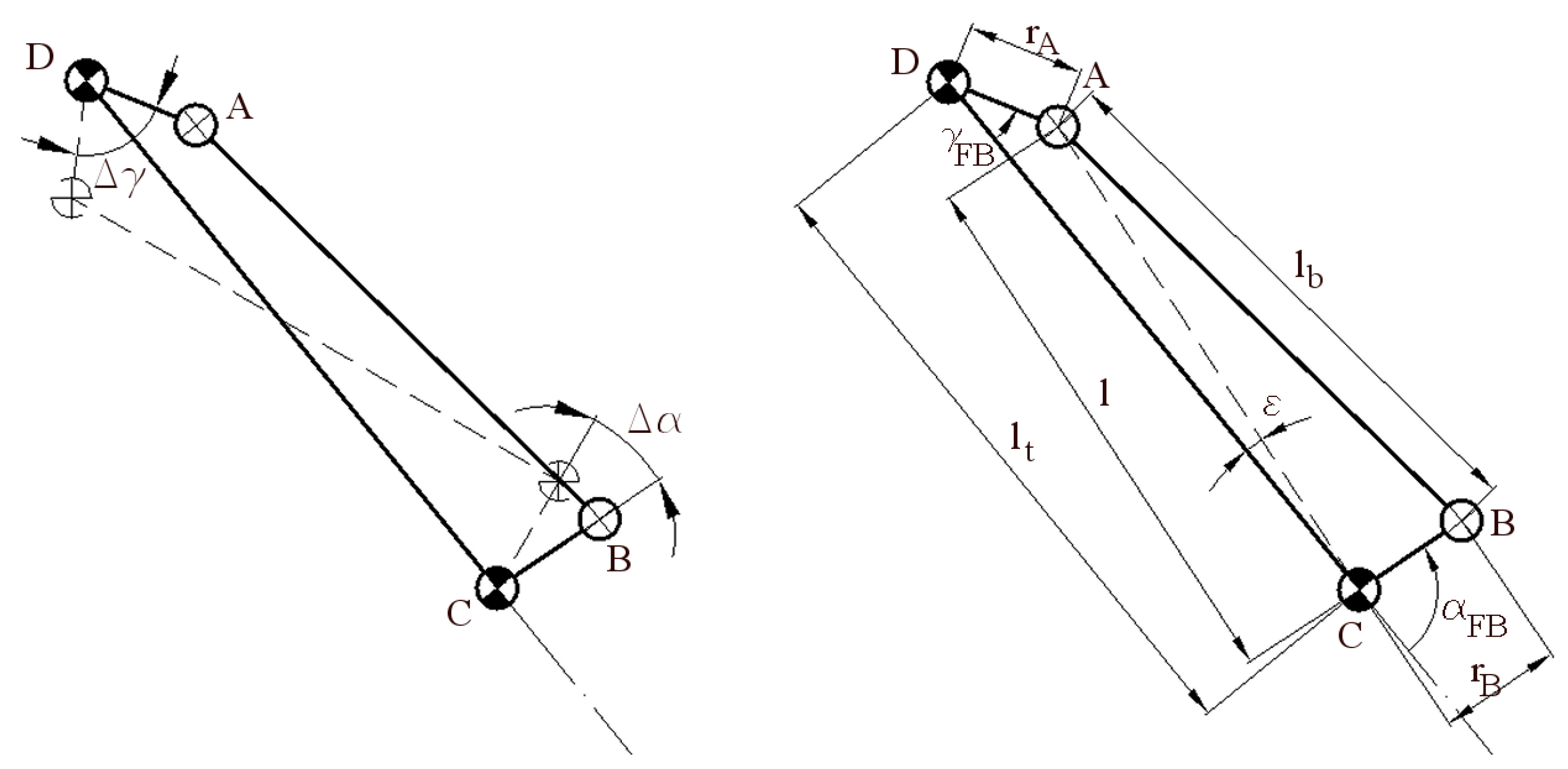
3. Kinematic Analysis

Figure 6 introduces some notations useful for the kinematic analysis. Angles δ and φ are constant parameters that must be properly chosen; they identify the orientation δ of the frame DC of the reconfiguration mechanism DCAB and the shift angle φ between the bogie arm CC_w1 and the rocker arm CB, respectively. Angles α and γ are variable and define the angular positions of the bogie and of the rocker arm DA with respect to the vertical direction, respectively; α_FB and γ_FB define the same locations, but measured from the reference line DC, so that $\alpha ={\alpha }_{FB}+\delta -\phi$ and $\gamma ={\gamma }_{FB}+\delta$.

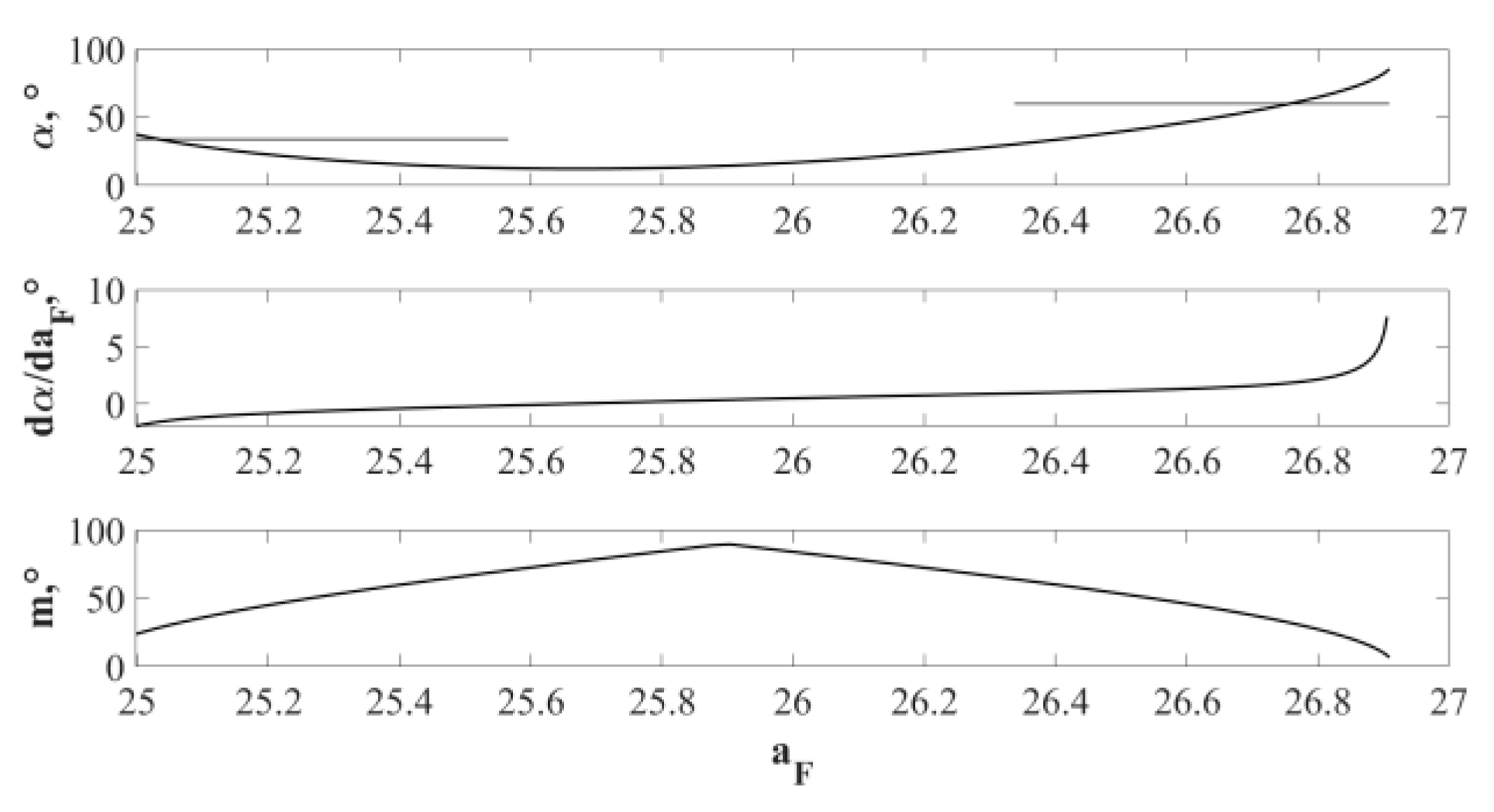
3.1. Amplification of the Output Range of Rotation

Moving from the four front-wheeled configuration to the two front-wheeled ones, the rocker DA of the reconfiguration mechanism has to overcome a dead point. Therefore, in order to obtain a reliable operation of the mechanism itself and to avoid undesired switches, the two limit positions of the rocker DA have to be kept far to each other. Choosing DA shorter than CB, the rotation Δα of the bogie needed to move from one configuration to the other results into a wider rotation Δγ of the rocker DA, reaching the goal. Furthermore, varying the shift angle ϕ between the rocker CB and the bogie arm CC_w1, Δα and Δγ can be placed at a convenient location. Figure 7 introduces the notations needed to determine the analytical relationship between α_FB and γ_FB.

It can be obtained that:

$${\alpha }_{FB}=\pi -ϵ-arcos\frac{l^2+{r_B}^2-{l_b}^2}{2·l·r_B}={\alpha }_{FB}\left({\gamma }_{FB}\right)$$

(1)

3.2. Actuation of the Mechanism

The rotation Δγ of the link DA can be driven by a linear actuator paired at one end to the front box, by means of the revolute joint E, and paired at the other end to the link DA, by means of the revolute joint F. As shown in Figure 8, the most convenient position of the second revolute joint F can be chosen, so to reorient Δγ, i.e., to limit the variability of the actuator transmission angle. The same figure highlights graphically the relationship between the desired γ rotation and the distance s_F between F and E, i.e., the parameter controlled by the actuator. The angles γ_A and γ_F identify the angular position of DA and DF with respect to the reference line DE, respectively: ${\gamma }_A={\gamma }_F+\eta$. The angle ψ is the angular shift of DE with respect to the vertical direction. It is also: ${\gamma }_A=\pi -\psi +\gamma$.

According to Figure 8, one has:

$$l_E+r_F \cos \left({\gamma }_F\right)=s_F·\cos \left(\xi \right)$$

(2)

$$r_F·\sin \left({\gamma }_F\right)=s_F·\sin \left(\xi \right)$$

(3)

For a certain value of the non-dimensional parameter $p_l=l_E/r_F$, using a numerical approach, the angle ξ can be worked out as a function of the input angle ${\gamma }_F$ as follows:

$$\xi =arctan\left(\frac{\sin \left({\gamma }_F\right)}{p_l+\cos \left({\gamma }_F\right)}\right)=\xi \left(p_l,{\gamma }_F\right)$$

(4)

In addition, the transmission angle μ can be worked out as:

$$\mu ={\gamma }_F-\xi ,\mathrm{if}({\gamma }_F-\xi )\le \mathsf{\pi }/2;\mu =\pi -({\gamma }_F-\xi ),\mathrm{if} ({\gamma }_F-\xi )>\mathsf{\pi }/2$$

(5)

Introducing the non-dimensional parameter $a_F=s_F/r_F$, it finally follows that:

$$a_F= \frac{s_F}{r_F}=\frac{\left(p_l+\cos \left({\gamma }_F\right)\right)}{\cos \left(\xi \left(p_l,{\gamma }_F\right)\right)}=w_C\left(p_l,{\gamma }_F\right)$$

(6)

3.3. Kinematic Results

Figure 9 shows the results obtained in terms of angular position α, instantaneous transmission ratio dα/da_F and transmission angle μ, as a function of the non-dimensional input a_F. Results are obtained setting DA = 44 mm, CB = 46 mm, DC = 230 mm, δ = 39°, ψ = 87°, DE = 400 mm, η = 33°, DF = 27 mm, and φ = 90°. The latter value of the shift angle was identified by the parametric analysis carried out in [11] as the better compromise between the need to avoid undesired switches of the reconfiguration mechanism and the need of an almost constant instantaneous transmission ratio, useful for motor optimization.

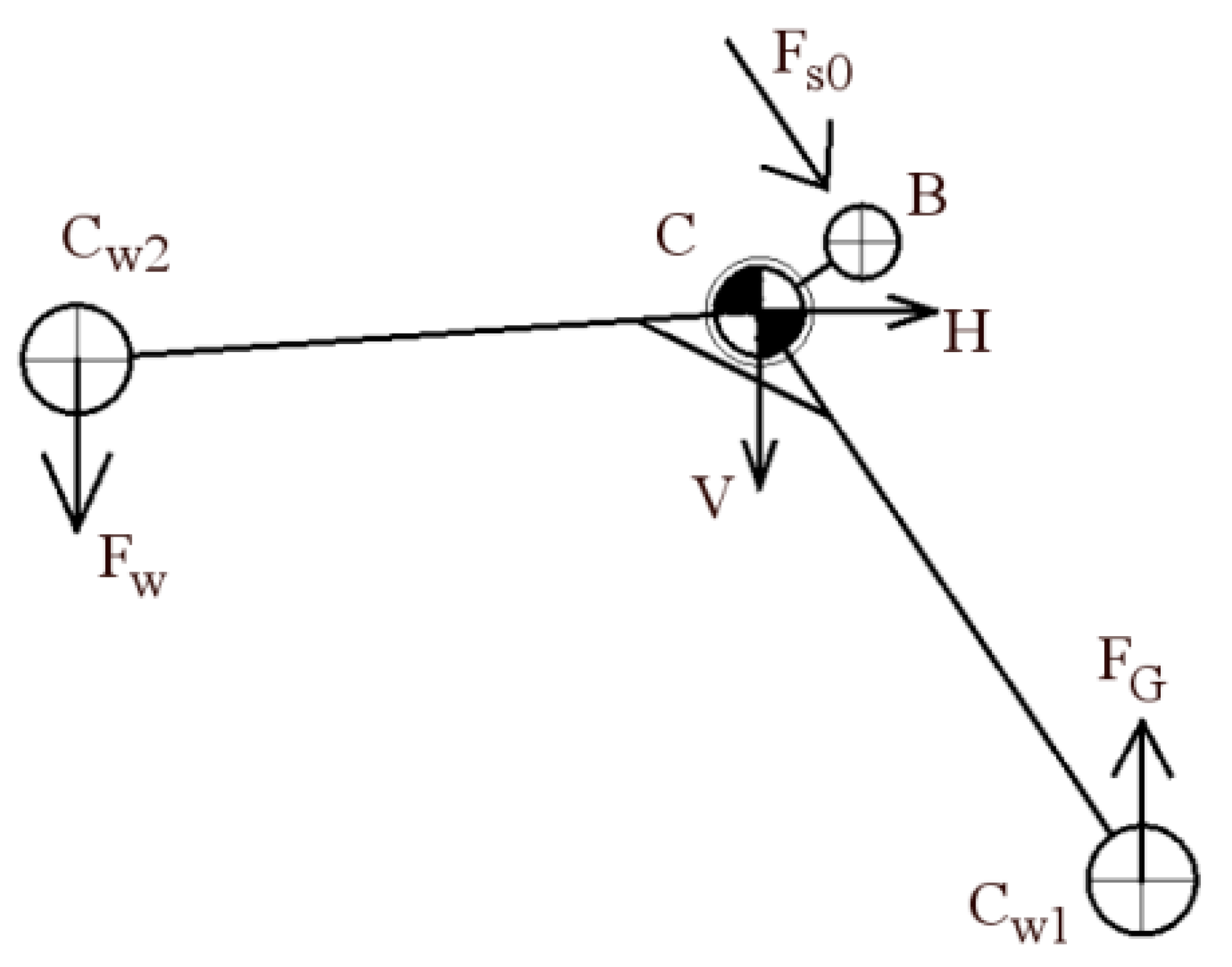
4. Dynamic Analysis

The following analysis refers to the rover in the two front-wheeled configuration: the reconfiguration mechanism is kept in contact with the limit stop, its hinge A acts now like a pivot joint fixed on the front box, and the shock absorber, characterized by a spring stiffness k and a damping coefficient c, is preloaded. Taking into account that the front and rear modules of the Agri_q rover are completely independent in terms of roll motion [20,21], the dynamic characteristics of the front suspended module are studied below.

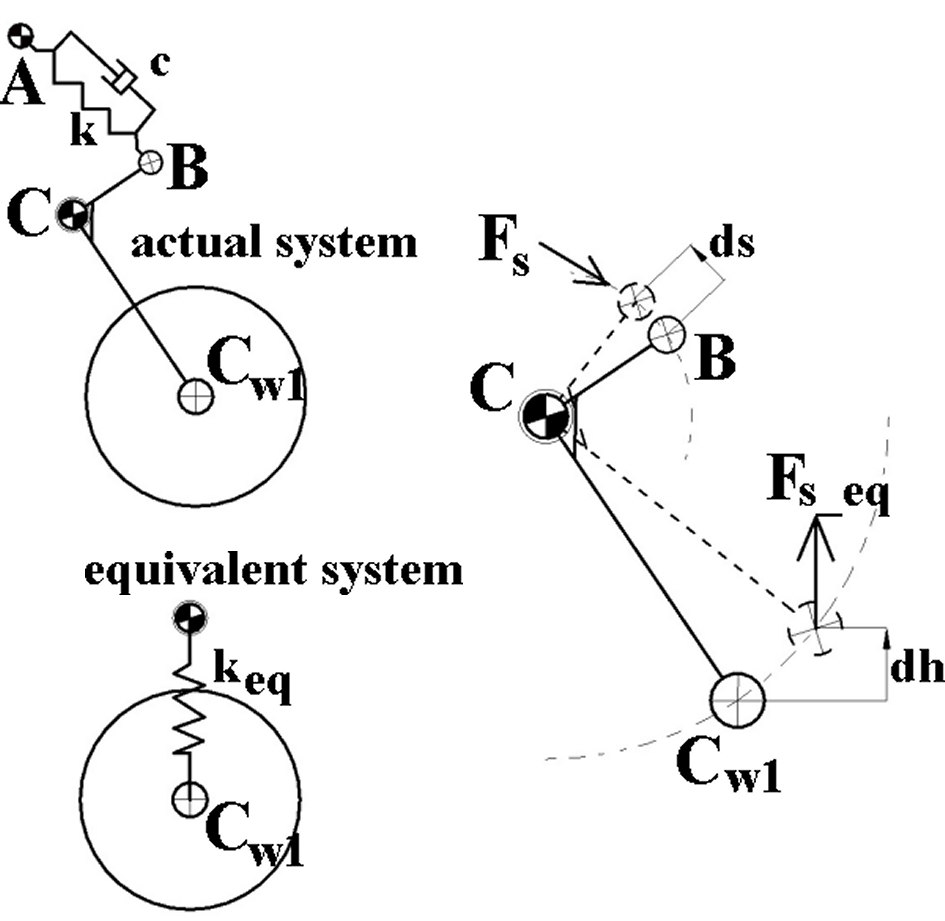
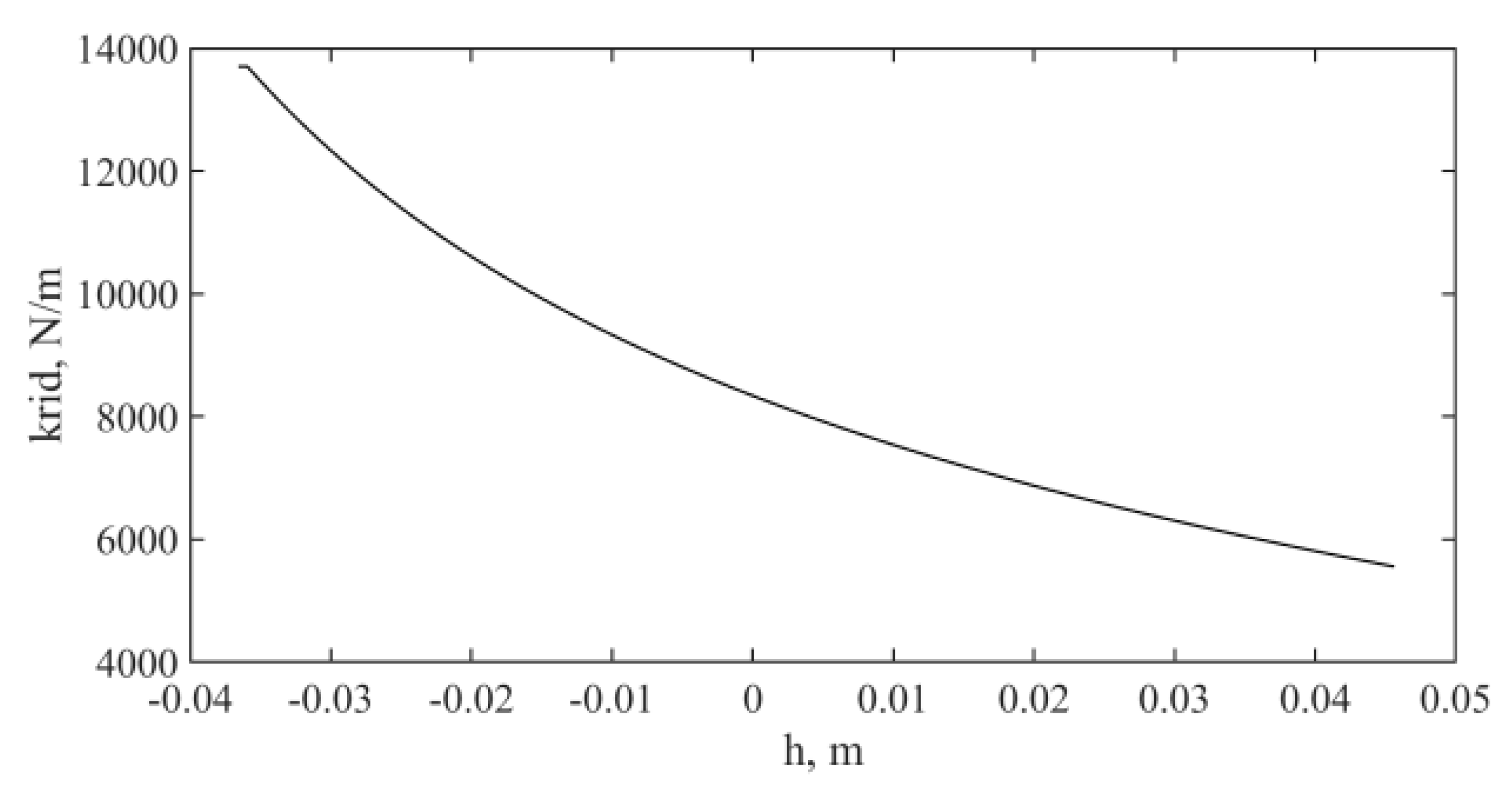
4.1. Suspension Force Reduction

In order to study the dynamics of the suspended mass, the force exerted by the suspension device on the swing arm has to be converted into an equivalent force, acting vertically on the wheel hub, as shown in Figure 10. In the figure, F_s denotes the force exerted by the shock absorber spring, F_{s_eq} represents the same force reduced at the wheel axle, while ds and dh are the shock-absorber travel and the wheel vertical displacement, respectively.

Applying the virtual work principle, one has:

$$F_s·ds=F_{s\_eq}·dh$$

(7)

Introducing the installation ratio $i_R=\frac{ds}{dh}$, which is also the leverage ratio throughout the range of motion, and taking into account that F_s = k∙ds and F_{s_eq} = k_eq·dh, it results:

$$k_{eq}=k·{i_R}^2$$

(8)

Similarly, an equivalent damping coefficient can be obtained:

$$c_{eq}=c·{i_R}^2$$

(9)

Figure 11 shows the trend of the suspension equivalent stiffness throughout the range of motion, obtained taking into account the characteristics of the commercial shock absorber and the swing arm geometry. As shown, the suspension device exhibits a non-linear regressive behavior, acceptable for off-road applications.

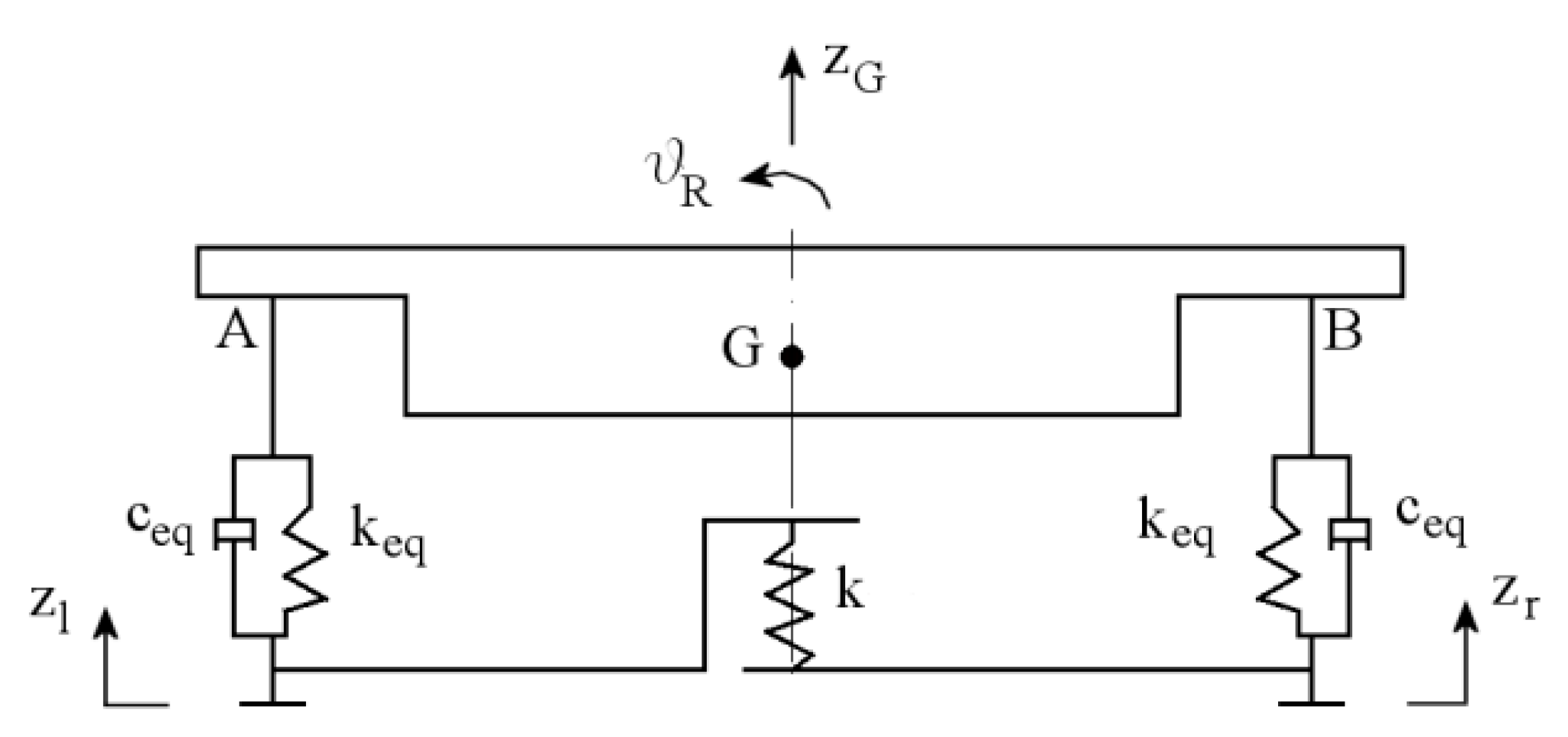
4.2. Front Box Model

The 2-DOF model shown in Figure 12 gives a description of the Agri_q front module roll and bounce dynamics. The motion of the suspended mass, characterized by the mass m and the mass moment of inertia I_xx, is described by the vertical position z_G and by the body roll angle θ_R. The two front suspension stiffness and damping, reduced at the wheel axle, are represented by k_eq and c_eq. The tyre stiffness and unsuspended mass oscillations are neglected. The surface excitation is introduced as the left and right displacements z_l and z_r. The displacements of the points of interest are described in the global coordinate system, whose origin is located on the flat ground.

The locations of the pivot linking the suspended mass to the suspensions depend on the vertical displacement z_G and on the roll angle θ_R of the suspended mass itself according to:

$$z_A=z_G-\frac{b}{2}·{\vartheta }_R$$

(10)

$$z_B=z_G+\frac{b}{2}·{\vartheta }_R$$

(11)

The total kinetic energy of the system is:

$$T=\frac{1}{2}·m·{\dot{z_G}}^2+\frac{1}{2}·I·{\dot{{\theta }_R}}^2$$

(12)

The elastic energy potential is:

$$V=\frac{1}{2}·k_{eq}·{\left(z_A-z_l\right)}^2+\frac{1}{2}·k_{eq}·{\left(z_B-z_r\right)}^2$$

(13)

The Rayleigh function of the energy dissipated in the shock absorbers can be written as follows:

$$D=\frac{1}{2}·k·c_{eq}·{\left(\dot{z_A}-\dot{z_l}\right)}^2+\frac{1}{2}·c_{eq}·{\left(\dot{z_B}-\dot{z_r}\right)}^2$$

(14)

The i-th equation of motion has the following Lagrange formulation:

$$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q_i}}\right)-\frac{\partial L}{\partial q_i}=Q_i$$

(15)

where $\{{q\}}^T=\left\{z_G {\vartheta }_R\right\}$ are the generalized lagrangian coordinates, L = T − V is the Lagrangian and

$$Q_i=-\frac{\partial D}{\partial \dot{q_i}}$$

(16)

In matrix form it is:

$$\begin{gathered} \left[\begin{array}{cc}m& 0\\ 0& I_{xx}\end{array}\right]\left\{\begin{array}{c}\ddot{z_G}\\ \ddot{{\vartheta }_R}\end{array}\right\}+\left[\begin{array}{cc}2·c_{eq}& 0\\ 0& c_{eq}·\frac{b^2}{2}\end{array}\right]\left\{\begin{array}{c}\dot{z_G}\\ \dot{{\vartheta }_R}\end{array}\right\}+\left[\begin{array}{cc}2·k_{eq}& 0\\ 0& k_{eq}·\frac{b^2}{2}\end{array}\right]\left\{\begin{array}{c}{z}_G\\ {\vartheta }_R\end{array}\right\} \\ =\left\{\begin{array}{c}{c}_{eq}·\dot{z_l}+c_{eq}·\dot{z_r}+k_{eq}·z_l+k_{eq}·z_r\\ c_{eq}·\frac{b}{2}·\dot{z_r}-c_{eq}·\frac{b}{2}·\dot{z_l}+k_{eq}·\frac{b}{2}·z_r-k_{eq}·\frac{b}{2}·z_{rl}\end{array}\right\} \end{gathered}$$

(17)

As can be seen, the hypothesis of a center of mass located at the middle of the wheelbase results in an uncoupled system of differential equations.

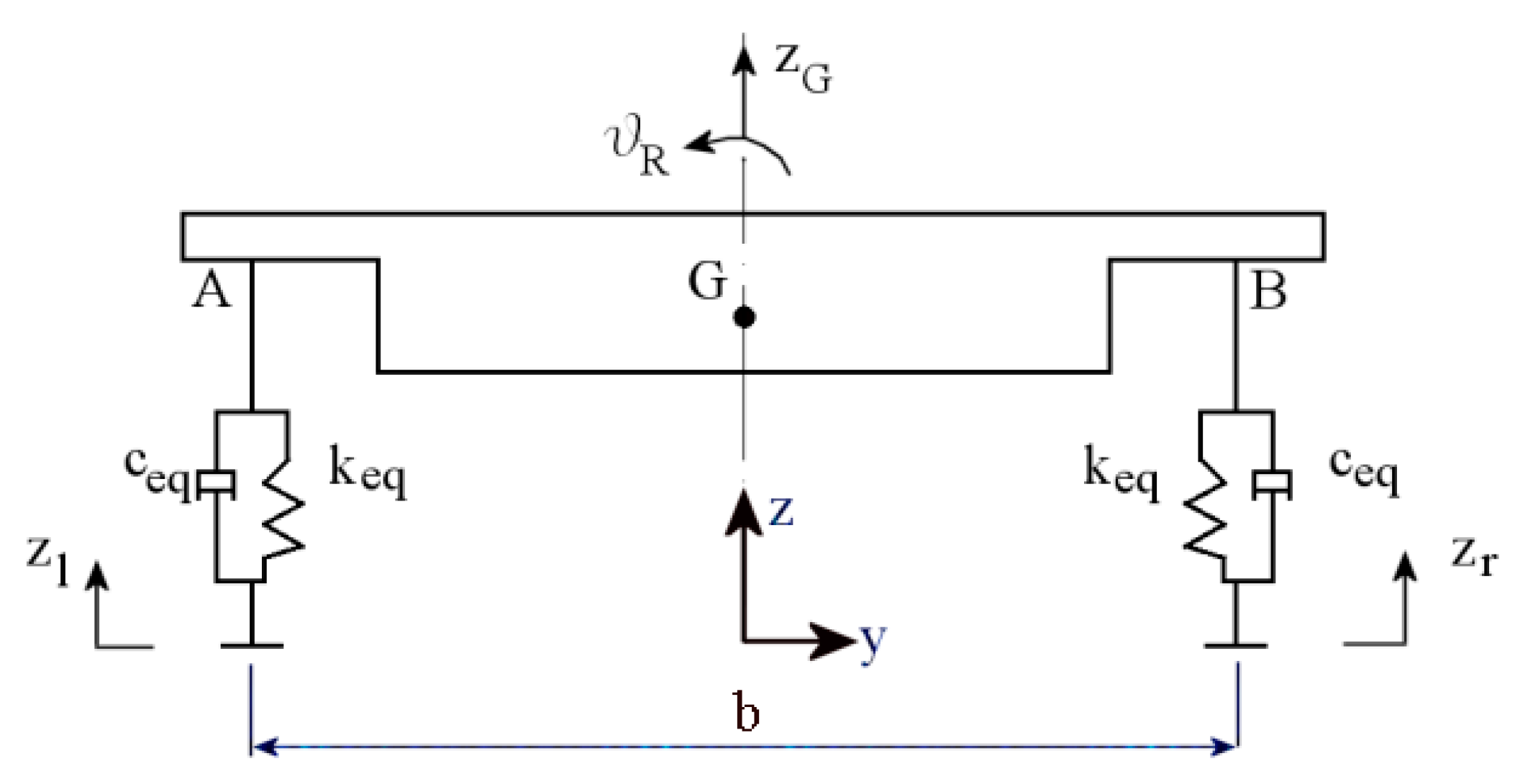
4.3. Linear Model

In order to evaluate the system response to an external surface excitation, a linear model of the system has been developed. In particular, the suspension spring characteristic has been linearized around the static preload condition (h = 0, in Figure 11), assuming constant values for k_eq and, similarly, for c_eq. Therefore, according to Equation (17), the undamped eigenfrequencies ω_n,z and ω_n,θ of the bounce and the roll motion, respectively, can be identified as:

$${\omega }_{n,z}=\sqrt{\frac{2·k_{eq}}{m}}\mathrm{and}{\omega }_{n,\vartheta }=\sqrt{\frac{k_{eq}·b^2}{2·I_{xx}}}$$

(18)

The corresponding damping factors are:

$${\zeta }_z=\frac{c_{eq}}{m·w_{n,z}}\mathrm{and}{\zeta }_{\vartheta }=\frac{c_{eq}·b^2}{4·I_{xx}·w_{n,\vartheta }}$$

(19)

Referring back to Figure 11, the surface input to the model is described by the displacements z_r and z_l, resulting in an external force F_z and moment $M_{\vartheta }$ on the model as:

$$F_z=c_{eq}·\dot{z_l}+c_{eq}·\dot{z_r}+k_{eq}·z_l+k_{eq}·z_r$$

(20)

$$M_{\vartheta }=c_{eq}·\frac{b}{2}·\dot{z_r}-c_{eq}·\frac{b}{2}·\dot{z_l}+k_{eq}·\frac{b}{2}·z_r-k_{eq}·\frac{b}{2}·z_{rl}$$

(21)

Assuming an asymmetric harmonic surface excitation $z_r=z_{r0} e^{i·\left(w·t\right)}$ and $z_l=0$, F_z can be expressed as:

$$F_z=F_{z0}·e^{i·\left(w·t+\chi \right)}$$

(22)

where:

$$F_{z0}=z_{r0}·\sqrt{{\left(\frac{k_{eq}}{m}\right)}^2+{\left(\frac{c_{eq}}{m}·\omega \right)}^2}$$

(23)

and:

$$\chi =atan\left(\frac{c_{eq}·\omega }{k_{eq}}\right)$$

(24)

Similarly, $M_{\vartheta }$ can be expressed as:

$$M_{\vartheta }=M_{\vartheta 0}·e^{i·\left(w·t+\chi \right)}$$

(25)

where:

$$M_{\vartheta 0}=z_{r0}·\sqrt{{\left(\frac{k_{eq}·l}{2·I_{xx}}\right)}^2+{\left(\frac{c_{eq}·l}{2·I_{xx}}·\omega \right)}^2}$$

(26)

$z_G=z_{G0}·e^{i·\left(w·t\right)}$ and ${\vartheta }_R={\vartheta }_{R0}·e^{i·\left(w·t\right)}$, the bounce transmissibility ${\alpha }_{z,r}$ (adimensional) and the roll transmissibility ${\alpha }_{\vartheta ,r}$ (dimensional, 1/m) can be calculated as:

$${\alpha }_{z,r}=\left|\frac{z_{G0}}{z_{r0}}\right|=\frac{\sqrt{{\left(\frac{k_{eq}}{m}\right)}^2+{\left(\frac{c_{eq}}{m}·\omega \right)}^2}·e^{i·\chi }}{\sqrt{{\left({{\omega }_{n,z}}^2-{\omega }^2\right)}^2+{\left(2·{\zeta }_z·\omega ·{\omega }_{n,z}\right)}^2}}$$

(27)

$${\alpha }_{\vartheta ,r}=\left|\frac{{\vartheta }_{R0}}{z_{r0}}\right|=\frac{\sqrt{{\left(\frac{k_{eq}·l}{2·I_{xx}}\right)}^2+{\left(\frac{c_{eq}·l}{2·I_{xx}}·\omega \right)}^2}·e^{i·\chi }}{\sqrt{{\left({{\omega }_{n,z}}^2-{\omega }^2\right)}^2+{\left(2·{\zeta }_z·\omega ·{\omega }_{n,z}\right)}^2}}$$

(28)

The bounce and roll transmissibilities have been analyzed setting m = 59 kg, I = 2.175 kg∙m², b = 1 m. Figure 13 and Figure 14 compares the results obtained from the linear model with those obtained numerically, solving the non-linear equation of motion in the Simulink environment. Two different values of z_r0, equal to 0.02 m or 0.2 m, have been imposed to simulate a more or less intense surface excitation. It can be noted that, in case of a high amplitude of the surface excitation, the non-linear numerical model picks the regressive behavior of the suspension device. A suspension that reacts softly to higher amplitude of the surface excitation helps reducing the transmissibility.

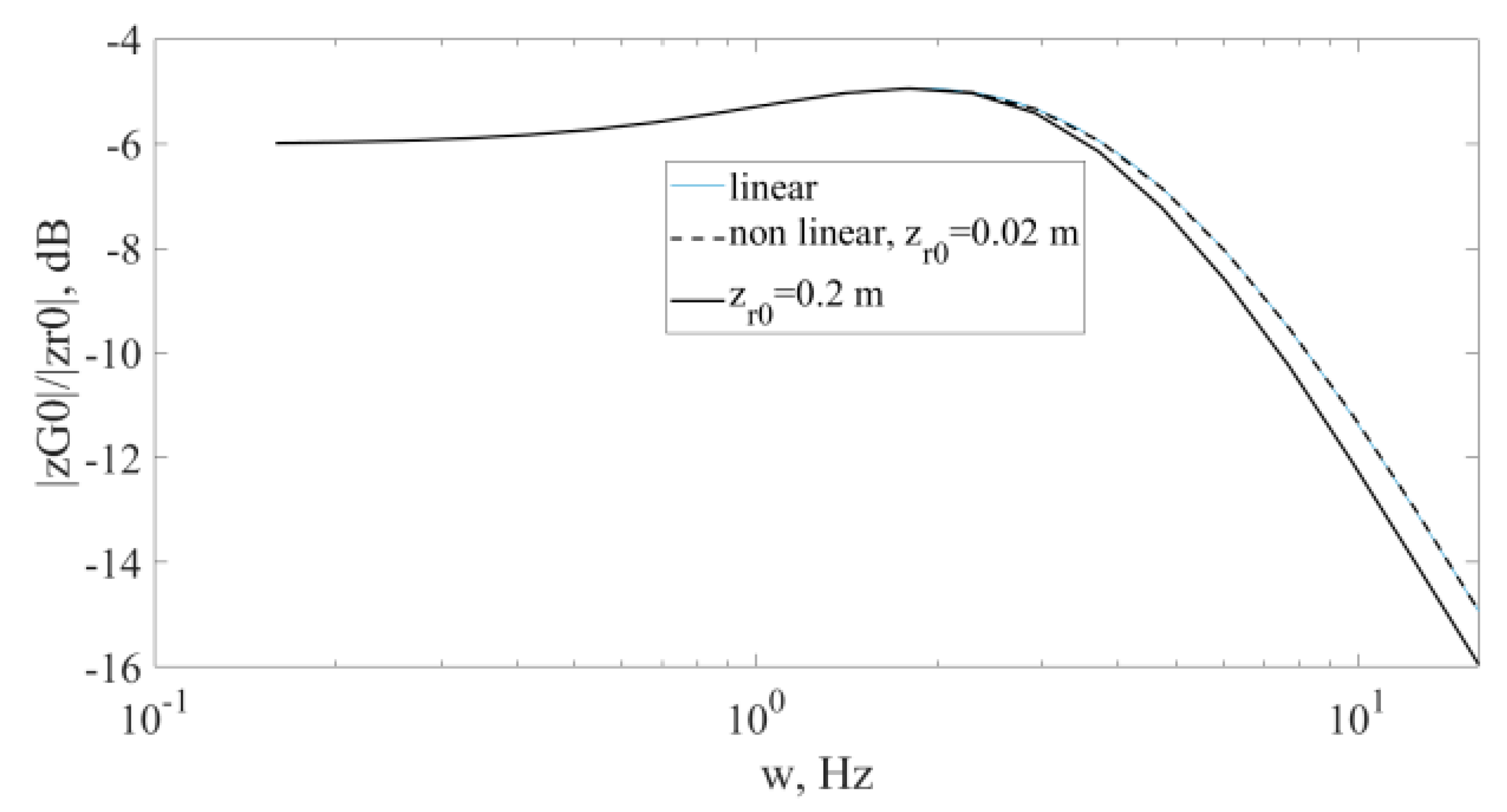
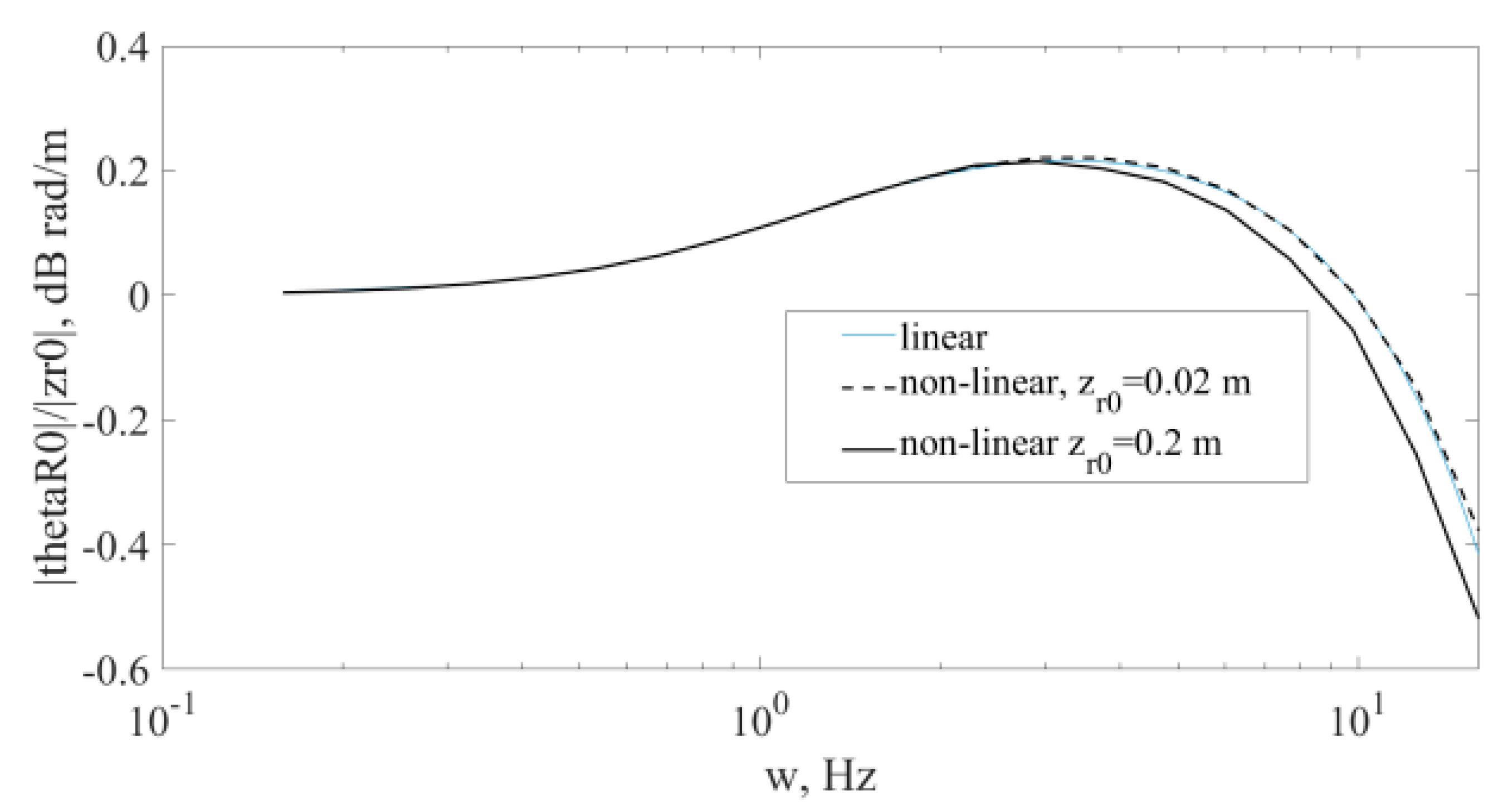
4.4. Roll Vibration Reduction

Having set ω_n,z conveniently, it is clear from the ratio $\frac{{\omega }_{n,\vartheta }}{{\omega }_{n,z}}=\sqrt{\frac{m·b^2}{4·I_{xx}}}$ that there is only a small intervention margin to obtain a ${\omega }_{n,\vartheta }$ lower than ω_n,z acting on I_xx. Choosing an appropriate distribution of the masses of the instrumentation contained inside the front box, I_xx could be increased without modifying the position of the centre of mass. Nevertheless, according to Equation (17), the most effective way to weaken the roll oscillations would be to limit the difference $\left(z_r-z_l\right)$. Therefore, in case torque absorption tests on Agri_q would prove that a 6-wheeled configuration is better than the current eight-wheeled configuration, an anti-roll bar could be connected to the Agri_q suspensions. It is worth noting that the introduction of such a device would modify the model under study as shown in Figure 15.

The additional contribution in terms of elastic energy potential is:

$$V_{add}=\frac{1}{2}·k·{\left(z_r-z_l\right)}^2$$

(29)

Therefore, the equation of motion (Equation (17)) and the undamped eigenfrequencies of the system remain unchanged, but the amplitude of the surface excitation for the roll motion is reduced.

5. Conclusions

A mechanism with an embedded suspension device has been studied to reconfigure the locomotion layout of the Agri_q agricultural rover. The mechanism permits to move from a four-front wheeled configuration, in which the ground excitation is filtered by a bogie, to a two front-wheeled configuration, in which a commercial shock absorber reduces the oscillation transmitted to the sub-chassis. Based on the shock absorber characteristic, the mechanism was dimensioned to ensure a reliable operation avoiding undesired switches and providing, at the same time, an almost constant instantaneous transmission ratio, useful for motor optimization. Focusing on the two-wheeled configuration, the device performance in terms of bounce and roll transmissibility to the rover front box has been studied, both by a linear analytical approach and by a non-linear numerical approach. Results suggest providing the rover front box by an anti-roll device, which does not affect the system eigenfrequencies and the system bounce response. In the future, the proposed mechanism will be integrated on the Agri_q prototype and experiments will be carried out to compare different locomotion layouts.