Rings, Hexagons, Petals, and Dipolar Moment Sink-Sources: The Fanciful Behavior of Water around Cyclodextrin Complexes
Abstract
1. Introduction
2. Materials and Methods
2.1. Set Up of the Simulation Boxes and MD Simulation Parameters
2.2. Parameterization Methods
2.3. Analysis of the Trajectories
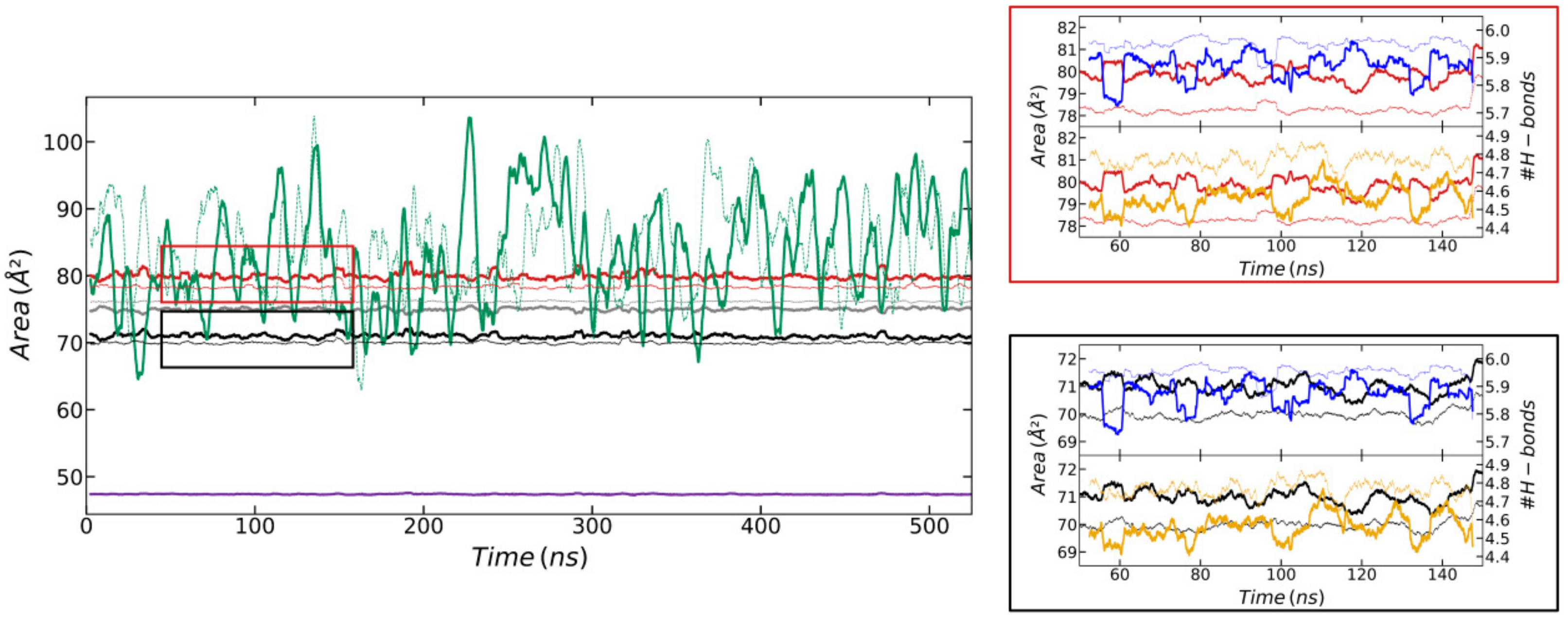
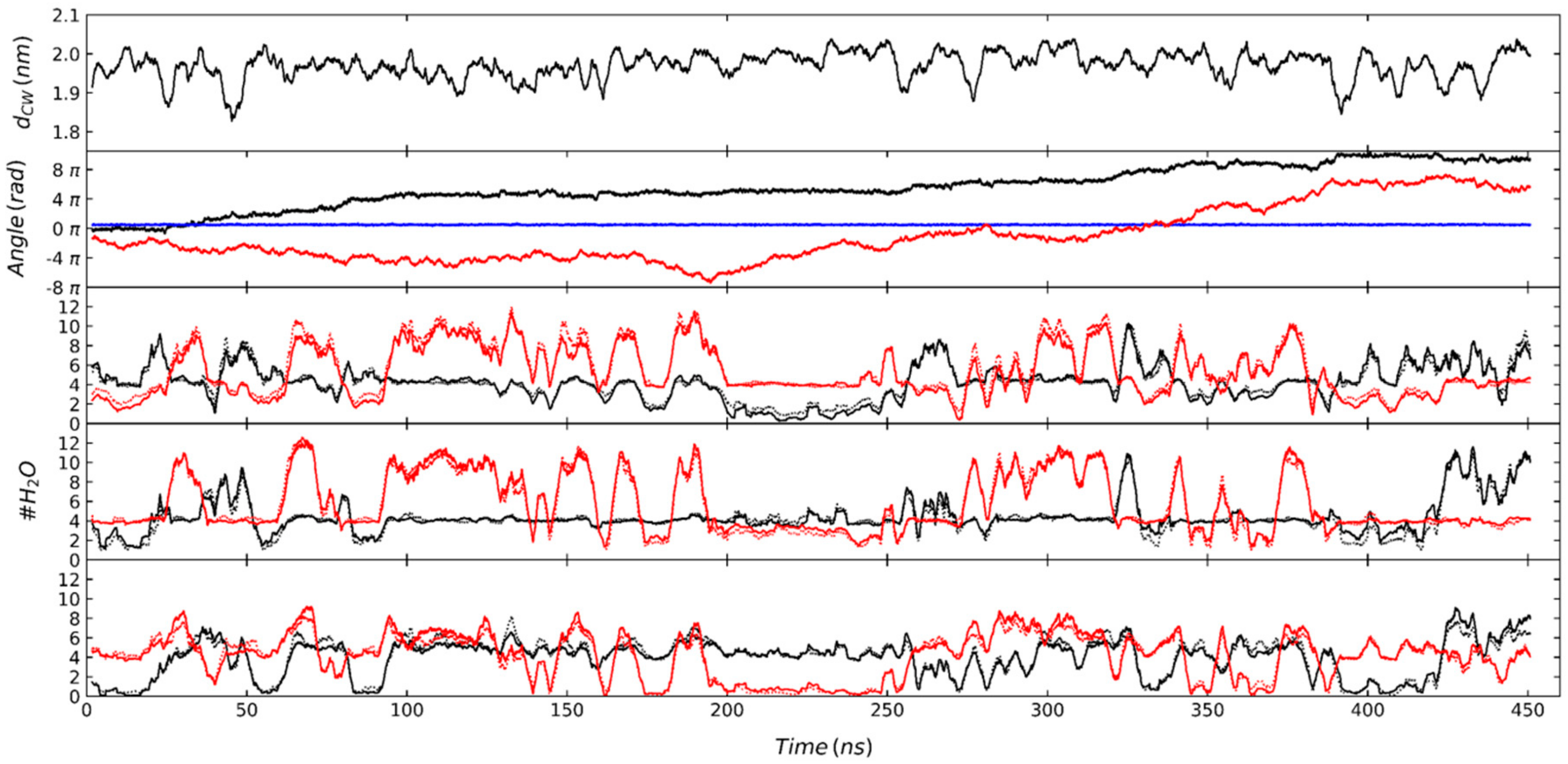
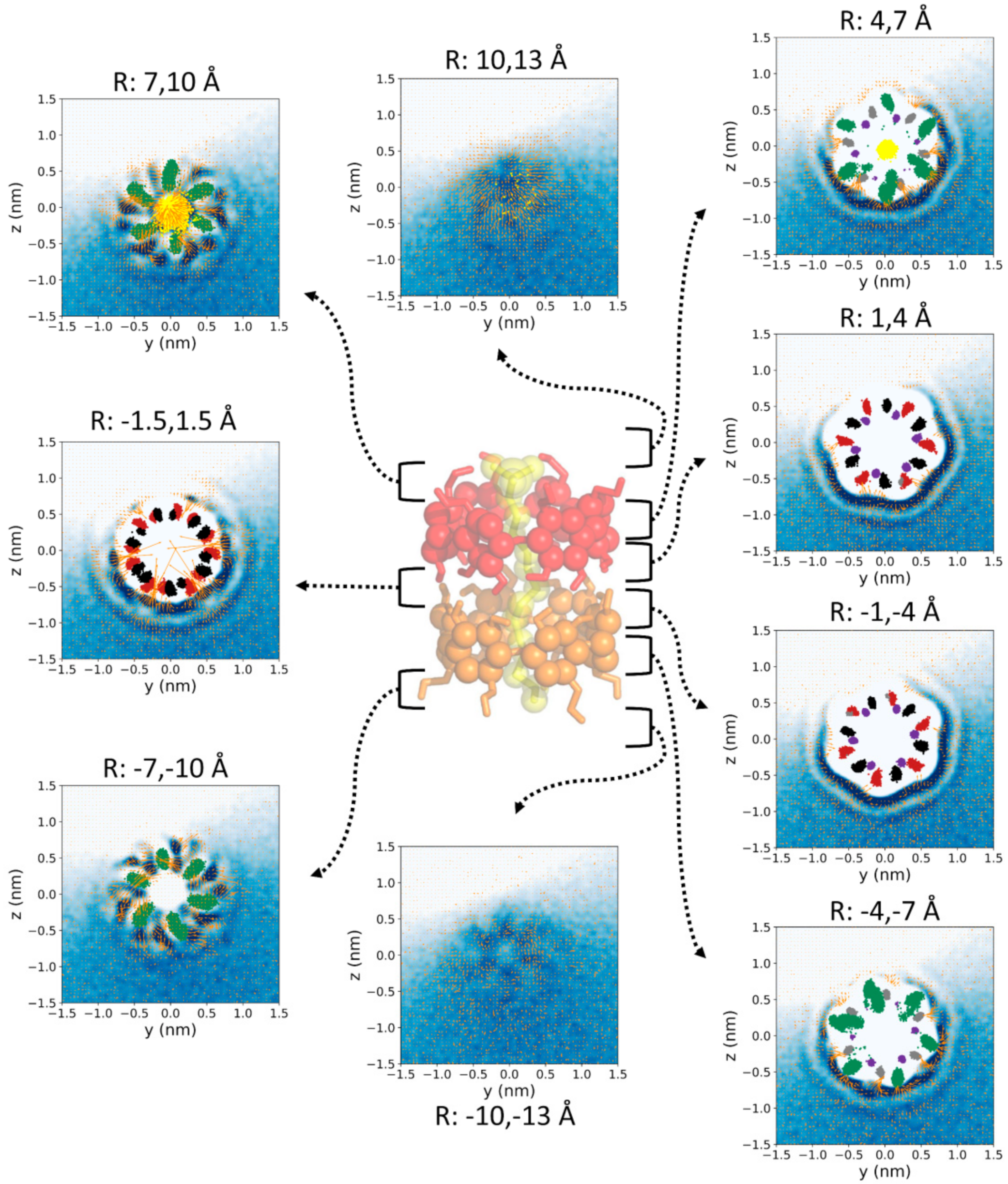
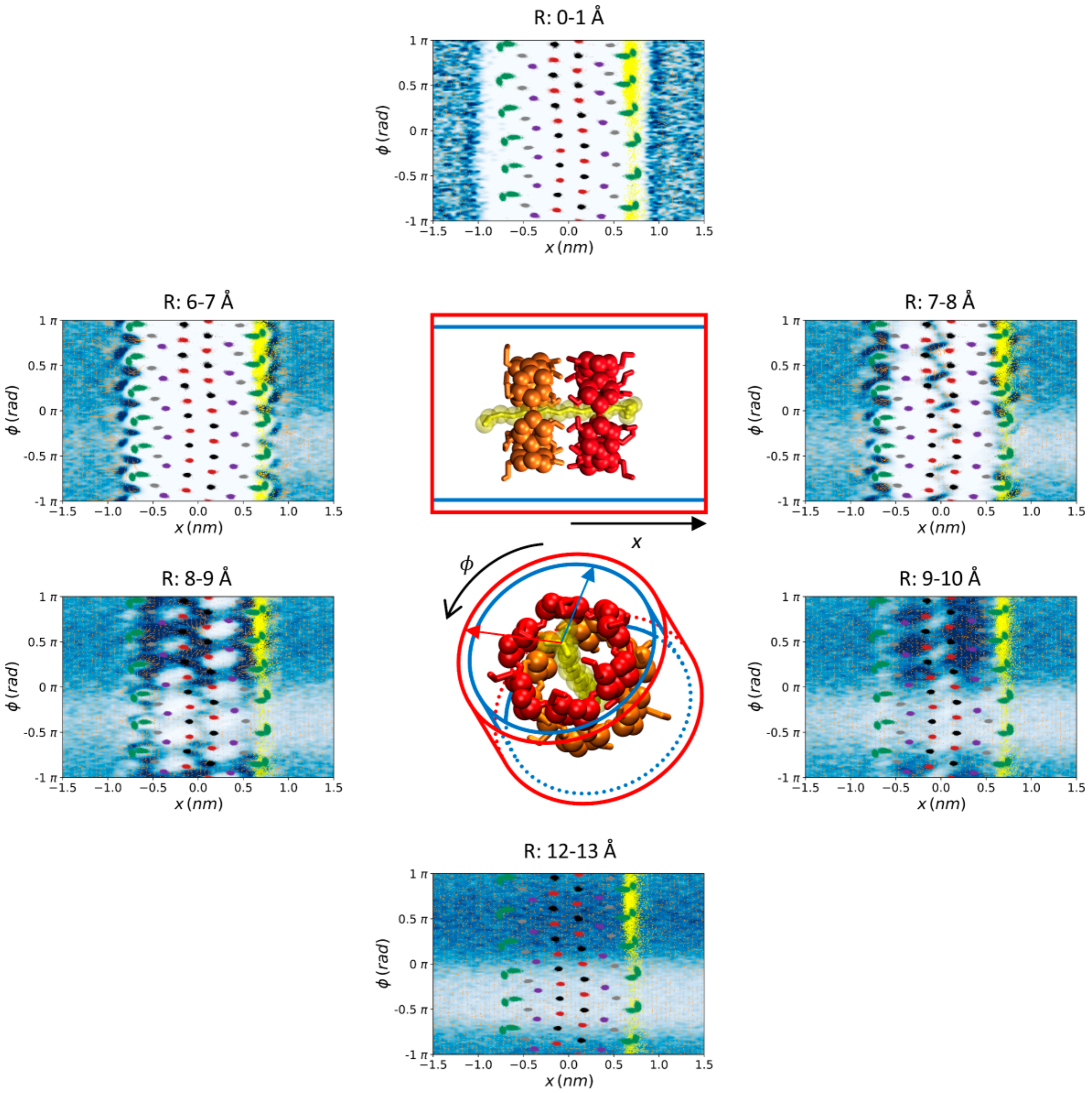
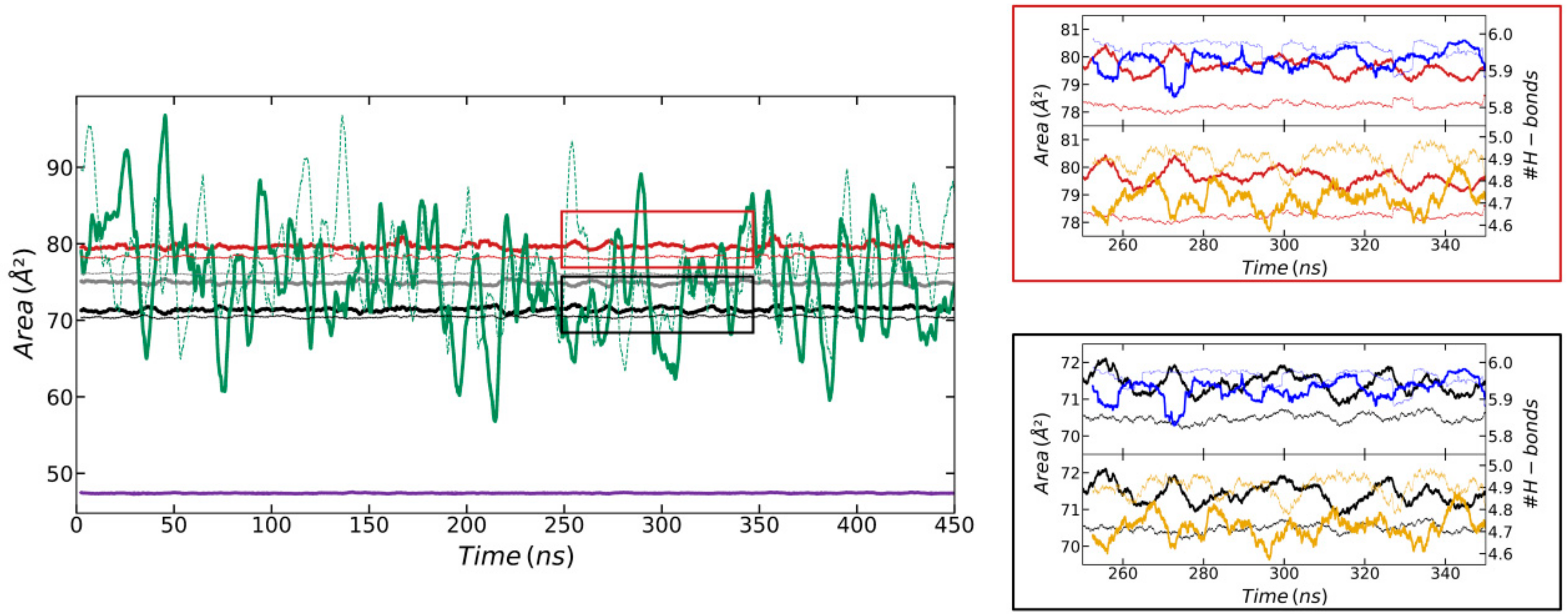
3. Results
3.1. Simulations in the Bulk Aqueous Solutions Using the G_2 Metho
3.2. Comparison between G_2 and Other Simulation Methods Using GROMOS and AMBER/GAFF Force Fields in the Bulk Aqueous Solution
3.3. H-Bond Analysis of Simulations in the Bulk Aqueous Solution
3.4. Simulations at the Water/Air Interface Using the Different Parameterizations of the GROMOS Force Field
3.5. H-Bond Analysis of Simulations at the Water/Air Interfaces Using the Different Parameterizations of the GROMOS Force Field
3.6. Analysis of Simulations Using the AMBER Force Field in the Presence of the Water/Air Interfaces
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Hernandez-Pascacio, J.; Piñeiro, A.; Ruso, J.M.; Hassan, N.; Campbell, R.A.; Campos-Terán, J.; Costas, M. Complex behavior of aqueous α-cyclodextrin solutions. Interfacial morphologies resulting from bulk aggregation. Langmuir 2016, 32, 6682–6690. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, M.; Bricout, H.; Azaroual, N.; Landy, D.; Tilloy, S.; Hapiot, F.; Monflier, E. Cyclodextrin/amphiphilic phosphane mixed systems and their applications in aqueous organometallic catalysis. Adv. Synth. Catal. 2012, 354, 1337–1346. [Google Scholar] [CrossRef]
- González-Gaitano, G.; Rodriguez, P.; Isasi, J.R.; Fuentes, M.; Tardajos, G.; Sánchez, M. The aggregation of cyclodextrins as studied by photon correlation spectroscopy. J. Incl. Phenom. Macrocycl. Chem. 2002, 44, 101–105. [Google Scholar] [CrossRef]
- Yang, S.; Yan, Y.; Huang, J.; Petukhov, A.V.; Kroon-Batenburg, L.M.; Drechsler, M.; Zhou, C.; Tu, M.; Granick, S.; Jiang, L. Giant capsids from lattice self-assembly of cyclodextrin complexes. Nat. Commun. 2017, 8, 15856. [Google Scholar] [CrossRef]
- Hernández-Pascacio, J.; Banquy, X.; Pérez-Casas, S.; Costas, M.; Amigo, A.; Piñeiro, Á. A small molecular size system giving unexpected surface effects: α-Cyclodextrin+ sodium dodecyl sulfate in water. J. Colloid Interface Sci. 2008, 328, 391–395. [Google Scholar] [CrossRef]
- Hernandez-Pascacio, J.; Garza, C.; Banquy, X.; Díaz-Vergara, N.; Amigo, A.; Ramos, S.; Castillo, R.; Costas, M.; Piñeiro, Á. Cyclodextrin-based self-assembled nanotubes at the water/air interface. J. Phys. Chem. B 2007, 111, 12625–12630. [Google Scholar] [CrossRef]
- Couto, A.R.S.; Aguiar, S.; Ryzhakov, A.; Larsen, K.L.; Loftsson, T. Interaction of native cyclodextrins and their hydroxypropylated derivatives with parabens in aqueous solutions. Part 1: Evaluation of inclusion complexes. J. Incl. Phenom. Macrocycl. Chem. 2019, 93, 309–321. [Google Scholar] [CrossRef]
- Hollingsworth, S.A.; Dror, R.O. Molecular dynamics simulation for all. Neuron 2018, 99, 1129–1143. [Google Scholar] [CrossRef]
- Marrink, S.J.; Corradi, V.; Souza, P.C.; Ingόlfsson, H.I.; Tieleman, D.P.; Sansom, M.S. Computational modeling of realistic cell membranes. Chem. Rev. 2019, 119, 6184–6226. [Google Scholar] [CrossRef]
- Chen, P.; Yao, S.; Chen, X.; Huang, Y.; Song, H. A new strategy for the construction of β-cyclodextrin-based magnetic nanocarriers: A molecular docking technique. New J. Chem. 2019, 43, 4282–4290. [Google Scholar] [CrossRef]
- Khuntawee, W.; Wolschann, P.; Rungrotmongkol, T.; Wong-Ekkabut, J.; Hannongbua, S. Molecular dynamics simulations of the interaction of beta cyclodextrin with a lipid bilayer. J. Chem. Inf. Model. 2015, 55, 1894–1902. [Google Scholar] [CrossRef] [PubMed]
- Nutho, B.; Nunthaboot, N.; Wolschann, P.; Kungwan, N.; Rungrotmongkol, T. Metadynamics supports molecular dynamics simulation-based binding affinities of eucalyptol and beta-cyclodextrin inclusion complexes. RSC Adv. 2017, 7, 50899–50911. [Google Scholar] [CrossRef]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; De Vries, A.H. The MARTINI force field: Coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef] [PubMed]
- Periole, X.; Cavalli, M.; Marrink, S.J.; Ceruso, M.A. Combining an elastic network with a coarse-grained molecular force field: Structure, dynamics, and intermolecular recognition. J. Chem. Theory Comput. 2009, 5, 2531–2543. [Google Scholar] [CrossRef]
- Otero-Mato, J.M.; Montes-Campos, H.; Calvelo, M.; Garcia-Fandino, R.; Gallego, L.J.; Piñeiro, A.; Varela, L.M. GADDLE Maps: General Algorithm for Discrete Object Deformations Based on Local Exchange Maps. J. Chem. Theory Comput. 2018, 14, 466–478. [Google Scholar] [CrossRef]
- Wassenaar, T.A.; Pluhackova, K.; Böckmann, R.A.; Marrink, S.J.; Tieleman, D.P. Going backward: A flexible geometric approach to reverse transformation from coarse grained to atomistic models. J. Chem. Theory Comput. 2014, 10, 676–690. [Google Scholar] [CrossRef]
- López, C.A.; De Vries, A.H.; Marrink, S.J. Computational microscopy of cyclodextrin mediated cholesterol extraction from lipid model membranes. Sci. Rep. 2013, 3, 2071. [Google Scholar] [CrossRef]
- Tuckerman, M.; Berne, B.J.; Martyna, G.J. Reversible multiple time scale molecular dynamics. J. Chem. Phys. 1992, 97, 1990–2001. [Google Scholar] [CrossRef]
- Ma, Q.; Izaguirre, J.A.; Skeel, R.D. Verlet-I/r-RESPA/Impulse is limited by nonlinear instabilities. SIAM J. Sci. Comput. 2003, 24, 1951–1973. [Google Scholar] [CrossRef]
- Sidler, D.; Lehner, M.; Frasch, S.; Cristófol-Clough, M.; Riniker, S. Density artefacts at interfaces caused by multiple time-step effects in molecular dynamics simulations. F1000Research 2018, 7. [Google Scholar] [CrossRef]
- Reißer, S.; Poger, D.; Stroet, M.; Mark, A.E. Real cost of speed: The effect of a time-saving multiple-time-stepping algorithm on the accuracy of molecular dynamics simulations. J. Chem. Theory Comput. 2017, 13, 2367–2372. [Google Scholar] [CrossRef] [PubMed]
- Feenstra, K.A.; Hess, B.; Berendsen, H.J. Improving efficiency of large time-scale molecular dynamics simulations of hydrogen-rich systems. J. Comput. Chem. 1999, 20, 786–798. [Google Scholar] [CrossRef]
- Luviano, A.S.; Hernández-Pascacio, J.; Ondo, D.; Campbell, R.A.; Piñeiro, Á.; Campos-Teránb, J.; Costas, M. Highly Viscoelastic Films at the Water/Air Interface: α-Cyclodextrin with anionic surfactants. J. Colloid Interface Sci. in press. [CrossRef] [PubMed]
- Hopkins, C.W.; Le Grand, S.; Walker, R.C.; Roitberg, A.E. Long-time-step molecular dynamics through hydrogen mass repartitioning. J. Chem. Theory Comput. 2015, 11, 1864–1874. [Google Scholar] [CrossRef] [PubMed]
- Balusek, C.; Hwang, H.; Lau, C.H.; Lundquist, K.; Hazel, A.; Pavlova, A.; Lynch, D.L.; Reggio, P.H.; Wang, Y.; Gumbart, J.C. Accelerating membrane simulations with Hydrogen Mass Repartitioning. J. Chem. Theory Comput. 2019, 15, 4673–4686. [Google Scholar] [CrossRef] [PubMed]
- Henriksen, N.M.; Gilson, M.K. Evaluating force field performance in thermodynamic calculations of cyclodextrin host–guest binding: Water models, partial charges, and host force field parameters. J. Chem. Theory Comput. 2017, 13, 4253–4269. [Google Scholar] [CrossRef]
- Jiang, L.; Peng, Y.; Yan, Y.; Deng, M.; Wang, Y.; Huang, J. “Annular Ring” microtubes formed by SDS@ 2β-CD complexes in aqueous solution. Soft Matter 2010, 6, 1731–1736. [Google Scholar] [CrossRef]
- Jiang, L.; Peng, Y.; Yan, Y.; Huang, J. Aqueous self-assembly of SDS@ 2 β-CD complexes: Lamellae and vesicles. Soft Matter 2011, 7, 1726–1731. [Google Scholar] [CrossRef]
- Mathapa, B.G.; Paunov, V.N. Cyclodextrin stabilised emulsions and cyclodextrinosomes. Phys. Chem. Chem. Phys. 2013, 15, 17903–17914. [Google Scholar] [CrossRef]
- Mathapa, B.G.; Paunov, V.N. Fabrication of viable cyborg cells with cyclodextrin functionality. Biomater. Sci. 2014, 2, 212–219. [Google Scholar] [CrossRef]
- Tanford, C. The hydrophobic effect and the organization of living matter. Science 1978, 200, 1012–1018. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Fandiño, R.; Piñeiro, A.; Trick, J.L.; Sansom, M.S. Lipid bilayer membrane perturbation by embedded nanopores: A simulation study. ACS Nano 2016, 10, 3693–3701. [Google Scholar] [CrossRef] [PubMed]
- Laage, D.; Elsaesser, T.; Hynes, J.T. Water dynamics in the hydration shells of biomolecules. Chem. Rev. 2017, 117, 10694–10725. [Google Scholar] [CrossRef] [PubMed]
- Bizzarri, A.R.; Cannistraro, S. Molecular dynamics of water at the Protein—Solvent interface. J. Phys. Chem. B 2002, 106, 6617–6633. [Google Scholar] [CrossRef]
- Jana, M.; Bandyopadhyay, S. Hydration Properties of α-, β-, and γ-Cyclodextrins from Molecular Dynamics Simulations. J. Phys. Chem. B 2011, 115, 6347–6357. [Google Scholar] [CrossRef]
- Bottari, C.; Comez, L.; Paolantoni, M.; Corezzi, S.; D’Amico, F.; Gessini, A.; Masciovecchio, C.; Rossi, B. Hydration properties and water structure in aqueous solutions of native and modified cyclodextrins by UV Raman and Brillouin scattering. J. Raman Spectrosc. 2018, 49, 1076–1085. [Google Scholar] [CrossRef]
- Jana, M.; Bandyopadhyay, S. Vibrational spectrum of water confined in and around cyclodextrins. Chem. Phys. Lett. 2011, 509, 181–185. [Google Scholar] [CrossRef]
- Schmid, N.; Eichenberger, A.P.; Choutko, A.; Riniker, S.; Winger, M.; Mark, A.E.; van Gunsteren, W.F. Definition and testing of the GROMOS force-field versions 54A7 and 54B7. Eur. Biophys. J. 2011, 40, 843. [Google Scholar] [CrossRef]
- Ponder, J.W.; Case, D.A. Force fields for protein simulations. In Advances in Protein Chemistry; Daggett, V., Ed.; Academic Press: Cambridge, MA, USA, 2003; Volume 66, pp. 27–85. [Google Scholar] [CrossRef]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef]
- Berendsen, H.J.; Postma, J.P.; van Gunsteren, W.F.; Hermans, J. Interaction models for water in relation to protein hydration. In Intermolecular Forces; Pullman, B., Ed.; Springer: Dordrecht, The Netherlands, 1981; Volume 14, pp. 331–342. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Brocos, P.; Díaz-Vergara, N.; Banquy, X.; Pérez-Casas, S.; Costas, M.; Pineiro, A. Similarities and Differences between Cyclodextrin—Sodium Dodecyl Sulfate Host—Guest Complexes of Different Stoichiometries: Molecular Dynamics Simulations at Several Temperatures. J. Phys. Chem. B 2010, 114, 12455–12467. [Google Scholar] [CrossRef]
- Berendsen, H.J.; van der Spoel, D.; van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [PubMed]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N log (N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Hockney, R.W.; Eastwood, J.W. Computer Simulation Using Particles, 1st ed.; CRC Press: Boca Raton, FL, USA, 1988. [Google Scholar] [CrossRef]
- Miyamoto, S.; Kollman, P.A. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.; Fraaije, J.G. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Mixcoha, E.; Campos-Terán, J.; Piñeiro, A. Surface adsorption and bulk aggregation of cyclodextrins by computational molecular dynamics simulations as a function of temperature: α-CD vs. β-CD. J. Phys. Chem. B 2014, 118, 6999–7011. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247260. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general AMBER force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Madura, J.D. Temperature and size dependence for monte carlo simulations of TIP4P water. Mol. Phys. 1985, 56, 1381–1392. [Google Scholar] [CrossRef]
- Gowers, R.J.; Linke, M.; Barnoud, J.; Reddy, T.J.E.; Melo, M.N.; Seyler, S.L.; Domanski, J.; Dotson, D.L.; Buchoux, S.; Kenney, I.M.; et al. MDAnalysis: A Python package for the rapid analysis of molecular dynamics simulations. In Proceedings of the 15th Python in Science Conference, Austin, TX, USA, 11 July 2016; Benthall, S., Rostrup, S., Eds.; SciPy: Austin, TX, USA, 2016. [Google Scholar] [CrossRef]
- Michaud-Agrawal, N.; Denning, E.J.; Woolf, T.B.; Beckstein, O. MDAnalysis: A toolkit for the analysis of molecular dynamics simulations. J. Comput. Chem. 2011, 32, 2319–2327. [Google Scholar] [CrossRef] [PubMed]
- Saenger, W.; Jacob, J.; Gessler, K.; Steiner, T.; Hoffmann, D.; Sanbe, H.; Koizumi, K.; Smith, S.M.; Takaha, T. Structures of the common cyclodextrins and their larger analogues—Beyond the doughnut. Chem. Rev. 1998, 98, 1787–1802. [Google Scholar] [CrossRef] [PubMed]
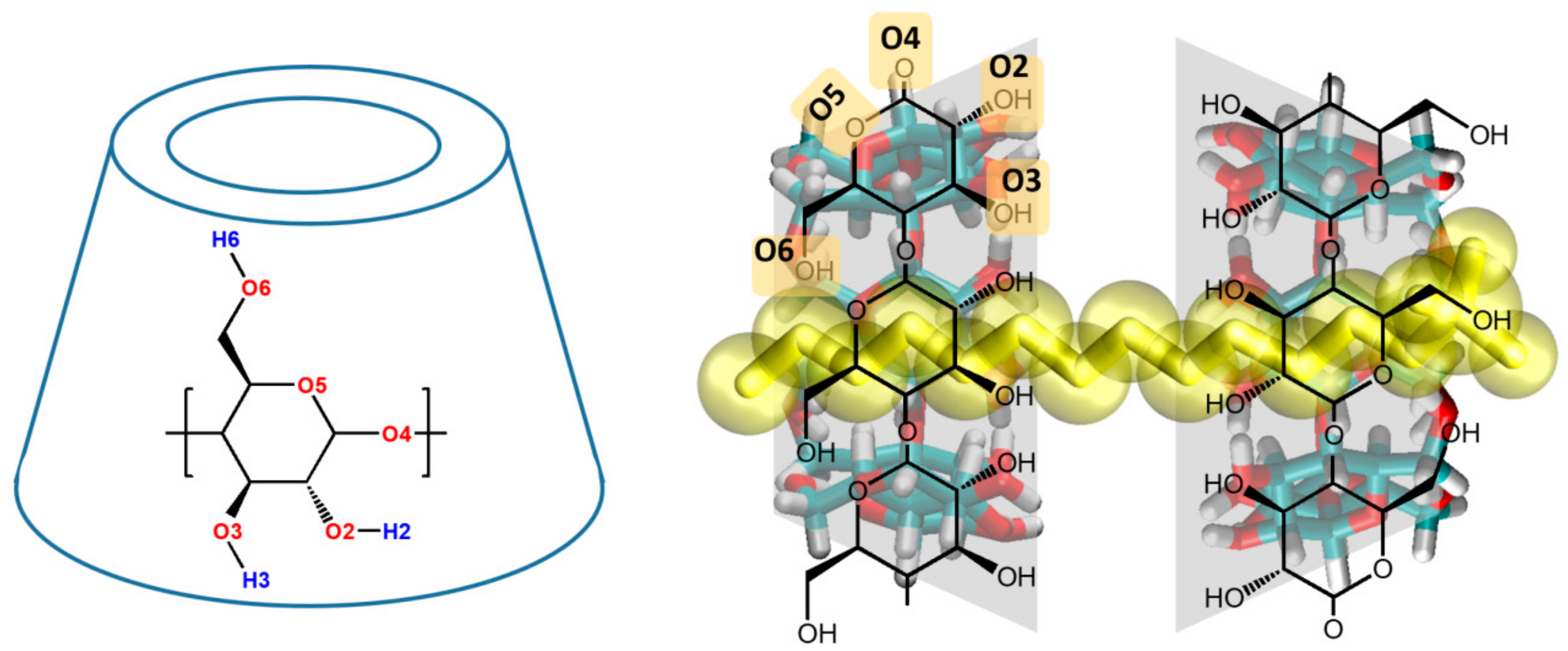

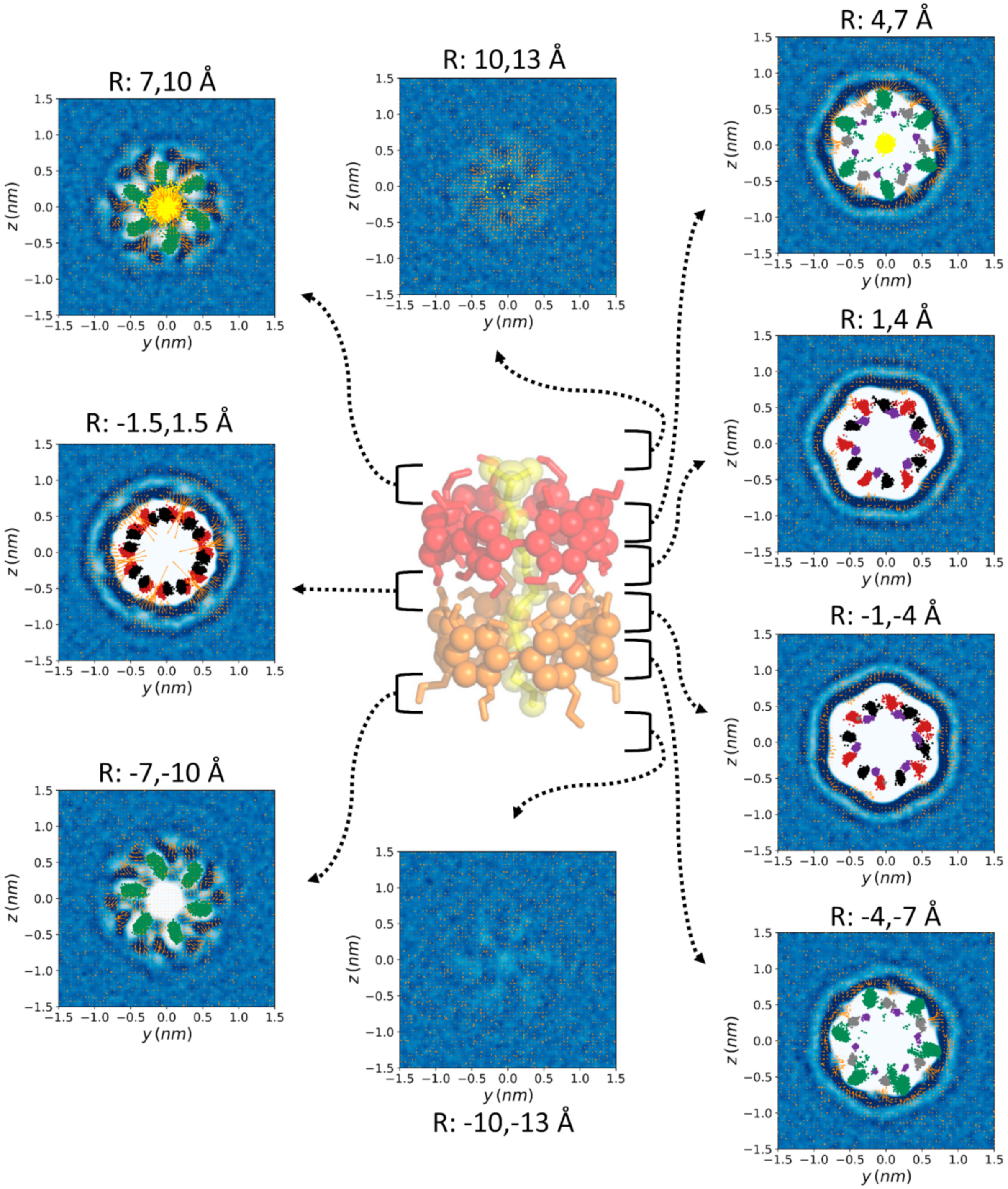
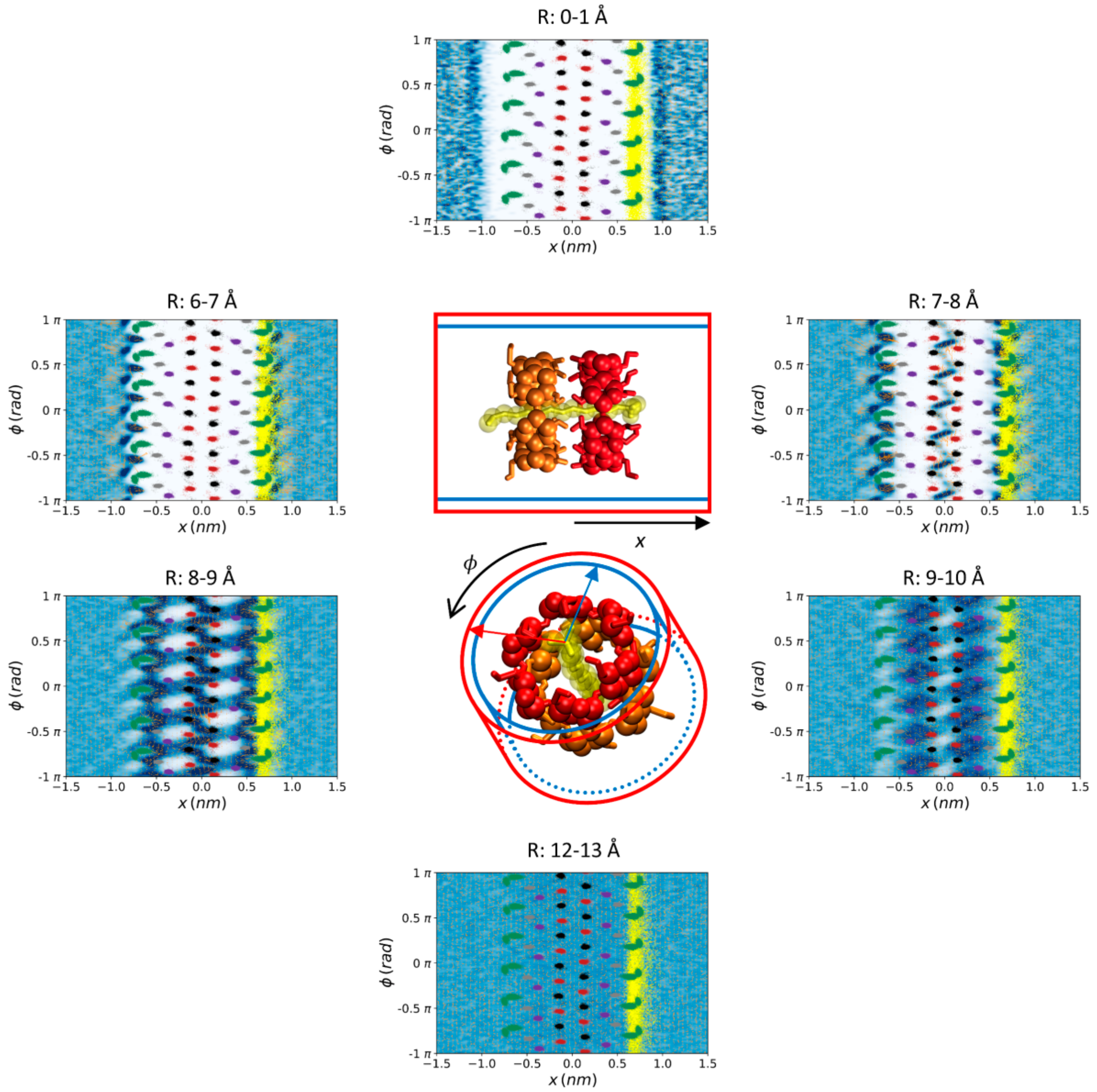
| Donor/Acceptor | G_2 | HMR_2 | HMR_7 | H2Q_2 | H2Q_7 | AMBER RESP | AMBER BB-RESP | AMBER BB-AM1 |
|---|---|---|---|---|---|---|---|---|
| CD1-CD2 | 9.37 (41.01) | 9.37 (41.00) | 9.47 (148.42) | 9.40 (41.75) | 9.42 (145.47) | 5.87 (20.56) | 5.45 (37.61) | 4.85 (18.21) |
| O2H2 (CD1)-O3H3 (CD2) | 4.55 (37.78) | 4.52 (37.87) | 4.60 (138.35) | 4.56 (38.63) | 4.59 (137.23) | 2.58 (21.42) | 1.57 (41.36) | 1.96 (18.64) |
| O2H2 (CD2)- O3H3 (CD1) | 4.76 (44.37) | 4.74 (43.93) | 4.77 (158.85) | 4.74 (44.78) | 4.74 (153.70) | 2.60 (21.51) | 1.59 (42.60) | 1.93 (18.81) |
| CD1-CD1 | 5.87 (852) | 5.82 (856) | 5.86 (2624) | 5.85 (849) | 5.87 (2696) | 5.80 (250.07) | 5.46 (145.83) | 5.73 (210.60) |
| O3H3 (CD1)- O2H2 (CD1) | 5.87 (856) | 5.82 (859) | 5.86 (2631) | 5.85 (853) | 5.87 (2701) | 5.77 (291.50) | 5.43 (155.73) | 5.71 (227.72) |
| CD1-SDS | 1.48 (52.26) | 1.35 (53.58) | 1.39 (93.65) | 1.55 (52.70) | 1.41 (89.89) | 2.02 (17.98) | 0.89 (19.63) | 2.55 (21.00) |
| CD2-CD2 | 5.94 (1640) | 5.93 (1437) | 5.92 (4484) | 5.92 (1678) | 5.92 (4586) | 5.89 (310.17) | 5.66 (209.38) | 5.81 (233.32) |
| O3H3 (CD2)- O2H2 (CD2) | 5.94 (1645) | 5.93 (1444) | 5.92 (4494) | 5.92 (1678) | 5.92 (4607) | 5.84 (400.60) | 5.64 (223.52) | 5.76 (271.77) |
| O2H2 (CD1)-water | 2.32 (6.90) | 2.37 (7.03) | 2.36 (19.47) | 2.34 (6.95) | 2.33 (19.35) | 3.45 (7.49) | 4.41 (9.72) | 3.14 (7.94) |
| O2H2 (CD2)-water | 1.97 (6.45) | 1.95 (6.54) | 2.01 (19.09) | 1.99 (6.65) | 2.01 (19.11) | 3.18 (7.24) | 3.91 (9.45) | 2.89 (7.85) |
| O3H3 (CD1)-water | 1.40 (6.23) | 1.43 (6.35) | 1.38 (18.64) | 1.39 (6.24) | 1.39 (18.73) | 2.98 (6.99) | 3.29 (8.39) | 3.26 (7.45) |
| O3H3 (CD2)-water | 1.19 (5.87) | 1.17 (5.82) | 1.18 (18.30) | 1.21 (5.85) | 1.20 (18.43) | 2.72 | 2.98 (8.27) | 3.00 (7.48) |
| (7.06) | ||||||||
| O5 (CD1)-water | 1.93 (6.60) | 1.93 (6.62) | 1.98 (18.79) | 1.95 (6.75) | 1.97 (18.77) | 2.80 (6.50) | 4.67 (9.43) | 2.78 (6.80) |
| O5 (CD2)-water | 1.63 (6.47) | 1.60 (6.43) | 1.64 (18.67) | 1.62 (6.50) | 1.62 (18.74) | 2.42 (6.33) | 4.40 (9.28) | 2.32 (6.55) |
| O6H6 (CD2)-water | 12.44 (14.49) | 12.46 (14.76) | 12.56 (27.73) | 12.45 (14.82) | 12.52 (28.27) | 9.71 (7.48) | 10.96 (7.96) | 9.53 (7.69) |
| O6H6 (CD1)-water | 11.59 (12.16) | 11.68 (12.36) | 11.73 (24.84) | 11.50 (12.30) | 11.72 (24.87) | 10.72 (8.16) | 11.31 (8.75) | 10.99 (8.32) |
| SDS-water | 3.69 (12.35) | 3.74 (12.53) | 3.74 (25.70) | 3.63 (12.38) | 3.72 (25.67) | 3.53 (8.96) | 3.75 (11.35) | 3.37 (8.64) |
| Donor/Acceptor | G_2 | HMR_2 | HMR_7 | H2Q_2 | H2Q_7 | AMBER RESP | AMBER BB-RESP | AMBER BB-AM1 |
|---|---|---|---|---|---|---|---|---|
| CD1-CD2 | 9.64 (46.60) | 9.65 (46.58) | 9.71 (166.19) | 9.61 (45.75) | 9.67 (163.43) | 5.87 (20.50) | 5.40 (36.66) | 4.86 (18.81) |
| O2H2 (CD1)-O3H3 (CD2) | 4.71 (42.81) | 4.72 (42.66) | 4.76 (155.15) | 4.69 (42.10) | 4.70 (147.75) | 2.55 (21.27) | 1.61 (39.79) | 1.98 (19.66) |
| O2H2 (CD2)- O3H3 (CD1) | 4.90 (50.71) | 4.91 (50.94) | 4.93 (178.41) | 4.89 (49.77) | 4.93 (181.16) | 2.64 (21.37) | 1.54 (41.16) | 1.98 (19.21) |
| CD1-CD1 | 5.91 (1248) | 5.92 (1381) | 5.93 (3852) | 5.91 (1298) | 5.90 (3662) | 5.79 (244.78) | 5.47 (151.57) | 5.73 (208.11) |
| O3H3 (CD1)- O2H2 (CD1) | 5.91 (1262) | 5.92 (1398) | 5.93 (3878) | 5.91 (1311) | 5.90 (3695) | 5.76 (284.60) | 5.45 (160.66) | 5.71 (223.89) |
| CD1-SDS | 2.09 (47.35) | 1.89 (48.18) | 1.99 (104.61) | 2.05 (56.39) | 2.16 (93.78) | 1.96 (18.15) | 1.01 (19.74) | 2.25 (20.96) |
| CD2-CD2 | 5.96 (1989) | 5.97 (2505) | 5.96 (5624) | 5.96 (2144) | 5.97 (8040) | 5.89 (318.85) | 5.56 (182.09) | 5.82 (251.10) |
| O3H3 (CD2)- O2H2 (CD2) | 5.96 (2117) | 5.96 (2632) | 5.96 (5869) | 5.96 (2307) | 5.96 (8421) | 5.84 (411.09) | 5.54 (191.28) | 5.78 (289.62) |
| O2H2 (CD1)-water | 2.51 (6.17) | 2.39 (6.19) | 2.76 (18.49) | 2.34 (6.22) | 2.28 (18.77) | 3.51 (7.42) | 4.53 | 3.17 (7.79) |
| (9.77) | ||||||||
| O2H2 (CD2)-water | 2.24 (5.85) | 2.16 (5.88) | 2.52 (18.24) | 2.08 (5.99) | 2.03 (18.43) | 3.23 (7.25) | 3.97 | 3.00 (7.86) |
| (9.35) | ||||||||
| O3H3 (CD1)-water | 1.87 (5.62) | 1.72 (5.65) | 2.10 (18.04) | 1.67 (5.68) | 1.62 (18.24) | 2.99 (7.03) | 3.37 | 3.33 (7.52) |
| (8.28) | ||||||||
| O3H3 (CD2)-water | 1.72 (5.45) | 1.61 (5.44) | 1.99 (17.94) | 1.51 (5.48) | 1.49 (17.95) | 2.79 (6.89) | 2.99 | 3.07 (7.36) |
| (8.23) | ||||||||
| O4 (CD1)-water | 0.56 (5.10) | 0.47 (5.09) | 0.69 (17.75) | 0.39 (5.09) | 0.40 (17.53) | -- | -- | -- |
| O4 (CD2)-water | 0.55 (5.10) | 0.50 (5.08) | 0.68 (17.50) | 0.44 (5.09) | 0.40 (17.58) | -- | -- | -- |
| O5 (CD1)-water | 2.05 (6.07) | 2.01 (6.13) | 2.27 (18.26) | 1.97 (6.10) | 1.94 (18.41) | 2.83 (6.48) | 4.70 | 2.82 (6.84) |
| (9.44) | ||||||||
| O5 (CD2)-water | 1.82 (5.95) | 1.75 (6.01) | 1.98 (18.07) | 1.68 (5.94) | 1.68 (18.40) | 2.46 (6.26) | 4.46 | 2.37 (6.45) |
| (9.07) | ||||||||
| O6H6 (CD2)-water | 11.33 (11.89) | 11.36 (12.13) | 11.74 (24.99) | 11.24 (12.12) | 11.12 (25.27) | 9.83 (7.48) | 10.98 (7.90) | 9.80 (7.65) |
| O6H6 (CD1)-water | 12.79 (15.68) | 12.70 (15.83) | 12.95 (31.75) | 12.74 (15.83) | 12.65 (32.11) | 10.89 (8.13) | 11.55 (8.55) | 11.17 (8.27) |
| SDS-water | 3.49 (11.01) | 3.59 (11.34) | 3.61 (24.84) | 3.42 (11.13) | 3.34 (25.07) | 3.62 (8.97) | 3.66 (11.18) | 3.62 (8.80) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
F. Garrido, P.; Calvelo, M.; Garcia-Fandiño, R.; Piñeiro, Á. Rings, Hexagons, Petals, and Dipolar Moment Sink-Sources: The Fanciful Behavior of Water around Cyclodextrin Complexes. Biomolecules 2020, 10, 431. https://doi.org/10.3390/biom10030431
F. Garrido P, Calvelo M, Garcia-Fandiño R, Piñeiro Á. Rings, Hexagons, Petals, and Dipolar Moment Sink-Sources: The Fanciful Behavior of Water around Cyclodextrin Complexes. Biomolecules. 2020; 10(3):431. https://doi.org/10.3390/biom10030431
Chicago/Turabian StyleF. Garrido, Pablo, Martín Calvelo, Rebeca Garcia-Fandiño, and Ángel Piñeiro. 2020. "Rings, Hexagons, Petals, and Dipolar Moment Sink-Sources: The Fanciful Behavior of Water around Cyclodextrin Complexes" Biomolecules 10, no. 3: 431. https://doi.org/10.3390/biom10030431
APA StyleF. Garrido, P., Calvelo, M., Garcia-Fandiño, R., & Piñeiro, Á. (2020). Rings, Hexagons, Petals, and Dipolar Moment Sink-Sources: The Fanciful Behavior of Water around Cyclodextrin Complexes. Biomolecules, 10(3), 431. https://doi.org/10.3390/biom10030431





