Measurements of Gaseous Hydrogen–Nitrogen Laser-Plasma
Abstract
:1. Introduction
2. Materials and Methods
3. Results
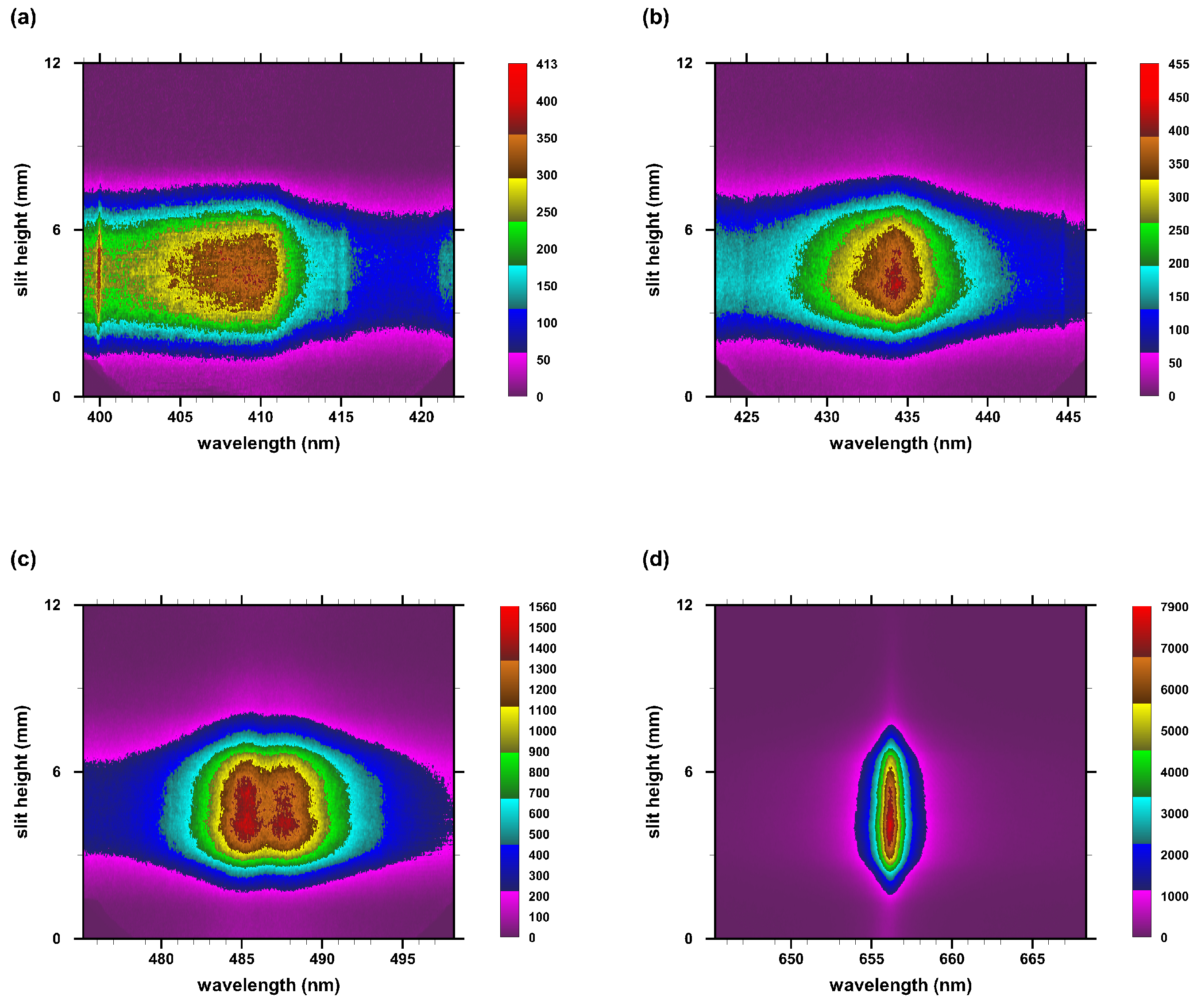
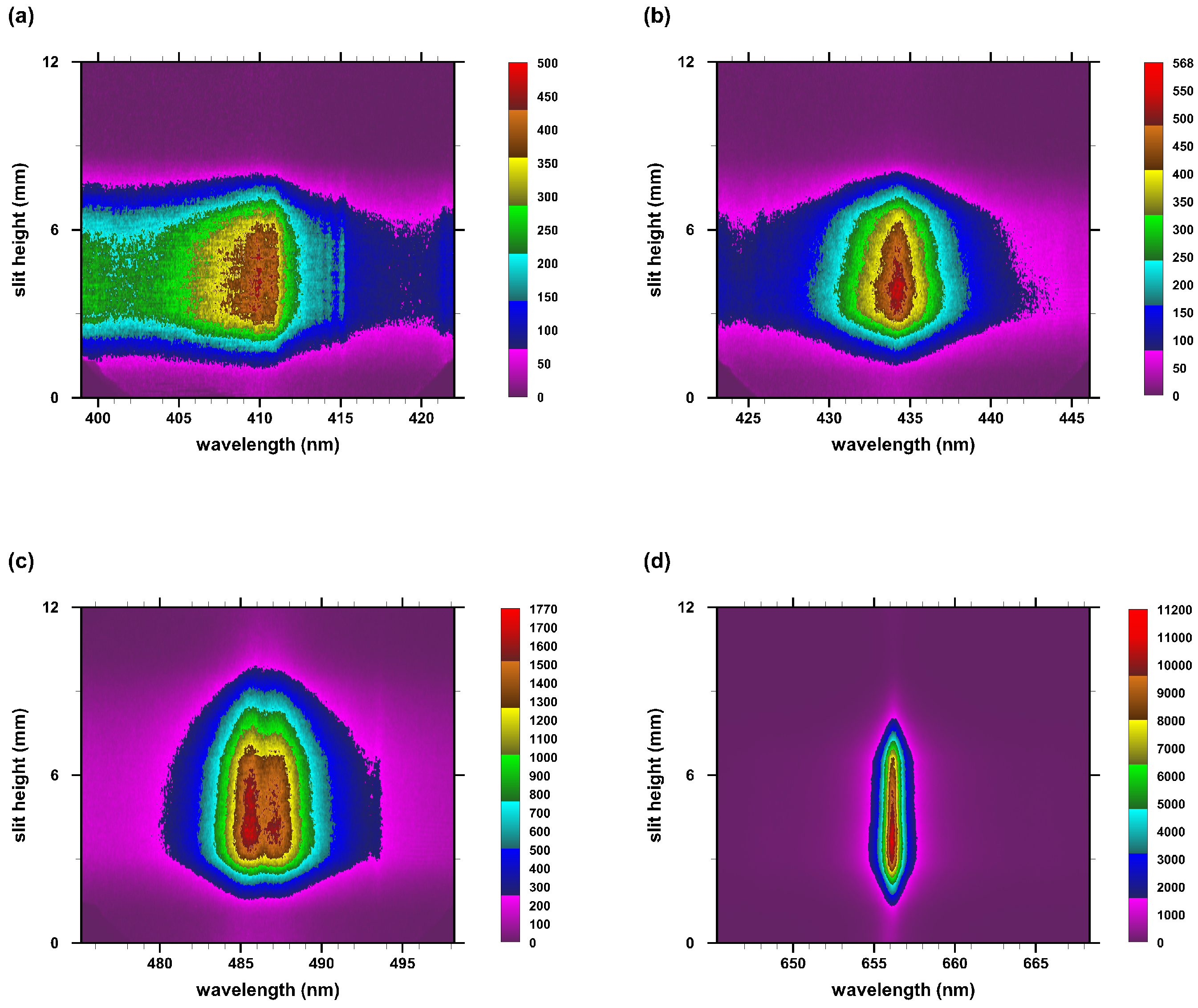
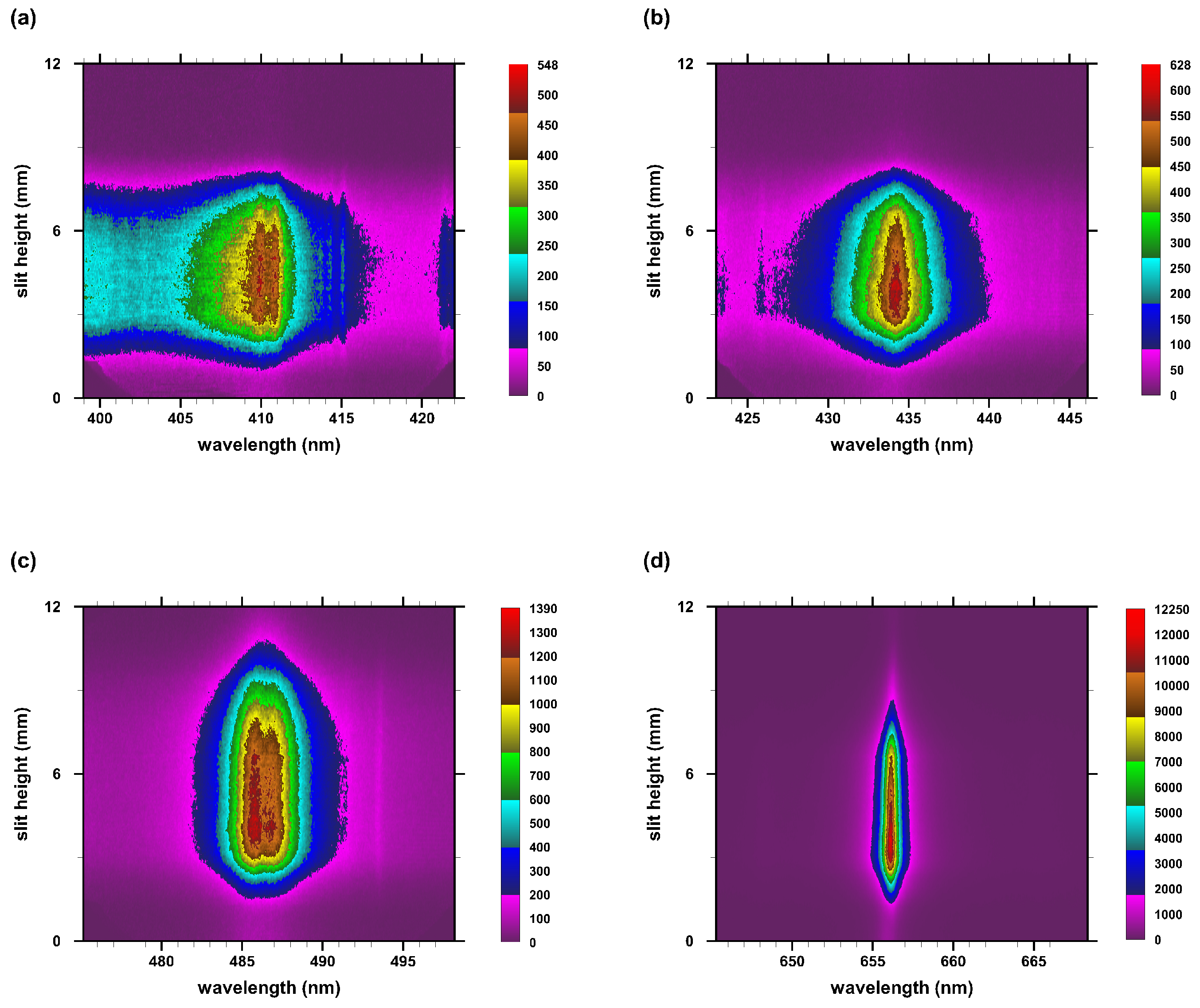
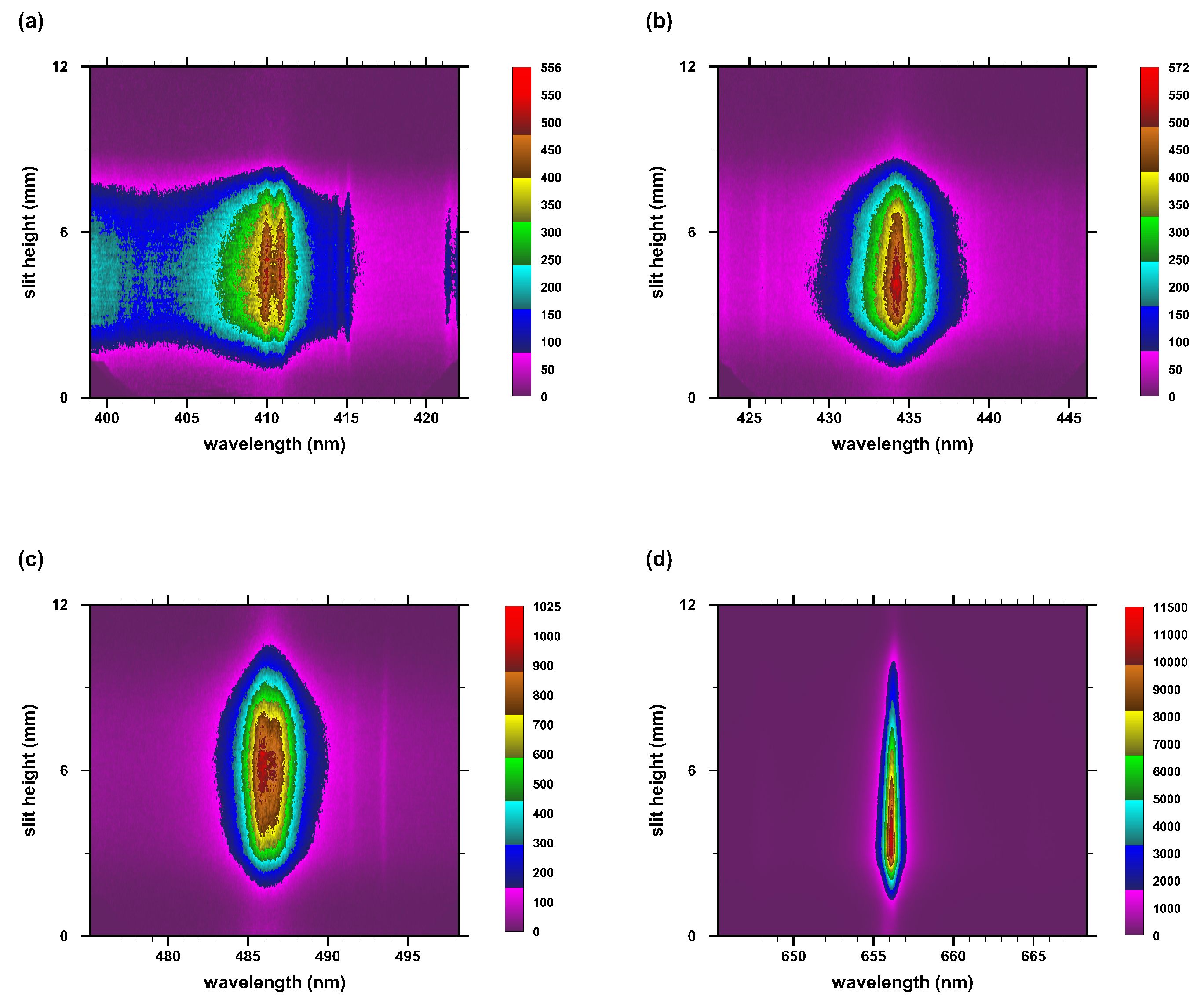
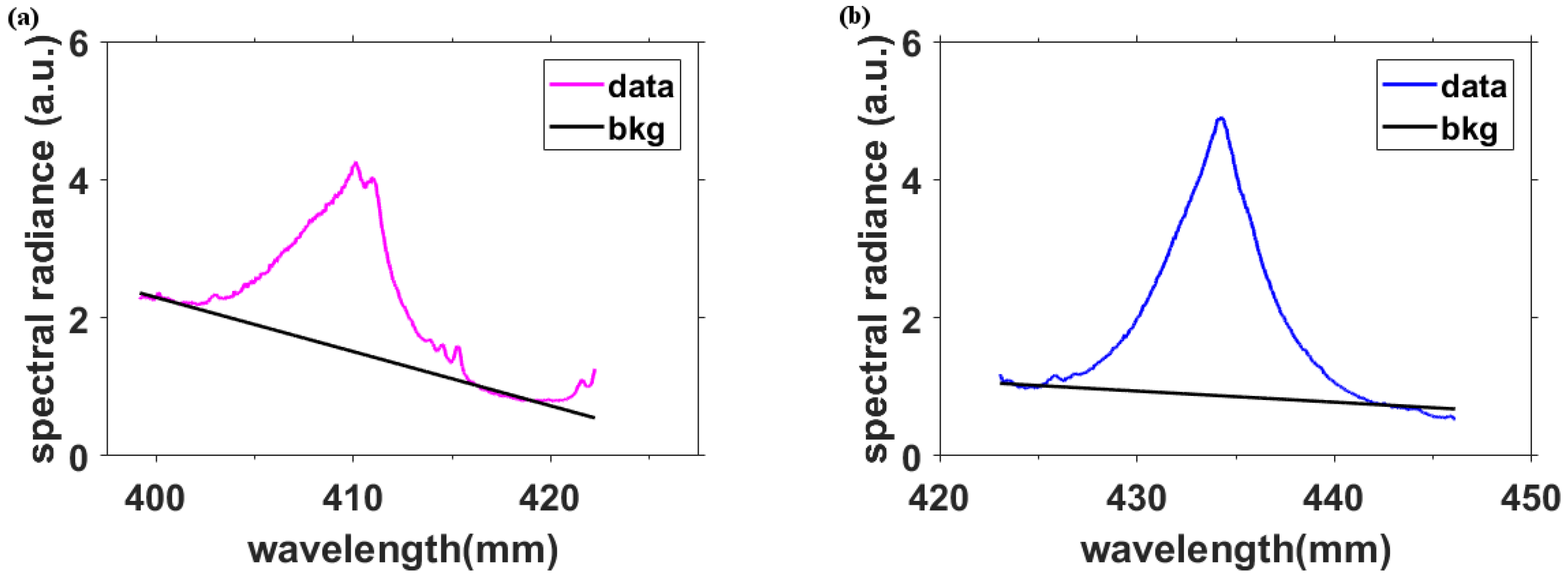
3.1. Line-of-Sight Measurements
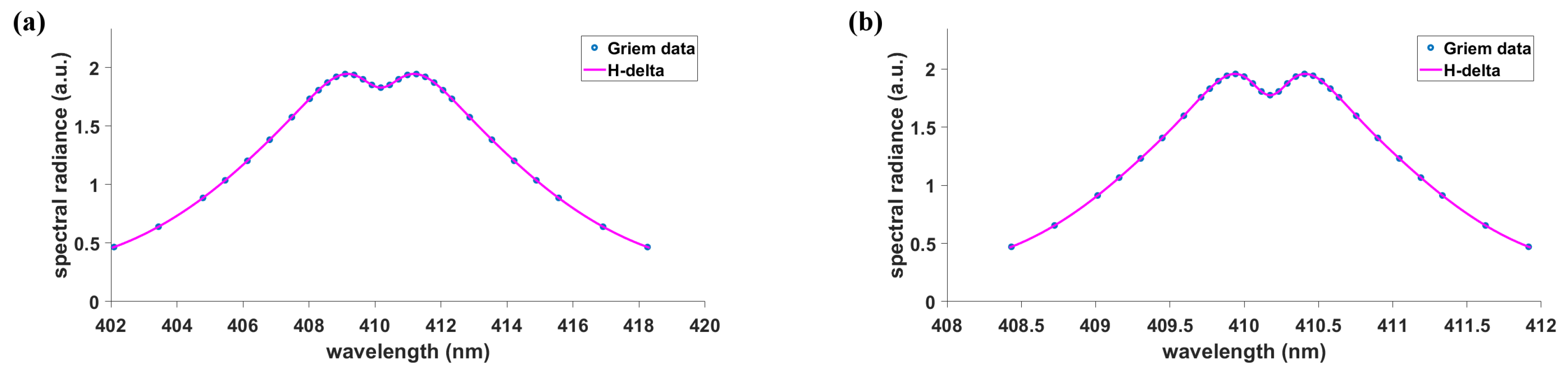
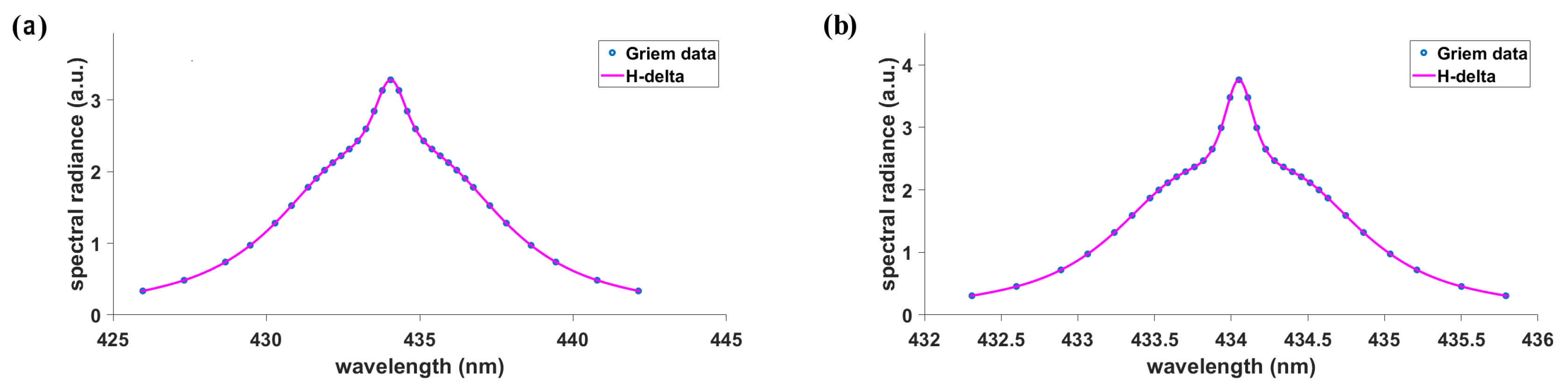
3.2. H and H Line Profiles
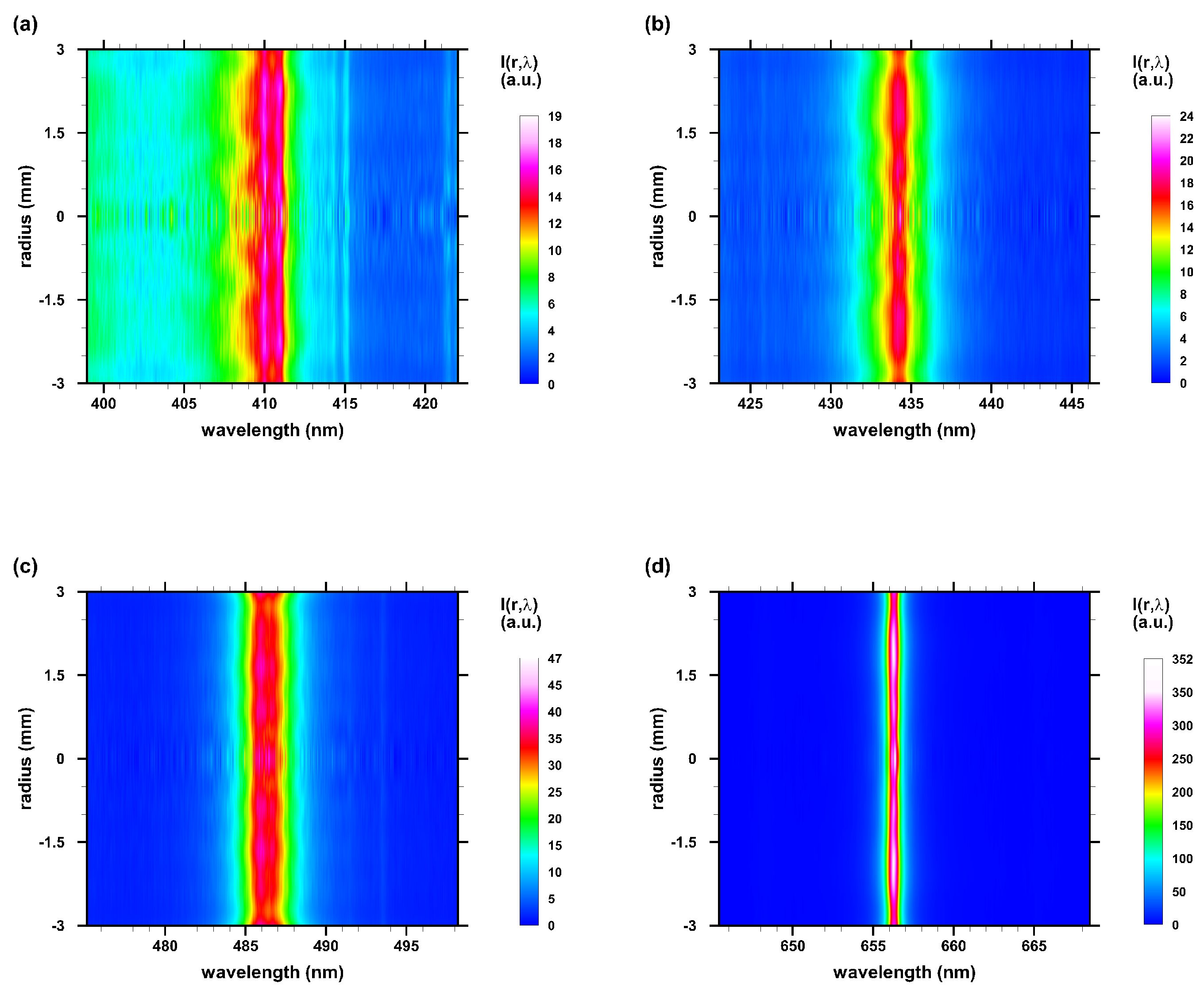
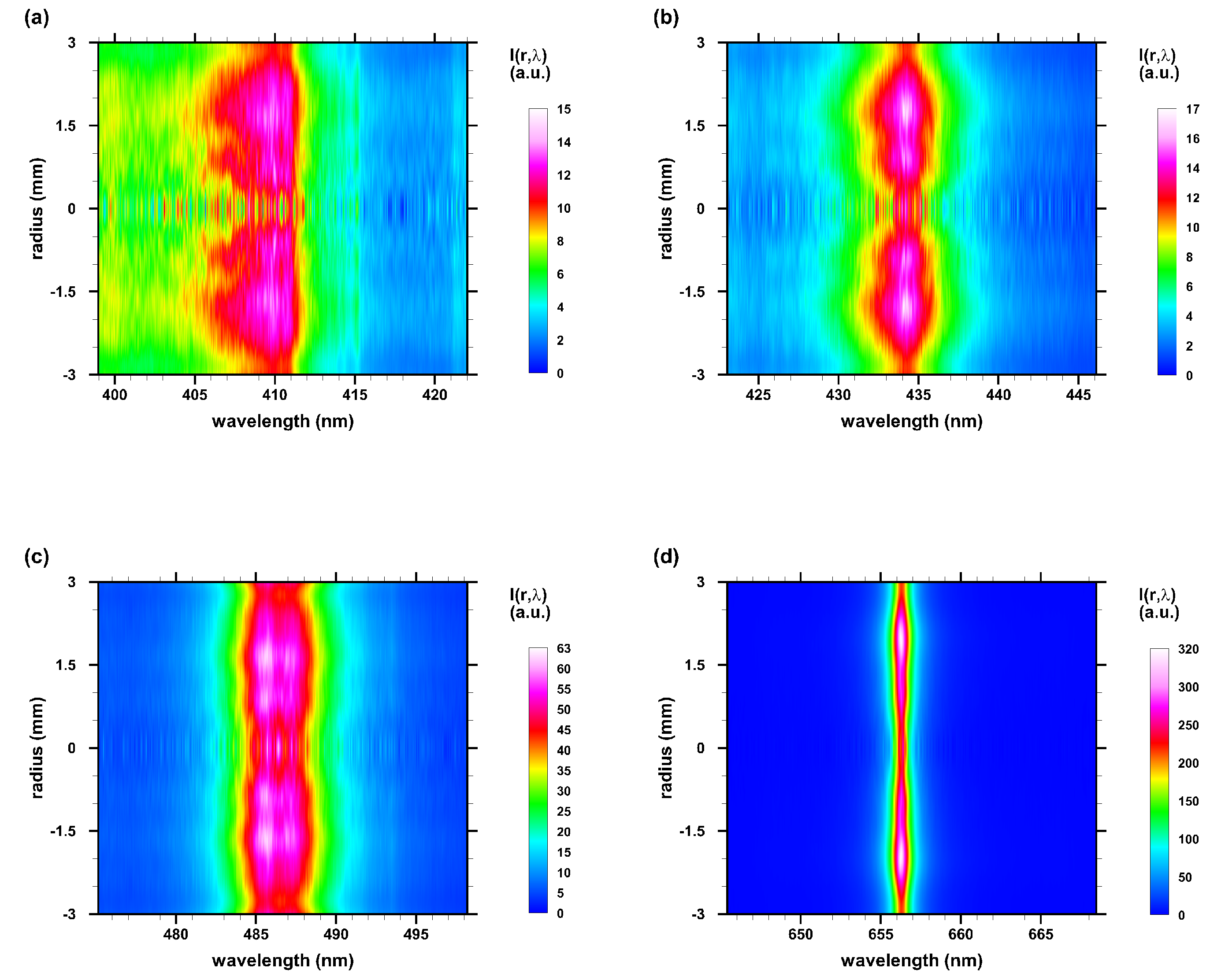
3.3. Abel-Inverted Spectral Maps
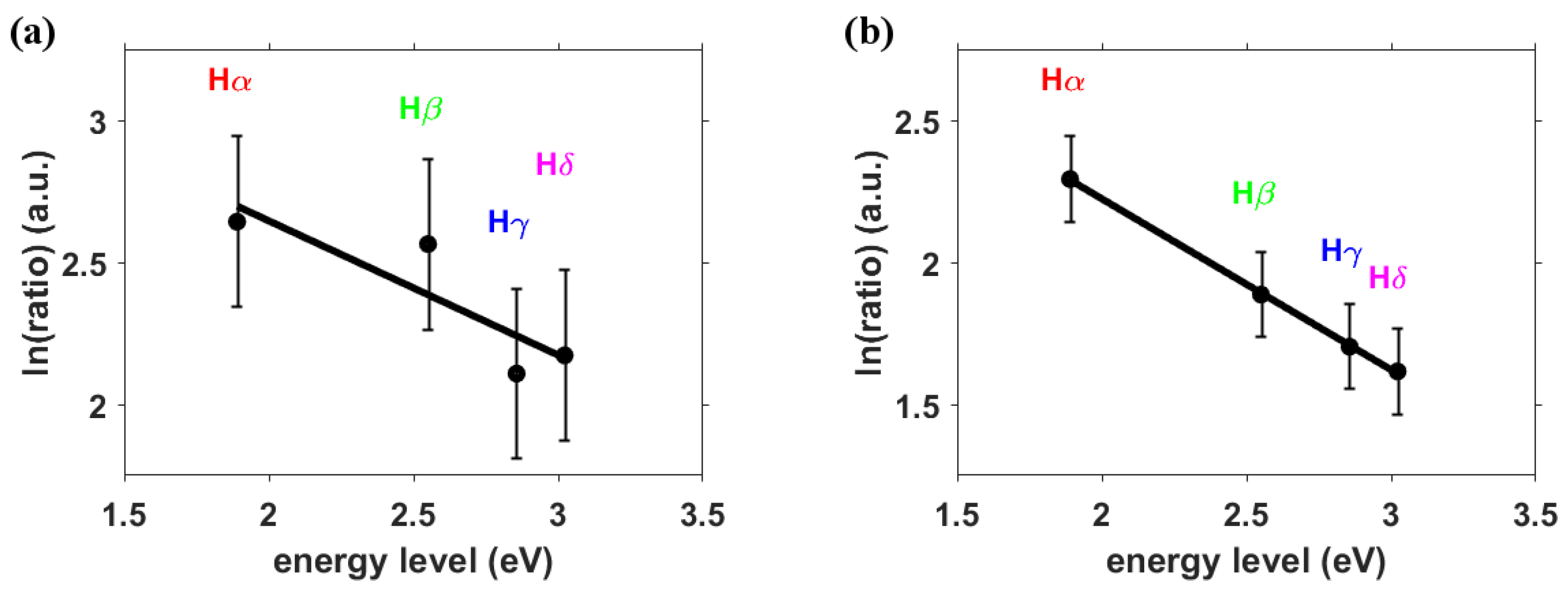
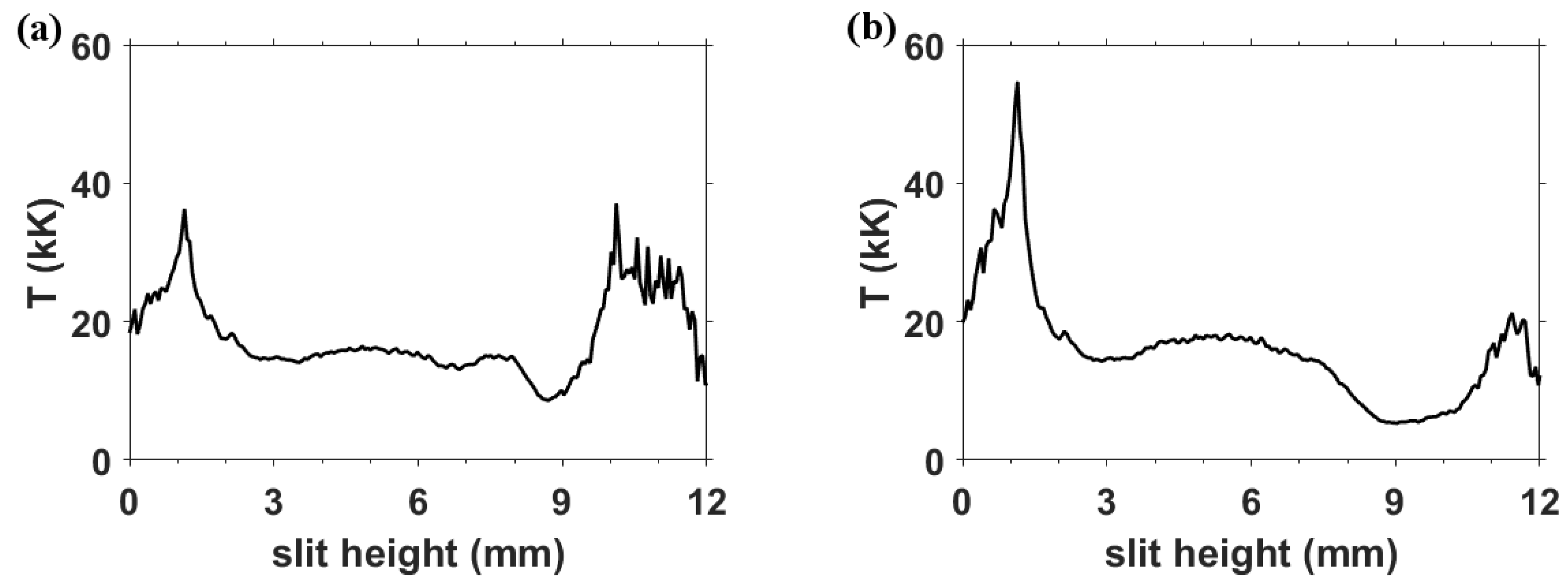
3.4. Electron Temperature and Density
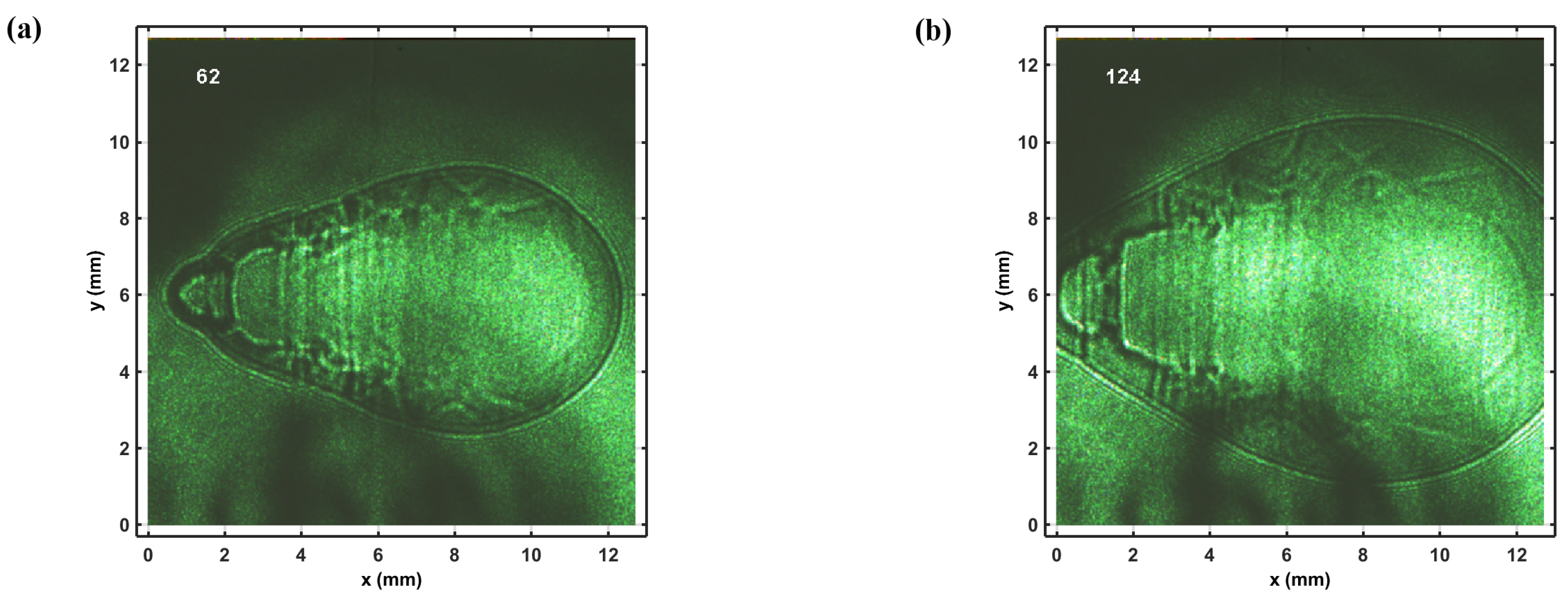
3.5. Plasma Expansion Dynamics
4. Discussion
Funding
Conflicts of Interest
References
- Miziolek, A.W.; Palleschi, V.; Schechter, I. (Eds.) Laser Induced Breakdown Spectroscopy; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Singh, J.P.; Thakur, S.N. (Eds.) Laser Induced Breakdown Spectroscopy; Elsevier Science: New York, NY, USA, 2019; in press. [Google Scholar]
- McWhirter, R.W.P. Spectral Intensities. In Plasma Diagnostic Techniques; Huddlestone, R.H., Leonard, S.L., Eds.; Academic Press: New York, NY, USA, 1965; pp. 201–264. [Google Scholar]
- Cristoforetti, G.; De Giacomo, A.; Dell’Aglio, M.; Legnaioli, S.; Tognoni, E.; Palleschi, V.; Omenetto, N. Local thermodynamic equilibrium in laser-induced breakdown spectroscopy: Beyond the McWhirter criterion. Spectrochim. Acta Part B At. Spectrosc. 2010, 65, 86–95. [Google Scholar] [CrossRef]
- Wiese, W.L. Line Broadening. In Plasma Diagnostic Techniques; Huddlestone, R.H., Leonard, S.L., Eds.; Academic Press: New York, NY, USA, 1965; pp. 265–317. [Google Scholar]
- Fujimoto, T. Plasma Spectroscopy; Clarendon Press: Oxford, UK, 2004. [Google Scholar]
- Kunze, H.-J. Introduction to Plasma Spectroscopy; Springer: New York, NY, USA, 2009; ISBN 978-3-642-02232-6. [Google Scholar]
- Pretzler, G.; Jäger, H.; Neger, T.; Philipp, H.; Woisetschläger, J. Comparison of Different Methods of Abel Inversion Using Computer Simulated and Experimental Side-On Data. Z. Naturforsch. 1992, 47a, 955–970. [Google Scholar]
- Parigger, C.G.; Drake, K.A.; Helstern, C.M.; Gautam, G. Laboratory Hydrogen-Beta Emission Spectroscopy for Analysis of Astrophysical White Dwarf Spectra. Atoms 2018, 6, 36. [Google Scholar] [CrossRef]
- Parigger, C.G.; Helstern, C.M.; Gautam, G.; Drake, K.A. Atomic and molecular line shapes in laboratory and selected astrophysical plasma. J. Phys. Conf. Ser. 2019, in press. [Google Scholar]
- Parigger, C.G.; Helstern, C.M.; Gautam, G. Laser-Plasma and Self-Absorption Measurements with Applications to Analysis of Atomic and Molecular Stellar Astrophysics Spectra. Atoms 2019, 7, 63. [Google Scholar] [CrossRef]
- Parigger, C.G.; Woods, A.C.; Witte, M.J.; Swafford, L.D.; Surmick, D.M. Measurement and Analysis of Atomic Hydrogen and Diatomic Molecular AlO, C2, CN, and TiO Spectra Following Laser-induced Optical Breakdown. J. Vis. Exp. 2014, 84, e51250. [Google Scholar]
- Parigger, C.G. Laser-plasma and stellar astrophysics spectroscopy. Contrib. Astron. Obs. Skaln. 2019. submitted. [Google Scholar]
- Tremblay, P.-E.; Bergeron, P. Spectroscopic Analysis of DA White dwarfs: Stark broadening of hydrogen lines including nonideal effects. Astrophys. J. 2009, 696, 1755–1770. [Google Scholar] [CrossRef]
- Gianninas, A.; Bergeron, P.; Ruiz, M.T. A spectroscopic survey and analysis of bright, hydrogen-rich white dwarfs. Astrophys. J. 2011, 743, 138–164. [Google Scholar] [CrossRef]
- Halenka, J.; Olchawa, W.; Madej, J.; Grabowski, B. Press. Shift Gravitational Redshift Balmer Lines White Dwarfs: Rediscussion. Astrophys. J. 2015, 808, 131–140. [Google Scholar] [CrossRef]
- Schrödinger, E. Quantisierung als Eigenwertproblem. Ann. Phys. 1926, 385, 437–490. [Google Scholar] [CrossRef]
- The Nobel Prize in Physics 1933. Available online: https://www.nobelprize.org/prizes/physics/1933/summary/ (accessed on 24 May 2019).
- Inglis, D.R.; Teller, E. Ionic depression of series limits in one-electron spectra. Astrophys. J. 1939, 90, 439–448. [Google Scholar] [CrossRef]
- Gigosos, M.A.; González, M.Á.; Cardeñoso, V. Computer simulated Balmer-alpha, -beta and -gamma Stark line profiles for non-equilibrium plasmas diagnostics. Spectrochim. Acta B At. Spectrosc. 2003, 58, 1489–1504. [Google Scholar] [CrossRef]
- Griem, H.R. Spectral Line Boradening by Plasmas; Academic Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Holtsmark, J. Über die Verbreiterung von Spectrallinien. Ann. Phys. 1919, 58, 577–630. [Google Scholar] [CrossRef]
- Greene, R.E., Jr. The Shift and Shape of Spectral Lines; Pergamon Press: Oxford, UK, 1961; Chapter 4; pp. 118–193. [Google Scholar]
- Oks, E. Diagnostics of Laboratory and Astrophysical Plasmas Using Spectral Lineshapes of One-, Two-, and Three-Electron Systems; World Scientific: Singapore, 2017; pp. 1–47. ISBN 9789814699075. [Google Scholar]
- Ivković, M.; Konjević, N.; Pavlović, Z. Hydrogen Balmer beta: The separation between line peaks for plasma electron density diagnostics and self-absorption test. J. Quant. Spectrosc. Radiat. Trans. 2015, 154, 1–8. [Google Scholar] [CrossRef]
- Parigger, C.G.; Gautam, G.; Surmick, D.M. Radial electron density measurements in laser-induced plasma from Abel inverted hydrogen Balmer beta line profiles. Int. Rev. At. Mol. Phys. 2015, 6, 43–55. [Google Scholar]
- Gautam, G.; Helstern, C.M.; Drake, K.A.; Parigger, C.G. Imaging of Laser-induced Plasma Expansion Dynamics in Ambient Air. Int. Rev. At. Mol. Phys. 2016, 7, 45–51. [Google Scholar]
- O’Haver, T.C. Command-line peak fitter for time-series signals. Version 9.0, January 2018; Mathworks File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/23611-peakfit-m (accessed on 4 June 2019).
- Beatrice Campanella, B.; Stefano Legnaioli, S.; Stefano Pagnotta, S.; Francesco Poggialini, F.; Palleschi, V. Shock Waves in Laser-Induced Plasmas. Atoms 2019, 7, 57. [Google Scholar]

| [s] | ||||||
|---|---|---|---|---|---|---|
| 1.50 | 7.5 ± 1.5 | 1.4 ± 0.8 | 5.0 ± 0.2 | 4.2 ± 0.25 | 1.2 ± 0.2 | 1.17 ± 0.1 |
| 3.25 | 5.8 ± 0.3 | 1.1 ± 0.2 | 3.2 ± 0.2 | 2.6 ± 0.25 | 0.8 ± 0.15 | 0.78 ± 0.1 |
| [s] | Average | ||||||
|---|---|---|---|---|---|---|---|
| 1.50 | 0.65 | 0.56 | 0.77 | 0.91 | 0.88 | 0.84 | 0.77 |
| 3.25 | 0.44 | 0.38 | 0.41 | 0.46 | 0.46 | 0.45 | 0.43 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parigger, C.G. Measurements of Gaseous Hydrogen–Nitrogen Laser-Plasma. Atoms 2019, 7, 61. https://doi.org/10.3390/atoms7030061
Parigger CG. Measurements of Gaseous Hydrogen–Nitrogen Laser-Plasma. Atoms. 2019; 7(3):61. https://doi.org/10.3390/atoms7030061
Chicago/Turabian StyleParigger, Christian G. 2019. "Measurements of Gaseous Hydrogen–Nitrogen Laser-Plasma" Atoms 7, no. 3: 61. https://doi.org/10.3390/atoms7030061
APA StyleParigger, C. G. (2019). Measurements of Gaseous Hydrogen–Nitrogen Laser-Plasma. Atoms, 7(3), 61. https://doi.org/10.3390/atoms7030061





