The Electron Impact Ionization Cross Sections of Methanol, Ethanol and 1-Propanol

Abstract

In the present investigation, the plane-wave Born approximation was employed to calculate the total ionization cross sections by electron impact of methanol, ethanol and 1-propanol from the threshold of ionization to 10 MeV. This method requires continuum generalized oscillator strengths (CGOSs). The two different semi-phenomenological expressions of CGOS, given by Mayol and Salvat and Weizsacker and Williams, along with approximated form of the continuum optical oscillator strength (COOS) by Khare et al. were used. Furthermore, the average of the above two CGOSs was also used. The calculated ionization cross sections were compared to the available previous theoretical results and experimental data. Out of three CGOSs, the present results with the average CGOS were found in good agreement with the available experimental results for all the considered molecules. Collision parameters C_RP were also calculated from 0.1 to 100 MeV and the calculations were found to be in excellent agreement with the experimental results of Reike and Prepejchal.

1. Introduction

The total ionization cross sections of organic and inorganic molecules have importance in many applications such as plasma modelling, astrophysics, atmospheric science and biological science [1,2,3]. The interaction of alcohols with electrons is a subject of interest because they are used as fuels which replace the traditional fossil fuels. Alcohols are efficient and renewable biofuels that can offer, as a solution to the problem of rural development, diversification of energy sources and fossil fuel saving. These fuels release fewer toxic gases and green-house gases on burning in internal combustion engines in comparison to fossil fuels. Plasma is created during the combustion of biofuels. Plasma modelling is required to make the theoretical model of car engines and the ionization cross sections may be used as an input parameter [4,5,6]. Furthermore, alcohols are detected in the interstellar space medium and also in the atmosphere of planets in the solar system. They play an important role in the chemistry of these environments [7]. Methanol, ethanol and propanol are very complex targets because methanol contains one atom of carbon, four atoms of hydrogen and one atom of oxygen, ethanol has two atoms of carbon, six atoms of hydrogen and one atom of oxygen and propanol contains three atoms of carbon, eight atoms of hydrogen and one atom of oxygen. Therefore, it is a very difficult task to evaluate the electron impact ionization cross sections theoretically. Many investigations were carried out for experimental and theoretical evaluations of the ionization cross sections of alcohols. Recently, Vinodkumar et al. [8] calculated the total ionization cross section for these molecules. They used the complex scattering potential ionization contribution method. Hudson et al. [9] calculated ionization cross section for all three alcohols from the ionization threshold to 300 eV using the Deutch–Mark (DM) and Kim binary-encounter-Bethe (BEB) models. Deutch et al. [10] calculated the ionization cross section of methanol. They used additive rule and weight factors, which depend on the atomic radii. Recently, Nixon’s group [6] measured the electron impact ionization cross section of methanol and ethanol energy range from 10 to 100 eV. They used a quadrupole mass spectrometer. Rejoub et al. [11] measured the absolute partial ionization cross section by electron impact of methanol, ethanol and propanol for energies from 13 to 1000 eV. The sum of the partial ionization cross sections of different fragments of a molecule provides the total ionization cross section. They used a time-of-flight mass spectrometer. Hudson et al. [9] measured the total ionization cross sections in the energy range 16 to 207 eV and Djuric et al. [12] also reported the total ionization cross sections of all three alcohols. Djuric et al. [12] employed the parallel plate method. Srivastava et al. [13] investigated the total ionization cross section of methanol using the quadrupole mass spectrometer filter and relative flow technique with He gas as the reference gas for energies from 20 to 500 eV. Pires et al. [14] also measured the total ionization cross sections by using a quadrupole mass spectrometer for 1-propanol. At relativistic energies, the theoretical calculations of the total ionization cross sections are also important to understanding the ionization process of molecules by electron impact. Rieke and Prepejchal [15] measured the total ionization cross sections for high energy ranges from 0.1 MeV to 2.7 MeV. A popular theoretical method to calculate the ionization cross sections for molecules is Kim binary-encounter-Bethe (BEB) model [16]. Kim and Rudd [16] combined the dipole interaction term of the plane-wave Born approximation, Bethe cross section and modified form of the Mott cross section to calculate the ionization cross section. In 1999, Khare et al. [17] proposed another binary-encounter-Bethe model to evaluate the total ionization cross sections of molecules. They started with the plane-wave Born approximation (PWBA) and employed the semi-phenomenological expression of Mayol and Salvat [18] for continuum generalized oscillator strengths (CGOSs). This expression of CGOS contains two terms, which depend on the continuum optical oscillator strengths (COOS). Furthermore, they took a simple approximated form of the COOS and also used some of the useful features of the Kim BEB model [16]. In the Khare BEB and Kim BEB models, expressions for the Mott cross section and Bethe cross sections are different but total ionization cross sections are very close to each other. The cross sections calculated by either model, the Khare BEB or Kim BEB model, are found in good agreement with the experimental data for a number of molecules. However, the cross sections calculated by using these models overestimate the experimental data for some heavy molecules. In the present investigation, we employed the Khare et al. [17] method by using the expression of CGOS by Weizsacker–Williams [18] instead of Mayol–Salvat [18] and the average of two CGOS, given by Weizsacker–Williams [18] and Mayol–Salvat [18]. To make the Khare BEB model simpler and suitable at relativistic energies, we replaced the incident kinetic energy, E, by $E^{\prime }=\frac{1}{2}m{v}^2$ in the upper limit of the integral of the Khare BEB-Bethe term [17], where m is the rest mass of the incident electron and v is the velocity of the incident electron. Furthermore, we modified the expression of recoil energy for relativistic energies for the Bethe term.

2. Theory

In the plane-wave Born approximation (PWBA), including longitudinal interaction through the static unretarded coulomb field and transverse interactions through the emission and reabsorption of virtual photons and also including exchange and relativistic corrections, the total ionization cross section of a molecule due to electron impact for the j_th molecular orbital is given by [17]

$${\sigma }_{jT}={\sigma }_{lj}+{\sigma }_{tj}$$

(1)

where ${\sigma }_{lj}$ is the cross section due to the longitudinal interaction and which is represented by

$${\sigma }_{lj}=\frac{4\pi a_0^2{R}^2}{\left[E^{\prime }+I+U\right]}\times {{\displaystyle \int }}_I^{W_{max}}\frac{1}{w}{{\displaystyle \int }}_{ln{\mathrm{Q}}_{min}}^{ln{\mathrm{Q}}_{max}}\frac{d{f}_j\left(w,Q\right)}{dw}{F}_{ex}\left(E,Q\right)d\left(lnQ\right)dw$$

(2)

and the cross section due to the transverse interaction is

$${\sigma }_{tj}=-\frac{4\pi a_0^{2}R}{E^{\prime }}{M}_j^2\left[\ln \left(1-{\beta }^2\right)+{\beta }^2\right]$$

(3)

The ionization cross section due to the transverse interaction, given by Equation (3), is significant only at high energies. In the above equations, R, $a_0$, F_ex, Q, w, I and U are the Rydberg energy, first Bohr radius, exchange factor, recoil energy, the energy lost by the incident electron in the collision, the ionization energy and the average kinetic energy of the bound electron, respectively. β is the ratio of the incident velocity, v, and the speed of light, c. $\frac{d{f}_j\left(w,Q\right)}{dw}$ is the CGOS per unit energy loss. $M_j^2$ is equal to the total dipole matrix squared measured in units of $a_0^2$ and given by

$$M_j^2={{\displaystyle \int }}_I^E\frac{R}{w}\frac{d{f}_j\left(w,0\right)}{dw}dw$$

(4)

where $\frac{d{f}_j\left(w,0\right)}{dw}$ is the COOS per unit energy range. The COOS may be experimentally known or computed. The values of the COOS are limited for the molecules. The simple analytic approximated form of the COOS, given by Khare et al. [17], is

$$\frac{d{f}_j\left(w,0\right)}{dw}=\frac{N{I}_j}{w^2}$$

(5)

where N is the occupation number of the molecular orbital.

For non-relativistic energies, the recoil energy is given by [17]

$$Q_{min,max}={\left(\sqrt{\mathrm{E}}\mp \sqrt{(E-w)}\right)}^2$$

(6)

It is very difficult to evaluate the CGOS quantum mechanically. Hence, Khare et al. [17] employed the semi phenomenological expression of Mayol and Salvat [18] for CGOS, which is expressed in terms of the COOS. It is given by

$${\left[\frac{d{f}_j\left(w,Q\right)}{dw}\right]}_{\mathrm{MS}}=h\left(Q\right)\mathsf{\delta }\left(w-Q\right)+\frac{d{f}_j\left(w,0\right)}{dw}\theta \left(w-Q\right)$$

(7)

where $\delta$ and $\theta$ are the delta and step functions, respectively, and

$$h\left(Q\right)={{\displaystyle \int }}_I^Q\frac{d{f}_j\left(w^{\prime },0\right)}{d{w}^{\prime }}d{w}^{\prime }$$

(8)

Another expression of CGOS, derived from the statistical model by Weizsacker–Williams [18], is given by Equation (38), by [18]

$${\left[\frac{d{f}_j\left(w,Q\right)}{dw}\right]}_{\mathrm{ww}}=h\left(Q\right)\mathsf{\delta }\left(w-Q\right)+\frac{d{f}_j\left(w,0\right)}{dw}\theta \left(\mathrm{I}-\mathrm{Q}\right)$$

(9)

where $h\left(Q\right)$ is same as given by Equation (8). Using Equations (5) and (7) with Equation (2), Khare and his associate [17] obtained the total ionization cross section due to longitudinal interaction in their BEB model given by [17] (omitting the subscript j)

$${\sigma }_l={\sigma }_{MK}+{\sigma }_{BK}$$

(10)

where the Mott cross section (the ionization cross section due to the hard collision), ${\sigma }_M,$ is given by

$${\sigma }_{MK}=\frac{AN}{\left[E^{\prime }+I+U\right]I}\left[\begin{array}{c}1-\frac{2}{t+1}+\frac{t-1}{2t^2}+\frac{5-t^2}{2{\left(t+1\right)}^2}\\ -\frac{1}{t\left(t+1\right)}-\frac{t+1}{t^2}\ln (\frac{t+1}{2})\end{array}\right]$$

(11)

where $t=E^{\prime }/I$ and $A=4\pi a_0^2{R}^2.$ The Bethe cross section (the ionization cross section due to the soft collision)$, {\sigma }_{BK},$ is

$${\sigma }_{BK}=\frac{AIN}{\left[E^{\prime }+I+U\right]}{{\displaystyle \int }}_I^E\frac{1}{w^3}\ln (\frac{w}{Q_{min}})dw$$

(12)

In the present investigation, we put the CGOS by Weizsacker–Williams from Equation (9) in Equation (2) and follow Khare et al. [17]. We get same expression for the Mott cross section but a different one for the Bethe cross section. The present Bethe cross section is obtained as

$${\sigma }_{BP}=\frac{ANI}{\left[E^{\prime }+I+U\right]}{{\displaystyle \int }}_I^E\frac{1}{w^3}\ln (\frac{I}{Q_{min}})dw$$

(13)

Similarly, with the average CGOS given by Equations (7) and (9), the Bethe cross section is obtained as

$${{\sigma }^{\prime }}_{BP}\left(Ave.\right)=\frac{ANI}{\left[E^{\prime }+I+U\right]}{{\displaystyle \int }}_I^E\frac{1}{w^3}\ln \left(\frac{\sqrt{\left(Iw\right)}}{Q_{min}}\right)dw$$

(14)

The above expression may be obtained by taking the average of Equations (12) and (13).

Now we replace E by $E^{\prime }$ in upper limit of integral of Equations (12)–(14) and in the expression of recoil energy, $Q_{min}$, given by Equation (7). With these two modifications, we integrate the Equations (12)–(14) and obtain

$${\sigma }_{BPK}=\frac{AN}{2\left[E^{\prime }+I+U\right]I}\left[\frac{1}{2}\left(1-\frac{1}{t^2}\right)-X\right]$$

(15a)

where the term X is given by

$$\begin{gathered} \mathrm{X}=2ln\left(\sqrt{t}-\sqrt{\left(t-1\right)}\right)+\frac{1}{2t^2}\left\{\begin{array}{c}1-\frac{1}{2}{\left(\frac{t}{t-\sqrt{t\left(t-1\right)}}\right)}^2\\ +\frac{1}{2}\left(\frac{t}{t+\sqrt{t\left(t-1\right)}}\right)-\left(\frac{t}{t-\sqrt{t\left(t-1\right)}}\right)\\ -\frac{3}{4}ln\left(\frac{t+\sqrt{t\left(t-1\right)}}{t-\sqrt{t\left(t-1\right)}}\right)\end{array}\right\} \\ {\sigma }_{BP}=\frac{AN}{2\left[E^{\prime }+I+U\right]I}\left[\frac{1}{t^2}ln\left(t\right)-X\right] \end{gathered}$$

(15b)

$${{\sigma }^{\prime }}_{BP}\left(Ave.\right)=\frac{AN}{2\left[E^{\prime }+I+U\right]I}\left[\frac{1}{4}\left(1-\frac{1}{t^2}\right)+\frac{1}{2t^2}ln\left(t\right)-X\right]$$

(15c)

Now, the present Khare BEB cross section,${\sigma }_{TPK}$, present cross section,${\sigma }_{TP}$ (obtained by using CGOS of Weizsacker–Williams), and the present average cross section (obtained by using the average CGOS), ${{\sigma }^{\prime }}_{TP}\left(Ave.\right),$ for each molecular orbital are

$${\sigma }_{TPK}={\sigma }_{BKH} + {\sigma }_{MK }+ {\sigma }_{t }$$

(16a)

$${\sigma }_{TP}={\sigma }_{BP} + {\sigma }_{MK }+ {\sigma }_t$$

(16b)

$${{\sigma }^{\prime }}_{TP}\left(Ave.\right)={\sigma }_B\left(Ave.\right) + {\sigma }_{MK }+ {\sigma }_{t }$$

(16c)

where ${\sigma }_{BPK},{\sigma }_{BP,} {{\sigma }^{\prime }}_B\left(Ave.\right), {\sigma }_{MK, }\mathrm{and} {\sigma }_t$ are given by Equations (15a), (15b), (15c), (11) and (3), respectively. A summation of cross sections $\{{\sigma }_{TPK} or {\sigma }_{TP} or {{\sigma }^{\prime }}_{TP}\left(Ave.\right)\}$ over all molecular orbitals gives the total ionization cross section for a molecule. The calculated total ionization cross sections are represented in Table 1. Rieke and Prepejchal [15] measured the total ionization cross sections of a number of molecules by electron impact in the energy range 0.1 and 2.7 MeV. They fitted their total ionization cross sections, in terms of two collisional parameters, ${\mathrm{C}}_{\mathrm{RP}}$ and $M^2,$ by Bethe cross section, given by

$${\sigma }_T=4\pi {\left(\frac{\hslash }{mc}\right)}^2\frac{1}{{\beta }^2}\left[M^2\left\{\ln \left(\frac{{\beta }^2}{1-{\beta }^2}\right)-{\beta }^2\right\}+{\mathrm{C}}_{\mathrm{RP}}\right]$$

(17)

Table 1. This table represents the calculated present Khare BEB cross sections ${\sigma }_{TPK}$, present cross sections ${\sigma }_{TP}$ (obtained by using CGOS of Weizsacker–Williams), and the present average cross sections (obtained by using the average CGOS) ${{\sigma }^{\prime }}_{TP}\left(Ave\right),$ using Equations (16a–c).

		CH3OH			C2H5OH			C3H7OH
E(eV)	$${\mathit{\sigma }}_{\mathit{T}\mathit{P}\mathit{K}}{(\mathbf{\AA })}^2$$	$${\mathit{\sigma }}_{\mathit{T}\mathit{P}}{(\mathbf{\AA })}^2$$	$${\mathit{\sigma }}_{\mathit{T}\mathit{P}}^{\prime }\left(\mathit{A}\mathit{v}\mathit{e}\right){(\mathbf{\AA })}^2$$	$${\mathit{\sigma }}_{\mathit{T}\mathit{P}\mathit{K}}{(\mathbf{\AA })}^2$$	$${\mathit{\sigma }}_{\mathit{T}\mathit{P}}{(\mathbf{\AA })}^2$$	$${\mathit{\sigma }}_{\mathit{T}\mathit{P}}^{\prime }\left(\mathit{A}\mathit{v}\mathit{e}\right){(\mathbf{\AA })}^2$$	$${\mathit{\sigma }}_{\mathit{T}\mathit{P}\mathit{K}}{(\mathbf{\AA })}^2$$	$${\mathit{\sigma }}_{\mathit{T}\mathit{P}}{(\mathbf{\AA })}^2$$	$${\mathit{\sigma }}_{\mathit{T}\mathit{P}}^{\prime }\left(\mathit{A}\mathit{v}\mathit{e}\right){(\mathbf{\AA })}^2$$
15	0.415	0.35	0.383	0.709	0.604	0.656	1.061	0.901	0.981
20	1.478	1.218	1.348	2.478	2.038	2.258	3.521	2.892	3.207
30	3.263	2.655	2.959	5.218	4.244	4.731	7.279	5.921	6.6
40	4.256	3.484	3.864	6.709	5.496	6.102	9.292	7.614	8.453
50	4.805	3.969	4.348	7.499	6.201	6.85	10.33	8.544	9.437
60	5.091	4.242	4.666	7.89	6.581	7.235	10.82	9.031	9.928
70	5.223	4.385	4.804	8.051	6.766	7.409	11.01	9.258	10.13
80	5.262	4.447	4.855	8.077	6.833	7.455	11.02	9.326	10.17
90	5.244	4.458	4.851	8.021	6.825	7.423	10.92	9.296	10.11
100	5.191	4.435	4.813	7.916	6.77	7.343	10.76	9.205	9.981
200	4.243	3.732	3.988	6.367	5.605	5.986	8.574	7.551	8.063
300	3.475	3.098	3.286	5.18	4.62	4.9	6.949	6.2	6.574
400	2.939	2.641	2.789	4.365	3.923	4.144	5.843	5.254	5.549
500	2.551	2.304	2.426	3.779	3.415	3.597	5.052	4.567	4.81
600	2.257	2.047	2.15	3.338	3.029	3.184	4.459	4.047	4.253
700	2.028	1.844	1.934	2.995	2.726	2.86	3.997	3.639	3.818
800	1.843	1.681	1.759	2.72	2.481	2.6	3.628	3.311	3.469
900	1.691	1.545	1.615	2.494	2.28	2.387	3.325	3.04	3.183
1 × 103	1.564	1.432	1.494	2.304	2.111	2.207	3.072	2.814	2.943
2 × 103	0.912	0.843	0.874	1.34	1.24	1.29	1.784	1.65	1.717
4 × 103	0.517	0.482	0.499	0.759	0.707	0.733	1.009	0.94	0.975
6 × 103	0.368	0.344	0.356	0.54	0.505	0.523	0.718	0.672	0.695
8 × 103	0.289	0.271	0.28	0.424	0.397	0.411	0.563	0.528	0.546
10 × 103	0.239	0.225	0.232	0.351	0.33	0.34	0.466	0.438	0.452
20 × 103	0.134	0.126	0.13	0.196	0.185	0.19	0.26	0.246	0.253
40 × 103	0.076	0.072	0.074	0.111	0.105	0.108	0.148	0.14	0.144
60 × 103	0.055	0.053	0.054	0.081	0.077	0.079	0.108	0.102	0.105
80 × 103	0.045	0.043	0.044	0.066	0.062	0.064	0.087	0.083	0.085
0.1 × 106	0.038	0.036	0.037	0.056	0.053	0.055	0.075	0.071	0.073
0.2 × 106	0.025	0.024	0.025	0.037	0.035	0.036	0.049	0.047	0.048
0.4 × 106	0.019	0.018	0.018	0.028	0.026	0.027	0.037	0.035	0.036
0.6 × 106	0.017	0.016	0.017	0.025	0.024	0.024	0.033	0.032	0.032
0.8 × 106	0.016	0.016	0.016	0.024	0.023	0.023	0.032	0.03	0.031
1 × 106	0.016	0.015	0.016	0.023	0.022	0.023	0.031	0.03	0.03
5 × 106	0.017	0.017	0.017	0.025	0.024	0.025	0.033	0.032	0.033
10 × 106	0.018	0.018	0.018	0.027	0.026	0.027	0.036	0.035	0.035

Putting Equation (3) in Equation (16c) and equating the result to Equation (17), we get

$${\mathrm{C}}_{\mathrm{RP}}=\frac{R{E}^{\prime }}{\mathrm{A}}{\displaystyle \sum }_{\mathrm{j}}\left({\sigma }_B\left(Ave.\right)+{\sigma }_M\right)-M^{2}ln{\beta }^2$$

(18)

where, $M^2={{\displaystyle \sum }}_j{M}^2$ and summation is over all molecular orbitals. We took $E^{\prime }+I+U=E^{\prime }$ at relativistic energies. $M^2$ is calculated from Equation (4), using the expression of the COOS, given by Equation (5). Calculated values of M² and C_RP are tabulated in Table 2.

Table 2. The present calculated values of collisional parameter C_RP and M² (in unit of $a_0^2$) are shown along with the experimental values, given by Rieke and Prepejchal [15]. The values of C_RP are calculated at incident energies 0.1, 1, 10 and 100 MeV using Equation (18).

Molecules	CRP (at 1MeV)	CRP (at 1MeV)	CRP (at 10MeV)	CRP (at 102MeV)	CRP (Exp. Rieke [15])	Present M2	M2(Exp. Rieke [15])
CH3OH	66.77	66.80	66.80	66.80	66.40	5.9	6.22
C2H5OH	97.87	97.89	97.89	97.89	97.66	8.65	9.94
1-C3H7OH	129.86	129.91	129.91	129.92	--------	11.46	-------

3. Results and Discussion

The theoretical methods described in the above section are employed to calculate the total ionization cross sections of three molecules—methanol, ethanol and 1-propanol. The required molecular parameters ionization energies, I, kinetic energies of bound electrons, U, and occupation numbers, N, are taken from Irikura [19]. The present cross sections, ${\sigma }_{TK},{\sigma }_{TP}\mathrm{and}{{\sigma }^{\prime }}_{TP}\left(Ave.\right)$, are tabulated in Table 1. It is clear from Table 1 that the present theoretical cross sections,${\sigma }_{TP}$, lie below ${{\sigma }^{\prime }}_{TP}\left(ave.\right)$. However,${\sigma }_{TK}$ are greater than ${{\sigma }^{\prime }}_{TP}\left(ave.\right)$. The Figure 1, Figure 2 and Figure 3 show the present cross sections, ${\sigma }_{TK}$, ${\sigma }_{TP}$ and ${{\sigma }^{\prime }}_{TP}\left(Ave.\right)$, along with the previous theoretical and experimental results available in literature for methanol, ethanol and 1-propanol at energies from the ionization threshold to 2 keV, respectively. We used Equation (16a–c) to calculate the present total ionization cross sections.

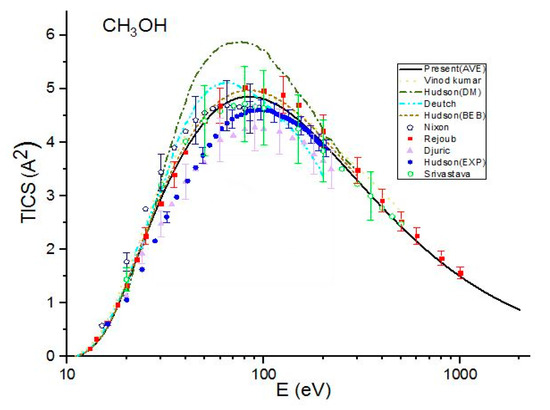
Figure 1. Total ionization cross sections (TICSs) for CH3OH in Å^2, the solid line represents the present (Ave.) results, the dash line represents the theoretical results measured by Vinod kumar et al. [8], the dash dot line represents the theoretical results measured by Hudson et al. [9] using Deutch–Mark (DM) formulism, the short dash dot line represents the theoretical results measured by Deutch et al. [10], the dot line represents the BEB calculations by Hudson et al. [9], the dash dot dot line represents the present (Khare BEB), and the short dash line represents the present results. Filled triangles, filled squares open circles, filled pentagons and open hexagons are the experimental results of Djuric et al. [11], Hudson et al. [9], Nixon et al. [6], Rejoub et al. [12] and Srivastava et al. [13], respectively.

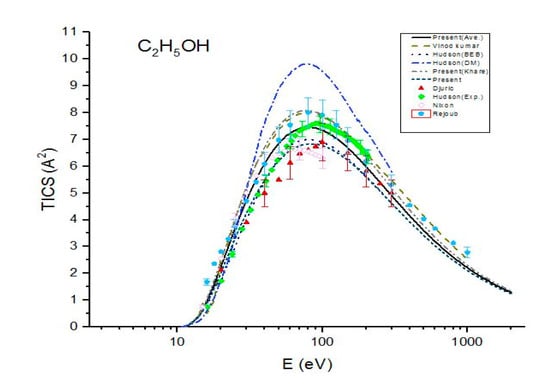
Figure 2. Total ionization cross sections (TICS) for C₂H₅OH in ${\AA }^2$, the solid line represents the present (Ave.) results, the dash line represents the theoretical results measured by Vinodkumar et al. [8], the dash dot line represents the theoretical results measured by Hudson et al. [9] using DM formulism, the dot line represents the BEB calculations by Hudson et al. [9], the dash dot dot line represents the present (Khare BEB), the short dash line represents the present results. Filled triangles, filled squares, open circles and filled pentagons are the experimental results of Djuric et al. [11], Hudson et al. [9], Nixon et al. [6] and Rejoub et al. [12], respectively.

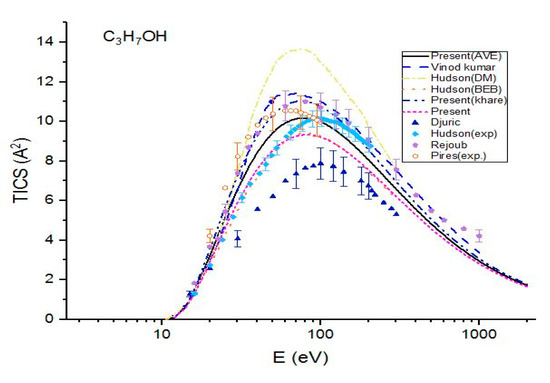
Figure 3. Total ionization cross sections (TICS) for C₃H₇OH in ${\AA }^2$, the solid line represents the present (Ave.) results, the dash line represents the theoretical results measured by Vinod kumar et al. [8], the dash dot represents the theoretical results measured by Hudson et al. [9] using DM formulism, the dot line represents the BEB calculations of Hudson et al. [9], the dash dot dot line represents the present (Khare BEB), the short dash represents the present results. Filled triangles, filled squares, filled pentagons and open hexagonals are the experimental results of Djuric et al. [11], Hudson et al. [9] Rejoub et al. [12] and Pires et al. [14], respectively.

Figure 1 shows a comparison of present cross sections with other previous theoretical results and experimental data for methanol. The present Khare BEB cross sections, ${\sigma }_{TPK}$, are in good agreement with the experimental results of Rejoub et al. [11] throughout the energy range. They are also in good agreement with the experimental data measured by Nixon et al. [6] up to E = 60 eV but are greater than experimental values for E > 60. However, ${\sigma }_{TPK}$ overestimate the experimental results measured by Hudson et al. [9], Srivastava et al. [13] and Djuric et al. [12]. A good agreement is found among the present calculations with average CGOS ${{\sigma }^{\prime }}_{TP}\left(Ave.\right)$, BEB calculations by Hudson [9], theoretical calculations by Vinodkumar et al. [8] and the experimental results measured by Srivastava et al. [13] and Rejoub et al. [11] over the full energy range studied by them. The cross sections ${{\sigma }^{\prime }}_{TP}\left(Ave.\right)$ are also in good agreement with the experimental data measured by Nixon et al. [6], except near threshold energy. ${{\sigma }^{\prime }}_{TP}\left(Ave.\right)$ over-estimate the experimental data of Hudson et al. [9] for E < 90 eV and tend to coincide with experimental values at higher energies. In the present calculations with the CGOS by Weizsacker–Williams, ${\sigma }_{TP}$ underestimate the experimental results of Rejoub et al. [11], Nixon et al. [6] and Srivastava et al. [13]. However, they are in good agreement with those measured by Hudson et al. [9] and Djuric et al. [12]. The theoretical results of Deutch et al. [10] do not agree with the present calculations as well as other reported results except near threshold energy.

In Figure 2, present ionization cross sections are compared with the previous theoretical results and experimental data for ethanol. Figure 2 shows a good agreement among the present cross sections ${\sigma }_{TPK}$, experimental measurements of Rejoub et al. [11] and theoretical results of Vinodkumar et al. [8] for the entire energy range. However, they overestimate the other reported experimental data. The cross sections ${{\sigma }^{\prime }}_{TP}\left(Ave.\right)$ are in good agreement with the experimental results measured by Rejoub et al. [11] and Hudson et al. [9]. They are also in good agreement with the experimental data measured by Nixon et al. [6] within 10% up to E = 70 eV but are greater than the experimental values by 15% at higher energies. A good agreement is found among the total ionization cross sections ${\sigma }_{TP}$, experimental data of Nixon et al. [6] and Djuric et al. [12]. ${\sigma }_{TP}$ also show a good agreement with the experimental data Hudson et al. [9] up to E = 49 eV but they are lower than these experimental data for E > 70 eV. Figure 2 shows an excellent agreement between ${\sigma }_{TP}$ and BEB calculations of Hudson [9].

The present calculations were compared with the theoretical results and experimental data in the Figure 3 for 1-propanol. The cross sections ${\sigma }_{TPK }\mathrm{consistently}$ show a good agreement with Rejoub et al. [11] and Vinodkumar et al. [8] over the full range of incident energies. However, they are greater than the experimental data measured by Hudson et al. [9]. The theoretical cross sections ${{\sigma }^{\prime }}_{TP}\left(Ave.\right)$ are greater than those measured by Hudson et al. [9] for E < 90 eV but are smaller than the experimental values for higher incident energies. However, the difference between these two sets is not large. The maximum value of cross section ${{\sigma }^{\prime }}_{TP}\left(Ave.\right)$ observed was 10.17 ${\AA }^2$ at E = 77 eV, while the maximum cross section measured by Hudson et al. [9] was 10.15 ${\AA }^2$ at E = 97 eV. The difference between the two maximum cross sections is very small. Except near the ionization threshold, the experimental data of Pires et al. [14] lie between two curves, i.e.$, {\sigma }_{TPK }\& {{\sigma }^{\prime }}_{TP}\left(Ave.\right)$. The cross sections ${\sigma }_{TP}$ are in excellent agreement with the experimental results measured by Hudson et al. [9] up to E = 69 eV, but they under-estimate the experimental values by 14% at higher energies. Again, ${\sigma }_{TP}$ show an excellent agreement with BEB results measured by Hudson et al. [9]. All three present calculations as well as other theoretical calculations and experimental ionization cross sections are higher than experimental data measured by Djuric et al. [12]. The DM calculations of Hudson et al. [9] are higher than present calculations as well as other theoretical and experimental data for all three molecules. In a comparison of the present three cross sections, it was observed that the total ionization cross sections ${{\sigma }^{\prime }}_{TP}\left(Ave.\right)$ calculated by using average CGOS are better than other two for all three alcohols in the energy range from the ionization threshold to 2 keV.

Figure 4, Figure 5 and Figure 6 show the present total ionization cross sections ${{\sigma }^{\prime }}_{TP}\left(Ave.\right)$ along with the experimental data measured by Rieke and Prepejchal [15] available in a range of 0.1 to 2.7 MeV. At relativistic energies, the cross sections ${{\sigma }^{\prime }}_{TP}\left(Ave.\right)$ are very close to ${\sigma }_{TP}$ and ${\sigma }_{TK}$, so the cross sections ${\sigma }_{TP}$ and ${\sigma }_{TK}$ are not shown in the figures. The collisional parameter C_RP and M² are listed in Table 2. We have calculated the collisional parameters C_RP by using Equation (18). The values of C_RP are unchanged on increasing the incident energies as expectations for all three molecules. Figure 4 shows a comparison between the present results and the experimental data of Rieke and Prepejchal [15] for methanol. The present ionization cross sections ${{\sigma }^{\prime }}_{TP}\left(Ave.\right)$ were found in excellent agreement with measured data. The present calculated values of C_RP and M² are 66.8 and 5.9, respectively. The present value of M² is lower than the experimental value by 5%. However, the value of C_RP is very close to the experimental value of Reike and Prapejchal [15]. A comparison between the present total ionization cross sections ${{\sigma }^{\prime }}_{TP}\left(Ave.\right)$ and the experimental data of Reike and Prapejchal [15] are shown in Figure 5 for ethanol. The present cross sections ${{\sigma }^{\prime }}_{TP}\left(Ave.\right)$ are in good agreement with experimental data within 2.6%. The present calculated values of C_RP and M² are 97.89 and 8.65, respectively. The present value of M² is lower by 13% than the experimental value. However, present C_RP is consistently very close to the experimental value of Rieke and Prepejchal [15]. Figure 6 shows the present calculations by using the average CGOS for 1-propanol. For this molecule, no other data are available for comparison. However, from our previous results, we are confident that the present values are quite reasonable.

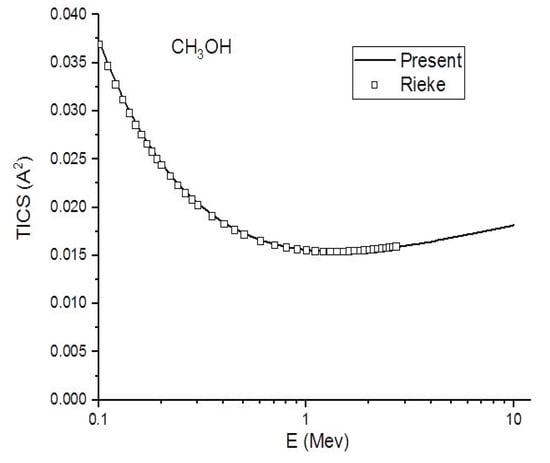
Figure 4. In this figure, we compare the present (Ave.) (-) total ionization cross section in ${\AA }^2$ to the experimental (☐) results of Rieke and Prepejchal [15] for CH₃OH at a high energy range.

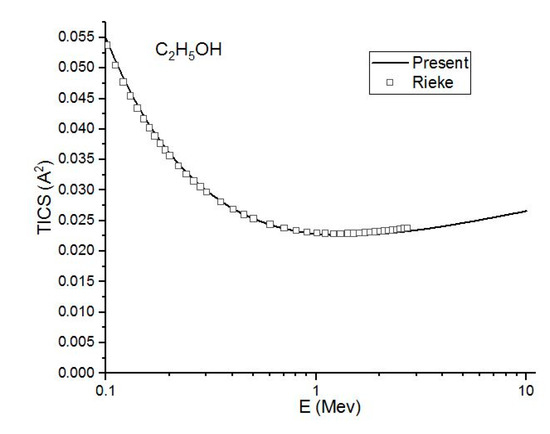
Figure 5. In this figure, we compare the present (Ave.) (-) theoretical total ionization cross sections in ${\AA }^2$ to the experimental (☐) results of Rieke and Prepejchal [15] for C₂H₅OH at a high energy range.

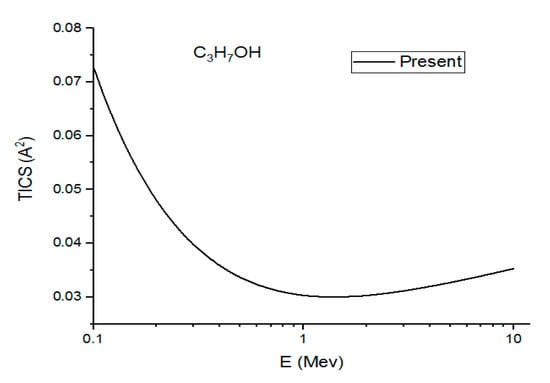
Figure 6. In this figure, we plot the present (Ave.) total ionization cross sections (TICS) in ${\AA }^2$ v/s a high energy range for C₃H₇OH.

4. Conclusions

Three different CGOSs, given by Mayol and Salvat [18], Weizsacker and Williams [18] and an average of the above two CGOSs, along with PWBA [17], were employed to calculate total ionization cross sections for methanol, ethanol and 1-propanol from an ionization threshold to 10 MeV. The present calculations with the average expression of CGOS provide better results that improve the agreement between theory and experiments for considered molecules. At relativistic energies, the calculated ionization cross sections ${{\sigma }^{\prime }}_{TP}\left(Ave.\right)$ are also found in good agreement with the experimental data of Rieke and Prepejchal [15] for methanol and ethanol. For a high incident energy range, these are the first calculations for methanol, ethanol and 1-propanol to the best of our knowledge. The application of the present method to calculate the total ionization cross sections of other heavy molecules is of interest.