Towards the Search for Thallium Nuclear Schiff Moment in Polyatomic Molecules: Molecular Properties of Thallium Monocyanide (TlCN)
Abstract
1. Introduction
2. Computational Methods
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Isaev, T.A.; Zaitsevskii, A.V.; Eliav, E. Laser-coolable polyatomic molecules with heavy nuclei. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 225101. [Google Scholar] [CrossRef]
- Norrgard, E.B.; Barker, D.S.; Eckel, S.P.; Fedchak, J.A.; Klimov, N.N.; Scherschligt, J. Nuclear-Spin Dependent Parity Violation in Optically Trapped Polyatomic Molecules. arXiv, 2018; arXiv:1812.00064. [Google Scholar]
- Kozyryev, I.; Hutzler, N. Precision measurement of time-reversal symmetry violation with laser-cooled polyatomic molecules. Phys. Rev. Lett. 2017, 119, 133002. [Google Scholar] [CrossRef] [PubMed]
- Shafer-Ray, N.E. Possibility of 0-g- factor paramagnetic molecules for measurement of the electron’s electric dipole moment. Phys. Rev. A 2006, 73, 034102. [Google Scholar] [CrossRef]
- DeMille, D. CeNTREX Experiment (DAMOP 2017 Report). 2017. Available online: http://meetings.aps.org/Meeting/DAMOP17/Session/B2.3 (accessed on 29 April 2019).
- Norrgard, E.B.; Edwards, E.R.; McCarron, D.J.; Steinecker, M.H.; DeMille, D.; Alam, S.S.; Peck, S.K.; Wadia, N.S.; Hunter, L.R. Hyperfine structure of the B3Π1 state and predictions of optical cycling behavior in the x→B transition of TlF. Phys. Rev. A 2017, 95, 062506. [Google Scholar] [CrossRef]
- Lanzisera, D.V.; Andrews, L. Reactions of Laser-Ablated Al, Ga, In, and Tl Atoms with Hydrogen Cyanide in Excess Argon. Matrix Infrared Spectra and Density Functional Theory Calculations on New Cyanide and Isocyanide Products. J. Phys. Chem. A 1997, 101, 9660. [Google Scholar] [CrossRef]
- Essers, R.; Tennyson, J.; Wormer, P. An SCF potential energy surface for Lithium Cyanide. Chem. Phys. Lett. 1982, 89, 223. [Google Scholar] [CrossRef]
- Van Vaals, J.; Meerts, W.L.; Dymanus, A. Structure of sodium cyanide by molecular beam electric resonance spectroscopy. J. Chem. Phys. 1982, 77, 5245. [Google Scholar] [CrossRef]
- Marsden, C. Ab initio correlated potential energy surfaces for monomeric sodium and potassium cyanides. J. Chem. Phys. 1982, 76, 6451. [Google Scholar] [CrossRef]
- Lee, D.-K.; Lim, I.S.; Lee, Y.S.; Hagebaum-Reignier, D.; Jeung, G.-H. Molecular properties and potential energy surfaces of the cyanides of the groups 1 and 11 metal atoms. J. Chem. Phys. 2007, 126, 244313. [Google Scholar] [CrossRef]
- Van Vaals, J.; Meerts, W.L.; Dymanus, A. Molecular beam electric resonance study of KCN, K13CN and KC15N. J. Mol. Spectrosc. 1984, 106, 280. [Google Scholar] [CrossRef]
- Törring, T.; Bekooy, J.; Meerts, W.L.; Hoeft, J.; Tiemann, E.; Dymanus, A. Rotational spectrum and structure of KCN. J. Chem. Phys. 1980, 73, 4875. [Google Scholar] [CrossRef]
- Petrie, S. Trends in M (CN) isomerism: A computational study of monocyanides of the main-group third row atoms. Phys. Chem. Chem. Phys. 1999, 1, 2897. [Google Scholar] [CrossRef]
- Hinds, E.A.; Sandars, P.G.H. Electric dipole hyperfine structure of TIF. Phys. Rev. A 1980, 21, 471. [Google Scholar] [CrossRef]
- Available online: http://www.qchem.pnpi.spb.ru (accessed on 29 April 2019).
- Vissher, L.; Lee, T.J.; Dyall, K.G. Formulation and implementation of a relativistic unrestricted coupled-cluster method including noniterative connected triples. J. Chem. Phys. 1996, 105, 8769. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007. [Google Scholar] [CrossRef]
- Zaitsevskii, A.; Eliav, E. Padé´ extrapolated effective Hamiltonians in the Fock space relativistic coupled cluster method. Int. J. Quantum Chem. 2018, 118, e25772. [Google Scholar] [CrossRef]
- Petersson, G.A.; Frisch, M.J. A journey from generalized valence bond theory to the full CI complete basis set limit. J. Phys. Chem. A 2000, 104, 2183. [Google Scholar] [CrossRef]
- Mourik, V.T.; Wilson, A.K.; Peterson, K.A.; Woon, D.E.; Dunning, J.T.H. Advances in Quantum Chemistry; Elsevier: Amsterdam, The Netherlands, 1998; Volume 31, pp. 105–135. [Google Scholar]
- van Wüllen, C. A quasirelativistic two-component density functional and hartree-fock program. Zeitschrift für Physikalische Chemie 2010, 224, 413–426. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158. [Google Scholar] [CrossRef]
- Godbout, N.; Salahub, D.R.; Andzelm, J.; Wimmer, E. Optimization of Gaussian-type basis sets for local spin density functional calculations. Part I. Boron through neon, optimization technique and validation. Can. J. Chem. 1992, 70, 560. [Google Scholar] [CrossRef]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 1995, 16, 1190. [Google Scholar] [CrossRef]
- Sushkov, O.P.; Flambaum, V.V.; Khriplovich, I.B. Possibility of investigating P-and T-odd nuclear forces in atomic and molecular experiments. Sov. Phys. JETP 1984, 87, 1521. [Google Scholar]
- Petrov, A.N.; Mosyagin, N.S.; Isaev, T.A.; Titov, A.V.; Ezhov, V.F.; Eliav, E.; Kaldor, U. Calculation of P,T-Odd Effects in 205TIF Including Electron Correlation. Phys. Rev. Lett. 2002, 88, 073001. [Google Scholar] [CrossRef] [PubMed]
- Titov, A.V.; Mosyagin, N.S.; Petrov, A.N.; Isaev, T.A.; DeMille, D.P. P, T-parity violation effects in polar heavy-atom molecules. Prog. Theor. Chem. Phys. 2006, 15, 253. [Google Scholar]
- Skripnikov, L.V.; Titov, A.V. Theoretical study of ThF+ in the search for T,P-violation effects: Effective state of a Th atom in ThF+ and ThO compounds. Phys. Rev. A 2015, 91, 042504. [Google Scholar] [CrossRef]
- Skripnikov, L.V.; Titov, A.V. LCAO-based theoretical study of PbTiO3 crystal to search for parity and time reversal violating interaction in solids. J. Chem. Phys. 2016, 145, 054115. [Google Scholar] [CrossRef] [PubMed]
- Skripnikov, L.V.; Titov, A.V.; Petrov, A.N.; Mosyagin, N.S.; Sushkov, O.P. Enhancement of the electron electric dipole moment in Eu2+. Phys. Rev. A 2011, 84, 022505. [Google Scholar] [CrossRef]
- Titov, A.V.; Mosyagin, N.S. Generalized relativistic effective core potential: Theoretical grounds. Int. J. Quantum Chem. 1999, 71, 359. [Google Scholar] [CrossRef]
- Mosyagin, N.S.; Zaitsevskii, A.V.; Titov, A.V. Shape-consistent relativistic effective potentials of small atomic cores. Rev. At. Mol. Phys. 2010, 1, 63. [Google Scholar]
- Mosyagin, N.S.; Zaitsevskii, A.V.; Skripnikov, L.V.; Titov, A.V. Generalized relativistic effective core potentials for actinides. Int. J. Quantum Chem. 2016, 116, 301. [Google Scholar] [CrossRef]
- Skripnikov, L.V. Combined 4-component and relativistic pseudopotential study of ThO for the electron electric dipole moment search. J. Chem. Phys. 2016, 145, 214301. [Google Scholar] [CrossRef] [PubMed]
- Skripnikov, L.V.; Mosyagin, N.S.; Titov, A.V. Relativistic coupled-cluster calculations of spectroscopic and chemical properties for element 120. Chem. Phys. Lett. 2013, 555, 79. [Google Scholar] [CrossRef]
- Visscher, L.; Jensen, H.J.A.; Bast, R.; Saue, T.; Bakken, V.; Dyall, K.G.; Dubillard, S.; Ekström, U.; Eliav, E.; Enevoldsen, T.; et al. DIRAC, a Relativistic Ab Initio Electronic Structure Program, Release DIRAC17 (2017). Available online: http://www.diracprogram.org (accessed on 29 April 2019).
- Kállay, M.; Rolik, Z.; Ladjánszki, I.; Szegedy, L.; Ladóczki, B.; Csontos, J.; Kornis, B. mrcc, a quantum chemical program suite. Available online: www.mrcc.hu (accessed on 29 April 2019).
- Rolik, Z.; Kállay, M. A general-order local coupled-cluster method based on the cluster-in-molecule approach. J. Chem. Phys. 2011, 135, 104111. [Google Scholar] [CrossRef]
- Ma, B.; Yamaguchi, Y.; Schaefer, H.F., III. Spectroscopic constants and potential energy surfaces for the possible interstellar molecules A1NC and A1CN. Mol. Phys. 1995, 86, 1331. [Google Scholar] [CrossRef]
- Fukushima, M. Laser induced fluorescence spectroscopy of AlNC/AlCN in supersonic free expansions. Chem. Phys. Lett. 1998, 283, 337. [Google Scholar] [CrossRef]
- Walker, K.A.; Evans, C.J.; Suh, S.-H.K.; Gerry, M.C.; Watson, J.K. Fourier Transform Microwave Spectroscopy of Cyanides and Isocyanides of Al, Ga, and In. J. Mol. Spectrosc. 2001, 209, 178. [Google Scholar] [CrossRef]
- Robinson, J.; Apponi, A.; Ziurys, L. The millimeter-wave spectrum of AlNC: chemical trends in metal isocyanide molecules. Chem. Phys. Lett. 1997, 278, 1. [Google Scholar] [CrossRef]
- Gerasimov, I.; Yang, X.; Dagdigian, P.J. Laser fluorescence excitation spectra of the AlNC and AlCN isomers. J. Chem. Phys. 1999, 110, 220. [Google Scholar] [CrossRef]
- Ismail, Z.K.; Hauge, R.H.; Margrave, J.L. Infrared spectra of matrix-isolated sodium and potassium cyanides. J. Mol. Spectrosc. 1973, 45, 304. [Google Scholar] [CrossRef]
- Kudashov, A.D.; Petrov, A.N.; Skripnikov, L.V.; Mosyagin, N.S.; Titov, A.V.; Flambaum, V.V. Calculation of the parity- and time-reversal-violating interaction in 225RaO. Phys. Rev. A 2013, 87, 020102(R). [Google Scholar] [CrossRef]
- Kudashov, A.D.; Petrov, A.N.; Skripnikov, L.V.; Mosyagin, N.S.; Isaev, T.A.; Berger, R.; Titov, A.V. Ab initio study of radium monofluoride (RaF) as a candidate to search for parity- and time-and-parity-violation effects. Phys. Rev. A 2014, 90, 052513. [Google Scholar] [CrossRef]
- Isaev, T.A.; Petrov, A.N.; Mosyagin, N.S.; Titov, A.V. Search for the nuclear Schiff moment in liquid xenon. Phys. Rev. A 2007, 75, 032515. [Google Scholar] [CrossRef]
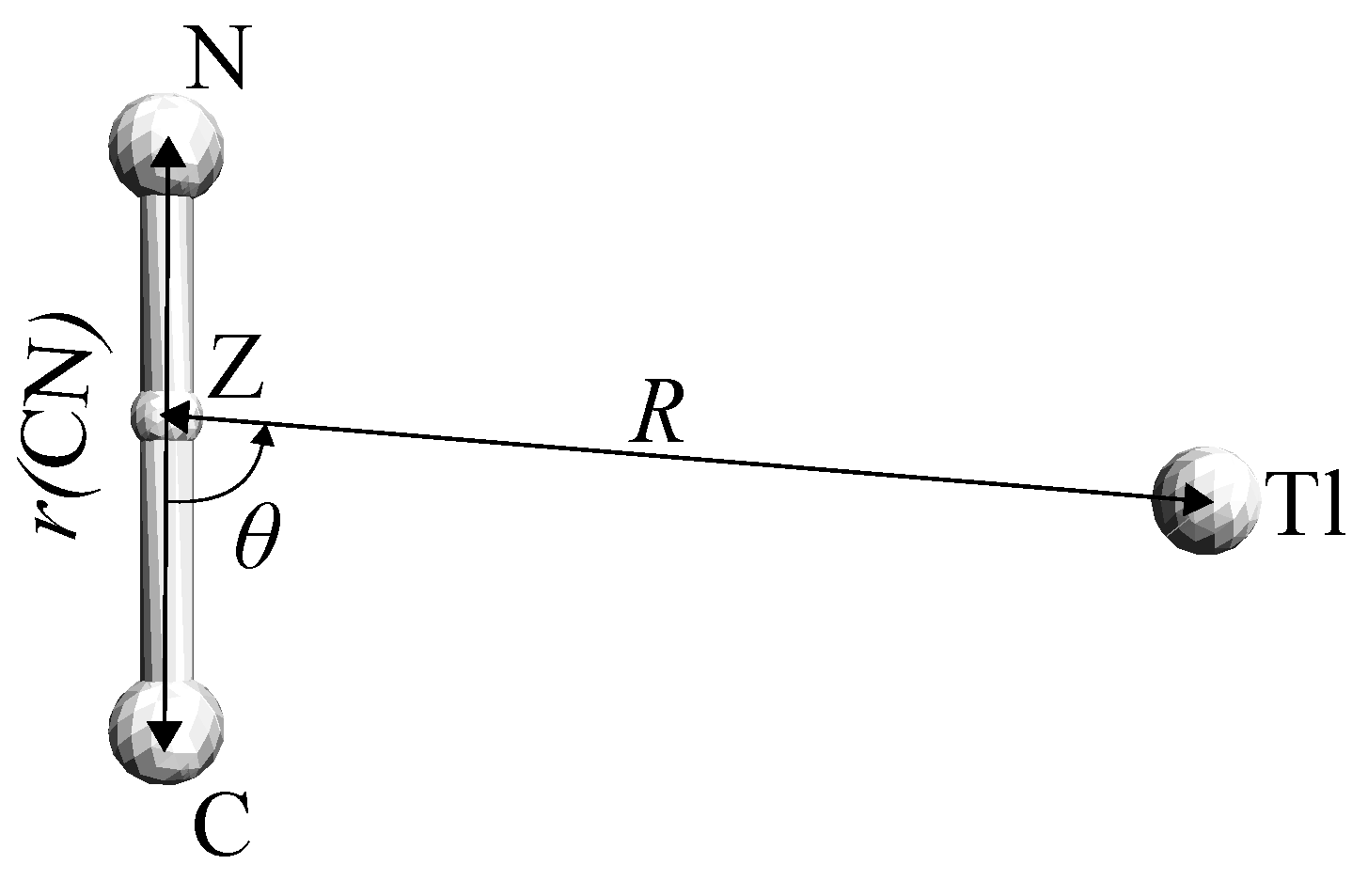
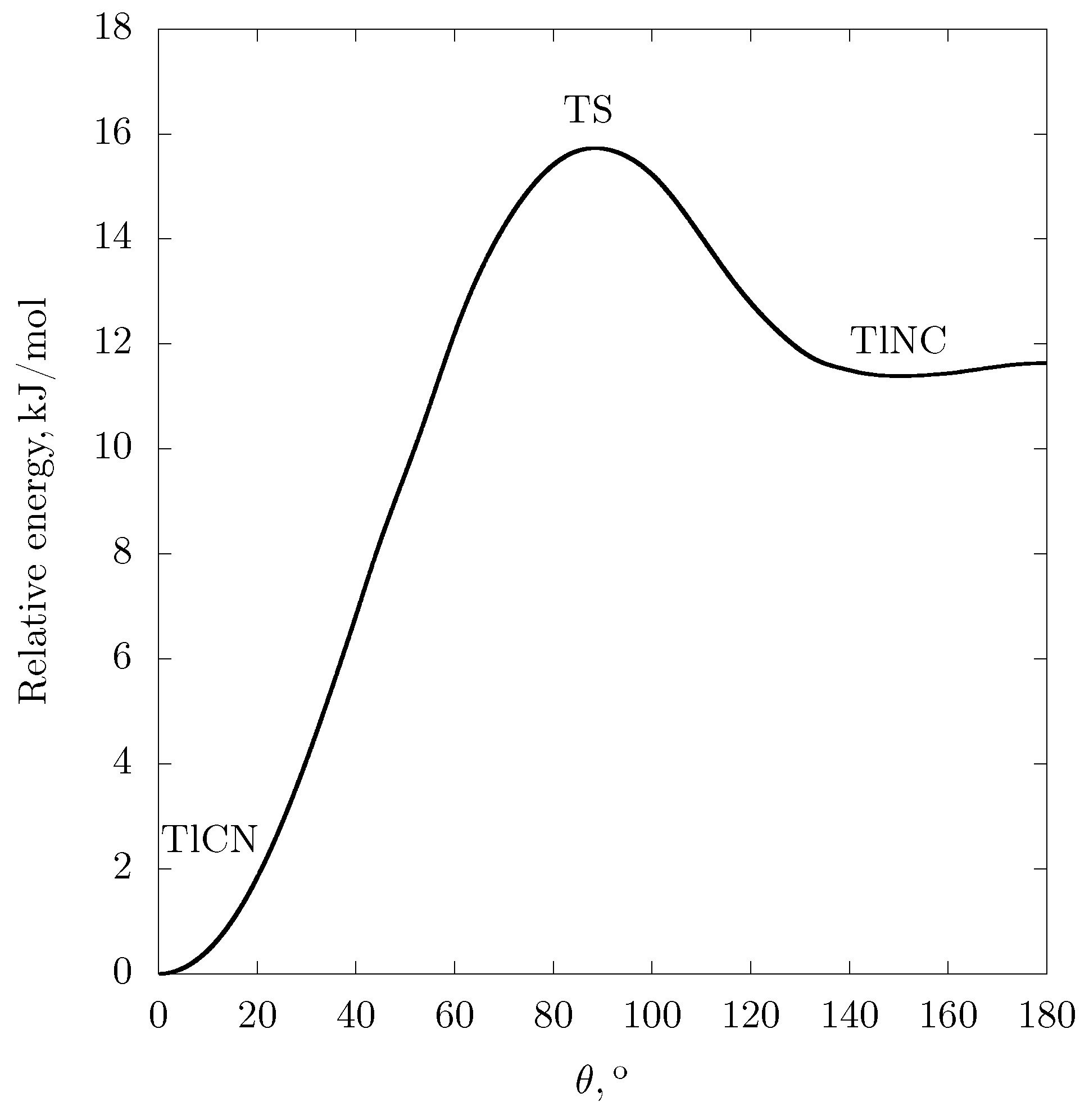
| M | Method | Source | MCN | TS | MNC | ||
|---|---|---|---|---|---|---|---|
| Minimum | Linear | ||||||
| Tl | RCCSD(T)/TZ | PW | 0 | 16.4 | 9.0 | ||
| RCCSD(T)/QZ | 0 | 16.0 | 9.9 | 11.2 | |||
| RCCSD(T)/CBS | 0 | 15.7 | 10.7 | 11.4 | |||
| RDFT/PBE0 | 0 | 13.4 | 14.5 | ||||
| Tl | DFT/BP89 | [7] | 0 | 6.2 | |||
| Al | CCSD | [40] | 25.7 | 55.5 | 0 | ||
| CCSD(T) | [40] | 23.2 | 0 | ||||
| QCISD(T) | [41] | 23.7 | 0 | ||||
| Ga | DFT/BP89 | [7] | 5.5 | 0 | |||
| DFT/B3LYP | [42] | 8.7 | 0 | ||||
| In | DFT/BP89 | [7] | 1.4 | 0 | |||
| MCN | TS | M[CN] | linear MNC | ||||
| Na | CCSD(T) | [11] | 10.1 | 15.8 | 0 | 11.2 | |
| K | CCSD(T) | [11] | 18.3 | 19.3 | 0 | 13.0 | — |
| Rb | CCSD(T) | [11] | 18.3 | 18.8 | 0 | 12.5 | |
| Molecule | Source | D | ||||||
|---|---|---|---|---|---|---|---|---|
| TlCN | RCCSD(T)/TZ, PW | 2.344 | 1.173 | |||||
| RCCSD(T)/QZ, PW | 2.333 | 1.170 | ||||||
| RCCSD(T)/CBS, PW | 2.324 | 1.166 | 294 | 101 | 2163 | 2.41 | ||
| RDFT/PBE0, PW | 2.358 | 1.178 | 277 | 104 | 2149 | 2.39 | ||
| TlCN | Exptl. [7] | 307(?) | 2126 | |||||
| TlNC(?) | Exptl. [7] | 2048 | ||||||
| AlCN | CCSD(T) [40] | 2.014 | 1.171 | 472 | 187 | 2479 | 3.49 | |
| Exptl. [41] | 524 | 133 | 1975 | |||||
| Exptl. [7] | 456 | 2144 | ||||||
| AlNC | CCSD(T) [40] | 1.861 | 1.187 | 584 | 131 | 2290 | 3.14 | |
| Exptl. [42] | 1.854 | 1.178 | 453 | 167 | ||||
| Exptl. [43] | 1.849 | 1.171 | ||||||
| Exptl. [44] | 549;557 | 100 | 2069 | |||||
| Exptl. [7] | 532 | 2069 | ||||||
| GaCN | Exptl. [42] | 2.062 | 1.158 | 304 | ||||
| Exptl. [7] | 2138 | |||||||
| GaNC | Exptl. [42] | 1.938 | 1.174 | 105 | ||||
| Exptl. [7] | 401 | 2046 | ||||||
| InCN | Exptl. [42] | 2.262 | 1.146 | 302 | ||||
| Exptl. [7] | 333 | 2132 | ||||||
| InNC | Exptl. [42] | 2.137 | 1.170 | 71 | ||||
| Exptl. [7] | 392 | 2151 | ||||||
| D | ||||||||
| Na[CN] | Exptl. [9] | 2.366 | 2.243 | 1.169 | ||||
| Exptl. [45] | 368 | 168 | 2047 | |||||
| CCSD(T) [11] | 2.39 | 2.23 | 1.18 | 3.48 | ||||
| K[CN] | Exptl. [12] | 2.716 | 2.549 | 1.169 | ||||
| Exptl. [45] | 288 | 139 | 2050 | |||||
| CCSD(T) [11] | 2.73 | 2.55 | 1.18 | 4.04 |
| Basis Set | X, a.u. | |||
|---|---|---|---|---|
| Tl | C, N | Hartree-Fock | RCCSD | RCCSD(T) |
| 8997 | 7119 | 6939 | ||
| 9093 | 7263 | 7076 | ||
| 9105 | 7351 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kudrin, A.V.; Zaitsevskii, A.; Isaev, T.A.; Maison, D.E.; Skripnikov, L.V. Towards the Search for Thallium Nuclear Schiff Moment in Polyatomic Molecules: Molecular Properties of Thallium Monocyanide (TlCN). Atoms 2019, 7, 62. https://doi.org/10.3390/atoms7030062
Kudrin AV, Zaitsevskii A, Isaev TA, Maison DE, Skripnikov LV. Towards the Search for Thallium Nuclear Schiff Moment in Polyatomic Molecules: Molecular Properties of Thallium Monocyanide (TlCN). Atoms. 2019; 7(3):62. https://doi.org/10.3390/atoms7030062
Chicago/Turabian StyleKudrin, A. V., A. Zaitsevskii, T. A. Isaev, D. E. Maison, and L. V. Skripnikov. 2019. "Towards the Search for Thallium Nuclear Schiff Moment in Polyatomic Molecules: Molecular Properties of Thallium Monocyanide (TlCN)" Atoms 7, no. 3: 62. https://doi.org/10.3390/atoms7030062
APA StyleKudrin, A. V., Zaitsevskii, A., Isaev, T. A., Maison, D. E., & Skripnikov, L. V. (2019). Towards the Search for Thallium Nuclear Schiff Moment in Polyatomic Molecules: Molecular Properties of Thallium Monocyanide (TlCN). Atoms, 7(3), 62. https://doi.org/10.3390/atoms7030062




