Developing the Techniques for Solving the Inverse Problem in Photoacoustics
Abstract
:1. Introduction
2. Generalized Model of PA Response—Direct Problem Solving
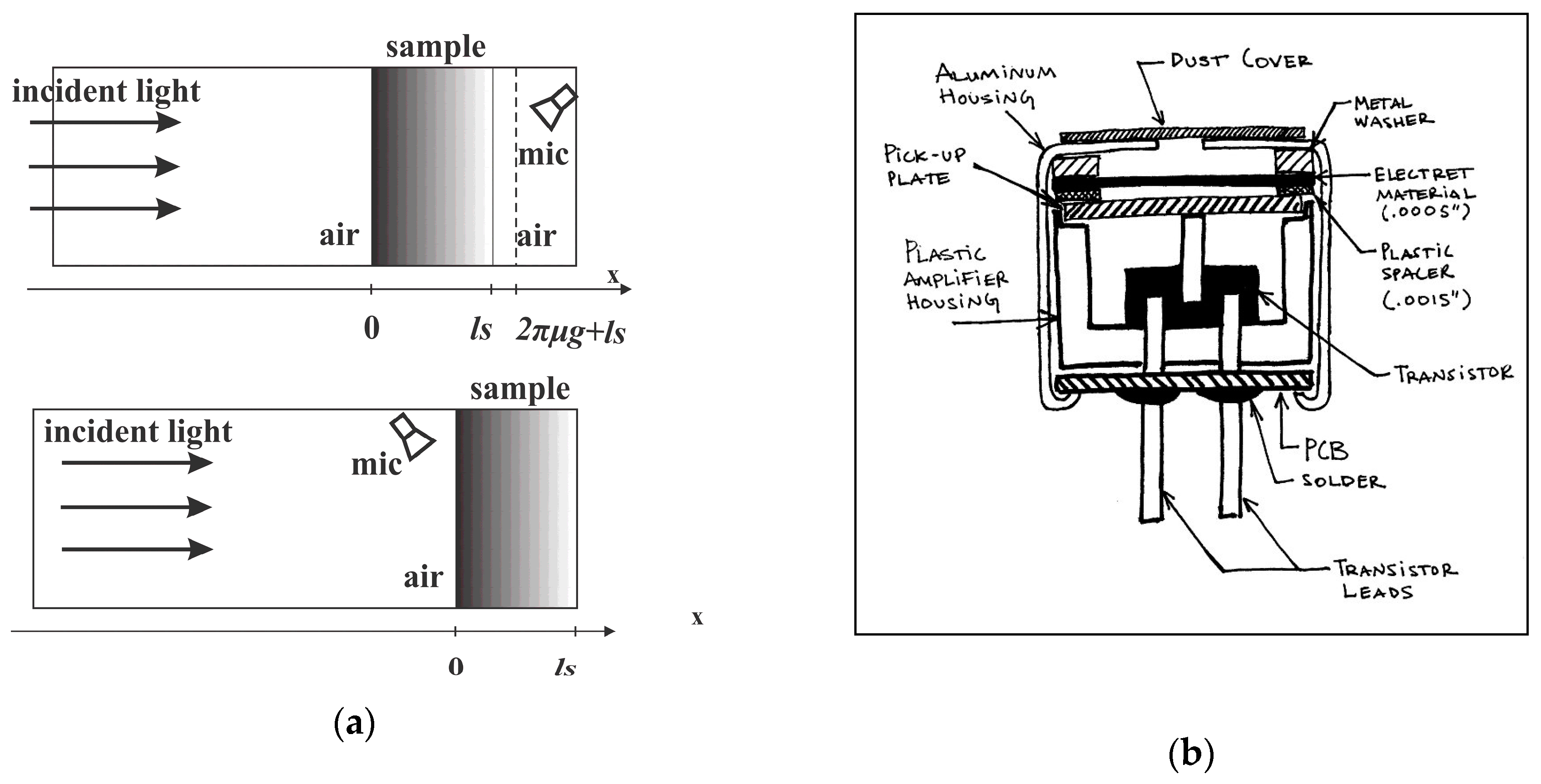
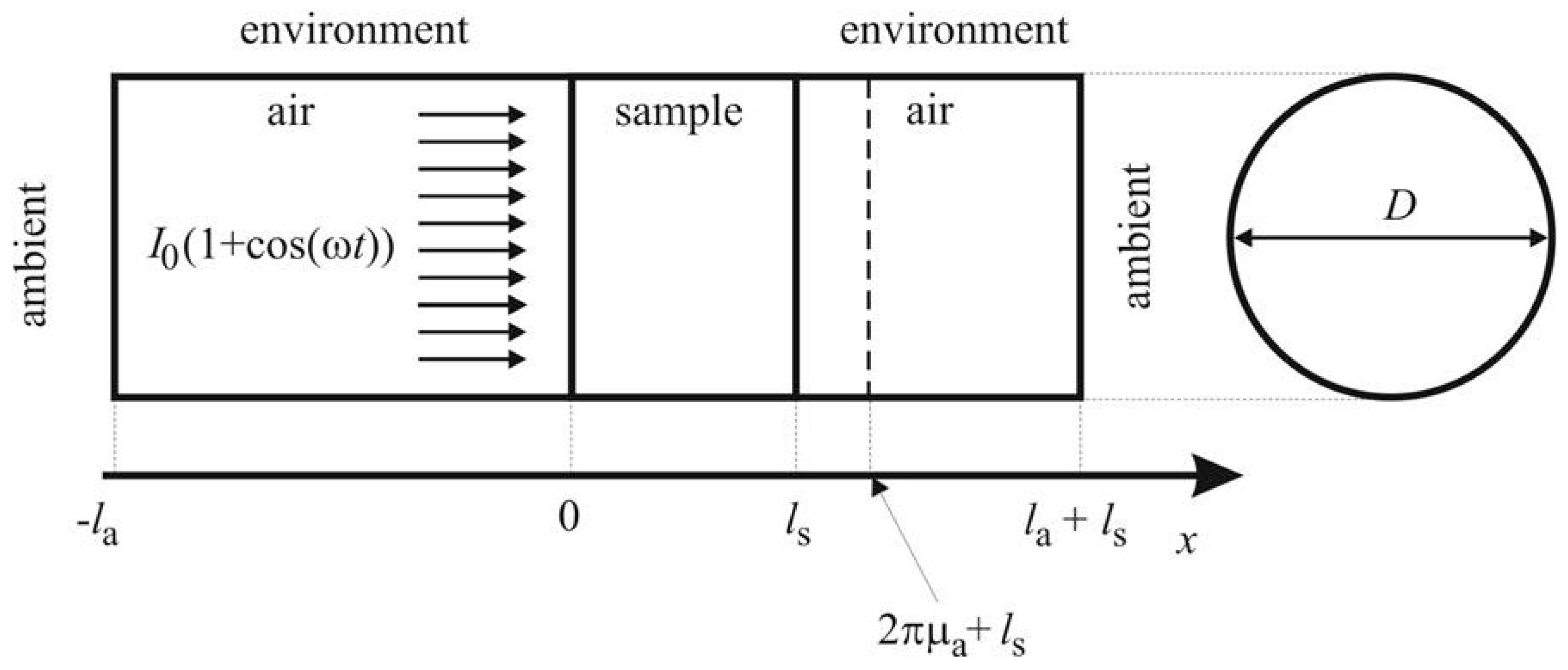
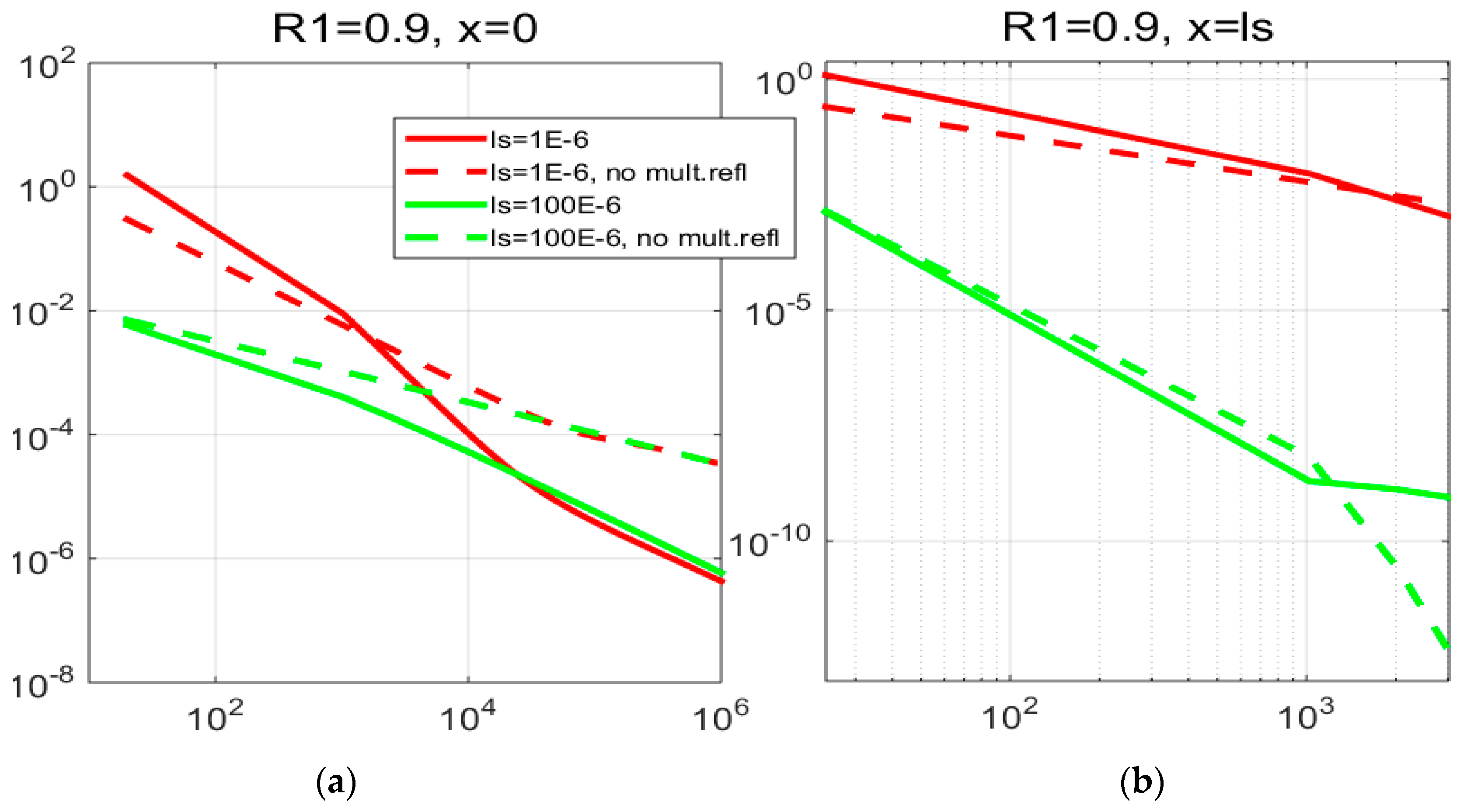
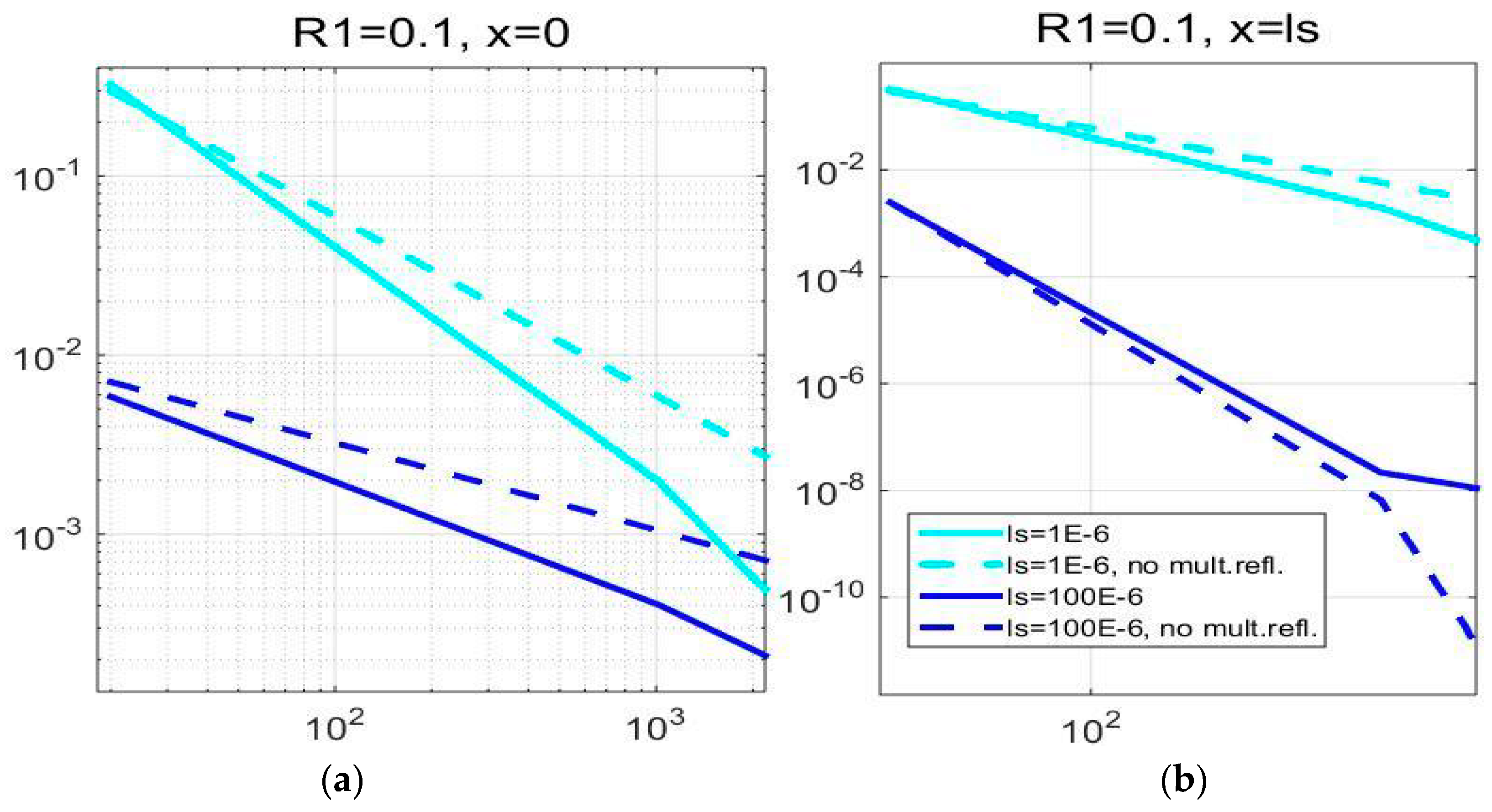
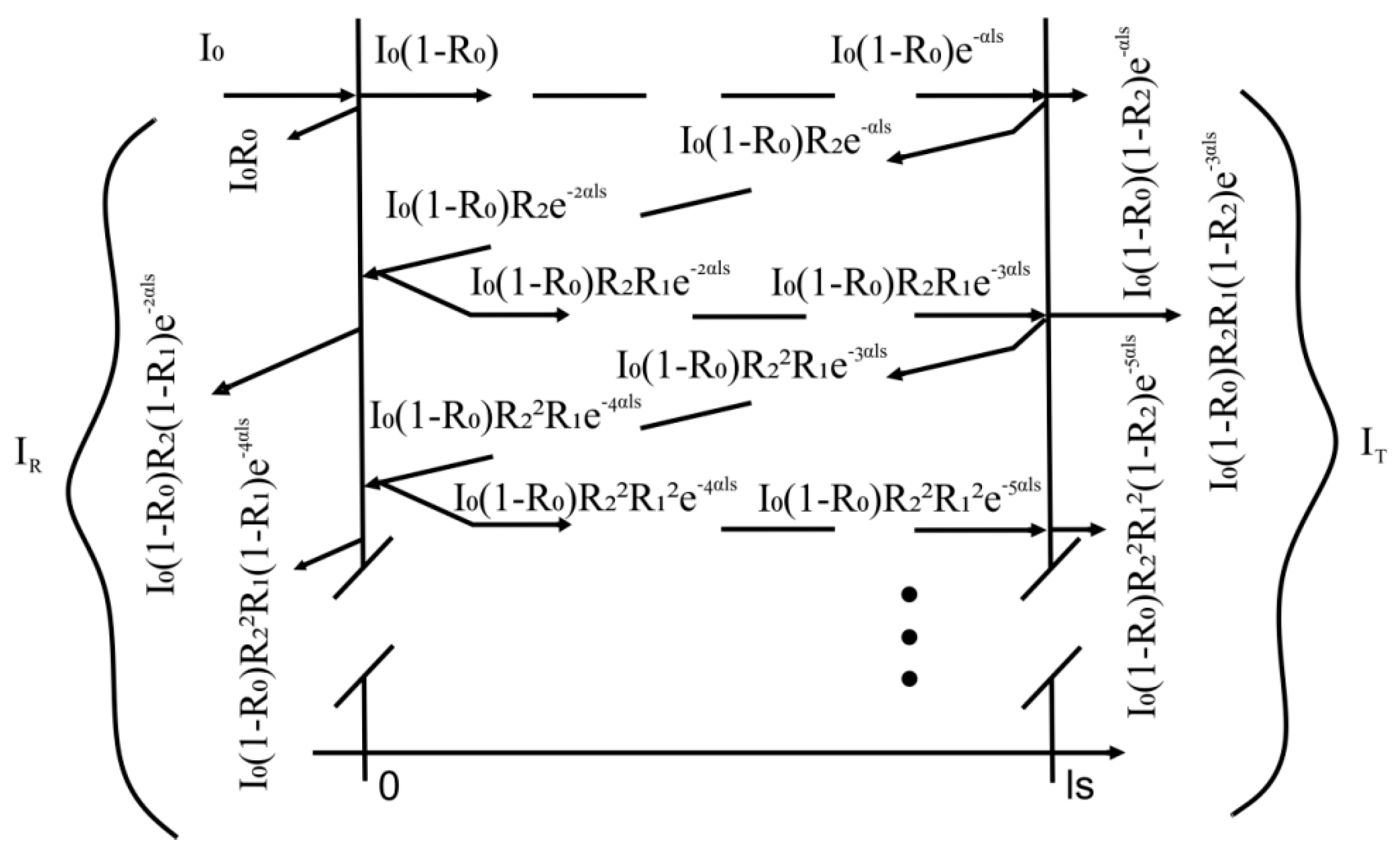
2.1. Multiple Optical Reflections—the Influence of Optical Properties
2.2. Thermal Memory Influence
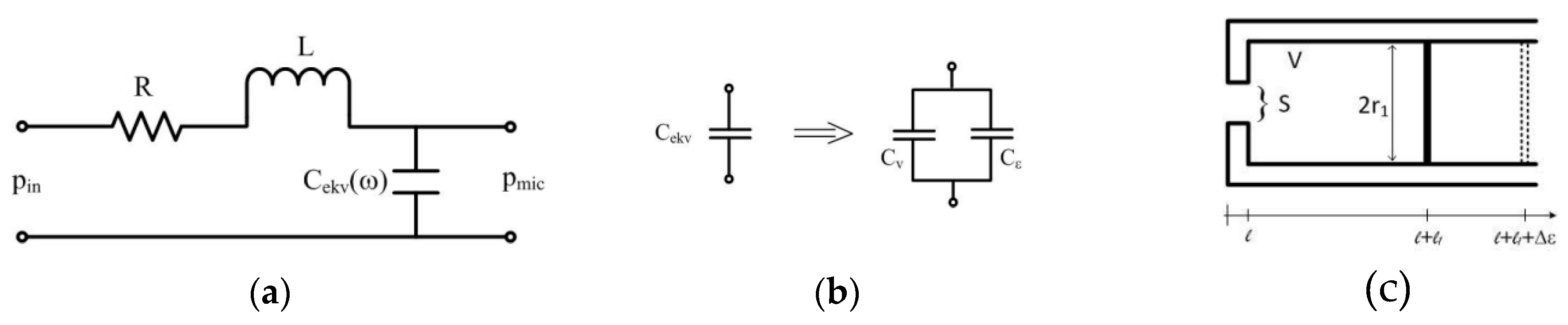
2.3. Helmholtz Resonances—the Influence of the Measurement Chain
3. Techniques for Inverse Solving of PA Response
- A self-consistent procedure for solving the exponential problems of mathematical physics;
- A well-trained three-layer perceptron with back propagation, based upon theory of neural networks.
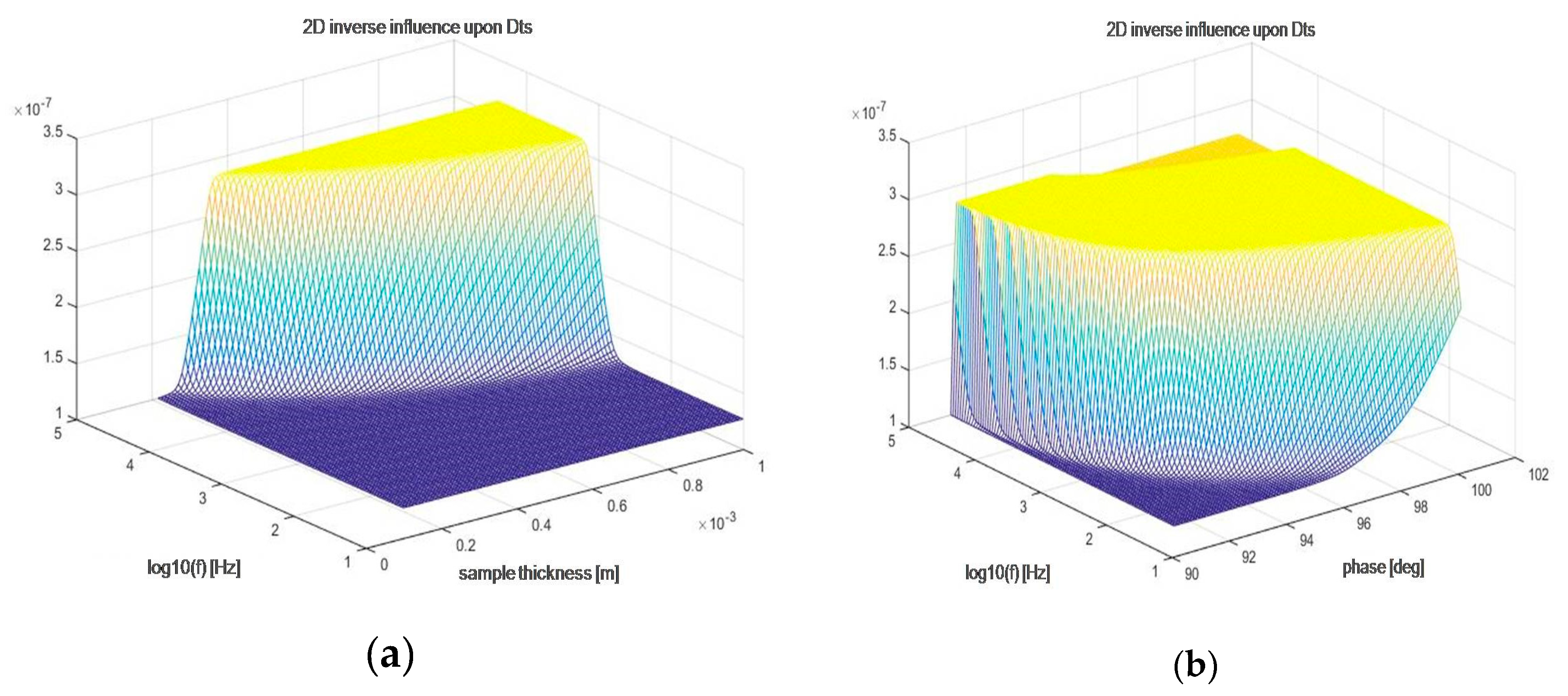
3.1. Self-Consistent Inverse PA Procedure
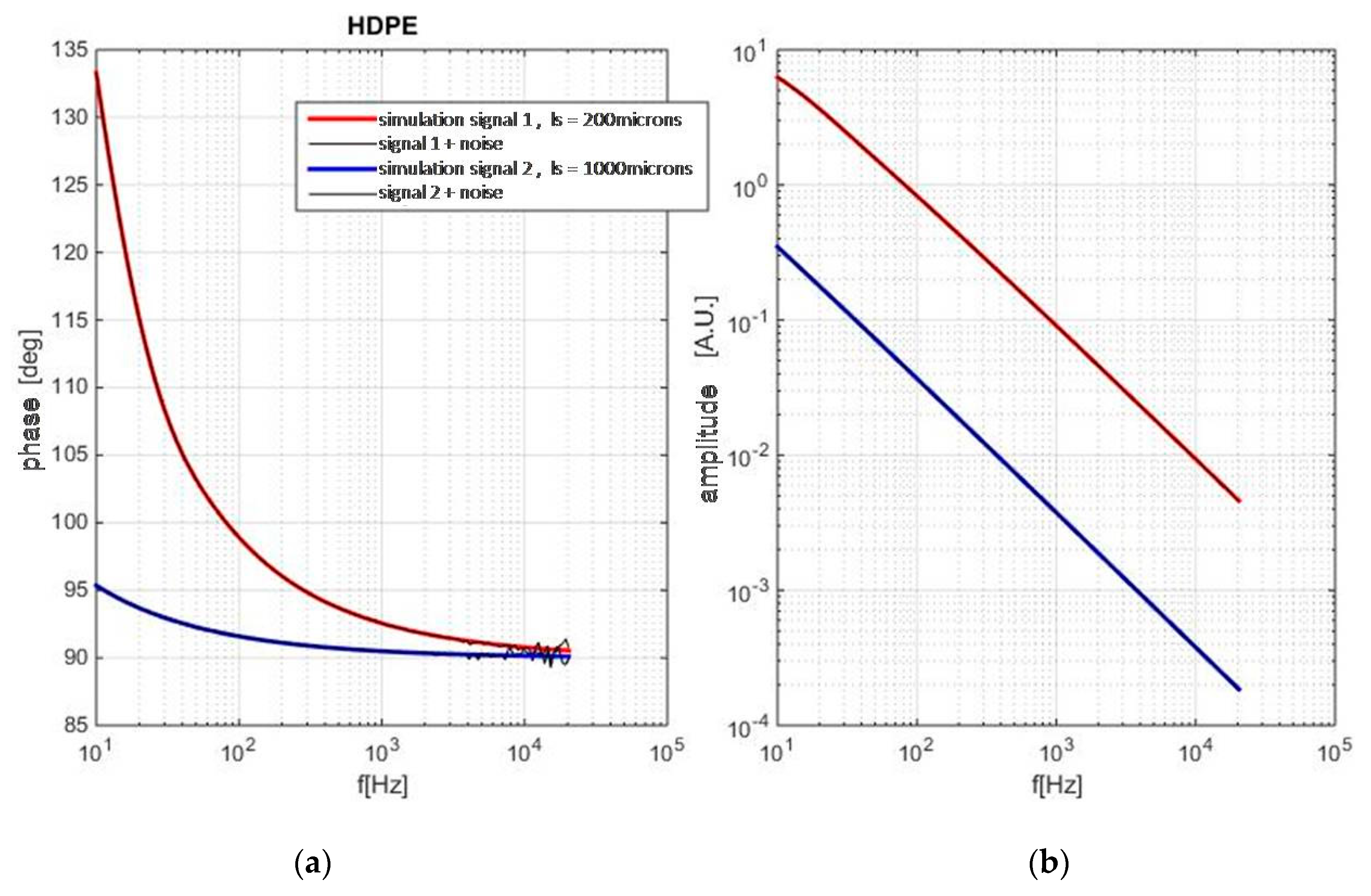
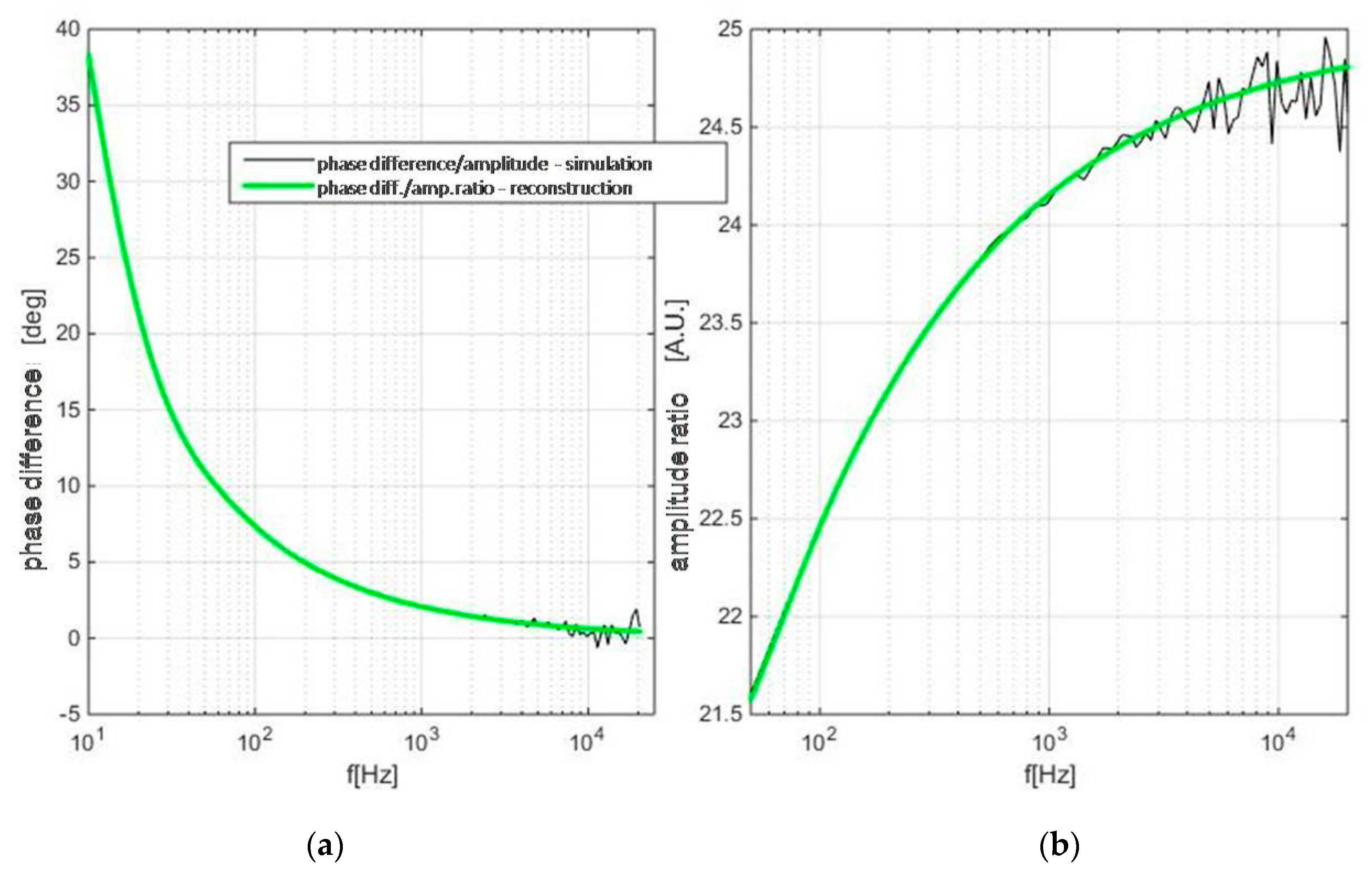
3.2. The Application of the Neural Network
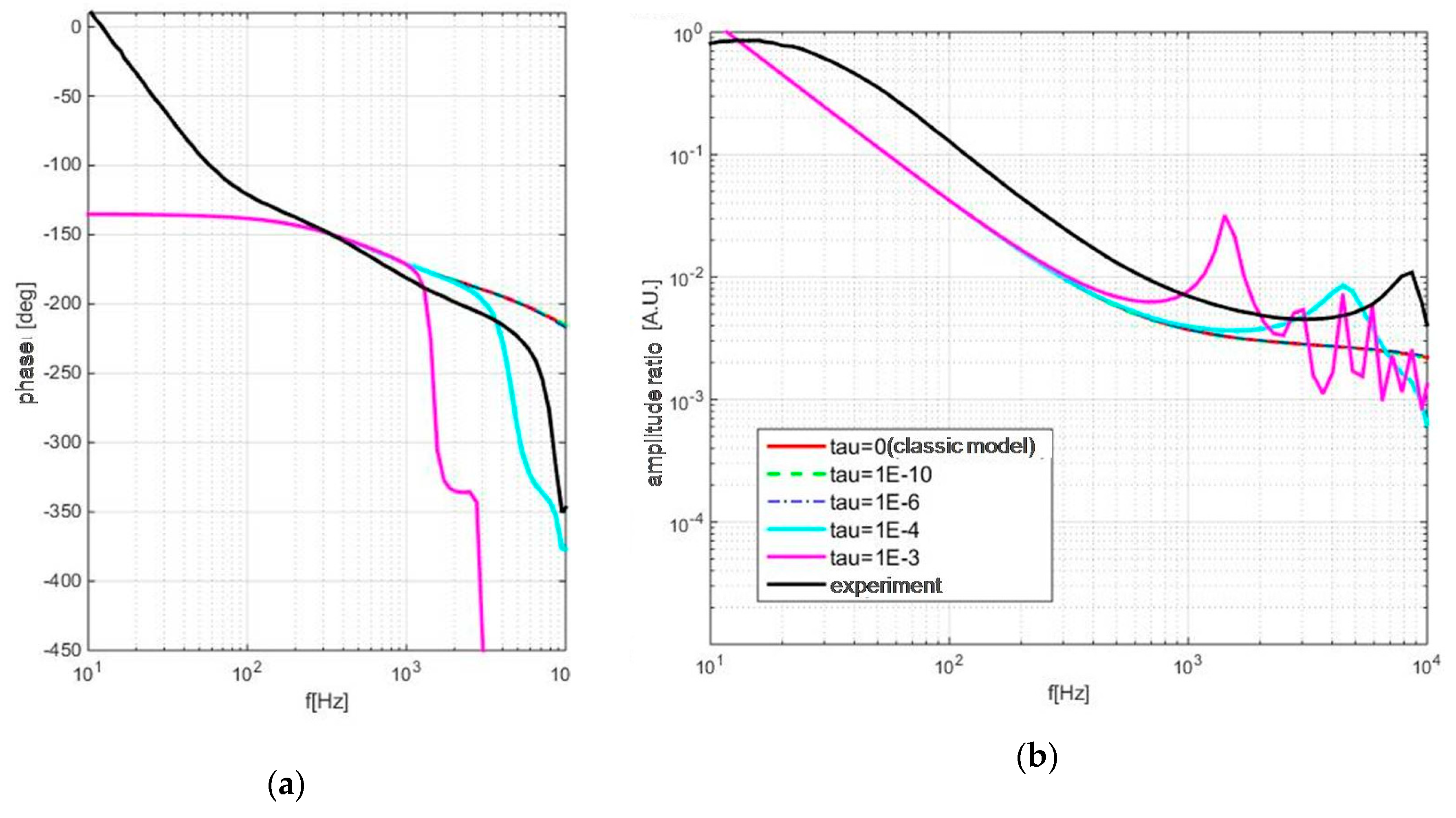
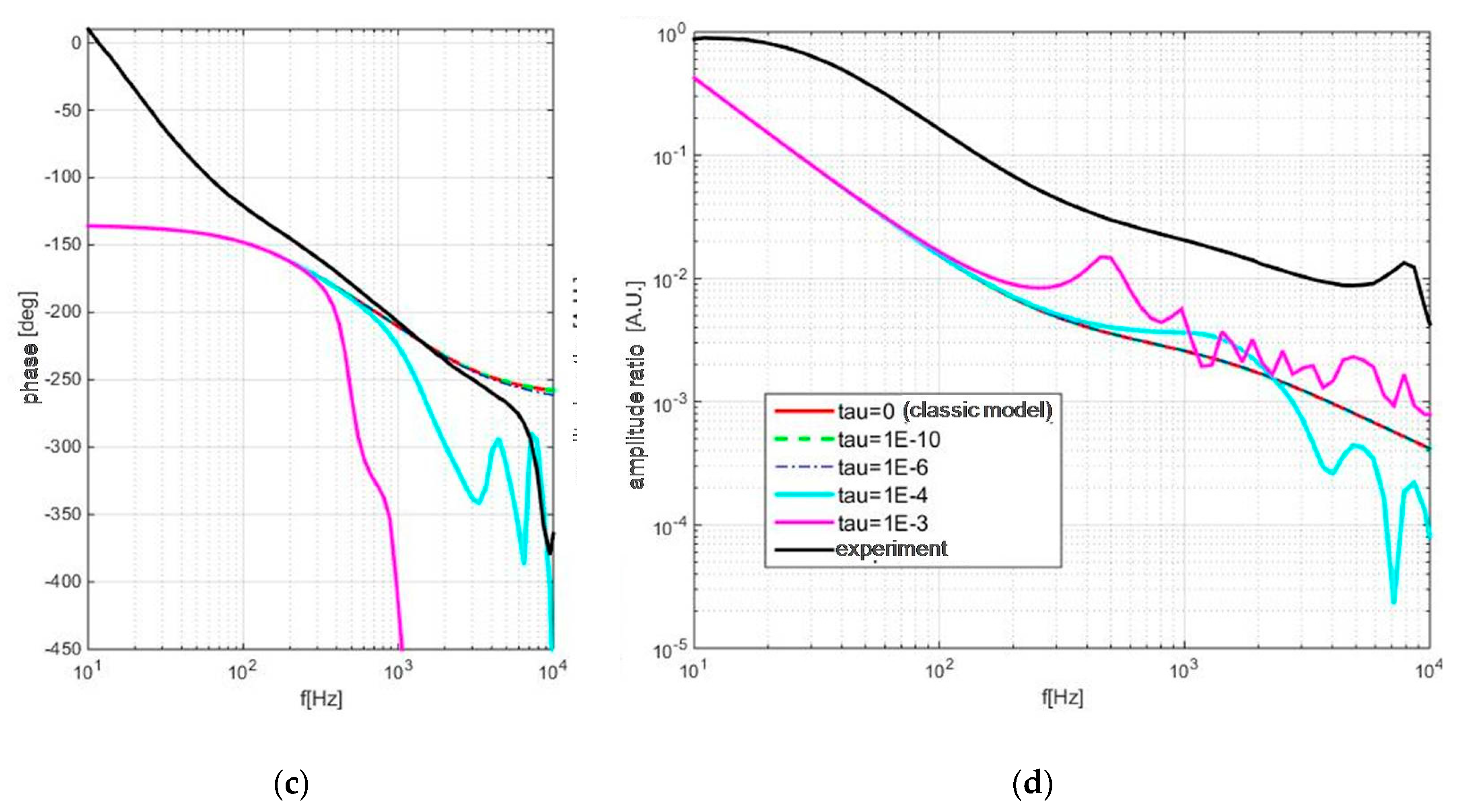
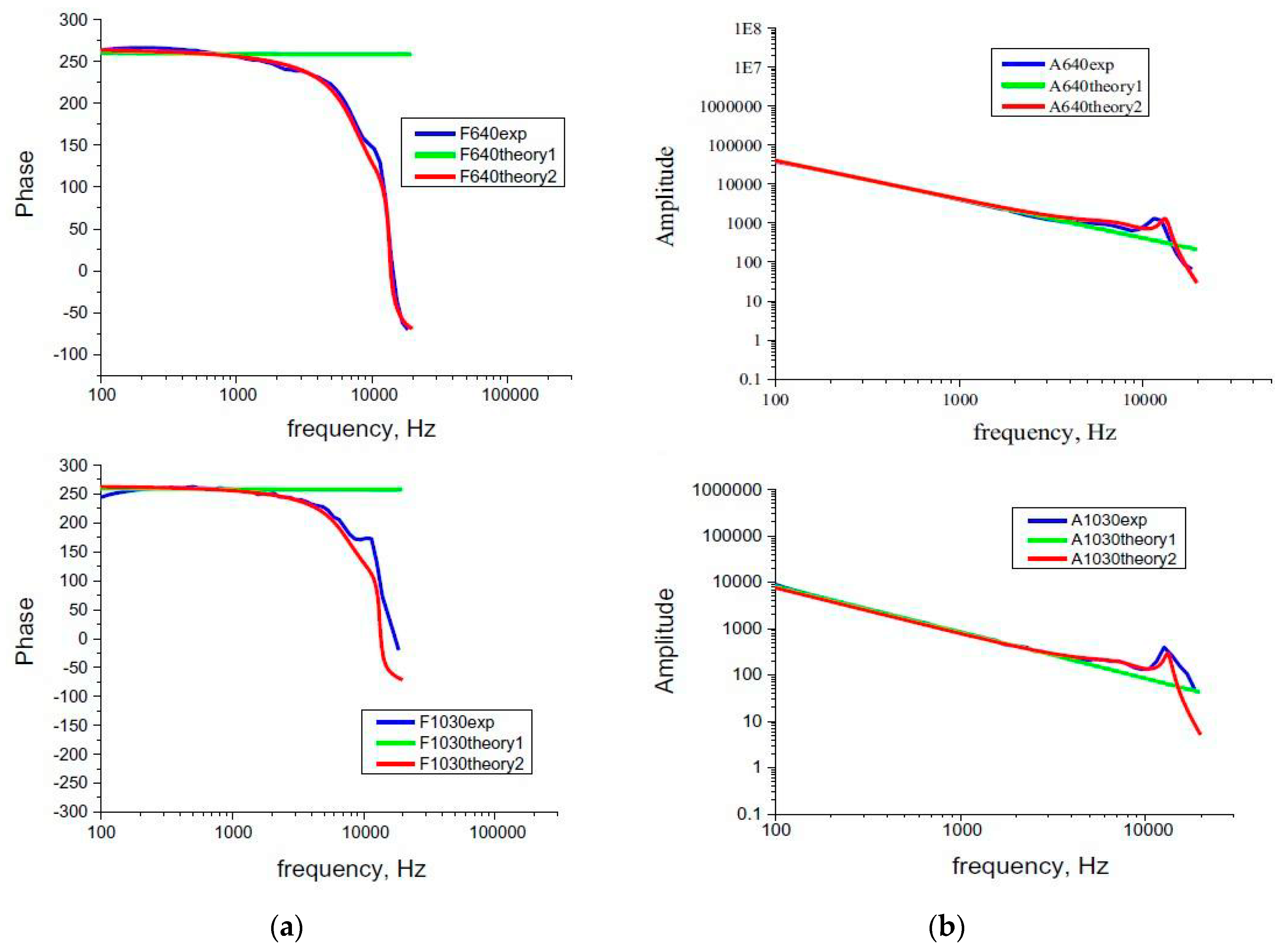
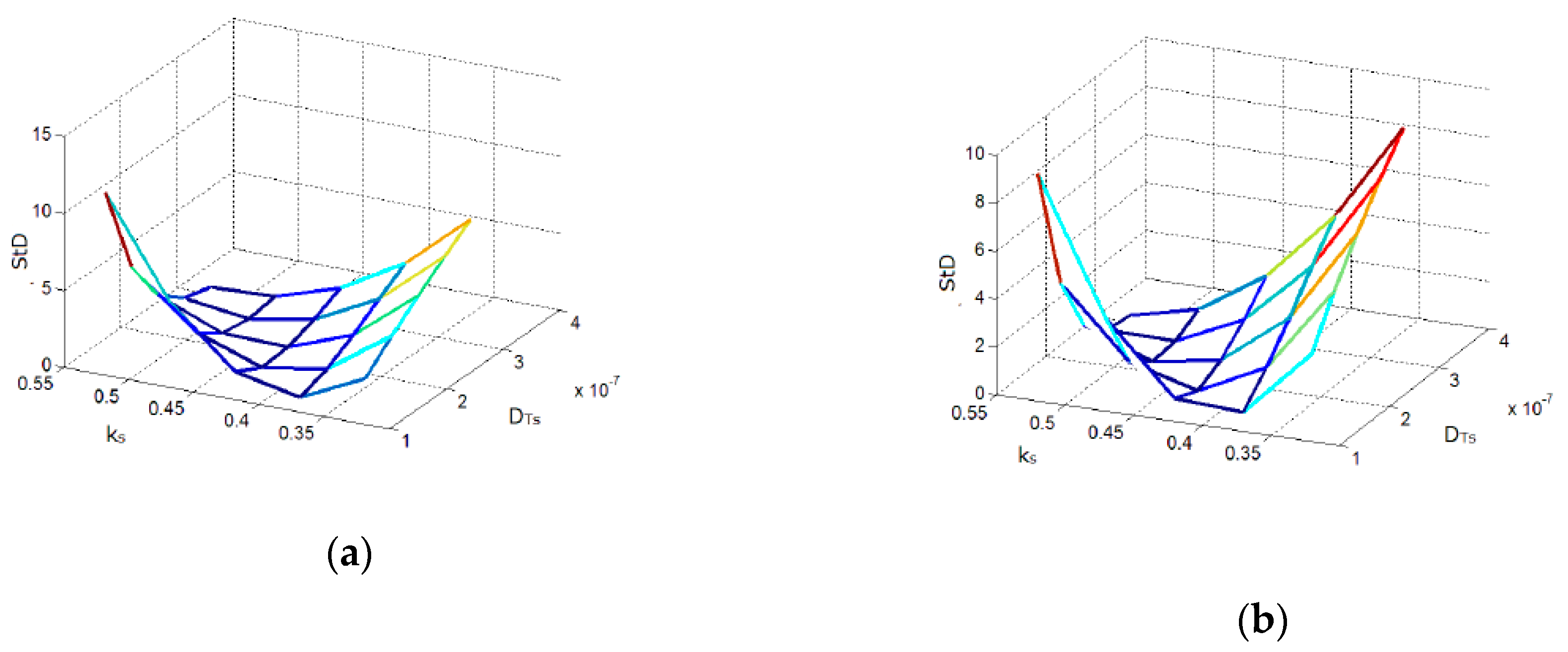
3.3. The Application on Experimental Data
4. Conclusions
- Generalized model of PA response as the consequence of finite heat propagation velocity was considered and its manifestations—thermal resonances—were described, with potential application in the determination of heat propagation velocity by making use of the location of the first peak;
- The influence of multiple optical reflections on PA response was considered for a specific class of soft matter materials and its potential application, as well as implications regarding fundamental heat transfer were pointed out;
- Minimum volume PA cell was successfully modeled as Helmholtz resonator and innovative applications of PA methods were potentiated;
- Simultaneous use of amplitude and phase measurements was proven to enable the estimation of thermal diffusivity, while difficulties in assessing the ratio of linear expansion coefficient and heat conductivity coefficient pointed out the necessity for the improvement of TMS modeling;
- The application of a neural network on the numerical experiment exposed the necessity for the reconsideration of the thermal piston model in materials with low levels of arrangement (macromolecules, tissue, soft matter);
- The application of self-consistent procedures on the experiment demonstrated the dependence of thermal properties upon thickness and crystallinity.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| TMS | theoretically/mathematically simulated (TMS) models |
| PA | photoacoustic/photoacoustics |
| EM | electromagnetic |
| 1D | one-dimensional |
| HDPE | High-Density Polyethylene |
| WAXD | wide angle X-ray diffraction |
| DSC | diffraction scanning calorimetry |
References
- Mandelis, A. Diffusion waves and their uses. Phys. Today 2000, 53, 29–34. [Google Scholar] [CrossRef]
- Todorović, D.M.; Nikolic, P.M. Carrier transport Contribution on Thermoelastic and Electronic Deformation in Semiconductors. In Progress in Photothermal and Photoacoustic Science and Technology; Mandelis, A., Hess, P., Eds.; SPIE Press: Washington, DC, USA, 2000; Volume 4, p. 272. [Google Scholar]
- Rabasovic, M.D.; Nikolic, M.G.; Dramicanin, M.D.; Franko, M.; Markushev, D.D. Low-cost, portable photoacoustic setup for solid samples. Meas. Sci. Technol. 2009, 20, 95902. [Google Scholar] [CrossRef]
- Perondi, L.F.; Miranda, L.C.M. Minimal-volume photoacoustic cell measurement of thermal diffusivity: Effect of the thermoelastic sample bending. J. Appl. Phys. 1987, 62, 2955–2959. [Google Scholar] [CrossRef]
- Terazima, M.; Hirota, N.; Braslavsky, S.E.; Mandelis, A.; Bialkowski, S.E.; Diebold, G.J.; Miller, R.J.D.; Fournier, D.; Palmer, R.A.; Tam, A. Quantities, Terminology, And Symbols In Photothermal And Related Spectroscopies. Pure Appl. Chem. 2004, 76, 1083–1111. [Google Scholar] [CrossRef]
- Nesic, M.V.; Popovic, M.N.; Stojanovic, Z.; Soskic, Z.N.; Galovic, S.P. Photoacoustic response of thin films: Thermal memory influence. Hem. Ind. 2013, 67, 139–146. [Google Scholar] [CrossRef]
- Markushev, D.D.; Ordonez-Miranda, J.; Rabasović, M.D.; Chirtoc, M.; Todorović, D.M.; Bialkowski, S.E.; Korte, D.; Franko, M. Thermal and elastic characterization of glassy carbon thin films by photoacoustic measurements. Eur. Phys. J. Plus 2017, 132, 1–9. [Google Scholar] [CrossRef]
- Pichardo-Molina, J.L.; Alvarado-Gil, J.J. Heat diffusion and thermolastic vibration influence on the signal of an open photoacoustic cell for two layer systems. J. Appl. Phys. 2004, 95, 6450–6456. [Google Scholar] [CrossRef]
- Galovic, S.P.; Kostoski, D. Photothermal wave propagation in media with thermal memory. J. Appl. Phys. 2003, 93, 3063–3070. [Google Scholar] [CrossRef]
- Nesic, M.V.; Galovic, S.P.; Soskic, Z.N.; Popovic, M.N.; Todorović, D.M. Photothermal thermoelastic bending for media with thermal memory. Int. J. Thermophys. 2012, 33, 2203–2209. [Google Scholar] [CrossRef]
- Galovic, S.P.; Soskic, Z.N.; Popovic, M.N.; Stojanovic, Z.; Cevizovic, D.; Stojanovic, Z. Theory of photoacoustic effect in media with thermal memory. J. Appl. Phys. 2014, 116, 024901. [Google Scholar] [CrossRef]
- Nesic, M.V.; Popovic, M.N.; Galovic, S.P. Influence of thermal memory on the thermoelastic bending component of photoacoustic response. Hem. Ind. 2011, 65, 219–227. [Google Scholar] [CrossRef]
- Gurevich, Y.; Logvinov, G.; Lashkevich, I. Effective thermal conductivity: application to photothermal experiments for the case of bulk light absorption. Phys. Stat. Solidi (b) 2004, 241, 1286–1298. [Google Scholar] [CrossRef]
- Gurevich, Y.; Logvinov, G.; de Rivera, L.N.; Titov, O. Nonstationary temperature distribution caused by bulk absorption of laser pulse. Rev. Sci. Instrum. 2003, 74, 441–443. [Google Scholar] [CrossRef]
- Logvinov, G.N.; Gurevich, Y.G.; Lashkevich, I.M. Surface Heat Capacity and Surface Heat Impedance: An Application to Theory of Thermal Waves. Jpn. J. Appl. Phys. 2003, 42, 4448–4452. [Google Scholar] [CrossRef]
- Rosencwaig, A.; Gerscho, A. Theory of the photoacoustic effect with solids. J. Appl. Phys. 1976, 47, 64–69. [Google Scholar] [CrossRef]
- McDonald, F.A.; Wetsel, G.C. Generalized theory of the photoacoustic effect. J. Appl. Phys. 1978, 49, 2313–2322. [Google Scholar] [CrossRef]
- Rousset, L.; Lepoutre, F.; Bertrand, L. Influence of thermoelastic bending on photoacoustic experiments related to measurements of thermal diffusivity of metals. J. Appl. Phys. 1983, 54, 2383–2391. [Google Scholar] [CrossRef]
- Mansanares, A.M.; Vargas, H.; Galembeck, F.; Buijs, J.; Bicanic, D. Photoacoustic characterization of a two-layer system. J. Appl. Phys. 1991, 70, 7046–7050. [Google Scholar] [CrossRef]
- Balderas-Lopez, J.A.; Mandelis, A. Thermal diffusivity measurements in the photoacoustic open-cell configuration using simple signal normalization techniques. J. Appl. Phys. 2001, 90, 2273–2279. [Google Scholar] [CrossRef]
- Nesic, M.V.; Gusavac, P.; Popovic, M.N.; Soskic, Z.N.; Galovic, S.P. Thermal memory influence on the thermoconducting component of indirect photoacoustic response. Phys. Scr. 2012, T149, 14018. [Google Scholar] [CrossRef]
- Cao, J. Interferential formulization and interpretation of the photoacoustic effect in multi-layered cells. J. Phys. D. Appl. Phys. 2000, 33, 200. [Google Scholar] [CrossRef]
- Lima, C.A.S.; Lima, M.B.S.; Miranda, L.C.M.; Baeza, J.; Freer, J.; Reyes, N.; Ruiz, J.; Silva, M.D. Photoacoustic characterization of bleached wood pulp and finished papers. Meas. Sci. Technol. 2000, 11, 504. [Google Scholar] [CrossRef]
- Bedoya, A.; Marin, E.; Mansanares, A.M.; Zambrano-Arjona, M.A.; Riech, I.; Calderon, A. On the thermal characterization of solids by photoacoustic calorimetry: Thermal diffusivity and linear thermal expansion coefficient. Thermochim. Acta 2015, 614, 52–58. [Google Scholar] [CrossRef]
- Nesic, M.V.; Popovic, M.N.; Galovic, S.P. The influence of multiple optical reflexions on the photoacoustic frequency response. Opt. Quantum Electron. 2016, 48, 7. [Google Scholar] [CrossRef]
- Novikov, I.A. Harmonic thermal waves in materials with thermal memory. J. Appl. Phys. 1997, 81, 1067–1072. [Google Scholar] [CrossRef]
- Todorović, D.M.; Rabasovic, M.D.; Markushev, D.D. Photoacoustic elastic bending in thin film—Substrate system. J. Appl. Phys. 2013, 114, 213510. [Google Scholar]
- Todorović, D.M.; Rabasovic, M.D.; Markushev, D.D.; Sarajlić, M. Photoacoustic elastic bending in thin film-substrate system: Experimental determination of the thin film parameters. J. Appl. Phys. 2014, 116, 053506. [Google Scholar] [CrossRef]
- Aleksic, S.M.; Markushev, D.K.; Pantic, D.S.; Rabasovic, M.D.; Markushev, D.D.; Todorović, D.M. Electro-Acustic Influence of the Measuring System on the Photo-Acustic Signal Amplitude and Phase in Frequency Domain. Univ. Facta. 2010, 14, 1–13. [Google Scholar]
- Popovic, M.N.; Nesic, M.V.; Ciric-Kostic, S.; Zivanov, M.; Markushev, D.D.; Rabasovic, M.D.; Galovic, S.P. Helmholtz Resonances in Photoacoustic Experiment with Laser-Sintered Polyamide Including Thermal Memory of Samples. Int. J. Thermophys. 2016, 37, 1–9. [Google Scholar] [CrossRef]
- Nesic, M.V.; Popovic, M.; Rabasovic, M.; Milicevic, D.; Suljovrujic, E.; Markushev, D.; Stojanovic, Z. Thermal Diffusivity of High-Density Polyethylene Samples of Different Crystallinity Evaluated by Indirect Transmission Photoacoustics. Int. J. Thermophys. 2018, 39, 24. [Google Scholar] [CrossRef]
- Soskic, Z.N.; Ciric-Kostic, S.; Galovic, S.P. An extension to the methodology for characterization of thermal properties of thin solid samples by photoacoustic techniques. Int. J. Therm. Sci. 2016, 109, 217–230. [Google Scholar] [CrossRef]
- Wunderlich, B. Thermal Analysis of Polymeric Materials; Springer: Berlin, Germany, 2005. [Google Scholar]
- Wunderlich, B.; Cormier, C.M. Heat of fusion of polyethylene. J. Polym. Sci. Part A-2 Polym. Phys. 1967, 5, 987–988. [Google Scholar] [CrossRef]
- Vonk, C.G. Computerization of Ruland’s X-ray method for determination of the crystallinity in polymers. J. Appl. Cryst. 1973, 6, 148–152. [Google Scholar] [CrossRef]
- Jokanovic, V. Instrumental Methods: Key to Understanding Nanotechnologies and Nanomedicine; Engineering Academy of Serbia: Belgrade, Serbia, 2014. [Google Scholar]
| χ (%) | 200 μm | 400 μm | 600 μm | |
|---|---|---|---|---|
| DSC | WAXD | DSC | DSC | |
| Fast Cooled | 51.7 | 50.5 | 57.4 | 59.3 |
| Slowly Cooled | 73.8 | 72.5 | 71.5 | 70.8 |
| Thickness [μm] | HDPE—High-Density Polyethylene | |||
|---|---|---|---|---|
| Fast Cooled | Slowly Cooled | Uncertainty | ||
| 400, 600 | ks | 0.33 | 0.33 | (±0.02) |
| DTs | 0.313 | 0.313 | (±0.019) | |
| 200 | ks | 0.48 | 0.53 | (±0.02) |
| DTs | 0.265 | 0.313 | (±0.019) | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nesic, M.; Popovic, M.; Galovic, S. Developing the Techniques for Solving the Inverse Problem in Photoacoustics. Atoms 2019, 7, 24. https://doi.org/10.3390/atoms7010024
Nesic M, Popovic M, Galovic S. Developing the Techniques for Solving the Inverse Problem in Photoacoustics. Atoms. 2019; 7(1):24. https://doi.org/10.3390/atoms7010024
Chicago/Turabian StyleNesic, Mioljub, Marica Popovic, and Slobodanka Galovic. 2019. "Developing the Techniques for Solving the Inverse Problem in Photoacoustics" Atoms 7, no. 1: 24. https://doi.org/10.3390/atoms7010024
APA StyleNesic, M., Popovic, M., & Galovic, S. (2019). Developing the Techniques for Solving the Inverse Problem in Photoacoustics. Atoms, 7(1), 24. https://doi.org/10.3390/atoms7010024






