BEAMDB and MOLD—Databases at the Serbian Virtual Observatory for Collisional and Radiative Processes

Abstract

In this contribution we present a progress report on two atomic and molecular databases, BEAMDB and MolD, which are web services at the Serbian virtual observatory (SerVO) and nodes within the Virtual Atomic and Molecular Data Center (VAMDC). The Belgrade Electron/Atom (Molecule) DataBase (BEAMDB) provides collisional data for electron interactions with atoms and molecules. The Photodissociation (MolD) database contains photo-dissociation cross sections for individual rovibrational states of diatomic molecular ions and rate coefficients for the chemi-ionisation/recombination processes. We also present a progress report on the major upgrade of these databases and plans for the future. As an example of how the data from the BEAMDB may be used, a review of electron scattering from methane is described.

1. Introduction

Databases in atomic and molecular physics have become essential for developing models and simulations of complex physical and chemical processes and for the interpretation of data provided by observations and measurements, e.g., in laboratory plasma [1], and studying plasma chemistries and reactions in planetary atmospheres [2]. In the last decade large amounts of data have been collected for medical applications including stopping powers in different media and tissues as well as cross sections for atomic particles (photons, electrons, positrons, ions) interacting with biomolecules and their constituents in order to achieve an insight, at the molecular level, of the radiation damage and radiotherapy [3]. In order to solve the problem of analysis and mining of such large amounts of data, the creation of Virtual Observatories and Virtual Data Centres have been crucial ([4] and refs. therein). In this contribution we present a progress report of two atomic and molecular databases, the Belgrade Electron/Atom (Molecule) DataBase (BEAMDB) and Photodissociation (MolD), which are web services at the Serbian virtual observatory (SerVO) [5] and nodes within the Virtual Atomic and Molecular Data Centre (VAMDC) [6].

This branch of science often entitled ‘Data management’ or ‘Data mining’ is undergoing rapid expansion and development such that nowadays it is not enough for these databases to satisfy the standards of Virtual centres, etc., but they have to deal with new challenges such as the input of large amounts of data, i.e., Big Data. Thus, we can expect major investment and activity in this field in the next decade. Indeed, in September 2018, the European Strategy Forum on Research Infrastructures (ESFRI) presented its Strategy Report and Roadmap 2018. As a strategic instrument that identifies Research Infrastructures (RI) of strategic interest for Europe and the wider research community, the document presented Big data and e-infrastructure needs and highlighted the Virtual Observatory (VO) and The International VO Alliance (IVOA) as very important initiatives with VAMDC relevant data standards as well as state-of-the-art data analysis tools being highlighted as evidence of good practice.

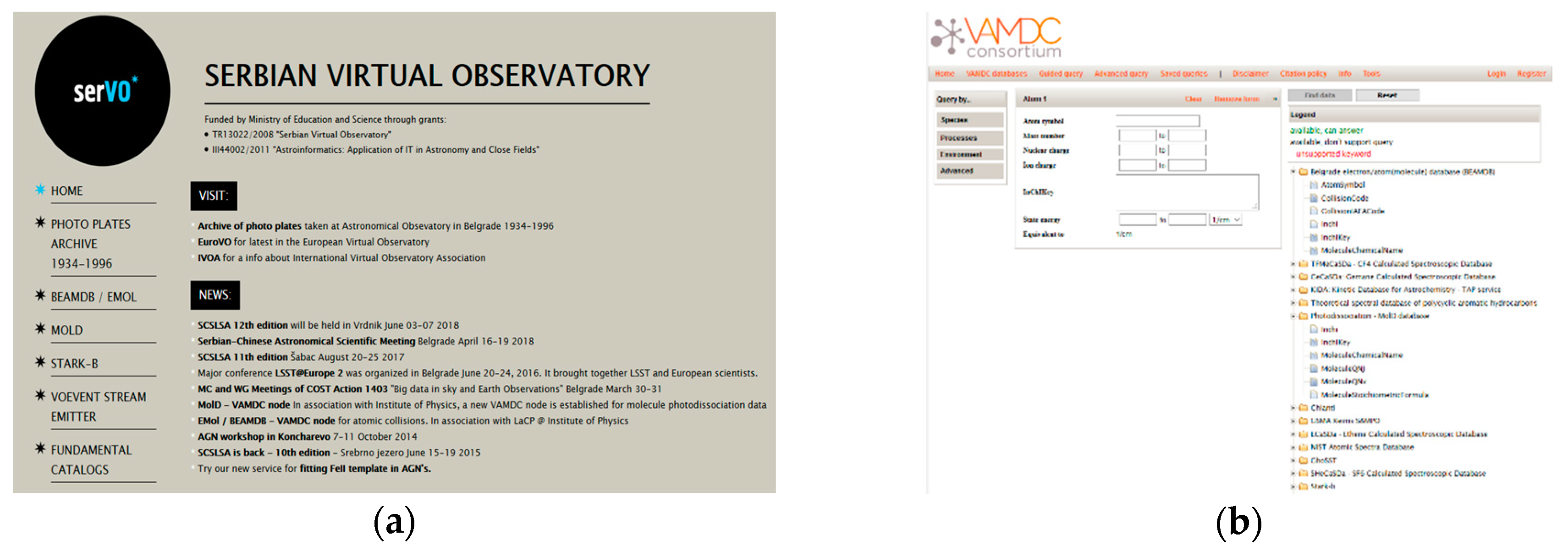
2. BEAMDB and MolD Database Nodes

The Belgrade nodes of VAMDC are hosted by SerVO (see Figure 1a) and currently consists of two databases BEAMDB (servo.aob.rs/emol) and MolD (servo.aob.rs/mold). These databases have been developed using the standards developed and operated by the VAMDC project [6] (see Figure 1b). VAMDC and SerVO have been through several different stages of development. SerVO (http://servo.aob.rs/) is a project formally created in 2008 but it originated in 2000, when the first attempts to organize data and to create a kind of web service were made in the BELDATA project, the precursor of SerVO. VAMDC started on 1 July 2009 as a FP7-funded project and originally was to be developed with about 20 databases, but the portal now has more than 33 operational databases [7].

We are currently in a transition phase updating the software “platform” (Python update, Django, XSAMS evolution, new Query Store on VAMDC, etc.) as the consequence of the rapid development and expansion of our two databases. Some current technical characteristics and aspects of these databases will be briefly introduced here (for details see [4]). Access to the BEAMDB and MolD data is possible via Table Access Protocol (TAP), a Virtual Observatory standard for a web service or via AJAX (Asynchronous JavaScript and XML)-enabled web interface (http://servo.aob.rs/). Both queries return data in XSAMS (XML Schema for Atoms, Molecules and Solids) format. The XSAMS schema provides a framework for a structured presentation of atomic, molecular, and particle‒solid interaction data in an XML file. The underlying application architecture is written in Django, a Python web framework, and represents a customization and extension of VAMDC’s NodeSoftware [8,9].

2.1. BEAMDB—Belgrade Electron/Atom(Molecule) DataBase

The origins of this database date from the early ideas of developing an Information System in Atomic Collision Physics [10] and at first it provided only cross sections for electron interactions with neutral atoms and molecules [11]. However the database has now been extended to cover electron spectra (energy loss and threshold) and ionic species [4].

Maintaining databases on cross sections and other collisional data, such as different types of spectra, is important for several reasons. One is to provide a comprehensive set of data to both researchers and applied scientists or engineers who need such data to design and make better devices and products. On the other hand, we need basic data to be able to include them in sophisticated models and to understand more complex processes, one of recent example is the use of electron cross section data for oxygen and water molecules in order to reveal for the role of electron induced processing in the coma of Comet 67P/Churyumov-Gerasimenko during the Rosetta mission [12]. Such an analysis clearly demonstrated the need for comprehensive datasets of electron‒molecule collisions in format that is readily accessible and understandable to the space community. Electron collision cross sections are also a subject of databases with the particular interest in plasma processes data. An overview of such databases is given by Huo and Kim [13] and White et al. [14], with the emphasis on the role of electron collisional data in gases and surfaces in plasma processes. Another database specialized for modelling in low-temperature plasma is the LXCat database [15]. The compilation of electron scattering data from atoms and molecules has a rich history. After the discovery of the electron in 1897 by J. J. Thompson (see more about his route and how he conducted the experiments in [16]), a series of experiments on how electron beams behave by passing through a gas started to develop. The discovery of electron was followed by intense research of its interactions with matter, such that several Nobel Prizes were awarded for such studies: in 1904 to Philipp E. A. von Lenard for his “work on cathode rays”; in 1906 to Joseph J. Thomson “in recognition of the great merits of his theoretical and experimental investigations on the conduction of electricity by gases”; and in 1925 to James Franck and Gustav Ludwig Hertz “for their discovery of the laws governing the impact of an electron upon an atom.” Carl W. Ramsauer at Danzig Technische Hochschule and Sir John S. Townsend at Oxford University independently studied the scattering of electrons of low energy by atoms and discovered an effect of occurrence of minima in total cross section that was named after them. The Ramsauer–Townsend effect was also observed in electron scattering from the methane molecule at the end of the 1920s and beginning of the 1930s, when electron collision studies were pioneered at St. John’s College and Trinity College, Cambridge. Dymond and Watson [17] made the first direct determination of the scattering curve for slow electrons by helium atom. Arnot [18] performed scattering experiments in mercury vapour, while Bullard and Massey [19] performed experiments over a wider range of scattering angles in order to observe maxima and minima in scattering curves by argon atoms demonstrating diffraction phenomena. In parallel, the theoretical description of elastic scattering emerged on the basis of quantum wave mechanics by Mott [20] and later was fully developed by Mott and Massey [21]. Theoretical calculations producing cross sections have advanced over the years as the use of quantum mechanics allowed new methods to be developed, such as the time-independent close-coupling approach and R-matrix approach used to study low-energy collisions [22], relativistic convergent close-coupling method [23], distorted-wave Born approach [24] absorption potential [25] and optical potential method [26] to study high-energy collisions [27]. A special advantage of the time-independent close-coupling approach is its possibility of providing a guide to uncertainty estimates of the calculated values.

As an example of how BEAMDB may be used, we will discuss a review of electron scattering from methane. The methane molecule as well as other hydrocarbons have been identified as sources of infrared absorption in the atmospheres of giant planets. Novel measurements of IR spectra allow more precise determination of the methane content in these atmospheres [28]. It is considered that it is constituent of the atmosphere of Uranus, with an abundance of 2.3%, and of Neptune of 1.5%. It plays a very important role in the photochemistry processes on Neptune [29]. It is also considered as one of the major greenhouse gases in the Earth’s atmosphere [30].

2.1.1. Elastic Electron Scattering by Methane Molecule—Early Experiments

The methane molecule is one of the molecules for which we have a relatively complete dataset for electron interactions. The electronic structure of methane is representative of most bio-molecules with its valence molecular orbitals being delocalized over the entire nuclear frame. As discussed by Herzberg [31], at first glance it is not obvious which conformation of C and H atoms would be the most stable and to which point group it should be attributed: a regular tetrahedron (T_d), a non-regular tetrahedron (C_3v), or square planar form (D_4h). In the T_d point group representation the highest occupied molecular orbitals (HOMO) of methane are of a₁ and t₁ symmetry, so the ground state of methane has a configuration 1(a₁)²2(a₁)²1(t_2x)²1(t_2y)²1(t_2z)² [32]. The pairing of all electrons in the HOMO makes methane a closed-shell compound. The binding energy of the lowest MO 2(a₁) is −18.8 eV, the energy of the three 1t₂ orbitals is −10.6 eV, while the first LUMO 3(a₁) is at +1.99 eV and the second 2t₂ is +3.90 eV [33].

The first measurements of electron differential elastic cross sections (DCS) for methane was performed in 1931 by Arnot [34] and by Bullard and Massey [35]. Arnot measured DCSs at higher impact energies of 30, 84, 205, 410 and 820 eV, while Bullard and Massey used lower incident electron energies of 4, 6, 10, 20 and 30 eV and covered an angular range from 20° to 120° in steps of 10°, except at an incident energy of 10 eV, where an additional point was measured at 125°. A close resemblance of between the DCS of methane and that of an argon atom was recognized. From this observation, the authors opened up the possibility of considering scattering by heavy atoms in terms of successive electron shells [35]. In 1932 Mohr and Nicoll [36] also measured DCS for methane at incident energies of 30, 52 and 84 eV, covering the full accessible angular range up to 150°. Hughes and McMillen [37] investigated the interference effects between the electron waves scattered by individual atoms as indicated by the presence of maxima in the curves for the ratios of the DCSs for different hydrocarbon molecules. For methane they measured DCS at 11 incident energies in the range from 10 eV to 800 eV and in the angular range from 10° to 150°.

2.1.2. Elastic Electron Scattering by Methane Molecule—Modern Experiments and Calculations

Gianturco and Thompson [32] used a model of scattering by a rigid molecule with inclusion of exchange and polarisation (with an ad hoc short range cutoff parameter) effects in an approximate way in order to calculate differential cross sections at low electron energies. For CH₄ they used the scattering states of symmetry A_l, T_I, T₂ and E, except A₂, was found to be of little importance for low-energy scattering, with A₁ and T₂ being found to be the most important. The exchange effects were included in each of these states. The results were presented graphically for 9.5 eV incident electron energy and for three cutoffs, r_o = 0.92; 0.88 and 0.84. The authors concluded that it was not possible to give a single r_o that gives complete agreement with the wide variety of experimental data, which reflects the crudeness of their model, but a good feature of the model is the correct incorporation of the static potential, calculated from good molecular wavefunctions. For intermediate and higher electron energies, from 205 to 820 eV, Dhal et al. [38] calculated DCS using the first Born, the Eikonal and the two-potential approximations including the polarisation and exchange effects. In these calculations no account was taken of the absorption effects that would certainly improve the accuracy of the calculated data.

New experiments exploring vibrationally elastic cross sections were performed by Rohr [39] at energies below 10 eV, i.e., at 1, 2 and 5 eV and from 10° to 120° using an spectrometer that consists of an electron monochromator to produce a high-resolution electron beam and a rotatable electron analyser capable of resolving the vibrational modes in energy loss mode, both systems had 127° electrostatic selectors. Absolute DCS were obtained by a normalization to the integral cross sections obtained in transmission experiments by other authors. A comprehensive study of differential, integral and momentum transfer cross sections was reported by Tanaka et al. [40] for elastic e/CH₄ scattering. They performed measurements using a crossed electron beam, molecular beam apparatus with the relative flow technique allowing the elastic DCS of CH₄ to be derived by comparison with those of He. DCSs were measured at electron impact energies of 3, 5, 6, 7.5, 9, 10, 15, and 20 eV for scattering angles from 30° to 140°. The authors concluded that the angular distribution in the energy region of 3 to 7.5 eV is dominated by a d-wave scattering as was theoretically predicted and also established experimentally at 5 eV. Later the same authors remeasured the elastic DCS with a new spectrometer for impact energies from 1.5–100 eV and scattering angles from (10°–130°) and it was found that the previous values were systematically lower by about 30–35% [41].

Using the same set of data for normalization, Vušković and Trajmar [42] obtained DCSs for elastic scattering as well as inelastic cross sections by recording energy-loss spectra at incident energies of 20, 30 and 200 eV. The set of data obtained at 200 eV was normalized to the data by Dhal et al. [38]. All measured relative angular dependences were corrected for effective path length variation with scattering angle.

A group from University College London used an electron spectrometer, incorporating hemispherical electrostatic energy analysers, and a crossed beam of target molecules in order to measure elastic and vibrational excitation cross sections at low incident electron energies from 7.5 to 20 eV and scattering angles from 32° to 142° [43].

After the measurements by Rohr [39] at the University of Kaiserslautern, Sohn et al. [44] investigated threshold structures in the cross sections of low-energy electron scattering of methane. They also presented the measurements of angular dependences (DCS) at 0.6 and 1.0 eV from 35° to 105° scattering angles. Müller et al. [45] investigated the rotational excitation in vibrationally elastic e/CH₄ collisions and presented vibrationally elastic (rotationally summed) differential cross sections at the primary energies 5, 7.5 and 10 eV. They normalized their results to the previous measurements of Tanaka et al. [40]. Sohn et al. [46], with an improved (in comparison with [45]) crossed-beam spectrometer, measured DCSs at low energies in the range from 0.2 to 5.0 eV in the angular range between 15° and 138°. With the aid of a phase-shift analysis, integrated cross sections were calculated as well, but the absolute DCS scale was obtained by the relative flow technique, using He as a reference gas.

Further DCS measurements at intermediate and high electron incident energies were made by Sakae et al. [47]. The angular range was 5°–135° and the electron energies were 75, 100, 150, 200, 300, 500 and 700 eV. Absolute DCS were determined by using He as the known reference DCS. Data were presented as rotationally and vibrationally summed elastic DCS, with the overall uncertainty being estimated at approximately 10%. Shyn and Cravens [48] measured differential vibrationally elastic scattering cross sections from 5 to 50 eV and from 12° to 156°. The beam of methane molecules was modulated at a frequency of 150 Hz so that the pure beam signal could be separated from the background using a phase-sensitive detector. The overall uncertainty of data was about 14%, including the uncertainty of the He cross sections (filled into the chamber for normalization), from which relative curves were placed on an absolute scale.

Jain and Thompson [49] calculated cross sections for low electron-molecule scattering using a local exchange potential and polarisation potential introducing a first-order wavefunction. DCS were calculated at 3 and 5 eV using three different types of potentials, one parameter-free polarisation potential and two phenomenological potentials. Abusalbi et al. [50] calculated ab initio interaction potentials for e/CH₄ scattering at 10 eV impact energy. Jain [51] exploited a spherical optical complex potential model to investigate, over a wide energy range (0.1–500 eV), electron interactions with methane. The whole energy range was divided into three regions; (i) from 0.1 to 1.0 eV in which a Ramsauer‒Townsend minimum is observed in the total cross section; (ii) between 2 and 20 eV where the scattering is dominated by a d-wave broad structure around 7–8 eV; and (iii) from 20 to 500 eV, where ionization and dissociation dominate over the elastic process. It was found that an absorption potential using the distorted charge density is more successful than one with polarized density and that the elastic cross sections are reduced significantly by including the imaginary part in the optical potential.

Gianturco et al. [52] used a parameter-free treatment of the interaction e/CH₄ and calculated cross sections for low energies. Functional forms of exchange and polarisation interactions were examined to find their importance over the whole range of collision energies. McNaughten et al. [53] reported rotationally elastic DCSs in the 0.1–20 eV energy region using the parameter-free model polarisation potential with electron exchange treated exactly and distortion effects included. Lengsfield, [54] used the complex Kohn method with polarized trial functions at incident energies from 0.2 to 10 eV. The latter was the first ab initio study to accurately characterize low-energy electron-methane scattering.

Later Gianturco et al. [55] calculated vibrational elastic, rotationally summed cross sections with ab initio static-exchange interactions and using a symmetry-adapted, single-centre expansion (SCE) representation for the close-coupling (CC) equations. Elastic DCS were obtained at energies 10, 15, 20, 30 and 50 eV. Nishimura and Itikawa [56] calculated vibrationally elastic DCS at 10 to 50 eV impact electron energies using an ab initio electrostatic potential and treating exchange and polarization in approximate way. Nestmann et al. [57] employed the variational R-matrix theory based on the fixed-nuclei approximation in order to calculate DCSs at low energies, i.e., 0.2, 0.5, 0.7, 1.5, 2.5, 3.5 and 5.0 eV. The structures in the calculated DCSs are shifted to smaller angles compared with the experimental results due to the omission of nonadiabatic effects.

Mapstone and Newell [58] reported measurements of hydrocarbon molecules at incident energies from 3.2 to 15.4 eV using electron spectrometer with hemispherical analysers both in monochromator and analyser. They first determined volume correction factors by using a phase shift analysis for helium DCS as a reference gas and then normalized relative values to the data of Tanaka et al. [32]. Bundschu et al. [59] performed a combined experimental and theoretical study for low-energy electron interactions with methane molecule. They determined absolute DCS at energies from 0.6 to 5.4 eV and within the angular range from 12° to 132.5°. Elastic differential cross sections were calculated using a body-fixed, SCE for the CC equations.

A group at Wayne State University, although primarily interested in positron scattering by methane [60], also measured electron elastic cross sections at 15, 20 and 200 eV. Their electron beam was produced as secondary electrons from the moderator with the energy spread of several electronvolts. Maji et al. [61] measured elastic DCSs for a number of carbon-containing molecules at the high-energy region from 300 to 1300 eV by the crossed-beam technique. They wanted to test the validity of the independent atom model for polyatomic molecules. The measurements of DCS were carried out with an energy resolution of about 1 eV and by using the relative flow method at 30° where the overall uncertainty was 15%. Basavaraju et al. [62] gave tabulated values for measured DCSs in [61] and obtained a scaled DCSs regarded as a universal function of a scaled momentum transfer for a number molecular targets.

Iga et al. [63] performed a joint theoretical (for 1–500 eV) and experimental (100–500 eV) investigation on e/CH₄ elastic scattering. Within the complex optical potential method they used the Schwinger variational iterative procedure combined with the distorted-wave approximation to calculate the scattering amplitudes. Experimentally, they used the relative flow technique and neon as the reference gas. The overall experimental uncertainty in the obtained absolute DCSs was about 10.3%. Lee et al. [64], on the basis of previous calculations, tested an improved version of the quasifree scattering model (QFSM) potential proposed by Blanco and García [25].

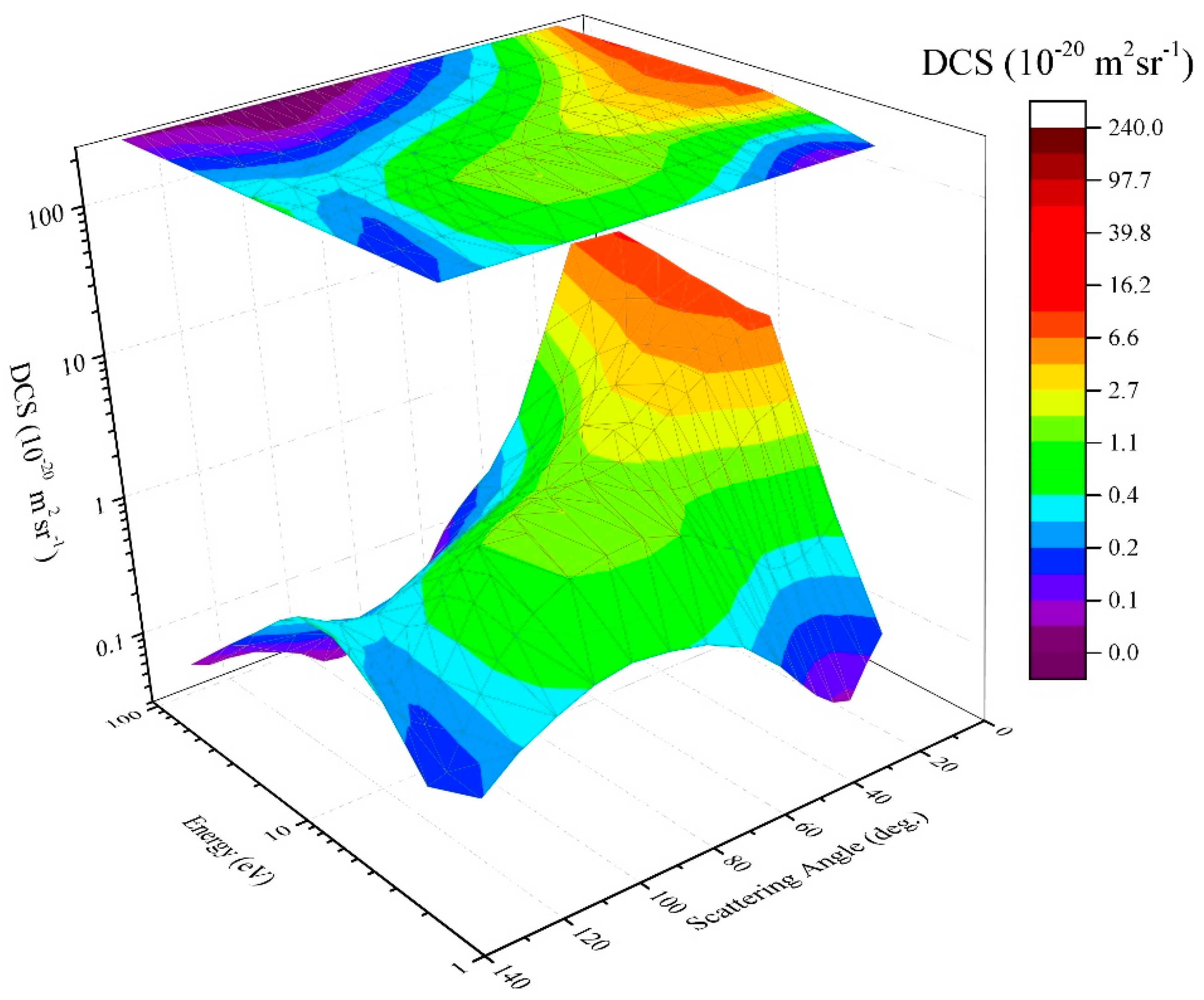
2.1.3. Elastic Electron Scattering by Methane Molecule—The Twenty-First Century Results

Bettega et al. [65] reported elastic DCSs for a class of molecules, (XH₄) among them methane, at incident electron energies between 3 and 10 eV using the Schwinger multichannel method with pseudopotentials. They demonstrated the importance of polarization effects in elastic collisions. Absolute differential elastic and vibrational excitation cross sections were measured by Allan [66] who exploited the improved resolution of the electron spectrometer in Fribourg to achieve the separation for all four vibrational modes within 0.4 eV from elastic peak at the impact energies from 0.1 to 1.5 eV. Varambhia et al. [67] and Tennyson [27] presented a sophisticated R-matrix approach to calculations of low-energy electron alkane collisions. DCSs were obtained for rotationally summed elastic scattering and the graphs were presented at 3.0 and 5.0 eV incident energies. Brigg et al. [68] performed R-matrix calculations at energies between 0.02 and 15 eV using a series of different ab initio models for both the target and the full scattering system.

Fedus and Karwasz [69] investigated the depth and position of the Ramsauer‒Townsend minimum in methane by applying the MERT theory (Modified Effective Range Theory). They presented the results at incident energies from 0.2 to 1.5 eV and compared them with other results. They were able to put forward the recommended set of data for integral and momentum transfer data for methane at energies from 10⁻³ to 2.0 eV. Sun et al. [70] used a difference converging method (DCM) to predict accurate values of experimentally unknown DCSs. They presented vibrationally elastic cross section at 5.0 eV.

2.1.4. Elastic Electron Scattering by Methane Molecule—Coverage in the BEAMDB

Elastic cross sections for electron scattering by molecular targets comprise the majority of data items within the BEAMDB. Molecular targets covered by the present database are: alanine, formamide, tetrahydrofuran, hydrogen sulfide, pyrimidine, N-methylformamide, water, furan, nitrous oxide, and newly added datasets for methane. Currently there are 17 datasets for elastic DCSs for methane, spanning from 1931 (Arnot [34] and Bullard and Massey [35]) to the most recent work by Iga et al. [63]. For example, in Figure 2 we present in 3D graphical form one of the rather complete sets of data by Boesten and Tanaka [41] that have been used by many researchers for comparison and/or normalization.

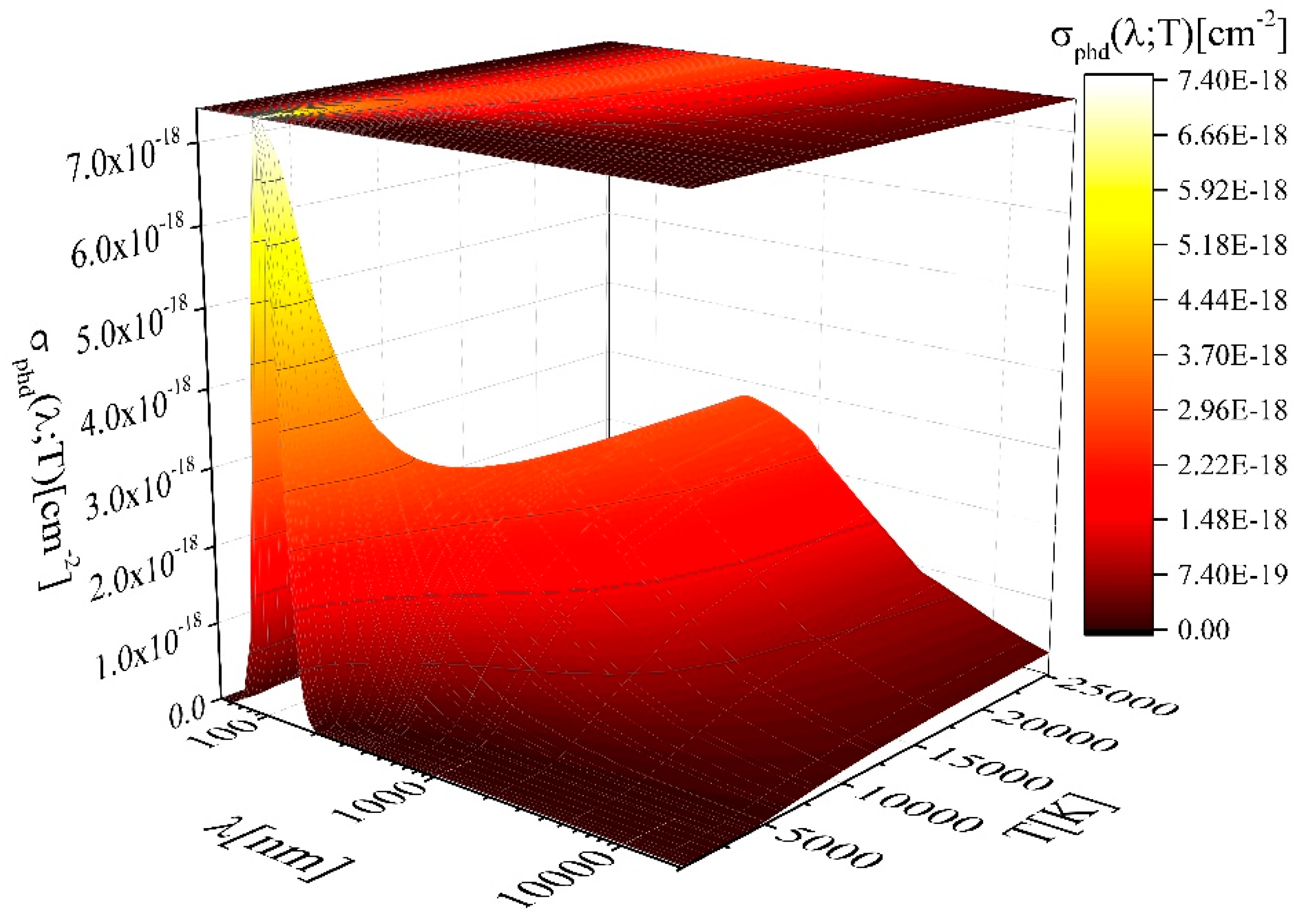
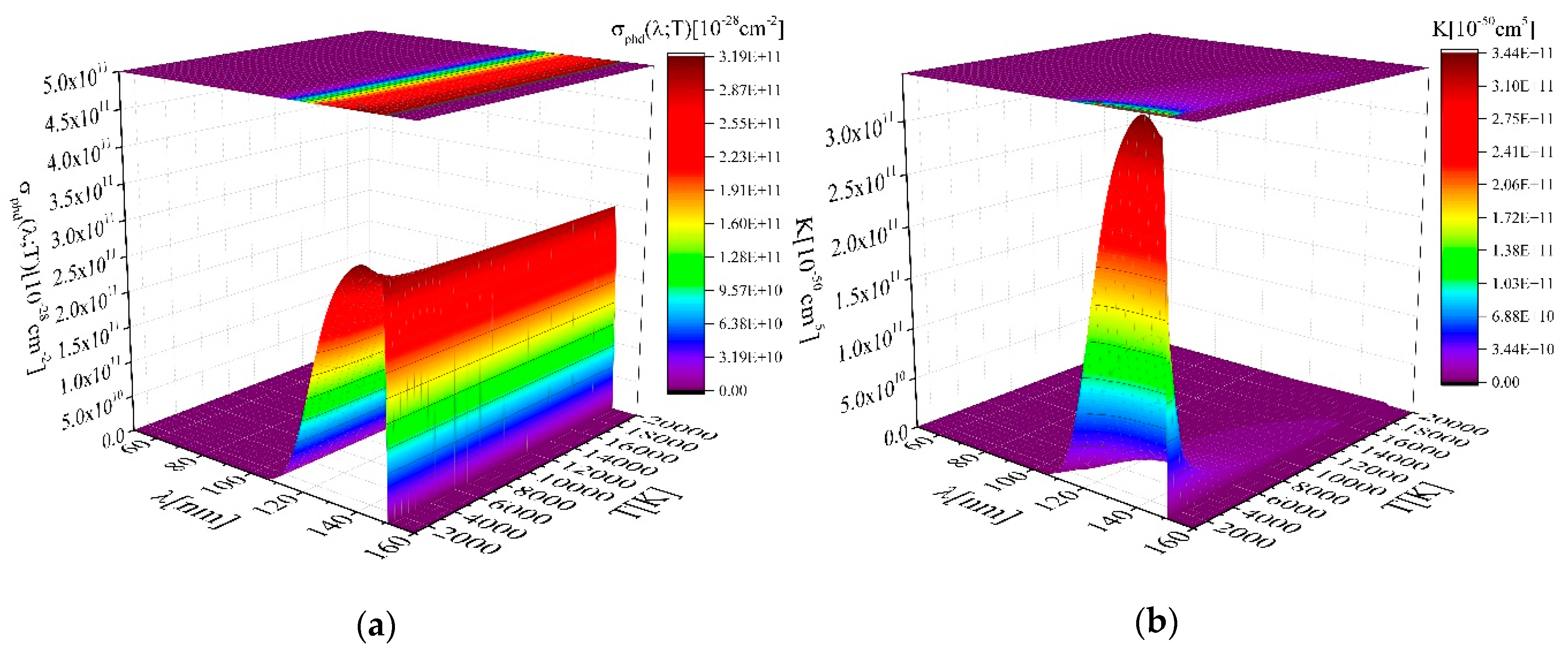
2.2. Photodissociation—The MolD Database

MolD as a part of SerVO and VAMDC is intensively used by astrophysicists for model atmosphere calculations of solar and near solar-type stars, atmospheric parameter determinations, etc. as well as for theoretical and laboratory plasma research [71,72,73,74,75,76]. Such data are also important for astrochemistry and especially for studies of early Universe chemistry (see e.g., Heathcote et al. [74]). MolD consists of several components such as data collection, and user interface tools (e.g., on-site AJAX enabled queries and visualizations).

The database contains photodissociation cross sections for the individual rovibrational states of the diatomic molecular ions as well as corresponding data on molecular species and molecular state characterizations (rovibrational energy states, etc.). These cross sections can be summed and averaged (Figure 3) for further applications, e.g., obtaining rate coefficients (see Figure 4) for non-local thermal equilibrium models of early universe chemistry (Coppola et al. [77]), models of the solar atmosphere, or models of the atmospheres of white dwarfs (Wen & Han [78]), etc.

The cross sections are obtained using a quantum mechanical method where the photodissociation process is treated as result of radiative transitions between the ground and the first excited adiabatic electronic state of the molecular ion (see e.g., Ignjatović et al., 2014b [79]). The transitions are the outcome of the interaction of the electronic component of ion-atom systems with the electromagnetic field in the dipole approximation.

MolD offers on-site services that include calculation of the average thermal cross sections based on temperature for a specific molecule and wavelength. Besides acting as a VAMDC compatible web service, accessible through VAMDC portal and other tools implemented using VAMDC standards, MolD offers additional on-site utilities enable the plotting of average thermal cross sections along available wavelengths for a given temperature.

The MolD database was developed in three stages [80,81]. The first, completed at the end of 2014, was characterized by the construction of the service for all photodissociation data for hydrogen H₂⁺ and helium He₂⁺ molecular ions, together with the development of web interface and some utility programs. In stage 2, completed at the end of 2016, to MolD have been added averaged thermal photodissociation cross sections for H₂⁺ and helium He₂⁺ molecular ions as well as new cross sections for processes that involve species like diatomic molecular ions HX⁺, where X = Mg, Li, Na. During 2017, in stage 3, MolD implemented cross section data for processes involving MgH⁺, HeH⁺, LiH⁺, NaH⁺, H₂⁺, He₂⁺. In this third stage, the design of the web interface was also improved and utility programs that allow online data visualization of a wide range of data were developed. The third stage of the MolD development was completed at the beginning of 2018 and has been followed by work on a major upgrade of the MolD database, including inserting new photodissociation data (for Na₂⁺, Li₂⁺ and LiNa⁺). All of these data have possible applications in spectroscopy, low-temperature laboratory plasma created in gas discharges, e.g., in microwave discharges at atmospheric pressure [82]. Processes that involve alkali metals are also important for the optical properties and modelling of weakly ionized layers of different stellar atmospheres and rate coefficients are also needed as input parameter for models of the Io atmosphere [83]. The data may also be important in the investigation of metal-polluted white dwarfs and dusty white dwarfs, interstellar gas chemistry, etc. [84].

2.3. Node Maintenance

As VAMDC recently introduced Query Store, a new paradigm for dataset citation (see Zwölf et al. [85]), NodeSoftware upgrade was necessary at the Belgrade server. In order for latest pull of NodeSoftware repository (v12.7) from GitHub to work, Django was upgraded from version 1.4 to 1.11.2. The code is still running on Python 2.7, due to requirements of some other services running at the same server, but will be transferred to Python 3.x in the near future [86].

VAMDC has accepted the suggestion of Research Data Alliance, a research community organization [87], to implement the concept of Query Store. Now that Query Store is enabled, each query is persisted as a unique resource (with an identifier) with its pertinent citations and can be recreated even if data or schema at the host node change, as explained by Moreau et al. [88]. In this way, the connection between the citation and the dataset is straightforward and it can be interconnected with existing scientific infrastructures via Zenodo DOI request. This will increase the impact of data producers and will give more reliable citation of datasets.

3. Conclusions

This review presents the continuation of the work performed on database development at Serbian Virtual Observatory. The SVO is now addressing the challenge of upgrading software and continuous improvements of data processing. The changes since the last publication in 2017 include data for new targets like methane, hydrogen sulfide and rare gas atoms. The upgrades and new standards for databases include:

• Developing of the VAMDC Portal as a Major Enabler of Atomic and Molecular Data Citation;
• Python, Django updates;
• Installing the Query Store on VAMDC node that could have a plan store for holding the execution plan information, and a runtime stats store for carrying on the execution statistics information.
• XSAMS evolution to deal with Big Data (resources to be accessed by diverse client platforms across the network; generating and transferring data over a network without requiring human-to-human or human-to-computer; provide security and data quality; etc.).

In this paper, as examples of exploitation of the datasets in the database, we have reviewed the available results on elastic scattering of electron by methane molecule for both experiments and theoretical treatments, covering the ranges of incident energies and scattering angles. By comparing the collected datasets for methane we have been able to show that, although it has been extensively studied in the past, there is a need for new measurements in the intermediate electron impact energy range. Hydrogen sulfide data should be contrasted with data for water molecule and that will be one of our future goals. Data for rare gas atoms, especially helium and argon, may serve as reference gases with the well-established cross sections in relative flow method for upbringing unknown cross sections on absolute scale.

We have also shown that MolD may be used to reveal the surface plot of the averaged cross section and rates for photodissociation of the HLi⁺ are given, as well as averaged cross sections for photodissociation of the hydrogen molecular ion H₂⁺ as a function of λ and T.