Abstract
Hydrogen atoms, being subjected to a strong magnetic field, exhibit an additional, delocalized potential well at almost a microscopic distance from the nucleus. We studied the influence of the delocalized states of hydrogen atoms on the number of observable hydrogen lines in strongly magnetized plasmas. We show that, for sufficiently large values of the pseudomomentum K (K being the integral of the motion controlling the separation of the center of mass and the relative motions), this effect dominates other factors potentially influencing the number of observable hydrogen lines in strongly magnetized plasmas. We provide examples for plasma parameters relevant to edge plasmas of contemporary and future tokamaks, as well as for DA white dwarfs. We demonstrate that our results open up an avenue for the experimental determination of the pseudomomentum K. This is the first proposed method for the experimental determination of the pseudomomentum—to the best of our knowledge.
1. Introduction
For hydrogenic atoms, there are numerous studies of the coupling of the relative and center-of-mass motions in a magnetic field B—see, e.g., papers [1,2,3,4,5,6,7,8] (listed in the reverse chronological order) and references therein. Due to the coupling, these two kinds of motion cannot be separated in the general case. Luckily, for hydrogen atoms, the situation allows a pseudoseparation. As a result, the relative motion is described by a Hamiltonian that does not depend on the coordinate R of the center of mass, but depends on the quantity canonically conjugated to R called the pseudomomentum K [6]. The latter is the integral of the motion, i.e., the conserved quantity.
In paper [9], it was shown that in a non-uniform electric field, these two motions cannot be separated exactly. They can be separated only by using the approximate analytical method of separating rapid and slow subsystems.
In paper [10] we wrote:
“Under a uniform magnetic field, the strongest center-of-mass effect is that the diamagnetic potential term in the Hamiltonian for the relative motion can become responsible for the formation of an additional potential well (hereafter, B-well)—far away from the hydrogen nucleus (proton). For relatively strong magnetic fields B, the new bound states inside the B-well are delocalized states of almost macroscopic dimensions”.
In the present paper, we consider the effect of the B-well on the number of observable hydrogen lines. We show that for sufficiently large values of the pseudomomentum K, this effect dominates the other factor (the Lorentz field) influencing the number of observable hydrogen lines in a strong magnetic field. We demonstrate that our results make possible the experimental determination of this atomic physics quantity—the pseudomomentum K.
2. Details of the Effect
In paper [10] we wrote:
“In the Hamiltonian of the relative (internal) motion for the hydrogen atom in a magnetic field B, the potential energy has the form (see, e.g., Schmelcher–Cederbaum paper [11], Equation (6))
where K is the pseudomomentum, M is the mass of the hydrogen atom, c is the speed of light, and e is the electron charge. We follow paper [11] in choosing e < 0; we also note that in paper [11] it was set at c = 1. In Equation (1), (B × K)r stands for the scalar product (also known as the dot product) of vector r and vector (B × K)”.
V = [e2/(2Mc2)](B × r)2 − [|e|/(Mc)B × K)r − e2/r,
The first term in Equation (1) is the diamagnetic one; the second term is due to the motional Stark effect; the third term represents the Coulomb interaction.
In paper [11], its authors chose the following configuration: B = (0, 0, B), K = (0, K, 0), where K > 0. Here, we use the same choice. Then, Equation (1) can be written as
V = [e2B2/(2Mc2)](x2 + y2) + [|e|BK/(Mc)]x − e2/(x2 + y2 + z2)1/2.
It is important to emphasize the following. The general expression for the pseudomomentum is (see, e.g., paper [2]):
where re and rp are the radius vectors of the electron and proton, respectively. For the values of K~102 a.u. (a.u. standing for atomic units) or greater, the last term in the right side of Equation (3) predominates, so that the pseudomomentum characterizes electron–proton separation rather than velocity—see, e.g., papers [1,2]. We are interested in the values of K~102 a.u. or greater, so that in view of the predominance of the last term in the right side of Equation (3), it is clear that vector K is practically perpendicular to the magnetic field B. Therefore, the choice of B = (0, 0, B), K = (0, K, 0) is appropriate. (In any case, it is the component of K perpendicular to B that causes the appearance of the second potential well and is responsible for the rich physics of the system.)
K = mp drp/dt + me dre/dt − (e/c) B × (re − rp),
We denote:
Vs = Mc2V/(e2B2).
Physically, the quantity Vs is the scaled potential energy. Then, Equation (2) takes the form:
Vs = (x2 + y2)/2 + [Kc/(|e|B)]x − Mc2/[B2(x2 + y2 + z2)1/2].
With respect to the y- and z-coordinates, the minimum of the potential occurs at y = z = 0 [9]. Then, we calculate
∂Vs/∂x = x + Kc/(|e|B) + Mc2x/[B2(x2 + y2 + z2)3/2].
Along the line of y = z = 0, Equation (6) simplifies to:
where, as usual, sign x = −1 for x < 0 or sign x = 1 for x > 0.
∂Vs/∂x = x + Kc/(|e|B) + (Mc2/B2) (sign x)/x2,
The right side of Equation (7) vanishes if
x3 + [Kc/(|e|B)]x2 + (Mc2/B2)(sign x) = 0.
For x > 0, Equation (8) reads as
x3 + [Kc/(|e|B)]x2 + (Mc2/B2) = 0.
It is easy to see that there are no positive roots of this equation.
For x < 0, Equation (8) reads as
which is mathematically equivalent to Equation (8b) from paper [9] (where their authors set e = −1 and c = 1.
|x|3 − [Kc/(|e|B)]|x|2 + (Mc2/B2) = 0.
In paper [10], we wrote:
“The polynomial in Equation (10) has either two or zero real roots. Thus, the total number of roots of Equation (8) is also either two or zero—since there are no positive roots.
We note in passing that the authors of paper [9] erroneously stated that ∂V/∂x, calculated at y = z = 0, can have three real roots. Their error originates from the fact that they missed the factor (sign x) in the corresponding equation.
We introduce the scaled magnetic field b and the scaled pseudomomentum k, as follows
where b has the dimension of cm−3/2 and k has the dimension of cm−1/2. Below, while using particular numerical values of b and k, we omit the dimensions for brevity”.
b = B/(cM1/2), k = K/(|e|M1/2),
In the scaled notations, Equation (10) reads as
|x|3 − (k/b)|x|2 + 1/b2 = 0.
This cubic equation has the following discriminant:
Δ = (4k3 − 27b)/b5.
If Δ > 0, i.e., if
k > kmin, kmin = 3(b/4)1/3 ≈ 1.89 b1/3.
Then, Equation (12) has two real negative roots different from each other.
In the non-scaled units:
Kmin(a.u.) ≈ 0.375 [B(Tesla)]1/3.
We remind that the atomic unit, in which Kmin is measured in the left side of Equation (15), is the atomic unit of any linear momentum—it is equal to
me|e|2/ħ ≈ 1.99 × 10−19 g cm/s.
Below is the Cardano’s solution for the two real roots x1 and x2 of the cubic Equation (12):
x1 = − k/(3b) − (1 + 31/2i) k2/{22/33b [27b − 2k3 + 33/2(27b2 − 4k3b)1/2]1/3} −
(1 − 31/2i) [27b − 2k3 + 33/2(27b2 − 4k3b)1/2]1/3/(21/36b).
(1 − 31/2i) [27b − 2k3 + 33/2(27b2 − 4k3b)1/2]1/3/(21/36b).
x2 = − k/(3b) − (1 − 31/2i) k2/{22/33b [27b − 2k3 + 33/2(27b2 − 4k3b)1/2]1/3} −
(1 + 31/2i) [27b − 2k3 + 33/2(27b2 − 4k3b)1/2]1/3/(21/36b).
(1 + 31/2i) [27b − 2k3 + 33/2(27b2 − 4k3b)1/2]1/3/(21/36b).
The above expressions yield real values for x1 and x2 under the condition (14)—regardless of the formal appearance of the imaginary unit i in these expressions. For example, for the root x2, this is analytically proven in Appendix A.
For sufficiently large values of the pseudomomentum K, such that
the expressions for the roots of Equation (12) simplify to:
k >> b1/3,
x1 ≈ –k/b, x2 ≈ 1/(kb)1/2.
Under condition (14), the scaled potential energy Vs reaches the maximum at x = x2 and exhibits the minimum at x = x1. At y = z = 0, the scaled potential energy Vs has the form:
Vs = x2/2 + kx/b − 1/(b2|x|).
Figure 1 depicts the dependence of the scaled potential energy Vs from Equation (21) on the coordinate x (in cm) for b = 1.04 × 109 (corresponding to B = 40,000 Tesla, such as, e.g., in the DA white dwarfs) and k = 19,200 corresponding to K = 60 a.u. (solid line). The dashed line corresponds to the energy Etop at the top of the potential barrier.
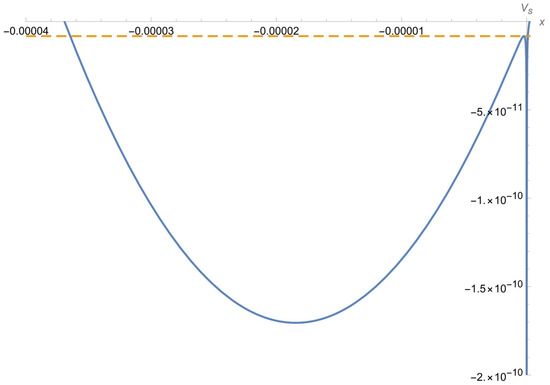
Figure 1.
The dependence of scaled potential energy Vs from Equation (21) on the coordinate x (in cm) for b = 1.04 × 109 (corresponding to B = 40,000 Tesla) and k = 19,200 corresponding to K = 60 a.u. (solid line). The dashed line corresponds to the energy at the top of the potential barrier.
Here, we come to the central point. For hydrogen energy levels below the top of the potential barrier (E < Etop), the atomic electron is confined in a relatively narrow potential well. However, for the energy levels at or above the top of the potential barrier, the width of the potential well increases by several orders of magnitude (for sufficiently large values of the pseudomomentum K). According to the uncertainty relation, this means that, in the latter case, the spacing of the energy levels decreases by several orders of magnitude. Since these energy levels have a finite width (e.g., due to the collisional and natural broadenings), the dramatic decrease of the spacing between these energy levels creates a quasi-continuum out of them and thus causes the atomic electron to be practically free from the proton. This is equivalent to the ionization on the atom.
Moreover, the above reasoning related only to the x-coordinate. However, in reality, the location of the B-well on the x-axis corresponds in three dimensions to the saddle point. Therefore, the atomic electron, excited to the top or above the top of the potential barrier, would get far away from the proton through the saddle point—even regardless of the one-dimensional considerations of the sudden decrease of the spacing of the energy levels and the formation of the quasi-continuum. In other words, in the three-dimensional picture, our main conclusion of the ionization of the atom (when the atomic electron is excited at or above the top of the potential barrier) would be actually reinforced.
Thus, this mechanism (the lowering of the top of the potential barrier) limits the number of the discrete energy levels En by the condition:
Etop > En = − mee4/(2 ħ2n2).
At the top of the potential barrier (i.e., at x = x2), under the condition (19) the scaled potential energy is
Vs,top ≈ −2k1/2/b3/2.
The corresponding value of the non-scaled potential energy is
Es = Vs,top ≈ −2|e|3/2[KB/(Mc)]1/2.
From Formulas (22) and (24), it is easy to obtain the following expression for the maximum principal quantum number nmax,B (caused by the presence of the B-well):
where a0 is the Bohr radius. The practical formula for nmax,B is:
where B is in Tesla and K is in atomic units (a.u.).
nmax,B = [|e|Mc/(16a02BK)]1/4,
nmax,B ≈ 72/(BK)1/4,
Hydrogen atoms moving across the magnetic field experience the Lorentz field ELT, whose average value is ELT = BvT/c, where vT = (2T/M)1/2 is the atomic thermal velocity. In papers [12,13], it was shown that, under the Lorentz field, the principal quantum number nmax,L of the last observable hydrogen line (while disregarding the effect of the B-well) is:
(the letter L in the subscript stands for Lorentz field).
nmax,L = [me2|e|5c/(3ħ4vTB)]1/5
By the way, in papers [12,13], it was shown that the average Lorentz field exceeds the most probable ion microfield Ei when the magnetic field B exceeds the following critical value: Bc(Tesla) = 4.69 × 10−7Ne(cm−3)2/3/[T(K)]1/2. Thus, under this condition, the effect of the ion microfield on the number of observable hydrogen lines can be neglected.
It is worth mentioning that the simultaneous usage of the average velocity vT and a certain value of the pseudomomentum K is legitimate. In paper [14], it was stated that the dependence of the energy E on the pseudomomentum (the latter being denoted as P in paper [14]) allows one to determine the mean velocity of the atom for a given (i.e., fixed) P:
<v> = ∂E/∂P.
By comparing Equations (25) and (27), it is easy to find out that the presence of the B-well controls the number of the observable hydrogen lines (i.e., nmax,B < nmax,L) for sufficiently large values of the pseudomomentum
K > Kcrit = (M/16)[81|e|cvT4/(a02B)]1/5.
The practical formula for the critical pseudomomentum value is:
where Kcrit is in a.u., T is in eV, and B is in Tesla.
Kcrit ≈ 57(T2/B)1/5,
Now, let us consider some examples. For B = 5 Tesla, Equation (25) yields nmax,B = 15 for K = 100 a.u. or nmax,B = 11 for K = 300 a.u. We note that B = 5 Tesla can be created in many labs—such magnets are used, e.g., in contemporary tokamaks.
Superconductive magnets, such as, e.g., the MIT fusion magnet, create B = 20 Tesla [15]. For B = 20 Tesla, Equation (25) yields nmax,B = 10 for K = 100 a.u. or nmax,B = 8 for K = 300 a.u.
The atmospheres of DA white dwarfs (i.e., of the white dwarfs emitting hydrogen lines) are characterized by magnetic fields B from 100 to 100,000 Tesla. For B = 2000 Tesla, Equation (25) yields nmax,B = 4 for K = 50 a.u.
In all of the above examples, the principal quantum number of the last observable hydrogen line is controlled by nmax,B < nmax,L.
Thus, the primary effect of the diamagnetic term in the Hamiltonian is the creation of the B-well causing the decrease of the number of observable hydrogen lines. Compared to this primary effect, other effects of the diamagnetic term—those discussed in paper [16]—are just minor, secondary outcomes.
Our results open up an avenue for the experimental determination of the pseudomomentum K. Indeed, from Equation (25) one gets:
K(a.u.) ≈ (nmax,B/72)4/B(Tesla).
Thus, from the experimental values of the magnetic field B and the number nmax,B of the last observable hydrogen line, it is possible to deduce the value of the pseudomomentum by using Equation (29). This is the first proposed method for the experimental determination of the pseudomomentum—to the best of our knowledge.
We remind again that for K~102 a.u. or greater, i.e., for the values of K considered in the present paper, from measuring the atomic velocity it is impossible to deduce the value of the pseudomomentum. At this range of values, K is controlled by the vector product of the magnetic field B and the electron proton separation (re − rp)—see Equation (3) and the paragraph after Equation (3). Therefore, for this range of K, there is no other method to measure K, except the method we suggest.
Now, we analyze the accuracy of Equations (25) and (29) obtained using the asymptotic result for the root x2 from Equation (20) valid for relatively large values of the pseudomomentum (such that k >> b1/3). For this purpose, we use the following exact expression for the root x2 in the trigonometric form, which is more compact than the corresponding exact result (18) and does not contain the imaginary unit i (see, e.g., handbooks [17,18])
where
x2 = −k/(3b) + [2k/(3b)] cos(α/3 + π/3),
α = arccos [1 − 27b/(2k3)].
Then, the scaled energy at the top of the potential barrier becomes:
Vs,top = {−k/(3b) + [2k/(3b)] cos(α/3 + π/3)}2/2 + k{−k/(3b) + [2k/(3b)] cos(α/3 + π/3)}/b −
1/{b2| − k/(3b) + [2k/(3b)] cos(α/3 + π/3)|}.
1/{b2| − k/(3b) + [2k/(3b)] cos(α/3 + π/3)|}.
Figure 2 presents the coordinate x2 of the top of the potential barrier versus the scaled pseudomomentum k for the scaled magnetic field b = 1.3 × 106 (corresponding to B = 5 Tesla). The solid line is the exact result from Equation (32), the dashed line—the asymptotic result from Equation (20). It is seen that for values of k close to kmin given by Equation (14), kmin being equal to 206 for b = 1.3 × 106, there is a significant difference between the exact and asymptotic results, but the difference becomes practically negligible for values of k just a few times greater than kmin.
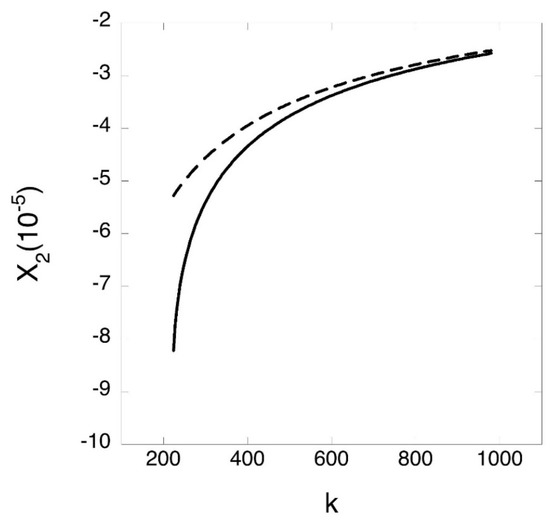
Figure 2.
The coordinate x2 of the top of the potential barrier versus the scaled pseudomomentum k for the scaled magnetic field b = 1.3 × 106 (corresponding to B = 5 Tesla). The solid line is the exact result from Equation (32), the dashed line—the asymptotic result from Equation (20).
Figure 3 shows the scaled energy Es = Vs,top at the top of the potential barrier versus the scaled pseudomomentum k for the scaled magnetic field b = 1.3 × 106 (corresponding to B = 5 Tesla). The solid line is the exact result from Equation (34), the dashed line—the asymptotic result from Equation (23). It is seen that even for values of k close to kmin, the difference is practically negligible. Thus, Equations (25) and (29), obtained by using the asymptotic value of Vs,top from Equation (23), yield the sufficient accuracy.
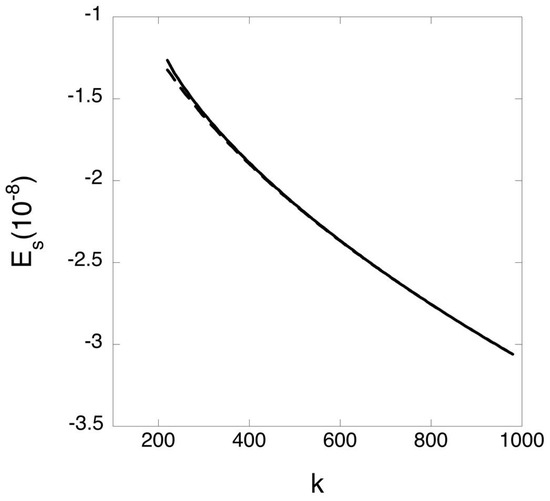
Figure 3.
The scaled energy Es = Vs,top at the top of the potential barrier versus the scaled pseudomomentum k for the scaled magnetic field b = 1.3 × 106 (corresponding to B = 5 Tesla). The solid line is the exact result from Equation (34), the dashed line—the asymptotic result from Equation (23).
3. Conclusions
We analyzed the influence of the delocalized states of hydrogen atoms (the B-well) on the number of observable hydrogen lines in strongly magnetized plasmas. We demonstrated that for sufficiently large values of the pseudomomentum K (K being the integral of the motion controlling the separation of the center of mass and the relative motions), this effect dominates the other factor—the Lorentz field—affecting the number of observable hydrogen lines. We gave examples for several, quite realistic values of the magnetic field.
We showed that our results open up an avenue for the experimental determination of the pseudomomentum K. This is the first proposed method for the experimental determination of this atomic physics quantity—the pseudomomentum—to the best of our knowledge.
The pseudomomentum seems to be the least-studied atomic physics quantity. In addition to the fundamental importance, the experimental determination of the pseudomomentum has, e.g., the practical relevance to the application of Dirac’s Generalized Hamiltonian Dynamics (GHD) to atomic systems. In Dirac’s GHD, the constraints are added to the Hamiltonian. For applying Dirac’s GHD to atomic/molecular systems and obtaining the detailed classical (rather than quantum) description of such systems, the authors of paper [19] successfully modified Dirac’s GHD by using integrals of the motion as the constraints added to the Hamiltonian. As a result, e.g., for hydrogen atoms, they obtained classical non-radiating states of the same discrete set of energies, as in the quantum description. In this respect, the knowledge of particular experimental values of the pseudomomentum, which is the integral of the motion, is crucial for applying the modified GHD from paper [19] to a hydrogen atom in a strong magnetic field and achieving the detailed classical description of the whole system (including the degrees of freedom corresponding not only to the relative motion, but also to the center-of-mass motion). We remind that the detailed classical description of atomic systems provides the physical insight that the quantum description lacks.
Finally, we note that in atomic experiments, hydrogen atoms could have one certain value of the pseudomomentum K. However, in plasma experiments, there could be a distribution of values of K over the ensemble—see, e.g., paper [1]. In this case, by using Equation (31), one would obtain the most probable value of K. This is similar to the situation where the number of the last observable hydrogen line nmax is controlled by the ion microfield F in plasmas: nmax was considered to be related to the most probable value of F—see, e.g., the Inglis–Teller paper [20] and the Griem book [21].
Author Contributions
All authors contributed equally to the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data are included in the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Analytical Proof that Equation (18) Yields Real Values
First, we note that in Equation (18) for x2
1 ± i31/2 = 2 exp(± iπ/3).
Any complex number γ + i δ can be written as
where Arctan(δ/γ) is a multibranch function and p is any positive or negative integer or zero. Consequently,
γ + i δ = (γ2 + δ2)1/2 exp{i [Arctan(δ/γ) + 2pπ]},
(γ + i δ)1/3 = (γ2 + δ2)1/6 exp{i [Arctan(δ/γ)]/3 + 2pπi/3}.
Then, Equation (18) can be represented in the form:
x2 = −k/(3b) − 2[β/(γ2 + δ2)1/6] exp{−i [Arctan(δ/γ)]/3 − (2p + 1)πi/3} −
2[(γ2 + δ2)1/6/ε] exp{i [Arctan(δ/γ)]/3 + (2p + 1)πi/3}.
2[(γ2 + δ2)1/6/ε] exp{i [Arctan(δ/γ)]/3 + (2p + 1)πi/3}.
In Equation (A4):
γ2 + δ2 = (27b − 2k3)2 + 27(4bk3 − 27b2), β = k2/(22/33b), ε = 21/36b.
Equation (A4) can be further rewritten as
x2 = −k/(3b) − u exp(−iv) − w exp(iv) = −k/(3b) − u(cos v − i sin v) − w(cos v + i sin v) =
−k/(3b) − (u + w)cos v + i(u − w)sin v.
−k/(3b) − (u + w)cos v + i(u − w)sin v.
In Equation (A6):
u = 2β/(γ2 + δ2)1/6, w = 2(γ2 + δ2)1/6/ε.
Now, we will show that u = w, that is,
or
2β/(γ2 + δ2)1/6 = 2(γ2 + δ2)1/6/ε
(γ2 + δ2)1/3 = βε.
By substituting into Equation (A9) the corresponding expressions from Equation (A5), we find that both the left and the right side of Equation (A9) are equal to 22/3k2. Thus, Equation (A8) is the identity, so that indeed u = w and the right side of Equation (18) is a real quantity.
References
- Potekhin, A.Y.; Shabrier, G.; Shibanov, Y.A. Partially ionized hydrogen plasma in strong magnetic fields. Phys. Rev. E 1999, 60, 2193. [Google Scholar] [CrossRef] [PubMed]
- Potekhin, A.Y. Hydrogen atom moving across a strong magnetic field: Analytical approximations. J. Phys. B At. Mol. Opt. Phys. 1998, 31, 49. [Google Scholar] [CrossRef]
- Schmelcher, P.; Cederbaum, L.S. Classical self-ionization of fast atomic ions in magnetic fields. Phys. Rev. Lett. 1995, 74, 662. [Google Scholar] [CrossRef] [PubMed]
- Schmelcher, P.; Cederbaum, L.S. Intermittent chaos in Hamiltonian systems: The three-dimensional hydrogen atom in magnetic fields. Phys. Rev. A 1993, 47, 2634. [Google Scholar] [CrossRef] [PubMed]
- Vincke, M.; le Dorneuf, M.; Baye, D. Hydrogen atom in crossed electric and magnetic fields: Transition from weak to strong electron-proton decentring. J. Phys. B At. Mol. Opt. Phys. 1992, 25, 2787. [Google Scholar] [CrossRef]
- Vincke, M.; Baye, D. Centre-of-mass effects on the hydrogen atom in a magnetic field. J. Phys. B At. Mol. Opt. Phys. 1988, 21, 2407. [Google Scholar] [CrossRef]
- Johnson, B.R.; Hirshfelder, J.O.; Yung, K.-H. Interaction of atoms, molecules, and ions with constant electric and magnetic fields. Rev. Mod. Phys. 1983, 55, 109. [Google Scholar] [CrossRef]
- Burkova, L.A.; Dzyaloshinskii, I.E.; Drukarev, G.F.; Monozon, B.S. Hydrogen-like system in crossed electric and magnetic fields. Sov. Phys. JETP 1976, 44, 276. [Google Scholar]
- Oks, E. Center-of-Mass Effects for Hydrogen Atoms in a Nonuniform Electric Field: Applications to Magnetic Fusion, Radiofrequency Discharges, and Flare Stars. J. Phys. Commun. 2018, 2, 045005. [Google Scholar] [CrossRef]
- Oks, E.; Dalimier, E.; Angelo, P. A Supersensitive Method for Spectroscopic Diagnostics of Electrostatic Waves in Magnetized Plasmas. Plasma 2021, 4, 780. [Google Scholar] [CrossRef]
- Schmelcher, P.; Cederbaum, L.S. Two-body effects of the hydrogen atom in crossed electric and magnetic fields. Chem. Phys. Lett. 1993, 208, 548–554. [Google Scholar] [CrossRef]
- Oks, E. Aspects of Lorentz-Stark broadening of hydrogen spectral lines in magnetized, turbulent and non-turbulent plasmas important for magnetic fusion and solar physics Intern. Intern. Rev. At. Mol. Phys. 2013, 4, 105–119. [Google Scholar]
- Oks, E. Role of Lorentz-Stark Broadening of Hydrogen Spectral Lines in Magnetized Plasmas: Applications to Magnetic Fusion and Solar Physics. J. Quant. Spectrosc. Rad. Transfer. 2015, 156, 24. [Google Scholar] [CrossRef]
- Pavlov, G.G.; Meszaros, P. Finite-velocity effects on atoms in strong magnetic fields and implications for neutron star atmospheres. Astrophys. J. 1993, 416, 752. [Google Scholar] [CrossRef]
- MIT-News. MIT-Designed Project Achieves Major Advance toward Fusion Energy. Available online: https://news.mit.edu/2021/MIT-CFS-major-advance-toward-fusion-energy-0908 (accessed on 16 August 2022).
- Rosato, J. Hydrogen Line Shapes in Plasmas with Large Magnetic Fields. Atoms 2020, 8, 74. [Google Scholar] [CrossRef]
- Korn, G.A.; Korn, T.M. Mathematical Handbook for Scientists and Engineers; McGraw Hill: New York, NY, USA, 1968. [Google Scholar]
- Polyanin, A.D.; Manzhirov, A.V. Handbook of Mathematics for Engineers and Scientists; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Oks, E.; Uzer, T. Application of Dirac’s generalized Hamiltonian dynamics to atomic and molecular systems. J. Phys. B At. Mol. Opt. Phys. 2002, 35, 165. [Google Scholar] [CrossRef]
- Inglis, D.R.; Teller, E. Ionic Depression of Series Limits in One-Electron Spectra. Astrophys. J. 1939, 90, 439. [Google Scholar] [CrossRef]
- Griem, H.R. Spectral Line Broadening by Plasmas; Academic: New York, NY, USA, 1974. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).