Cooling Process of White Dwarf Stars in Palatini f(R) Gravity
Abstract
1. Introduction
2. Basic Formalism of Palatini Gravity and Hydrostatic Balance Equations
3. Temperature Gradient Equation and Cooling Timescale of White Dwarfs in Gravity
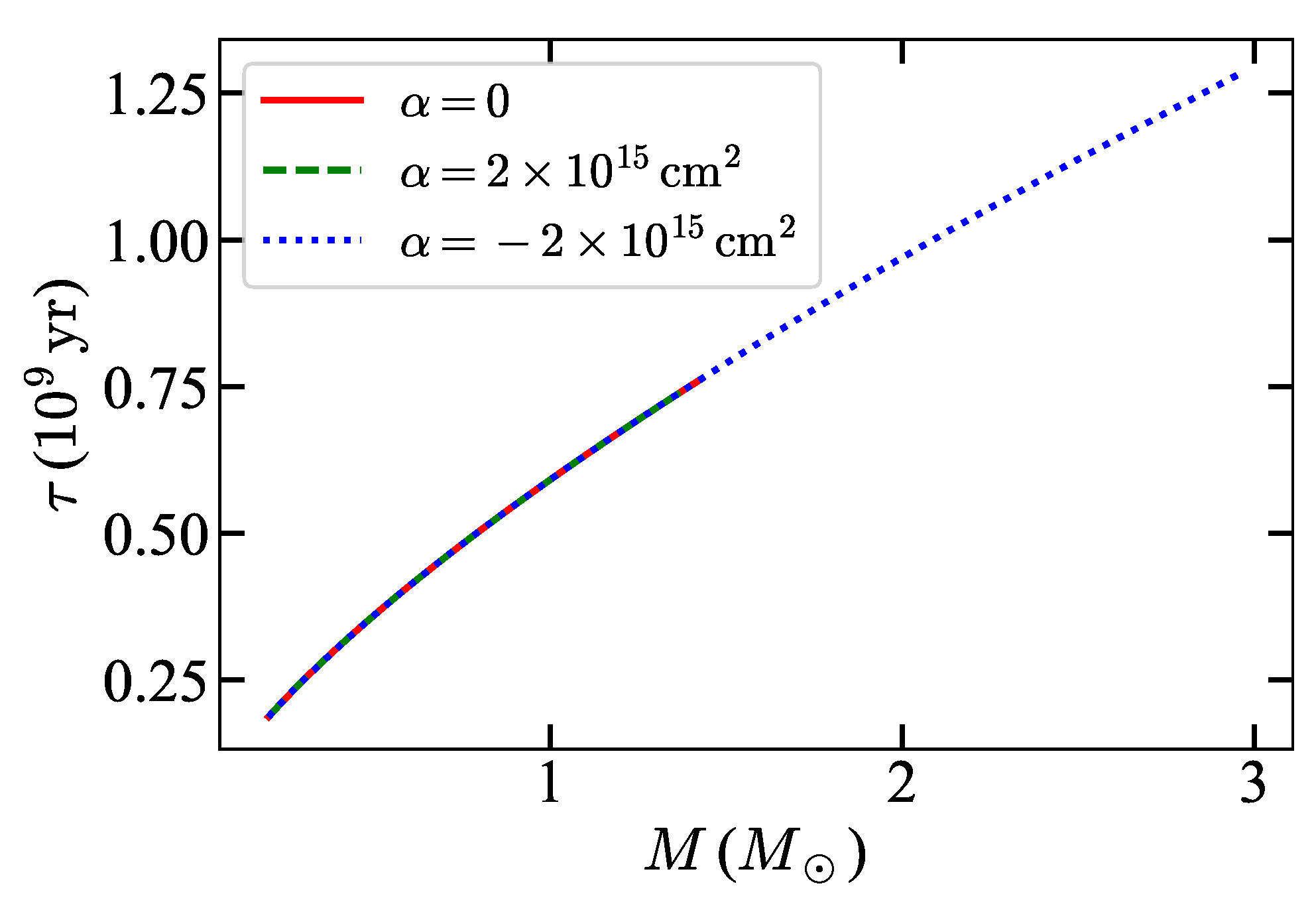
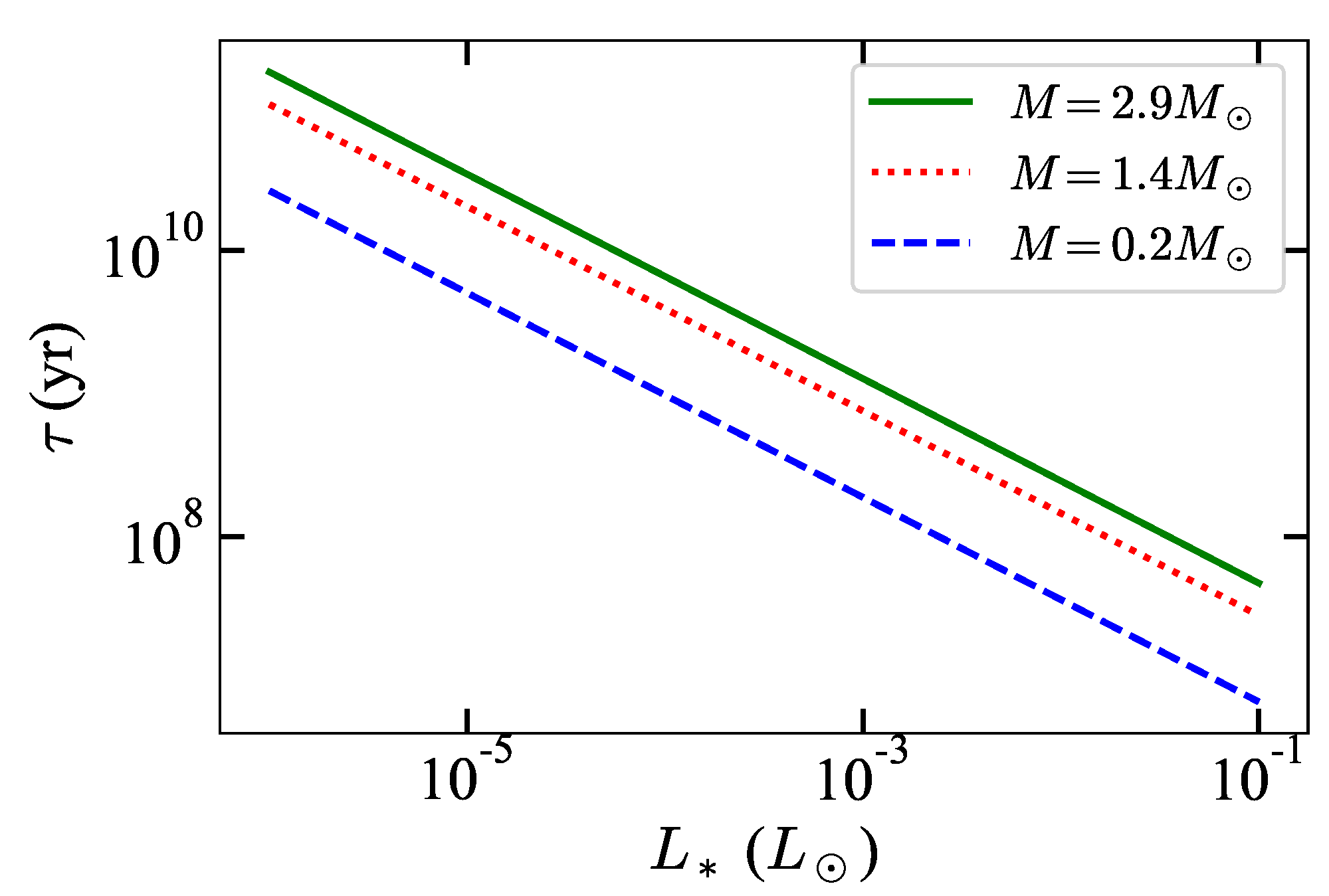
4. Mass–Radius Relation and Cooling Age of White Dwarfs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Although, one can rewrite the equations as second-order differential equations for the metric, and the additional one for the curvature scalar, which arises to a dynamical field in this theory. |
| 2 | This fact arises as a conclusion from the field equations and it will be evident in the next section, whereas in the metric formalism, the connection is assumed to be the Levi–Civita one of the spacetime metric. |
| 3 | To see the relativistic hydrostatic equilibrium equation for Palatini gravity, see [88]. |
| 4 | Let us notice that this form differs slightly from the one obtained in [43]. This is so because of different assumptions on the matter description and its behavior under the conformal transformation. |
| 5 | Of course, there are other processes, such as magnetic field [91,92], noncommutative geometry [93,94], ungravity effect [95], consequence of total lepton number violation [96], generalized Heisenberg uncertainty principle [97] and many more which can also explain massive white dwarfs but they are failing to explain the sub-Chandrasekhar mass-limit. |
References
- Carroll, S.M. Spacetime and Geometry: An Introduction to General Relativity; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Poisson, E.; Will, C.M. Gravity: Newtonian, Post-Newtonian, Relativistic; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astron. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Coles, P. Book Review: Cosmological inflation and large-scale structure/Cambridge University Press, 2000. Astron. Geophys. 2003, 44, 32. [Google Scholar]
- Huterer, D.; Turner, M.S. Prospects for probing the dark energy via supernova distance measurements. Phys. Rev. D 1999, 60, 081301. [Google Scholar] [CrossRef]
- Battaner, E.; Florido, E. The Rotation Curve of Spiral Galaxies and its Cosmological Implications. Fund. Cosmic. Phys. 2000, 21, 1–154. [Google Scholar]
- Gaskins, J.M. A review of indirect searches for particle dark matter. Contemp. Phys. 2016, 57, 496–525. [Google Scholar] [CrossRef]
- Taoso, M.; Bertone, G.; Masiero, A. Dark matter candidates: A ten-point test. J. Cosmol. Astropart. Phys. 2008, 2008, 22. [Google Scholar] [CrossRef]
- Bullock, J.S.; Boylan-Kolchin, M. Small-Scale Challenges to the ΛCDM Paradigm. arXiv 2017, arXiv:1707.04256. [Google Scholar] [CrossRef]
- Del Popolo, A.; Le Delliou, M. Small Scale Problems of the ΛCDM Model: A Short Review. Galaxies 2017, 5, 17. [Google Scholar] [CrossRef]
- Guzmán, F.S.; Matos, T.; Villegas, H.B. Scalar fields as dark matter in spiral galaxies: Comparison with experiments. Astron. Nachrichten 1999, 320, 97. [Google Scholar] [CrossRef]
- Gutiérrez-Luna, E.; Carvente, B.; Jaramillo, V.; Barranco, J.; Escamilla-Rivera, C.; Espinoza, C.; Mondragón, M.; Núñez, D. Scalar field dark matter with two components: Combined approach from particle physics and cosmology. Phys. Rev. D 2022, 105, 083533. [Google Scholar] [CrossRef]
- Borowiec, A.; Kamionka, M.; Kurek, A.; Szydłowski, M. Cosmic acceleration from modified gravity with Palatini formalism. J. Cosmol. Astropart. Phys. 2012, 2012, 27. [Google Scholar] [CrossRef]
- Koivisto, T.; Kurki-Suonio, H. Cosmological perturbations in the Palatini formulation of modified gravity. Class. Quantum Gravity 2006, 23, 2355. [Google Scholar] [CrossRef]
- Flanagan, E.E. Palatini form of 1/R gravity. Phys. Rev. Lett. 2004, 92, 071101. [Google Scholar] [CrossRef] [PubMed]
- Fay, S.; Tavakol, R.; Tsujikawa, S. f(R) gravity theories in Palatini formalism: Cosmological dynamics and observational constraints. Phys. Rev. D 2007, 75, 063509. [Google Scholar] [CrossRef]
- Sotiriou, T.P. Unification of inflation and cosmic acceleration in the Palatini formalism. Phys. Rev. D 2006, 73, 063515. [Google Scholar] [CrossRef]
- Dioguardi, C.; Racioppi, A.; Tomberg, E. Slow-roll inflation in Palatini F(R) gravity. J. High Energy Phys. 2022, 6, 106. [Google Scholar] [CrossRef]
- Gialamas, I.D.; Karam, A.; Racioppi, A. Dynamically induced Planck scale and inflation in the Palatini formulation. J. Cosmol. Astropart. Phys. 2020, 11, 14. [Google Scholar] [CrossRef]
- Dimopoulos, K.; Karam, A.; Sánchez López, S.; Tomberg, E. Palatini R2 Quintessential Inflation. J. Cosmol. Astropart. Phys. 2022, 2022, 76. [Google Scholar] [CrossRef]
- Szydłowski, M.; Stachowski, A.; Borowiec, A.; Wojnar, A. Do sewn up singularities falsify the Palatini cosmology? Eur. Phys. J. C 2016, 76, 567. [Google Scholar] [CrossRef]
- Szydłowski, M.; Stachowski, A.; Borowiec, A. Emergence of running dark energy from polynomial f(R) theory in Palatini formalism. Eur. Phys. J. C 2017, 77, 603. [Google Scholar] [CrossRef]
- Stachowski, A.; Szydłowski, M.; Borowiec, A. Starobinsky cosmological model in Palatini formalism. Eur. Phys. J. C 2017, 77, 406. [Google Scholar] [CrossRef]
- Allemandi, G.; Borowiec, A.; Francaviglia, M.; Odintsov, S.D. Dark energy dominance and cosmic acceleration in first order formalism. Phys. Rev. D 2005, 72, 063505. [Google Scholar] [CrossRef]
- Allemandi, G.; Borowiec, A.; Francaviglia, M. Accelerated cosmological models in Ricci squared gravity. Phys. Rev. D 2004, 70, 103503. [Google Scholar] [CrossRef]
- Allemandi, G.; Borowiec, A.; Francaviglia, M. Accelerated cosmological models in first order nonlinear gravity. Phys. Rev. D 2004, 70, 043524. [Google Scholar] [CrossRef]
- Capozziello, S.; de Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Lazkoz, R.; Salzano, V.; Moniz, P.V.; Capozziello, S.; Beltrán Jiménez, J.; De Laurentis, M.; Olmo, G.J. Modified Gravity and Cosmology; An Update by the CANTATA Network; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Heisenberg, L. Scalar-vector-tensor gravity theories. J. Cosmol. Astropart. Phys. 2018, 2018, 54. [Google Scholar] [CrossRef]
- Ferraro, R.; Fiorini, F. Modified teleparallel gravity: Inflation without an inflaton. Phys. Rev. D 2007, 75, 084031. [Google Scholar] [CrossRef]
- Buchdahl, H.A. Non-linear Lagrangians and cosmological theory. Mon. Not. R. Astron. Soc. 1970, 150, 1–8. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) theories of gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- Sotiriou, T.P. Constraining f(R) gravity in the Palatini formalism. Class. Quantum Gravity 2006, 23, 1253–1267. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified Gravity with ln R Terms and Cosmic Acceleration. Gen. Relativ. Gravit. 2004, 36, 1765–1780. [Google Scholar] [CrossRef]
- Amarzguioui, M.; Elgarøy, Ø.; Mota, D.F.; Multamäki, T. Cosmological constraints on f(R) gravity theories within the Palatini approach. Astron. Astrophys. 2006, 454, 707–714. [Google Scholar] [CrossRef]
- Borowiec, A.; Stachowski, A.; Szydłowski, M.; Wojnar, A. Inflationary cosmology with Chaplygin gas in Palatini formalism. J. Cosmol. Astropart. Phys. 2016, 2016, 40. [Google Scholar] [CrossRef]
- Järv, L.; Karam, A.; Kozak, A.; Lykkas, A.; Racioppi, A.; Saal, M. Equivalence of inflationary models between the metric and Palatini formulation of scalar-tensor theories. Phys. Rev. D 2020, 102, 044029. [Google Scholar] [CrossRef]
- Teppa Pannia, F.A.; García, F.; Perez Bergliaffa, S.E.; Orellana, M.; Romero, G.E. Structure of compact stars in R-squared Palatini gravity. Gen. Relativ. Gravit. 2017, 49, 25. [Google Scholar] [CrossRef]
- Herzog, G.; Sanchis-Alepuz, H. Neutron stars in Palatini R+αR2 and R+αR2+βQ theories. Eur. Phys. J. C 2021, 81, 888. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D.; Wojnar, A. Minimum main sequence mass in quadratic Palatini f(R) gravity. Phys. Rev. D 2019, 100, 044020. [Google Scholar] [CrossRef]
- Wojnar, A. Early evolutionary tracks of low-mass stellar objects in modified gravity. Phys. Rev. D 2020, 102, 124045. [Google Scholar] [CrossRef]
- Wojnar, A. Lithium abundance is a gravitational model dependent quantity. Phys. Rev. D 2021, 103, 044037. [Google Scholar] [CrossRef]
- Benito, M.; Wojnar, A. Cooling process of brown dwarfs in Palatini f(R) gravity. Phys. Rev. D 2021, 103, 064032. [Google Scholar] [CrossRef]
- Wojnar, A. Jupiter and jovian exoplanets in Palatini f(R¯) gravity. Phys. Rev. D 2021, 104, 104058. [Google Scholar] [CrossRef]
- Wojnar, A. Giant planet formation in Palatini gravity. Phys. Rev. D 2022, 105, 124053. [Google Scholar] [CrossRef]
- Kozak, A.; Wojnar, A. Metric-affine gravity effects on terrestrial exoplanet profiles. Phys. Rev. D 2021, 104, 084097. [Google Scholar] [CrossRef]
- Kozak, A.; Wojnar, A. Non-homogeneous exoplanets in metric-affine gravity. Int. J. Geom. Meth. Mod. Phys. 2022, 19, 2250157. [Google Scholar] [CrossRef]
- Kozak, A.; Wojnar, A. Interiors of Terrestrial Planets in Metric-Affine Gravity. Universe 2021, 8, 3. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D.; Wojnar, A. Stellar structure models in modified theories of gravity: Lessons and challenges. Phys. Rept. 2020, 876, 1–75. [Google Scholar] [CrossRef]
- Wojnar, A. Stellar and substellar objects in modified gravity. arXiv 2022, arXiv:2205.08160. [Google Scholar]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs and Neutron Stars: The Physics of Compact Objects; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Lauffer, G.R.; Romero, A.D.; Kepler, S.O. New full evolutionary sequences of H- and He-atmosphere massive white dwarf stars using MESA. Mon. Not. R. Astron. Soc. 2018, 480, 1547–1562. [Google Scholar] [CrossRef]
- Kalita, S.; Mukhopadhyay, B. Modified Einstein’s gravity to probe the sub- and super-Chandrasekhar limiting mass white dwarfs: A new perspective to unify under- and over-luminous type Ia supernovae. J. Cosmol. Astropart. Phys. 2018, 2018, 7. [Google Scholar] [CrossRef]
- Kalita, S.; Mukhopadhyay, B. Gravitational Wave in f(R) Gravity: Possible Signature of Sub- and Super-Chandrasekhar Limiting-mass White Dwarfs. Astron. J. 2021, 909, 65. [Google Scholar] [CrossRef]
- Wojnar, A. White dwarf stars in modified gravity. Int. J. Geom. Methods Mod. Phys. 2021, 18, 2140006. [Google Scholar] [CrossRef]
- Kalita, S.; Sarmah, L. Weak-field limit of f(R) gravity to unify peculiar white dwarfs. Phys. Lett. B 2022, 827, 136942. [Google Scholar] [CrossRef]
- Sarmah, L.; Kalita, S.; Wojnar, A. Stability criterion for white dwarfs in Palatini f(R) gravity. Phys. Rev. D 2022, 105, 024028. [Google Scholar] [CrossRef]
- Das, U.; Mukhopadhyay, B. Modified Einstein’s gravity as a possible missing link between sub- and super-Chandrasekhar type Ia supernovae. J. Cosmol. Astropart. Phys. 2015, 2015, 45. [Google Scholar] [CrossRef]
- Das, U.; Mukhopadhyay, B. Imprint of modified Einstein’s gravity on white dwarfs: Unifying Type Ia supernovae. Int. J. Mod. Phys. D 2015, 24, 1544026. [Google Scholar] [CrossRef]
- García-Berro, E.; Hernanz, M.; Isern, J.; Mochkovitch, R. The rate of change of the gravitational constant and the cooling of white dwarfs. Mon. Not. R. Astron. Soc. 1995, 277, 801–810. [Google Scholar] [CrossRef]
- Althaus, L.G.; Córsico, A.H.; Torres, S.; Lorén-Aguilar, P.; Isern, J.; García-Berro, E. The evolution of white dwarfs with a varying gravitational constant. Astron. Astrophys. 2011, 527, A72. [Google Scholar] [CrossRef]
- Córsico, A.H.; Althaus, L.G.; García-Berro, E.; Romero, A.D. An independent constraint on the secular rate of variation of the gravitational constant from pulsating white dwarfs. J. Cosmol. Astropart. Phys. 2013, 2013, 32. [Google Scholar] [CrossRef]
- Benvenuto, O.G.; Garcia-Berro, E.; Isern, J. Asteroseismological bound on Ġ/G from pulsating white dwarfs. Phys. Rev. D 2004, 69, 082002. [Google Scholar] [CrossRef]
- Saltas, I.D.; Sawicki, I.; Lopes, I. White dwarfs and revelations. J. Cosmol. Astropart. Phys. 2018, 2018, 28. [Google Scholar] [CrossRef]
- Liu, H.L.; Lü, G.L. Properties of white dwarfs in Einstein-Λ gravity. J. Cosmol. Astropart. Phys. 2019, 2019, 40. [Google Scholar] [CrossRef]
- Carvalho, G.A.; Lobato, R.V.; Moraes, P.H.R.S.; Arbañil, J.D.V.; Otoniel, E.; Marinho, R.M.; Malheiro, M. Stellar equilibrium configurations of white dwarfs in the f(R,T) gravity. Eur. Phys. J. C 2017, 77, 871. [Google Scholar] [CrossRef]
- Eslam Panah, B.; Liu, H.L. White dwarfs in de Rham-Gabadadze-Tolley like massive gravity. Phys. Rev. D 2019, 99, 104074. [Google Scholar] [CrossRef]
- Biesiada, M.; Malec, B. A new white dwarf constraint on the rate of change of the gravitational constant. Mon. Not. R. Astron. Soc. 2004, 350, 644–648. [Google Scholar] [CrossRef]
- Benvenuto, O.; Althaus, L.; Torres, D.F. Evolution of white dwarfs as a probe of theories of gravitation: The case of Brans—Dicke. Mon. Not. R. Astron. Soc. 1999, 305, 905–919. [Google Scholar] [CrossRef][Green Version]
- Bienaymé, O.; Turon, C.; Isern, J.; GarcíaBerro, E.; Salaris, M. White dwarfs as tools of fundamental physics: The gravitational constant case. Eur. Astron. Soc. Publ. Ser. 2002, 2, 123–128. [Google Scholar]
- Babichev, E.; Koyama, K.; Langlois, D.; Saito, R.; Sakstein, J. Relativistic stars in beyond Horndeski theories. Class. Quantum Gravity 2016, 33, 235014. [Google Scholar] [CrossRef]
- Crisostomi, M.; Lewandowski, M.; Vernizzi, F. Vainshtein regime in scalar-tensor gravity: Constraints on degenerate higher-order scalar-tensor theories. Phys. Rev. D 2019, 100, 024025. [Google Scholar] [CrossRef]
- Wibisono, C.; Sulaksono, A. Information-entropic method for studying the stability bound of nonrelativistic polytropic stars within modified gravity theories. Int. J. Mod. Phys. D 2018, 27, 1850051. [Google Scholar] [CrossRef]
- Biesiada, M.; Malec, B. White dwarf cooling and large extra dimensions. Phys. Rev. D 2002, 65, 043008. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. White dwarf cooling via gravity portals. Phys. Rev. D 2020, 101, 023017. [Google Scholar] [CrossRef]
- Isern, J.; García-Berro, E. White dwarf stars as particle physics laboratories. Nucl. Phys. B Proc. Suppl. 2003, 114, 107–110. [Google Scholar] [CrossRef]
- Banerjee, S.; Shankar, S.; Singh, T.P. Constraints on modified gravity models from white dwarfs. J. Cosmol. Astropart. Phys. 2017, 2017, 4. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) Theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef]
- Chavanis, P.H. Statistical mechanics of self-gravitating systems in general relativity: I. The quantum Fermi gas. Eur. Phys. J. Plus 2020, 135, 1–79. [Google Scholar] [CrossRef]
- Wojnar, A. Fermi gas and modified gravity. arXiv 2022, arXiv:2208.04023. [Google Scholar]
- Borowiec, A.; Ferraris, M.; Francaviglia, M.; Volovich, I. Universality of Einstein equations for the Ricci squared Lagrangians. Class. Quant. Grav. 1998, 15, 43–55. [Google Scholar] [CrossRef]
- Beltrán Jiménez, J.; Delhom, A. Ghosts in metric-affine higher order curvature gravity. Eur. Phys. J. C 2019, 79, 656. [Google Scholar] [CrossRef]
- Afonso, V.I.; Olmo, G.J.; Rubiera-Garcia, D. Mapping Ricci-based theories of gravity into general relativity. Phys. Rev. D 2018, 97, 021503. [Google Scholar] [CrossRef]
- Afonso, V.I.; Olmo, G.J.; Orazi, E.; Rubiera-Garcia, D. Mapping nonlinear gravity into General Relativity with nonlinear electrodynamics. Eur. Phys. J. C 2018, 78, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Afonso, V.I.; Olmo, G.J.; Orazi, E.; Rubiera-Garcia, D. Correspondence between modified gravity and general relativity with scalar fields. Phys. Rev. D 2019, 99, 044040. [Google Scholar] [CrossRef]
- Wojnar, A. On stability of a neutron star system in Palatini gravity. Eur. Phys. J. C 2018, 78, 421. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The highly collapsed configurations of a stellar mass (Second paper). Mon. Not. R. Astron. Soc. 1935, 95, 207–225. [Google Scholar] [CrossRef]
- Mestel, L. On the theory of white dwarf stars. I. The energy sources of white dwarfs. Mon. Not. R. Astron. Soc. 1952, 112, 583. [Google Scholar] [CrossRef]
- Das, U.; Mukhopadhyay, B. New Mass Limit for White Dwarfs: Super-Chandrasekhar Type Ia Supernova as a New Standard Candle. Phys. Rev. Lett. 2013, 110, 071102. [Google Scholar] [CrossRef]
- Kalita, S.; Mukhopadhyay, B. Continuous gravitational wave from magnetized white dwarfs and neutron stars: Possible missions for LISA, DECIGO, BBO, ET detectors. Mon. Not. R. Astron. Soc. 2019, 490, 2692–2705. [Google Scholar] [CrossRef]
- Kalita, S.; Mukhopadhyay, B.; Govindarajan, T.R. Significantly super-Chandrasekhar mass-limit of white dwarfs in noncommutative geometry. Int. J. Mod. Phys. D 2021, 30, 2150034. [Google Scholar] [CrossRef]
- Kalita, S.; Govindarajan, T.R.; Mukhopadhyay, B. Super-Chandrasekhar limiting mass white dwarfs as emergent phenomena of noncommutative squashed fuzzy spheres. Int. J. Mod. Phys. D 2021, 30, 2150101. [Google Scholar] [CrossRef]
- Bertolami, O.; Mariji, H. White dwarfs in an ungravity-inspired model. Phys. Rev. D 2016, 93, 104046. [Google Scholar] [CrossRef]
- Belyaev, V.B.; Ricci, P.; Šimkovic, F.; Adam, J.; Tater, M.; Truhlík, E. Consequence of total lepton number violation in strongly magnetized iron white dwarfs. Nucl. Phys. A 2015, 937, 17–43. [Google Scholar] [CrossRef][Green Version]
- Ong, Y.C. Generalized uncertainty principle, black holes, and white dwarfs: A tale of two infinities. J. Cosmol. Astropart. Phys. 2018, 9, 15. [Google Scholar] [CrossRef]
- Kozak, A.; Soieva, K.; Wojnar, A. Cooling process of substellar objects in scalar-tensor gravity. arXiv 2022, arXiv:2205.12812. [Google Scholar]
- Auddy, S.; Basu, S.; Valluri, S.R. Analytic models of brown dwarfs and the substellar mass limit. Adv. Astron. 2016, 2016, 5743272. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalita, S.; Sarmah, L.; Wojnar, A. Cooling Process of White Dwarf Stars in Palatini f(R) Gravity. Universe 2022, 8, 647. https://doi.org/10.3390/universe8120647
Kalita S, Sarmah L, Wojnar A. Cooling Process of White Dwarf Stars in Palatini f(R) Gravity. Universe. 2022; 8(12):647. https://doi.org/10.3390/universe8120647
Chicago/Turabian StyleKalita, Surajit, Lupamudra Sarmah, and Aneta Wojnar. 2022. "Cooling Process of White Dwarf Stars in Palatini f(R) Gravity" Universe 8, no. 12: 647. https://doi.org/10.3390/universe8120647
APA StyleKalita, S., Sarmah, L., & Wojnar, A. (2022). Cooling Process of White Dwarf Stars in Palatini f(R) Gravity. Universe, 8(12), 647. https://doi.org/10.3390/universe8120647







