Weak Field Limit for Embedding Gravity

Abstract

We study a perturbation theory for embedding gravity equations in a background for which corrections to the embedding function are linear with respect to corrections to the flat metric. The remaining arbitrariness after solving the linearized field equations is fixed by an assumption that the solution is static in the second order. A nonlinear differential equation is obtained, which allows for finding the gravitational potential for a spherically symmetric case if a background embedding is given. An explicit form of a spherically symmetric background parameterized by one function of radius is proposed. It is shown that this function can be chosen in such a way that the gravitational potential is in a good agreement with the observed distribution of dark matter in a galactic halo.

1. Introduction

Embedding gravity (also called embedding theory) [1] is a modified theory of gravity based on the idea of our spacetime as a 4D surface in a 10D flat space. From a geometric point of view, this approach renders the theory of gravity similar to string theory. In this case, the space–time metric is considered to be induced and has the form

$$g_{\mu \nu }=\left({\partial }_{\mu }{y}^a\right)\left({\partial }_{\nu }{y}^b\right){\eta }_{ab},$$

(1)

where ${\eta }_{ab}$ is a flat metric of the ambient space, and $y^a\left(x^{\mu }\right)$ is an embedding function defining the shape of the surface. Here and further $\mu ,\nu ,\dots =0,\dots ,3$ and $a,b,\dots =0,\dots ,9$. After the pioneering work of [1], the ideas of the embedding approach were repeatedly used in the works of various authors to describe gravity, including the problem of its quantization; see, for example, [2,3,4,5,6,7,8,9,10,11].

The embedding gravity equations of motion, called Regge–Teitelboim equations, are more general in comparison with Einstein’s equations $G^{\mu \nu }=\varkappa T^{\mu \nu }$ and have the following form:

$$\left(G^{\mu \nu }-\varkappa T^{\mu \nu }\right)b_{\mu \nu }^a=0,$$

(2)

where $b_{\mu \nu }^a$ is a second fundamental form of a 4D surface defined by an embedding function $y^a\left(x^{\mu }\right)$. All “Einsteinian” (i.e., satisfying Einstein’s equations) solutions satisfy the Regge–Teitelboim equations, but they do not exhaust the full set of solutions. There may be additional solutions for which $G^{\mu \nu }\ne \varkappa T^{\mu \nu }$; nevertheless, (2) is satisfied. Initially, this was seen as a disadvantage of the approach, since embedding gravity was understood as some reformulation of GR, potentially more convenient for quantization due to the presence of a flat ambient space. Therefore, it was proposed to additionally introduce Einstein constraints into the theory, rendering it truly equivalent to GR [1,12]. However, the presence of extra solutions in the theory can be considered to be an advantage.

If we assume that just the Regge–Teitelboim equations describe the gravitational interaction, from the point of view of describing observations in terms of the usual GR, extra solutions manifest themselves as an additional contribution to the right side of Einstein’s equations. It can be interpreted as the presence of some additional fictitious embedding matter that has nothing to do with ordinary matter. This contribution depends solely on the gravitational variables (which, in embedding theory, are $y^a\left(x^{\mu }\right)$), and its appearance is connected only with an attempt to reformulate a new theory in the old language. Since the direct detection of dark matter does not currently yield results [13,14], it is of interest to try to treat the embedding matter of the embedding theory as dark matter (and possibly as dark energy). Then, the effects associated with dark matter and energy are purely gravitational. In this way, observational problems that have no explanation within the framework of GR can be solved. The Regge–Teitelboim Equation (2) can be rewritten as a pair of equations

$$G^{\mu \nu }=\varkappa \left(T^{\mu \nu }+{\tau }^{\mu \nu }\right),$$

(3)

$${\tau }^{\mu \nu }{b}_{\mu \nu }^a=0,$$

(4)

i.e., in the form of a set of Einstein’s equations with the contribution of an energy–momentum tensor ${\tau }^{\mu \nu }$ of fictitious embedding matter and its equations of motion. This was first indicated in [15]. There are also modified theories of gravity which are alternative to the embedding gravity, equations of motion of which can be written in the form of Einstein’s equations supplemented by other equations. The most famous is mimetic gravity [16,17].

In order to obtain the properties of the embedding matter generated by embedding gravity (and thereby to understand whether they are similar to the properties of dark matter), it is necessary to investigate solutions of Equation (2). In general, due to their nonlinearity, this is too difficult a mathematical problem. So, we limit ourselves to the most physically interesting case of weak gravity, when metric $g_{\mu \nu }$ is close to flat metric ${\eta }_{\mu \nu }$. In this case, the problem arises in choosing a background value ${\overline{y}}^a\left(x^{\mu }\right)$ of the embedding function that would correspond to the flat metric. The simplest choice in the form of ${\overline{y}}^a\left(x^{\mu }\right)$, which defines a 4D plane in the ambient space, is unsuitable since, in such a background, Regge–Teitelboim Equations (2) are not linearized [2]. To linearize the equations, it is necessary to choose "unfolded" embedding [18] as the background, which means that the second fundamental form of the surface is nondegenerate in some sense.

In this paper, we use the unfolded embedding of the Minkowski metric, which is the product of a timelike line $y^I=const$ (we use indices $I,K,\dots =1,\dots ,9$; $i,k,\dots =1,2,3$) on 9D unfolded embedding ${\overline{y}}^I\left(x^i\right)$ of the euclidean 3D metric, i.e.,

$${\overline{y}}^a=\left(\begin{array}{c}{x}^0\\ {\overline{y}}^I\left(x^i\right)\end{array}\right),{\partial }_i{\overline{y}}^I{\partial }_k{\overline{y}}^I={\delta }_{ik}.$$

(5)

With such a choice of background embedding, a nonrelativistic motion of embedding matter is possible [19].

The purpose of this work is to study Regge-Teitelboim Equation (2), linearized in the background of (5). We look for a solution that corresponds to a galaxy that rotates so slowly that the effect of the rotation can be neglected, i.e., the distribution of ordinary matter is static and spherically symmetric on average. At the same time, we assume that metric (1) is also static (and spherically symmetric), which corresponds to the time independence of value ${\tau }^{\mu \nu }$ describing embedding matter. The resulting solution determines the dependence of the gravitational potential on the distance to the center of the galaxy, and it can be compared with observations of the rotation curves of galaxies.

In Section 2 and Section 3, we obtain linearized equations and find their solution. In Section 4, the influence of the assumption of the exact static nature of the solution on its behavior in a linear approximation is investigated. In Section 5, we study how the problem is simplified in the case of spherical symmetry. We propose an explicit form of a spherically symmetric background embedding in Section 6. In Section 7, we study the possibility of choosing this embedding in such a way that the corresponding gravitational potential is in agreement with the observed rotation curves of galaxies.

2. Linearization of Regge–Teitelboim Equations

Let us recall some formulas of embedding theory. All convolutions by Latin indices are carried out using the flat metric of ambient space ${\eta }_{ab}$. The induced metric is expressed in terms of the embedding function by Formula (1). We use space–time signature $(-,+,+,+)$. The signature is changed by changing the sign of ${\eta }_{ab}$, and the induced metric changes the sign as a consequence. The second fundamental form of a 4D surface is expressed in terms of the covariant derivative $D_{\mu }$ of the embedding function, consistent with the metric or through projector ${\Pi }_{\perp }{}_b^a$ on a subspace transverse to the surface (see, for example, [12]):

$$b_{\mu \nu }^a=D_{\mu }{\partial }_{\nu }{y}^a={\Pi }_{\perp }{}_b^a{\partial }_{\mu }{\partial }_{\nu }{y}^b.$$

(6)

We mark with a line the values corresponding to background embedding function $\overline{y}{}^a$ (5); for example, $\overline{b}{}_{\mu \nu }^a$ is the second fundamental form of the background surface. We raise and lower the 4D indices of values with a line using the background metric. Since it is flat, the background connection is zero, and the covariant derivative in (6) is reduced to the usual one. The second derivatives of $\overline{y}{}^0$ and the derivatives by $x^0$ of $\overline{y}{}^I$ are zero; hence, the nonzero components of $\overline{b}{}_{\mu \nu }^a$ are:

$$\overline{b}{}_{ij}^I={\partial }_i{\partial }_j{\overline{y}}^I.$$

(7)

Through index I, this value is transverse to the 3D surface in 9D space described by embedding function $\overline{y}{}^I\left(x^i\right)$. Thus, index I at each point effectively runs through 6 values, exactly like multi-index $\left\{ij\right\}$. Therefore, $\overline{b}{}_{ij}^I$ can be represented as a $6\times 6$ matrix. Since this matrix is nonsingular for “unfolded” embeddings (see details in [18]), you can introduce symmetric by $l,m$ and transverse by I value ${\overline{\alpha }}_I^{lm}$, which is inverse to $\overline{b}{}_{ij}^I$ in the matrix sense:

$${\overline{\alpha }}_I^{lm}\overline{b}{}_{ij}^I=\frac{1}{2}\left({\delta }_i^l{\delta }_j^m+{\delta }_j^l{\delta }_i^m\right).$$

(8)

We look for solutions of the equations in the form of Systems (3) and (4) as a perturbation theory series in degrees of the gravitational constant $\varkappa$ in the background (5):

$$y^a={\overline{y}}^a+\varkappa \stackrel{{}_{\left(1\right)}}{y}{}^a+{\varkappa }^2\stackrel{{}_{\left(2\right)}}{y}{}^a+\dots .$$

(9)

We write similar expansions in a series of $\varkappa$ for any other quantities, including ${\tau }^{\mu \nu }$ and the energy–momentum tensor of ordinary matter $T^{\mu \nu }$. Substituting expansions into Systems (3) and (4), in the first nonvanishing order, we obtain

$$\stackrel{{}_{\left(1\right)}}{G}{}^{\mu \nu }={\overline{T}}^{\mu \nu }+{\overline{\tau }}^{\mu \nu },$$

(10)

$${\overline{\tau }}^{ik}{\overline{b}}_{ik}^I=0.$$

(11)

Due to the nonsingularity of the (7) mentioned above, the last equation corresponds to Condition

$${\overline{\tau }}^{ik}=0.$$

(12)

Of the 10 linearized Einstein Equations (10), only six (for $\mu =i$, $\nu =k$) are equations for the first correction $\stackrel{{}_{\left(1\right)}}{y}{}^a$ to the embedding function and hence for the first correction $\stackrel{{}_{\left(1\right)}}{g}{}_{\mu \nu }$ to the metric, as follows from (1). The remaining four equations define the components of ${\overline{\tau }}^{0\mu }$; therefore, they do not restrict the embedding function.

Only the transverse contributions to the background surface in $\stackrel{{}_{\left(1\right)}}{y}{}^a$ change the shape of the surface, so that only six components of $\stackrel{{}_{\left(1\right)}}{y}{}^a$ make physical sense. The others four components correspond to the longitudinal deformations of the surface, which are equivalent to diffeomorphisms. Therefore, in order to uniquely find all 10 components of $\stackrel{{}_{\left(1\right)}}{y}{}^a$, it is necessary to impose some coordinate conditions.

3. Solving of the Linearized Equations

Assume that at least in the zero order the distribution of ordinary matter is static, i.e., ${\partial }_0{\overline{T}}^{\mu \nu }=0$. We look for solutions of linearized Equation (10) that correspond to the static addition to the metric, i.e., ${\partial }_0\stackrel{{}_{\left(1\right)}}{g}{}_{\mu \nu }=0$. This corresponds to the fact that, in the main order, the distribution of embedding matter is also static, i.e., ${\partial }_0{\overline{\tau }}^{\mu \nu }=0$.

Instead of solving only 6 out of 10 Equations (10) (which can be performed and gives the same result), it is convenient to solve all 10 equations, treating the quantities of ${\overline{\tau }}^{0\mu }$ as independent variables describing embedding matter. Then, the linearized Regge–Teitelboim equations are simply reduced to linearized Einstein Equation (10). We assume that ordinary matter is dustlike (as can be performed for the matter in galaxies) and is at rest in zero order; then,

$${\overline{T}}_{\mu \nu }=\overline{\rho }\left(x^i\right){\delta }_{\mu }^0{\delta }_{\nu }^0.$$

(13)

Equation (10) can be considered to be an equation not directly for $\stackrel{{}_{\left(1\right)}}{y}{}^a$, but as an equation for the correction to metric $\stackrel{{}_{\left(1\right)}}{g}{}_{\mu \nu }$, from which $\stackrel{{}_{\left(1\right)}}{y}{}^a$ is then found by solving embedding Equation (1).

The equations for $\stackrel{{}_{\left(1\right)}}{g}{}_{\mu \nu }$ take a simple form:

$$\Delta \stackrel{{}_{\left(1\right)}}{g}{}_{00}=-(\overline{\rho }\left(x^i\right)+{\overline{\tau }}_{00}),\Delta \stackrel{{}_{\left(1\right)}}{g}{}_{jk}=-(\overline{\rho }\left(x^i\right)+{\overline{\tau }}_{00}){\delta }_{jk},$$

(14)

$$\Delta \stackrel{{}_{\left(1\right)}}{g}{}_{0k}=-2{\overline{\tau }}_{0k}$$

(15)

(where $\Delta$ is the Laplacian operator) if we choose harmonic coordinates and assume that $\stackrel{{}_{\left(1\right)}}{g}{}_{\mu \nu }$ does not depend on time. In addition, we assume that $\stackrel{{}_{\left(1\right)}}{g}{}_{\mu \nu }$ is decreasing at spatial infinity. The conditions for the harmonic coordinates are reduced to only one additional equation:

$${\partial }_k\stackrel{{}_{\left(1\right)}}{g}{}_{0k}=0.$$

(16)

Introducing gravitational potential $\phi \left(x^i\right)$ (we did not include the gravitational constant $\varkappa$ in it for convenience) as a solution of Poisson equation

$$\Delta \phi \left(x^i\right)=\frac{1}{2}(\overline{\rho }\left(x^i\right)+{\overline{\tau }}_{00})$$

(17)

and taking into account that the solutions are decreasing at spatial infinity, we obtain

$$\stackrel{{}_{\left(1\right)}}{g}{}_{00}=-2\phi \left(x^i\right),\stackrel{{}_{\left(1\right)}}{g}{}_{jk}=-2\phi \left(x^i\right){\delta }_{jk}.$$

(18)

Now, we find correction $\stackrel{{}_{\left(1\right)}}{y}{}^a$ to the embedding function that corresponds to an arbitrary correction $\stackrel{{}_{\left(1\right)}}{g}{}_{\mu \nu }$ to the metric. From Formula (1), in the first order by $\varkappa$, we have:

$$\stackrel{{}_{\left(1\right)}}{g}{}_{\mu \nu }=\left({\partial }_{\mu }{\overline{y}}^a\right)\left({\partial }_{\nu }\stackrel{{}_{\left(1\right)}}{y}{}_a\right)+\left({\partial }_{\nu }{\overline{y}}^a\right)\left({\partial }_{\mu }\stackrel{{}_{\left(1\right)}}{y}{}_a\right).$$

(19)

Let us introduce a parameterization for the correction to the embedding function as the sum of a tangent and orthogonal to the background components:

$$\stackrel{{}_{\left(1\right)}}{y}{}^a=\stackrel{{}_{\left(1\right)}}{y}{}_{\parallel }^{\gamma }{\partial }_{\gamma }{\overline{y}}^a+\stackrel{{}_{\left(1\right)}}{y}{}_{\perp }^a.$$

(20)

The structure of Background Embedding (5) leads to relation $\stackrel{{}_{\left(1\right)}}{y}{}^0=\stackrel{{}_{\left(1\right)}}{y}{}_{\parallel }^0$. Substituting Representation (20) in (19) yields a system of differential equations for $\stackrel{{}_{\left(1\right)}}{y}{}_{\parallel }^{\gamma }$ and $\stackrel{{}_{\left(1\right)}}{y}{}_{\perp }^a$:

$${\eta }_{\gamma \nu }{\partial }_{\mu }\stackrel{{}_{\left(1\right)}}{y}{}_{\parallel }^{\gamma }+{\eta }_{\gamma \mu }{\partial }_{\nu }\stackrel{{}_{\left(1\right)}}{y}{}_{\parallel }^{\gamma }-2\stackrel{{}_{\left(1\right)}}{y}{}_{\perp }^I{\overline{b}}_{\mu \nu }^I=\stackrel{{}_{\left(1\right)}}{g}{}_{\mu \nu }.$$

(21)

Writing out its components, we obtain a system of equations:

$$\begin{array}{c}-2{\partial }_0\stackrel{{}_{\left(1\right)}}{y}{}^0=\stackrel{{}_{\left(1\right)}}{g}{}_{00},\\ -{\partial }_k\stackrel{{}_{\left(1\right)}}{y}{}^0+{\partial }_0\stackrel{{}_{\left(1\right)}}{y}{}_{\parallel }^k=\stackrel{{}_{\left(1\right)}}{g}{}_{0k},\\ {\partial }_i\stackrel{{}_{\left(1\right)}}{y}{}_{\parallel }^j+{\partial }_j\stackrel{{}_{\left(1\right)}}{y}{}_{\parallel }^i-2\stackrel{{}_{\left(1\right)}}{y}{}_{\perp }^I{\overline{b}}_{ij}^I=\stackrel{{}_{\left(1\right)}}{g}{}_{ij}.\end{array}$$

(22)

This can be solved by integrating the equations over time and taking into account the static $\stackrel{{}_{\left(1\right)}}{g}{}_{\mu \nu }$. Denoting the integration constants as ${\tilde{y}}^a\left(x^i\right)$, we write the answer as follows:

$$\begin{array}{c}\stackrel{{}_{\left(1\right)}}{y}{}^0=-{\displaystyle \frac{1}{2}}\stackrel{{}_{\left(1\right)}}{g}{}_{00}{x}^0+{\tilde{y}}^0\left(x^i\right)=\phi \left(x^i\right)x^0+\tilde{y}{}^0\left(x^i\right),\\ \stackrel{{}_{\left(1\right)}}{y}{}_{\parallel }^k=\int \left(\stackrel{{}_{\left(1\right)}}{g}{}_{0k}+{\partial }_k\stackrel{{}_{\left(1\right)}}{y}{}^0\right)d{x}^0+{\tilde{y}}^k\left(x^i\right),\\ \stackrel{{}_{\left(1\right)}}{y}{}_{\perp }^I={\displaystyle \frac{1}{2}}{\overline{\alpha }}_I^{kj}\left(-\stackrel{{}_{\left(1\right)}}{g}{}_{kj}+2{\partial }_k\stackrel{{}_{\left(1\right)}}{y}{}_{\parallel }^j\right)={\overline{\alpha }}_I^{kj}\left(\phi \left(x^i\right){\delta }_{kj}+{\partial }_k\stackrel{{}_{\left(1\right)}}{y}{}_{\parallel }^j\right),\end{array}$$

(23)

where (18) was also used.

Substituting these expressions into (20), we lastly obtain

$$\begin{array}{c}\stackrel{{}_{\left(1\right)}}{y}{}^a={\delta }_0^a\left(\phi \left(x^i\right)x^0+\tilde{y}{}^0\left(x^i\right)\right)+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\delta }_I^a\left(\left(\int \left(\stackrel{{}_{\left(1\right)}}{g}{}_{0k}+{\partial }_k\stackrel{{}_{\left(1\right)}}{y}{}^0\right)d{x}^0+{\tilde{y}}^k\left(x^i\right)\right){\partial }_k{\overline{y}}^I+{\overline{\alpha }}_I^{kj}\left(\phi \left(x^i\right){\delta }_{kj}+{\partial }_k\stackrel{{}_{\left(1\right)}}{y}{}_{\parallel }^j\right)\right).\end{array}$$

(24)

This expression gives the solution of the linearized Regge–Teitelboim equations. It is parameterized by the gravitational potential $\phi \left(x^i\right)$ that, via Equation (17), is associated with the zero-order ${\overline{\tau }}_{00}$ of the density of embedding matter, and via the components of metric $\stackrel{{}_{\left(1\right)}}{g}{}_{0k}$ that, via Equation (15), are related to the zero-order ${\overline{\tau }}_{0k}$ of the flux density of this matter. Due to (15) and (16), the components of ${\overline{\tau }}_{0k}$ obey condition ${\partial }_k{\overline{\tau }}_{0k}=0$ (it has the meaning of the embedding matter conservation condition in the case under consideration), so only two of these three components can be considered as independent.

It is interesting to compare this result with the one obtained in [19] in the framework of the nonrelativistic approximation. For this purpose, let us write down the time derivative of Solution (24):

$$\begin{array}{c}{\partial }_0\stackrel{{}_{\left(1\right)}}{y}{}^0=\phi \left(x^i\right),\\ {\partial }_0\stackrel{{}_{\left(1\right)}}{y}{}^I=\left(\stackrel{{}_{\left(1\right)}}{g}{}_{0k}+{\partial }_k\stackrel{{}_{\left(1\right)}}{y}{}^0\right){\partial }_k{\overline{y}}^I+{\overline{\alpha }}_I^{ij}{\partial }_i\left(\stackrel{{}_{\left(1\right)}}{g}{}_{0j}+{\partial }_j\stackrel{{}_{\left(1\right)}}{y}{}^0\right).\end{array}$$

(25)

The second equation reproduces Equation (62) from [19], taking into account the assumption $\stackrel{{}_{\left(1\right)}}{g}{}_{0j}=0$ there. However, the first equation differs from Equation (61) of [19] through the absence of a quadratic contribution. Of course, this is not surprising, since the solution of (24) is obtained in the linear approximation and hence with the rejection of the quadratic contributions. However, when analyzing the nonrelativistic limit in [19], it was taken into account that for the large intervals of time $x^0$ (when time $x^0$ is replaced by nonrelativistic time $t=x^0/c$, where c is the speed of light) quadratic corrections can give a comparable contribution to the linear ones.

4. Accounting for Equations in the Next Order

The solution obtained above in the first order of perturbation theory depends on the choice of the distribution of embedding matter in zero order characterized by ${\overline{\tau }}_{0\mu }$. Let us find restrictions on this distribution, assuming that both ${\tau }^{\mu \nu }$ characterizing embedding matter and the energy–momentum tensor of ordinary matter $T^{\mu \nu }$ are static not only in the zero approximation, but also exactly. In particular, it follows that the metric is also exactly static. When considering a galaxy, this means that the configuration of both ordinary and embedding matter at some point passed into a stationary state. We investigate just this particular case.

Let us write down Equation (4) in the next order in $\varkappa$, compared to already studied Equation (11), and use it:

$$\stackrel{{}_{\left(1\right)}}{\tau }{}^{jk}{\overline{b}}_{jk}^a+{\overline{\tau }}^{00}\stackrel{{}_{\left(1\right)}}{b}{}_{00}^a+2{\overline{\tau }}^{0k}\stackrel{{}_{\left(1\right)}}{b}{}_{0k}^a=0.$$

(26)

Due to (6) and the properties of Background Embedding (5), we have $\stackrel{{}_{\left(1\right)}}{b}{}_{0\mu }^a={\overline{\Pi }}_{\perp }{}_b^a{\partial }_0{\partial }_{\mu }\stackrel{{}_{\left(1\right)}}{y}{}^b$. This allows for us to express $\stackrel{{}_{\left(1\right)}}{\tau }{}^{jk}$ from (26) in the form:

$$\stackrel{{}_{\left(1\right)}}{\tau }{}^{jk}=-\left(\overline{\tau }{}^{00}{\partial }_0{\partial }_0\stackrel{{}_{\left(1\right)}}{y}{}^I+2\overline{\tau }{}^{i0}{\partial }_i{\partial }_0\stackrel{{}_{\left(1\right)}}{y}{}^I\right){\overline{\alpha }}_I^{jk}.$$

(27)

Therefore, the assumed time independence of ${\tau }^{\mu \nu }$ leads to additional restrictions on the quantities in the right-hand side. The time derivative of Equation (27) with (25) and condition ${\partial }_0\stackrel{{}_{\left(1\right)}}{\tau }{}^{jk}=0$ provide the equation

$$\overline{\tau }{}^{i0}\left(\left({\delta }_i^j{\delta }_l^k+{\delta }_l^j{\delta }_i^k\right){\partial }_l\phi +2{\partial }_i\left({\overline{\alpha }}_I^{lm}{\partial }_l{\partial }_m\phi \right){\overline{\alpha }}_I^{jk}\right)=0.$$

(28)

Then, we can also write down Equation (3) in the next order, and it provides the next correction $\stackrel{{}_{\left(2\right)}}{g}{}_{\mu \nu }$ to the metric. However, it is possible to write down a consequence of this equation in which the determined correction does not enter. This is the corresponding order of equation $D_{\mu }{\tau }^{\mu \nu }=0$, reflecting the conservation (with covariant corrections) of embedding matter. In the lowest order, this equation has the form ${\partial }_{\mu }{\overline{\tau }}^{\mu \nu }=0$ and is satisfied given (12), (15) and (16). In the next order, it looks like

$${\partial }_{\mu }\stackrel{{}_{\left(1\right)}}{\tau }{}^{\mu \nu }+\stackrel{{}_{\left(1\right)}}{\Gamma }{}_{\mu \gamma }^{\mu }{\overline{\tau }}^{\gamma \nu }+\stackrel{{}_{\left(1\right)}}{\Gamma }{}_{\mu \gamma }^{\nu }{\overline{\tau }}^{\mu \gamma }=0.$$

(29)

Taking $\nu =k$ in this equation, and using Equation (27) and the assumed time independence of ${\tau }^{\mu \nu }$ in all orders, from condition ${\partial }_0\stackrel{{}_{\left(1\right)}}{\tau }{}^{0k}=0$ we obtain an equation:

$$\begin{array}{c}{\partial }_j\left(\left(\overline{\tau }{}^{00}{\partial }_0{\partial }_0\stackrel{{}_{\left(1\right)}}{y}{}^I+2\overline{\tau }{}^{i0}{\partial }_i{\partial }_0\stackrel{{}_{\left(1\right)}}{y}{}^I\right){\overline{\alpha }}_I^{jk}\right)-\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\overline{\tau }{}^{0k}{\eta }^{\mu \alpha }\left({\partial }_{\alpha }{\overline{y}}_a\right){\partial }_{\mu }{\partial }_0\stackrel{{}_{\left(1\right)}}{y}{}^a-\overline{\tau }{}^{00}\left({\partial }_k{\overline{y}}_a\right){\partial }_0{\partial }_0\stackrel{{}_{\left(1\right)}}{y}{}^a-2\overline{\tau }{}^{j0}\left({\partial }_k{\overline{y}}_a\right){\partial }_j{\partial }_0\stackrel{{}_{\left(1\right)}}{y}{}^a=0,\end{array}$$

(30)

where (12) and an expression for connectivity are used (see, for example, [12])

$${\Gamma }_{\mu \gamma }^{\nu }=g^{\nu \alpha }\left({\partial }_{\alpha }{y}_a\right){\partial }_{\mu }{\partial }_{\gamma }{y}^a,$$

(31)

from which it can be found that

$$\stackrel{{}_{\left(1\right)}}{\Gamma }{}_{\mu 0}^{\nu }={\eta }^{\nu \alpha }\left({\partial }_{\alpha }{\overline{y}}_a\right){\partial }_{\mu }{\partial }_0\stackrel{{}_{\left(1\right)}}{y}{}^a.$$

(32)

Using Formulas (25) in (30), we obtain an equation that, together with (28), restricts the choice of the background embedding ${\overline{y}}^a$ and ${\overline{\tau }}^{0\mu }$, which parameterize the solution of the linear approximation found in the previous section. From the remaining Equation (29) at $\nu =0$, variable $\stackrel{{}_{\left(1\right)}}{\tau }{}^{k0}$ is not excluded, so this equation does not provide a new restrictions on the above quantities.

The background embedding of the form (5) is parameterized by three functions, since nine components of ${\overline{y}}^I\left(x^i\right)$ are imposed by six conditions that the metric of the surface described by this function is flat Euclidean. At first sight, the resulting number of equations for the background and ${\overline{\tau }}^{0\mu }$ seems too large—six Equation (28) and three Equation (30) for six unknowns (as noted after (24)), only two of the three components ${\overline{\tau }}^{0k}$ are independent). However, it is easy to see that a solution nevertheless exists, since the six Equations (28) can be satisfied by choosing three quantities ${\overline{\tau }}^{0k}$ as

$${\overline{\tau }}^{0k}=0.$$

(33)

We study the solutions corresponding just to such a choice. Physically, it means that, in the zero approximation, embedding matter is at rest. Using Background (5) leads to the fact that time independence ${\overline{\tau }}^{\mu \nu }$ actually leads to (33) (otherwise, there are fewer unknowns than equations), i.e., to Embedding Matter at rest in the zero approximation. In the analysis of the nonrelativistic limit in [19], such a background was found when discussing the nonrelativistic character of motion of embedding matter. Taking into account (15) and assuming decreasing corrections to the metric at 3D infinity, it follows from (33) that $\stackrel{{}_{\left(1\right)}}{g}{}_{0k}=0$.

Given that ${\overline{\tau }}^{0k}=0$, the remaining Equations (30) are simplified. Using (25), we can now rewrite them as

$${\partial }_j\left((2\Delta \phi -\overline{\rho }){\overline{\alpha }}_I^{jk}{\overline{\alpha }}_I^{lm}{\partial }_l{\partial }_m\phi \right)-(2\Delta \phi -\overline{\rho }){\partial }_k\phi =0,$$

(34)

where $\overline{\tau }{}^{00}$ was expressed from (17).

These are three equations for four quantities, namely, three that parameterize the background embedding function ${\overline{y}}^I\left(x^i\right)$ and one describing the density of embedding matter ${\overline{\tau }}^{00}$. Thus, linearized Regge–Teitelboim equations, supplemented by the condition of exact statics of solutions, leave an arbitrariness in the choice of one function of coordinates $x^i$. The physical meaning of this arbitrariness lies in the presence of arbitrariness in the general case when specifying the distribution of embedding matter at the initial moment of time.

5. The Case of Spherical Symmetry

Let us consider the situation when ordinary matter is distributed in a spherically symmetric way. Then, the solution can also be sought in the class of spherically symmetric functions. In this case, both gravitational potential $\phi$ and the distribution density of ordinary matter $\overline{\rho }$ depend only on the radial coordinate $r=\sqrt{x^i{x}^i}$.

The question of how to formulate a condition of any kind of symmetry for an embedding function is rather nontrivial; see, for example, [20]. Since the background embedding function ${\overline{y}}^I\left(x^i\right)$ enters Equation (34) only as a quantity

$$A^{lm,jk}={\overline{\alpha }}_I^{lm}{\overline{\alpha }}_I^{jk},$$

(35)

it is possible to directly impose symmetry constraints on this. Taking into account all index permutation symmetries, in the case of spherical symmetry, quantity A can be written in the form

$$\begin{array}{c}{A}^{lm,jk}=f_1\left(r\right){\delta }^{lm}{\delta }^{jk}+{\displaystyle \frac{1}{2}}{f}_2\left(r\right)\left({\delta }^{lj}{\delta }^{mk}+{\delta }^{lk}{\delta }^{mj}\right)+{\displaystyle \frac{1}{2r^2}}{f}_3\left(r\right)\left({\delta }^{lm}{x}^j{x}^k+{\delta }^{jk}{x}^l{x}^m\right)+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +{\displaystyle \frac{1}{4r^2}}{f}_4\left(r\right)\left({\delta }^{lj}{x}^m{x}^k+{\delta }^{lk}{x}^m{x}^j+{\delta }^{jm}{x}^k{x}^l+{\delta }^{mk}{x}^j{x}^l\right)+{\displaystyle \frac{1}{r^4}}{f}_5\left(r\right)x^l{x}^m{x}^j{x}^k.\end{array}$$

(36)

Here, functions $f_1\dots f_5$ are characteristics of the particular background embedding used. If we substitute this representation into (34), a common multiplier $x^k$ appears, and the three equations turn into one scalar equation. Introducing notations for different combinations of functions $f_1\dots f_5$, the resulting equation can be written in the following form:

$${\left(\left({\phi }^{″}+{\displaystyle \frac{2}{r}}{\phi }^{\prime }-{\displaystyle \frac{1}{2}}\overline{\rho }\right)\left({\phi }^{″}{F}_1+{\displaystyle \frac{1}{r}}{\phi }^{\prime }{F}_2\right)\right)}^{\prime }+{\displaystyle \frac{2}{r}}\left({\phi }^{″}+{\displaystyle \frac{2}{r}}{\phi }^{\prime }-{\displaystyle \frac{1}{2}}\overline{\rho }\right)\left({\phi }^{″}{F}_3+{\displaystyle \frac{1}{r}}{\phi }^{\prime }{F}_4\right)=0,$$

(37)

where

$$\begin{array}{cc}\hfill F_1& =f_1+f_2+f_3+f_4+f_5,\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill F_2& =2f_1+f_3,\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill F_3& =f_2+{\displaystyle \frac{1}{2}}{f}_3+f_4+f_5,\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill F_4& =-f_2+f_3-{\displaystyle \frac{r^2}{2}}.\hfill \end{array}$$

(41)

Equation (37) allows for us to determine gravitational potential $\phi \left(r\right)$ if the distribution of ordinary matter $\overline{\rho }\left(r\right)$ and the background embedding function defining $f_1\dots f_5$ are known. Since (37) is a nonlinear differential equation, in the general case, its solution can only be sought numerically. First of all, it is necessary to find all the functions $f_1\dots f_5$ included in the equation using the given embedding function, which requires first finding the value of ${\overline{\alpha }}_I^{lm}$.

Finding it directly with Formula (8) is a nontrivial task for specific embeddings. Let us find a simpler way that allows for us to find functions $f_1\dots f_5$ included in the expansion of (36) without explicit knowledge of ${\overline{\alpha }}_I^{lm}$. When writing this expansion, we took into account three types of symmetry by permutations of indices following from the definition of (35): inside the first pair, inside the second, and when replacing the first pair with the second. As a consequence, we have five independent coefficients $f_1\dots f_5$. However, in fact, there are fewer independent variables parameterizing A. To show this, we define quantity B:

$$B_{jk,is}={\overline{b}}_{jk}^I{\overline{b}}_{is}^I=\left({\partial }_j{\partial }_k{\overline{y}}^I\right){\partial }_i{\partial }_s{\overline{y}}^I.$$

(42)

It is easy to see that this quantity is symmetric through the permutation of any two indices due to the orthogonality of the first and second derivatives of ${\overline{y}}^I$:

$$B_{jk,is}=\left({\partial }_j{\partial }_k{\overline{y}}^I\right){\partial }_i{\partial }_s{\overline{y}}^I=-\left({\partial }_i{\partial }_j{\partial }_k{\overline{y}}^I\right){\partial }_s{\overline{y}}^I=\left({\partial }_i{\partial }_k{\overline{y}}^I\right){\partial }_j{\partial }_s{\overline{y}}^I=B_{ik,js}.$$

(43)

Hence, in the spherically symmetric case, it can be parameterized not by five but only by three radial functions:

$$\begin{array}{c}{B}_{jk,is}={\displaystyle \frac{1}{3}}{g}_1\left(r\right)\left({\delta }^{jk}{\delta }^{is}+{\delta }^{js}{\delta }^{ik}+{\delta }^{ji}{\delta }^{sk}\right)+{\displaystyle \frac{1}{6r^2}}{g}_2\left(r\right)({\delta }^{jk}{x}^i{x}^s+{\delta }^{ji}{x}^k{x}^s+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\delta }^{js}{x}^i{x}^k+{\delta }^{ik}{x}^j{x}^s+{\delta }^{is}{x}^j{x}^k+{\delta }^{sk}{x}^j{x}^i)+{\displaystyle \frac{1}{r^4}}{g}_3\left(r\right)x^j{x}^k{x}^i{x}^s.\end{array}$$

(44)

There is a connection between A and B that follows from (8):

$$A^{lm,jk}{B}_{jk,is}={\displaystyle \frac{1}{2}}\left({\delta }_i^l{\delta }_s^m+{\delta }_s^l{\delta }_i^m\right).$$

(45)

It can be used to express five functions $f_1\dots f_5$ through three functions $g_1\dots g_3$:

$$\begin{array}{cc}\hfill f_1& ={\displaystyle \frac{-24g_1^2+(-24g_2-36g_3)g_1+3g_2^2}{4(20g_1^2+(20g_2+24g_3)g_1-g_2^2)g_1}},\hfill \\ \hfill f_2& ={\displaystyle \frac{3}{2g_1}},\hfill \\ \hfill f_3& ={\displaystyle \frac{(12g_2+36g_3)g_1-3g_2^2}{2(20g_1^2+(20g_2+24g_3)g_1-g_2^2)g_1}},\hfill \\ \hfill f_4& ={\displaystyle \frac{-3g_2}{g_1(2g_1+g_2)}},\hfill \\ \hfill f_5& ={\displaystyle \frac{-360g_1^2{g}_3+(138g_2^2+108g_2{g}_3)g_1-3g_2^3}{4(20g_1^2+(20g_2+24g_3)g_1-g_2^2)g_1(2g_1+g_2)}}.\hfill \end{array}$$

(46)

As a result, to find the functions $f_1\dots f_5$ corresponding to a specific background embedding, we first need to calculate the second fundamental form $\overline{b}{}_{ij}^I={\partial }_i{\partial }_j{\overline{y}}^I$. Then, we have to determine quantity $B_{jk,is}$ according to (42). Comparing the result with the (44) expansion, we can find functions $g_1\dots g_3$, and then find functions $f_1\dots f_5$ by (46).

6. Explicit Unfolded Spherically Symmetric Embedding

Let us present an embedding ${\overline{y}}^I\left(x^i\right)$ of the flat Euclidean 3D metric into 9D Euclidean space that would be spherically symmetric in the sense discussed in [20] and would also be unfolded in terms of [18]. The latter means that, for such a surface, the second fundamental form (7) is nonsingular as a $6\times 6$ matrix; see the text after (7).

We consider basis ${\lambda }_{ij}^A$ in the space of symmetric traceless matrices, numbered by index A, which runs through values $4,\dots ,8$. We subject this basis to the orthonormality condition in the space of such matrices:

$${\lambda }_{ij}^A{\lambda }_{lm}^A={\displaystyle \frac{1}{2}}\left({\delta }_{il}{\delta }_{jm}+{\delta }_{im}{\delta }_{jl}\right)-{\displaystyle \frac{1}{3}}{\delta }_{ij}{\delta }_{lm},{\lambda }_{ij}^A{\lambda }_{ij}^B={\delta }^{AB}.$$

(47)

We take the embedding function ${\overline{y}}^I\left(x^i\right)$ with components

$$\begin{array}{cc}\hfill & {\overline{y}}^k\left(x^i\right)=f\left(r\right)x^k,\hfill \\ \hfill & {\overline{y}}^A\left(x^i\right)=g\left(r\right){\lambda }_{lm}^A{x}^l{x}^m,\hfill \\ \hfill & {\overline{y}}^9\left(x^i\right)=h\left(r\right),\hfill \end{array}$$

(48)

it is parameterized by three radial functions. One can check that this embedding function describes a surface with spherical symmetry. This means that there is such a representation (generally speaking, reducible) of the group of 3D rotations under the action of which in the space ${\overline{y}}^I$ the surface transforms to itself (see [20] for details). The three independent functions $f,g,h$ are related to its irreducible parts, and the reducible representation as a whole can be described as “3+5+1”.

Let us select, among all the embeddings of type (48), those that correspond to a flat metric. Calculating for (48) the components of the induced metric, we obtain the equations

$$\begin{array}{cc}\hfill & f^2+2r^2{g}^2=1,\hfill \\ \hfill & {\left(rf\right)}^{\prime 2}+{\displaystyle \frac{2}{3}}{\left(r^{2}g\right)}^{\prime 2}+h^{\prime 2}=1.\hfill \end{array}$$

(49)

Expressing from these equations functions g and h through f we obtain the desired spherically symmetric embedding of the flat Euclidean 3D metric into 9D Euclidean space. It is parameterized by choosing one function of radius $f\left(r\right)$. The fact that such an embedding is unfolded by a non-special choice of this function can be checked directly by computing the second fundamental form ${\partial }_i{\partial }_j{\overline{y}}^I$ (7) and making sure that it is nonsingular.

Calculating this quantity and Expression (42) constructed from it lead to the following expressions for the coefficients $g_1\dots g_3$ of its expansion (44):

$$\begin{array}{cc}\hfill g_1& =6g^2,\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill g_2& =6\left(f^{\prime 2}+2r^2{g}^{\prime 2}+4rg{g}^{\prime }\right),\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill g_3& =r^2{\left({\displaystyle \frac{h^{\prime }}{r}}\right)}^{\prime 2}+r^2{f}^{″2}+2r{f}^{\prime }{f}^{″}-3f^{\prime 2}+{\displaystyle \frac{2}{3}}{r}^4{g}^{″2}+4r^3{g}^{\prime }{g}^{″}+4r^{2}g{g}^{″}-2r^2{g}^{\prime 2}-4rg{g}^{\prime },\hfill \end{array}$$

(52)

where the functions g and h must be expressed through a single arbitrary function $f\left(r\right)$ according to (49).

7. Inverse Problem

Equation (37) obtained above in Section 5 allows for searching for the gravitational potential $\phi \left(r\right)$ if the distribution of ordinary matter $\overline{\rho }\left(r\right)$ and the background embedding function ${\overline{y}}^I\left(x^i\right)$ are known. It is easy to see that, among the solutions of this equation, there is an Einsteinian solution for which

$${\phi }^{″}+{\displaystyle \frac{2}{r}}{\phi }^{\prime }-{\displaystyle \frac{1}{2}}\overline{\rho }=0.$$

(53)

However, there are other solutions too. In the galactic halo region where the contribution of $\overline{\rho }$ can be neglected, we have a Newtonian behavior of the gravitational potential $\phi \sim 1/r$ for the Einsteinian solution. Such a behavior does not agree well with the data of the rotation curves of galaxies. To find other solutions in this area, it is sufficient to know background embedding ${\overline{y}}^I\left(x^i\right)$.

The background embedding constructed in the previous section has ambiguity in the choice of one function $f\left(r\right)$. There is no highlighted natural way to choose this function. As a consequence, there is also no possibility to uniquely find the gravitational potential $\phi \left(r\right)$ as a result of solving Equation (37), since changing $f\left(r\right)$ also changes $\phi \left(r\right)$. Therefore, we focus on investigating the inverse problem by posing the question: can we find such a background embedding ${\overline{y}}^I\left(x^i\right)$ (i.e., such a function $f\left(r\right)$) so that the solution of Equation (37) corresponds to the gravitational potential in good agreement with galactic halo observations?

As a good fitting of observational data, we take the Burkert profile [21] of the dark matter density; see, for example, review [22]:

$${\rho }_B\left(r\right)=\frac{{\rho }_0{r}_0^3}{(r+r_0)(r^2+r_0^2)},$$

(54)

where $r_0$ is the core radius, ${\rho }_0$ is the density at the center of the galaxy. In order to find a behavior of the gravitational potential that agrees well with the observations, one needs to solve the equation

$${\phi }^{″}+\frac{2}{r}{\phi }^{\prime }=\frac{1}{2}(\overline{\rho }+{\rho }_B).$$

(55)

The solution of this equation in the galactic halo has the form:

$$\phi \left(r\right)=\frac{M}{r}+\frac{{\rho }_0}{2}\left(\left(1+\frac{r_0}{r}\right)\left(arctan\frac{r}{r_0}-ln\left(1+\frac{r}{r_0}\right)\right)+\frac{1}{2}\left(1-\frac{r_0}{r}\right)ln\left(1+\frac{r^2}{r_0^2}\right)\right),$$

(56)

where M is the mass of ordinary matter in the galaxy. To avoid introducing this quantity as an additional parameter, we further assume that the proportional contribution to M to the gravitational potential in the halo region can be neglected compared with the contribution of dark matter. The trivial substitution of Function (56) with $M=0$ into Equation (37) leads to a very complicated (so we do not show it here) third-order nonlinear differential equation for the unknown function $f\left(r\right)$ parameterizing the background embedding. This equation fails to be solved analytically. We numerically solved the Cauchy problem for Equation obtained, choosing different values of the initial data at the value of the radius $r=r_0/2$, which is usually about the visual size of the galaxy. We solve Equation (37) with a zero contribution of ordinary matter, so it is applicable only in the region of the galactic halo.

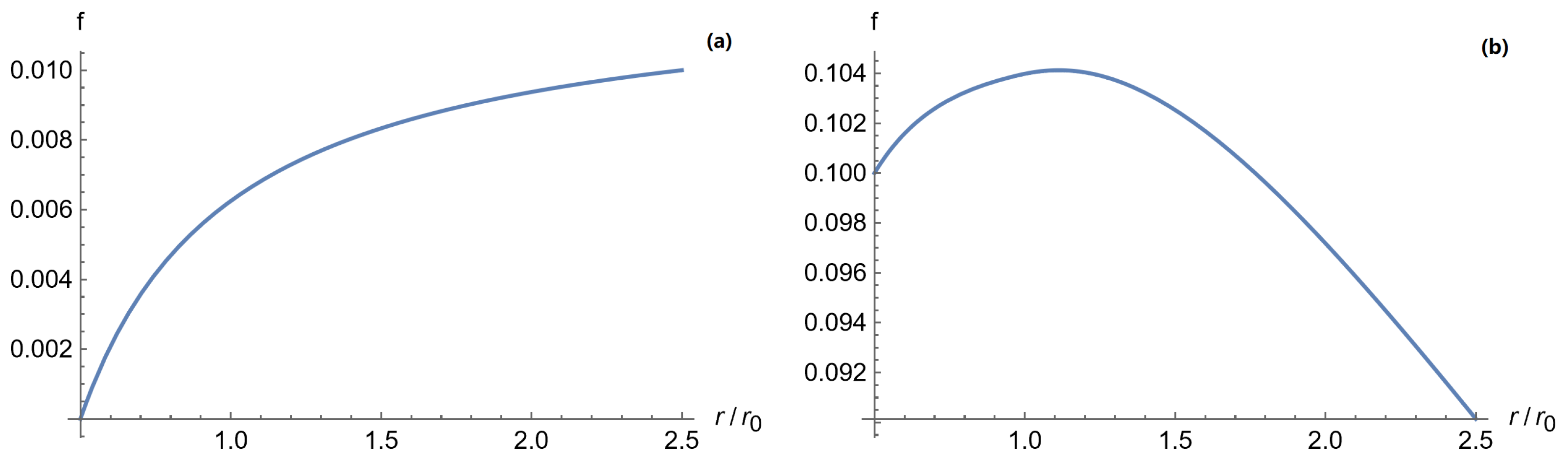
A typical view of the obtained solutions is shown in Figure 1. The existence of such solutions shows the possibility to choose parameterizing embedding (48) function $f\left(r\right)$ in a special way. For this choice, equations of motion in the framework of linearization of the embedding theory in this background lead to the same gravitational potential as the dark matter with Burkert profile (54) in the framework of ordinary GR. With a significant change in the chosen values of the initial data, the algorithm used for the numerical solution of the nonlinear differential equation no longer made it possible to extend the solution into the region $r\gtrsim 0.95r_0$. This can be explained by the fact that in the differential equation being solved, the coefficient at the major derivative (which itself is a compound quantity that also depends on the minor derivatives) may become too small, which prevents the correct behavior of the algorithm.

8. Conclusions

We considered the problem of constructing a perturbation theory for Regge-Teitelboim Equation (2) for some background. The background was chosen to be (5), which corresponded to a 4D surface that is a direct product of the timelike straight line on the 9D unfolded embedding of the euclidean 3D metric. This formulation of the problem is a special case of the weak gravitational field approximation in the embedding theory, in which the corrections to the embedding function are linear to the corrections to the metric; see (23). The analysis is simplified if the Regge–Teitelboim equations are rewritten as a set of Einstein Equation (3) with the contribution of fictitious embedding matter and Equation (4) describing the behavior of this matter.

First, the Einstein equations were linearized in the usual way and solved using harmonic coordinates. The result depended on the energy-momentum tensor of embedding matter specified arbitrarily in the lower order. Further, we restricted ourselves to the class of solutions for which both ordinary matter and embedding matter are in a stationary state, which corresponded to the description of an already fully formed galaxy. Taking this condition into account in the second order of perturbation theory leads to additional restrictions on the solutions found in the linear one. As a result, Equation (37) arises in the case of spherical symmetry, which allows for finding the gravitational potential $\phi \left(r\right)$ if the background embedding is given. The nonlinear form of this equation is explained by the fact that it arises as a result of accounting for the static character of the metric in the second (following the linear) order.

It is possible to find a class of spherically symmetric surfaces (48) and (49) that have all necessary properties for their use as a background embedding. These embeddings are parameterized by a single function $f\left(r\right)$. This function could be chosen, so that the solution of Equation (37) led to a gravitational potential that corresponded well (if we neglected deviations from spherical symmetry for real galaxies) to the observed distribution of dark matter in the galactic halo.

In our analysis we used the following assumptions. We assumed that ordinary matter has, on average, static spherically symmetric distribution. As a consequence, the energy–momentum tensor of ordinary matter $T^{\mu \nu }$ has exactly spherically symmetric and static character (we use this fact in the first two orders of perturbation theory: for ${\overline{T}}^{\mu \nu }$ and $\stackrel{{}_{\left(1\right)}}{T}{}^{\mu \nu }$). We further assumed that the metric had an exactly spherically symmetric and static character, and we used this for corrections to the metric $\stackrel{{}_{\left(1\right)}}{g}{}_{\mu \nu }$ and $\stackrel{{}_{\left(2\right)}}{g}{}_{\mu \nu }$. Given the restrictions on $T^{\mu \nu }$, imposing such an assumptions on the metric is the same as imposing them on the energy-momentum tensor of embedding matter in the first two orders: for ${\overline{\tau }}^{\mu \nu }$ and $\stackrel{{}_{\left(1\right)}}{\tau }{}^{\mu \nu }$. As a background embedding function ${\overline{y}}^a\left(x^{\mu }\right)$ that corresponded to the flat metric ${\eta }_{\mu \nu }$, we took the Product (5) of a timelike line on 9D unfolded and the spherically-symmetric embedding (48) of the euclidean 3D metric. The assumptions were internally consistent, but for real galaxies, they are satisfied only approximately. The strongest ones are the deviations from the spherical symmetry.

We discussed the behavior of the gravitational potential $\phi \left(r\right)$ only in the galactic halo. In order to study the behavior of $\phi \left(r\right)$ inside the galaxy where the influence of ordinary matter cannot be neglected, one must additionally find an explicit form of its distribution, which is beyond the scope of this paper. At the same time, deviations of embedding gravity predictions from GR arise at scales where energy–momentum tensor ${\tau }^{\mu \nu }$ of embedding matter becomes significant compared to the energy–momentum tensor $T^{\mu \nu }$ of ordinary matter. We assumed that, at the scale of the galaxy, these two quantities were comparable, but at smaller distances, the influence of the embedding matter could be neglected, and the laws of GR would start to be satisfied with good accuracy.