Non-Perturbative Propagators in Quantum Gravity
Abstract
1. Introduction
- The spin two and spin zero modes of the graviton feature qualitative and quantitative differences in their momentum dependence.
- The overall gauge and gap dependence is small, see Figures 4 and 5.
- Quantum corrections to the free propagator decrease exponentially with increasing dimension, see (78) and Figure 3.
2. Functional Renormalisation Group
3. Momentum Dependence in Quantum Gravity
3.1. Fluctuation Approach
3.2. General Structure of the RG Flows
3.3. On the Relation between Form Factors and Anomalous Dimensions
3.4. Momentum-Dependent Anomalous Dimension versus Wave Function Renormalisation
4. Momentum-Dependent Fluctuation RG Flow: Analytical Structure
4.1. Behaviour at Small Momentum
4.2. Behaviour at Large Momentum
4.2.1. Spin Two Sector
4.2.2. Spin Zero Sector
4.2.3. Ghost Sector
4.3. Limit of Large Dimension
4.4. The Flow for Positive
5. Momentum-Dependent Fluctuation RG Flow: Numerical Results
5.1. Numerical Strategy
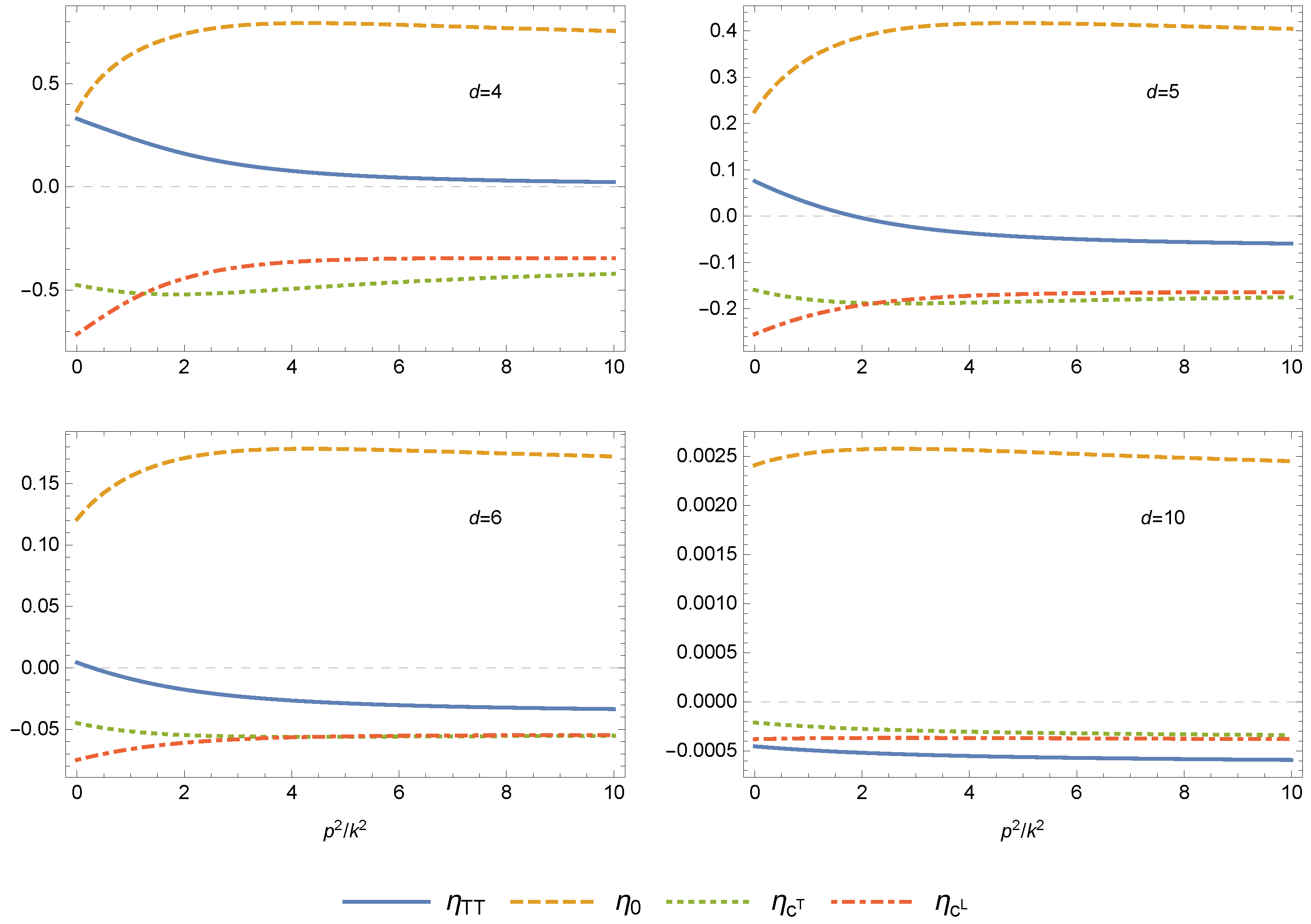
5.2. Dimensional Dependence
5.3. Gap Dependence
5.4. Gauge Dependence
5.5. Form Factors and the Derivative Expansion
6. Momentum-Dependent Background RG Flow
7. Comparing Background and Fluctuation Results
8. Summary and Outlook
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Asymptotic Expansion of Form Factors
Appendix B. Calculation of the Background form Factors Induced by GR
Appendix B.1. Early Time Heat Kernel Expansion
Appendix B.2. Some Integral Transformations in d = 4
Appendix B.3. Trace Contribution of the Spin Zero Part
Appendix B.4. Trace Contribution of the Ghost
Appendix B.5. Trace Contribution of the Spin Two Part
Appendix B.6. Background Flow Equations
Appendix B.7. Fixed Point Structure
| 1 | We refer to as the dimensionless wave function renormalisation, since its canonical mass dimension and the anomalous dimension cancel at the fixed point. |
| 2 | A correlation function is called momentum-local in this context if the ratio of its flow to the correlator itself vanishes for large momenta. |
References
- Weinberg, S. Ultraviolet divergences in quantum theories of gravitation. General Relativity: An Einstein Centenary Survey; Hawking, S.W., Israel, W., Eds.; Cambridge University Press: Cambridge, UK, 1979; pp. 790–831. [Google Scholar]
- Gies, H.; Scherer, M.M. Asymptotic safety of simple Yukawa systems. Eur. Phys. J. C 2010, 66, 387–402. [Google Scholar] [CrossRef]
- Gies, H.; Rechenberger, S.; Scherer, M.M. Towards an Asymptotic-Safety Scenario for Chiral Yukawa Systems. Eur. Phys. J. C 2010, 66, 403–418. [Google Scholar] [CrossRef]
- Braun, J.; Gies, H.; Scherer, D.D. Asymptotic safety: A simple example. Phys. Rev. 2011, D83, 085012. [Google Scholar] [CrossRef]
- Gies, H.; Rechenberger, S.; Scherer, M.M.; Zambelli, L. An asymptotic safety scenario for gauged chiral Higgs-Yukawa models. Eur. Phys. J. C 2013, 73, 2652. [Google Scholar] [CrossRef]
- Reuter, M. Nonperturbative evolution equation for quantum gravity. Phys. Rev. 1998, D57, 971–985. [Google Scholar] [CrossRef]
- Souma, W. Nontrivial ultraviolet fixed point in quantum gravity. Prog. Theor. Phys. 1999, 102, 181–195. [Google Scholar] [CrossRef]
- Reuter, M.; Saueressig, F. Renormalization group flow of quantum gravity in the Einstein-Hilbert truncation. Phys. Rev. 2002, D65, 065016. [Google Scholar] [CrossRef]
- Lauscher, O.; Reuter, M. Ultraviolet fixed point and generalized flow equation of quantum gravity. Phys. Rev. 2002, D65, 025013. [Google Scholar] [CrossRef]
- Litim, D.F. Fixed points of quantum gravity. Phys. Rev. Lett. 2004, 92, 201301. [Google Scholar] [CrossRef]
- Machado, P.F.; Saueressig, F. On the renormalization group flow of f(R)-gravity. Phys. Rev. 2008, D77, 124045. [Google Scholar] [CrossRef]
- Codello, A.; Percacci, R.; Rahmede, C. Investigating the Ultraviolet Properties of Gravity with a Wilsonian Renormalization Group Equation. Ann. Phys. 2009, 324, 414–469. [Google Scholar] [CrossRef]
- Benedetti, D.; Machado, P.F.; Saueressig, F. Asymptotic safety in higher-derivative gravity. Mod. Phys. Lett. 2009, A24, 2233–2241. [Google Scholar] [CrossRef]
- Machado, P.F.; Percacci, R. Conformally reduced quantum gravity revisited. Phys. Rev. 2009, D80, 024020. [Google Scholar] [CrossRef]
- Manrique, E.; Reuter, M. Bimetric Truncations for Quantum Einstein Gravity and Asymptotic Safety. Ann. Phys. 2010, 325, 785–815. [Google Scholar] [CrossRef]
- Manrique, E.; Reuter, M.; Saueressig, F. Bimetric Renormalization Group Flows in Quantum Einstein Gravity. Ann. Phys. 2011, 326, 463–485. [Google Scholar] [CrossRef]
- Groh, K.; Saueressig, F. Ghost wave-function renormalization in Asymptotically Safe Quantum Gravity. J. Phys. 2010, A43, 365403. [Google Scholar] [CrossRef]
- Eichhorn, A.; Gies, H. Ghost anomalous dimension in asymptotically safe quantum gravity. Phys. Rev. 2010, D81, 104010. [Google Scholar] [CrossRef]
- Benedetti, D.; Groh, K.; Machado, P.F.; Saueressig, F. The Universal RG Machine. J. High Energy Phys. 2011, 2011, 079. [Google Scholar] [CrossRef]
- Manrique, E.; Rechenberger, S.; Saueressig, F. Asymptotically Safe Lorentzian Gravity. Phys. Rev. Lett. 2011, 106, 251302. [Google Scholar] [CrossRef] [PubMed]
- Reuter, M.; Saueressig, F. Quantum Einstein Gravity. New J. Phys. 2012, 14, 055022. [Google Scholar] [CrossRef]
- Benedetti, D.; Caravelli, F. The Local potential approximation in quantum gravity. J. High Energy Phys. 2012, 2012, 017. [Google Scholar] [CrossRef]
- Rechenberger, S.; Saueressig, F. A functional renormalization group equation for foliated spacetimes. J. High Energy Phys. 2013, 2013, 10. [Google Scholar] [CrossRef]
- Christiansen, N.; Litim, D.F.; Pawlowski, J.M.; Rodigast, A. Fixed points and infrared completion of quantum gravity. Phys. Lett. 2014, B728, 114–117. [Google Scholar] [CrossRef]
- Dietz, J.A.; Morris, T.R. Asymptotic safety in the f(R) approximation. J. High Energy Phys. 2013, 2013, 108. [Google Scholar] [CrossRef]
- Ohta, N.; Percacci, R. Higher Derivative Gravity and Asymptotic Safety in Diverse Dimensions. Class. Quant. Grav. 2014, 31, 015024. [Google Scholar] [CrossRef]
- Falls, K.; Litim, D.; Nikolakopoulos, K.; Rahmede, C. A Bootstrap towards Asymptotic Safety; University of Sussex: Brighton, UK, 2013. [Google Scholar]
- Falls, K.; Litim, D.F.; Nikolakopoulos, K.; Rahmede, C. Further evidence for asymptotic safety of quantum gravity. Phys. Rev. 2016, D93, 104022. [Google Scholar] [CrossRef]
- Christiansen, N.; Knorr, B.; Pawlowski, J.M.; Rodigast, A. Global Flows in Quantum Gravity. Phys. Rev. 2016, D93, 044036. [Google Scholar] [CrossRef]
- Becker, D.; Reuter, M. En route to Background Independence: Broken split-symmetry, and how to restore it with bi-metric average actions. Ann. Phys. 2014, 350, 225–301. [Google Scholar] [CrossRef]
- Christiansen, N.; Knorr, B.; Meibohm, J.; Pawlowski, J.M.; Reichert, M. Local Quantum Gravity. Phys. Rev. 2015, D92, 121501. [Google Scholar] [CrossRef]
- Morris, T.R.; Slade, Z.H. Solutions to the reconstruction problem in asymptotic safety. J. High Energy Phys. 2015, 2015, 094. [Google Scholar] [CrossRef]
- Ohta, N.; Percacci, R.; Vacca, G.P. Flow equation for f(R) gravity and some of its exact solutions. Phys. Rev. 2015, D92, 061501. [Google Scholar] [CrossRef]
- Ohta, N.; Percacci, R.; Vacca, G.P. Renormalization Group Equation and scaling solutions for f(R) gravity in exponential parametrization. Eur. Phys. J. 2016, C76, 46. [Google Scholar] [CrossRef]
- Gies, H.; Knorr, B.; Lippoldt, S. Generalized Parametrization Dependence in Quantum Gravity. Phys. Rev. 2015, D92, 084020. [Google Scholar] [CrossRef]
- Demmel, M.; Saueressig, F.; Zanusso, O. A proper fixed functional for four-dimensional Quantum Einstein Gravity. J. High Energy Phys. 2015, 2015, 113. [Google Scholar] [CrossRef]
- Biemans, J.; Platania, A.; Saueressig, F. Quantum gravity on foliated spacetimes: Asymptotically safe and sound. Phys. Rev. 2017, D95, 086013. [Google Scholar] [CrossRef]
- Gies, H.; Knorr, B.; Lippoldt, S.; Saueressig, F. Gravitational Two-Loop Counterterm Is Asymptotically Safe. Phys. Rev. Lett. 2016, 116, 211302. [Google Scholar] [CrossRef]
- Denz, T.; Pawlowski, J.M.; Reichert, M. Towards apparent convergence in asymptotically safe quantum gravity. Eur. Phys. J. 2018, C78, 336. [Google Scholar] [CrossRef] [PubMed]
- Platania, A.; Saueressig, F. Functional Renormalization Group Flows on Friedman–Lemaître–Robertson–Walker backgrounds. Found. Phys. 2018, 48, 1291–1304. [Google Scholar] [CrossRef]
- Falls, K.; King, C.R.; Litim, D.F.; Nikolakopoulos, K.; Rahmede, C. Asymptotic safety of quantum gravity beyond Ricci scalars. Phys. Rev. 2018, D97, 086006. [Google Scholar] [CrossRef]
- Knorr, B.; Lippoldt, S. Correlation functions on a curved background. Phys. Rev. 2017, D96, 065020. [Google Scholar] [CrossRef]
- Christiansen, N.; Falls, K.; Pawlowski, J.M.; Reichert, M. Curvature dependence of quantum gravity. Phys. Rev. 2018, D97, 046007. [Google Scholar] [CrossRef]
- De Brito, G.P.; Ohta, N.; Pereira, A.D.; Tomaz, A.A.; Yamada, M. Asymptotic safety and field parametrization dependence in the f(R) truncation. Phys. Rev. 2018, D98, 026027. [Google Scholar] [CrossRef]
- Falls, K.G.; Litim, D.F.; Schröder, J. Aspects of asymptotic safety for quantum gravity. Phys. Rev. D 2019, 99, 126015. [Google Scholar] [CrossRef]
- Kluth, Y.; Litim, D.F. Fixed Points of Quantum Gravity and the Dimensionality of the UV Critical Surface. arXiv 2020, arXiv:2008.09181. [Google Scholar]
- Falls, K.; Ohta, N.; Percacci, R. Towards the determination of the dimension of the critical surface in asymptotically safe gravity. Phys. Lett. B 2020, 810, 135773. [Google Scholar] [CrossRef]
- Knorr, B. The derivative expansion in asymptotically safe quantum gravity: General setup and quartic order. arXiv 2021, arXiv:2104.11336. [Google Scholar]
- Narain, G.; Percacci, R. Renormalization Group Flow in Scalar-Tensor Theories. I. Class. Quant. Grav. 2010, 27, 075001. [Google Scholar] [CrossRef]
- Shaposhnikov, M.; Wetterich, C. Asymptotic safety of gravity and the Higgs boson mass. Phys. Lett. 2010, B683, 196–200. [Google Scholar] [CrossRef]
- Donà, P.; Eichhorn, A.; Percacci, R. Matter matters in asymptotically safe quantum gravity. Phys. Rev. 2014, D89, 084035. [Google Scholar] [CrossRef]
- Meibohm, J.; Pawlowski, J.M.; Reichert, M. Asymptotic safety of gravity-matter systems. Phys. Rev. 2016, D93, 084035. [Google Scholar] [CrossRef]
- Donà, P.; Eichhorn, A.; Labus, P.; Percacci, R. Asymptotic safety in an interacting system of gravity and scalar matter. Phys. Rev. 2016, D93, 044049, Erratum in Phys. Rev. 2016, D93, 129904. [Google Scholar] [CrossRef]
- Oda, K.y.; Yamada, M. Non-minimal coupling in Higgs–Yukawa model with asymptotically safe gravity. Class. Quant. Grav. 2016, 33, 125011. [Google Scholar] [CrossRef]
- Eichhorn, A.; Lippoldt, S. Quantum gravity and Standard-Model-like fermions. Phys. Lett. 2017, B767, 142–146. [Google Scholar] [CrossRef]
- Wetterich, C.; Yamada, M. Gauge hierarchy problem in asymptotically safe gravity–the resurgence mechanism. Phys. Lett. B 2017, 770, 268–271. [Google Scholar] [CrossRef]
- Biemans, J.; Platania, A.; Saueressig, F. Renormalization group fixed points of foliated gravity-matter systems. J. High Energy Phys. 2017, 2017, 093. [Google Scholar] [CrossRef]
- Christiansen, N.; Litim, D.F.; Pawlowski, J.M.; Reichert, M. Asymptotic safety of gravity with matter. Phys. Rev. 2018, D97, 106012. [Google Scholar] [CrossRef]
- Hamada, Y.; Yamada, M. Asymptotic safety of higher derivative quantum gravity non-minimally coupled with a matter system. JHEP 2017, 08, 070. [Google Scholar] [CrossRef]
- Eichhorn, A.; Hamada, Y.; Lumma, J.; Yamada, M. Quantum gravity fluctuations flatten the Planck-scale Higgs potential. Phys. Rev. 2018, D97, 086004. [Google Scholar] [CrossRef]
- Eichhorn, A.; Held, A. Top mass from asymptotic safety. Phys. Lett. 2018, B777, 217–221. [Google Scholar] [CrossRef]
- Eichhorn, A.; Lippoldt, S.; Skrinjar, V. Nonminimal hints for asymptotic safety. Phys. Rev. D 2018, 97, 026002. [Google Scholar] [CrossRef]
- Alkofer, N.; Saueressig, F. Asymptotically safe f(R)-gravity coupled to matter I: The polynomial case. Ann. Phys. 2018, 396, 173–201. [Google Scholar] [CrossRef]
- Eichhorn, A.; Labus, P.; Pawlowski, J.M.; Reichert, M. Effective universality in quantum gravity. Sci. Post Phys. 2018, 5, 31. [Google Scholar] [CrossRef]
- Eichhorn, A.; Lippoldt, S.; Pawlowski, J.M.; Reichert, M.; Schiffer, M. How perturbative is quantum gravity? Phys. Lett. 2019, B792, 310–314. [Google Scholar] [CrossRef]
- Eichhorn, A.; Lippoldt, S.; Schiffer, M. Zooming in on fermions and quantum gravity. Phys. Rev. 2019, D99, 086002. [Google Scholar] [CrossRef]
- Pawlowski, J.M.; Reichert, M.; Wetterich, C.; Yamada, M. Higgs scalar potential in asymptotically safe quantum gravity. Phys. Rev. 2019, D99, 086010. [Google Scholar] [CrossRef]
- Knorr, B.; Ripken, C.; Saueressig, F. Form Factors in Asymptotic Safety: Conceptual ideas and computational toolbox. Class. Quant. Grav. 2019, 36, 234001. [Google Scholar] [CrossRef]
- Bürger, B.; Pawlowski, J.M.; Reichert, M.; Schaefer, B.J. Curvature dependence of quantum gravity with scalars. arXiv 2019, arXiv:1912.01624. [Google Scholar]
- Eichhorn, A.; Schiffer, M. d=4 as the critical dimensionality of asymptotically safe interactions. Phys. Lett. 2019, B793, 383–389. [Google Scholar] [CrossRef]
- Reichert, M.; Smirnov, J. Dark Matter meets Quantum Gravity. Phys. Rev. D 2020, 101, 063015. [Google Scholar] [CrossRef]
- Kurov, A.; Saueressig, F. On characterizing the Quantum Geometry underlying Asymptotic Safety. Front. Phys. 2020, 8, 187. [Google Scholar] [CrossRef]
- Daas, J.; Oosters, W.; Saueressig, F.; Wang, J. Asymptotically safe gravity with fermions. Phys. Lett. B 2020, 809, 135775. [Google Scholar] [CrossRef]
- Eichhorn, A.; Pauly, M. Safety in darkness: Higgs portal to simple Yukawa systems. arXiv 2020, arXiv:2005.03661. [Google Scholar]
- Eichhorn, A.; Pauly, M. Constraining power of asymptotic safety for scalar fields. Phys. Rev. D 2021, 103, 026006. [Google Scholar] [CrossRef]
- Ali, P.; Eichhorn, A.; Pauly, M.; Scherer, M.M. Constraints on discrete global symmetries in quantum gravity. J. High Energy Phys. 2021, 2021, 036. [Google Scholar] [CrossRef]
- Harst, U.; Reuter, M. QED coupled to QEG. JHEP 2011, 1105, 119. [Google Scholar] [CrossRef]
- Eichhorn, A.; Gies, H. Light fermions in quantum gravity. New J. Phys. 2011, 13, 125012. [Google Scholar] [CrossRef]
- Christiansen, N.; Eichhorn, A. An asymptotically safe solution to the U(1) triviality problem. Phys. Lett. 2017, B770, 154–160. [Google Scholar] [CrossRef]
- Eichhorn, A.; Versteegen, F. Upper bound on the Abelian gauge coupling from asymptotic safety. J. High Energy Phys. 2018, 2018, 030. [Google Scholar] [CrossRef]
- Gies, H.; Martini, R. Curvature bound from gravitational catalysis. Phys. Rev. D 2018, 97, 085017. [Google Scholar] [CrossRef]
- Eichhorn, A.; Held, A. Mass difference for charged quarks from asymptotically safe quantum gravity. Phys. Rev. Lett. 2018, 121, 151302. [Google Scholar] [CrossRef]
- Alkofer, R.; Eichhorn, A.; Held, A.; Nieto, C.M.; Percacci, R.; Schröfl, M. Quark masses and mixings in minimally parameterized UV completions of the Standard Model. Ann. Phys. 2020, 421, 168282. [Google Scholar] [CrossRef]
- de Brito, G.P.; Eichhorn, A.; Schiffer, M. Light charged fermions in quantum gravity. Phys. Lett. B 2021, 815, 136128. [Google Scholar] [CrossRef]
- Gies, H.; Salek, A.S. A curvature bound from gravitational catalysis in thermal backgrounds. arXiv 2021, arXiv:2103.05542. [Google Scholar]
- Bonanno, A.; Platania, A. Asymptotically safe inflation from quadratic gravity. Phys. Lett. B 2015, 750, 638–642. [Google Scholar] [CrossRef]
- Alkofer, N.; D’Odorico, G.; Saueressig, F.; Versteegen, F. Quantum Gravity signatures in the Unruh effect. Phys. Rev. 2016, D94, 104055. [Google Scholar] [CrossRef]
- Bonanno, A.; Koch, B.; Platania, A. Cosmic Censorship in Quantum Einstein Gravity. Class. Quant. Grav. 2017, 34, 095012. [Google Scholar] [CrossRef]
- Bonanno, A.; Gionti, S.J.G.; Platania, A. Bouncing and emergent cosmologies from Arnowitt–Deser–Misner RG flows. Class. Quant. Grav. 2018, 35, 065004. [Google Scholar] [CrossRef]
- Bonanno, A.; Platania, A.; Saueressig, F. Cosmological bounds on the field content of asymptotically safe gravity–matter models. Phys. Lett. 2018, B784, 229–236. [Google Scholar] [CrossRef]
- Gubitosi, G.; Ooijer, R.; Ripken, C.; Saueressig, F. Consistent early and late time cosmology from the RG flow of gravity. JCAP 2018, 1812, 004. [Google Scholar] [CrossRef]
- Platania, A. The inflationary mechanism in Asymptotically Safe Gravity. Universe 2019, 5, 189. [Google Scholar] [CrossRef]
- Platania, A. From renormalization group flows to cosmology. Front. Phys. 2020, 8, 188. [Google Scholar] [CrossRef]
- Bonanno, A.; Reuter, M. Quantum gravity effects near the null black hole singularity. Phys. Rev. D 1999, 60, 084011. [Google Scholar] [CrossRef]
- Falls, K.; Litim, D.F. Black hole thermodynamics under the microscope. Phys. Rev. 2014, D89, 084002. [Google Scholar] [CrossRef]
- Koch, B.; Saueressig, F. Structural aspects of asymptotically safe black holes. Class. Quant. Grav. 2014, 31, 015006. [Google Scholar] [CrossRef]
- Koch, B.; Saueressig, F. Black holes within Asymptotic Safety. Int. J. Mod. Phys. 2014, A29, 1430011. [Google Scholar] [CrossRef]
- Bonanno, A.; Koch, B.; Platania, A. Gravitational collapse in Quantum Einstein Gravity. Found. Phys. 2018, 48, 1393–1406. [Google Scholar] [CrossRef]
- Adeifeoba, A.; Eichhorn, A.; Platania, A. Towards conditions for black-hole singularity-resolution in asymptotically safe quantum gravity. Class. Quant. Grav. 2018, 35, 225007. [Google Scholar] [CrossRef]
- Platania, A. Dynamical renormalization of black-hole spacetimes. Eur. Phys. J. C 2019, 79, 470. [Google Scholar] [CrossRef]
- Bosma, L.; Knorr, B.; Saueressig, F. Resolving Spacetime Singularities within Asymptotic Safety. Phys. Rev. Lett. 2019, 123, 101301. [Google Scholar] [CrossRef]
- Held, A.; Gold, R.; Eichhorn, A. Asymptotic safety casts its shadow. J. Cosmol. Astropart. Phys. 2019, 2019, 029. [Google Scholar] [CrossRef]
- Percacci, R. An Introduction to Covariant Quantum Gravity and Asymptotic Safety; 100 Years of General Relativity; World Scientific: Singapore, 2017; Volume 3. [Google Scholar] [CrossRef]
- Eichhorn, A. An asymptotically safe guide to quantum gravity and matter. Front. Astron. Space Sci. 2019, 5, 47. [Google Scholar] [CrossRef]
- Reuter, M.; Saueressig, F. Quantum Gravity and the Functional Renormalization Group; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Reichert, M. Lecture notes: Functional Renormalisation Group and Asymptotically Safe Quantum Gravity. PoS 2020, Modave2019, 005. [Google Scholar] [CrossRef]
- Pawlowski, J.M.; Reichert, M. Quantum gravity: A fluctuating point of view. arXiv 2021, arXiv:2007.10353. [Google Scholar]
- Donoghue, J.F. A Critique of the Asymptotic Safety Program. Front. Phys. 2020, 8, 56. [Google Scholar] [CrossRef]
- Bonanno, A.; Eichhorn, A.; Gies, H.; Pawlowski, J.M.; Percacci, R.; Reuter, M.; Saueressig, F.; Vacca, G.P. Critical reflections on asymptotically safe gravity. Front. Phys. 2020, 8, 269. [Google Scholar] [CrossRef]
- Ambjorn, J.; Jurkiewicz, J.; Loll, R. Reconstructing the universe. Phys. Rev. D 2005, 72, 064014. [Google Scholar] [CrossRef]
- Laiho, J.; Coumbe, D. Evidence for Asymptotic Safety from Lattice Quantum Gravity. Phys. Rev. Lett. 2011, 107, 161301. [Google Scholar] [CrossRef] [PubMed]
- Ambjorn, J.; Goerlich, A.; Jurkiewicz, J.; Loll, R. Nonperturbative Quantum Gravity. Phys. Rept. 2012, 519, 127–210. [Google Scholar] [CrossRef]
- Coumbe, D.; Laiho, J. Exploring Euclidean Dynamical Triangulations with a Non-trivial Measure Term. J. High Energy Phys. 2015, 2015, 028. [Google Scholar] [CrossRef]
- Laiho, J.; Bassler, S.; Coumbe, D.; Du, D.; Neelakanta, J.T. Lattice Quantum Gravity and Asymptotic Safety. Phys. Rev. 2017, D96, 064015. [Google Scholar] [CrossRef]
- Ambjørn, J.; Gizbert-Studnicki, J.; Görlich, A.; Jurkiewicz, J.; Németh, D. The phase structure of Causal Dynamical Triangulations with toroidal spatial topology. J. High Energy Phys. 2018, 2018, 111. [Google Scholar] [CrossRef]
- Loll, R. Quantum Gravity from Causal Dynamical Triangulations: A Review. Class. Quant. Grav. 2020, 37, 013002. [Google Scholar] [CrossRef]
- Ambjorn, J.; Drogosz, Z.; Gizbert-Studnicki, J.; Görlich, A.; Jurkiewicz, J.; Nèmeth, D. CDT Quantum Toroidal Spacetimes: An Overview. Universe 2021, 7, 79. [Google Scholar] [CrossRef]
- Bassler, S.; Laiho, J.; Schiffer, M.; Unmuth-Yockey, J. The de Sitter Instanton from Euclidean Dynamical Triangulations. Phys. Rev. D 2021, 103, 114504. [Google Scholar] [CrossRef]
- Bonanno, A.; Denz, T.; Pawlowski, J.M.; Reichert, M. Reconstructing the graviton. arXiv 2021, arXiv:2102.02217. [Google Scholar]
- Platania, A.; Wetterich, C. Non-perturbative unitarity and fictitious ghosts in quantum gravity. Phys. Lett. B 2020, 811, 135911. [Google Scholar] [CrossRef]
- Wetterich, C. Exact evolution equation for the effective potential. Phys.Lett. 1993, B301, 90–94. [Google Scholar] [CrossRef]
- Ellwanger, U. FLow equations for N point functions and bound states. Z. Phys. C 1994, 62, 503–510. [Google Scholar] [CrossRef]
- Morris, T.R. The Exact renormalization group and approximate solutions. Int. J. Mod. Phys. 1994, A9, 2411–2450. [Google Scholar] [CrossRef]
- Berges, J.; Tetradis, N.; Wetterich, C. Nonperturbative renormalization flow in quantum field theory and statistical physics. Phys. Rept. 2002, 363, 223–386. [Google Scholar] [CrossRef]
- Pawlowski, J.M. Aspects of the functional renormalisation group. Ann. Phys. 2007, 322, 2831–2915. [Google Scholar] [CrossRef]
- Gies, H. Introduction to the functional RG and applications to gauge theories. Lect. Notes Phys. 2012, 852, 287–348. [Google Scholar] [CrossRef]
- Berges, J.; Mesterhazy, D. Introduction to the nonequilibrium functional renormalization group. Nucl. Phys. Proc. Suppl. 2012, 228, 37–60. [Google Scholar] [CrossRef]
- Dupuis, N.; Canet, L.; Eichhorn, A.; Metzner, W.; Pawlowski, J.M.; Tissier, M.; Wschebor, N. The nonperturbative functional renormalization group and its applications. Phys. Rep. 2020. [Google Scholar] [CrossRef]
- Demmel, M.; Nink, A. Connections and geodesics in the space of metrics. Phys. Rev. 2015, D92, 104013. [Google Scholar] [CrossRef]
- Houthoff, W.B.; Kurov, A.; Saueressig, F. Impact of topology in foliated Quantum Einstein Gravity. Eur. Phys. J. 2017, C77, 491. [Google Scholar] [CrossRef] [PubMed]
- Knorr, B. Lorentz symmetry is relevant. Phys. Lett. 2019, B792, 142–148. [Google Scholar] [CrossRef]
- Baldazzi, A.; Percacci, R.; Skrinjar, V. Wicked metrics. Class. Quant. Grav. 2019, 36, 105008. [Google Scholar] [CrossRef]
- Eichhorn, A.; Platania, A.; Schiffer, M. Lorentz invariance violations in the interplay of quantum gravity with matter. Phys. Rev. D 2020, 102, 026007. [Google Scholar] [CrossRef]
- Nagy, S.; Sailer, K.; Steib, I. Renormalization of Lorentzian conformally reduced gravity. Class. Quantum Gravity 2019, 36, 155004. [Google Scholar] [CrossRef]
- Kawai, H.; Kitazawa, Y.; Ninomiya, M. Scaling exponents in quantum gravity near two-dimensions. Nucl. Phys. 1993, B393, 280–300. [Google Scholar] [CrossRef]
- Aida, T.; Kitazawa, Y.; Nishimura, J.; Tsuchiya, A. Two loop renormalization in quantum gravity near two-dimensions. Nucl. Phys. 1995, B444, 353–380. [Google Scholar] [CrossRef]
- Nink, A. Field Parametrization Dependence in Asymptotically Safe Quantum Gravity. Phys. Rev. 2015, D91, 044030. [Google Scholar] [CrossRef]
- Percacci, R.; Vacca, G.P. Search of scaling solutions in scalar-tensor gravity. Eur. Phys. J. 2015, C75, 188. [Google Scholar] [CrossRef]
- Labus, P.; Percacci, R.; Vacca, G.P. Asymptotic safety in O(N) scalar models coupled to gravity. Phys. Lett. 2016, B753, 274–281. [Google Scholar] [CrossRef]
- Ohta, N.; Percacci, R. Ultraviolet Fixed Points in Conformal Gravity and General Quadratic Theories. Class. Quant. Grav. 2016, 33, 035001. [Google Scholar] [CrossRef]
- Falls, K. On the renormalisation of Newton’s constant. Phys. Rev. 2015, D92, 124057. [Google Scholar] [CrossRef]
- Ohta, N.; Percacci, R.; Pereira, A.D. Gauges and functional measures in quantum gravity I: Einstein theory. J. High Energy Phys. 2016, 2016, 115. [Google Scholar] [CrossRef]
- Falls, K.; Ohta, N. Renormalization Group Equation for f(R) gravity on hyperbolic spaces. Phys. Rev. 2016, D94, 084005. [Google Scholar] [CrossRef]
- Percacci, R.; Vacca, G.P. The background scale Ward identity in quantum gravity. Eur. Phys. J. 2017, C77, 52. [Google Scholar] [CrossRef][Green Version]
- Knorr, B. Infinite order quantum-gravitational correlations. Class. Quant. Grav. 2018, 35, 115005. [Google Scholar] [CrossRef]
- Reuter, M.; Weyer, H. Background Independence and Asymptotic Safety in Conformally Reduced Gravity. Phys. Rev. 2009, D79, 105005. [Google Scholar] [CrossRef]
- Manrique, E.; Reuter, M.; Saueressig, F. Matter Induced Bimetric Actions for Gravity. Ann. Phys. 2011, 326, 440–462. [Google Scholar] [CrossRef]
- Donkin, I.; Pawlowski, J.M. The phase diagram of quantum gravity from diffeomorphism-invariant RG-flows. arXiv 2012, arXiv:1203.4207. [Google Scholar]
- Codello, A.; D’Odorico, G.; Pagani, C. Consistent closure of renormalization group flow equations in quantum gravity. Phys. Rev. 2014, D89, 081701. [Google Scholar] [CrossRef]
- Becker, D.; Reuter, M. Propagating gravitons vs. ‘dark matter’ in asymptotically safe quantum gravity. J. High Energy Phys. 2014, 2014, 025. [Google Scholar] [CrossRef]
- Demmel, M.; Saueressig, F.; Zanusso, O. RG flows of Quantum Einstein Gravity in the linear-geometric approximation. Ann. Phys. 2015, 359, 141–165. [Google Scholar] [CrossRef]
- Dietz, J.A.; Morris, T.R. Background independent exact renormalization group for conformally reduced gravity. J. High Energy Phys. 2015, 2015, 118. [Google Scholar] [CrossRef]
- Safari, M. Splitting Ward identity. Eur. Phys. J. 2016, C76, 201. [Google Scholar] [CrossRef][Green Version]
- Wetterich, C. Gauge invariant flow equation. Nucl. Phys. B 2018, 931, 262–282. [Google Scholar] [CrossRef]
- Wetterich, C. Gauge symmetry from decoupling. Nucl. Phys. 2017, B915, 135–167. [Google Scholar] [CrossRef]
- Morris, T.R.; Preston, A.W.H. Manifestly diffeomorphism invariant classical Exact Renormalization Group. J. High Energy Phys. 2016, 2016, 012. [Google Scholar] [CrossRef]
- Safari, M.; Vacca, G.P. Covariant and single-field effective action with the background-field formalism. Phys. Rev. 2017, D96, 085001. [Google Scholar] [CrossRef]
- Safari, M.; Vacca, G.P. Covariant and background independent functional RG flow for the effective average action. J. High Energy Phys. 2016, 2016, 139. [Google Scholar] [CrossRef]
- Labus, P.; Morris, T.R.; Slade, Z.H. Background independence in a background dependent renormalization group. Phys. Rev. 2016, D94, 024007. [Google Scholar] [CrossRef]
- Morris, T.R. Large curvature and background scale independence in single-metric approximations to asymptotic safety. J. High Energy Phys. 2016, 2016, 160. [Google Scholar] [CrossRef]
- Meibohm, J.; Pawlowski, J.M. Chiral fermions in asymptotically safe quantum gravity. Eur. Phys. J. 2016, C76, 285. [Google Scholar] [CrossRef] [PubMed]
- Ohta, N. Background Scale Independence in Quantum Gravity. PTEP 2017, 2017, 033E02. [Google Scholar] [CrossRef]
- Nieto, C.M.; Percacci, R.; Skrinjar, V. Split Weyl transformations in quantum gravity. Phys. Rev. D 2017, 96, 106019. [Google Scholar] [CrossRef]
- Gies, H. Running coupling in Yang-Mills theory: A flow equation study. Phys. Rev. D 2002, 66, 025006. [Google Scholar] [CrossRef]
- Litim, D.F.; Pawlowski, J.M. Renormalization group flows for gauge theories in axial gauges. J. High Energy Phys. 2002, 2002, 049. [Google Scholar] [CrossRef]
- Brizuela, D.; Martin-Garcia, J.M.; Mena Marugan, G.A. xPert: Computer algebra for metric perturbation theory. Gen. Rel. Grav. 2009, 41, 2415–2431. [Google Scholar] [CrossRef]
- Martín-García, J.M.; Portugal, R.; Manssur, L.R.U. The Invar tensor package. Comput. Phys. Commun. 2007, 177, 640–648. [Google Scholar] [CrossRef]
- Martín-García, J.M.; Yllanes, D.; Portugal, R. The Invar tensor package: Differential invariants of Riemann. Comput. Phys. Commun. 2008, 179, 586–590. [Google Scholar] [CrossRef]
- Martín-García, J.M. xPerm: Fast index canonicalization for tensor computer algebra. Comput. Phys. Commun. 2008, 179, 597–603. [Google Scholar] [CrossRef]
- Nutma, T. xTras: A field-theory inspired xAct package for mathematica. Comput. Phys. Commun. 2014, 185, 1719–1738. [Google Scholar] [CrossRef]
- Cyrol, A.K.; Mitter, M.; Strodthoff, N. FormTracer - A Mathematica Tracing Package Using FORM. Comput. Phys. Commun. 2017, 219, 346–352. [Google Scholar] [CrossRef]
- Knorr, B.; Saueressig, F. Towards reconstructing the quantum effective action of gravity. Phys. Rev. Lett. 2018, 121, 161304. [Google Scholar] [CrossRef]
- Belgacem, E.; Dirian, Y.; Foffa, S.; Maggiore, M. Nonlocal gravity. Conceptual aspects and cosmological predictions. J. Cosmol. Astropart. Phys. 2018, 2018, 002. [Google Scholar] [CrossRef]
- Belgacem, E.; Dirian, Y.; Finke, A.; Foffa, S.; Maggiore, M. Gravity in the infrared and effective nonlocal models. J. Cosmol. Astropart. Phys. 2020, 2020, 10. [Google Scholar] [CrossRef]
- Knorr, B. Lessons from conformally reduced quantum gravity. Class. Quant. Grav. 2021, 38, 065003. [Google Scholar] [CrossRef]
- Wetterich, C. Quantum correlations for the metric. Phys. Rev. D 2017, 95, 123525. [Google Scholar] [CrossRef]
- Christiansen, N. Four-Derivative Quantum Gravity Beyond Perturbation Theory. arXiv 2016, arXiv:1612.06223. [Google Scholar]
- Reichert, M. Towards a UV-Complete Standard Model: From Baryogenesis to Asymptotic Safety. Ph.D. Thesis, Heidelberg University, Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Boyd, J. Orthogonal rational functions on a semi-infinite interval. J. Comp. Phys. 1987, 70, 63–88. [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods, 2nd ed.; Dover Publications: Mignola, NY, USA, 2000. [Google Scholar]
- Borchardt, J.; Knorr, B. Global solutions of functional fixed point equations via pseudospectral methods. Phys. Rev. 2015, D91, 105011, Erratum: Phys. Rev. 2016, D93, 089904. [Google Scholar] [CrossRef]
- Borchardt, J.; Knorr, B. Solving functional flow equations with pseudo-spectral methods. Phys. Rev. 2016, D94, 025027. [Google Scholar] [CrossRef]
- Grossi, E.; Wink, N. Resolving phase transitions with Discontinuous Galerkin methods. arXiv 2019, arXiv:1903.09503. [Google Scholar]
- Becker, D.; Ripken, C.; Saueressig, F. On avoiding Ostrogradski instabilities within Asymptotic Safety. J. High Energy Phys. 2017, 2017, 121. [Google Scholar] [CrossRef]
- Draper, T.; Knorr, B.; Ripken, C.; Saueressig, F. Finite Quantum Gravity Amplitudes: No Strings Attached. Phys. Rev. Lett. 2020, 125, 181301. [Google Scholar] [CrossRef]
- Draper, T.; Knorr, B.; Ripken, C.; Saueressig, F. Graviton-Mediated Scattering Amplitudes from the Quantum Effective Action. J. High Energy Phys. 2020, 2020, 136. [Google Scholar] [CrossRef]
- Codello, A.; Zanusso, O. On the non-local heat kernel expansion. J. Math. Phys. 2013, 54, 013513. [Google Scholar] [CrossRef]

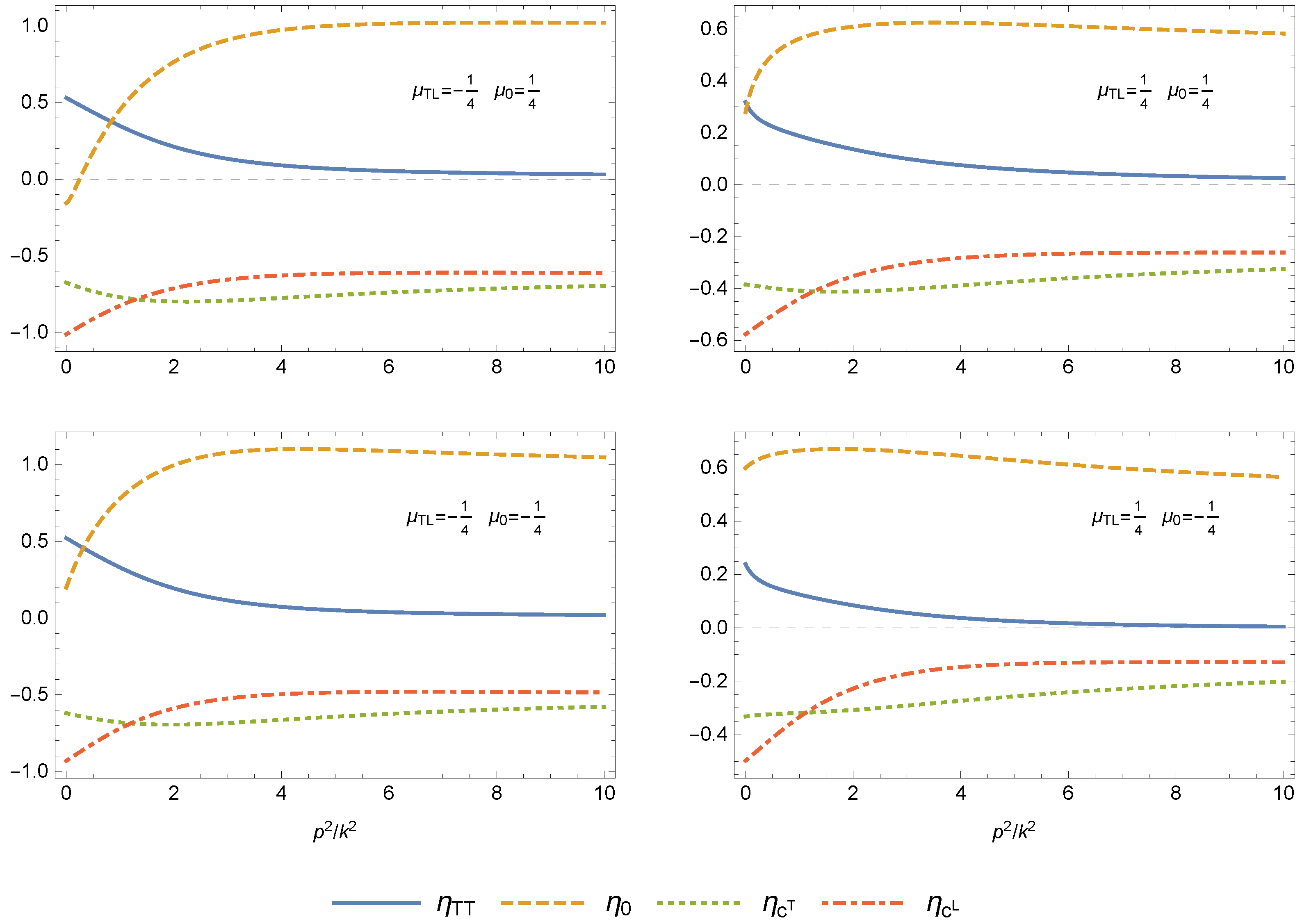

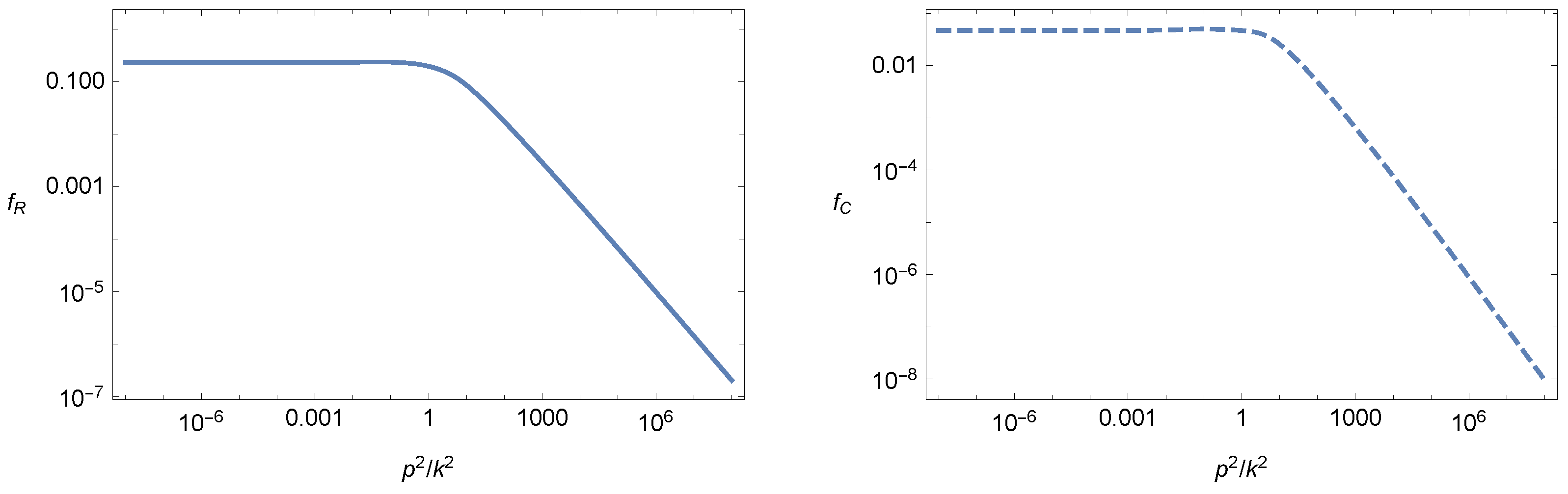
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Knorr, B.; Schiffer, M. Non-Perturbative Propagators in Quantum Gravity. Universe 2021, 7, 216. https://doi.org/10.3390/universe7070216
Knorr B, Schiffer M. Non-Perturbative Propagators in Quantum Gravity. Universe. 2021; 7(7):216. https://doi.org/10.3390/universe7070216
Chicago/Turabian StyleKnorr, Benjamin, and Marc Schiffer. 2021. "Non-Perturbative Propagators in Quantum Gravity" Universe 7, no. 7: 216. https://doi.org/10.3390/universe7070216
APA StyleKnorr, B., & Schiffer, M. (2021). Non-Perturbative Propagators in Quantum Gravity. Universe, 7(7), 216. https://doi.org/10.3390/universe7070216





