1. Introduction
The introduction of dark matter, along with modified theories of gravity (such as modified Newtonian dynamics (MoND) [
1,
2], entropic gravity [
3] and quantised inertia [
4]), is used to explain various astrophysical and cosmological phenomena such as distinctive shapes of the rotation curves of galaxies, dynamics of galaxy clusters, and effects of gravitational lensing and microlensing. However, nowadays, dark matter is a commonly accepted explanation of these phenomena, and there are various models to describe its interaction with baryonic matter.
WIMPs (Weakly Interacted Massive Particles) are well-known candidates for dark matter. It is assumed that our Galaxy is surrounded by a WIMP halo with WIMPs having masses ranging from 1 GeV to 100 TeV. The idea of direct detection of WIMPs is based on the assumption that a wind of WIMPs with Maxwell velocity distributions with an average velocity of 220 km/s “blows” on our Earth in the Solar system as it rotates around the center of the Galaxy [
5]. In this scenario, WIMPs should be able to interact elastically with detector material producing recoil nuclei, which can be registered and measured. Some experiments are designed in such a way so as to allow for the determination of the recoil nuclei directions and, thus, the directions of WIMP momenta prior to their interaction with a target. The examples of such detectors are time-projection proportional chambers [
6], micro pattern gaseous detectors [
7], graphene-based detectors [
8], and other detectors using advanced technologies.
The maximum of the assumed WIMP velocity distribution corresponds to the direction to the Cygnus constellation. Background events related to elastic neutrino interactions should be either isotropic (like the ones from both atmospheric and supernova neutrinos) or correlate with the position of the Sun (events from solar neutrinos). Consequently, the detection of excess events with directions pointing to the Cygnus constellation could serve as an unambiguous proof of the presence of dark matter in the form of a galactic halo [
9].
In the present work, we provide the model constraints on the possibility of WIMP detection in a directional experiment with a light target, such as hydrogen nuclei (H), nuclei of carbon–oxygen–nitrogen group (CNO), as well as fluorine nuclei (F). This work is organized as follows. In
Section 2, we briefly describe a classical scheme of WIMP elastic interactions with recoil nuclei of the detector and provide the characteristics of WIMPs with different masses. In
Section 3, we describe the scheme for modeling of recoil nuclei tracks in the detector material and study the features of tracks in nuclear emulsion, liquid propane
, and liquid octafluoropropane
.
Section 4 is devoted to numerical estimates of a possible WIMP signal obtained using the micrOMEGAs code [
10]. Since solar neutrinos represent a directional background for WIMP search experiments,
Section 5 considers recoil tracks from directional (solar) neutrinos and provides the main formulas for calculation of energy and angular distributions of recoil nuclei from neutrino elastic interactions with detector material nuclei, as well as the features of recoil nuclei tracks in nuclear emulsion, propane, and octafluoropropane. Finally, in
Section 6 we discuss the possible number of recoil nuclei from WIMP and solar neutrino interactions with detector material, and draw conclusions concerning preferred targets for visualizing and directional WIMP experiments with WIMPs having the lowest supposed masses of 4–10 GeV.
2. Scheme of WIMP Elastic Interaction with Detector Material. Energy and Angular Distributions of Recoil Nuclei
Three models of tracking detectors with significantly different densities of sensitive materials have been considered. The first one is the NEWSdm nuclear emulsion detector [
11] with density
, which uses nanoemulsion NIT (Nano Imaging Tracker) with grain sizes of 20–40–80 nm [
12]. This is a huge improvement over a typical nuclear emulsion used, for example, in the OPERA
neutrino oscillation search experiment [
13], where the emulsion grain size was approximately 200 nm. The second model is that a detector in the form of 500 L of liquid propane
with density
, which works as a bubble chamber. As the third model we considered the sensitive material of the projected PICO experiment detector [
14]—a bubble chamber filled with 500 L of octafluoropropane
with density
.
The elastic interaction of WIMPs on target nuclei has been described in numerous works, e.g., [
15,
16]. Its general scheme is shown in
Figure 1.
To model the tracks of recoil nuclei in the detectors of directional experiments one could use a double differential distribution of recoil nuclei by energy and direction described by the following formula [
16]:
where
,
is the WIMP local density,
m is the WIMP mass,
M is the mass of the target nucleus,
is the reduced mass of the WIMP-nucleus system.
is the minimal WIMP velocity necessary for the transfer of energy E to a target with the mass M.
Just as it was done in [
16], we take a modified Maxwell distribution as a
function:
where
is the WIMP velocity before the scattering, and
is the direction of recoil nucleus velocity
after the WIMP scattering on them.
and
are set with regard to the direction corresponding to the maximum of WIMP velocity distribution—
.
The cross section of WIMP scattering on nuclei consists of two parts: spin-dependent (SD) and spin-independent (SI).
Correspondingly, one can separate the spin-independent and spin-dependent contributions to the directional recoil rate.
The spin-independent part could be written as:
where
,
are amplitudes for DM scattering on nucleons; Z and A are nucleus mass number and charge, respectively, and
is the Helm form-factor [
17]:
where
q is the momentum of the recoil nucleus,
,
,
,
The spin-dependent (
is the spin of the nucleus) part of the cross section
[
18]
is defined through functions
,
, and
, which play the same role as the nuclear form-factor
in the spin-independent case and are defined as [
19]:
where
,
, and
are the nuclear spin structure functions [
19].
If the spin of the nucleus can be approximated by the spin of an odd nucleon only, then for a nucleus with an odd proton we have:
and for a nucleus with an odd neutron we get:
Values of
were taken from [
15,
20].
As targets we considered light H,C,N,O nuclei, which make up the nuclear emulsion is the sensitive part of the NEWSdm detector [
11], model propane bubble chamber, as well as fluorine F, which is part of
detector in the PICO experiment [
14].
Hydrogen and fluorine nuclei have spins of , while carbon and oxygen have zero spins. Another component of one of the targets considered by us is nitrogen, which has nuclei of a similar mass and a spin of 1. However, unfortunately, we were not able to find any information on its structure function for an odd-odd nucleus, which is necessary for calculating the spin-dependent part, so for N we used a spin-independent approximation instead.
Formula (
1) was used to calculate the two-dimensional probability density functions of energy
E and direction
distributions of various recoil nuclei. Then, in accordance to these distributions we simulated sets of individual recoil nuclei with fixed
E and
for WIMPs with masses 10, 60, 100, and 1000 GeV, see
Figure 2,
Figure 3 and
Figure 4.
The absolute values of WIMP-nucleon interaction cross-sections as well as the number of events per unit mass of the material have been obtained using the publicly available micrOMEGAs toolkit [
10] for specific models of WIMPs.
Figure 2,
Figure 3 and
Figure 4 show the examples of distributions of
simulated hydrogen (H), carbon (C), and fluorine (F) recoil nuclei over their energies
and the projection of a 3D recoil nucleus incidence angle on a 2D detector plane
for various WIMP masses. For the task of reconstructing the recoil nuclei track directions it is the projection of the 3D incidence angle
on the detector plane (e.g., on the plane of an emulsion plate) that represents the angle corresponding to the track direction, which can be studied in the experiment, most accurately.
It is worth mentioning that there are noticeable differences in the energies of hydrogen, carbon and fluorine nuclei as well as almost indistinguishable shapes of angular distributions for H, C and F for different WIMP masses.
3. Scheme of Track Modeling in GEANT4
Modeling of the recoil nuclei tracks in the detector material has been done using GEANT4 toolkit. More specifically, we have used StandardNR—Nuclear Recoil Physics List) [
21].
Examples of hydrogen and carbon nuclei tracks are shown in
Figure 5. This figure also demonstrates the lines that represent best fits (according to the least squares method) of all the track points. Lengths and orientations of these tracks are then used to determine lengths and directions of recoil nuclei tracks.
The first step of our simulation included studying the tracks from monoenergetic hydrogen H (2, 5, 10, 30 keV) and carbon C (10, 30, 60, 100 keV) nuclei with fixed energies, which were emitted as a focused beam and interacted with nuclear emulsion material with density
. This modeling is necessary to estimate the extent of scattering of recoil nuclei and resulting track lengths of nuclei with various energies. The track lengths of carbon (C) and hydrogen (H) nuclei in the emulsion as well as angular distributions over the angle defined as an angle between the best fit of track points and the original direction of the recoil nucleus are shown in
Figure 6 and
Figure 7 for various energies.
Distributions of
hydrogen (H) and carbon (C) nuclei recoil tracks in a nuclear emulsion over the tracks length and angular distributions relative to the direction “toward the Cygnus constellation” are shown in
Figure 8 and
Figure 9 for WIMP masses 10 and 100 GeV. The tracks was modeled with GEANT4 StandardNR Physics List. The initial nuclear recoil energies
was simulated based on the two-dimensional probability density functions (
1) and shown in
Figure 2 and
Figure 3.
Only tracks with a length greater than 80 nm are considered.
As an alternative option for the detector material we considered liquid propane
with density
g/cm
, which could be used as a tracker in the bubble chamber mode, and the target of the PICO detector [
14]—octafluoropropane
with density
g/cm
. As for the case of the nuclear emulsion, we simulated
recoil nuclei tracks from WIMPs with masses 10 and 100
.
Distributions of track lengths in liquid propane for hydrogen and carbon recoil nuclei and WIMPs with masses 10 and 100 GeV are shown in
Figure 8 and
Figure 9, right.
The significantly lower density of propane makes it possible to visualize a substantially larger number of tracks of recoil nuclei compared to the number of tracks in a denser emulsion. Since the original WIMP angular distribution is rather wide (see
Figure 2,
Figure 3 and
Figure 4), the directions of the tracks of the recoil nuclei are correspondingly wide.
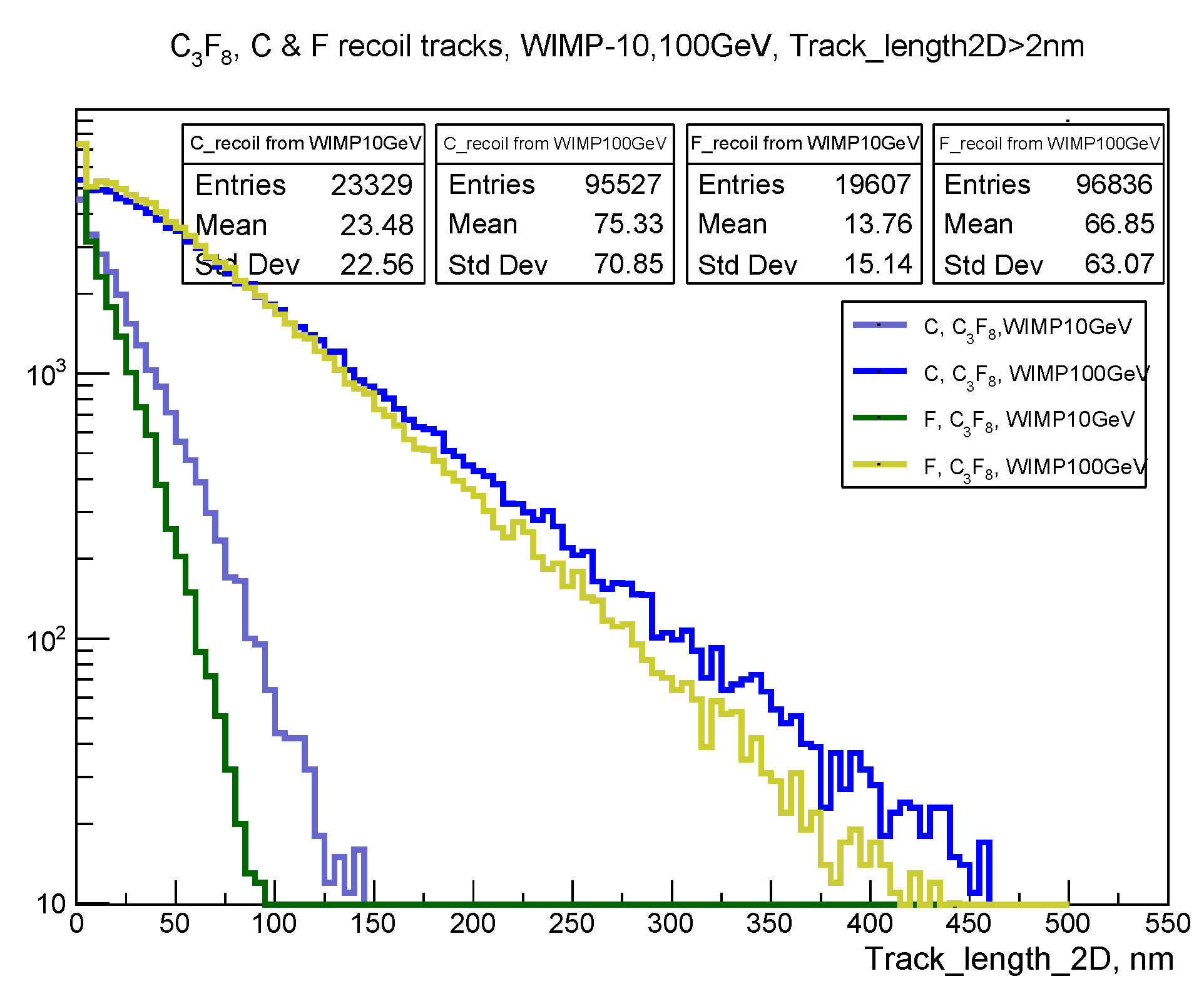
Figure 10 and
Figure 11 illustrate the fact that WIMPs with small masses (∼10 GeV) do not couple effectively with C and F nuclei and do not create recoil nuclei tracks with track lengths more than 100 nm in the octafluoropropane, while such coupling is possible for WIMPs with masses 100 GeV. This means that the PICO detector as well as the XENON1T detector would exhibit the best sensitivity to WIMPs with masses ≲100 GeV.
The angular distribution of recoil nuclei tracks in has a similar shape as that for both denser (nuclear emulsion) and less dense () material. However, the track length cuts ≥80 nm for WIMPs with masses 10 GeV impoverish the statistics of heavier recoil nuclei in a much more significant way.
Calculations of recoil nuclear track lengths and angular distributions from WIMPs with various masses in NIT and UNIT emulsions using SRIM simulations are presented in [
22]. An additional modeling scenario, taking into account the crystal structure of the emulsion grains is also considered. Compared to the GEANT4 StandardNR model we used, SRIM simulated tracks, as indicated in [
22], are somewhat longer, and the angular distributions of the tracks are wider.
The average values of track length distributions in a standard nuclear emulsion for WIMPs of different masses are given in [
23]:
μm for
and
μm for
. The characteristics of the track length distributions from this work are shown in
Figure 8.
4. Models of Cold Dark Matter (WIMP) in micrOMEGAs. Constraints on WIMP Fluxes for Various Models
We used the micrOMEGAs 5.2.4 software package [
24]—the code for calculating the cold dark matter properties for various supersymmetric extensions of the Standard Model—for quantitative estimation of the WIMP signal. In the MSSM (Minimal Supersymmetric Standard Model) [
25] a candidate for the role of a dark matter particle is a light neutralino, which has a spin 1/2 and is a linear combination of superpartners of gauge bosons and Higgs doublet—
,
,
and
:
It is now believed that the neutralino in MSSM as a cold dark matter model is almost completely ruled out by experimental constraints [
26].
To estimate the cross sections we used the NMSSM (Next-to-Minimal Supersymmetric Standard Model) [
27,
28] and the IDM (Inert Doublet Model) [
29] models for minimal WIMP masses (approximately 10 GeV or less). Higher masses have been ruled out by XENON1T experiment [
30].
In the NMSSM a particle with spin 1/2 is assumed as a dark matter particle. Like in the MSSM, it is a linear combination of
,
,
, and
, but in this case a new superpartner is added—
:
For the NMSSM we considered the SUGRA [
31] scenario. For a wide range of model parameters we calculated WIMP masses and values of cross sections of dark matter particle interactions with nucleons (proton and neutron)
,
. In the “Direct Detection” scenario we also calculated the number of WIMP events per kg of target per day for hydrogen, carbon, and oxygen targets (see
Figure 12).
The calculations show (see
Figure 12) that the NMSSM is also practically ruled out for WIMP masses starting from several GeV by the XENON1T [
30] data. DarkSide [
32] and CRESST [
33] experiments have set the constraints on the WIMP-nucleon interaction cross sections for WIMP masses ∼1 GeV.
The IDM [
29] turned out to be the most promising model in terms of experimental constraints. This model contains, in addition to the Standard Model (SM) particle content, a second complex scalar doublet. The IDM has four new physical states: two charged
and two neutral
and
, the neutral ones of them can be a cold dark matter particle candidate. Here we consider
, the lightest particle of the four,
as a DM particle candidate. Moreover, in the IDM, a DM particle is a scalar, which means that one does not need to consider the spin-dependent interactions. Thus, the DM interactions with nitrogen and fluorine nuclei could be treated in the same way as the ones with carbon and oxygen nuclei.
Firstly, we need to verify that different IDM options (i.e., different choice of model parameters) do not contradict with the constraints set by the relic density. This comparison is shown in
Figure 13.
Figure 14, left shows different IDM models along with existing experimental constraints for different WIMP masses. It can be seen that there are numerous model options which do not contradict the constraints.
Figure 14, right shows the IDM simulations in the “WIMP mass—number of events per day per kg of target” parameter space.
For the numerical estimates we considered WIMPs with mass 10 GeV. We also chose the IDM option with the maximal WIMP-nucleon cross section that does not contradict the existing experimental constraints. The corresponding values of WIMP events per day per kg of target are shown in the conlusive table below.
5. Elastic Interaction of Solar Neutrinos with Detector Material as a Directional Background for WIMP Observations
In this work we study the possibility of analyzing the directions and track lengths of recoil nuclei from WIMP-target interactions to search the excess WIMP signal in the direction to the Cygnus constellation. Recoil nuclei from solar neutrino interactions could represent a directional background for such a task.
The expressions for cross sections of neutrino-nucleus elastic scattering used to estimate the neutrino background are presented in, e.g., [
34]. The solar neutrino energies were modeled after the corresponding spectrum [
35] starting from the energy
MeV.
Figure 15 shows the distributions of the recoil nuclei from solar neutrino interactions in denser (nuclear emulsion) and less dense (
and
) material in the “neutrino energy-recoil nucleus track length” parameter space. It is evident from this figure that hydrogen recoil nuclei from elastic scattering of neutrinos with energies
MeV can form tracks with track lengths more than 2 nm. For carbon nuclei the same is true for neutrinos with energies
MeV. Thus, the contribution from the carbon recoil nuclei is expected to be minimal. A characteristic congestion of dots in the solar neutrino energy region (∼1–2) MeV) is due to the form of the intrinsic neutrino spectrum.
Figure 16 shows the distributions of the recoil nuclei from solar neutrinos in
,
, and nuclear emulsion over track lengths. If one applies cuts on track lengths according to the sensitivity of nanoemulsions to the directions of recoil nuclei tracks (≥60–80 nm), it becomes evident that the main contribution to the directional solar neutrino signal would be from hydrogen nuclei.
6. Discussion and Conclusions
In this work we estimated the annual signal from a WIMP with a mass of 10 GeV in 30 kg of nuclear emulsion, of liquid , and 500 L of liquid . It was found that approximately 1 event per year is expected in the considered sensitive volume of the emulsion. Accordingly, in order to register approximately 10 events related to WIMPs, it is necessary to expose and scan approximately 300 kg of emulsion, which requires significant material and human resources. In targets with a lower density, and , entirely consisting of light nuclei, and also providing long track lengths of nuclei, there will be 24 and 194 events from WIMPs per year.
These estimates allow us to conclude that, taking into account the existing experimental constraints on the elastic interaction cross sections of the WIMP-nucleus interactions, it makes sense in the direct detection scenario to consider lighter and less dense targets as a sensitive element of the detector system.
These results, as well as estimates of recoil events number from solar neutrinos, are presented in the table (see
Figure 17).