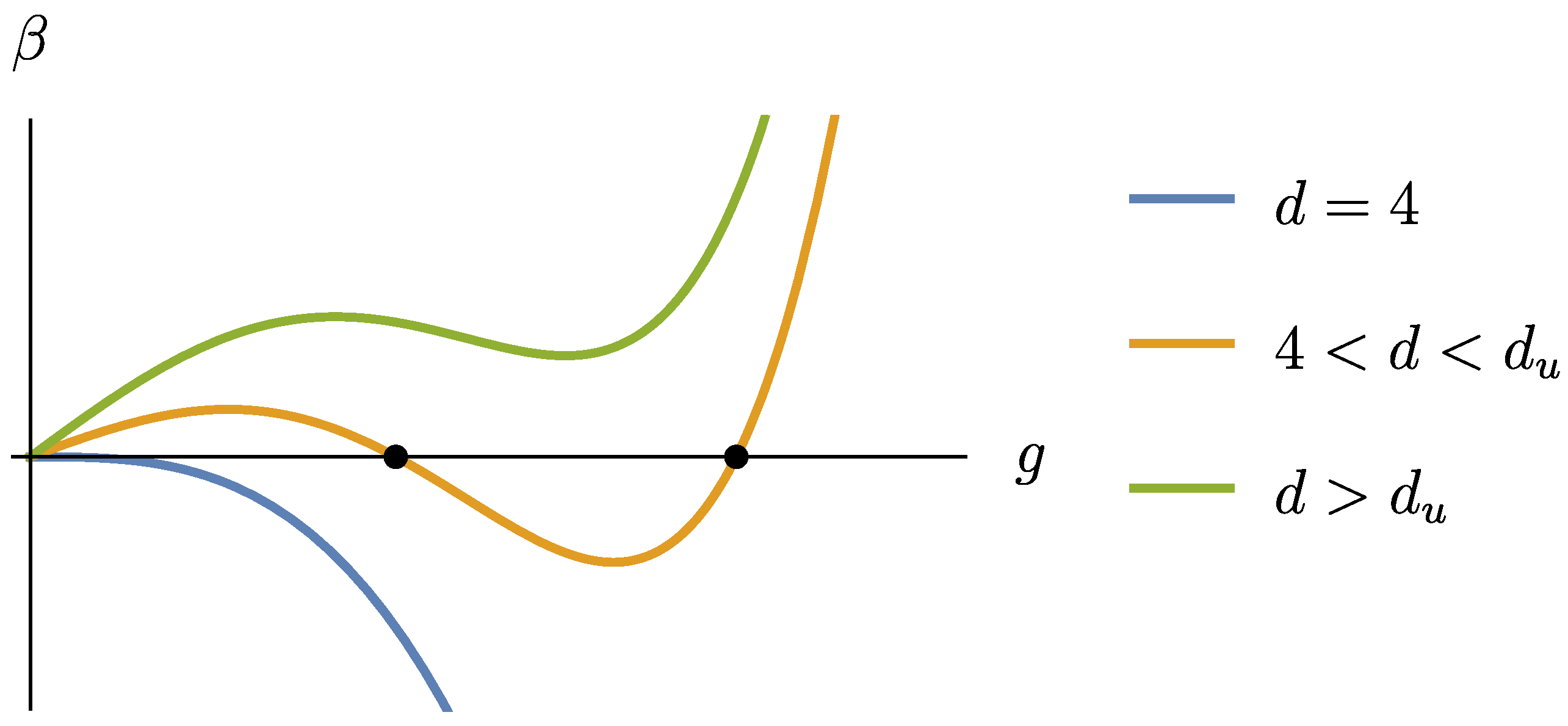Abstract
On the basis of a limited number of reasonable axioms, we discuss the classification of all the possible universality classes of diffeomorphisms invariant metric theories of quantum gravity. We use the language of the renormalization group and adopt several ideas which originate in the context of statistical mechanics and quantum field theory. Our discussion leads to several ideas that could affect the status of the asymptotic safety conjecture of quantum gravity and give universal arguments towards its proof.
1. Introduction
A well-known fact is that in four dimensions a quantum theory of Einstein–Hilbert gravity displays perturbatively non-renormalizable divergences starting at two loops [1,2]. This happens because Newton’s constant has negative mass dimension, which in turn requires a re-interpretation of the perturbative series as an effective expansion in inverse powers of the Planck mass, making the theory an effective IR model, rather than a UV complete one [3].
It was suggested by Weinberg that the UV limit of metric gravity could still be meaningful if the theory was asymptotically safe, namely, if it had an ultraviolet fixed point with a finite number of relevant directions in its renormalization group flow [4]. Since its inception, the idea of asymptotically safe gravity was linked to the proposal of continuing two-dimensional gravity, which is asymptotically free, in dimensions [5], where it could be asymptotically safe [6].
The proposal was early on investigated perturbatively continuing from two dimensions [7,8], but, given the obvious limitations of the -expansion, the main tool to explore the conjecture soon became the non-perturbative functional renormalization group, starting from the pivotal work of Reuter [9]. One difficulty, which is caused by the use of the average effective action of the functional approach, is that it is sometimes difficult to eliminate parametric and gauge dependences from the action, see for example [10], making the physical interpretation of the results unclear. To this day, the possibility that quantum gravity is asymptotically safe is still a conjecture, and most theoretists working on quantum gravity have strong opinions on the matter, either in favor or against it [11,12].
The discussion on the early approach to the conjecture brings forward a dilemma: on the one hand, using perturbation theory, we have that gravity in is a well-defined theory with no gauge or parametric dependence on-shell, but we are limited to , so we cannot access the physically interesting four dimensional theory located at (a meaningful resummation would require many more orders than the available ones). On the other hand, the non-perturbative approach has access to directly, but has general scheme and background/gauge dependences and no obvious way to eliminate them. The natural question is, which method should one choose? Our suggestion is simple, both. The seach for the ultraviolet completion of metric gravity should be pursued on both the perturbative and non-perturbative sides, and both sides should learn lessons from each other.
If we are to accept the idea that the UV complete theory of quantum gravity in comes from the model in , which is an idea based entirely on perturbation theory, then we might ask whether there are obstructions to the continuation of this solution to . In this paper, we discuss possible mechanisms that could either allow or prevent the -expansion from reaching the physical case . One natural mechanism is that of collision of fixed points, which is difficult to capture perturbatively, unless all involved players are in the weak-coupling regime. For this reason, it is important to have an idea of all the possible critical theories that are described by a metric effective action.
In the next two sections we use general arguments to discuss metric-based diffeomorphisms invariant theories that can be constructed perturbatively at a given critical dimension . We also argue if and how these theories can be continued either below or above their critical dimension to the physically interesting case .
2. The Diffeomorphisms Group and Its Siblings
The first ingredient of our construction requires the choice of the symmetry group. There are in principle several possible options of symmetry groups that lead to sensible gravitational actions. A discussion on some possibilities and the degrees of freedom that they propagate can be found in [13]. In order to contain the proliferation of possibilities, we mostly limit ourselves to the diffeomorphisms group and close relatives.
Einstein’s general relativity is an example of theory which is invariant under general diffeomorphisms. Infinitesimally, the general transformation can be parametrized locally with a vector field , so that coordinates change nonlinearly as . The metric transforms as
These infinitesimal transformations generate the algebra of the diffeomorphisms group, denoted Diff, which is isomorphic to the one of vector fields with Lie brackets as internal commutator
where are the Lie brackets of two vectors.
If one chooses to rewrite the metric as a conformal factor times another metric, , the symmetry is generally enhanced by a Weyl factor related to the combined rescaling of the two terms. By requiring that transformations on preserve the volume form , it is possible to break the enhanced symmetry down to a subgroup, , for which
where indices are lowered with on the right hand side. The subgroup preserves the volume, therefore is a unimodular metric, while is referred to as the dilaton. The interesting part is that this symmetry group is isomorphic to itself, as seen from proving that
A transformation can be seen as a volume preserving diffeomorphism combined to a conformal transformation, which together return a general diffeomorphism on the original metric. They propagate the same degrees of freedom, but the two groups generally differ when considered in a path-integral.
Another possiblity would be to not break the Weyl factor and construct a theory that is invariant under the full conformal group, , which would require the theory to be invariant under both Equation (1) and the local rescalings of the form . In a conformally invariant theory one does not naturally have scales, such as masses, therefore, in order to reproduce the physical world that includes Newton’s constant for gravity, one should invoke a spontaneous breaking mechanism at lower energies [14]. One point has to be made on the conformal group, and in particular on the subgroup, as it does not seem to have a nonzero Noether current in simple scalar models, which could make one question its role in the construction of a dynamical theory [15]. This is a particularly delicate issue that deserves more attention.
The symmetries that we described here are but two of a more general list of examples discussed in Ref. [13]. In fact, specific breaking patterns of the conformal group actually generate the aforementioned and [13,16], so we could reasonably expect them as outcomes of obtaining Planck mass at low energies from conformal symmetry. Another natural symmetry that emerges in this context is the group of volume preserving diffeomorphisms, that is the symmetry of unimodular gravity which has been introduced to relax the tension between the values of cosmological and Newton’s constants (see for example Refs. [17,18]).
3. Guiding Principles and Illustrative Examples
Now we articulate the guiding principles, inspired by the application of the renormaliation group to the theory of critical and multicritical phenomena in a Ginzburg–Landau description, that we are then going to apply to the case of metric-based theories. Some of the following ideas might be familiar to all readers, in that they are based on the textbook examples of and Yang–Mills gauge theories. Some others might be less familiar, especially those based on less-traditional examples, so we hope that they are met by open-minded readers. Rather than appliying directly any idea to the metric case, we prefer to discuss the principles using as many examples coming from the field-theoretical approach to statistical mechanics as possible.
Guiding principle 1: The theory admits a critical dimension at which a certain finite set of operators are canonically marginal.
Notice that we do not assume here that equals four, even though it may do so. The idea behind this principle is that from the set of operators we can construct an action , which is parametrized by the set of couplings that, by definition, have zero mass dimension . The first term, , is some opportune free action that has no coupling, which can be used to fix the canonical dimensions of the fields, and consequently of the couplings . The operators could be all possible operators compatible with a given symmetry for the model. On this couplings’ basis, the theory is power counting renormalizable at , that, to state the obvious is not necessarily equal to four. We also do not assume that is the upper critical dimension of the theory, which instead we denote . The upper critical dimension is defined as the dimension above which the theory is Gaussian. It might as well be , as we discuss below. There can even be a lower critical dimension, but we assume that it is sufficiently low in all the examples below.
Guiding principle 2: The operators govern a well-defined renormalizable perturbative expansion at the critical dimension , which expresses everything as an expansion in powers of the couplings .
This is the essential requirement of perturbative renormalizability of S at the critical dimension. Since the theory is perturbatively renormalizable all divergences are local and have the structure of the operators . Divergences can be eliminated through the introduction of the finite number of counterterms order-by-order in the perturbative expansion. Generically, we expect that, if we use the method of dimensional regularization and the modified minimal subtraction scheme , all counterterms will result in renormalized couplings , denoted with the same symbol as the bare ones for simplicity, which make the path integral finite. If is the scale of dimensional regularization at which the divergences are subtracted, then the couplings will flow with beta functions . With only one exception given in Section 5, all the beta functions discussed in this paper should be understood as being derived using minimal subtraction and dimensional regularization methods. We also reserve the symbol for the running of the couplings at .
Guiding principle 3: The renormalized theory can be continued to a finite interval of d which includes .
The continuation of the renormalized theory in to another dimension could begin with an -expansion in , however the emphasis on the latter principle is on the word “finite”, so it is assumed that the theory can be meaningfully extended to finite values of . This finite value, say , can still be very small, though not infinitesimal; in fact, it might not even intercept any physically interesting value for d, which is a possibility that we have to deal with, in some way.
Even though we are interested in finite extensions away from , still the -expansion gives us particularly strong insights on how and where the theory could be extended in d. To elaborate on this point, consider the action S, which is traditionally extended to dimensions as , where we include the scale and some positive contants in such a way that the couplings remain dimensionless. For infinitesimally small , this implies that the couplings now obey the new scale transformations, (no summation over i), that now include a scaling term.
Here and in the following, we reserve the symbol for the beta function of the coupling at the critical dimension, while the general beta function in d dimensions is denoted . For example, a scalar -theory with coupling has and requires the subtraction from the bare coupling of a counterterm of the form for some positive constant A when the theory is regularized in dimensions [19]. In the loop expansion, A is determined from three one-loop diagrams with four external legs pairwise inserted in the loops. The scale appears as a byproduct of continuing the theory away from , where the coupling is no longer dimensionless, but, instead, has dimension ( in the notation of the main text). The independence of the bare coupling from the scale implies that the renormalized coupling runs as when (both sides are correctly dimensionless at the upper critical dimension), which defines . Instead, in , it is customary to measure in units of in order to still have a dimensionless coupling. This is achieved through the replacement , as shown in the main text. The counterterm in the new units becomes and the requirement that the bare coupling is independent of translates to a running of the renormalized one, , which correctly interpolates the limit for .
To better understand the implication of the new running, we momentarily restrict our attention to a single coupling g, which has a polynomial beta function . We also assume that the leading term of the beta function in is and that is required for boundedness, although these requirement can be dropped with minor modifications on the final arguments. The important point is that, according to the sign of , the model can be either asymptotically free () or Landau-trivial (). This happens because for , according to the signs of and , there can be an interesting scale invariant fixed point defined implicitly as a solution of .
- If , that is, if the theory is Landau-trivial at , we have that is a physically interesting fixed point for , implying that the theory could be extended nontrivially to . In this case, coincides with the upper critical dimension, . The natural interpretation is that the fixed point is infrared, because it governs the scale dependence of the model at low energies, , that can be seen from a simple stability analysis. When the model is trivial, meaning that the IR is governed by the Gaussian point, with at most logarithmic corrections to scaling. An example of Landau-trivial theory would be in ;
- If , that is, if the theory is asymptotically free, we have that is physical for . This suggests that the theory can be extended nontrivially to , mirroring the previous case, at least from a formal point of view. In this case, we can assume that , however we do not know if is big enough to include interesting physical values. The mirroring continues in that the fixed point is ultraviolet, because it governs the scale dependence of the model at high energies, . An example of asymptotically free theory would be a gauge theory in .
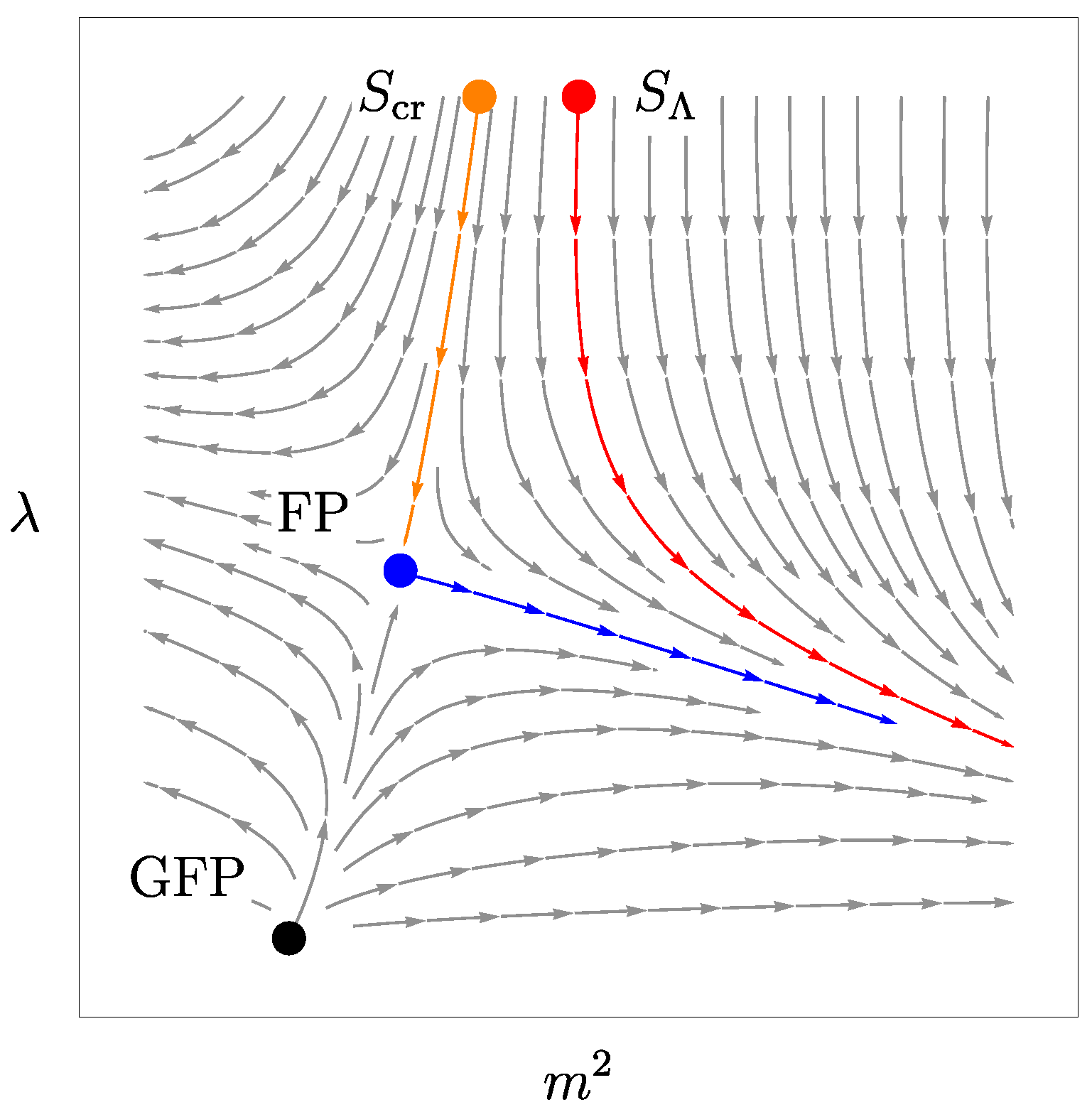
A well-known example of a theory for which and that can be continued below its critical dimension is the Wilson–Fisher model with interaction, also known as the linear sigma model (LSM) [20]. In fact, the interaction is Landau-trivial at , but has a nontrivial fixed point for , which encapsculates the large-scale behavior of a universality class of models which includes the three-dimensional lattice Ising model for . An example of theory for which and that can be continued above its critical dimension is the nonlinear sigma model (NLSM) [21]. The NLSM is asymptotically free in and can be continued to to describe a critical point which is believed to be the same as the LSM universality class for . One intuitive way to understand why they should belong to the same universality class is to realize that the NLSM can be interpreted as a LSM in which the radial mode has been integrated-out, or, alternatively, the LSM can be interpreted as a NLSM in which the radial mode reappears as a bound state [22]. The relation between LSM and NLSM can be visualized in Figure 1. Since the two models share the same universality, it is implied that they should share the upper critical dimension, which in the case of the Wilson–Fisher is . There is thus a finite interval of existence for the critical point of the NLSM above , even though a naive extrapolation of the leading order of the -expansion would suggest otherwise.
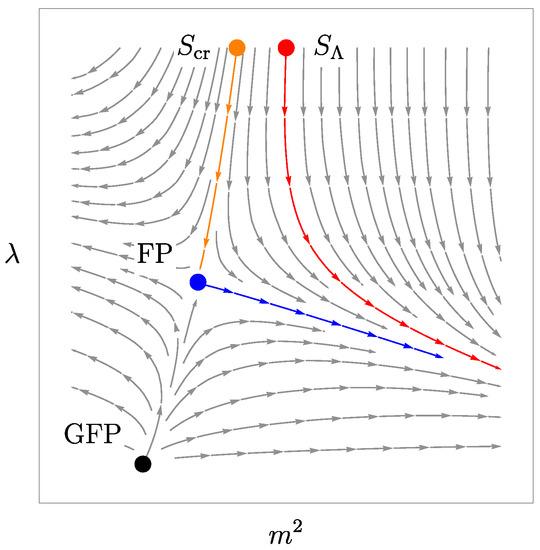
Figure 1.
RG diagram illustrating the relation between the linear and nonlinear sigma models; the trajectories represent lines of constant physics at large scales. The couplings are a quartic self interaction of the linear model and a squared mass in units of the RG scale, and their RG system has a nontrivial fixed point (FP) that is distinguished from the Gaussian fixed point (GFP). The fixed point controls the infrared behavior of the linear sigma model, as can be seen from the red trajectory that spawns from the point that represents a given “bare” theory characterized by a microscopic scale a or an ultraviolet energy . The fixed point drives the red trajectory to some infrared limit, located on the right in this example, that is representative of a macroscopic phase (e.g., broken or unbroken symmetry). In statistical mechanical models, can be tuned to a critial value (for example moving it towards the left in the picture), so that the trajectory would fall towards the fixed point itself following the orange trajectory and the theory becomes scale invariant by construction. The tuning is often achieved by changing the temperature to its critical value, , in the thermodynamical limit and under the assumption that the parameters of depend on T. The same fixed point, however, is seen as an ultraviolet one for the theories located on the blue trajectory, which represent the nonlinear sigma model. In the infrared limit the red and blue trajectories are taken to the same macroscopic phases, because they follow the same RG directions asymptotically, and thus belong to the same universality class. One important message is that the two models, linear vs. nonlinear, see the same fixed points in two rather different lights, infrared vs. ultraviolet, however it is perfectly legitimate to talk about the notion of universality class for both models. A useful remark for gravity is the following: an asymptotically safe trajectory for gravity would be the blue curve, since it is ultraviolet complete, while the rest of the RG diagram could represent any lattice-based attempt to find the continuum limit of gravity based on some lattice scale (e.g., any approach based on Regge’s discretization [26,27], such as EDT or CDT [28,29]), in which case the ultraviolet critical point for quantum gravity is seen as a standard fixed point associated to a second order phase transition in the lattice (see also the appropriate discussion on Section 5).
In fact, the examples of LSM versus NLSM illustrate a number of interesting points. The first one is that different models may share the same universality class at a critical point, which is a well-known fact of the theory of critical phenomena. Another one is that, from the point of view of the renormalization group, infrared and ultraviolet are relative concepts. Loosely speaking, one could imagine the critical point of the LSM in as lying on an RG phase diagram parametrized by mass and self-interaction. The RG flow would then swing close to the fixed point, because there are a relevant and an irrelevant directions, approximately identified with mass and self-interaction, respectively. The swung trajectories are then collected by the RG and driven to some infrared phase with macroscopic interpretation (for example zero or non-zero magnetization in the case of the sigma models), giving to the fixed point a natural infrared interpretation. However, in the same plane it is possible to identify the unique trajectory that departs from the critical point towards the infrared, that is, the infrared-relevant direction. In this case, the fixed point has a natural ultraviolet interpretation in agreement with the point of view of the analysis of the NLSM.
This picture that we just described is shared qualitatively by other models [23]. Another interesting and rather general aspect is that for models with a sufficiently large number of scalar degrees of freedom, but presumably for many other models too, it can actually be shown that there is no absolute infrared fixed point in the most general RG space of theories [24].
All the above considerations can be generalized to the case of multiple couplings if the opportune care is given. In general, the action S will have to satisfy some positivity conditions on the couplings in order to generate a meaningful path-integral. Furthermore some additional constraints could be imposed on the basis of unitarity for Lorentzian models, reflection positivity for Euclidean models [25], and stability. On the basis of accumulated experience, we expect that a general solution, which comes from the set of fixed point equations, can be either continued above or below , or maybe even both. For a meaningful theory of gravity the crucial question is, for obvious reasons, whether it can be continued to .
The -expansion, if combined with the sign of the perturbative beta function at , guarantees that a fixed point can be continued at least to some infinitesimally small value and . From our point of view this in enough to begin speculating on the continuation of perturbative fixed points as reasonable candidates of quantum theories of gravity. We also want to conjecture on which could be the actual mechanisms that prevent a theory from being useful for finite values of . In the assumption that fixed points do not simply “come and go”, but that there must be a mechanism that makes them appear and disappear, we are led to including another guiding principle.
Guiding principle 4: Distinct critical points do not simply exist in a vacuum: they can collide with each other, resulting, for example, in complex conjugate pairs as a function of the parameters of the theory.
This is by far our most speculative statement, so we are urged to try and justify it. There is a well-known statistical model, the lattice q-states Potts model, which is believed to display an annihilation of fixed points as a function of the number of states q [30]. In the continuum, the universality class of the Potts model is described by the Landau–Potts model, which is a scalar model with interaction constructed to be invariant under symmetry. The Landau–Potts theory admits a perturbative expansion in , and an -expansion in . Likewise the theory, the critical point exists and can be continued up at least to . In the range , it is assumed to satisfy a condition in the number of states, that is, there must be a critical value of the number of states, , which separates a second order phase transition for from a first order phase transition for .
For example, in it is well-known that the critical value of q is [30]. It has been conjectured that in arbitrary d, the critical value of the number of states must be d dependent, thus drawing a curve in the plane [31]. The different order of the phase transition stems from the presence or absence of the nontrivial fixed point as a function of q: if there is a nontrivial real fixed point the standard argument of phase transitions is that there is a second order phase, if instead there is only the Gaussian fixed point the system undergoes a first order phase transition.
Perhaps more interesting is the mechanism with which the theory’s transition changes from second to first order as a function of q, which is well-established in and conjectured to hold in any dimension. There are actually two fixed points, a critical and a multicritical one, that are distinct for , but that collide at and then become a complex conjugate pair for , leaving only the Gaussian fixed point. This mechanism has the added value of explaining why, for some values of q close to and above , the transition is weakly first order: if the two fixed points just collided the complex conjugate pair that is left makes the transition almost second order because it is still “close” to the real axis, in some sense that must be made precise [30].
Several analyses of perturbative renormalization groups see fixed points that collide for some parametric value. An example could be the analysis of the hypercubic model in , which has the symmetry group of the hypercube , in which it is easy to see that a fixed point with genuine hypercubic symmetry and the isotropic fixed point with symmetry collide at a value . In the hypercubic example, the critical value can be determined as a function of , hence of the dimension, and, from careful analysis, is very close to for (perturbatively, it is at , and it is a difficult to estimate that in from perturbation theory) [32]. The hypercubic example is interesting, but somehow simplifies the general case because both the and critical points “live” in the same perturbative RG diagram, meaning that their perturbative series can be described by the same set of RG beta functions.
Returning to the example of the Potts model, we see that the annihilation of fixed points is even less simple in this case, precisely for the reason that we have just mentioned. While the Landau–Potts theory is governed by the interaction in , the multicritical parter, with which the standard Potts annihilates, is not. A reasonable conjecture is that, in a Landau free-energy description, such multicritical model is described by a higher order interaction, with the simplest candidate pushed forward being in . The point is that the critical and multicritical models have different , 6 and , respectively, so it is impossible to see them in the same perturbative RG diagram. In fact, they are governed by two different perturbative series, or, in other words, they can at most appear in the strongly-interacting regime of each other [31].
We stress that there are several other interesting examples of colliding fixed points in gauge theories (e.g., see [33], which we return to in Section 5 from an unusual perspective. These mechanisms generally lead to conformal windows that depend on the number of flavors, but we anticipate that these ideas resonate also with part of the discussion that we are going to give in Section 4.1, where the number of flavors is replaced by the dimension of the system. Among these, we find particularly important the discussions that lead to the dynamical symmetry breaking in three-dimensional QED [34,35] and the chiral symmetry breaking of QCD with many flavors [36].
4. The Candidate Metric Theories
For the construction of the possible candidate metric theories that satisfy the first guiding principle, we assume that the only field at our disposal is the metric , that the connection is the Levi–Civita one, and that the theory must be covariant either under or . We also choose to work with covariant tensors that are constructed from the metric, namely the Riemannian curvatures, and that can be defined unambiguously in any dimension, for obvious reasons.
If we engineer coordinates to be dimensionless, then the metric tensor has mass dimension negative two, canonically, like a length square. The Riemann tensor with three indices down and one up, , is dimensionless; likewise the Ricci tensor is dimensionless ; finally the curvature scalar has mass dimension two being contracted with an inverse metric, . These three tensors, together with the covariant derivative , are the covariant quantities that we have at our disposal to construct an action.
It is easy to see that operators constructed with n powers of the curvatures, such as for example have dimension , while all lower powers of the curvatures could be studied as composite operators [37]. If we take into account the invariant volume element, , then the couplings multiplying an n-th power of the curvatures have canonical dimension . To satisfy the first principle, we seek for canonically dimensionless couplings at , which imply the solutions . The application of the first principle thus leaves us with the even natural numbers as candidate theories to look forward to. In the next sections we briefly review the work that has been done for the first few examples and collect some additional ideas.
4.1. Gravity in
We have that the only available local operator built from the metric of dimension two is the curvature scalar, so in two dimensions the gravitational coupling itself, the Newton’s constant, becomes dimensionless and must be used to construct a perturbative expansion. In the simplest units, the action is
and it is easy to see that the perturbative coupling is G by expanding the metric around a flat background, . However, in two dimensions several things happen at the same time: the curvature becomes a topological invariant when integrated, the action is conformally invariant modulo boundary terms, and the Lagrangian is zero on-shell. The handling of these problems results in a rather different way of treating the conformal mode between the and realizations. In the first case, the action (5) is complemented with a cosmological constant term that is renormalized simultaneously and allows to go on-shell consistently. In the second case, the conformal mode is separated and the corresponding scalar-tensor theory is renormalized. The invariant result can be evinced easily from String Theory in that it is related to the leading contribution to the string’s dilaton effective action in a non-critical dimension.
Either way, at the leading order the beta function for Newton’s constant is of the form
and for [7], for [38], and for [39,40,41], which can be obtained from the coupling of (5) to an additional scalar. The Newton’s constant is obviously asymptotically free in for the pure gravity model, while there is a conformal window if matter fields are included in the problem. In , following the discussion of the previous section, the theory is asymptotically safe because it has a fixed point, , however we do not know how far this fixed point can actually extend.
The combination of functional renormalization group (FRG) and background approach, with some approximations, seems to suggest that such fixed point exists up to [42]. This fact, however, is not backed by a computation that discusses all possible parametrization dependences in the construction [10], so we argue that it is an artifact of the approximation made in background projection (in fact, the same effect can be seen in the application of FRG to the NLSM [43], but we know that the NLSM universality class has upper critical dimension equal to four). In a previous work, we have discussed that there should be a conformal window in d, which could be thought of as a parameter analog to N in gauge theories, and we have also given a reliable estimate for the size of the window in the case of symmetry that agrees with previous cutoff-based work. The d-dependent beta function becomes
and we find that the fixed point exists for , modulo further corrections from higher loops, which seems reasonably bigger than four to justify the conjecture of asymptotic safety in [44]. It would be interesting, and certainly fruitful for the entire discussion of this paper, to formalize the continuation to arbitrary continuous dimension d. A possible starting point, at least for the Euclidean theory, could be the method discussed in Ref. [45], in which it is made sense of “symmetry” for arbitrary values of n, however it is still an open problem to generalize that method to gauge symmetries.
It is natural to ask which is the mechanism that would make this fixed point disappear. In the NSLM example the fixed point collides with the Gaussian one at , so the same could happen to the asymptotically safe fixed point of gravity. Another possibility, that we would like to push forward here, is that this fixed point collides and annihilates with the one of a higher derivative generalization of (5). This last possibility is of course purely conjectural, but it is the reason why we spend some words on the next two higher derivative models of gravity.
4.2. Higher Derivative Gravity in
In four dimensions the couplings multiplying operators that are quadratic in the curvatures are dimensionless, and thus suitable to construct a perturbatively renormalizable quantum theory. The action is often parametrized as
where we have defined the square of the Weyl tensor and the four-dimensional Euler density G; we have also neglected the boundary term . The conformal limit of (8) is obtained by taking . This model was shown to be renormalizable a long time ago already [46], but, most importantly, it was shown that is can be asymptotically free [47,48] if . Notice that earlier computations included some mistakes, we refer the reader to more recent papers, such as [49,50], for the correct results. The problem is that the same interaction is required to be positive, , by physically motivated constraints [49] which are relevant also for cosmology [51]. As it stands, for physical parameters, the model described by (8) is thus asymptotically free in , but Landau-trivial in (the integration of the perturbative beta function would hit a Landau pole at a finite energy).
Nevertheless, the action (8) has all the features that would make a natural complement to the Standard Model of particle physics, in fact it compares well with the curvature square terms that give dynamic to the gauge fields, but also it is asymptotically free, at least in part. For these reasons, the model was revived several times over the years [52,53,54].
Among its features, we notice that it has been proposed as an ultraviolet completion of quantum gravity and the standard model in the agravity proposal [53], which essentially suggests a regime beyond Planckian energies, E, in which the renormalization group is controlled by (8) for and its conformal version for . The decoupling of conformal models in the ultraviolet is the mechanism that the agravity proposal has to avoid the perturbative Landau-pole. However, the action (8) has an additional problem in that it violates unitarity, unless some clever prescription generalizing the Wick rotation is chosen to project away negative norm ghost modes [54], or a new symmetry is imposed on the spectrum [55].
The RG behavior of (8) is known at the leading one loop order for the standard realization, but also for the one in which there is no term [56]. It would be interesting to extend these results to the next-to-leading order; furthermore, to the best of our knowledge, nobody has studied in depth the realization [57], even though the structure of the conformal anomaly in four dimensions is known to an extent similar to the previous case [58]. Since the couplings in (8) all have Gaussian fixed points, it is customary to introduce the ratios and , so that the perturbative series is controlled only by (also seen through the expansion ). For the standard diffeomorphisms symmetry, we have the beta functions
instead for the conformal model ()
For all betas are automatically zero, however the true fixed points are obtained by solving the system as goes to zero, so in units of a different RG “time”, . A simple analysis shows that the first system has two nontrivial negative roots for , one of which is clarly unphysical [59], while the other one is argued to lead to an ill-defined Newtonian potential [49]. This means that the physically interesting action is supposed to have , where only is asymptotically free, but is Landau-trivial [53]. Nevertheless, the RG system induces nontrivial fractal properties for the effective structure of spacetime at small distances [60].
In relation to the discussion of the previous model in , it would be tempting to ask whether the fixed points of the higher derivative model have an interplay with the one which is in . The answer is that we do not know, but evidence based on FRG methods suggest that this is not the case, since both two- and four-dimensional fixed points can be seen in the same RG diagram if quadratic divergences are taken into account [59], though a more scheme independent statement would be desirable. Before concluding, it is interesting to notice that both gauge theories and general NLSMs admit very similar higher derivative generalizations, see for example [61,62]. These higher derivative generalizations are also asymptotically free, at least in some couplings, and require a similar rescaling of the RG time by a single coupling, say , which is thus required to control the perturbative series.
4.3. Cubic Gravity in
We are approaching terra incognita, because very little has been done in dimensions higher than four in relation to the purposes of the guiding principles that we stated. In six dimensions there are ten distinct operators that are constructed from three powers of the curvatures, modulo total derivatives. We can parametrize the action as
and the couplings for are correctly dimensionless in . This action is power counting renormalizable, so it is realistic to assume that the couplings are sufficient to remove the divergences at least at one loop in the perturbative expansion, if not at all orders like in the previous case.
To state the obvious, the action (11) evidently is much longer and more complicate than the two and four dimensional counterparts. In fact, we believe that it has not been renormalized at one loop for the or realizations, yet. Nevertheless, it has been considered in the case using functional RG methods and background field approach in Ref. [63]. The conformally invariant action includes the manifestly invariant operators multiplying and , but also a linear combination of the others [63], which can be related to a six dimensional Q-curvature. The Q-curvature needed here is often denoted , or for the dimensional continuation [64]. In general is the tensor defined as the constant part of an operator with leading part and that transforms as for . Since the operator has “nice” transformation properties under Weyl rescalings, it is possible to construct an interesting curvature from its constant part, , and couple it to topological charges. In the examples of the previous sections, one can find relations of the monomials with and (modulo boundary terms), which is a proof of concept for the utility of these curvatures in the context of critical models of quantum gravity. However the Einstein’s backgrounds for the metric that have been chosen in Ref. [63] are not enough to uniquely assign a beta function to the three couplings left, resulting in an incomplete RG flow, but the result is still impressive given the tensorial nature of the action.
An interesting aspect of (11) is that it contains the notorious Goroff–Sagnotti term, , which is used to argue the perturbative non-renormalizability of the traditional Einstein–Hilbert action in dimension [1]. The Goroff–Sagnotti term appears as a non-subtractable divergence when renormalizing (5) at two loops in , and it was included in functional truncations for the first time in Ref. [65]. Its tensor structure appears by expressing the Weyl tensor in terms of the Riemann tensor in the last two monomials. It is also necessary to realize that in a totally antisymmetric expression with more than four indices is necessarily zero (one can have at most four antisymmetric indices through the tensor ) so we can prove that .
A complete RG analysis of (11) would be an important theoretical achievement, which could have strong implications as suggested by our discussion, through a potential interplay with the lower dimensional universality classes in their strongly interacting regimes, and which we hope is undertaken in the future.
4.4. A Final Remark: Unitarity
The discussion that we have presented in this section is based on the guiding principles that we have listed in Section 3. The core of our idea is to use the four guiding principles constructively, but the resulting theories have to be tested for their physical validity. The guiding principles themselves are based on ideas coming from the theory of critical phenomena and are expressed in the language of the renormalization group. One particular aspect of the theory of critical phenomena, especially when applied to low dimensional condensed matter systems, is that it is not essential that the considered models are unitary. In fact, a critical phenomenon can manifest in the mesoscopic description of systems that otherwise have a physical built-in cutoff (for example, the scale of their microscopic components). Such systems do not have to be unitary, or, equivalently, reflection-positive in case that they are Euclidean, because they are supposed to have a unitary completion from their fundamental constituents.
On the other hand, ultraviolet complete theories of gravity, such as for example the conjectured asymptotically safe Einstein gravity, are not supposed to either have or need a further ultraviolet completion. This is an especially delicate issue, because unitarity is not always easy to prove, both inside and outside perturbation theory. We touched very briefly the problem of unitarity for the higher derivative model in Section 4.2, but there is an extensive literature which recently has seen the influx of new ideas [25,54,55]. We do not explore this issue further, but we dare add a fifth principle, upon which one should test the aforementioned theories (kindly suggested by a helpful referee).
Guiding principle 5: Any constructed critical theory that also wants to be an ultraviolet completion should be unitary.
5. A Toy-Model: Gauge Theory in
Now that we have listed the first few potential candidates for a universal theory of metric quantum gravity following the reasonable guiding principles for their constructions at a given critical dimension, it is time to collect ideas on what could be done with them. Since its early inception, the idea of an asymptotically safe, ultraviolet complete, theory of quantum gravity in has been associated with the continuation to of the Einstein–Hilbert action in of Section 4.1. The most notable exceptions, in this sense, would be some early work of Niedermaier on the conjecture, incorporating the perturbative RG of higher derivative gravity given in Section 4.1 as well as powerlaw divergences to “see” a nontrivial RG for the lower derivative terms that are in a strong coupling regime [66], and the works of Falls discussing universal physical properties of asymptotic safety [44,67,68].
Using the continuation of the theory in as a working hypothesis, we think that the paramount problem is to assess its existence in and, more generally, in . The natural general question becomes: is it possible to extend an asymptotically free theory in a certain critical dimension and obtain an asymptotically safe theory for some natural-valued dimension ? We have already given a known example, in the form of the NLSM, which is asymptotically free in , but also belongs to the same universality class as the linear model, that is nontrivial up to . In fact, the NLSM has been used as a toy-model for asymptotic safety in the past using functional methods [43,62], however some conclusions seem unnatural; for example in Ref. [43] it is predicted that the NLSM has a nontrivial critical point for all in contrast with the above argument. This is most likely caused by the lack of control of the operator expansion and cutoff parametric dependence, which generally affects the application of functional methods to theories with nonlinearly realized symmetries like the NLSM. The problem is shared, of course, by all metric theories of gravity that we listed.
As mentioned before, there are indications, based both on perturbation theory and Wilsonian methods that there should be a conformal window for the existence of the critical point of gravity, and that this window should extend above , thus validating the conjecture [10,16,44]. In particular, Refs. [16,44] predict the conformal window from the leading order of perturbation theory, using two separate methods. The result might be subject to radiative corrections, but it is further validated by qualitatively agreeing with the functional approach with minimal dependence on the cutoff of Ref. [10].
It would be desirable, at this point, to have a toy-model, other than the NLSM, which exihibits similar properties as the conjectured ones for gravity. The reason is that the NLSM is not entirely a perfect guiding principle, because we know that its universality is captured by the one of the linear model for . The toy-model should also be under better control than gravity, meaning that it should be known to a higher extent as a quantum field theory, both perturbatively and nonperturbatively. A simple candidate that fullfills all the requisites is a gauge theory: it is asymptotically free in , where its perturbative series is known to a reasonable amout of loops and where the growth of the coupling towards the infrared makes the model approach a strongly-interacting phase. We could argue that it should be asymptotically safe in , at least for reasonably small values of .
Earlier works have suggested, on the basis of the perturbative series, that the Yang–Mills gauge theory is asymptotically safe above , therefore it has a second order phase transition, but also that the conformal window might extend up to [69,70]. The critical properties change in such a way to suggest that the transition might become first order at the effective upper critical dimension [69]. To corroborate the end of the conformal window comes the picture suggested in Ref. [71], where it is shown, using functional RG methods, that, for small , there is always an ultraviolet fixed point, but also another nonperturbative fixed point besides it. For increasing values of d, and therefore of , the two fixed points collide leaving us with no zeroes for the beta function at .
To explain what is going on in Ref. [71] from a different perspective, imagine that in the square of the dimensionless gauge coupling has a beta function of the form
for some nonperturbative beta function in . The nonperturbative beta contains the leading order of perturbation theory, and , but also hides in the dots additional nonperturbative information coming from the strong coupling regime. If we only use the perturbative part, there is always a solution of . However, if the nonperturbative part contributes so that for , we must have at least another fixed point, and, for increasing , this latter fixed point will collide with the perturbative one. Here we implitictly assume that there are no singularities in the beta function, so the form is different from the one given in [72,73], for example. An illustration of the behavior of the beta function is given in Figure 2.
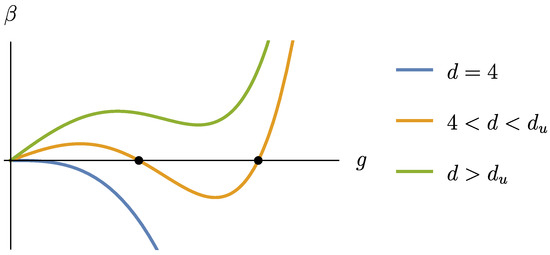
Figure 2.
Conjectured behavior of the beta function of the Yang–Mills coupling in various dimensions d, for which the slope at is proportional to . The blue function is the asymptotically free beta function of standard four dimensional Yang–Mills. For an interval of dimensions between the critical value, , and a speculative upper critical value, , the model admits two nontrivial fixed points, which are highlighted with dots in the figure. One is of ultraviolet nature, while the other one is infrared and assumed to be associated to a multicritical theory in the main text. Any change in d corresponds to a change in the initial slope of the beta function, so at the two fixed points collide and above the curve is not able to intercept the horizontal axis any longer [71].
The presence of a new fixed point is reminiscent of the Banks-Zaks one [33,74] and, as such, it leads to a more complicate phase-diagram, but with d as “parameter” this time. The collision would also explain why at there should be the onset of a first order transition, in fact the two fixed points should collide and form a complex conjugate pair, so we would expect that, slightly above the effective upper critical dimension , there is a weak first order transition (it is still affected by the complex pair of fixed point that are close to the real axis). More precisely, the transition should become infinite order exactly at —sufficiently far away and above the effective critical dimension the transition to properly become first order.
In order to validate or disprove the possibility that a gauge theory in is asymptotically safe, the natural option would be to perform lattice simulations of some discretized action with and , which is the simplest configuration that is reasonably expected to have an ultraviolet fixed point and hence a second order critical point. The use of the lattice Wilson’s action with the traces of plaquettes in the fundamental representation seems to lead only to a first order phase transition, but it could be argued that the inlusion of another bare parameter could be enough to see that the first order point actually belongs to a first order line that terminates in a second order point. The idea was explored early on in Ref. [75], but there was no clear signal of second order behavior, though this could be related to the size of the lattices being a bit small for today’s standards. The problem has been readdressed recently in Ref. [76], in which some signals of second order behavior are seen, though more work has to be done in this direction.
One interesting aspect of the search for the critical point in lattice Yang–Mills gauge theory is that it shares striking similarities with the search for the lattice gravitational critical point performed both with Euclidean and causal dynamical triangulations (EDT and CDT) [28,29]. In fact, in both cases it is known that the Regge discretization with fixed triangles and total spacetime volume of the Einstein–Hilbert action leads to a first order behavior if the only bare parameter is (related to) the Newton’s constant. However, if another bare parameter is added to the discretized action, a measure term in the case of EDT and a parameter measuring microscopic causality in CDT, then there are signs of more complicate phase behaviors, which can include a first order line (interpolating with the first order point of the case with only Newton’s constant) that terminates in a second order critical point. See also the comment given at the end of the caption of Figure 1 for further points on the relation between lattice simulations and quantum gravity.
These examples open up the possibility that it might simply be necessary to include one additional bare parameter to see the critical point of either gravity or gauge theory above their respective critical dimensions. It is tempting to speculate that the new operators that are introduced with the new bare parameter are those responsible for the second order behavior and, in the RG description, must be related to the nature of the second nontrivial fixed point. We know that the new operators must be in the strong coupling regime, but they could still be related to a multicritical generalization of the Yang–Mills gauge theory that has a critical dimension different than four. A candidate for such multicritical generalization has already appeared in the literature and has higher derivative interactions of the gauge field with critical dimension [61,77]. This candidate can be found by following the same logic of our guiding principles, but applying it to the gauge degrees of freedom, rather than to the metric. An interesting aspect of this idea is that a higher multicriticality should emerge from the competition of derivative interactions of various orders, which is known to lead to critical field theories in the scalar case [78,79]. Some of us plan to come back to this topic soon.
6. Conclusions
We have tried to push-forward five reasonable guiding principles to attempt a classification of critical theories which depend on a metric. The principles are inspired by ideas coming from the application of field-theoretical methods in statistical mechanics and are motivated by several examples. The resulting classification begins as perturbative, in the sense that we classify critical theories on the basis of a critical dimension that is assumed to allow for a perturbative definition of the field theory in its proximity, but becomes non-perturbative when we argue that these critical theories could be extended away from their critical dimensions (and how).
Our main purpose is twofold. On the one hand, we want to suggest reasonable candidate universality classes that can be relevant for the conjecture of asymptotic safety, but also, on the other hand, we simply want to promote the role of more perturbative and universal arguments in the literature of asymptotic safety. In recent years, the discussion on the conjecture has been mainly based on the application of functional RG methods and the Wetterich Equation [80], or, more appropriately, its background version, which could be called the Reuter Equation [9].
The main candidate for the critical model behind the conjecture is of course the extension to of Einstein–Hilbert gravity in , which is known since the inception of the idea of asymptotic safety itself. In an earlier work [16], we discussed that the perturbative renormalization of this theory can be done close to two dimensions, but all other instances of the dimensionality can be continued analytically, confirming the presence of a conformal window in d for the existence of the fixed point that can be computed perturbatively and should include the physical case [44].
However, we believe that, in such context, it is important to explain why there should be a conformal window. In this contribution we have discussed a number of conjectures and similar open problems that emerge from our analysis. In particular, we have discussed how the conformal window could be caused by an interplay, happening in the strong-coupling regime, between fixed points which have different critical dimensions (so they cannot be perturbative at the same time). Our arguments in this direction are admittedly very conjectural, but have been presented here in the hope of stimulating further research and discussions on these topics.
Even if very conjectural, our discussion has left out several important contributions that are not covered by our classification, but still are important in the ecosystem of the application of perturbative and field-theoretical methods to quantum gravity. A prominent approach could be the one of Ref. [81] in which, following the results of [82,83,84] a construction of a nonlocal super-renormalizable theory in is attempted, that of course differs from our suggested perturbatively (power-counting) renormalizable models. Similar ideas have appeared in [85,86]. We have not discussed changing the degrees of freedom either, for example introducing a scalar field, which is known to be related to gravity [87]. The finite parts of the quantum effective action of any theory of quantum gravity is well-known to include nonlocal form factors in the curvatures, both in two [88] and four dimensions [89,90], which become very important in a cosmological setting [91,92].
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
The research of AU was funded by the Deutsche Forschungsgemeinschaft under the Grant No. Za 958/2-1.
Acknowledgments
OZ is grateful to C. Bonati, A. Codello, H. Gies and R. Percacci for inspiring discussions on these topics over the years. We are especially grateful to H. Gies for comments on an earlier version of the draft. We are also grateful to a helpful referee suggesting the inclusion of unitarity as a guiding principle.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Goroff, M.H.; Sagnotti, A. The Ultraviolet Behavior of Einstein Gravity. Nucl. Phys. B 1986, 266, 709–736. [Google Scholar] [CrossRef]
- Van de Ven, A.E.M. Two loop quantum gravity. Nucl. Phys. B 1992, 378, 309–366. [Google Scholar] [CrossRef]
- Donoghue, J.F. General relativity as an effective field theory: The leading quantum corrections. Phys. Rev. D 1994, 50, 3874–3888. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, S. Critical Phenomena for Field Theorists. In Understanding the Fundamental Constituents of Matter; Zichichi, A., Ed.; The Subnuclear Series; Springer: Berlin/Heidelberg, Germany, 2012; Volume 14. [Google Scholar]
- Kawai, H.; Ninomiya, M. Renormalization Group and Quantum Gravity. Nucl. Phys. B 1990, 336, 115–145. [Google Scholar] [CrossRef]
- Weinberg, S. Ultraviolet divergences in quantum theories of gravitation. In General Relativity: An Einstein Centenary Survey; Hawking, S.W., Israel, W., Eds.; Cambridge University Press: Cambridge, UK, 2010; Chapter 16; pp. 790–831. [Google Scholar]
- Jack, I.; Jones, D.R.T. The Epsilon expansion of two-dimensional quantum gravity. Nucl. Phys. B 1991, 358, 695. [Google Scholar] [CrossRef]
- Aida, T.; Kitazawa, Y. Two loop prediction for scaling exponents in (2+epsilon)-dimensional quantum gravity. Nucl. Phys. B 1997, 491, 427. [Google Scholar] [CrossRef]
- Reuter, M. Nonperturbative evolution equation for quantum gravity. Phys. Rev. D 1998, 57, 971–985. [Google Scholar] [CrossRef]
- Gies, H.; Knorr, B.; Lippoldt, S. Generalized Parametrization Dependence in Quantum Gravity. Phys. Rev. D 2015, 92, 084020. [Google Scholar] [CrossRef]
- Donoghue, J.F. A Critique of the Asymptotic Safety Program. Front. Phys. 2020, 8, 56. [Google Scholar] [CrossRef]
- Bonanno, A.; Eichhorn, A.; Gies, H.; Pawlowski, J.M.; Percacci, R.; Reuter, M.; Saueressig, F.; Vacca, G.P. Critical reflections on asymptotically safe gravity. Front. Phys. 2020, 8, 269. [Google Scholar] [CrossRef]
- Gielen, S.; de León Ardón, R.; Percacci, R. Gravity with more or less gauging. Class. Quant. Grav. 2018, 35, 195009. [Google Scholar] [CrossRef]
- ’t Hooft, G. A class of elementary particle models without any adjustable real parameters. Found. Phys. 2011, 41, 1829–1856. [Google Scholar] [CrossRef]
- Jackiw, R.; Pi, S.Y. Fake Conformal Symmetry in Conformal Cosmological Models. Phys. Rev. D 2015, 91, 067501. [Google Scholar] [CrossRef]
- Martini, R.; Ugolotti, A.; Porro, F.D.; Zanusso, O. Gravity in d = 2 + ϵ dimensions and realizations of the diffeomorphisms group. arXiv 2021, under review. arXiv:2103.12421. [Google Scholar]
- Benedetti, D. Essential nature of Newton’s constant in unimodular gravity. Gen. Rel. Grav. 2016, 48, 68. [Google Scholar] [CrossRef]
- de Brito, G.P.; Pereira, A.D. Unimodular quantum gravity: Steps beyond perturbation theory. JHEP 2020, 9, 196. [Google Scholar] [CrossRef]
- Kleinert, H.; Schulte-Frohlinde, V. Critical Properties of ϕ4 Theories; World Scientific: Singapore, 2001. [Google Scholar]
- Wilson, K.G.; Fisher, M.E. Critical exponents in 3.99 dimensions. Phys. Rev. Lett. 1972, 28, 240–243. [Google Scholar] [CrossRef]
- Brezin, E.; Zinn-Justin, J. Renormalization of the nonlinear sigma model in 2 + epsilon dimensions. Application to the Heisenberg ferromagnets. Phys. Rev. Lett. 1976, 36, 691–694. [Google Scholar] [CrossRef]
- Bardeen, W.A.; Lee, B.W.; Shrock, R.E. Phase Transition in the Nonlinear σ Model in 2 + ϵ Dimensional Continuum. Phys. Rev. D 1976, 14, 985. [Google Scholar] [CrossRef]
- Janssen, L.; Herbut, I.F. Phase diagram of electronic systems with quadratic Fermi nodes in 2 < d < 4: 2+ϵ expansion, 4-ϵ expansion, and functional renormalization group. Phys. Rev. B 2017, 95, 075101. [Google Scholar]
- Osborn, H.; Stergiou, A. Heavy Handed Quest for Fixed Points in Multiple Coupling Scalar Theories in the ε Expansion. JHEP 2021, 04, 128. [Google Scholar] [CrossRef]
- Arici, F.; Becker, D.; Ripken, C.; Saueressig, F.; van Suijlekom, W.D. Reflection positivity in higher derivative scalar theories. J. Math. Phys. 2018, 59, 082302. [Google Scholar] [CrossRef]
- Regge, T. GENERAL RELATIVITY WITHOUT COORDINATES. Nuovo Cim. 1961, 19, 558–571. [Google Scholar] [CrossRef]
- Hamber, H.W. Quantum Gravitation: The Feynman Path Integral Approach; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Ambjorn, J.; Jurkiewicz, J.; Loll, R. A Nonperturbative Lorentzian path integral for gravity. Phys. Rev. Lett. 2000, 85, 924–927. [Google Scholar] [CrossRef] [PubMed]
- Coumbe, D.; Laiho, J. Exploring Euclidean Dynamical Triangulations with a Non-trivial Measure Term. JHEP 2015, 4, 028. [Google Scholar] [CrossRef]
- Gorbenko, V.; Rychkov, S.; Zan, B. Walking, Weak first-order transitions, and Complex CFTs II. Two-dimensional Potts model at Q>4. SciPost Phys. 2018, 5, 050. [Google Scholar] [CrossRef]
- Codello, A.; Safari, M.; Vacca, G.P.; Zanusso, O. Multicritical Landau–Potts field theory. Phys. Rev. D 2020, 102, 125024. [Google Scholar] [CrossRef]
- Pelissetto, A.; Vicari, E. Critical phenomena and renormalization group theory. Phys. Rept. 2002, 368, 549–727. [Google Scholar] [CrossRef]
- Kaplan, D.B.; Lee, J.W.; Son, D.T.; Stephanov, M.A. Conformality Lost. Phys. Rev. D 2009, 80, 125005. [Google Scholar] [CrossRef]
- Kubota, K.I.; Terao, H. Dynamical symmetry breaking in QED(3) from the Wilson RG point of view. Prog. Theor. Phys. 2001, 105, 809–825. [Google Scholar] [CrossRef]
- Kaveh, K.; Herbut, I.F. Chiral symmetry breaking in QED(3) in presence of irrelevant interactions: A Renormalization group study. Phys. Rev. B 2005, 71, 184519. [Google Scholar] [CrossRef]
- Gies, H.; Jaeckel, J. Chiral phase structure of QCD with many flavors. Eur. Phys. J. C 2006, 46, 433–438. [Google Scholar] [CrossRef]
- Houthoff, W.; Kurov, A.; Saueressig, F. On the scaling of composite operators in asymptotic safety. JHEP 2020, 04, 099. [Google Scholar] [CrossRef]
- Polyakov, A.M. Quantum Gravity in Two-Dimensions. Mod. Phys. Lett. A 1987, 2, 893. [Google Scholar] [CrossRef]
- Polyakov, A.M. Quantum Geometry of Bosonic Strings. Phys. Lett. B 1981, 103, 207–210. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Shapiro, I.L. One loop renormalization of two-dimensional induced quantum gravity. Phys. Lett. B 1991, 263, 183–189. [Google Scholar] [CrossRef]
- Elizalde, E.; Odintsov, S.D. Dilatonic gravity near two-dimensions as a string theory. Mod. Phys. Lett. A 1995, 10, 2001–2008. [Google Scholar] [CrossRef]
- Litim, D.F. Fixed points of quantum gravity. Phys. Rev. Lett. 2004, 92, 201301. [Google Scholar] [CrossRef] [PubMed]
- Codello, A.; Percacci, R. Fixed Points of Nonlinear Sigma Models in d>2. Phys. Lett. B 2009, 672, 280–283. [Google Scholar] [CrossRef]
- Falls, K. Renormalization of Newton’s constant. Phys. Rev. D 2015, 92, 124057. [Google Scholar] [CrossRef]
- Binder, D.J.; Rychkov, S. Deligne Categories in Lattice Models and Quantum Field Theory, or Making Sense of O(N) Symmetry with Non-integer N. JHEP 2020, 04, 117. [Google Scholar] [CrossRef]
- Stelle, K.S. Renormalization of Higher Derivative Quantum Gravity. Phys. Rev. D 1977, 16, 953. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Tseytlin, A.A. Renormalizable asymptotically free quantum theory of gravity. Nucl. Phys. B 1982, 201, 469. [Google Scholar] [CrossRef]
- Avramidi, I.G.; Barvinsky, A.O. Asymptotic freedom in higher derivative quantum gravity. Phys. Lett. B 1985, 159, 269–274. [Google Scholar] [CrossRef]
- Salvio, A. Quadratic Gravity. Front. Phys. 2018, 6, 77. [Google Scholar] [CrossRef]
- Jack, I. One-loop beta-functions for renormalisable gravity. arXiv 2020, arXiv:2002.12661. [Google Scholar]
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- de Berredo-Peixoto, G.; Shapiro, L. Higher derivative quantum gravity with Gauss–Bonnet term. Phys. Rev. D 2005, 71, 064005. [Google Scholar] [CrossRef]
- Salvio, A.; Strumia, A. Agravity up to infinite energy. Eur. Phys. J. C 2018, 78, 124. [Google Scholar] [CrossRef]
- Anselmi, D.; Piva, M. The Ultraviolet Behavior of Quantum Gravity. JHEP 2018, 1805, 027. [Google Scholar] [CrossRef]
- Mannheim, P.D. Ghost problems from Pauli–Villars to fourth-order quantum gravity and their resolution. Int. J. Mod. Phys. D 2020, 29, 2043009. [Google Scholar] [CrossRef]
- de Berredo-Peixoto, G.; Shapiro, I.L. Conformal quantum gravity with the Gauss–Bonnet term. Phys. Rev. D 2004, 70, 044024. [Google Scholar] [CrossRef]
- Hamada, K.J. Resummation and higher order renormalization in 4-D quantum gravity. Prog. Theor. Phys. 2002, 108, 399–433. [Google Scholar] [CrossRef]
- Antoniadis, I.; Mazur, P.O.; Mottola, E. Conformal symmetry and central charges in four-dimensions. Nucl. Phys. B 1992, 388, 627–647. [Google Scholar] [CrossRef]
- Groh, K.; Rechenberger, S.; Saueressig, F.; Zanusso, O. Higher Derivative Gravity from the Universal Renormalization Group Machine. Available online: https://arxiv.org/abs/1111.1743 (accessed on 24 April 2021).
- Becker, M.; Pagani, C.; Zanusso, O. Fractal Geometry of Higher Derivative Gravity. Phys. Rev. Lett. 2020, 124, 151302. [Google Scholar] [CrossRef] [PubMed]
- Casarin, L.; Tseytlin, A.A. One-loop β-functions in 4-derivative gauge theory in 6 dimensions. JHEP 2019, 08, 159. [Google Scholar] [CrossRef]
- Percacci, R.; Zanusso, O. One loop beta functions and fixed points in Higher Derivative Sigma Models. Phys. Rev. D 2010, 81, 065012. [Google Scholar] [CrossRef]
- Pang, Y. One-Loop Divergences in 6D Conformal Gravity. Phys. Rev. D 2012, 86, 084039. [Google Scholar] [CrossRef]
- Chernicoff, M.; Giribet, G.; Grandi, N.; Lavia, E.; Oliva, J. Q-curvature and gravity. Phys. Rev. D 2018, 98, 104023. [Google Scholar] [CrossRef]
- Gies, H.; Knorr, B.; Lippoldt, S.; Saueressig, F. Gravitational Two-Loop Counterterm Is Asymptotically Safe. Phys. Rev. Lett. 2016, 116, 211302. [Google Scholar] [CrossRef]
- Niedermaier, M.R. Gravitational Fixed Points from Perturbation Theory. Phys. Rev. Lett. 2009, 103, 101303. [Google Scholar] [CrossRef] [PubMed]
- Falls, K. Physical renormalization schemes and asymptotic safety in quantum gravity. Phys. Rev. D 2017, 96, 126016. [Google Scholar] [CrossRef]
- Falls, K.; Herrero-Valea, M. Frame (In)equivalence in Quantum Field Theory and Cosmology. Eur. Phys. J. C 2019, 79, 595. [Google Scholar] [CrossRef] [PubMed]
- Peskin, M.E. Critical point behavior of the wilson loop. Phys. Lett. B 1980, 94, 161–165. [Google Scholar] [CrossRef]
- Morris, T.R. Renormalizable extra-dimensional models. JHEP 2005, 01, 002. [Google Scholar] [CrossRef]
- Gies, H. Renormalizability of gauge theories in extra dimensions. Phys. Rev. D 2003, 68, 085015. [Google Scholar] [CrossRef]
- Sannino, F.; Schechter, J. Nonperturbative Results for Yang–Mills Theories. Phys. Rev. D 2010, 82, 096008. [Google Scholar] [CrossRef]
- Ryttov, T.A.; Sannino, F. Supersymmetry inspired QCD beta function. Phys. Rev. D 2008, 78, 065001. [Google Scholar] [CrossRef]
- Banks, T.; Zaks, A. On the Phase Structure of Vector-Like Gauge Theories with Massless Fermions. Nucl. Phys. B 1982, 196, 189–204. [Google Scholar] [CrossRef]
- Kawai, H.; Nio, M.; Okamoto, Y. On existence of nonrenormalizable field theory: Pure SU(2) lattice gauge theory in five-dimensions. Prog. Theor. Phys. 1992, 88, 341–350. [Google Scholar] [CrossRef][Green Version]
- Florio, A.; Lopes, J.M.V.P.; Matos, J.; Penedones, J. Searching for Continuous Phase Transitions in 5D SU(2) Lattice Gauge Theory. Available online: https://arxiv.org/abs/2103.15242 (accessed on 24 April 2021).
- Gracey, J.A. Six dimensional QCD at two loops. Phys. Rev. D 2016, 93, 025025. [Google Scholar] [CrossRef]
- Safari, M.; Vacca, G.P. Multicritical scalar theories with higher-derivative kinetic terms: A perturbative RG approach with the ϵ-expansion. Phys. Rev. D 2018, 97, 041701. [Google Scholar] [CrossRef]
- Safari, M.; Vacca, G.P. Uncovering novel phase structures in □k scalar theories with the renormalization group. Eur. Phys. J. C 2018, 78, 251. [Google Scholar] [CrossRef]
- Wetterich, C. Exact evolution equation for the effective potential. Phys. Lett. B 1993, 301, 90–94. [Google Scholar] [CrossRef]
- Modesto, L. Super-renormalizable Quantum Gravity. Phys. Rev. D 2012, 86, 044005. [Google Scholar] [CrossRef]
- Krasnikov, N.V. Nonlocal gauge theories. Theor. Math. Phys. 1987, 73, 1184–1190. [Google Scholar] [CrossRef]
- Kuzmin, Y.V. The convergent nonlocal gravitation. Sov. J. Nucl. Phys. 1989, 50, 1011–1014. (In Russian) [Google Scholar]
- Tomboulis, E.T. Superrenormalizable Gauge and Gravitational Theories. Available online: https://arxiv.org/abs/hep-th/9702146 (accessed on 24 April 2021).
- Biswas, T.; Gerwick, E.; Koivisto, T.; Mazumdar, A. Towards singularity and ghost free theories of gravity. Phys. Rev. Lett. 2012, 108, 031101. [Google Scholar] [CrossRef] [PubMed]
- Koshelev, A.S.; Kumar, K.S.; Starobinsky, A.A. R2 inflation to probe non-perturbative quantum gravity. JHEP 2018, 03, 071. [Google Scholar] [CrossRef]
- Ruf, M.S.; Steinwachs, C.F. One-loop divergences for f(R) gravity. Phys. Rev. D 2018, 97, 044049. [Google Scholar] [CrossRef]
- Ribeiro, T.G.; Shapiro, I.L.; Zanusso, O. Gravitational form factors and decoupling in 2D. Phys. Lett. B 2018, 782, 324–331. [Google Scholar] [CrossRef]
- Franchino-Viñas, S.A.; de Paula Netto, T.; Shapiro, O.; Zanusso, L.I. Form factors and decoupling of matter fields in four-dimensional gravity. Phys. Lett. B 2019, 790, 229–236. [Google Scholar] [CrossRef]
- Knorr, B.; Ripken, C.; Saueressig, F. Form Factors in Asymptotic Safety: Conceptual ideas and computational toolbox. Class. Quant. Grav. 2019, 36, 234001. [Google Scholar] [CrossRef]
- Maggiore, M.; Mancarella, M. Nonlocal gravity and dark energy. Phys. Rev. D 2014, 90, 023005. [Google Scholar] [CrossRef]
- Codello, A.; Jain, R.K. On the covariant formalism of the effective field theory of gravity and leading order corrections. Class. Quant. Grav. 2016, 33, 225006. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).