Abstract
The crust region is a tiny fraction of neutron stars, but it has a variety of physical properties and plays an important role in astronomical observations. One of the properties characterizing the crust is elasticity. In this review, with the approach of asteroseismology, we systematically examine neutron star oscillations excited by crust elasticity, adopting the Cowling approximation. In particular, by identifying the quasi-periodic oscillations observed in magnetar flares with the torsional oscillations, we make a constraint on the nuclear saturation parameters. In addition, we also discuss how the shear and interface modes depend on the neutron star properties. Once one detects an additional signal associated with neutron star oscillations, one can obtain a more severe constraint on the saturation parameters and/or neutron star properties, which must be a qualitatively different constraint obtained from terrestrial experiments and help us to complementarily understand astrophysics and nuclear physics.
1. Introduction
Neutron stars produced through the core-collapse supernova at the last moment of the massive star’s life can enter extreme states, which is quite difficult to realize on Earth. For example, their density easily exceeds the standard nuclear density, fm−3, and the gravitational and magnetic fields around/inside the star become much stronger than those observed in our solar system [1]. Therefore, physics in such extreme states may inversely be revealed through the observations of neutron stars and/or their phenomena.
The stellar structure depends on the equation of state (EOS) for neutron star matter, which is under beta-equilibrium and charge neutrality. However, the determination of EOS for neutron star matter from the experiments is still difficult. This is because the density of nuclei is around the saturation density almost independently of nuclear species due to the nature of nuclear saturation properties. Namely, the experimental data concentrate around/below the saturation density, while the neutron star properties are mainly determined from the EOS for higher-density regions. The saturation parameters characterizing the EOS in a lower-density region are gradually constrained through terrestrial experiments, e.g., [2,3,4,5,6,7,8,9,10], which are strongly associated with low-mass (or low central density) neutron star properties.
Meanwhile, it is better to note that experiments cannot directly measure the saturation parameters, where one has to estimate them from a kind of empirical relations (or strong correlations) between the saturation parameters and experimental data, suggested by theoretical studies, e.g., [11,12,13,14,15]. Thus, even if the experimental accuracy would be improved well, because of the theoretical uncertainties in these relations, it is not always true that the constraints on the saturation parameters improve [16,17,18]. In practice, the estimation of the density-dependence of the nuclear symmetry energy, the so-called slope parameter L (see Equation (1) for the definition), from the parity asymmetry of the polarized electron scattering cross section of 208Pb strongly depends on the model [19,20]. This means that the theoretical study must be vitally significant for deriving a technique to directly estimate the saturation parameters from the experimental data, although this is out of scope in this review.
On the other hand, astronomical observations are important for constraining the EOS in a higher-density region. For example, the discovery of massive neutron stars, whose mass is , excluded soft EOSs, whose maximum mass does not reach the observed mass [21,22,23,24]. The observation of gravitational waves from GW170817 [25] could restrict the dimensionless tidal deformability of neutron stars, which leads to the constraint that the neutron star radius should be less than 13.6 km [26]. In addition, through the observation of the pulsar light curve, one may constrain the neutron star properties, especially the stellar compactness, , with stellar mass M and radius R, e.g., [27,28,29,30,31,32]. This is because the trajectory of the photon radiating from the neutron star’s surface can bend due to the strong gravitational field induced by the neutron star, which is a relativistic effect. In practice, the Neutron Star Interior Composition Explorer (NICER) is now operating on the International Space Station, which successfully constrained the neutron star mass and radius for PSR J0030-0451 [33,34] and PSR J0740-6620 [35,36].
In such a way, the neutron star mass and radius would be constrained more and more in a higher-density region with astronomical observations and in a lower-density region with terrestrial experiments, e.g., [37,38,39] (also see Figure 1). Then, as these constraints from observations and experiments become more and more severe, one may eventually constrain the EOS for neutron star matter.
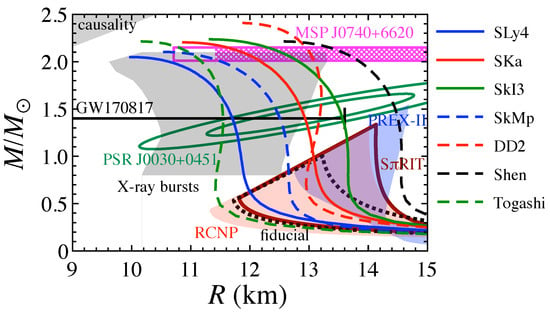
Figure 1.
Several constraints on the neutron star mass and radius obtained from astronomical observations and terrestrial experiments. MSP J0740+6620 is one of the largest neutron stars discovered up until now, whose mass is [24], while the radius (and mass) of this object is constrained via NICER as well as PSR J0030-0451. The tidal deformability restricted from the GW170817 event tells us the upper limit of the radius of the neutron star, i.e., km [26]. The observation of the X-ray bursts from neutron stars also provides us with the constraint on the neutron star mass and radius, although they depend on the theoretical model [40]. In addition, one can theoretically exclude the top-left shaded region due to the causality [41]. On the other hand, the terrestrial experiments, e.g., by PREX-II [19], SRIT [42], and at RCNP [43], provide us with the constraint on the stellar models constructed with a lower central density (bottom-right region), adopting the mass formula for low-mass neutron stars [44], where the constraints expected with the fiducial value of the nuclear saturation parameters, i.e., MeV [3,7,10] and MeV [2], are also shown (see Equation (1) for the definition of L and ). Furthermore, for reference, the mass and radius relations constructed with several EOSs, i.e., SLy4 [45,46], SKa [47], SkI3 [48], SkMp [49], DD2 [50], Shen [51], and Togashi [52], are plotted. Taken from [37].
In addition to the observations (or estimations) of the neutron star mass and radius, oscillation signals (and also the gravitational waves) from neutron stars, if observed, are another important piece of information used to extract neutron star properties. Since the objects have their own specific oscillation frequencies, one may determine interior information via the observation of their frequencies as an inverse problem. This technique is known as asteroseismology, which is similar to seismology on Earth and helioseismology on the Sun. In fact, the neutron star has a lot of oscillation modes, where each mode can be excited due to the corresponding physics [53]. For example, it is well-known that the frequency of fundamental oscillations in a neutron star is strongly associated with the square root of the stellar average density because the fundamental oscillations are acoustic oscillations. The gravitational waves from neutron stars may be suitable astronomical information to adopt asteroseismology; however, they have never been observed from an isolated neutron star. Even so, neutron star mass, radius, and EOS can be suggested by observing the gravitational waves from (cold) neutron stars, e.g., [54,55,56,57,58,59,60,61,62,63,64]. Moreover, this technique is also adopted to extract information concerning protoneutron stars from supernova gravitational waves, e.g., [65,66,67,68,69,70,71].
Instead of gravitational waves, quasi-periodic oscillations (QPOs) discovered in the afterglow following magnetar giant flares [72,73,74,75,76,77,78] are also valuable for adopting asteroseismology, where magnetars are strongly magnetized neutron stars. Here, the observed QPO frequencies are in the range of tens of Hz to kHz (see Section 2 for details). Although the emission mechanism of the flare activity in magnetar flares is still up for debate, the observed QPOs are considered to be strongly associated with neutron star oscillations. Taking into account the dynamical time of neutron stars, which is around 0.1 ms, it may be more difficult to theoretically explain lower frequencies among the observed frequencies. The possible candidates may be crustal torsional oscillations, magnetic oscillations, or magneto-elastic oscillations if one assumes that the observed QPO frequencies come from the neutron star oscillations. However, the magnetic oscillations strongly depend on the magnetic field strength and its geometry inside the star, e.g., [79,80,81], while our understanding of them is quite poor. Thus, here we discuss the crustal properties by identifying the observed QPO frequencies with crustal torsional oscillations, neglecting magnetic effects (see Section 2 for the magnetic effects on crustal torsional oscillations). In this way, the crustal properties are constrained, e.g., [82,83,84,85,86,87,88].
Through the asteroseismology approach, it is shown that the observed QPO frequencies can be identified with neutron star oscillations. On the other hand, there are still open issues in magnetar QPOs. For instance, all the observed QPOs are not simultaneously excited after magnetar flares, some of the QPOs are excited first, then others. This phenomenon cannot be explained using linear analysis. To understand the time dependence of QPO frequency excitation, one may have to look beyond linear analysis, for example, nonlinear coupling. Moreover, to discuss crustal oscillations, one must estimate the crustal elasticity, which is characterized by shear modulus. The details are shown in Section 4.
The oscillation frequencies in a spherically symmetric neutron star model can be classified into two families with parity, i.e., axial and polar oscillations, where axial-type oscillations can be excited independently of polar-type oscillations. The crustal torsional oscillations belong to the axial type oscillations. Since axial type oscillations do not involve density variation, they are relatively easily excited but less important in gravitational wave observations. On the other hand, polar-type oscillations involve density variation and stellar deformations, where various oscillation modes can exist.
Owing to crust elasticity, the shear and interface modes, which are polar-type oscillations, are also excited, as well as torsional oscillations, even though they are not so discussed well compared to torsional oscillations. The interface modes, whose frequencies are less than 100 Hz, may be excited in binary neutron stars by resonating with the orbital frequency. In fact, the precursors have been observed just before the main flare activity of a gamma-ray burst at a binary neutron star merger [89], which may be a result of the resonant shattering of neutron star crusts induced by the binary orbital motion [90,91]. If so, one could extract the neutron star properties by carefully observing the precursors and identifying them with neutron star oscillations [92,93,94,95]. To extract the properties from the resonant shattering of neutron star crust, one must examine the shear and interface modes systematically.
In this review, which mainly focuses on the torsional oscillations excited in the neutron star, we extract the neutron star properties by identifying the observed QPO frequencies using torsional oscillations. For this purpose, we simply assume the Cowling approximation in this review, i.e., we only consider fluid oscillations with the (unperturbed) background metric. The perturbation equations are derived from the linearized energy–momentum conservation law. By imposing appropriate boundary conditions on the numerical boundary, the problem to solve becomes an eigenvalue problem. The neutron star crust is mainly composed of spherical nuclei, but the non-spherical nuclei may appear in the vicinity of the boundary of crust and core, depending on the nuclear parameters (or EOS). First, we begin by discussing the observed QPO frequencies with the crustal torsional oscillations excited in the region only composed of spherical nuclei. Then, the discussion is extended to the more realistic situation with the non-spherical nuclei. Through these attempts, we successfully identify all the observed QPOs with crustal torsional oscillations, and finally, derive the constraint on the slope parameter as 58–73 MeV. Furthermore, we also discuss the identification of high-frequency QPOs observed in GRB 200415A with overtones of crustal torsional oscillations. Through this identification, we make a constraint on the neutron star mass and radius for GRB 200415A, adopting the fiducial values of nuclear saturation parameters. In addition, we systematically examine the shear and interface modes for various neutron star models, with which we determine the relation between the frequencies and the neutron star properties independently of the stiffness of EOS for the core region.
This manuscript is organized as follows. In Section 2, we briefly mention the observed QPO frequencies in magnetar giant flares, which will be considered as evidence of neutron star oscillations. In Section 3, we show the equilibrium neutron star models and the EOS considered in this study. In Section 4, we briefly mention the shear modulus inside the neutron star crust, which is an important property for considering crustal oscillations. In Section 5, we extract the crustal information in practice by identifying the observed QPOs with crustal torsional oscillations. In Section 6, we also show the behavior of the shear and interface modes, specifically focusing on their association with neutron star properties. Finally, we conclude in Section 7. Unless otherwise mentioned, we adopt the following geometric units: , where c and G denote the speed of light and the gravitational constant, respectively.
2. Magnetar QPOs and Magneitc Effects on Crustal Oscillations
Compared to usual pulsars whose surface magnetic field strength is ∼– G, the existence of neutron stars with strong magnetic fields, such as ∼– G, is observationally known. This strongly magnetized neutron star is known as a magnetar. In a rotating neutron star, the magnetic stress induced by the stellar rotation gradually accumulates in the crust, which is usually supported by crustal elasticity. But, once the magnetic stress becomes significantly strong and the crust elasticity cannot support it, the crust eventually breaks out, and the magnetic energy is released through flare activities [96,97], where star quakes may also occur. This scenario could be the origin of the QPOs observed in the afterglow following magnetar giant flares.
In practice, QPOs have been discovered in giant flares observed in soft-gamma repeaters (SGRs). There have been three events detected up until now in which QPOs are found, i.e., SGR 0526-66 in 1979 [98,99], SGR 1900+14 in 1998 [100], and SGR 1806-20 in 2004 [101,102]. In particular, in the events concerning SGR 1900+14 and SGR 1806-20, several QPOs were found [72,73,74], i.e., 28, 54, 84, and 155 Hz in SGR 1900+14, and 18, 26, 29 (or 30), 92.5, 150, 626.5, and 1837 Hz in SGR 1806-20. Using Bayesian analysis, the existence of additional QPOs was also reported in SGR 1806-20 [77]. Moreover, even without giant flares, QPOs have been found from less energetic recurrent bursts, i.e., 93 and 127 Hz in SGR J1550-5418 [75] and 57 Hz in SGR 1806-20 [76]. In addition to the QPOs observed in SGRs, several high QPO frequencies have been found in GRB 200415A, i.e., 836, 1444, 2132, and 4250 Hz [78].
Assuming that these QPOs derive from neutron star oscillations, one may identify the higher QPO frequencies with polar-type oscillations of neutron stars, e.g., Figure 25, but the lower frequencies are more difficult to identify with neutron star oscillations. Maybe the possible candidates are only the crustal torsional oscillations or magnetic oscillations (or magneto-elastic oscillations). Meanwhile, the magnetic oscillations definitely depend on the geometry and strength of magnetic fields, which are not understood well yet. In addition, it is pointed out that crustal torsional oscillations can be excited in the vicinity of the neutron star surface, while magnetic oscillations are confined only to the core region if magnetic fields are not so strong. This is because the shear velocity is higher than the Alfvén velocity, , with the magnetic field strength, B, and density, , at the basis of the crust, which leads to the oscillations being controlled by shear properties. In general, the critical field strength, above which magnetic oscillations become dominant, depends on the EOS (or crust properties), which is considered around a few times G [79,81,103]. Therefore, to avoid uncertainty in the magnetic geometry and profile, assuming that the field strength is not so strong, we focus on only crustal oscillations without magnetic effects in this review.
As an advantage, without the magnetic effect, crustal torsional oscillations are completely confined inside the crust since axial-type oscillations do not involve radial variations. That is, one can avoid large uncertainties in EOSs of the core region and directly discuss the crust properties by comparing the observed frequencies to the crustal torsional oscillations. On the other hand, if one takes into account the magnetic effects, even torsional oscillations can be coupled with the core region through the magnetic fields, where oscillations are easily damped out via magnetic coupling if the magnetic fields are relatively large [104,105]. We note that one has to consider polar-type oscillations in the whole region of a neutron star, even if the magnetic effects are neglected because polar-type oscillations involve radial variations.
We only focus on neutron star oscillations associated with crust elasticity in this review; however, we briefly mention the magnetic oscillations in the neutron star here. Since the existence of magnetic fields inside the star breaks a spherically symmetric configuration, one cannot examine magnetic oscillations (and also magneto-elastic oscillations) in the same way as spherically symmetric objects (as mentioned in the following sections). Assuming a specific distribution of magnetic fields, one may study them by decomposing perturbative variables with spherical harmonic function, where ℓ-th order perturbation equations are generally coupled with ℓ-th order equations of other values [79,106]. Alternatively, one may solve a time evolution of two-dimensional perturbation equations and determine frequencies via FFT.
With the latter approach, it has been shown that axial-type magnetic oscillations are on a continuous spectrum compared to discrete ones [107,108,109]. This is because the frequencies of magnetic oscillations are characterized by the propagation time determined with the magnetic field length inside the star and Alfvén velocity, while the magnetic field length inside the star continuously changes from the axis to the position related to the closed field line close to the equatorial plane [108]. This phenomenon may also be understood with a toy model suggested in [110,111]. In any case, taking into account coupling with the crust, i.e., magneto-elastic oscillations, one may identify the observed QPO frequencies [80,105,112,113]. Furthermore, one may constrain the magnetic geometry from the QPO frequencies and estimated field strength of magnetic fields, i.e., the case that the magnetic fields are confined in the crust due to the type I superconductor in the core region can be excluded [114].
Compared to extensive studies on axial-type magnetic oscillations, the study of polar-type magnetic oscillations is relatively poor. Even so, unlike axial-type oscillations, polar-type magnetic oscillations seem to be on a discrete spectrum [115], and they definitely play an important role in gravitational wave radiations [116,117].
3. Crustal Equilibrium
Although the details of a neutron star structure depend on the EOS for neutron star matter, its conceptual structure is generally accepted. Under the thin envelope of the atmosphere and/or ocean, the matter forms a Coulomb lattice, which behaves as a solid. This region corresponds to the neutron star crust. Most of the crust region is composed of spherical nuclei with a body-centered cubic (bcc) lattice, while the shape of stable nuclei changes into cylindrical, slablike, cylindrical hole, and spherical hole, and eventually becomes uniform matter as density increases [118,119]. The region composed of non-spherical nuclei is the so-called pasta phase, which behaves as a liquid crystal. Meanwhile, the region whose density is higher than the transition density from the non-uniform to the uniform matter is the neutron star core. This transition density depends on the neutron star EOS, which becomes ∼(1/3–1/2) of the nuclear saturation density. The transition density where the nuclear shape changes inside the crust also depends on the EOS, especially on the density dependence of the symmetry energy, L, in Equation (1) [120,121,122]. In addition, the crust thickness is at most of the stellar radius, which depends on stellar compactness, , and nuclear saturation parameters [119,123] (see Figure 2 for an example of the concrete stellar model). In general, the ratio of crust thickness to stellar radius decreases as the stellar compactness and L increases. In particular, for MeV, the pasta phase disappears, where the crust is composed of only spherical nuclei and directly transitions into uniform matter [120,121,122] (also see Table 1).
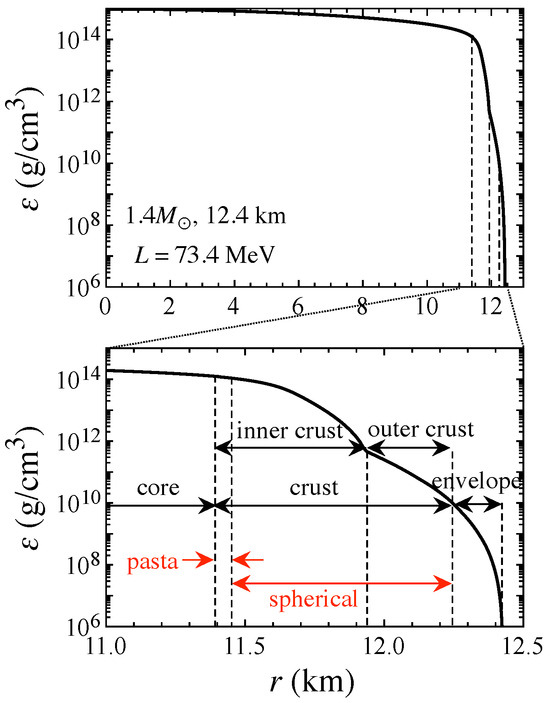
Figure 2.
Example of the energy density profile inside the neutron star with and km constructed with a specific EOS with MeV and MeV, where L and are the nuclear saturation parameters provided by Equation (1). The bottom panel is an enlarged view of the above panel. Taken from [124].

Table 1.
The EOS parameters for the OI-EOS family adopted in this review, where y is defined as . SP-C, C-S, S-CH, CH-SH, and SH-U denote the transition densities for each EOS parameter set. The asterisk at the value of denotes the EOS model with which some pasta phases are not predicted to appear, i.e., the values with , , and denote the transition densities from cylindrical nuclei to uniform matter, from cylindrical-hole nuclei to uniform matter, and from spherical nuclei to uniform matter, respectively.
The EOS for neutron star matter generally depends on the adopted nuclear interaction, nuclear models, and compositions. But for any EOSs, the bulk energy per baryon for the zero-temperature nuclear matter can be expanded in the vicinity of the saturation density, fm−3, of symmetric nuclear matter as a function of the baryon number density, , and neutron excess, , via the following [125]:
where , while and are provided by and using the neutron and proton number density, and . We note that the matter with corresponds to a symmetric nuclear matter, i.e., , while that with is a pure neutron matter, i.e., . The coefficients in this expansion are the nuclear saturation parameters, which characterize each EOS, and the term inside the brackets in front of corresponds to the nuclear symmetry energy. In particular, and are the binding energy and incompressibility of symmetric nuclear matter at , while is the symmetry energy at .
Owing to the nature of nuclear saturation properties, , , and are well determined via experiments, i.e., 0.15–0.16 fm−3, MeV [9], and MeV [10]. In contrast, and L are more difficult to determine experimentally because they are a density derivative at , i.e., one needs to know the nuclear information in a somewhat wide density range around the saturation point. Nevertheless, the constraints on these two parameters are improved, where their fiducial values are MeV [2,4] and MeV [3,7,10]. We note that the constraint on L still seems to have large uncertainties, e.g., MeV with PREX-II carried out by the Thomas Jefferson National Accelerator Facility in Virginia [19], or MeV with SRIT by the Radioactive Isotope Beam Factory at RIKEN in Japan [42].
In this review, to systematically discuss the dependence of crustal oscillations on nuclear saturation parameters, we adopt a phenomenological EOS proposed by Oyamatsu and Iida [120,121] (hereafter referred to as OI-EOS). For given values of and L, the OI-EOS family is constructed by optimizing the values of , , and to reproduce experimental data for masses and charge radii of stable nuclei in such a way that the bulk energy reduces to Equation (1) in the limit of and , adopting the extended Thomas–Fermi theory. The EOS parameters adopted in this review are listed in Table 1. We note that some of the EOS parameter sets are out of the range of fiducial values for and L, but we adopt such a wide range to systematically discuss the dependence on saturation parameters.
As an equilibrium crust model (or a neutron star model), we simply consider a non-rotating, strain-free, and spherically symmetric neutron star model in this review. The metric describing such a stellar model is provided by the following equation:
where and are the metric functions depending on only the radial coordinate, r. is directly associated with the mass function, , which corresponds to the enclosed gravitational mass inside position r, i.e., . Adopting an appropriate EOS, e.g., the OI-EOS family in this review, one can construct the stellar model by integrating the Tolman–Oppenheimer–Volkoff (TOV) equation. In general, to construct a stellar model, one integrates the TOV equation outward from the center to the surface, assuming a central density, i.e., the neutron star models become one parameter family for each EOS. In fact, we construct the stellar model in this way to discuss the shear and interface modes in Section 6 because these modes are polar-type oscillations, which are excited not only in the crust region but also inside the core. On the other hand, the torsional oscillations discussed in Section 5, which are axial-type oscillations, are confined inside the crust (elastic) region. Therefore, to remove the uncertainties of the core EOS, we construct only the crust equilibrium to discuss torsional oscillations, where we integrate TOV equations inward from the stellar surface to the base of the crust, assuming the stellar mass and radius as a boundary condition at the stellar surface.
4. Shear Modulus
The elasticity inside the crust can be characterized by the shear modulus, . The shear modulus, , in a phase of spherical nuclei with a bcc lattice is approximately described in the limit of zero-temperature as follows:
where , Z, and a are the ion number density, charge number of the ion, and Wigner–Seitz cell radius, i.e., [126]. This expression is derived by averaging the overall direction, assuming that each nucleus is only a point particle [127]. The shear modulus in the phase of spherical nuclei has been discussed more by including the phonon contribution [128], the electron-screening effect [129,130,131,132], the effect of polycrystal properties [133], and effects of finite size of atomic nuclei [134], which can modify the shear modulus more or less. However, in this review, we simply adopt given by Equation (3) as the shear modulus in the phase of spherical nuclei.
Compared to the shear modulus in the phase of spherical nuclei, the discussion for the shear modulus in the pasta phases is very poor. Nevertheless, according to [135], the shear modulus, , in the phase of cylindrical nuclei can be estimated as follows:
where and denote the Coulomb energy per volume of a Wigner–Seitz cell and the volume fraction of cylindrical nuclei, while the shear modulus, , in the phase of slablike nuclei is as follows:
i.e., the matter composed of slablike nuclei behaves as a fluid within the linear response. This is because the deformation energy in slablike nuclei becomes of higher order with respect to displacement [135]. So, in this review, we simply adopt Equations (4) and (5) as the shear modulus in the phases of cylindrical and slablike nuclei. But, it has also been suggested that the elastic constant in the poly-crystalline lasagna (which corresponds to slablike nuclei) may become a (nonzero) tiny value [136,137]. If one considers the nonzero shear modulus inside the slablike nuclei, the results shown in this review may be changed.
Furthermore, the shear modulus in the phase of cylindrical-hole, , and spherical-hole nuclei, , may be considered in a similar way to that in the phase of cylindrical and spherical nuclei. This is because liquid crystalline structures in the phase of cylindrical-hole and spherical-hole nuclei are basically the same as in the phase of cylindrical and spherical nuclei. Thus, we adopt Equations (4) and (3) for and by appropriately replacing the quantities in the formulae [88,138]. That is, in Equation (4) is replaced by the volume fraction of gas of dripped neutron for , while and Z in Equation (3) are replaced by the number density of spherical-holes (bubbles) and the effective charge number, , of spherical-hole nuclei for , where is estimated as with the effective charge number density of the spherical-hole nuclei, , and the volume of the spherical-hole nuclei, . is given by the difference of the charge number density inside the spherical-hole from that outside the spherical-hole, i.e., , using the proton number density outside the spherical-hole nuclei, , and the number density of uniform electron gas, .
In Figure 3, we show an example of the distribution of shear modulus inside the crust for the stellar model shown in Figure 2, where the right panel is an enlarged view of the shaded region in the left panel.
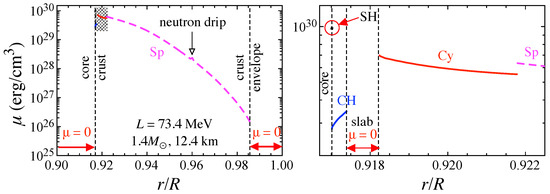
Figure 3.
Shear modulus inside the neutron star model provided in Figure 2, where Sp, Cy, CH, and SH, respectively, denote the phases composed of spherical, cylindrical, cylindrical-hole, and spherical-hole nuclei. The right panel is an enlarged view of the shaded region in the left panel. Taken from [124].
5. Crustal Torsional Oscillations
Concerning the crustal equilibrium models mentioned in the previous section, we carry out a linear perturbation analysis to determine the specific frequencies of crustal torsional oscillations. In this review, we examine the oscillation frequencies within the relativistic framework, which has also been discussed within the Newtonian framework, e.g., [126,139,140]. To derive the perturbation equations, we simply adopt the Cowling approximation, where the metric perturbation is neglected during fluid oscillations. We note that one can expect to accurately determine the frequencies of axial-type oscillations even with the Cowling approximation because axial-type oscillations do not involve density variations, i.e., metric perturbations (corresponding to the perturbations of gravitational potential) should be too small. The perturbation equation can be derived from the linearized energy–momentum conservation law. In practice, when introducing the component of Lagrangian displacement, , where denotes the ℓ-th order Legendre polynomial, and the perturbation equation is as follows [79,141]:
where the dash denotes the derivative with r, and denotes the effective enthalpy contributing to oscillations.
for spherical or cylindrical nuclei [85,142], while
for cylindrical-hole or spherical-hole nuclei [88].
In the expression of effective enthalpy, H denotes the local enthalpy provided by with the energy density, , and pressure, p, while A is the baryon number density inside a Wingner–Seitz cell, is the number of neutrons inside a Wingner–Seitz cell that do not commove with protons in the nuclei, is the number of neutrons inside cylindrical-hole or spherical-hole nuclei, and is a parameter characterizing a participant ratio in the oscillations, i.e., the ratio of nucleons outside cylindrical-hole or spherical-hole nucleu that commove non-dissipatively. That is, all the nucleons inside a Wingner–Seitz cell contribute to the effective enthalpy with (maximum enthalpy), while no nucleons outside the cylindrical-hole or spherical-hole nuclei do so with (minimum enthalpy). We note that, in a phase of spherical-hole nuclei, is predicted as ∼0.34–0.38 at fm−3 using band calculations [143]. Meanwhile, assuming that comes only from a part of the dripped neutrons inside a Wingner–Seitz cell, , the parameter can control the fraction of neutrons contributing to oscillations, i.e., corresponds to the situation that all dripped neutrons commove with protons (maximum enthalpy), while denotes that all dripped neutrons behave as a superfluid and do not contribute to oscillations (minimum enthalpy).
To determine the frequencies, one must impose appropriate boundary conditions in the perturbation Equation (6) at the basis of the crust (the boundary between the core and crust) and the surface of the crust (or the boundary between the crust and envelope). Both boundaries are essentially equivalent to the boundary between the elastic and fluid region, where we impose the condition that the traction force vanishes [79,141], which reduces to . On the other hand, at the interface between elastic regions with different shapes of nuclei, e.g., between spherical and cylindrical nuclei, we impose a continuous traction condition, i.e., should be continuous at such an interface. Then, the problem to solve becomes an eigenvalue problem with respect to the eigenvalue, . The resultant value of provides us the frequency, f, via for each value of ℓ. In this review, we use the notation of n for expressing the eigenfrequencies of torsional oscillations with the angular index ℓ and the nodal number in the eigenfunction (although the notation is different from the usual one, such as ℓ).
5.1. Torsional Oscillations Excited in Spherical Nuclei
Even though the crust is not only composed of the spherical nuclei as mentioned above, to determine the dependence of frequencies of the torsional oscillations on the EOS parameters and stellar properties, we first consider the torsional oscillations excited in the elastic region composed of only spherical nuclei. As a first step, we examine the frequencies without neutron superfluidity, i.e., (or ). As mentioned in Section 3, to construct the equilibrium model, we select two parameters for EOS, i.e., and L, and two for stellar models, M and R. In the left panel of Figure 4, we show the fundamental frequencies of torsional oscillations for a neutron star model with and 12 km, using the EOSs with some parameter sets listed in Table 1 (see Ref. [86] for the concrete parameter sets adopted here) as a function of L. From this figure, one can observe that the frequencies are less sensitive to . Thus, we will discuss the dependence of the fundamental frequency as a function of L through the fitting formula by assuming the polynomial form as follows:
where with are the adjustable parameters depending on M and R (and ), while is the value of L normalized by 100 MeV. Using this fitting formula, one can estimate the frequency of with less than accuracy for a neutron star model with and 12 km (Table 2 in [86]). In the left panel of Figure 4, we also show the expected frequencies with the fitting formula provided by Equation (9) by the thick, solid line.
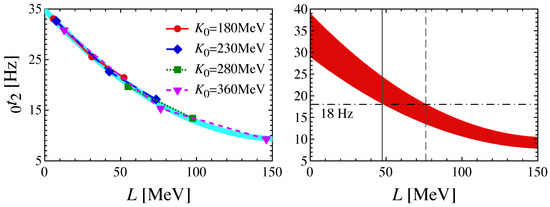
Figure 4.
In the left panel, the fundamental frequencies of torsional oscillations for a neutron star model with and 12 km constructed with several EOS parameter sets are shown as a function of L. The thick, solid line is the expected frequency using the fitting formula provided by Equation (9). In the right panel, the expected fundamental frequency of torsional oscillations as a function of L, assuming that the neutron star mass and radius are in the range of and 10 km 14 km, where for reference the lowest QPO frequency observed in SGR 1806-20, i.e., 18 Hz, is also shown. The vertical solid and broken lines correspond to and 76.2 MeV, respectively. Taken from [86].
One may be able to understand the dependence of on L as follows. As the value of L increases, the nuclear symmetry energy conversely decreases at the sub-nuclear density, considering the density dependence of the bulk energy provided by Equation (1). As a result, protons easily turn into neutrons, which leads to the situation that the charge number of nuclei becomes smaller. This means that decreases using Equation (3). On the other hand, the fundamental frequency of ℓ-th torsional oscillations, 0, are estimated as 0 with the shear velocity, [139]. Thus, one can expect that 0 decreases with L.
Now, assuming the neutron star mass and radius would be in the range of and 10 km 14 km, which are reasonable assumptions for a neutron star model, the resultant fundamental frequency of torsional oscillations is shifted, depending on stellar models. In the right panel of Figure 4, we show the expected region of 0 for such neutron star models as a function of L. We note that 0 decreases with R and M. So, the lower bound of the shaded region corresponds to the stellar model with and 14 km. On the other hand, the lowest QPO frequency observed in the SGR 1806-20, i.e., 18 Hz, is also shown in the right panel of Figure 4. Since , fundamental torsional oscillations are theoretically the lowest frequency among many eigenfrequencies of torsional oscillations, 0 should be equal to or even lower than the observed lowest QPO frequency on the assumption that magnetar QPOs come from crustal torsional oscillations. Then, from the right panel of Figure 4, one can obtain the constraint on L as MeV if the central object of SGR 1806-20 is a neutron star with and km [84,86]. Similarly, if the central object is a typical neutron star with and 10 km, L is constrained as MeV.
Next, we take into account neutron superfluidity in crustal torsional oscillations, i.e., . To see how the frequencies depend on , we calculate 0, assuming that is constant inside the inner crust. We confirm that 0 for a given neutron star model can be well expressed as a function of L using Equation (9), even for . In Figure 5, we show the L dependence of 0 for a neutron star model with and 14 km by varying the ratio of with each 0.2 from 0 to 1 (the solid lines from bottom to top). The tendency of why the frequency increases with can also be understood by the dependence of frequency on the shear velocity. As mentioned above, the effective enthalpy, , decreases with , which leads to an increase in the shear velocity. As a result, one can expect that the frequency also increases since 0. We note that the neutron star model discussed for the L dependence of 0 in Figure 5 corresponds to the stellar model, which provides the lower boundary of the shaded region in Figure 4. That is, assuming that the central object in SGR 1806-20 is a neutron star with and km, and also assuming that the lowest QPO frequency observed in SGR 1806-20 comes from 0, one can obtain the constraint on L as with a lower limit of , depending on , where is determined as the intersection of the L dependence of 0 and 18 Hz (dot-dashed line) in Figure 5, i.e., increases with [85].
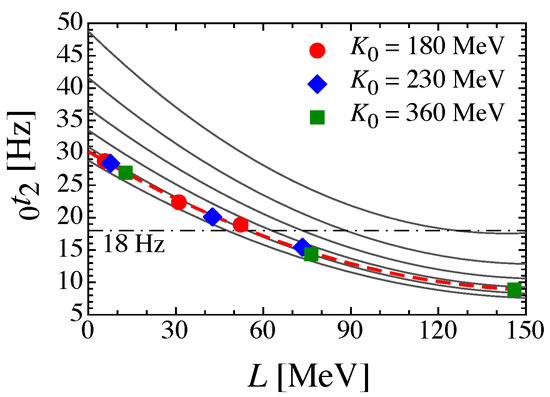
Figure 5.
For a neutron star model with and 14 km, the fundamental frequency of torsional oscillations is plotted as a function of L, changing the ratio of with each 0.2 from 0 to 1, where is assumed to be constant inside the inner crust. Meanwhile, the marks denote the frequencies, determined using the density-dependent derived in [143], and the dashed line is their fitting with Equation (9). Taken from [85].
In a realistic stellar model, should depend on the density. According to the band calculations in [143], the ratio of is only of the order of percent at , even though the ratio of is still under debate, e.g., in [144,145,146]. The fundamental frequencies determined with this density dependence of are also shown in Figure 5 with marks (and the dashed line for their fitting), which are close to the results obtained with . Anyway, since the frequencies of torsional oscillations strongly depend on the ratio of , it is quite important to understand the ratio of in a realistic situation.
In a similar way to the fundamental frequencies of torsional oscillations, one can discuss the L dependence of ℓ-th torsional oscillations. Actually, if one systematically examines the frequencies, one can determine that 0 is also well fitted as a function of L, which weakly depends on , as follow:
where with are also the adjustable parameters depending on M and R (and ) [85]. Using this L dependence of 0, we will discuss the QPO frequencies observed in SGR 1806-20 and 1900+14, even though one should also consider the effect of the existence of pasta (see Section 5.2 and Section 5.3 and also [147,148]). In Figure 6, we show the fundamental frequencies of torsional oscillations with specific values of ℓ for a neutron star model with and 12 km, adopting the results in [143] for . From the left panel, one can observe that the 18, 26, 30, and 92.5 Hz QPOs in SGR 1806-20 are well identified with fundamental oscillations if MeV; meanwhile, from the right panel, one can observe that the 28, 54, and 84 Hz QPOs in SGR 1900+14 are have fundamental oscillations if MeV. We note that other low-lying QPO frequencies discovered later can also be identified with torsional oscillations with different values of ℓ in the same framework [88,131,142] (also see Section 5.2 and Section 5.3).
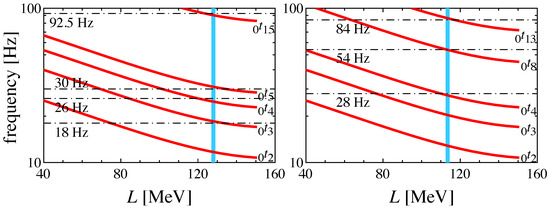
Figure 6.
The fundamental frequencies of torsional oscillations with several values of ℓ for a neutron star model with and 12 km are shown as a function of L. The QPO frequencies observed in SGR 1806-20 and SGR 1900+14 are compared with them in the left and right panels. Taken from [86].
Since the neutron star mass and radius in SGR 1806-20 and SGR 1900+14 are not constrained, it may be better to consider the stellar models with a typical range of mass and radius. In practice, if the stellar mass and radius are changed in a certain range, the resultant L dependence of 0 is shifted up and down in Figure 6 with the same combination of ℓ-th oscillations. As a result, the optimal value of L, with which the QPOs observed in SGRs are well identified with torsional oscillations, is also shifted left and right. In the left panel of Figure 7, the optimal values of L, with which the QPO frequencies observed in SGR 1806-20 (with filled marks) and in SGR 1900+14 (with open marks) are well identified as shown in Figure 6, are shown for various neutron star models. From this figure, one can see that L should be in the range of MeV for explaining SGR 1806-20 and MeV for explaining SGR 1900+14 if the central objects of both SGRs are neutron stars with and 10 km 14 km. Meanwhile, since the value of L should be universal, i.e., independent of the astronomical events, one has to simultaneously explain both events, SGR 1806-20 and SGR 1900+14, with the same value of L. Thus, we get a more stringent constraint on L, i.e., MeV [86], which is shown in the left panel of Figure 7 with the shaded region. Furthermore, since the symmetry energy at , is approximately estimated as a function of L [120] through the following:
one can constrain to explain the QPOs observed in the SGRs as MeV.
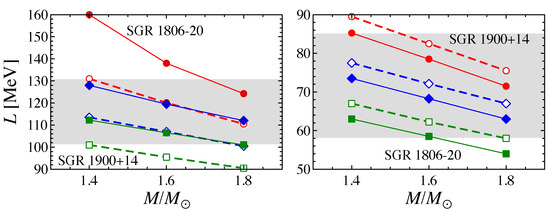
Figure 7.
The values of L, with which the QPOs observed in SGR 1806-20 (SGR 1900+14) are well identified by fundamental torsional oscillations, are shown with filled marks with solid lines (open marks with dashed lines) for different neutron star models, i.e., circles, diamonds, and squares correspond to the stellar models with a 10, 12, and 14 km radius. The left and right panels correspond to the identification shown in Figure 6 and Figure 8, respectively. The shaded region is the constraint on L, with which the QPOs observed in both SGR 1806-20 and 1900+14 are simultaneously explained by the torsional oscillations. Taken from [86].
On the other hand, considering the constraints on L obtained from terrestrial experiments whose fiducial value is MeV [3,7,10], the resultant constraint on L may be too large, although a larger value of L has also been reported [19,42]. So, if any, it may be better to consider an alternative possible correspondence to explain the QPO frequencies observed in SGRs with fundamental torsional oscillations. As an alternative possible correspondence, we determine that the 18, 30, and 92.5 Hz QPOs in SGR 1806-20 are identified with fundamental torsional oscillations, while the 28, 54, and 84 Hz in SGR 1900+14 are determined with oscillations, as shown in Figure 8 for a neutron star model with and 12 km, where the value of L should be MeV in SGR 1806-20 and MeV in 1900+14. We note that the 26 Hz QPO in SGR 1806-20 cannot be identified with this correspondence (see Section 5.3 for this missing identification). Considering a typical neutron star model with and 10 km 14 km, one can obtain the optimal values of L as shown in the right panel of Figure 7. To simultaneously explain the QPOs observed in the SGRs, we obtain the constraint on L as MeV (shaded region in the right panel), assuming that the central object in the SGR 1806-20 and SGR 1900+14 is a neutron star with and 10 km 14 km [86]. This constraint on L additionally provides us the constraint on as MeV, using Equation (11). We note that the fundamental frequencies of ℓ-th torsional oscillations excited inside the phase of spherical nuclei can be expressed as a function of ℓ, L, stellar mass, and radius [149].
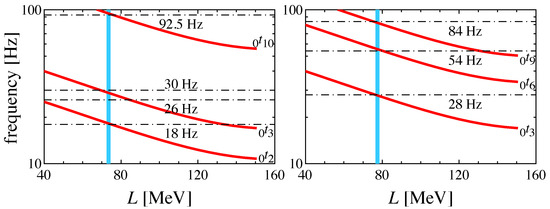
Figure 8.
Alternative possible correspondence of the QPO frequencies observed in SGR 1806-20 (left panel) and SGR 1900+14 (right panel) with fundamental torsional oscillations for a neutron star model with and 12 km. Taken from [86].
5.2. Torsional Oscillations Excited in Spherical and Cylindrical Nuclei
Since, in this review, we simply consider that the shear modulus inside the phase of slablike nuclei is zero, as mentioned in Section 4, torsional oscillations in the region composed of spherical and cylindrical nuclei can be excited independently from those in the region composed of cylindrical-hole and spherical-hole nuclei. That is, torsional oscillations are excited independently in two layers across the phase of slablike (lasagna) nuclei as “a lasagna sandwich” [88]. In this subsection, we discuss the torsional oscillations excited in the outer layer, i.e., the phase of spherical and cylindrical nuclei, while those excited in the inner layer, i.e., the phase of cylindrical-hole and spherical-hole nuclei, will be discussed in the next subsection (Section 5.3).
Unlike the phase of spherical nuclei, the understanding of the ratio of in the phase of cylindrical nuclei is poor. So, we simply consider the extreme case, i.e., and 1 in the phase of cylindrical nuclei. On the other hand, we adopt the result obtained in [143] for in the phase of spherical nuclei, as in the previous subsection. Then, one can determine the frequencies of torsional oscillations by solving an eigenvalue problem.
To see how the frequency of torsional oscillation changes due to the existence of cylindrical nuclei, in Figure 9, we show 0 as a function of L for a neutron star model with and 12 km using EOSs with some parameter sets listed in Table 1 (see [142] for the concrete parameter sets adopted here), where the left and right panels correspond to the results with and 1, respectively, and the thick, solid line is the fitting with Equation (9). For reference, we also show the L dependence of 0 excited in the phase of only spherical nuclei discussed in Section 5.1 with the dashed line. From this figure, one can observe that the modification in 0 due to the existence of cylindrical nuclei appears only for a neutron star model with a lower value of L. This is because the phase of cylindrical nuclei, as well as the other pasta phases, becomes narrower with L [120,121,122], i.e., one can neglect the existence of cylindrical nuclei in the stellar model with larger L. In any case, fundamental torsional oscillations hardly depend on , and one can discuss the L dependence through the fitting provided by Equation (10).
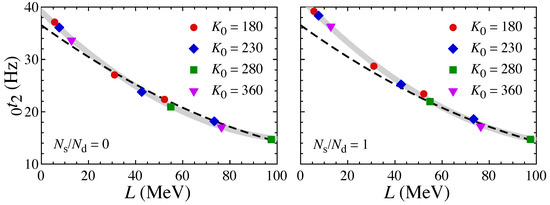
Figure 9.
The fundamental frequencies of torsional oscillations excited in the phase of spherical and cylindrical nuclei for a neutron star model with and 12 km are shown with various marks. The left and right panels are results with and 1, respectively. The thick-solid line denotes fitting with Equation (9), while the dashed line denotes the L dependence of 0 exited in the phase of only spherical nuclei discussed in Section 5.1. Taken from [142].
Using the L dependence of 0 with in the phase of cylindrical nuclei, in Figure 10, we compare fundamental torsional oscillations with various ℓ for a neutron star model with and 12 km to the low-lying QPO frequencies observed in SGR 1806-20 (left panel) and SGR 1900+14 (right panel), where the horizontal dashed and dotted lines denote the observed QPO frequencies and the solid lines denote the L dependence of 0. We note that we focus on only the correspondence of the observed low-lying QPOs except for the 26 Hz QPO in SGR 1806-20 here because the optimal value of L becomes larger than 100 MeV to identify all the observed low-frequency QPOs in terms of the crustal torsional oscillations, as discussed in Section 5.1, which may be inconsistent with the constraint in existing nuclear experiments. We also note that the 57 Hz QPO additionally discovered in [76] is taken into account this time. From this figure, one sees that the observed QPOs (except for the 26 Hz QPO) in SGR 1806-20 can be identified if MeV and those in SGR 1900+14 can be identified if MeV.
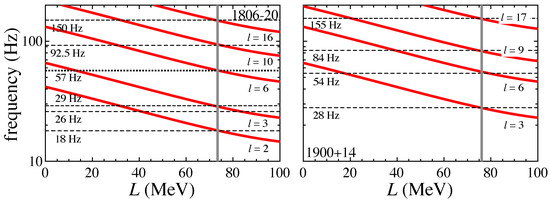
Figure 10.
Correspondence of the low-lying QPO frequencies (except for the 26 Hz QPO) observed in SGR 1806-20 (left panel) and 1900+14 (right panel) with several fundamental torsional oscillations for a neutron star model with and 12 km, assuming that in the cylindrical phase. Taken from [142].
Similarly, one can determine the optimal value of L to identify the observed QPOs with the same set of the fundamental torsional oscillations shown in Figure 10 for various neutron star models with and 1 in the phase of cylindrical nuclei. Assuming that and 10 km 14 km as a typical neutron star model, the optimal value of L for identifying the QPO frequencies observed in the SGRs with the same correspondence, as shown in Figure 10, are plotted in Figure 11 for in the left panel and in the right panel. In this figure, the filled marks with solid lines correspond to the resultant values of L for SGR 1806-20, while the open marks with dashed lines are for SGR 1900+14. Again, since the value of L should be independent of astronomical events, one must simultaneously explain both events, SGR 1806-20 and SGR 1900+14, with a specific value of L. Thus, we can obtain the constraint on L as MeV for and MeV for , assuming that the central object of SGR 1806-20 and SGR 1900+14 is a neutron star with and 10 km 14 km. These constraints on L are shown in the shaded region in Figure 11. Namely, the uncertainty in in the phase of cylindrical nuclei makes only a little difference in the constraint on L, where the allowed L lies in the range of 53.9–85.1 MeV, even if the uncertainty in in the phase of cylindrical nuclei is taken into account. This constraint on L provides us with the constraint of as 32.0–34.4 MeV, using the correlation between L and provided by Equation (11).
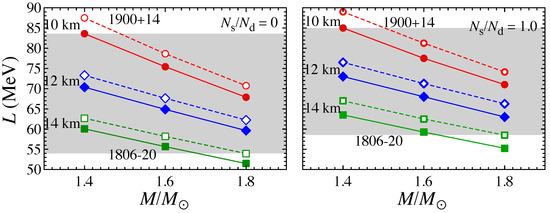
Figure 11.
The optimal value of L for identifying the low-lying QPO frequencies (except for the 26 Hz QPO) observed in SGR 1806-20 (filled marks with solid lines) and SGR 1900+14 (open marks with dashed lines) for various neutron star models, where the left and right panels are the results with and 1, respectively. Taken from [142].
On the other hand, since torsional oscillations are confined inside the phase of spherical and cylindrical nuclei, we can also discuss the overtone(s) of torsional oscillations. The n-th overtone frequency of ℓ-th torsional oscillations, n, is theoretically estimated with the crust thickness (or the thickness of elastic region), , as n [139,150]. Meanwhile, depends on EOS parameters L and , mainly through the neutron chemical potential at the crust-core boundary [123], when the neutron star mass and radius are fixed. Thus, via the identification of the relatively high-frequency QPO observed in SGR 1806-20, i.e., 626.5 Hz, as the first overtone of crustal torsional oscillations, one may obtain information regarding the EOS parameters [84,142].
Since n depends on and L through , it is of great use to determine a parameter constructed by a combination of and L, which can characterize n. To this end, assuming the combination of with integer numbers i and j, we finally determine an appropriate combination of and L as follows:
In Figure 12, we show the first overtones of torsional oscillations for a neutron star model with and 12 km constructed with various EOS parameters, where the thick, solid line denotes the fitting formula for the first overtones of torsional oscillations provided by [103,142]
where for are the adjustable parameters depending on M, R, and in the phase of cylindrical nuclei. We will, hereafter, discuss the dependence of n.
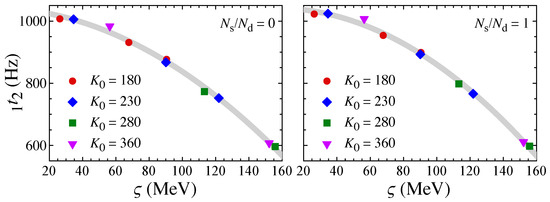
Figure 12.
The first overtones of torsional oscillations for a neutron star model with and 12 km constructed with various EOS parameters are shown as a function of defined by Equation (12), where the left and right panels, respectively, denote the results with and 1 in the phase of cylindrical nuclei. The thick, solid line denotes the fitting formula provided by Equation (13). Taken from [142].
It is well known that overtone frequencies of torsional oscillations weakly depend on ℓ, unlike the fundamental oscillations [139]. As an example, in the left panel of Figure 13, we show the first overtones of (solid lines) and 10 (dashed lines) torsional oscillations as a function of for neutron star models with , , and with in the phase of cylindrical nuclei. From this figure, one confirms that 1 weakly depends on ℓ, while one also determines that 1 strongly depends on stellar models. Hereafter, we focus only on n to discuss the dependence of overtones. In addition, in the right panel of Figure 13, we show the dependence of 1 for neutron star models with different radii with in the phase of cylindrical nuclei together with the 626.5 Hz QPO observed in SGR 1806-20. From this figure, one can observe that the optimal values of are 178.5, 149.7, and 107.1 MeV for neutron stars of , 12, and 14 km, respectively, if one identifies the 626.5 Hz QPO with the first overtone.
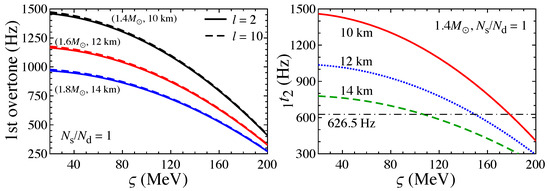
Figure 13.
In the left panel, we show the first overtones of (solid lines) and 10 (dashed lines) torsional oscillations as a function of for neutron star models with , , and with in the phase of cylindrical nuclei. In the right panel, the dependence of the first overtone of torsional oscillations for neutron star models with km (solid line), 12 km (dotted line), and 14 km (dashed line) with in the phase of cylindrical nuclei is compared to the 626.5 Hz QPO observed in SGR 1806-20 (dot-dashed line). Taken from [142].
In a similar way, one can obtain the optimal values of for various neutron star models. In the left panel of Figure 14, the resultant optimal values of are plotted for neutron star models with and 10 km 14 km for in the phase of cylindrical nuclei. One can observe that for each R, the optimal increases with M. This behavior comes from the fact that (or with fixed R) decreases with compactness, [123], which leads to the increases in 1 (through 1), meaning the optimal value of increases.
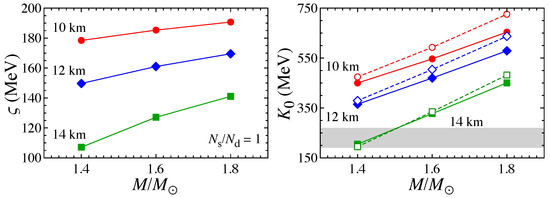
Figure 14.
In the left panel, the optimal value of to identify the 626.5 Hz QPO observed in SGR 1806-20 with the first overtone of the torsional oscillations is plotted for various neutron star models with and 10 km 14 km for in the phase of cylindrical nuclei. In the right panel, the constraint on obtained by combining the optimal values of shown in the left panel (and also those obtained with ) and the optimal values of L shown in Figure 11 is plotted for each stellar model, where filled marks with solid lines (open marks with dashed lines) denote the results for (0) in the phase of cylindrical nuclei. Meanwhile, the shaded region denotes the experimental constraint on obtained in [4], i.e., MeV. Taken from [142].
Furthermore, we also derive the constraint on through the definition of provided by Equation (12), i.e., , using the optimal values of for identifying the 626.5 Hz QPO with the first overtone frequency shown in the left panel of Figure 14 and the optimal values of L for identifying the low-lying QPO frequencies shown in Figure 11. In the right panel of Figure 14, such constraints on are plotted for various neutron star models, where the filled marks with solid lines denote the results for , while the open marks with dashed lines denote the results for . In the same panel, we also show the experimental constraint on , i.e., MeV [4]. Adopting this constraint on as a typical one, although it may still be model dependent, e.g., [5], from the right panel of Figure 14, one can observe that the neutron star models with 1.4–1.5M⊙ for km, and presumably, 1.2–1.4M⊙ for km are favored by the QPOs observed in SGR 1806-20 up to 626.5 Hz (except for the 26 Hz QPO). That is, a central object in SGR 1806-20 would have a relatively low mass and large radius. We note in passing that a neutron star model with still lower mass and smaller radius than that mentioned above might be acceptable from the right panel of Figure 14, but one must assume a larger value of L to construct such a stellar model, which would be presumably inconsistent with the systematic analysis of the mass-radius relation for low-mass neutron stars [44].
Finally, adopting the resultant constraint on the neutron star model of SGR 1806-20, i.e., 1.4–1.5M⊙ for km and 1.2–1.4M⊙ for km, the constraints on L shown in Figure 11 are dramatically improved. Namely, the optimal value of L should be 62–73 MeV for and 58–70 MeV for in the phase of cylindrical nuclei. Therefore, we obtain the constraint on L as 58–73 MeV independently of the uncertainty in in the phase of cylindrical nuclei, which is consistent with the existing constraint on L, e.g., [3,7,10]. Using the correlation between L and (Equation (11)), one can estimate the corresponding value of as 32.4–33.5 MeV.
5.3. Torsional Oscillations Excited in Cylindrical-Hole and Spherical-Hole Nuclei
In Section 5.1 and Section 5.2, we discussed that the QPO frequencies observed in SGR 1806-20 and SGR 1900+14 are well identified with torsional oscillations excited in the phase of spherical and cylindrical nuclei. In particular, by identifying the 626.5 Hz QPO with the first overtone of torsional oscillations, we showed the possibility that a central object in SGR 1806-20 would be a neutron star with a relatively low mass and large radius, and determined the constraint on L as more severe. However, we still have a missing piece in the identification of the observed QPO frequencies, i.e., the 26 Hz QPO observed in SGR 1806-20. In this subsection, we discuss the possibility of identifying the 26 Hz QPO (and the QPOs additionally discovered in [77]) in SGR 1806-20 with torsional oscillations excited in the phase of cylindrical-hole and spherical-hole nuclei, maintaining the consistency with the identification discussed in Section 5.2.
To determine the frequencies of torsional oscillations excited in the phase of cylindrical-hole and spherical-hole nuclei, one must know the value of in Equation (8) in the phases of cylindrical-hole and spherical-hole nuclei, but it is still quite uncertain. Here, we simply consider extreme cases, i.e., for maximum enthalpy and 0 for minimum enthalpy. In Figure 15, we show the fundamental frequencies of torsional oscillations excited in the phase of cylindrical-hole and spherical-hole nuclei for a neutron star model with and 12 km, using the EOSs with some parameter sets listed in Table 1 (see [88] for the concrete parameter sets adopted here), where the left and right panels correspond to the results with and 0 in the phase of cylindrical-hole and spherical-hole nuclei, respectively. From this, we determine that the fundamental frequencies excited in the phase of cylindrical-hole and spherical-hole nuclei weakly depend on and the dependence on L is well-fitted with the functional form provided by the following equation:
where for are the adjustable parameters depending on M, R, and in the phase of cylindrical-hole and spherical-hole nuclei [88]. Using this L dependence of 0 excited in the phase of cylindrical-hole and spherical-hole nuclei, we see the correspondence of the observed QPOs.
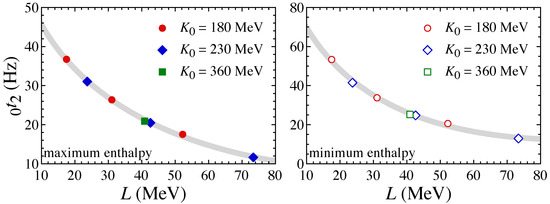
Figure 15.
The fundamental frequencies of torsional oscillations excited in the phase of cylindrical-hole and spherical-hole nuclei for a neutron star model with and 12 km. The thick, solid line corresponds to the fitting formula provided by Equation (14). The left and right panels, respectively, correspond to the results with (maximum enthalpy) and (minimum enthalpy). Taken from [88].
In the left panel of Figure 16, we show the identification of low-lying QPOs observed in SGR 1806-20 with fundamental frequencies of torsional oscillations excited in the phase of spherical and cylindrical nuclei and the phase of cylindrical-hole and spherical-hole nuclei for a neutron star model with and 13 km. As shown in the left panel of Figure 10, 18, 29, 57, and 92.5 Hz QPOs can be identified with the fundamental frequencies of , 3, 6, 10 torsional oscillations excited in the phase of spherical and cylindrical nuclei. With this correspondence, we determine the optimal values of L as MeV for and MeV for in the phase of cylindrical nuclei. We note that, in Figure 16, the solid lines denote the fundamental frequencies of torsional oscillations excited in the phase of spherical and cylindrical nuclei with in the phase of cylindrical nuclei. On the other hand, we also show the fundamental frequencies of torsional oscillations excited in the phase of cylindrical-hole and spherical-hole nuclei by the shaded regions, assuming that . From this figure, one can observe that the 26 Hz QPO, which cannot be identified with the torsional oscillations in the phase of spherical and cylindrical nuclei, can be identified with fundamental torsional oscillations excited in the phase of cylindrical-hole and spherical-hole nuclei consistently with the optimal value of L given by the identification of other QPOs with torsional oscillations in the phase of spherical and cylindrical nuclei.
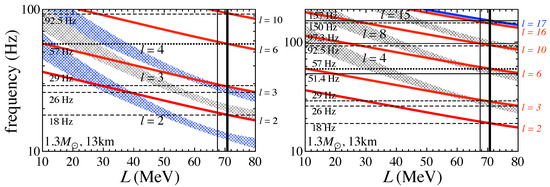
Figure 16.
The correspondence of the QPO frequencies observed in SGR 1806-20 and the fundamental frequencies of torsional oscillations with various values of ℓ excited in the phase of spherical and cylindrical nuclei with in the cylindrical nuclei (solid lines) and the phase of cylindrical-hole and spherical-hole nuclei for (shaded regions) for a neutron star model with and 13 km. We focus on only low-lying QPOs in the left panel, while in the right panel, we also consider the QPOs discovered in [77] together with the QPOs considered in the left panel. The vertical lines denote the optimal values of L to identify the low-lying QPO frequencies observed in SGR 1806-20, except for the 26 Hz QPO with the torsional oscillations excited in the phase of spherical and cylindrical nuclei discussed in Section 5.2, where the thick line ( MeV) and thin line ( MeV), respectively, correspond to the optimal values of L with and 0 in the phase of cylindrical nuclei. Taken from [88].
In addition, using this double layer model (the lasagna sandwich model), we determine that one can identify the QPOs originally discovered in SGR 1806-20 together with the QPOs additionally discovered by the Bayesian procedure, e.g., 51.4, 97.3, and 157 Hz QPOs [77], as shown in the right panel of Figure 16. That is, as shown in the left panel of Figure 10, 18, 29, 57, 92.5, and 150 Hz QPOs can be identified with the fundamental frequencies of , and 16 torsional oscillations excited in the phase of spherical and cylindrical nuclei. In a similar way, the 157 Hz QPO can be identified with fundamental torsional oscillations in the phase of spherical and cylindrical nuclei, while the 26, 51.4, and 97.3 Hz QPOs are the , and 15 fundamental torsional oscillations in the phase of cylindrical-hole and spherical-hole nuclei.
5.4. Constraint on a Neutron Star Model for GRB 200415A
So far, we considered the correspondence between crustal torsional oscillations and QPO frequencies observed in giant flares. In addition to these observations, another magnetar flare, GRB 200415A, was also detected in the direction of the NGC253 galaxy, where several high-frequency QPOs with varying significance were found at 836, 1444, 2132, and 4250 Hz [78]. We note that only high-frequency QPOs were detected from this event due to the short observation interval. So, considering the dynamical time of neutron stars, it may be possible to identify these observed QPOs with neutron star oscillations other than torsional oscillations, such as the fundamental (f-), gravity (-), or shear (-) modes (e.g., see Figure 25). Nevertheless, since these QPOs come from magnetar flares, here we consider identification with crustal torsional oscillations, which is the same framework as discussed in the case of QPOs observed in giant flares (Section 5.1, Section 5.2 and Section 5.3).
Since the observed QPOs are too high to identify fundamental torsional oscillations, we consider identifying them with overtones of torsional oscillations, as in Section 5.2. Using the fitting of the overtone frequencies provided by Equation (13), we plot the dependence of n in the left panel of Figure 17 for a neutron star model with and 12 km with in the phase of cylindrical nuclei, where the horizontal shaded regions denote the QPOs observed in GRB 200415A. We note that the overtone frequencies weakly depend on the ratio of in the phase of cylindrical nuclei [103]. In this subsection, we only consider the case with in the phase of cylindrical nuclei. From this figure, one can observe that four QPOs can be identified well with the 1st, 2nd, 4th, and 10th overtones of torsional oscillations, which tells us the optimal value of is 121.7 MeV.
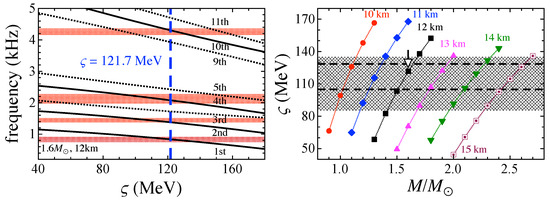
Figure 17.
In the left panel, we show the identification of four QPO frequencies observed in GRB 200415A [78] (shaded horizontal regions) with several overtones of torsional oscillations excited in the phase of spherical and cylindrical nuclei for a neutron star model with and 12 km with in the phase of cylindrical nuclei, where is the optimal value with this correspondence. In the right panel, we show the optimal values of to identify four QPOs in GRB 200415A with the same combinations of overtones as in the left panel for various neutron star models. The shaded region is the range of 85.3–135.1 MeV estimated with the fiducial value of MeV and MeV, while the region in the dashed lines is the range of 104.9–128.4 MeV with the optimal values of L discussed in Section 5.2, i.e., 58–73 MeV, together with MeV. The arrow in the right panel indicates the neutron star model considered in the left panel. Taken from [103].
In a similar way, one can determine the optimal values of for various neutron star models. In practice, the optimal values of determined with the same combination of the overtones as shown in the left panel of Figure 17 are plotted in the right panel of Figure 17. In particular, the neutron star model considered in the left panel is indicated with an arrow. Meanwhile, the value of is also estimated with the fiducial value of L and , i.e., 83.5–135.1 MeV with MeV and MeV [2], or with the optimal value of L obtained in Section 5.2 to identify the QPO frequencies observed in the giant flares with the torsional oscillations, such as 58–73 MeV, with the fiducial value of , i.e., 104.9–128.4 MeV. These estimations of are also shown in the right panel of Figure 17 with the shaded region and the enclosed region with the dashed lines. That is, considering these estimations, the stellar model with and 11 km can be excluded. Consequently, we can obtain the constraint on the neutron star mass and radius as shown in the left panel of Figure 18, where the shaded region corresponds to the results with 83.5–135.1 MeV, while the bound region by solid lines is those with 104.9–128.4 MeV.
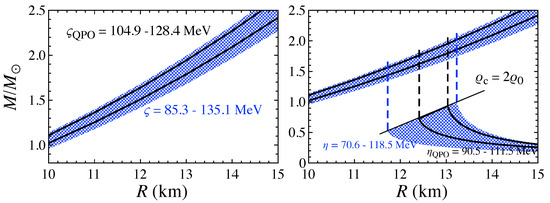
Figure 18.
In the left panel, the constraint on the neutron star mass and radius for GRB 200415A obtained from the optimal values of to identify the high-frequency QPOs with 1st, 2nd, 4th, and 10th overtones of torsional oscillations, adopting the range of 85.3–135.1 MeV estimated with the fiducial value of L and (shaded region) or 104.9–128.4 MeV with the optimal value of L to identify the magnetar QPOs (bound by solid lines). In the right panel, we show the constraint on the neutron star mass and radius obtained from the QPOs in GRB 200415A (the same as the left panel) together with those estimated with the mass formula for a low-mass neutron star as a function of derived in [44] (the right-bottom region), assuming that the central density of neutron stars should be less than twice the nuclear saturation density. Taken from [103].
One may make the constraint on the mass and radius of the neutron star model for GRB 200415A more severe if one knows the EOSs (or mass–radius relations) corresponding to the estimations of . For this purpose, the mass formula for a low-mass neutron star [44] must be crucial. The low-mass neutron star structures may strongly depend on the nuclear saturation parameters because the central density for such an object is very low. In fact, the mass and gravitational redshift, z, defined by , can be expressed as a function of the stellar central density and a new parameter provided by the following:
such that
where is the central density of the neutron star normalized by the saturation density and is the value of normalized by 100 MeV [44]. We note that these empirical formulae are valid in the range of . Since z is a combination of M and R, one can plot the mass and radius relation once one selects the value of .
The values of and , which are adopted to make a constraint on the mass and radius of the neutron star shown in the left panel of Figure 18, are provided by MeV and 58–73 with MeV, which correspond to the value of as 70.6–118.5 MeV and 90.5–111.5 MeV, respectively. Using this range of , one can estimate the stellar mass and radius, whose central density is less than twice the saturation density, as in the right-bottom region in the right panel of Figure 18. Furthermore, assuming that the radius of the neutron star whose central density is larger than twice the saturation density would be almost constant as shown with the dashed lines corresponding to , 12.41, 13.03, and 13.23 km for , 90.5, 111.5, and 118.5 MeV, we can obtain the overlap region with the constraint on the neutron star mass and radius to identify the QPOs with the overtones of torsional oscillations shown in the left panel of Figure 18. In such a way, we can obtain the neutron star mass and radius constraint for GRB 200415A. The resultant mass and radius constraint is shown in Figure 19 with a double-parallelogram, together with the other constraints obtained from the astronomical observations and experimental constraints.
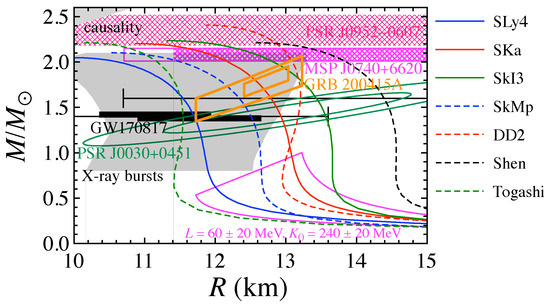
Figure 19.
Mass and radius of GRB 200415A constrained by identifying the observed high-frequency QPOs with the overtones of crustal torsional oscillations (double-parallelogram), adopting the fiducial values of L and (or the optimal value of L to identify the magnetar QPOs). For reference, the other constraints obtained from the astronomical observations and experimental restrictions are also shown. For astronomical observations, as well as those shown in Figure 1, we plot the constraints of the neutron star radius, i.e., km [151], the neutron star radius, i.e., km [152] or km [153] obtained from the GW170817, and the massive neutron star mass of PSR J0952-0607, i.e., [154]. Additionally, the mass and radius relations for neutron stars constructed with several EOSs, as in Figure 1, are also plotted. Taken from [103].
Finally, we comment on the alternative identification of QPOs observed in GRB 200415A with overtones of torsional oscillations. To obtain the neutron star mass and radius constraint shown in Figure 19, we identify the lowest QPO observed in GRB 200415A, i.e., 835.9 Hz QPO, with the first overtone of torsional oscillations, but it may be possible to identify it with the second overtone. In the left panel of Figure 20, we compare the lowest QPO observed in GRB 200415A with the first (dotted line) and second (solid line) overtones for a neutron star model with and 14 km. In this figure, we also show the range of with the fiducial value of L and (shaded region) and that with the optimal value of L to identify the QPOs observed in the giant flares (the region between the vertical dashed lines). From this figure, one can determine that the lowest QPO observed in GRB 200415A cannot be identified with the second overtone at least with this stellar model, consistent with the region of estimated with the fiducial value of saturation parameters. In practice, one can identify four QPOs observed in GRB 200415A with the 2nd, 5th, 8th, and 16th overtones if MeV, as shown in the right panel of Figure 20. Still, it is inconsistent with the range of with the fiducial value of saturation parameters. We note that the stellar model considered here is a little larger than the constraint from GW170817, i.e., the neutron star radius should be less than 13.6 km. But, as shown in the right panel of Figure 17, the optimal value of to identify the observed QPO frequencies becomes larger as the stellar radius decreases with fixed mass. That is, if one considers the neutron star model with a radius smaller than 13.6 km, the optimal value of is more distant from the estimation of using the fiducial values of and L.
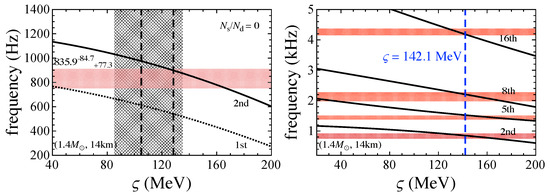
Figure 20.
An alternative possibility to identify the observed QPOs in GRB 200415A with the overtones of torsional oscillations, i.e., the lowest QPO frequency is identified with the 2nd overtone instead of the 1st overtone. In the left panel, the lowest QPO frequency (shaded horizontal region) is compared with the 1st (dotted line) and 2nd (solid line) overtones as a function of for a neutron star model with and 12 km. The vertical shaded region corresponds to 85.3–135.1 MeV with fiducial values of L and , while the region between the vertical dashed lines is 104.9–128.4 MeV. In the right panel, the four observed QPOs are identified with the 2nd, 5th, 8th, and 16th overtones for a neutron star model with and 14 km. The vertical dashed line denotes the optimal value of with this correspondence. Taken from [103].
6. Shear and Interface Oscillations
Owing to the presence of crust elasticity, the shear (s-) and interface (i-) modes are also excited, as are torsional oscillations. To determine the behavior of the s and i mode frequencies, we consider the stellar model with pasta phases, where the elasticity in the phase composed of slablike nuclei is assumed to be zero. Similar to torsional oscillations, one must consider the effect of neutron superfluidity, i.e., , to estimate the value of in Equation (7) and in Equation (8), but for simplicity, we consider only the situation of the maximum enthalpy here, i.e., the dripped neutrons commove with the protons.
In this review, we simply adopt the Cowling approximation to examine s- and i-mode oscillations. Therefore, the perturbation equations for the s and i modes are derived from linearized energy–momentum conservation laws, which are completely the same as those for the f, , and modes if one neglects the elasticity. One can find the concrete perturbation equations in [124,155], even though they are not shown explicitly here. We note that perturbation equations without the Cowling approximation are also found in [61], which can be obtained from the linearized Einstein equations. We note that one can qualitatively discuss the behavior of the frequencies determined with the Cowling approximation, but the quantitative discussion may be problematic, at least for the f and p modes, which deviate from those determined without the Cowling approximation [156]. On the other hand, since the damping rate for the s and i modes is too small to calculate numerically, the s and i modes might be determined relatively well, even with the Cowling approximation. In fact, it has been shown that the g modes excited with density discontinuity, whose damping rate is too low, are accurately determined with the Cowling approximation [56]. Anyway, one must discuss the accuracy of the s and i mode frequencies with the Cowling approximation somewhere.
As the boundary conditions, one should impose the regularity condition at the center and the condition that the Lagrangian perturbation of pressure should be zero at the stellar surface. In addition, at the interface where the elasticity discontinuously becomes zero, one has to impose junction conditions, such as the continuity of radial displacement, radial and transverse tractions, and the Lagrangian perturbation of pressure [155,157]. In practice, with our stellar models, one has to impose junction conditions at the four interfaces, i.e., between the fluid core and the phase of spherical-hole nuclei, between the phase of cylindrical-hole nuclei and the phase of slablike nuclei, between the phase of slablike nuclei and the phase of cylindrical nuclei, and between the surface of the outer crust and envelope.
The transition density at these interfaces becomes crucial for s- and i-mode oscillations. The transition density where the nuclear shape would be changed is determined from the EOS depending on the saturation parameters, e.g., [120,121,122]. On the other hand, the transition density at the outer crust surface is more or less complicated. This is because the density to determine such properties is too low to neglect the thermal effect, even though the thermal effect on the neutron star structure is negligible when the density is very high [158]. In this review, we simply consider that the transition density at the surface of the outer crust is g/cm3. In addition, we set the surface density, , as g/cm3.
In Figure 21, as an example, we show the radial profile of the amplitude of the Lagrangian displacement for the modes ( 1–4) in the radial (W) and angular directions (V) for a stellar model with and 10.2 km constructed with the EOS with MeV and MeV. The classification of the i mode is not uniquely fixed, but here we identify that the mode is mainly excited at the interface between the crust surface and envelope; the mode is excited at the interface between the crust surface and envelope and at the interface between the phase of slablike nuclei and the phase of cylindrical nuclei; the and modes are mainly excited at the interface associated with the cylindrical-hole and spherical-hole nuclei. Since the i modes are eigenmodes excited due to the existence of the interface where the elasticity discontinuously becomes zero [159], the number of the excited i modes is generally equivalent to the number of interfaces [124,160]. With our classification, the order of the i modes generally becomes -, -, -, and , from the lowest to highest, and typically, the frequencies are less than Hz. Moreover, in Figure 22, we show how i-mode frequencies depend on the surface density, , by fixing the other transition density. From this figure, one can observe that the i-mode frequencies hardly depend on .
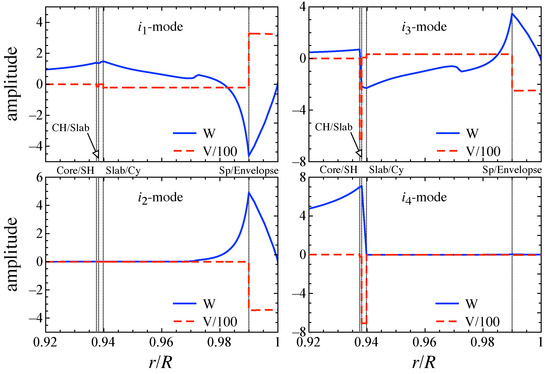
Figure 21.
The radial profile of the amplitude of the Lagrangian displacement for the modes in the radial (W) and angular direction (V) for a stellar model with and 10.2 km constructed with the EOS with MeV and MeV. The vertical dotted lines from left to right denote the interface between the fluid core and the phase of spherical-hole nuclei, the interface between the phase of cylindrical-hole and the phase of slablike nuclei, the interface between the phase of slablike nuclei and the phase of cylindrical nuclei, and the interface between the surface of crust and envelope. Taken from [160].
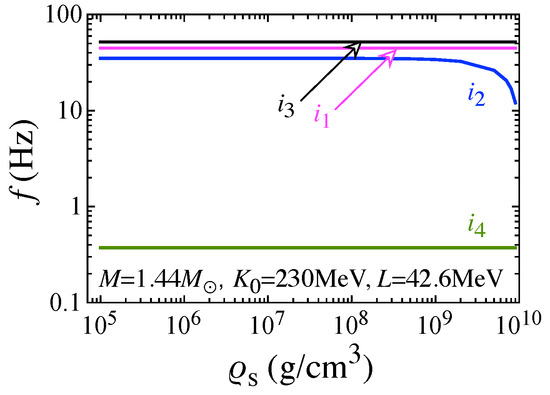
Figure 22.
Dependence of the i-mode frequencies on the surface density, , for a neutron star model with constructed with MeV and MeV. The other transition density between the phases with and without elasticity is fixed. Taken from [160].
On the other hand, in Figure 23, we show the radial profile of the amplitude of the Lagrangian displacement for the - and modes in the radial (W) and angular directions (V) for a neutron star model with and 12.4 km constructed with the EOS with MeV and MeV. Unlike the i modes, there are an infinite number of s modes. As shown in Figure 23, s modes are excited almost only inside the elastic region. Thus, in principle, one may find the s modes excited inside the phase of cylindrical-hole and spherical-hole nuclei. Even so, we could not find them in the frequency range of less than a few kHz. This situation could be understood as follows. Focusing on the angular displacement, V, in Figure 23, one may see that the wavelength of the mode, , is roughly estimated as follows:
where denotes the thickness of the elastic region where the s mode is confined. Meanwhile, the mode frequency may be estimated as follows:
using the shear velocity, , [61]. With this simple estimation, one can expect that, even if the s modes are excited inside the phase of cylindrical-hole and spherical-hole nuclei, their frequencies must become much higher than those excited in the phase of spherical and cylindrical nuclei. Namely, for the phase of cylindrical-hole and spherical-hole nuclei, , is much thinner than for the phase of spherical and cylindrical nuclei, , i.e., , which leads to the estimation that the s-mode frequencies excited in the phase of cylindrical-hole and spherical-hole nuclei must be times higher than those excited in the phase of spherical and cylindrical nuclei.
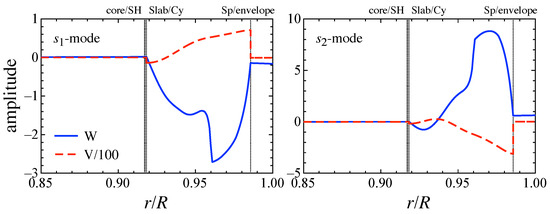
Figure 23.
The radial profile of the amplitude of the Lagrangian displacement for the and modes in the radial (W) and angular direction (V) for a neutron star model with and 12.4 km constructed with the EOS with MeV and MeV. Taken from [124].
Since the crust thickness, , also depends on the stellar compactness [119,123], to determine the dependence of the s and i mode frequencies on the neuron star properties, we consider not only the neutron star models constructed with the original OI-EOSs but also those constructed with the EOS, which is constructed in such a way that the OI-EOS for a lower density region () is connected to a one-parameter EOS provided by the following equation:
for a higher density region (), where we especially adopt that is equivalent to twice the saturation density [161]. In the one-parameter EOS, is given from the OI-EOS at , and is related to the sound velocity, , as . Thus, is a kind of indicator for expressing the stiffness of the core (or higher density) region. In this review, we focus on .
Through a systematical study, we determine empirical relations for the mode frequency, , and the mode frequency, . That is, and can be expressed as a function of the stellar compactness, x, given by with and , almost independently of the stiffness of the core region, i.e., the value of :
where , , , , and are the adjusted coefficients depending on the crust properties [124]. As an example, in Figure 24, we show the results for the mode (left panel) and the mode (right panel), where the solid lines denote the fitting given by Equations (21) and (22). Thus, once one simultaneously observes the shear and interface mode frequencies from a neutron star, one might extract the neutron star mass and radius via the empirical relations given by Equations (21) and (22) with the help of the constraint on the crust stiffness obtained from terrestrial experiments. Furthermore, the coefficients in Equations (21) and (22) can be well fitted as a function of a suitable combination of and L [124]. Namely, and can be expressed as a function of and a combination of and L. In practice, the s mode frequency for a canonical neutron star can be estimated within accuracy.
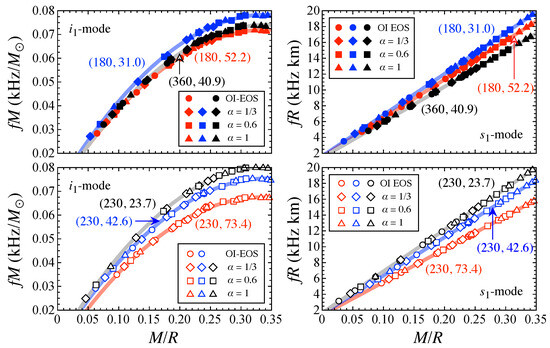
Figure 24.
For various neutron star models, and are, respectively, plotted as a function of in the left and right panels, where the circles, diamonds, squares, and triangles denote the results for stellar models constructed with the original OI-EOS, OI-EOS connected to the EOS with , 0.6, and 1, respectively. The solid lines denote fitting by Equation (21) in the left panel and (22) in the right panel, while the values of the EOS parameters are also shown on each line. Taken from [160].
In the end, we consider the possibility of applying the s mode frequency to identify the QPO observations. As discussed in Section 5.4, one can identify the high-frequency QPOs observed in GRB 200415A with the overtones of crustal torsional oscillations. Since only high-frequency QPOs have been observed in this event, one may identify them with other neutron star oscillations. In practice, as shown in Figure 25, where the f and mode frequencies for the stellar models with are shown as a function of the stellar compactness, together with the QPO frequencies observed in GRB 200415A, one can identify them with the s modes. Namely, the observed QPOs are identified with the , , , and mode frequencies if for (left panel) or for (right panel). One could discuss the constraint on the saturation parameters through the identification of QPOs with torsional oscillations in Section 5 because torsional oscillations are confined inside the elastic region. On the other hand, since s-mode oscillations depend on not only the crust region (elastic region) but also the (fluid) core region, it may be more difficult to discuss the crust properties via the identification of QPOs with s modes. Anyway, to obtain a severe constraint on the neutron star properties or to validate a theoretical model, we must wait for the next signals from a neutron star.
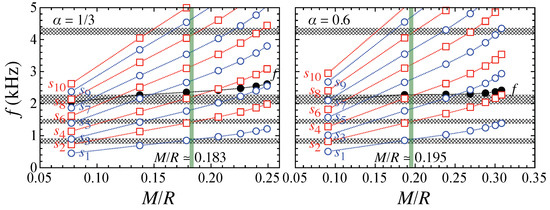
Figure 25.
The f and mode ( 1–10) frequencies are shown as a function of for neutron star models constructed with the EOS parameter of , where the left and right panels correspond to the results for and 0.6, respectively. The horizontal shaded regions denote the QPO frequencies observed in GRB 200415A [78]. The vertical lines denote the optimal value of to identify the four observed QPOs with the modes, i.e., for and for . Taken from [160].
7. Discussion and Conclusions
In this review, we discussed neutron star oscillations excited by crust elasticity, such as torsional, interface, and shear oscillations, adopting the Cowling approximation. Since torsional oscillations are axial-type oscillations, one can fully discuss them even with the Cowling approximation. On the other hand, since interface and shear oscillations are polar-type oscillations, one can qualitatively discuss them with the Cowling approximation, but one may have to check the accuracy of the interface and shear mode frequencies by comparing them to metric perturbations. In any case, through the identification of QPOs observed in magnetar flares with torsional oscillations, we successfully obtained the constraint on the nuclear saturation parameters, especially the density dependence of the nuclear symmetry energy, L, as 58–73 MeV. On the other hand, via the systematical study of interface and shear oscillations, we determined empirical relations almost independent of the stiffness of the core region.
To determine these frequencies, the effect of superfluidity is also important concerning input physics, as well as the shear modulus. To deal with superfluidity, in this review, we introduces a parameter, such as or , which is still quite uncertain. In addition, the understanding of the shear modulus inside the pasta phases may still be poor, where one has room for improvement. One may have to improve these properties to consider a more realistic situation.
As shown in this review, the observed QPO frequencies can be identified with crustal torsional oscillations; however, one must solve the time-dependence of QPO excitations. For this purpose, one may have to examine crustal oscillations beyond linear analysis, e.g., taking into account nonlinear coupling, and discuss the energy transfer from specific modes to other modes.
Moreover, in this review, we only considered the oscillations excited due to the crust elasticity. Meanwhile, the existence of quark matter inside the neutron star was theoretically suggested. In such a situation, the hadronic matter would transition into quark matter, and the mixed phase may appear at the transition region, where the structure becomes similar to the pasta structure in the crust [162,163]. So, such a mixed phase behaves as a liquid crystal, i.e., the elasticity becomes non-zero. That is, if such a phase exists, one can expect that torsional oscillations and/or shear and interface oscillations are excited in the hadron-quark mixed phase [164,165]. Through observations of these oscillation modes, one may probe the properties of quark matter.
Funding
This research was funded by the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Numbers JP19KK0354, JP21H01088, and JP24KF0090, and by the FY2023 RIKEN Incentive Research Project.
Data Availability Statement
Dataset available on request from the authors.
Acknowledgments
We are grateful to Kazuhiro Oyamatus for providing the EOS data, which is crucial for calculations in this study, and also to Kei Iida, Ken’ichiro Nakazato, Kostas D. Kokkotas, and Nick Stergioulas for their valuable comments.
Conflicts of Interest
The author declares no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| QPOs | Quasi-periodic oscillations |
| SGR | Soft-gamma repeater |
| EOSs | Equations of state |
| TOV | Tolman–Oppenheimer–Volkoff |
References
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; Wiley-Interscience: New York, NY, USA, 1983. [Google Scholar]
- Shlomo, S.; Kolomietz, V.M.; Colò, G. Deducing the nuclear-matter incompressibility coefficient from data on isoscalar compression modes. Eur. Phys. J. A 2006, 30, 23. [Google Scholar] [CrossRef]
- Tsang, M.B.; Stone, J.R.; Camera, F.; Danielewicz, P.; Gandolfi, S.; Hebeler, K.; Horowitz, C.J.; Lee, J.; Lynch, W.G.; Kohley, Z.; et al. Constraints on the symmetry energy and neutron skins from experiments and theory. Phys. Rev. C 2012, 86, 015803. [Google Scholar] [CrossRef]
- Khan, E.; Margueron, J. Determination of the density dependence of the nuclear incompressibility. Phys. Rev. C 2013, 88, 034319. [Google Scholar] [CrossRef]
- Stone, J.R.; Stone, N.J.; Moszkowski, S.A. Incompressibility in finite nuclei and nuclear matter. Phys. Rev. C 2014, 89, 044316. [Google Scholar] [CrossRef]
- Viñas, X.; Centelles, M.; Roca-Maza, X.; Warda, M. Density dependence of the symmetry energy from neutron skin thickness in finite nuclei. Eur. Phys. J. A 2014, 50, 27. [Google Scholar] [CrossRef]
- Newton, W.G.; Hooker, J.; Gearheart, M.; Murphy, K.; Wen, D.H.; Fattoyev, F.J.; Li, B.A. Constraints on the symmetry energy from observational probes of the neutron star crust. Eur. Phys. J. A 2014, 50, 41. [Google Scholar] [CrossRef]
- Tews, I.; Lattimer, J.M.; Ohnishi, A.; Kolomeitsev, E.E. Symmetry Parameter Constraints from a Lower Bound on Neutron-matter Energy. Astrophys. J. 2017, 848, 105. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Li, B.A.; Krastev, P.G.; Wen, D.H.; Zhang, N.B. Towards understanding astrophysical effects of nuclear symmetry energy. Eur. Phys. J. A 2019, 55, 117. [Google Scholar] [CrossRef]
- Blaizot, P.J. Nuclear compressibilities. Phys. Rep. 1980, 64, 171. [Google Scholar] [CrossRef]
- Piekarewicz, J. Why is the equation of state for tin so soft? Phys. Rev. C 2007, 76, 031301. [Google Scholar] [CrossRef]
- Garg, U.; Colò, G. The compression-mode giant resonances and nuclear incompressibility. Prog. Part. Nucl. Phys. 2018, 101, 55. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Centelles, M.; Viñas, X.; Warda, M. Neutron Skin of 208Pb, Nuclear Symmetry Energy, and the Parity Radius Experiment. Phys. Rev. Lett. 2011, 106, 252501. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Brenna, M.; Colò, G.; Centelles, M.; Viñas, X.; Agrawal, B.K.; Paar, N.; Vretenar, D.; Piekarewicz, J. Electric dipole polarizability in 208Pb: Insights from the droplet model. Phys. Rev. C 2013, 88, 024316. [Google Scholar] [CrossRef]
- Erler, J.; Horowitz, C.J.; Nazarewicz, W.; Rafalski, M.; Reinhard, P.-G. Energy density functional for nuclei and neutron stars. Phys. Rev. C 2013, 87, 044320. [Google Scholar] [CrossRef]
- Kurasawa, H.; Suzuki, T. The mean-square radius of the neutron distribution in the relativistic and non-relativistic mean-field models. Prog. Theor. Exp. Phys. 2022, 2022, 023D03. [Google Scholar] [CrossRef]
- Naito, T.; Roca-Maza, X.; Colò, G.; Liang, H.; Sagawa, H. Isospin symmetry breaking in the charge radius difference of mirror nuclei. Phys. Rev. C 2022, 106, L061306. [Google Scholar] [CrossRef]
- Reed, B.T.; Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J. Implications of PREX-2 on the Equation of State of Neutron-Rich Matter. Phys. Rev. Lett. 2021, 126, 172503. [Google Scholar] [CrossRef]
- Reinhard, P.-G.; Roca-Maza, X.; Nazarewicz, W. Information Content of the Parity-Violating Asymmetry in 208Pb. Phys. Rev. Lett. 2021, 127, 232501. [Google Scholar] [CrossRef]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef] [PubMed]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72. [Google Scholar] [CrossRef]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined Mass and Geometric Measurements of the High-mass PSR J0740+6620. Astrophys. J. 2021, 915, L12. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [The LIGO Scientific Collaboration and the Virgo Collaboration] GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Vuorinen, A. Gravitational-Wave Constraints on the Neutron-Star-Matter Equation of State. Phys. Rev. Lett. 2018, 120, 172703. [Google Scholar] [CrossRef] [PubMed]
- Pechenick, K.R.; Ftaclas, C.; Cohen, J.M. Hot spots on neutron stars—The near-field gravitational lens. Astrophys. J. 1983, 274, 846. [Google Scholar] [CrossRef]
- Leahy, D.A.; Li, L. Including the effect of gravitational light bending in X-ray profile modelling. Mon. Not. R. Astron. Soc. 1995, 277, 1177. [Google Scholar] [CrossRef]
- Poutanen, J.; Gierlinski, M. On the nature of the X-ray emission from the accreting millisecond pulsar SAX J1808.4-3658. Mon. Not. R. Astron. Soc. 2003, 343, 1301. [Google Scholar] [CrossRef]
- Psaltis, D.; Özel, F. Pulse Profiles from Spinning Neutron Stars in the Hartle-Thorne Approximation. Astrophys. J. 2014, 792, 87. [Google Scholar] [CrossRef]
- Sotani, H.; Miyamoto, U. Systematical study of pulsar light curves with special relativistic effects. Phys. Rev. D 2018, 98, 103019. [Google Scholar] [CrossRef]
- Sotani, H. Light curves from highly compact neutron stars with spot size effect. Phys. Rev. D 2020, 101, 063013. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. 2019, 887, L21. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. 2019, 887, L24. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. 2021, 918, L27. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. 2021, 918, L28. [Google Scholar] [CrossRef]
- Sotani, H.; Nishimura, N.; Naito, T. New constraints on the neutron-star mass and radius relation from terrestrial nuclear experiments. Prog. Theor. Exp. Phys. 2022, 2022, 041D01. [Google Scholar] [CrossRef]
- Sotani, H.; Ota, S. Neutron star mass formula with nuclear saturation parameters for asymmetric nuclear matter. Phys. Rev. D 2022, 106, 103005. [Google Scholar] [CrossRef]
- Sotani, H.; Naito, T. Empirical neutron star mass formula based on experimental observables. Phys. Rev. C 2023, 107, 035802. [Google Scholar] [CrossRef]
- Steiner, A.W.; Lattimer, J.M.; Brown, E.F. The Neutron Star Mass-Radius Relation and the Equation of State of Dense Matter. Astrophys. J. 2013, 765, L5. [Google Scholar] [CrossRef]
- Lattimer, J.M. The Nuclear Equation of State and Neutron Star Masses. Annu. Rev. Nucl. Part. Sci. 2012, 62, 485. [Google Scholar] [CrossRef]
- Estee, J.; Lynch, W.G.; Tsang, C.Y.; Barney, J.; Jhang, G.; Tsang, M.B.; Wang, R.; Kaneko, M.; Lee, J.W.; Isobe, T.; et al. Probing the Symmetry Energy with the Spectral Pion Ratio. Phys. Rev. Lett. 2021, 126, 162701. [Google Scholar] [CrossRef] [PubMed]
- Zenihiro, J.; Sakaguchi, H.; Murakami, T.; Yosoi, M.; Yasuda, Y.; Terashima, S.; Iwao, Y.; Takeda, H.; Itoh, M.; Yoshida, H.P.; et al. Neutron density distributions of 204,206,208Pb deduced via proton elastic scattering at Ep = 295 MeV. Phys. Rev. C 2010, 82, 044611. [Google Scholar] [CrossRef]
- Sotani, H.; Iida, K.; Oyamatsu, K.; Ohnishi, A. Mass and radius formulas for low-mass neutron stars. Prog. Theor. Exp. Phys. 2014, 2014, 051E01. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities Part II. Nuclei far from stabilities. Nucl. Phys. A 1998, 635, 231. [Google Scholar] [CrossRef]
- Douchin, F.; Haensel, P. A unified equation of state of dense matter and neutron star structure. Astron. Astrophys. 2001, 380, 151. [Google Scholar] [CrossRef]
- Köhler, H.S. Skyrme force and the mass formula. Nucl. Phys. A 1976, 258, 301. [Google Scholar] [CrossRef]
- Reinhard, P.-G.; Flocard, H. Nuclear effective forces and isotope shifts. Nucl. Phys. A 1995, 584, 467. [Google Scholar] [CrossRef]
- Bennour, L.; Heenen, P.-H.; Bonche, P.; Dobaczewski, J.; Flocard, H. Charge distributions of 208Pb, 206Pb, and 205Tl and the mean-field approximation. Phys. Rev. C 1989, 40, 2834. [Google Scholar] [CrossRef] [PubMed]
- Typel, S. Neutron skin thickness of heavy nuclei with α-particle correlations and the slope of the nuclear symmetry energy. Phys. Rev. C 2014, 89, 064321. [Google Scholar] [CrossRef]
- Shen, H.; Toki, H.; Oyamatsu, K.; Sumiyoshi, K. Relativistic equation of state of nuclear matter for supernova and neutron star. Nucl. Phys. A 1998, 637, 435. [Google Scholar] [CrossRef]
- Togashi, H.; Nakazato, K.; Takehara, Y.; Yamamuro, S.; Suzuki, H.; Takano, M. Nuclear equation of state for core-collapse supernova simulations with realistic nuclear forces. Nucl. Phys. A 2017, 961, 78. [Google Scholar]
- Kokkotas, K.D.; Schmidt, B.G. Quasi-Normal Modes of Stars and Black Holes. Living Rev. Rel. 1999, 2, 2. [Google Scholar] [CrossRef] [PubMed]
- Andersson, N.; Kokkotas, K.D. Gravitational Waves and Pulsating Stars: What Can We Learn from Future Observations? Phys. Rev. Lett. 1996, 77, 4134. [Google Scholar] [CrossRef] [PubMed]
- Andersson, N.; Kokkotas, K.D. Towards gravitational wave asteroseismology. Mon. Not. R. Astron. Soc. 1998, 299, 1059. [Google Scholar] [CrossRef]
- Sotani, H.; Tominaga, K.; Maeda, K.I. Density discontinuity of a neutron star and gravitational waves. Phys. Rev. D 2001, 65, 024010. [Google Scholar] [CrossRef]
- Sotani, H.; Kohri, K.; Harada, T. Restricting quark matter models by gravitational wave observation. Phys. Rev. D 2004, 69, 084008. [Google Scholar] [CrossRef]
- Sotani, H.; Yasutake, N.; Maruyama, T.; Tatsumi, T. Signatures of hadron-quark mixed phase in gravitational waves. Phys. Rev. D 2011, 83, 024014. [Google Scholar] [CrossRef]
- Passamonti, A.; Andersson, N. Towards real neutron star seismology: Accounting for elasticity and superfluidity. Mon. Not. R. Astron. Soc. 2012, 419, 638. [Google Scholar] [CrossRef]
- Doneva, D.D.; Gaertig, E.; Kokkotas, K.D.; Kruüger, C. Gravitational wave asteroseismology of fast rotating neutron stars with realistic equations of state. Phys. Rev. D 2013, 88, 044052. [Google Scholar] [CrossRef]
- Kruüger, C.J.; Ho, W.C.G.; Andersson, N. Seismology of adolescent neutron stars: Accounting for thermal effects and crust elasticity. Phys. Rev. D 2015, 92, 063009. [Google Scholar] [CrossRef]
- Sotani, H. Neutron star asteroseismology and nuclear saturation parameter. Phys. Rev. D 2021, 103, 123015. [Google Scholar] [CrossRef]
- Sotani, H.; Kumar, B. Universal relations between the quasinormal modes of neutron star and tidal deformability. Phys. Rev. D 2021, 104, 123002. [Google Scholar] [CrossRef]
- Sotani, H.; Dohi, A. Gravitational wave asteroseismology on cooling neutron stars. Phys. Rev. D 2022, 105, 023007. [Google Scholar] [CrossRef]
- Sotani, H.; Takiwaki, T. Gravitational wave asteroseismology with protoneutron stars. Phys. Rev. D 2016, 94, 044043. [Google Scholar] [CrossRef]
- Sotani, H.; Kuroda, T.; Takiwaki, T.; Kotake, K. Probing mass-radius relation of protoneutron stars from gravitational-wave asteroseismology. Phys. Rev. D 2017, 96, 063005. [Google Scholar] [CrossRef]
- Morozova, V.; Radice, D.; Burrows, A.; Vartanyan, D. The Gravitational Wave Signal from Core-collapse Supernovae. Astrophys. J. 2018, 861, 10. [Google Scholar] [CrossRef]
- Torres-Forné, A.; Cerdá-Durán, P.; Passamonti, A.; Obergaulinger, M.; Font, J.A. Towards asteroseismology of core-collapse supernovae with gravitational wave observations - II. Inclusion of space-time perturbations. Mon. Not. R. Astron. Soc. 2019, 482, 3967. [Google Scholar] [CrossRef]
- Sotani, H.; Sumiyoshi, K. Determination of properties of protoneutron stars toward black hole formation via gravitational wave observations. Phys. Rev. D 2019, 100, 083008. [Google Scholar] [CrossRef]
- Sotani, H.; Takiwaki, T. Avoided crossing in gravitational wave spectra from protoneutron star. Mon. Not. R. Astron. Soc. 2020, 498, 3503. [Google Scholar] [CrossRef]
- Sotani, H.; Takiwaki, T.; Togashi, H. Universal relation for supernova gravitational waves. Phys. Rev. D 2021, 104, 123009. [Google Scholar] [CrossRef]
- Israel, G.L.; Belloni, T.; Stella, L.; Rephaeli, Y.; Gruber, D.E.; Casella, P.; Dall’Osso, S.; Rea, N.; Persic, M.; Rothschild, R.E. The Discovery of Rapid X-Ray Oscillations in the Tail of the SGR 1806-20 Hyperflare. Astrophys. J. 2005, 628, L53. [Google Scholar] [CrossRef]
- Strohmayer, T.E.; Watts, A.L. Discovery of Fast X-Ray Oscillations during the 1998 Giant Flare from SGR 1900+14. Astrophys. J. 2005, 632, L111. [Google Scholar] [CrossRef]
- Strohmayer, T.E.; Watts, A.L. The 2004 Hyperflare from SGR 1806-20: Further Evidence for Global Torsional Vibrations. Astrophys. J. 2006, 653, 593. [Google Scholar] [CrossRef]
- Huppenkothen, D.; D’Angelo, C.; Watts, A.L.; Heil, L.; van der Klis, M.; van der Horst, A.J.; Kouveliotou, C.; Baring, M.G.; Gogus, E.; Granot, J.; et al. Quasi-periodic oscillations in short recurring bursts of the soft gamma repeater J1550-5418. Astrophys. J. 2014, 787, 128. [Google Scholar] [CrossRef]
- Huppenkothen, D.; Heil, L.M.; Watts, A.L.; Göğüş, E. Quasi-Periodic Oscillations in Short Recurring Bursts of the magnetars SGR 1806-20 and SGR 1900+14 Observed with RXTE. Astrophys. J. 2014, 795, 114. [Google Scholar] [CrossRef]
- Miller, M.C.; Chirenti, C.; Strohmayer, T.E. On the Persistence of QPOs during the SGR 1806-20 Giant Flare. Astrophys. J. 2019, 871, 95. [Google Scholar] [CrossRef]
- Castro-Tirado, A.J.; ∅stgaard, N.; Göğüş, E.; Sánchez-Gil, C.; Pascual-Granado, J.; Reglero, V.; Mezentsev, A.; Gabler, M.; Marisaldi, M.; Neubert, T.; et al. Very-high-frequency oscillations in the main peak of a magnetar giant flare. Nature 2021, 600, 621. [Google Scholar] [CrossRef] [PubMed]
- Sotani, H.; Kokkotas, K.D.; Stergioulas, N. Torsional oscillations of relativistic stars with dipole magnetic fields. Mon. Not. Roy. Astron. Soc. 2007, 375, 261. [Google Scholar] [CrossRef]
- Gabler, M.; Cerdá-Durán, P.; Font, J.A.; Müller, E.; Stergioulas, N. Magneto-elastic oscillations of neutron stars II: Exploring different magnetic field configurations. Mon. Not. Roy. Astron. Soc. 2013, 430, 1811. [Google Scholar] [CrossRef]
- Gabler, M.; Cerdá-Durán, P.; Stergioulas, N.; Font, J.A.; Müller, E. Constraining properties of high-density matter in neutron stars with magneto-elastic oscillations. Mon. Not. Roy. Astron. Soc. 2018, 476, 4199. [Google Scholar] [CrossRef]
- Steiner, A.W.; Watts, A.L. Constraints on Neutron Star Crusts from Oscillations in Giant Flares. Phys. Rev. Lett. 2009, 103, 181101. [Google Scholar] [CrossRef]
- Gearheart, M.; Newton, W.G.; Hooker, J.; Li, B.A. Upper limits on the observational effects of nuclear pasta in neutron stars. Mon. Not. Roy. Astron. Soc. 2011, 418, 2343. [Google Scholar] [CrossRef]
- Sotani, H.; Nakazato, K.; Iida, K.; Oyamatsu, K. Probing the Equation of State of Nuclear Matter via Neutron Star Asteroseismology. Phys. Rev. Lett. 2012, 108, 201101. [Google Scholar] [CrossRef]
- Sotani, H.; Nakazato, K.; Iida, K.; Oyamatsu, K. Effect of superfluidity on neutron star oscillations. Mon. Not. Roy. Astron. Soc. 2013, 428, L21. [Google Scholar] [CrossRef]
- Sotani, H.; Nakazato, K.; Iida, K.; Oyamatsu, K. Possible constraints on the density dependence of the nuclear symmetry energy from quasi-periodic oscillations in soft gamma repeaters. Mon. Not. Roy. Astron. Soc. 2013, 434, 2060. [Google Scholar] [CrossRef]
- Deibel, A.T.; Steiner, A.W.; Brown, E.F. Magnetar giant flare oscillations and the nuclear symmetry energy. Phys. Rev. C 2014, 90, 025802. [Google Scholar] [CrossRef]
- Sotani, H.; Iida, K.; Oyamatsu, K. Astrophysical implications of double-layer torsional oscillations in a neutron star crust as a lasagna sandwich. Mon. Not. Roy. Astron. Soc. 2019, 489, 3022. [Google Scholar] [CrossRef]
- Troja, E.; Rosswog, S.; Gehrels, N. Precursors of short gamma-ray bursts. Astrophys. J. 2010, 723, 1711. [Google Scholar] [CrossRef]
- Tsang, D.; Read, J.S.; Hinderer, T.; Piro, A.L.; Bondarescu, R. Resonant Shattering of Neutron Star Crusts. Phys. Rev. Lett. 2012, 108, 011102. [Google Scholar] [CrossRef]
- Tsang, D. Shattering Flares During Close Encounters of Neutron Stars. Astrophys. J. 2013, 777, 103. [Google Scholar] [CrossRef]
- Suvorov, A.G.; Kokkotas, K.D. Precessing magnetars as central engines in short gamma-ray bursts. Mon. Not. Roy. Astron. Soc. 2021, 502, 2482. [Google Scholar] [CrossRef]
- Neill, D.; Newton, W.G.; Tsang, D. Resonant shattering flares as multimessenger probes of the nuclear symmetry energy. Mon. Not. Roy. Astron. Soc. 2021, 504, 1129. [Google Scholar] [CrossRef]
- Kuan, H.-J.; Krüger, C.J.; Suvorov, A.G.; Kokkotas, K.D. Constraining equation-of-state groups from g-mode asteroseismology. Mon. Not. Roy. Astron. Soc. 2022, 513, 4045. [Google Scholar] [CrossRef]
- Neill, D.; Preston, R.; Newton, W.G.; Tsang, D. Constraining the Nuclear Symmetry Energy with Multimessenger Resonant Shattering Flares. Phys. Rev. Lett. 2023, 130, 112701. [Google Scholar] [CrossRef] [PubMed]
- Duncan, R.C.; Thompson, C. Formation of Very Strongly Magnetized Neutron Stars: Implications for Gamma-Ray Bursts. Astrophys. J. 1992, 392, L9. [Google Scholar] [CrossRef]
- Thompson, C.; Duncan, R.C. The soft gamma repeaters as very strongly magnetized neutron stars—I. Radiative mechanism for outbursts. Mon. Not. R. Astron. Soc. 1995, 275, 255. [Google Scholar] [CrossRef]
- Mazets, E.P.; Golentskii, S.V.; Il’inskii, V.N.; Aptekar, R.L.; Guryan, Y.A. Observations of a flaring X-ray pulsar in Dorado. Nature 1979, 282, 587. [Google Scholar] [CrossRef]
- Barat, C.; Hayles, R.I.; Hurley, K.; Niel, M.; Vedrenne, G.; Desai, U.; Kurt, V.G.; Zenchenko, V.M.; Estulin, I.V. Fine time structure in the 1979 March 5 gamma ray burst. Astron. Astrophys. 1983, 126, 400. [Google Scholar]
- Hurley, K.; Cline, T.; Mazets, E.; Barthelmy, S.; Butterworth, P.; Marshall, F.; Palmer, D.; Aptekar, R.; Golenetskii, S.; Il’Inskii, V.; et al. A giant periodic flare from the soft γ-ray repeater SGR 1900+14. Nature 1999, 397, 41. [Google Scholar] [CrossRef]
- Terasawa, T.; Tanaka, Y.T.; Takei, Y.; Kawai, N.; Yoshida, A.; Nomoto, K.; Yoshikawa, I.; Saito, Y.; Kasaba, Y.; Takashima, T.; et al. Repeated injections of energy in the first 600 ms of the giant flare of SGR 1806-20. Nature 2005, 434, 1100. [Google Scholar] [CrossRef]
- Palmer, D.M.; Barthelmy, S.; Gehrels, N.; Kippen, R.M.; Cayton, T.; Kouveliotou, C.; Eichler, D.; Wijers, R.A.M.J.; Woods, P.M.; Granot, J.; et al. A giant γ-ray flare from the magnetar SGR 1806-20. Nature 2005, 434, 1107. [Google Scholar] [CrossRef]
- Sotani, H.; Kokkotas, K.D.; Stergioulas, N. Neutron star mass-radius constraints using the high-frequency quasi-periodic oscillations of GRB 200415A. Astron. Astrophys. 2023, 676, A65. [Google Scholar] [CrossRef]
- Gabler, M.; Cerdá-Durán, P.; Font, J.A.; Müller, E.; Stergioulas, N. Magneto-elastic oscillations and the damping of crustal shear modes in magnetars. Mon. Not. Roy. Astron. Soc. 2011, 410, L37. [Google Scholar] [CrossRef]
- Gabler, M.; Cerdá-Durán, P.; Stergioulas, N.; Font, J.A.; Müller, E. Magnetoelastic oscillations of neutron stars with dipolar magnetic fields. Mon. Not. Roy. Astron. Soc. 2012, 421, 2054. [Google Scholar] [CrossRef]
- Lee, U. Axisymmetric toroidal modes of magnetized neutron stars. Mon. Not. Roy. Astron. Soc. 2008, 385, 2069. [Google Scholar] [CrossRef]
- Sotani, H.; Kokkotas, K.D.; Stergioulas, N. Alfven quasi-periodic oscillations in magnetars. Mon. Not. Roy. Astron. Soc. 2008, 385, L5. [Google Scholar] [CrossRef]
- Colaiuda, A.; Beyer, H.; Kokkotas, K.D. On the quasi-periodic oscillations in magnetars. Mon. Not. Roy. Astron. Soc. 2009, 396, 1441. [Google Scholar] [CrossRef]
- Cerdá-Durán, P.; Stergioulas, N.; Font, J.A. Alfvén QPOs in magnetars in the anelastic approximation. Mon. Not. Roy. Astron. Soc. 2009, 397, 1607. [Google Scholar] [CrossRef]
- Levin, Y. QPOs during magnetar flares are not driven by mechanical normal modes of the crust. Mon. Not. Roy. Astron. Soc. 2006, 368, L35. [Google Scholar] [CrossRef]
- Levin, Y. On the theory of magnetar QPOs. Mon. Not. Roy. Astron. Soc. 2007, 377, 159. [Google Scholar] [CrossRef]
- Colaiuda, A.; Kokkotas, K.D. Magnetar oscillations in the presence of a crust. Mon. Not. Roy. Astron. Soc. 2011, 414, 3014. [Google Scholar] [CrossRef]
- Colaiuda, A.; Kokkotas, K.D. Coupled polar-axial magnetar oscillations. Mon. Not. Roy. Astron. Soc. 2012, 423, 811. [Google Scholar] [CrossRef]
- Sotani, H.; Colaiuda, A.; Kokkotas, K.D. Constraints on the Magnetic Field Geometry of Magnetars. Mon. Not. Roy. Astron. Soc. 2008, 385, 2161. [Google Scholar] [CrossRef]
- Sotani, H.; Kokkotas, K.D. Alfven Polar Oscillations of Relativistic Stars. Mon. Not. Roy. Astron. Soc. 2009, 395, 1163. [Google Scholar] [CrossRef]
- Levin, Y.; van Hoven, M. On the excitation of f modes and torsional modes by magnetar giant flares. Mon. Not. Roy. Astron. Soc. 2011, 418, 659. [Google Scholar] [CrossRef]
- Kashiyama, K.; Ioka, K. Magnetar asteroseismology with long-term gravitational waves. Phys. Rev. D 2011, 83, 081302(R). [Google Scholar] [CrossRef]
- Oyamatsu, K. Nuclear shapes in the inner crust of a neutron star. Nucl. Phys. A 1993, 561, 431. [Google Scholar] [CrossRef]
- Pethick, J.; Ravenhall, D.G. Matter at Large Neutron Excess and the Physics of Neutron-Star Crusts. Annu. Rev. Nucl. Part. Sci. 1995, 45, 429. [Google Scholar] [CrossRef]
- Oyamatsu, K.; Iida, K. Saturation of Nuclear Matter and Radii of Unstable Nuclei. Prog. Theor. Phys. 2003, 109, 631. [Google Scholar] [CrossRef]
- Oyamatsu, K.; Iida, K. Symmetry energy at subnuclear densities and nuclei in neutron star crusts. Phys. Rev. C 2007, 75, 015801. [Google Scholar] [CrossRef]
- Oyamatsu, K. Nuclear masses and the equation of state of nuclear matter. Prog. Theor. Exp. Phys. 2023, 2023, 063D03. [Google Scholar] [CrossRef]
- Sotani, H.; Iida, K.; Oyamatsu, K. Probing crustal structures from neutron star compactness. Mon. Not. R. Astron. Soc. 2017, 470, 4397. [Google Scholar] [CrossRef]
- Sotani, H. Shear and interface modes in neutron stars with pasta structures. Phys. Rev. D 2023, 107, 123025. [Google Scholar] [CrossRef]
- Lattimer, J.M. The Equation of State of Hot Dense Matter and Supernovae. Annu. Rev. Nucl. Part. Sci. 1981, 31, 337. [Google Scholar] [CrossRef]
- Strohmayer, T.; van Horn, H.M.; Ogata, S.; Iyetomi, H.; Ichimaru, S. The Shear Modulus of the Neutron Star Crust and Nonradial Oscillations of Neutron Stars. Astrophys. J. 1991, 375, 679. [Google Scholar] [CrossRef]
- Ogata, S.; Ichimaru, S. First-principles calculations of shear moduli for Monte Carlo-simulated Coulomb solids. Phys. Rev. A 1990, 42, 4867. [Google Scholar] [CrossRef]
- Baiko, D.A. Shear modulus of neutron star crust. Mon. Not. R. Astron. Soc. 2011, 416, 22. [Google Scholar] [CrossRef]
- Kobyakov, D.; Pethick, C.J. Dynamics of the inner crust of neutron stars: Hydrodynamics, elasticity, and collective modes. Phys. Rev. C 2013, 87, 055803. [Google Scholar] [CrossRef]
- Sotani, H. Electron screening effects on crustal torsional oscillations. Phys. Lett. B 2014, 730, 166. [Google Scholar] [CrossRef]
- Sotani, H.; Iida, K.; Oyamatsu, K. Possible identifications of newly observed magnetar quasi-periodic oscillations as crustal shear modes. New Astron. 2016, 43, 80. [Google Scholar] [CrossRef]
- Tews, I. Spectrum of shear modes in the neutron-star crust: Estimating the nuclear-physics uncertainties. Phys. Rev. C 2017, 95, 015803. [Google Scholar] [CrossRef]
- Kobyakov, D.; Pethick, C.J. Elastic properties of polycrystalline dense matter. Mon. Not. R. Astron. Soc. 2015, 449, L110. [Google Scholar] [CrossRef]
- Sotani, H.; Togashi, H.; Takano, M. Effects of finite sizes of atomic nuclei on shear modulus and torsional oscillations in neutron stars. Mon. Not. R. Astron. Soc. 2022, 516, 5440. [Google Scholar] [CrossRef]
- Pethick, C.J.; Potekhin, A.Y. Liquid crystals in the mantles of neutron stars. Phys. Lett. B 1998, 427, 7. [Google Scholar] [CrossRef]
- Caplan, M.E.; Schneider, A.S.; Horowitz, C.J. Elasticity of Nuclear Pasta. Phys. Rev. Lett. 2018, 121, 132701. [Google Scholar] [CrossRef]
- Pethick, C.J.; Zhang, Z.-W.; Kobyakov, D.N. Elastic properties of phases with nonspherical nuclei in dense matter. Phys. Rev. C 2020, 101, 055802. [Google Scholar] [CrossRef]
- Sotani, H.; Iida, K.; Oyamatsu, K. Probing nuclear bubble structure via neutron star asteroseismology. Mon. Not. Roy. Astron. Soc. 2017, 464, 3101. [Google Scholar] [CrossRef]
- Hansen, C.J.; Cioffi, D.F. Torsional oscillations in neutron star crusts. Astrophys. J. 1980, 238, 740. [Google Scholar] [CrossRef]
- McDermott, P.N.; van Horn, H.M.; Hansen, C.J. Nonradial Oscillations of Neutron Stars. Astrophys. J. 1988, 325, 725. [Google Scholar] [CrossRef]
- Schumaker, B.L.; Thorne, K.S. Torsional oscillations of neutron stars. Mon. Not. Roy. Astron. Soc. 1983, 203, 457. [Google Scholar] [CrossRef]
- Sotani, H.; Iida, K.; Oyamatsu, K. Constraints on the nuclear equation of state and the neutron star structure from crustal torsional oscillations. Mon. Not. Roy. Astron. Soc. 2018, 479, 4735. [Google Scholar] [CrossRef]
- Chamel, N. Neutron conduction in the inner crust of a neutron star in the framework of the band theory of solids. Phys. Rev. C 2012, 85, 035801. [Google Scholar] [CrossRef]
- Chamel, N. Band structure effects for dripped neutrons in neutron star crust. Nucl. Phys. A 2005, 747, 109. [Google Scholar] [CrossRef]
- Carter, B.; Chamel, N.; Haensel, P. Entrainment coefficient and effective mass for conduction neutrons in neutron star crust: Simple microscopic models. Nucl. Phys. A 2005, 748, 675. [Google Scholar] [CrossRef]
- Watanabe, G.; Pethick, C.J. Superfluid Density of Neutrons in the Inner Crust of Neutron Stars: New Life for Pulsar Glitch Models. Phys. Rev. Lett. 2017, 119, 062701. [Google Scholar] [CrossRef]
- Sotani, H. Constraints on Pasta Structure of Neutron Stars from Oscillations in Giant Flares. Mon. Not. Roy. Astron. Soc. 2011, 417, L70. [Google Scholar] [CrossRef]
- Passamonti, A.; Pons, J.A. Quasi-periodic oscillations in superfluid, relativistic magnetars with nuclear pasta phases. Mon. Not. Roy. Astron. Soc. 2016, 463, 1173. [Google Scholar] [CrossRef]
- Sotani, H. Empirical formula of crustal torsional oscillations. Phys. Rev. D 2016, 93, 044059. [Google Scholar] [CrossRef]
- Samuelsson, L.; Andersson, N. Neutron Star Asteroseismology. Axial Crust Oscillations in the Cowling Approximation. Mon. Not. Roy. Astron. Soc. 2007, 374, 256. [Google Scholar] [CrossRef]
- Bauswein, A.; Just, O.; Janka, H.-T.; Stergioulas, N. Neutron-star Radius Constraints from GW170817 and Future Detections. Astrophys. J. 2017, 850, L34. [Google Scholar] [CrossRef]
- Capano, C.D.; Tews, I.; Brown, S.M.; Margalit, B.; De, S.; Kumar, S.; Brown, D.A.; Krishnan, B.; Reddy, S. Stringent constraints on neutron-star radii from multimessenger observations and nuclear theory. Nat. Astron. 2020, 4, 625. [Google Scholar] [CrossRef]
- Dietrich, T.; Coughlin, M.W.; Pang, P.T.H.; Bulla, M.; Heinzel, J.; Issa, L.; Tews, I.; Antier, S. Multimessenger constraints on the neutron-star equation of state and the Hubble constant. Science 2020, 370, 1450–1453. [Google Scholar] [CrossRef]
- Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. PSR J0952-0607: The Fastest and Heaviest Known Galactic Neutron Star. Astrophys. J. 2022, 934, L17. [Google Scholar] [CrossRef]
- Yoshida, S.; Lee, U. Nonradial oscillations of neutron stars with a solid crust. Astron. Astrophys. 2002, 395, 201. [Google Scholar] [CrossRef]
- Yoshida, S.; Kojima, Y. Accuracy of the relativistic Cowling approximation in slowly rotating stars. Mon. Not. Roy. Astron. Soc. 1997, 289, 117. [Google Scholar] [CrossRef]
- Finn, L.S. Non-radial pulsations of neutron stars with a crust. Mon. Not. Roy. Astron. Soc. 1990, 245, 82. [Google Scholar] [CrossRef]
- Gudmundsson, E.H.; Pethick, C.J.; Epstein, R.I. Structure of neutron star envelopes. Astrophys. J. 1983, 272, 286. [Google Scholar] [CrossRef]
- Piro, A.L.; Bildsten, L. Neutron Star Crustal Interface Waves. Astrophys. J. 2005, 619, 1054. [Google Scholar] [CrossRef]
- Sotani, H. Shear oscillations in neutron stars and the nuclear symmetry energy. Phys. Rev. D 2024, 109, 023030. [Google Scholar] [CrossRef]
- Sotani, H. Effect of nuclear saturation parameters on a possible maximum mass of neutron stars. Phys. Rev. C 2017, 95, 025802. [Google Scholar] [CrossRef]
- Maruyama, T.; Chiba, S.; Schulze, H.-J.; Tatsumi, T. Hadron-quark mixed phase in hyperon stars. Phys. Rev. D 2007, 76, 123015. [Google Scholar] [CrossRef]
- Xia, C.-J.; Maruyama, T.; Yasutake, N.; Tatsumi, T.; Shen, H.; Togashi, H. Systematic study on the quark-hadron mixed phase in compact stars. Phys. Rev. D 2020, 102, 023031. [Google Scholar] [CrossRef]
- Sotani, H.; Maruyama, T.; Tatsum, T. Shear oscillations in the hadron-quark mixed phase. Nucl. Phys. A 2013, 906, 37. [Google Scholar] [CrossRef]
- Lau, S.Y.; Yagi, K. Probing hybrid stars with gravitational waves via interfacial modes. Phys. Rev. D 2021, 103, 063015. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).