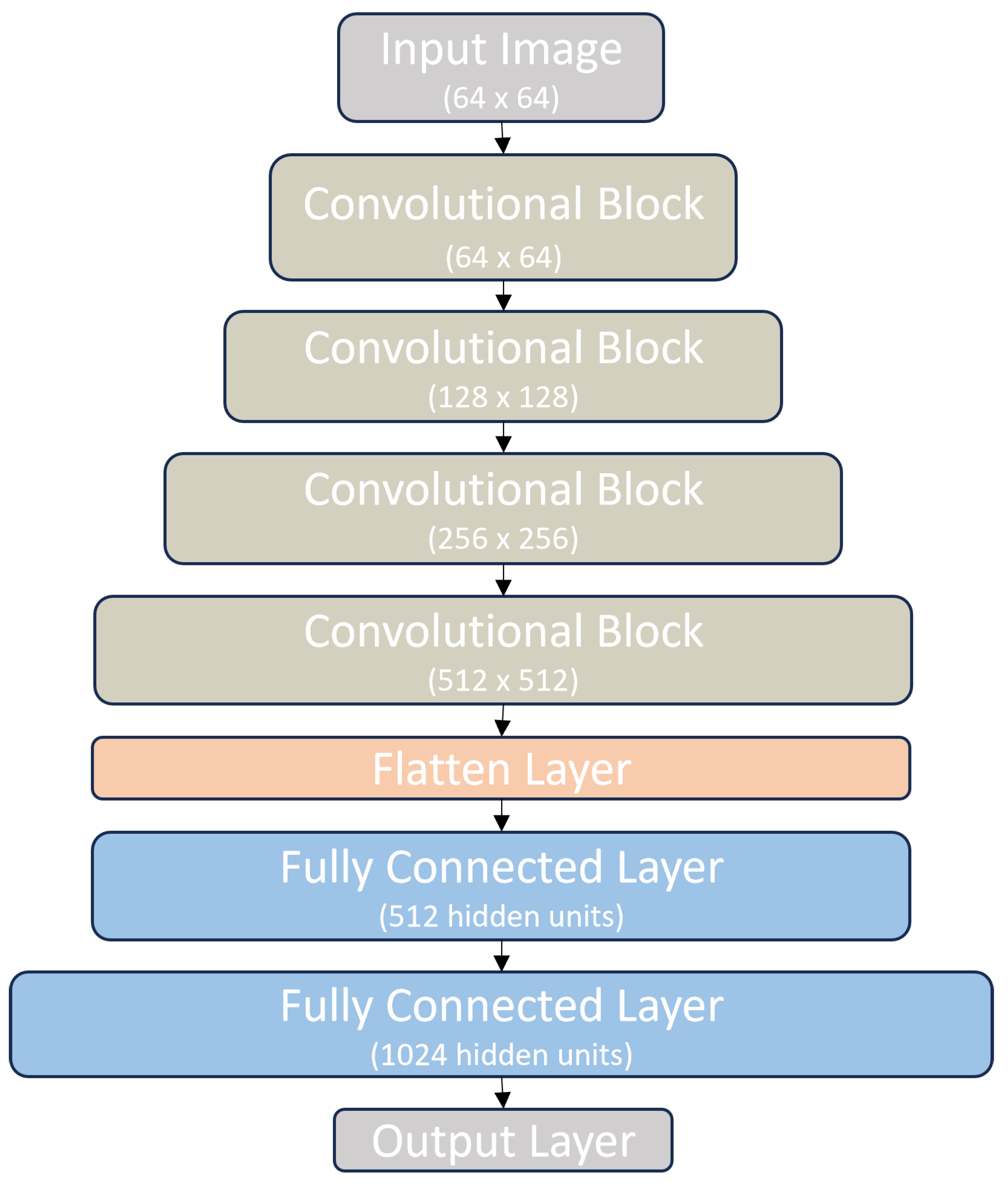
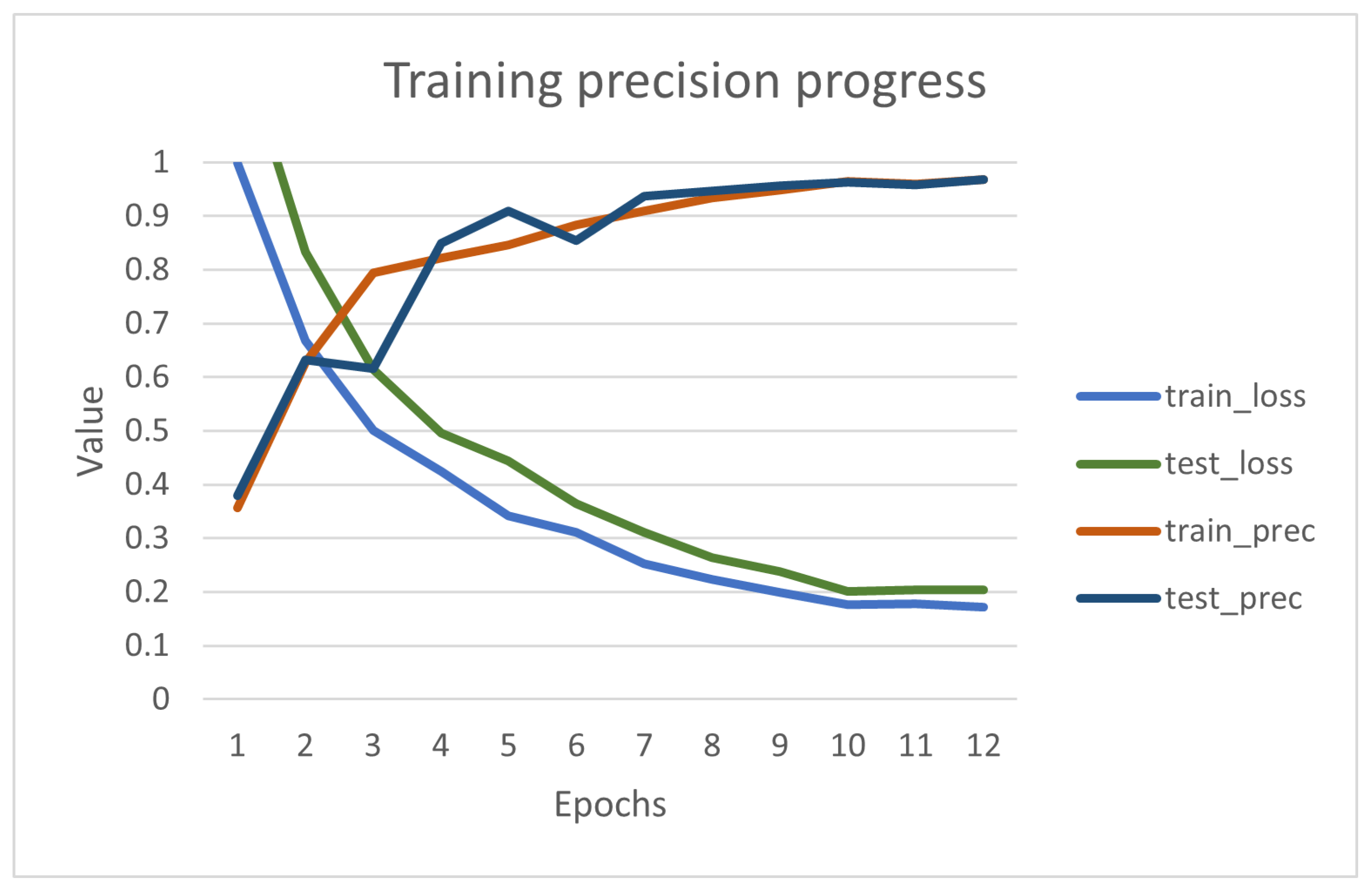
5.1. Summary of Results
The comparison between the classes, as depicted in the confusion matrix from
Table 5, provides a detailed look into the neural network’s performance across the distinct categories of classes. Notably, the matrix exhibits a strong diagonal pattern with bold values, representing correct predictions for each class. For Class 0, the model achieves 3472 correct predictions, making it the most accurately classified class. Similarly, Class 1 demonstrates high accuracy with 4878 correct predictions, indicating a model that effectively discerns instances from this category. Moving to Class 2, we find 1141 correct predictions, revealing the network’s capacity to accurately classify instances from this class. Despite being less frequent in the dataset, Classes 3 and 4 are also correctly identified with 439 and 1947 predictions, respectively. This confirms the model’s reliable performance across all classes, highlighting its strong multi-class classification capabilities.
To further analyze our class-based comparison, we randomly split our analysis into training and validation data subsets. This differentiation allows us to study how our CNN performs on individual classes during both the validation and testing phases. By evaluating the precision, recall, and F1 score for each class in these distinct datasets, we obtain valuable insights into the model’s ability to generalize its learning from the training set to previously unseen validation data. This partitioned examination enables a better understanding of performance across diverse classes and helps to optimize our model more efficiently.
To better understand the data behind these confusion matrices, in this section, we switch our focus to a class-based comparison of the results. This helps us to better understand how our neural network performs across individual classes. Through an examination of class-specific precision, recall, and F1 scores, we gain a better understanding of the model’s performance and the disparities among various categories.
The comparison between the classes in the multi-class classification problem, as shown in
Table 6, reveals valuable information about the model’s performance across multiple categories. Notably, Class 1 stands out with an impressive accuracy rate of 99.03%, accompanied by precision and recall metrics at the same elevated level. This demonstrates the model’s remarkable consistency in accurately classifying instances from this category. This can also be correlated to the fact it has the biggest sample size. Similarly, Class 0 exhibits strong performance with an accuracy of 98.92%, indicating a high degree of precision and recall. This level of accuracy across two classes underlines the model’s reliability and accuracy in correctly identifying instances from these groups. As we progress to Class 2, an accuracy of 96.12% is maintained, accompanied by parallel precision and recall scores. This reflects the model’s proficiency in recognizing instances from Class 2, offering a robust multi-class classification solution. The results further demonstrate the model’s capability to handle Classes 3 and 4 with accuracy rates of 91.46% and 97.35%, respectively, and precision and recall metrics mirroring these percentages. These close values in performance showcase the model’s consistency in correctly categorizing instances from these classes, more so from the first two and the last one, making it a reliable classifier for this multi-class problem.
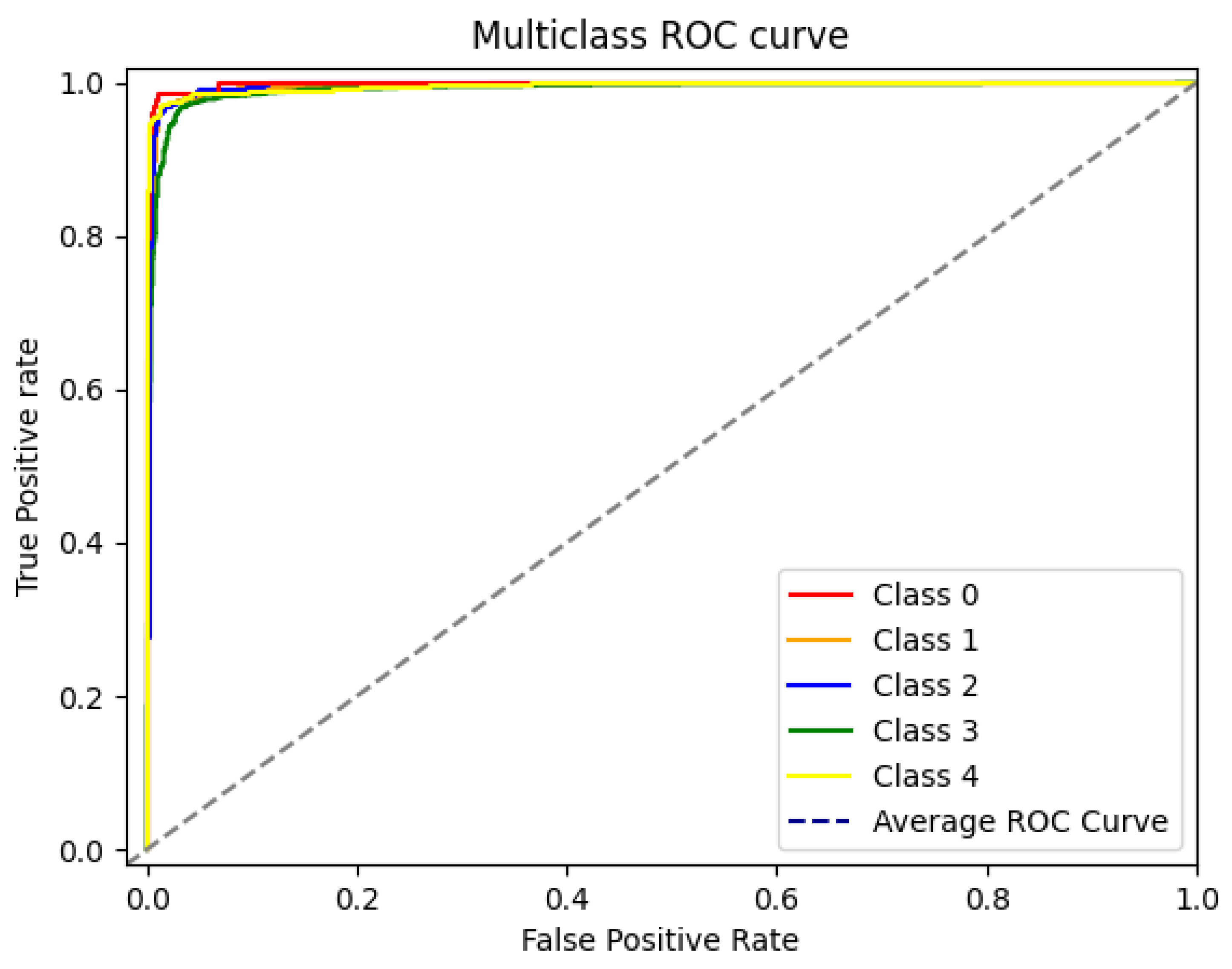
Figure 8 illustrates the ROC curve for our model’s classification of the five classes on the testing set. Each distinct color within the graph corresponds to a specific class. The proximity of the True Positive Rate (TPR) to 1 and the False Positive Rate (FPR) to 0, as evidenced by the ROC, showcases the performance of our model on each class. In essence, the closer the curve aligns with the upper-left corner, the more accurate the predictions. Cf.
Figure 8, the ROC curve for each class exhibits good performance. Notably, the 1st class achieves the highest predictive accuracy, while the 3rd class lags slightly in performance, primarily attributed to the scarcity of available cigar-shaped images in the dataset. Furthermore, the average AUC for our model amounts to an impressive 0.9921, indicative of the model’s exceptional overall predictive capabilities. The diagonal line showcased in
Figure 8 represents the performance of a random classifier.
5.2. Comparison with Other Methods
In this section, we compare the proposed architecture and its results with other CNNs and related works proposed in the literature, as mentioned earlier.
We must first understand the architecture and the main features of some state-of-the-art neural networks. The distinguishing feature of ResNet-50 [
22] is the use of residual blocks. These blocks contain skip connections, or shortcuts, that allow the network to skip over one or more layers. This skip connection enables the network to learn residual functions, making it easier to train very deep networks. For DenseNet [
23], these outstanding features are its densely connected layers. In traditional neural networks, each layer receives input only from the previous layer. In contrast, DenseNet connects each layer to all subsequent layers. This dense connectivity facilitates feature reuse and encourages gradient flow, making it easier to train very deep networks. The Inception architecture [
21], also known as GoogleNet, introduces the concept of inception modules, which are building blocks for the network. These modules perform multiple convolutions of different kernel sizes (1 × 1, 3 × 3, 5 × 5) and max-pooling operations on the input data in parallel. The outputs of these operations are concatenated along the depth dimension, allowing the network to capture features at various scales. The core idea behind EfficientNet [
24] is to achieve model scalability by uniformly scaling three critical dimensions of a CNN architecture: depth, width, and resolution. By systematically and uniformly scaling these dimensions, EfficientNet models maintain a balance between model capacity and computational efficiency. And, lastly, MobileNet [
25] introduces a significant innovation in the use of depthwise separable convolutions, which replace traditional convolutions. Depthwise separable convolutions consist of two layers: depthwise convolutions (pointwise convolutions) and 1 × 1 pointwise convolutions. These layers are computationally more efficient than standard convolutions. Also, this network is a more lightweight version of neural networks compared with its previous counterparts.
It is important to note that these networks were trained with the same set of hyperparameters that the proposed network was trained on. These hyperparameters are a batch size of 16, a learning rate of 0.001, categorical cross-entropy as a loss function, and an Adam optimizer. Besides these parameters, in order to attain convergence on each of the trained networks, we used early stopping, as we did for the proposed network mentioned in
Section 4.2.
Table 7 shows the comparison between the proposed network architecture and state-of-the-art counterparts previously described. It can be noticed that our designed CNN provides better results than the rest. The proposed CNN achieved a testing accuracy of 96.83%. This marked an improvement beyond the accuracy rates attained by the competitors, which hovered around 94% after the validation. This was also the case when compared with [
20], which obtained an accuracy of 95.2% on a classification problem with the same number of five classes. Also, Ref. [
19] have a good accuracy of 94.47%, with the main reason for a lower accuracy being the class imbalance present in it. This results in the fact that the proposed network was better at training on a limited number of images compared with the proposed research from Zhang.
Because of the class imbalance, cf.
Table 6, under the sample size column, accuracy can be unreliable on its own. For this reason, other metrics such as precision, recall, and the F1 score can be helpful. If all these metrics give good results, we are looking at a general solution for our problem, whereas if these values are unsatisfactory, the model needs improvements. While precision is important when false positives need to be reduced, the recall is mostly used to evaluate the miss rate of true positive values. For the problem of class imbalance, the most important metric is the F1 score, as it allows for a comprehensive assessment of the model’s performance, taking both false positives and false negatives into account.
With values of 96.75%, 96.52%, and 96.72% for precision, recall, and the F1 score, our proposed CNN provides a better solution to the problem of galaxy classification. This can be observed in the comparison with other networks, where most of them obtained values of around 94%, as well as the architecture proposed by [
20], which provided values of 95.12%, 95.21% and 95.15% for precision, recall, and the F1 score.
Another comparison can be made when we inspect the number of nodes of each network. In this comparison, we do not see a big difference between the proposed network and the state-of-the-art ones. The fact that the number of features is similar to theirs while achieving higher accuracy suggests that the layers used are more suitable for the suggested problem.
These features are represented by the total number of neurons in the fully connected layers of this neural network; the number of units in these layers can be added up, and the results are represented in
Table 8.
The performance of our network is also validated by the lower values obtained by the loss function.
Table 7 summarizes the results. Achieving the lowest value of the tested networks suggests that the results that were predicted by the proposed network are closest to the truth. Achieving a difference of around 0.04 from the best performer, DenseNet obtained a loss value of 0.2174.
Accuracy and loss are inversely correlated. As accuracy increases, loss decreases. As the model becomes better at minimizing the error represented by the loss function, its accuracy increases. The proposed architecture achieved a remarkable accuracy of 96.83%, with a very low loss of 0.1718. This indicates that the model excels at correctly classifying galaxies and does so with high confidence, compared with the other solutions peaking at 95.20% accuracy with a slightly higher loss of 0.1908. All the training of the state-of-the-art networks is conducted using early stopping, achieving their convergence. While the other models perform well, they have a lower accuracy compared with the proposed model, and the loss indicates slightly less precise class predictions.
Evaluating the performance of CNNs often means relying on point estimates like accuracy or loss. However, these metrics might not fully capture all the properties of CNNs, particularly when dealing with tasks involving uncertainty or risk. In [
40], the authors leverage the concept of stochastic ordering to provide a comprehensive comparison of neural networks. Similarly, we compare the proposed network architecture against established state-of-the-art models in the following paragraphs. Stochastic ordering allows us to assess which model offers a more favorable distribution of outcomes for the task at hand. This approach goes beyond traditional point estimates and provides valuable insights into the relative risk profiles and potential benefits of each tested architecture.
We applied this technique on our proposed network’s and established architectures (ResNet-50, DenseNet, Inception, EfficientNet, MobileNet). We leveraged the GZ2 dataset, randomly selecting 4511 images for evaluation. For each image, all six networks provided a prediction confidence value between 0 and 1. For each image, the statewise dominant is chosen based on the network that predicted the correct class with the highest confidence value. In stochastic ordering, a statewise dominant variable guarantees at least equal or better results compared with all others, with at least one scenario offering a strictly better outcome. This approach allowed us to analyze the distribution of confidence scores across the entire dataset. Also, this provides insights into which network consistently produces not only accurate classifications but also the most reliable confidence estimates for the task of galaxy morphology classification in the GZ2 dataset. Based on this stochastic ordering, other metrics are computed to further the understanding of the network’s performance. These metrics are the confidence mean, median, SD, and variation.
The proposed network demonstrates the highest count of dominant instances, with a total number of 2465 samples having the best confidence. This is more than half of the 4511 evaluated images, making it the “stochastic dominant”. This indicates that the network’s predictions were not only precise, but also the most confident (with the highest score) for a significant portion of the dataset in comparison to other models.
The proposed network also presents the highest average and median confidence with values of 0.9457 and 0.9992. This suggests a strong tendency to be highly confident in its classifications. The SD and coefficient of variation for the proposed network’s confidence scores also have the lowest values of 0.1129 and 0.0127. This shows a more consistent level of confidence across its predictions compared with other models.
An interesting event to be observed happens between the ResNet-50 and DenseNet networks. In
Table 9, even if the DenseNet architecture obtained more dominant instances, all the other metrics indicate that ResNet-50 is more reliable and consistent. This tells us that the ResNet-50 architecture is more confident and robust in its predictions, but DenseNet is a better network for a large number of detections.
According to the stochastic ordering analysis, the proposed network shows strong performance in categorizing galaxy morphology. It has a high frequency of dominant instances, indicating that its predictions are often the most confident and precise. Furthermore, the reduced variability in confidence scores suggests a consistent level of reliability in the network’s outputs.
5.3. Examples
To better showcase the results obtained by the proposed neural network, this section presents some prediction examples for the multi-class classification problem. This section also contains a comprehensive display of image examples representing all five distinct classes. The examples, analyzed and predicted by the proposed neural network, offer a visual aid to better asses the model’s strengths and weaknesses. They provide a visual understanding of its ability to discern and categorize various objects, patterns, or entities and showcase the challenges of the dataset itself.
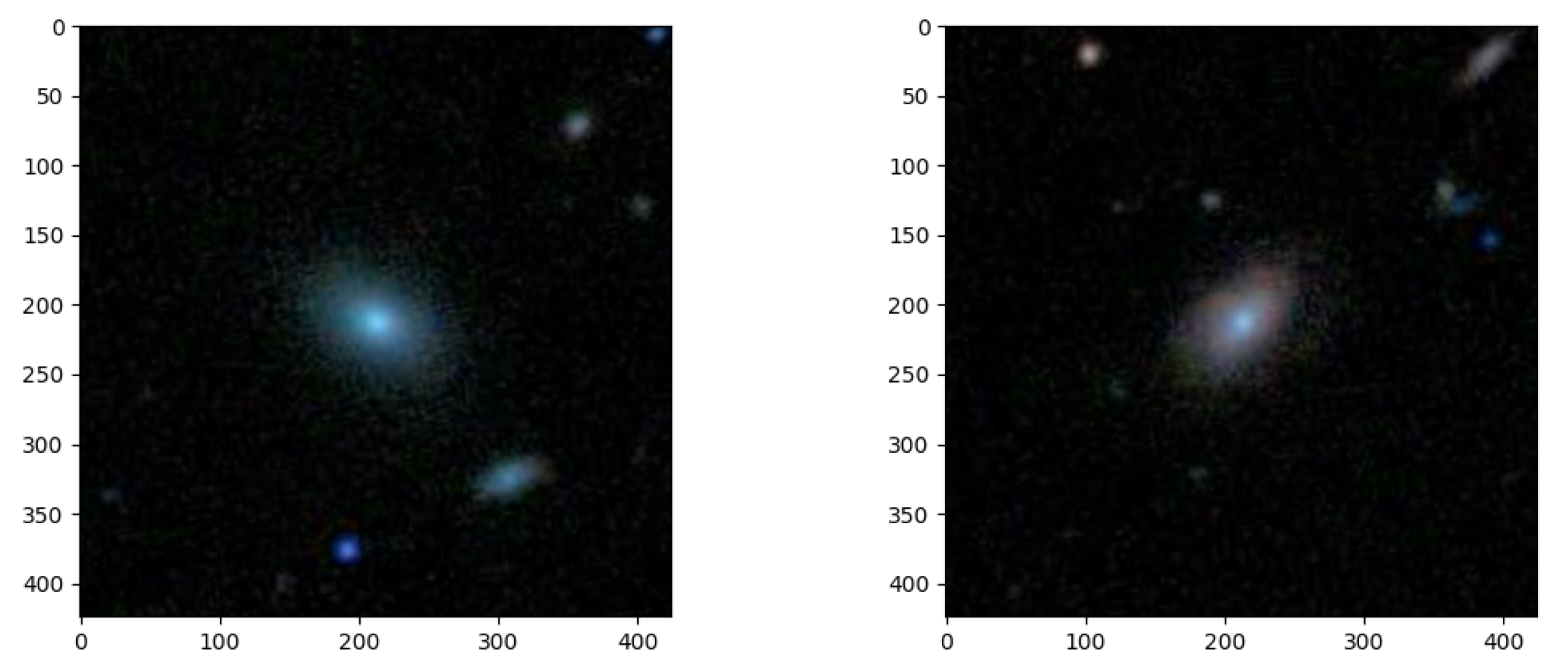
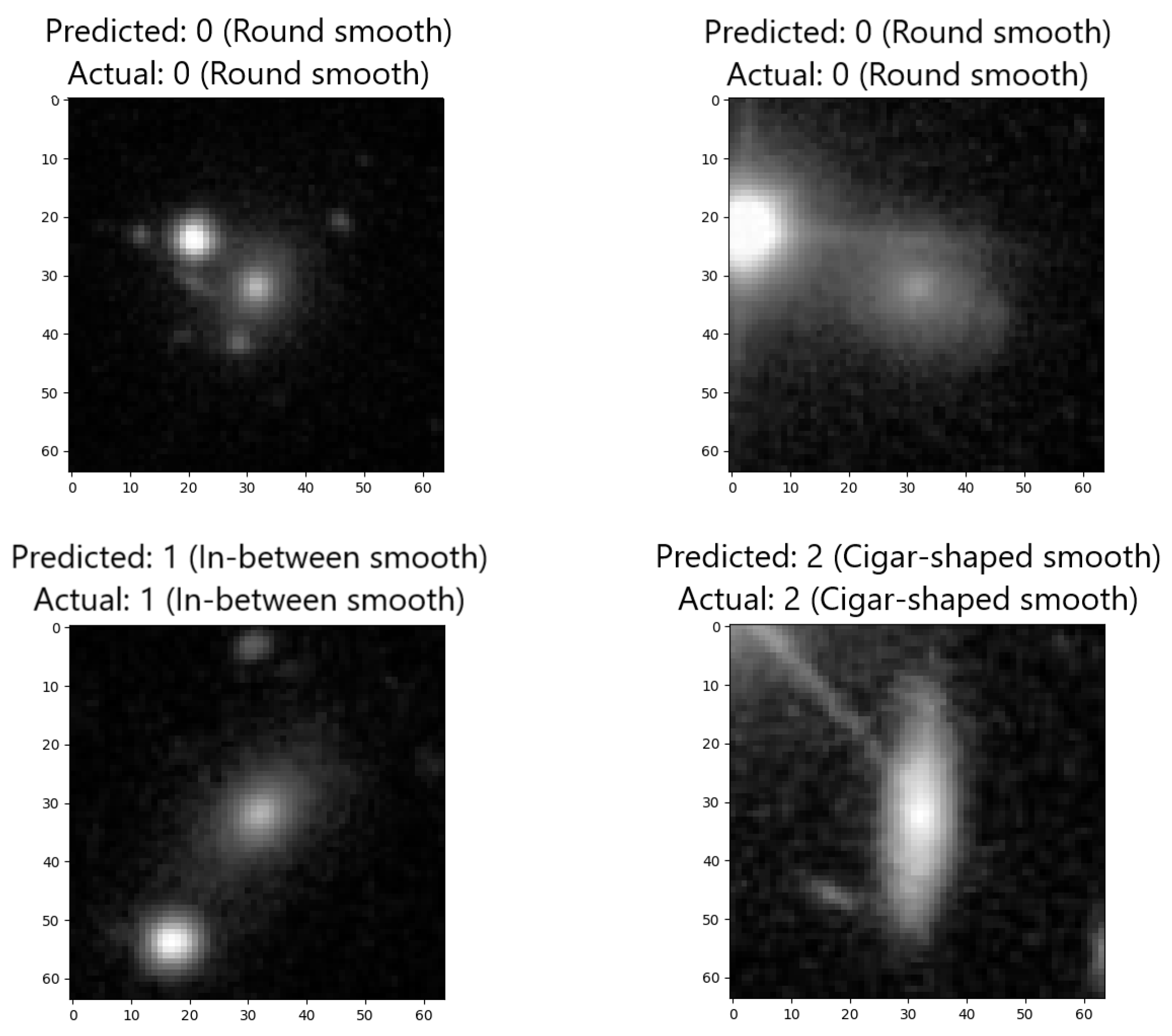
Among the predictions generated by our CNN, there exist instances that pose unique challenges due to the presence of artifacts or complexities within the images, cf.
Figure 9. These difficult, yet ultimately correct predictions showcase the model’s ability to understand subtle details and overcome visual challenges found in multi-class classification. In the face of artifacts, noise, or strange patterns that may confuse other systems, our neural network showcases its accuracy and adaptability. These successful classifications provide proof of the network’s robustness and its capacity to make well-informed decisions even when faced with challenging real-world data. Such capabilities are mandatory in applications where image quality and content can vary widely and where the presence of artifacts is a common occurrence. These challenging but accurate predictions exemplify the neural network’s potential to contribute to the advancement of various domains by providing reliable multi-class categorization, even in the presence of complex image artifacts.
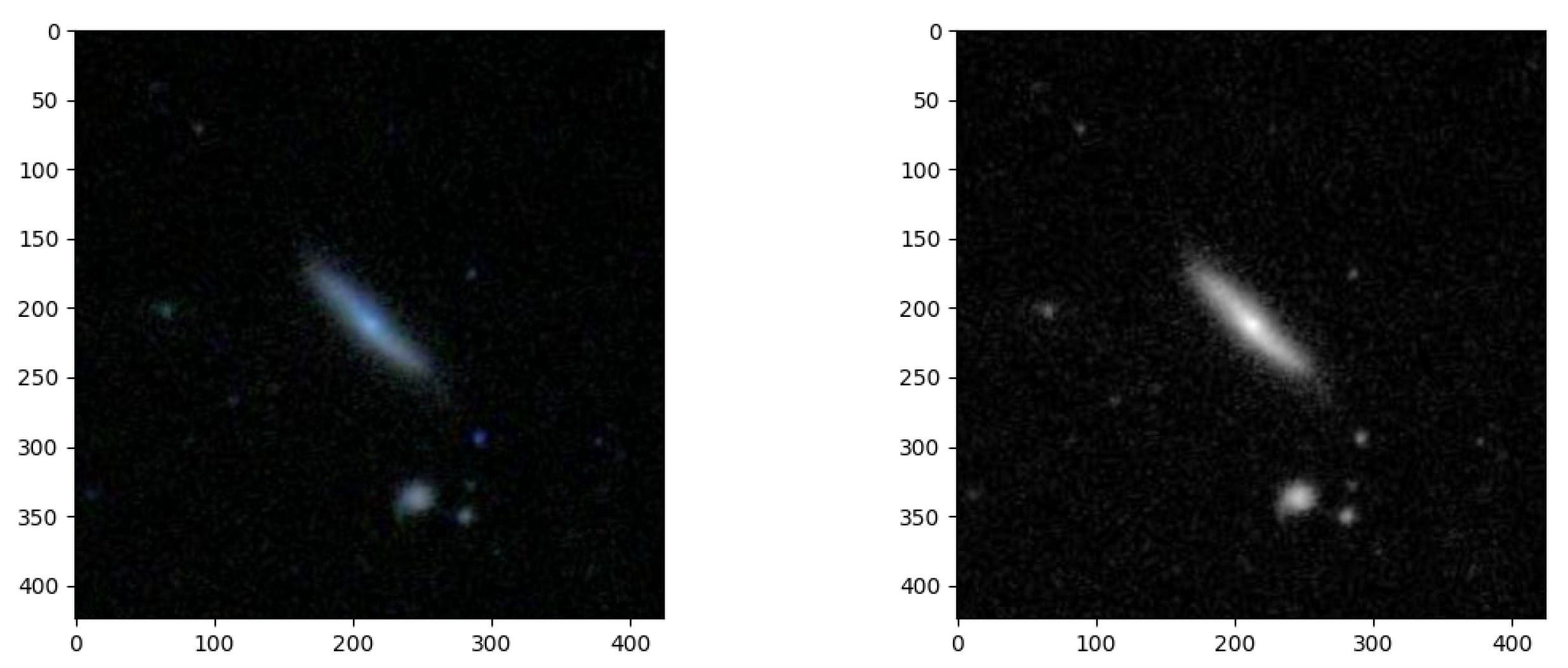
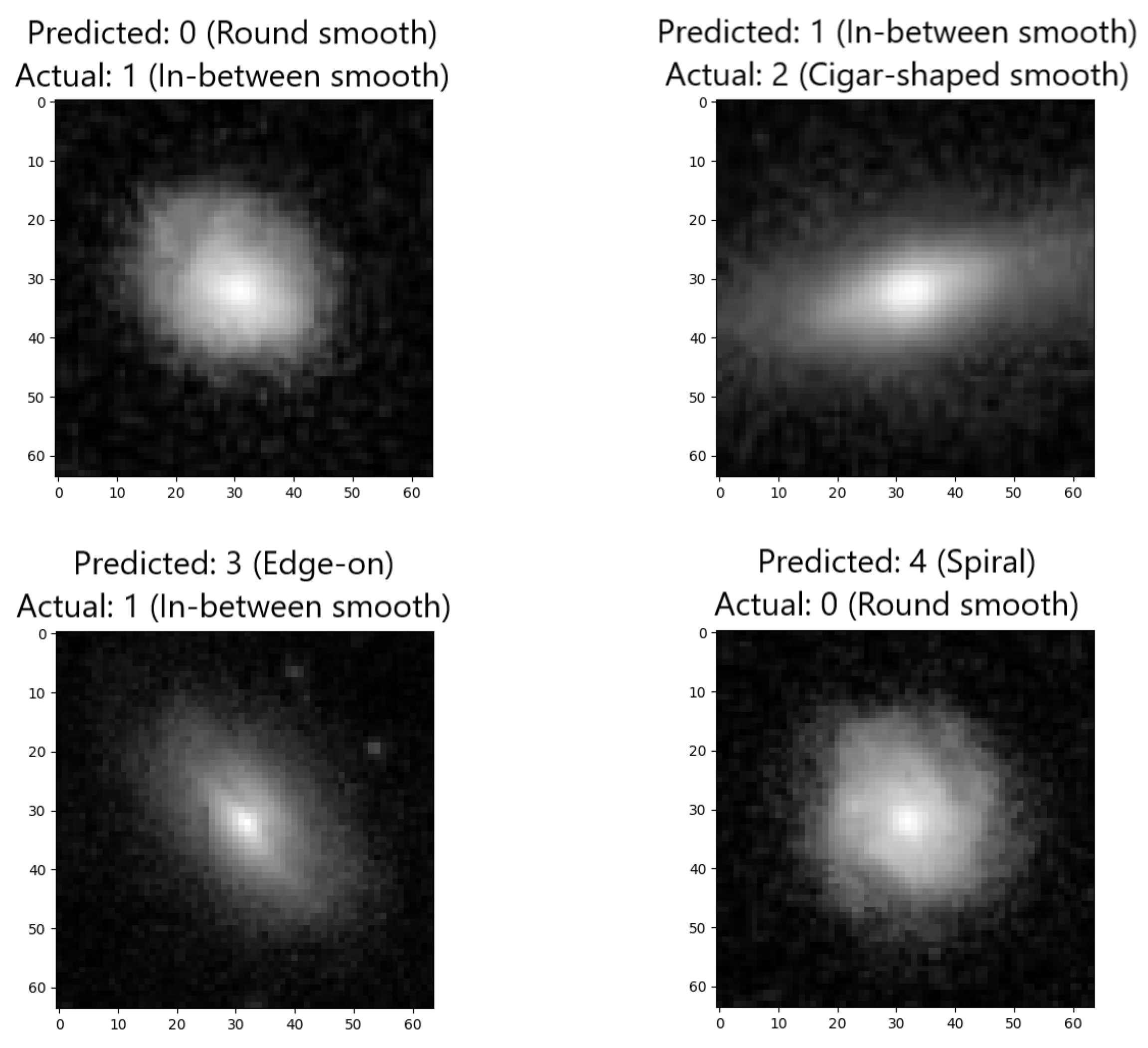
While the performance is satisfactory, occasional predictions were missed, as presented in
Figure 10. These instances, where the model assigns an incorrect label, provide insights into the boundaries of its capabilities and the complexity of real-world data. These missed predictions may appear due to complex image content, ambiguous patterns, or unexpected variations within the dataset. While they underscore the challenges associated with multi-class classification, they also drive us to continually refine and optimize the model. Understanding the nature of these missed predictions serves as valuable information for model improvement and fine-tuning. By addressing the details and complexities that lead to these cases, we aim to enhance the network’s robustness and further its potential in applications where precision and accuracy are key factors. These missed predictions remind us of the ongoing process to advance and better the state of the proposed network, promoting the development of more intelligent and adaptable neural networks.
To further evaluate the effectiveness of our proposed algorithm, we applied it to a set of 50 galaxy images obtained from the James Webb Space Telescope (JWST)’s deep field observations. By testing our algorithm on this challenging dataset containing previously unseen and potentially unique galaxy morphologies, we can assess its robustness and generalizability to a wider range of astronomical objects, compared with traditional datasets.
In [
41], the process used to obtain JWST’s images is explained. They are taken using various infrared filters and then combined. JWST utilizes its infrared cameras to acquire multiple grayscale intensity images. These images correspond to distinct wavelengths of infrared light, invisible to the human eye, captured through a set of six specialized filters. Following data acquisition, scientists assign a corresponding visible color to each filter’s dataset. The longest wavelengths are mapped to red, while the shortest wavelengths are assigned blue, with intermediate wavelengths represented by a spectrum of intervening colors. Finally, by combining these color-coded images, a composite image is produced, revealing the full spectrum of color observed in the now-famous astronomical photographs.
To prepare the data for analysis with our proposed algorithm, individual galaxies were extracted from the deep field image. Following extraction, each galaxy was cropped to isolate the object of interest. Finally, the cropped images were resized to a standardized size of 64 × 64 pixels and converted to a grayscale format to ensure compatibility with our model’s input requirements. The resulted images and the predictions of the network can be observed in
Figure 11.