Phantom Scalar Field Cosmologies Constrained by Early Cosmic Measurements
Abstract
1. Introduction
2. Phantom Scalar Field Cosmology Background
3. Methodology
Observational Baselines
- Late-time baselines:
- Supernovae Type Ia (SNIa) Pantheon: We used the 1048 data points provided by the Pantheon [57]. This baseline measures the apparent distance for several SNIa events in . Furthermore, this catalog provides SN magnitudes corrected for stretch and color effects along with the maximum brightness, the mass of the host galaxy, and sky position bias. To compute a cosmological useful quantity, we can calculate the distance modulus , where m is the apparent magnitude, and M is the absolute magnitude that is considered a fixed value for our analyses. Furthermore, the for the Pantheon sample iswhere is the total covariance matrix for the data, is the model vector parameter, S is the sum of all components of the inverse of the matrix, and , using . Furthermore, the distance modulus can be computed using the expressionand where is the luminosity distance given aswhere c is the speed of light and is the Hubble parameter.
- Cosmic clocks (CCs): This sample offers a good tool to constrain the Hubble rate at different z. To this end, the final catalog considered came from the differential age method [58]. In particular, we considered the Cosmick clocks 2016 catalog [59]. The CC method consists of using spectroscopic dating techniques on passively-evolving galaxies to compute the age difference between two galaxies at different z. By measuring this age difference, , we can compute . For our MCMC analysis, we computed to compare the agreement between the theoretical Hubble parameter values , with model parameters , and the observational Hubble data values , with an observational error of . Therefore, the is calculated using the following expression:
- Baryon Acoustic Oscillations (BAOs): In this work, we included measurements of the Hubble parameter and the corresponding comoving angular diameter at , which were obtained from the third generation of the SDSS mission (SDSS BOSS DR12) [60]. For this BAO baseline, we computed the Hubble distance given by . We also used the angular diameter distance given bywhere the first is the comoving angular diameter distance given trough , and the second one is the volume average distance given byAfterwards, we calculated the corresponding combination of results and . For this, we required the comoving sound horizon at the end of the baryon drag epoch at [15], which can be calculated throughwhere is the sound speed, and we have considered a fiducial value of [15] with an assumption of [15] and . The corresponding is given bywhere and is the corresponding covariance matrix for the BAO observations.
- Early-time baselines:
- Planck 2018: For these CMB observations, we took the high-ℓ TTTEE, low-ℓ EE, low-ℓ TT, and lensing likelihoods [15]. Furthermore, polarization and temperature TT-TE-EE baselines were used at high multipole likelihood Plik and at low multipoles TT-EE for .
- ACTPol DR-4: This is the third CMB catalog considered coming from the Data Release 4 measured by the Atacama Telescope (ACT) Collaboration [21]. To use this catalog along with MontePython, we utilised the pyactlike Python package devised by the ACT Collaboration (https://github.com/ACTCollaboration/pyactlike (accessed on 21 April 2022)). This likelihood also includes a Gaussian prior on .
- WMAP9: The final CMB catalog was the Wilkinson Microwave Anisotropy Probe and we took the results from the ninth year [53]. To use this catalog along with others in MontePython, we used the clik software 16.0 (https://github.com/benabed/clik (accessed on 12 March 2024)) that enabled us to install the WMAP9 likelihood and use it inside MontePython.
- Planck 2018+BAO+Pantheon+Cosmic clocks;
- SPT-3G+WMAP9+BAO+Pantheon+Cosmic clocks;
- ACTPol DR-4+WMAP9+BAO+Pantheon+Cosmic clocks.
4. Cosmological Tensions Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CDM | Lambda cold dark matter |
| CMB | Cosmic Microwave Background |
| SNeIa | Type Ia Supernovae |
| BAOs | Baryon Acoustic Oscillations |
References
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Jaffe, A.H.; Ade, P.A.R.; Balbi, A.; Bock, J.J.; Bond, J.R.; Borrill, J.; Boscaleri, A.; Coble, K.; Crill, B.P.; de Bernardis, P.; et al. Cosmology from MAXIMA-1, BOOMERANG and COBE/DMR CMB observations. Phys. Rev. Lett. 2001, 86, 3475–3479. [Google Scholar] [CrossRef] [PubMed]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.-J.; Tegmark, M.; Zheng, Z.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Anderson, L.; Aubourg, E.; Bailey, S.; Beutler, F.; Bhardwaj, V.; Blanton, M.; Bolton, A.S.; Brinkmann, J.; Brownstein, J.R.; Burden, A.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples. Mon. Not. Roy. Astron. Soc. 2014, 441, 24–62. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Abdalla, F.B.; Alarcon, A.; Allam, S.; Allen, S.; Amara, A.; Annis, J.; Asorey, J.; Avila, S.; Bacon, D.; et al. Dark Energy Survey year 1 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2018, 98, 043526. [Google Scholar] [CrossRef]
- Brout, D.; Scolnic, D.; Popovic, B.; Riess, A.G.; Carr, A.; Zuntz, J.; Kessler, R.; Davis, T.M.; Hinton, S.; Jones, D.; et al. The Pantheon+ Analysis: Cosmological Constraints. Astrophys. J. 2022, 938, 110. [Google Scholar] [CrossRef]
- Scolnic, D.; Perlmutter, S.; Aldering, G.; Brout, D.; Davis, T.; Filippenko, A.; Foley, R.; Hlozek, R.; Hounsell, R.; Jha, S.; et al. The Next Generation of Cosmological Measurements with Type Ia Supernovae. arXiv 2019, arXiv:1903.05128. [Google Scholar] [CrossRef]
- Lu, J.; Wang, L.; Chen, X.; Rubin, D.; Perlmutter, S.; Baade, D.; Mould, J.; Vinko, J.; Regős, E.; Koekemoer, A.M. Constraints on Cosmological Parameters with a Sample of Type Ia Supernovae from JWST. Astrophys. J. 2022, 941, 71. [Google Scholar] [CrossRef]
- Di Valentino, E.; Anchordoqui, L.A.; Akarsu, O.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Basilakos, S.; Battistelli, E.; et al. Cosmology Intertwined III: fσ8 and S8. Astropart. Phys. 2021, 131, 102604. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Planck evidence for a closed Universe and a possible crisis for cosmology. Nat. Astron. 2019, 4, 196–203. [Google Scholar] [CrossRef]
- Handley, W. Curvature tension: Evidence for a closed universe. Phys. Rev. D 2021, 103, L041301. [Google Scholar] [CrossRef]
- Di Valentino, E.; Anchordoqui, L.A.; Akarsu, O.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Basilakos, S.; Battistelli, E.; et al. Snowmass2021—Letter of interest cosmology intertwined IV: The age of the universe and its curvature. Astropart. Phys. 2021, 131, 102607. [Google Scholar] [CrossRef]
- Di Valentino, E.; Anchordoqui, L.A.; Akarsu, Ö.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Basilakos, S.; Battistelli, E.; et al. Snowmass2021—Letter of interest cosmology intertwined II: The hubble constant tension. Astropart. Phys. 2021, 131, 102605. [Google Scholar] [CrossRef]
- Aghanim, N.; Anchordoqui, L.A.; Akarsu, O.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Basilakos, S.; Battistelli, E.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Abdalla, E.; Abellán, G.F.; Aboubrahim, A.; Agnello, A.; Akarsu, O.; Akrami, Y.; Alestas, G.; Aloni, D.; Amendola, L.; Anchordoqui, L.A.; et al. Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies. JHEAp 2022, 34, 49–211. [Google Scholar] [CrossRef]
- Abbott, T.; Abdalla, F.B.; Aleksic, J.; Allam, A.; Amara, A.; Bacon, D.; Balbinot, E.; Banerji, M.; Bachtol, K.; Bernstein, M.; et al. The Dark Energy Survey: More than dark energy—An overview. Mon. Not. Roy. Astron. Soc. 2016, 460, 1270–1299. [Google Scholar] [CrossRef]
- Aghamousa, A.; Aguilar, J.; Ahlen, S.; Alam, S.; Allen, L.E.; Prieto, C.A.; Annis, J.; Bailey, S.; Balland, C.; Ballester, O.; et al. The DESI Experiment Part I: Science, Targeting, and Survey Design. arXiv 2016, arXiv:1611.00036. [Google Scholar]
- Mandelbaum, R.; Eifler, T.; Hlozek, R.; Collett, T.; Gawiser, E.; Scolnic, D.; Alonso, D.; Awan, H.; Biswas, R.; Blazek, J.; et al. The LSST Dark Energy Science Collaboration (DESC) Science Requirements Document. arXiv 2018, arXiv:1809.01669. [Google Scholar]
- Amendola, L.; Appleby, S.; Avgoustidis, A.; Bacon, D.; Baker, T.; Baldi, M.; Bartolo, N.; Blanchard, A.; Bonvin, C.; Borgani, S.; et al. Cosmology and fundamental physics with the Euclid satellite. Living Rev. Relativ. 2018, 21, 2. [Google Scholar] [CrossRef]
- Aiola, S.; Calabrese, E.; Maurin, L.; Naess, S.; Schmitt, B.L.; Abitbol, M.H.; Addison, G.E.; Ade, P.A.; Alonso, D.; Amiri, M.; et al. The Atacama Cosmology Telescope: DR4 maps and cosmological parameters. J. Cosmol. Astropart. Phys. 2020, 2020, 047. [Google Scholar] [CrossRef]
- Dutcher, D.; Balkenhol, L.; Ade, P.; Ahmed, Z.; Anderes, E.; Anderson, A.; Archipley, M.; Avva, J.; Aylor, K.; Barry, P.; et al. Measurements of the E-mode polarization and temperature-E-mode correlation of the CMB from SPT-3G 2018 data. Phys. Rev. D 2021, 104, 022003. [Google Scholar] [CrossRef]
- Escamilla-Rivera, C.; Capozziello, S. Unveiling cosmography from the dark energy equation of state. Int. J. Mod. Phys. D 2019, 28, 1950154. [Google Scholar] [CrossRef]
- Escamilla-Rivera, C. Status on bidimensional dark energy parameterizations using SNe Ia JLA and BAO datasets. Galaxies 2016, 4, 8. [Google Scholar] [CrossRef]
- Escamilla, L.A.; Giarè, W.; Di Valentino, E.; Nunes, R.C.; Vagnozzi, S. The state of the dark energy equation of state circa 2023. arXiv 2023, arXiv:2307.14802. [Google Scholar] [CrossRef]
- Escamilla-Rivera, C.; Nájera, A. Dynamical dark energy models in the light of gravitational-wave transient catalogues. JCAP 2022, 3, 060. [Google Scholar] [CrossRef]
- Escamilla-Rivera, C.; Quintero, M.A.C.; Capozziello, S. A deep learning approach to cosmological dark energy models. JCAP 2020, 3, 008. [Google Scholar] [CrossRef]
- Zhang, H.C. Dynamical dark energy can amplify the expansion rate of the Universe. Phys. Rev. D 2023, 107, 103529. [Google Scholar] [CrossRef]
- Jaime, L.G.; Jaber, M.; Escamilla-Rivera, C. New parametrized equation of state for dark energy surveys. Phys. Rev. D 2018, 98, 083530. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified Gravity and Cosmology. Phys. Rep. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Amendola, L.; Gannouji, R.; Polarski, D.; Tsujikawa, S. Conditions for the cosmological viability of f(R) dark energy models. Phys. Rev. D 2007, 75, 083504. [Google Scholar] [CrossRef]
- Bahamonde, S.; Dialektopoulos, K.F.; Escamilla-Rivera, C.; Farrugia, G.; Gakis, V.; Hendry, M.; Hohmann, M.; Levi Said, J.; Mifsud, J.; Di Valentino, E. Teleparallel gravity: From theory to cosmology. Rept. Prog. Phys. 2023, 86, 026901. [Google Scholar] [CrossRef] [PubMed]
- de Ritis, R.; Marino, A.A.; Rubano, C.; Scudellaro, P. Quintessence duality. Int. J. Mod. Phys. D 2001, 10, 921–926. [Google Scholar] [CrossRef]
- Alho, A.; Uggla, C.; Wainwright, J. Tracking Quintessence. Phys. Dark Univ. 2024, 44, 101433. [Google Scholar] [CrossRef]
- Banerjee, A.; Cai, H.; Heisenberg, L.; Colgáin, E.Ó.; Sheikh-Jabbari, M.M.; Yang, T. Hubble sinks in the low-redshift swampland. Phys. Rev. D 2021, 103, L081305. [Google Scholar] [CrossRef]
- Lee, B.H.; Lee, W.; Colgáin, E.Ó.; Sheikh-Jabbari, M.; Thakur, S. Is local H 0 at odds with dark energy EFT? J. Cosmol. Astropart. Phys. 2022, 2022, 004. [Google Scholar] [CrossRef]
- Cai, Y.F.; Saridakis, E.N.; Setare, M.R.; Xia, J.Q. Quintom cosmology: Theoretical implications and observations. Phys. Rep. 2010, 493, 1–60. [Google Scholar] [CrossRef]
- Setare, M.; Saridakis, E. Coupled oscillators as models of quintom dark energy. Phys. Lett. B 2008, 668, 177–181. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Teng, Y.P.; Lee, W.; Ng, K.W. Constraining the dark-energy equation of state with cosmological data. Phys. Rev. D 2021, 104, 083519. [Google Scholar] [CrossRef]
- Gangopadhyay, M.R.; Sami, M.; Sharma, M.K. Phantom dark energy as a natural selection of evolutionary processes â la genetic algorithm and cosmological tensions. Phys. Rev. D 2023, 108, 103526. [Google Scholar] [CrossRef]
- Yashar, M.; Bozek, B.; Abrahamse, A.; Albrecht, A.; Barnard, M. Exploring Parameter Constraints on Quintessential Dark Energy: The Inverse Power Law Model. Phys. Rev. D 2009, 79, 103004. [Google Scholar] [CrossRef]
- Ureña López, L.A.; Roy, N. Generalized tracker quintessence models for dark energy. Phys. Rev. D 2020, 102, 063510. [Google Scholar] [CrossRef]
- Roy, N.; Ureña López, L.A. Tracker behaviour of quintom dark energy and the Hubble tension. arXiv 2023, arXiv:2312.04003. [Google Scholar]
- Adil, A.; Albrecht, A.; Knox, L. Quintessential cosmological tensions. Phys. Rev. D 2023, 107, 063521. [Google Scholar] [CrossRef]
- Copeland, E.J.; Moss, A.; Sevillano Muñoz, S.; White, J.M.M. Scaling solutions as Early Dark Energy resolutions to the Hubble tension. arXiv 2023, arXiv:2309.15295. [Google Scholar] [CrossRef]
- Caldwell, R.R. A phantom menace? Cosmological consequences of a dark energy component with super-negative equation of state. Phys. Lett. B 2002, 545, 23–29. [Google Scholar] [CrossRef]
- Ratra, B.; Peebles, P.J. Cosmological consequences of a rolling homogeneous scalar field. Phys. Rev. D 1988, 37, 3406. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Wang, L.; Zlatev, I. Cosmological tracking solutions. Phys. Rev. D 1999, 59, 123504. [Google Scholar] [CrossRef]
- Roy, N.; Gonzalez-Morales, A.X.; Ureña-López, L.A. New general parametrization of quintessence fields and its observational constraints. Phys. Rev. D 2018, 98, 063530. [Google Scholar] [CrossRef]
- Cedeño, F.X.L.; Roy, N.; Ureña-López, L.A. Tracker phantom field and a cosmological constant: Dynamics of a composite dark energy model. Phys. Rev. D 2021, 104, 123502. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Anand, G.S.; Breuval, L.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km s- 1 Mpc- 1 Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.; Dunkley, J.; Nolta, M.; Halpern, M.; Hill, R.; Odegard, N.; et al. Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Cosmological parameter results. Astrophys. J. Suppl. Ser. 2013, 208, 19. [Google Scholar] [CrossRef]
- Blas, D.; Lesgourgues, J.; Tram, T. The cosmic linear anisotropy solving system (CLASS). Part II: Approximation schemes. J. Cosmol. Astropart. Phys. 2011, 2011, 034. [Google Scholar] [CrossRef]
- Audren, B.; Lesgourgues, J.; Benabed, K.; Prunet, S. Conservative constraints on early cosmology with MONTE PYTHON. J. Cosmol. Astropart. Phys. 2013, 2013, 001. [Google Scholar] [CrossRef]
- Brinckmann, T.; Lesgourgues, J. MontePython 3: Boosted MCMC sampler and other features. Phys. Dark Universe 2019, 24, 100260. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.; Rest, A.; Pan, Y.; Chornock, R.; Foley, R.; Huber, M.; Kessler, R.; Narayan, G.; Riess, A.; et al. The complete light-curve sample of spectroscopically confirmed SNe Ia from Pan-STARRS1 and cosmological constraints from the combined pantheon sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Jimenez, R.; Loeb, A. Constraining cosmological parameters based on relative galaxy ages. Astrophys. J. 2002, 573, 37. [Google Scholar] [CrossRef]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jimenez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D. A 6% measurement of the Hubble parameter at z 0.45: Direct evidence of the epoch of cosmic re-acceleration. J. Cosmol. Astropart. Phys. 2016, 2016, 014. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.H.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. R. Astron. Soc. 2017, 470, 2617–2652. [Google Scholar] [CrossRef]
- Chudaykin, A.; Gorbunov, D.; Nedelko, N. Exploring Λ CDM extensions with SPT-3G and Planck data: 4σ evidence for neutrino masses, full resolution of the Hubble crisis by dark energy with phantom crossing, and all that. arXiv 2022, arXiv:2203.03666. [Google Scholar]
- Gelman, A.; Rubin, D.B. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Sharma, M.K.; Pacif, S.K.J.; Yergaliyeva, G.; Yesmakhanova, K. The Oscillatory Universe, phantom crossing and the Hubble tension. Ann. Phys. 2023, 454, 169345. [Google Scholar] [CrossRef]

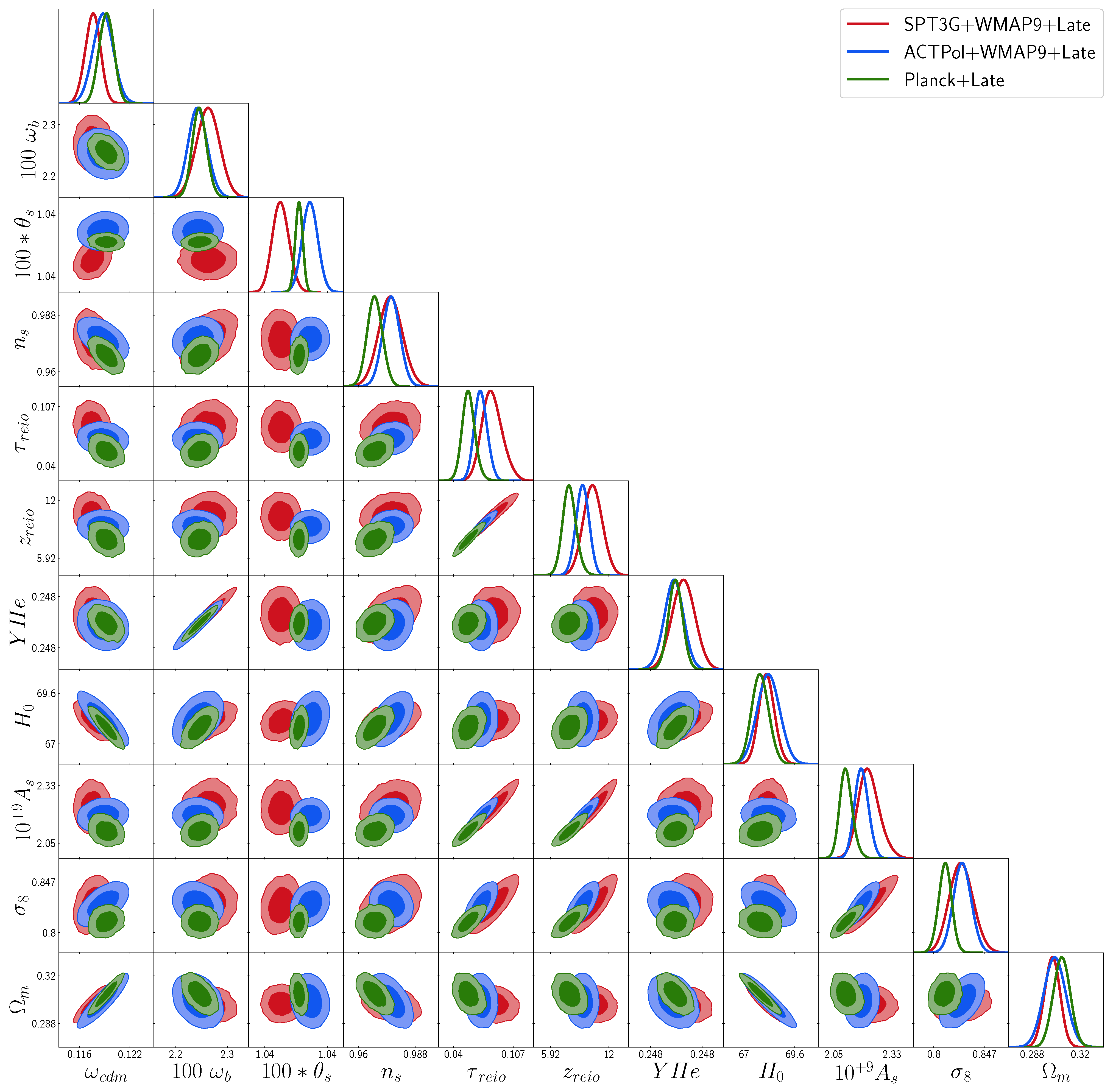
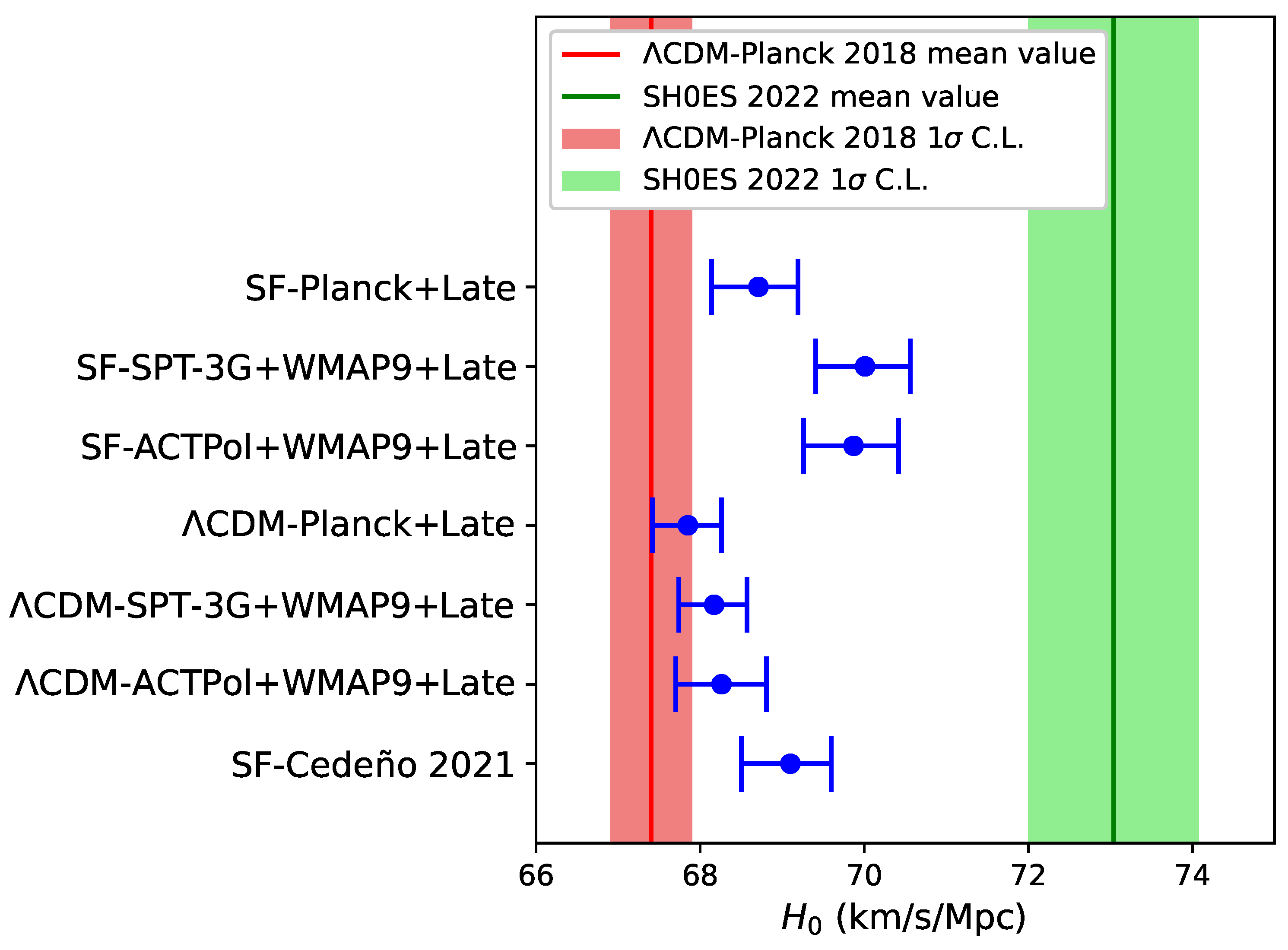
| Parameter | Planck 2018+Late | SPT-3G+WMAP9+Late | ACTPol DR-4+WMAP9+Late |
|---|---|---|---|
| 4.01 | 2.80 | 2.92 |
| Parameter | Planck 2018+Late | SPT-3G+WMAP9+Late | ACTPol DR-4+WMAP9+Late |
|---|---|---|---|
| 4.87 | 4.60 | 4.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nájera, J.A.; Escamilla-Rivera, C. Phantom Scalar Field Cosmologies Constrained by Early Cosmic Measurements. Universe 2024, 10, 232. https://doi.org/10.3390/universe10060232
Nájera JA, Escamilla-Rivera C. Phantom Scalar Field Cosmologies Constrained by Early Cosmic Measurements. Universe. 2024; 10(6):232. https://doi.org/10.3390/universe10060232
Chicago/Turabian StyleNájera, José Antonio, and Celia Escamilla-Rivera. 2024. "Phantom Scalar Field Cosmologies Constrained by Early Cosmic Measurements" Universe 10, no. 6: 232. https://doi.org/10.3390/universe10060232
APA StyleNájera, J. A., & Escamilla-Rivera, C. (2024). Phantom Scalar Field Cosmologies Constrained by Early Cosmic Measurements. Universe, 10(6), 232. https://doi.org/10.3390/universe10060232







