Thermodynamics of Magnetic Black Holes with Nonlinear Electrodynamics in Extended Phase Space

Abstract

We study Einstein’s gravity in AdS space coupled to nonlinear electrodynamics. Thermodynamics in extended phase space of magnetically charged black holes is investigated. We compute the metric and mass functions and their asymptotics, showing that black holes may have one or two horizons. The metric function is regular, $f\left(0\right)=1$, and corrections to the Reissner–Nordström solution are in the order of $\mathcal{O}\left(r^{-3}\right)$ when the Schwarzschild mass is zero. We prove that the first law of black hole thermodynamics and the generalized Smarr relation hold. The magnetic potential and vacuum polarization conjugated to coupling are computed and depicted. We calculate the Gibbs free energy and the heat capacity showing that first-order and second-order phase transitions take place.

1. Introduction

Black hole thermodynamics has been of great interest in recent decades [1,2,3]. It was understood that the black hole area corresponds to the entropy, and the temperature is connected to surface gravity [4,5]. Later, researchers reached the conclusion that black hole thermodynamic properties possess rich phase structures with critical phenomena similar to ordinary thermodynamics. To formulate the first law of black hole thermodynamics, including the $VdP$ term, it was necessary to introduce a negative cosmological constant as the positive pressure. As a result, one comes to Anti de Sitter (AdS) space. Einstein’s gravity in AdS space is of interest because of a gauge duality description (the holographic principle) [6] that possesses some applications in condensed matter physics. The correspondence of quantum field theory to AdS gravity allows us to study the behavior of quark–gluon plasma and other condensed matter phenomena. Hawking and Page [7] studied phase transitions in the phase space of non-rotating uncharged Schwarzschild–AdS black holes. Then, their work was extended to study more complicated backgrounds [8,9]. The first-order phase transitions were discovered in Refs. [10,11] for charged and non-rotating Reissner–Nordström black holes in AdS spacetime. Such transitions show the classical critical behavior which is similar to van der Waals liquid–gas phase transitions. To formulate the first law of black hole thermodynamics, the cosmological constant has to be variable [12,13,14,15,16,17,18]. But in Einstein–AdS gravity, the cosmological constant is a constant parameter. Therefore, an alteration in the cosmological constant can be treated as a consideration of black hole ensembles having different asymptotics. The cosmological constant represents a vacuum energy which can be altered. Therefore, $\Lambda$ can enter the first law of black hole thermodynamics [19,20]. But if the cosmological constant is a real constant, the Smarr relation does not hold [21], and neither does the first law of black hole thermodynamics [13]. When $\Lambda$ is included in the first law of black hole thermodynamics, the black hole mass M has to be considered as enthalpy [13]. In this case, $\Lambda$ corresponds to positive pressure, $P=-\Lambda /\left(8\pi \right)$ ($\Lambda$ is negative for AdS space), and its conjugate variable is the volume $V=4\pi r_{+}^3/3$, where $r_{+}$ is the event horizon radius of a black hole [22,23,24].

In this work, we investigate Einstein–AdS theory coupled to nonlinear electrodynamics (NED) to smooth out singularities which are present in linear Maxwell electrodynamics. For the weak-field limit, our NED is converted into Maxwell’s theory. Born—Infeld (BI) electrodynamics [25] was the first form of NED without the singularities of point-like charges, and it has finite electric self-energy. In weak fields, BI electrodynamics becomes Maxwell’s electrodynamics. The black hole solutions in Einstein’s gravity coupled to BI NED was studied in Refs. [26,27,28,29,30,31]. In quantum electrodynamics, loop corrections to Maxwell’s electrodynamics, due to the virtual creation of electron–positron pairs, lead to NED [32]. The one-parameter NED explored in this paper is a particular case of a more general form of two-parameter NED [33]. Solutions obtained in this work are expressed through elementary functions compared to solutions in [33] in the form of special functions. Therefore, formulas for the Hawking temperature, EoS, heat capacity, and Gibbs free energy are in the form of elementary functions. As a result, the analysis in this work is more transparent.

The paper is structured as follows: In Section 2, we find the black hole solution in Einstein–AdS gravity coupled to nonlinear electrodynamics. The metric and mass functions and their asymptotics are obtained. We show that the black hole magnetic mass is finite. Corrections to the Reissner–Nordström metric, when the cosmological constant vanishes, are found. The first law of black hole thermodynamics and Smarr relation are formulated in Section 3. The magnetic potential and a conjugate to coupling are computed and plotted. In Section 4, to study the local stability, we calculate the heat capacity and investigate the phase transitions. We compute the Gibbs free energy, critical temperatures, and pressures. Phase transitions of the first and second order are investigated. Section 5 is devoted to a summary.

The units with $c=\hslash =1$ are employed.

2. Black Hole Solution in Einstein–AdS Theory

The Einstein’s gravity in AdS space is described by the action

$$I=\int d^{4}x\sqrt{-g}\left(\frac{R-2\Lambda }{16\pi G_N}+\mathcal{L}\left(\mathcal{F}\right)\right),$$

(1)

where $\Lambda =-3/l^2$ is the negative cosmological constant and l is the AdS radius. Here, we employ the source of gravity to be NED with the Lagrangian [34,35]

$$\mathcal{L}=-\frac{\mathcal{F}}{4\pi {(1+2\beta \mathcal{F})}^2}.$$

(2)

$\mathcal{F}=F^{\mu \nu }{F}_{\mu \nu }/4=(B^2-E^2)/2$, and E and B being the electric and magnetic fields, respectively. At the weak-field limit, Lagrangian (2) becomes Maxwell’s Lagrangian. Einstein’s and field equations follow from action (1),

$$R_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }R+\Lambda g_{\mu \nu }=8\pi G_N{T}_{\mu \nu },$$

(3)

$${\partial }_{\mu }\left(\sqrt{-g}{\mathcal{L}}_{\mathcal{F}}{F}^{\mu \nu }\right)=0,$$

(4)

with ${\mathcal{L}}_{\mathcal{F}}=\partial \mathcal{L}\left(\mathcal{F}\right)/\partial \mathcal{F}$. The energy–momentum tensor is given by

$$T_{\mu \nu }=F_{\mu \rho }{F}_{\nu }^{\rho }{\mathcal{L}}_{\mathcal{F}}+g_{\mu \nu }\mathcal{L}\left(\mathcal{F}\right).$$

(5)

We will study spherical symmetrical solutions of Einstein’s Equation (3) with the line element squared

$$d{s}^2=-f\left(r\right)d{t}^2+\frac{1}{f\left(r\right)}d{r}^2+r^2\left(d{\theta }^2+{sin}^2\left(\theta \right)d{\varphi }^2\right).$$

(6)

Let us consider black holes as a magnetic monopole possessing the magnetic field $B=q/r^2$, and q is the magnetic charge. The metric function can be found as [36]

$$f\left(r\right)=1-\frac{2m\left(r\right)G_N}{r},$$

(7)

where the mass function is given by

$$m\left(r\right)=m_0+4\pi \int \rho \left(r\right)r^{2}dr.$$

(8)

The $m_0$ is the Schwarzschild mass (an integration constant), and $\rho$ is the total energy density. From Equation (5), we find the magnetic energy density ${\rho }_m$. Then, the total energy density is given by

$$\rho ={\rho }_m-\frac{3}{8\pi G_N{l}^2},{\rho }_m=\frac{q^2{r}^4}{8\pi {(r^4+q^2\beta )}^2}.$$

(9)

Making use of Equations (8) and (9), one obtains the mass function

$$m\left(r\right)=m_0+\frac{q^{2}g\left(r\right)}{64}-\frac{r^3}{2G_N{l}^2},$$

$$g\left(r\right)=\frac{3\sqrt{2}}{\sqrt[4]{q^2\beta }}ln\frac{r^2-\sqrt{2}\sqrt[4]{q^2\beta }r+q\sqrt{\beta }}{r^2+\sqrt{2}\sqrt[4]{q^2\beta }r+q\sqrt{\beta }}-\frac{8r^3}{r^4+q^2\beta }$$

$$-\frac{6\sqrt{2}}{\sqrt[4]{q^2\beta }}\left(arctan\left(1-\frac{\sqrt{2}r}{\sqrt[4]{q^2\beta }}\right)-arctan\left(1+\frac{\sqrt{2}r}{\sqrt[4]{q^2\beta }}\right)\right).$$

(10)

By virtue of Equations (7) and (10), we obtain the metric function

$$f\left(r\right)=1-\frac{2m_0{G}_N}{r}-\frac{q^2{G}_{N}g\left(r\right)}{32r}+\frac{r^2}{l^2}.$$

(11)

Then, one finds the asymptotic as $r\to 0$, when the Schwarzschild mass is zero ($m_0=0$),

$$f\left(r\right)=1+\frac{r^2}{l^2}-\frac{G_N{r}^6}{7q^2{\beta }^2}+\frac{2G_N{r}^{10}}{11q^4{\beta }^3}+\mathcal{O}\left(r^{14}\right),$$

(12)

From Equation (12), we obtain $f\left(0\right)=1$, which is a necessary condition for regular spacetime. When $\Lambda =0$ ($l\to \infty$) and as $r\to \infty$ one finds from Equation (11)

$$f\left(r\right)=1-\frac{2M{G}_N}{r}+\frac{q^2{G}_N}{r^2}+\mathcal{O}\left(r^{-3}\right),$$

(13)

were ADM mass is $M=m_0+m_m$ and the magnetic mass is given by

$$m_m=4\pi {\int }_0^{\infty }{\rho }_m\left(r\right)r^{2}dr=\frac{3\sqrt{2}\pi q^{3/2}}{32{\beta }^{1/4}}\approx \frac{0.417q^{3/2}}{{\beta }^{1/4}}.$$

(14)

Equation (13) shows that black holes have corrections to the Reissner–Nordström solution in the order of $\mathcal{O}\left(r^{-3}\right)$. In the limit $\beta \to 0$ Equation (13) becomes the metric function of Reissner–Nordström spacetime. The plot of metric function (11) is depicted in Figure 1 at $m_0=0$, $G_N=1$, $q=1$, and $l=10$.

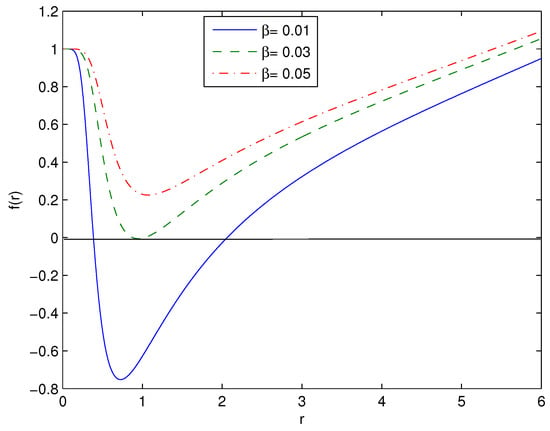
Figure 1. The function $f\left(r\right)$ at $m_0=0$, $G_N=1$, $q=1$, and $l=10$. Figure 1 shows that black holes could have one or two horizons.

According to Figure 1, when parameter $\beta$ increases, the event horizon radius decreases. In accordance with Figure 1, black holes can have one or two horizons.

3. First Law of Black Hole Thermodynamics and Smarr Relation

The pressure in extended phase space thermodynamics is given by $P=-\Lambda /\left(8\pi \right)$ [8,13,15,37,38], and $\beta$ represents the thermodynamic value. The black hole mass M should be treated as the enthalpy, $M=U+PV$, where U is the internal energy. Note that in general relativity, the ADM mass is a notion of total mass contained in asymptotically flat spacetime, but AdS is not asymptotically flat space. In AdS space and in extended phase space, the M is the enthalpy and is not ADM mass. For this case, instead of ADM mass, one can consider the internal energy of a black hole, which is $U=M-PV$. With the help of Euler’s dimensional analysis with $G_N=1$ [13,21], one finds that

$$M=2S\frac{\partial M}{\partial S}-2P\frac{\partial M}{\partial P}+q\frac{\partial M}{\partial q}+2\beta \frac{\partial M}{\partial \beta },$$

(15)

and we do not consider rotational black holes. The so-called vacuum polarization is the thermodynamic conjugate to coupling $\beta$ [23] $\mathcal{B}=\partial M/\partial \beta$. The black hole entropy S, volume V, and pressure P are given by

$$S=\pi r_{+}^2,V=\frac{4}{3}\pi r_{+}^3,P=-\frac{\Lambda }{8\pi }=\frac{3}{8\pi l^2}.$$

(16)

From Equations (11) and (14) and equation $f\left(r_{+}\right)=0$, defining the event horizon radius $r_{+}$, we obtain

$$M\left(r_{+}\right)=\frac{r_{+}}{2G_N}+\frac{r_{+}^3}{2G_N{l}^2}-\frac{q^{2}g\left(r_{+}\right)}{64}+\frac{3\sqrt{2}\pi q^{3/2}}{32{\beta }^{1/4}}.$$

(17)

The Hawking temperature is defined by the relation

$$T=\frac{f^{\prime }{\left(r\right)|}_{r=r_{+}}}{4\pi },$$

(18)

where $f^{\prime }\left(r\right)=\partial f\left(r\right)/\partial r$. Making use of Equations (11) and (18), one obtains the Hawking temperature

$$T\left(r_{+}\right)=\frac{1}{4\pi }\left[\frac{1}{r_{+}}+\frac{3r_{+}}{l^2}-\frac{q^2{r}_{+}^5}{{(r_{+}^4+q^2\beta )}^2}\right].$$

(19)

At the limit $\beta \to 0$, Equation (19) becomes the Hawking temperature of a Maxwell-AdS black hole. With the help of Equations (16), (17), and (19), we obtain the first law of black hole thermodynamics

$$dM=TdS+VdP+\Phi dq+\mathcal{B}d\beta .$$

(20)

Making use of Equations (17) and (20), one finds the magnetic potential $\Phi$ and the vacuum polarization $\mathcal{B}$ as follows:

$$\Phi =\frac{\partial M}{\partial q}=\frac{q{r}_{+}^7}{4{(r_{+}^4+q^2\beta )}^2}-\frac{3qg\left(r_{+}\right)}{128}+\frac{9\sqrt{2}\pi \sqrt{q}}{64{\beta }^{1/4}},$$

$$\mathcal{B}=\frac{\partial M}{\partial \beta }=\frac{q^2{r}_{+}^7}{8\beta {(r_{+}^4+q^2\beta )}^2}-\frac{3\sqrt{2}\pi q^{3/2}}{128{\beta }^{5/4}}+\frac{q^{2}g\left(r_{+}\right)}{256}.$$

(21)

The functions $\Phi$ and $\mathcal{B}$ versus $r_{+}$ are depicted in Figure 2.

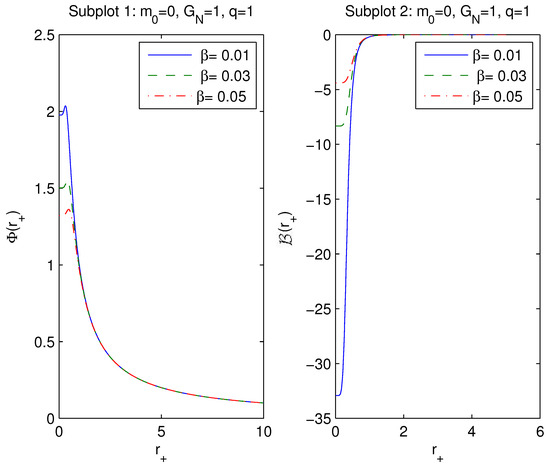
Figure 2. The functions $\Phi$ and $\mathcal{B}$ vs. $r_{+}$ at $q=1$. The solid curve in subplot 1 is for $\beta =0.01$, the dashed curve is for $\beta =0.03$, and the dashed–dotted curve is for $\beta =0.05$. It follows that the magnetic potential $\Phi$ is finite at $r_{+}=0$ and becomes zero as $r_{+}\to \infty$. The function $\mathcal{B}$ in subplot 2 vanishes as $r_{+}\to \infty$ and is finite at $r_{+}=0$.

The left panel of Figure 2 shows that as $r_{+}\to \infty$, the $\Phi$ goes to zero ($\Phi (\infty )=0$), and $\Phi$ is finite at $r_{+}=0$. If the parameter $\beta$ increases, the magnetic potential decreases. In accordance with the right panel of Figure 2, the vacuum polarization is finite at $r_{+}=0$, and $\mathcal{B}$ becomes zero as $r_{+}\to \infty$ ($\mathcal{B}(\infty )=0$). If the coupling $\beta$ increases, $\mathcal{B}\left(0\right)$ also increases. By virtue of Equations (16), (19), and (21), we obtain the generalized Smarr relation

$$M=2ST-2PV+q\Phi +2\beta \mathcal{B}.$$

(22)

4. Thermodynamics of Black Hole

The local stability of black holes can be investigated by analyzing the heat capacity that is given by

$$C_q=T{\left(\frac{\partial S}{\partial T}\right)}_q=\frac{T\partial S/\partial r_{+}}{\partial T/\partial r_{+}}=\frac{2\pi r_{+}T}{G_N\partial T/\partial r_{+}}.$$

(23)

Making use of Equation (19), we depict the Hawking temperature in Figure 3.

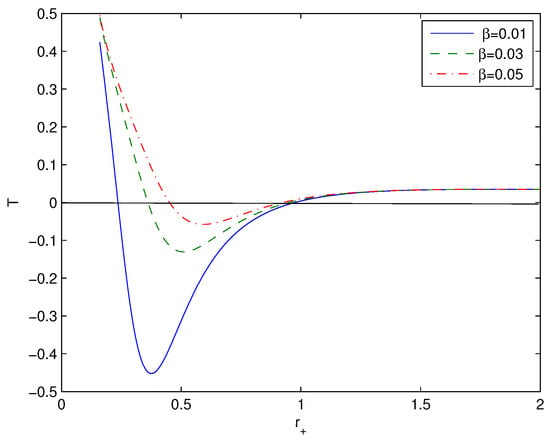
Figure 3. The functions T vs. $r_{+}$ at $q=1$ and $l=10$. The solid curve is for $\beta =0.01$, the dashed curve is for $\beta =0.03$, and the dashed–dotted curve is for $\beta =0.05$. In some range of $r_{+}$, the Hawking temperature is negative where black holes do not exist. In the extremum of the Hawking temperature, phase transitions take place.

In accordance with Equation (23), the heat capacity has a singularity when the Hawking temperature possesses an extremum. In this case, the black hole phase transition occurs. From Equation (19), we obtain

$$\frac{\partial T}{\partial r_{+}}=\frac{1}{4\pi }\left[-\frac{1}{r_{+}^2}+\frac{3}{l^2}-\frac{q^2{r}_{+}^4(5q^2\beta -3r_{+}^4)}{{(r_{+}^4+q^2\beta )}^3}\right].$$

(24)

The heat capacity (23) is defined by Equations (19) and (24). In Figure 4, we depict the heat capacity (23) versus $r_{+}$.

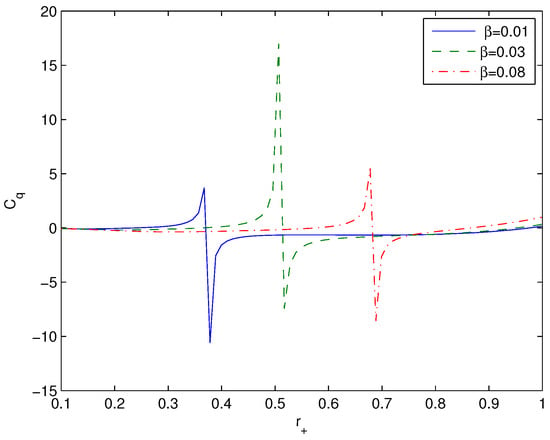
Figure 4. The functions $C_q$ vs. $r_{+}$ at $q=1$ and $l=10$. The solid curve is for $\beta =0.01$, the dashed curve is for $\beta =0.03$, and the dashed–dotted curve is for $\beta =0.08$. In points where second-order phase transitions take place, the heat capacity diverges.

Figure 4 shows that second-order phase transitions in the canonical ensemble occur where there are singularities of the heat capacity. Zeros of the heat capacity occur when the Hawking temperature vanishes (see Equation (19)) and correspond to first-order phase transitions. It follows from Equation (23) that the heat capacity is zero when the Hawking temperature is zero. In Table 1 and Table 2, we present approximate solutions for the heat capacity of zero and infinity, respectively.

Table 1. $C_q=0$, $q=1$, and $l=10$.

$\beta$	0.01	0.03	0.05
$r_{+}$	0.2357	0.3611	0.4507

Table 2. $C_q=\infty$, $q=1$, and $l=10$.

$\beta$	0.01	0.03	0.05
$r_{+}$	0.3752	0.5097	0.5921

From Table 1 and Table 2, we observe that for intervals $0.3752>r_{+}>0.2357$ ($\beta =0.01$), $0.5097>r_{+}>0.3611$ ($\beta =0.03$), and $0.5921>r_{+}>0.4507$ ($\beta =0.05$), the heat capacity is positive. When the heat capacity is positive, a black hole is locally stable; otherwise, it is unstable. It is worth noting that the Hawking temperature is negative in Figure 3, and, therefore, in such parameters black holes do not exist. As a result, the example presented in Figure 4 corresponds to a non-physical situation. It is worth noting that in the canonical ensemble, the charge q, pressure, and $\beta$ are fixed, and the Hessian matrix has only one component, ${\mathbf{H}}_{S,S}^M={\partial }^{2}M/\partial S^2$. In addition, the Hessian matrix is a function of the heat capacity $C_q$, ${\mathbf{H}}_{S,S}^M=T/C_q$. Therefore, if the heat capacity is positive, $T>0$, and ${\mathbf{H}}_{S,S}^M>0$, one has the local thermal stability in the phase space [39,40]. It should be stressed that to verify the local thermodynamic stability in extended phase space, one has to consider the full Hessian matrix of the system. The stability requirement is ${\mathbf{H}}_{Q_A,Q_B}^M\ge 0$, where $Q_A=S,q,P,\beta$. To find the region of thermodynamic stability, $\det \left[{\mathbf{H}}_{Q_A,Q_B}^M\right]>0$ is required [39].

Making use of Equation (19) we obtain the black hole equation of state (EoS)

$$P=\frac{T}{2r_{+}}-\frac{1}{8\pi r_{+}^2}+\frac{q^2{r}_{+}^4}{8\pi {(r_{+}^4+16q^2\beta )}^2}.$$

(25)

As $\beta \to 0$, Equation (25) becomes EoS of charged Maxwell-AdS black hole [37]. If the specific volume is defined as $v=2l_P{r}_{+}$ ($l_P=\sqrt{G_N}=1$) [37], Equation (25) is similar to the van der Waals EoS. Replacing $v=2l_P{r}_{+}$ into Equation (25) one finds

$$P=\frac{T}{v}-\frac{1}{2\pi v^2}+\frac{2q^2{v}^4}{\pi {(v^4+16q^2\beta )}^2}.$$

(26)

The plot of P versus v is depicted in Figure 5 for $q=1$ and $T=0.05$.

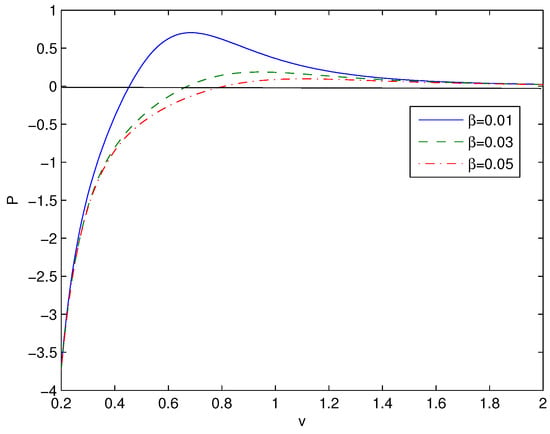
Figure 5. The functions P vs. v at $T=0.05$. The solid curve is for $\beta =0.01$, the dashed curve is for $\beta =0.03$, and the dashed–dotted curve is for $\beta =0.05$.

For some values of specific volume v, the pressure becomes negative (non-physical). The inflection points (critical points) can be found by equations $\partial P/\partial v=0$, ${\partial }^{2}P/\partial v^2=0$. From Equation (26), we obtain

$$\frac{\partial P}{\partial v}=-\frac{T}{v^2}+\frac{1}{\pi v^3}+\frac{8q^2{v}^3(a-v^4)}{\pi {(a+v^4)}^3},$$

$$\frac{\partial P}{\partial v^2}=\frac{2T}{v^3}-\frac{3}{\pi v^4}+\frac{8q^2{v}^2[3a^2-16a{v}^4+5v^8]}{\pi {(a+v^4)}^4},$$

(27)

where $a=16q^2\beta$. Then, from equations $\partial P/\partial v={\partial }^{2}P/\partial v^2=0$, we find the equation for critical points

$$-{(a+v_c^4)}^4+16q^2{v}_c^6(a^2-v_c^8)+8q^2{v}_c^6[3a^2-16a{v}_c^4+5v_c^8]=0.$$

(28)

By virtue of Equation (27), one obtains the critical temperature and pressure

$$T_c=\frac{1}{\pi v_c}+\frac{8q^2{v}_c^5(a-v_c^4)}{\pi {(a+v_c^4)}^3},$$

$$P_c=\frac{1}{2\pi v_c^2}+\frac{2q^4{v}_c^4(5a-3v_c^4)}{\pi {(a+v_c^4)}^3}.$$

(29)

There are no analytical solutions to Equation (28) for critical points. The approximate solutions to Equation (28) and critical temperatures and pressures are given in Table 3. We present only solutions for critical values of the specific volume when $T_c$ and $P_c$ are positive values.

Table 3. Critical values of the specific volume, temperatures, and pressures at $q=1$.

$\beta$	0.04	0.05	0.06	0.07	0.08	0.09	0.1
$v_c$	4.8731	4.8664	4.8597	4.8529	4.8461	4.8391	4.8321
$T_c$	0.0434	0.0434	0.0435	0.0435	0.0435	0.0435	0.0436
$P_c$	0.0033	0.0033	0.0033	0.0033	0.0034	0.0034	0.0034

At the critical values, $P-v$ diagrams for some parameters look like van der Waals liquid diagrams possessing inflection points. For small coupling $\beta$, we obtain from Equations (28) and (29) that

$$v_c^2=24q^2+\mathcal{O}\left(\beta \right),T_c=\frac{1}{3\sqrt{6}q\pi }+\mathcal{O}\left(\beta \right),P_c=\frac{1}{96q^2\pi }+\mathcal{O}\left(\beta \right).$$

(30)

From Equation (30), one finds the critical ratio

$${\rho }_c=\frac{v_c{P}_c}{T_c}=\frac{3}{8}+\mathcal{O}\left(\beta \right).$$

(31)

The value ${\rho }_c=3/8$ corresponds to the van der Waals fluid. When M is treated as the chemical enthalpy, the Gibbs free energy is given by

$$G=M-TS.$$

(32)

With the help of Equations (17), (19), and (32) we find

$$G=\frac{r_{+}}{4}-\frac{2\pi r_{+}^{3}P}{3}-\frac{q^{2}g\left(r_{+}\right)}{64}+\frac{3\sqrt{2}\pi q^{3/2}}{32{\beta }^{1/4}}+\frac{q^2{r}_{+}^7}{4{(r_{+}^4+q^2\beta )}^2}.$$

(33)

The critical ’swallowtail’ behavior with first-order phase transitions between small and large black holes is shown in subplots 1 and 2 for $P<P_c$. In this case, one has the multi-valuedness of the Gibbs free energy, and it is continuous but not differentiable. Subplot 3 is for the case of the critical point with the second-order phase transition at $P_c$≈ 0.003. This case is similar to liquid–gas phase transitions. We have here a kink for the second-order phase transition. Subplot 4 corresponds to non-critical behavior of the Gibbs free energy for $P>P_c$. For this case, there is a smooth behavior of the Gibbs free energy.

The plot of G versus T is depicted in Figure 6 for $\beta =0.01$ and $q=1$.

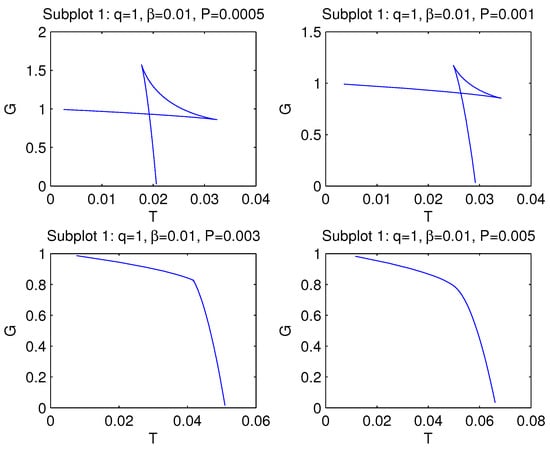
Figure 6. The functions G vs. T at $\beta =0.01$ for $P=0.0005$, $P=0.001$, $P=0.003$, and $P=0.005$.

5. Summary

Magnetic black hole solutions in Einstein–AdS gravity coupled to NED have been obtained. We found the metric and mass functions and their asymptotics. Corrections to the Reissner–Nordström solution were obtained when the cosmological constant is zero. If the Schwarzschild mass is zero ($m_0=0$) the asymptotic of the metric function as $r\to 0$ is $f\left(r\right)=1+\mathcal{O}\left(r^2\right)$ with the de Sitter core. The magnetic mass of a black hole is found to be finite. By plotting the metric function, we observe that black holes can have one or two horizons, and when coupling $\beta$ increases, the event horizon radius decreases. We have studied black hole thermodynamics in an extended phase space in Einstein–AdS gravity coupled to NED. The thermodynamic quantity (so-called vacuum polarization) conjugated to coupling $\beta$, and thermodynamic potential, conjugated to magnetic charge, were obtained and plotted. We have proved that the first law of black hole thermodynamics and the generalized Smarr relation take place. We have analyzed first-order and second-order phase transitions by computing the heat capacity and Gibbs free energy. It was shown that the critical ratio is ${\rho }_c=3/8+\mathcal{O}\left(\beta \right)$ with $3/8$ being the critical ratio for the van der Waals liquid. The black hole thermodynamics of our model is similar to the van der Waals liquid–gas thermodynamics. We leave the study of the global structure of the spacetime by presenting the Penrose diagram for further reference. It is also interesting to study thermodynamic behavior of modified gravity $f\left(R\right)$ coupled to NED presented in this paper. Thermodynamics for pure $f\left(R\right)$-gravity was studied in Refs. [41,42,43,44,45,46,47]. We leave this for further investigation.